1 Introduction

In the realm of electronic circuits, oscillators play a crucial role in generating repetitive waveforms, a fundamental function in various applications such as signal processing, communications, and timing circuits. The traditional electronics oscillators are designed using energy storage elements, inductors, capacitors along with the locally active nonlinear resistors, transistors and op-amp [1]. The working mechanism of these conventional oscillators are based on the charging and discharging principle of capacitors/inductors and locally active nature of the nonlinear resistors, transistors and op-amp. While traditional oscillators have been widely utilized across various applications, their advancements have reached a maximum-limit due to their complex structures and limitations imposed by transistor sizes. Conversely, the emergence of memristors, a novel fourth circuit element [2, 3] conceptualized by Leon Chua, has sparked significant interest in the development of memristor-based electronic oscillators [4,5,6,7]. However, these oscillators typically incorporate memristors with locally active devices, transistors and energy storage components such as capacitors and inductors. On the other hand, we introduced the simplest design of electronic oscillators by utilizing a locally active second-order memristor [8]. This design involves connecting just two “uncoupled” first-order voltage-controlled positive temperature coefficient (PTC) and negative temperature coefficient (NTC) memristors in series, eliminating the need for additional energy storage elements and transistors. Our simplest model of this oscillator consists of only two differential equations to generate sinusoidal oscillation. The circuit-theoretic analysis and characterizations of this simplest oscillator were presented by small-signal analysis, local activity principle, edge of chaos and Hopf bifurcations theorem. We have shown the memristor oscillator spawns sinusoidal oscillations starting from the either boundary of the edge of chaos regime of the memristor via a super-critical Hopf bifurcation. Though, the waveforms in this oscillator were shown by solving the differential equations, the actual global nonlinear dynamical bifurcations caused by the core circuit hidden inside the small signal model known as edge of chaos kernel that plays an important role to produce oscillation in the simplest model of memristor oscillator was not covered. The term edge of chaos kernel recently introduced by Leon Chua is a simple 1-port electrical circuit in a series connection of negative resistance (R < 0) and negative inductance (L < 0) which exhibits edge of chaos phenomenon of being potentially stable yet, but unstable when a dissipation is added [9]. Such a shocking and magical events occurred in edge of chaos kernel leads to the generation of action potential in neurons, resolving the Turing’s instability and Smale’s paradox [10,11,12]. This is a significant discovery from Chua’s riddle that finally succeed to resolve the Galvani’s 240-year old unresolved enigma [13]. This paper aims to elucidate and resolve the nonlinear dynamic bifurcations using the powerful 1-port edge of chaos kernel circuit from the small-signal equivalent model of the PTC-NTC memristors oscillator as well as exploring its potential application in the voltage control sensing circuit.

2 Edge of Chaos Kernel

The concept “edge of chaos kernel” incarnated from Chua’s riddle is the simplest 1-port circuit with negative resistance(R < 0) and negative inductance (L < 0) having potential to create action potential in nature’s optimum. The “edge of chaos” is a phase transition region between stable and unstable in a system. The concept “edge of chaos kernel” could be applied to various systems, including electronic circuits like memristors to explore their capabilities at the boundary.

In context of this study, the concept suggests that harnessing the dynamical behavior of memristors at the edge of chaos could lead to novel and efficient approaches for information and computations processing. Table 1 presents comprehensive diverse cases of the edge of chaos kernel circuit. This exploration illustrates a spectrum of scenarios, each offering a unique perspective on how this powerful edge of chaos kernel circuit transforms from stability to instability by adding dissipation of a resistor or an energy storage element inductorFootnote 1, revealing a deep understanding of dynamic behavior at the edge of chaos kernel. These cases allow us to uncover how the circuit’s dynamics unfold in the presence of small disturbances, offering valuable information about its stability, sensitivity, and potential for chaotic behavior. Through these detailed case studies and understanding, we provide the transformative impact of the edge of chaos kernel circuit that sheds light on the potential application in the design of the memristor based electronic oscillator.

Table 1 Effects on stability when resistance or inductance is added in the edge of chaos kernel circuit
Full size table

3 Edge of Chaos Kernel in the Simplest Memristor Oscillator

Memristors with their unique property to remember the past history serve as the foundational components in oscillator design to generate periodic signals. The distinctive features of these oscillators lie in their purported blessing with an “edge of chaos kernel”. This section introduces the crucial role of edge of chaos kernel circuit via the small-signal model of PTC-NTC oscillator to establish a formal proof that the simplest memristor oscillator is blessed with an “edge of chaos kernel”.

3.1 PTC-NTC Memristors Oscillator

Positive temperature coefficient (PTC) memristor whose resistance increases as the temperature increases is defined by the following equations [5]:

$$\,i_{1} = G(x_{1} )\,v_{1}$$
(1a)
$$G(x_{1} ) = \left( {K_{1} e^{{\beta_{1} \left( {x_{1} - \gamma_{1} } \right)}} } \right)^{ - 1}$$
(1b)
$$\frac{{dx_{1} }}{dt} = \frac{1}{{\alpha_{1} }}\left[ {\delta_{1} \left( {\gamma_{1} - x_{1} } \right) + G(x_{1} )v_{1}^{2} } \right]$$
(1c)

where K1, α1 β1, δ1 and γ1 are the device parameters. The parameters values for the PTC memristor used in this paper are K1 = 103, α1 = 0.8, β1 = 104, δ1 = 0.8 and γ1 = 300.

Similarly, negative temperature coefficient (NTC) memristor whose resistance decreases as the temperature increases is defined by the following equations [14]:

$$\,i_{2} = G(x_{2} )\,v_{2}$$
(2a)
$$G(\,x_{2} ) = \left( {K_{2} e^{{\beta_{2} \left( {\frac{1}{{x_{2} }} - \frac{1}{{\gamma_{2} }}} \right)}} } \right)^{ - 1}$$
(2b)
$$\frac{{dx_{2} }}{dt} = \frac{1}{{\alpha_{2} }}\left[ {\delta_{1} \left( {\gamma_{2} - x_{2} } \right) + G(x_{2} )v_{2}^{2} } \right]$$
(2c)

where K2, α2 β2, δ2 and γ2 are the device parameters. The parameters values specified for the NTC memristor are K2 = 105, α2 = 0.2, β2 = 107, δ2 = 0.1 and γ2 = 300.

PTC memristor, characterized by an increase in resistance with rising temperature, and NTC memristor, marked by a decrease in resistance under similar conditions form a compelling duo when connected in series. This configuration, blending the opposing temperature-dependent behaviors of PTC and NTC memristors, holds the promise of creating oscillator with inherent temperature sensitivity and voltage-regulation. The inherent temperature sensitivity of PTC-NTC refers to their ability to exhibit changes in electrical resistance in response to changes in temperature. This sensitivity is an intrinsic property of the material from which the thermistor is made and is typically quantified by the temperature coefficient, which describes how much the resistance changes per unit change in temperature. The nonlinear differential equations associated with the series connection of PTC and NTC memristors are given by following state dependent Ohm’s law equations:

$$i = G(x_{1} ,\,\,x_{2} )\,v$$
(3a)
$$G(x_{1} ,\,\,x_{2} ) = \frac{1}{{\left( {K_{1} e^{{\beta_{1} \left( {x_{1} - \gamma_{1} } \right)}} } \right) + \left( {K_{2} e^{{\beta_{2} \left( {\frac{1}{{x_{2} }} - \frac{1}{{\gamma_{2} }}} \right)}} } \right)}}$$
(3b)
$$\frac{{dx_{1} }}{dt} = \frac{1}{{\alpha_{1} }}\left[ {\delta_{1} \left( {\gamma_{1} - x_{1} } \right) + \frac{{K_{1} e^{{\beta_{1} \left( {x_{1} - \gamma_{1} } \right)}} }}{{\left( {\left( {K_{1} e^{{\beta_{1} \left( {x_{1} - \gamma_{1} } \right)}} } \right) + \left( {K_{2} e^{{\beta_{2} \left( {\frac{1}{{x_{2} }} - \frac{1}{{\gamma_{2} }}} \right)}} } \right)} \right)^{2} }}v^{2} } \right]$$
(3c)
$$\frac{{dx_{2} }}{dt} = \frac{1}{{\alpha_{2} }}\left[ {\delta_{2} \left( {\gamma_{2} - x_{2} } \right) + \frac{{K_{2} e^{{\beta_{2} \left( {\frac{1}{{x_{2} }} - \frac{1}{{\gamma_{2} }}} \right)}} }}{{\left( {\left( {K_{1} e^{{\beta_{1} \left( {x_{1} - \gamma_{1} } \right)}} } \right) + \left( {K_{2} e^{{\beta_{2} \left( {\frac{1}{{x_{2} }} - \frac{1}{{\gamma_{2} }}} \right)}} } \right)} \right)^{2} }}v^{2} } \right]$$
(3d)

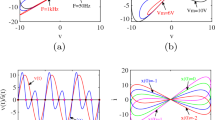
The series configuration and its equivalent small-signal model derived using Taylor series expansion and Laplace transform are shown in Fig. 1a and b respectively. The small-signal admittance function and frequency response at an equilibrium point are given by,

$$Y\left( {s;\;V_{Q} } \right) = \frac{{k(s - z_{1} )(s - z_{2} )}}{{(s - p_{1} )(s - p_{2} )}}$$
(4a)
$$\begin{gathered} Y\left( {i\omega \,;\,\,V_{Q} } \right) = \left[ {\frac{{(a_{0} - a_{2} \omega^{2} )(b_{0} - b_{2} \omega^{2} ) + a_{1} b_{1} \omega^{2} }}{{(a_{0} - a_{2} \omega^{2} )^{2} + a_{1}^{2} \omega^{2} }}} \right] \hfill \\ \, \quad+ \,\,i\,\left[ {\frac{{[(a_{0} - a_{2} \omega^{2} )b_{1} - a_{1} (b_{0} - b_{2} \omega^{2} )]\omega }}{{(a_{0} - a_{2} \omega^{2} )^{2} + a_{1}^{2} \omega^{2} }}} \right] \hfill \\ \end{gathered}$$
(4b)

where

(4c)
Fig. 1
figure 1

a Series connection of two uncouple first order PTC-NTC memristor. b Small-signal equivalent circuit of the PTC-NTC memristors. c Inductances and resistances of the small-signal equivalent circuit of the PTC-NTC memristors at the DC equilibrium voltage V

Full size image

The derivations of these equations are omitted here to avoid the clutter. For detailed explanation and coefficient values, readers are encouraged to refer our article [8].

The plots of small signal inductances and resistances L1, R1, Ra and L2, R2, Rb of the PTC-NTC memristors are shown in Fig. 1c. Observe that the inductance L1 and resistance R1 derived from the small signal model of the PTC memristor are always negative for any DC equilibrium voltage V. The negative values of inductance and resistance signify the edge of chaos kernel, representing a range from potentially stable to unstable dynamics. Analyzing this representation offers valuable insights into the system’s behavior, emphasizing the significance of the edge of chaos kernel in understanding the stability characteristics of the nonlinear system. The stability characteristics of a nonlinear system involves analyzing how the system responds to disturbances or changes from its equilibrium state. This analysis often utilizes method such as small signal equivalent circuit by linearization of the nonlinear system to determine if the system will remain stable over time or if its behavior will become unpredictable or divergent. This understanding is vital for designing oscillator circuits, control systems and predicting the system’s behavior accurately.

Table 2 provides a comprehensive view of the system’s behavior via detailed analyses of currents, inductances, resistances, Re(iω; VQ) and poles in response to varying DC voltage levels. Notably, the inclusion of negative inductance (L1) and resistance(R1) values signify the presence of an edge of chaos kernel. As the DC voltage varies, the table reveals the dynamic shifts in Re(iω; VQ) and poles, emphasizing critical points where the system makes a transition from a potentially stable state to an unstable state. The presence of negative inductance and negative resistance at the DC equilibrium provides compelling evidence that the PTC-NTC oscillator is endowed with an edge of chaos kernel.

Table 2 Currents, inductances, resistances, Re(iω; VQ) and poles of the small-signal admittance function of the PTC-NTC memristors at different DC equilibrium voltages, V
Full size table

3.1.1 Edge of Chaos Kernel in Locally Passive Regime

A locally passive typically refers to a property where the circuit behaves passively within a certain local region of its operation. The depiction of the edge of chaos kernel within a locally passive regime, highlighted by the blue color in Table 2, presents an intriguing scenario where the inductance(L1) and resistance(R1) exhibit negative values. However, the expression ReY(iω;VQ) > 0 and the presence of negative poles suggest the stability within the system, particularly aligning with the cases 2 and 3 from Table 1 for the stable condition. This suggests that despite the presence of other positive values of inductances and resistances in the small signal equivalent circuit, the system exhibits stable behavior, indicating a robust stable condition in locally passive regime.

In order to verify the stability condition of PTC-NTC oscillator in a locally passive regime, we have shown the small signal equivalent circuit, the plot of ReY(iω;VQ) vs. ω, and current(I) vs. time(t), x2 vs. x1, in Fig. 2a, b, c and d, respectively at DC equilibrium voltage V = 5.7 V. The numerical computation of corresponding poles (p1, p2) with values of p1 = −0.1844 and p2 = −0.8188 signify that these poles are located in the left-hand plane of the complex plane, suggesting the nonlinear system is stable. The small signal model shown in Fig. 2a provides insights into the linearized behavior of the system around equilibrium points with edge of chaos kernel circuit R1 = −3.91 kΩ, L1 = −3.11 kH, while the ReY(iω;VQ) > 0 plot shown in Fig. 2b illustrates the stabile region. Additionally, waveform analyses of I vs. t, and x2 vs. x1, depict the system’s response shown in Fig. 2c and d confirm its convergence to DC equilibrium and thus ensuring stability and dissipation of energy over time. These plotted analyses collectively validate the expected behavior of the PTC-NTC oscillator within the locally passive regime.

Fig. 2
figure 2

a Small-signal equivalent circuit model at DC voltage V = 5.7 V in locally passive regime. b Small-signal admittance frequency ReY(iω;VQ) with respect to ω. c Output current (I) with respect to time. d Plot of x2 vs. x1. Observe that R1 = −3.91 kΩ, L1 = −3.11 kH signify the presence of edge of chaos kernel circuit and ReY(iω;Vm(Q)) > 0 illustrates the local passivity

Full size image

3.1.2 Edge of Chaos Kernel in Edge of Chaos Regime

The concept of the “edge of chaos” in a dynamical system suggests that within a narrow region of parameter space lies a critical zone where complex and interesting phenomena are most likely to emerge [15,16,17,18]. This region is characterized by key properties of admittance function ReY(iω, VQ) < 0 (locally active) and real part of poles are negative (stable). In the edge of chaos regime, the system is locally active, meaning it is not passive but rather actively exhibits non-trivial dynamics. On the other hand, negative real part of the poles in the system’s transfer function indicate that the poles are located in the left-half of the complex plane and signify the stability of nonlinear system. By combining these two conditions, the Table 2 highlighted by green color over the region 6.209 V < V < 6.38820157073 V and 7.6613678261 < V < ∞ confirm the existence of edge of chaos regime 1 and edge of chaos regime 2 respectively, which satisfy the both criteria for locally active and stable. The rows highlighted with green color in Table 2 emphasizes the fulfillment of these conditions, indicating that this region of the parameter space is where complex phenomena are likely to emerge due to the delicate balance between activity and stability. The presence of components with negative resistance and negative inductance suggest that the circuit contains an “edge of chaos kernel” operating within the edge of chaos regime which is a particular case of 2 and 3 illustrated in Table 1 for the condition of stability. This implies that even in the presence of other positive values of inductances and resistances in the small signal equivalent circuit, the PTC-NTC memristor oscillator demonstrates stable behavior as expected from locally active and stable condition.

The illustration of the locally active and stable condition of the PTC-NTC oscillator in the edge of chaos regime 1 and edge of chaos regime 2 at V = 6.32 V and V = 8.58 V are shown in Figs. 3 and 4 respectively with small-signal equivalent model, plot of ReY(iω; VQ) vs. ω, current (I) vs. time(t), and x2 vs. x1. The extensive computation of the corresponding poles(p) at V = 6.32 V and V = 8.58 V, with values of p = −0.0293 ± 0.467 i and p = −0.314 ± 0.9302 i, respectively, indicate that these poles lie in the left-hand plane of the complex plane, implying stability. Similarly, the presence of R1 = −3.083 kΩ, L1 =−1.388 kH in small-signal equivalent circuit model of Fig. 3a and R1 = −24.268 kΩ, L1 = −5.231 kH in small-signal equivalent circuit model of Fig. 4a signify the existence of edge of chaos kernels in the edge of chaos regime 1 and edge of chaos regime 2, respectively. Similarly, the plot of the small signal admittance function ReY(iω, VQ) vs. ω is negative, indicating locally active dynamics. Moreover, the waveform analyses of the current (I) vs. time(t), x2 vs. x1 illustrate the system’s response affirming it’s convergence to DC equilibrium state. These plotted analyses collectively validate the anticipated behavior of the PTC-NTC memristors oscillator in the edge of chaos regime.

Fig. 3
figure 3

a Small-signal equivalent circuit model at DC voltage V = 6.32 V in edge of chaos regime 1. b small-signal admittance frequency ReY(iω;VQ) with respect to ω. c Output current (I) with respect to time. d Plot of x2 vs. x1. Please note that R1 = −3.083 kΩ, L1 =−1.388 kH ndicate the presence of edge of chaos kernel circuit and ReY(iω;VQ) < 0 depicts a state of local activity

Full size image
Fig. 4
figure 4

a Small-signal equivalent circuit model at DC voltage V = 8.58 V in edge of chaos regime 2. b small-signal admittance frequency ReY(iω;VQ) with respect to ω. c Output current (I) with respect to time. d Plot of x2 vs. x1. Please note that R1 =−24.268 kΩ, L1 = −5.231 kH indicate the presence of edge of chaos kernel circuit and ReY(iω;VQ) < 0 depicts a state of local activity

Full size image

3.1.3 Edge of Chaos Kernel in Locally Active Unstable Regime

In a locally active unstable regime, the real part of the admittance function evaluated at a specific frequency, Re(Y(iω; VQ)) < 0 and the real parts of the poles of the system lie in open right hand plane. The condition Re(Y(iω; VQ)) < 0 indicates that the real part of the admittance function evaluated at a particular frequency ω is negative. This condition suggests that the system is locally active, meaning there is dynamic activity or response to perturbations, rather than being in a stable, quiescent state. Furthermore, the positive real part of the poles which lie in the open right-hand plane implies the DC equilibrium points in this regime is unstable. Therefore, within the locally active and unstable regime, complex behaviors emerge, encompassing a spectrum of dynamic phenomena such as oscillations and chaos. Table 2 highlighted by the red color between the two purely imaginary bifurcation points corresponding to poles ± 0.50372249 i and ± 0.82930627 i confirm the existence of a locally active and unstable regime. The presence of a components with negative resistance and negative inductance suggest that the circuit contains an “edge of chaos kernel” operating within the locally active and unstable regime. The combination of the edge of chaos kernel with positive inductances and resistances in the small-signal model aligns with cases 2 and 3 illustrated in Table 1 for the condition of instability. Positive values of inductances and resistances, alongside the characteristics of the edge of chaos kernel, contribute to the system’s instability, creating a sinusoidal oscillation in PTC-NTC memristors.

Figure 5 depict the small-signal equivalent model, plots of ReY(iω; VQ) vs. t, current (I) vs. t, x2 vs. x1 at V = 7.20 V at the locally active and unstable regime. Extensive computations of the corresponding poles p = 0.084 ± 0.7393 i at V = 7.20 V reveal that, these poles reside in the right half-plane of the complex plane, indicating instability. Furthermore, the presence of R1=−8.072 kΩ and L1=−2.348 kH in the small-signal equivalent circuit model signifies the existence of an edge of chaos kernel in the locally active and unstable regime. The plot of the small-signal admittance functions, Re(Y(iω;VQ) vs. ω exhibit negativity, indicating locally active dynamics. Moreover, waveform analyses of the I vs. t, and x2 vs. x1 illustrate the system’s response, affirming its convergence to oscillation. These plotted analyses collectively validate the anticipated behavior of the PTC-NTC memristor oscillator in the unstable regime.

Fig. 5
figure 5

a Small-signal equivalent circuit model at DC voltage V = 7.20 V in the locally active unstable regime. b small-signal admittance frequency ReY(iω;VQ) with respect to ω. c Output current (I) with respect to time. d Plot of x2 vs. x1. The presence of R1 =−8.072 kΩ and L1 = −2.348 kH in the small signal model illustrates the edge of chaos kernel circuit and ReY(iω;VQ) < 0 depicts a state of local activity

Full size image

4 Application of PTC-NTC Oscillator in Voltage Control Sensing

One of the potential applications of our PTC-NTC oscillator is in the voltage control sensing circuit, as illustrated in Fig. 6. The PTC-NTC oscillator is connected to the inverting terminal of the operational amplifier (OPAMP). When the oscillator is biased at the locally active and unstable regime over the input DC voltage 6.38820157073 < V < 7.66131678261, it generates the oscillation as discussed in the previous section. For the input DC voltage V = 7.20 V, as depicted in Fig. 7a, the change in the temperature(x1), resistance (Rp) and voltage (vp) of the PTC memristor is observed as shown in the Fig. 7b, c and d, respectively. The OPAMP is configured as a voltage comparator with the reference voltage \(v_{f} = \frac{{R_{2} \times V}}{{R_{1} + R_{2} }} = 2.05\;{\text{V}}\) applied to the non-inverting terminal. The relay turns “ON” when the voltage at point vp is less than the voltage at point vf.. This configuration enables the circuit to function as a voltage control switch, when the output of the oscillator drops below 2.05 V, as demonstrated in Fig. 7e.

Fig. 6
figure 6

Application of PTC-NTC oscillator to the voltage control sensing circuit

Full size image
Fig. 7
figure 7

Waveform of the application circuit of Fig. 6. a DC input voltage 7.20 V. b Change in the temperature of PTC memristor. c Change in the resistance of the PTC memristor. d Voltage vp across the PTC memristor. e Output when the relay switch is ON

Full size image

5 Conclusion

This paper introduced the memristor oscillator designed with the series connection of PTC-NTC memristors was found to be blessed by an “edge of chaos kernel circuit” and characterized by negative resistance and negative inductance hidden inside the small signal model. Through our detailed analyses, we observed how this innovative circuit pushed the boundaries of nonlinear systems from potentially stable to unstable with the addition of positive resistance or inductance, harnessing unique properties to achieve complex dynamics. We showed that the stable and periodic oscillations observed in the simplest model of memristor oscillator was not possible without the presence of the edge of chaos kernel. We provided compelling evidences that the edge of chaos kernel circuit functions as the foundational circuit for generating diverse complex dynamics in nonlinear systems. Furthermore, the application of the simplest oscillator in the voltage control sensing circuit underscores its potential contribution to scientific innovation in the field of nonlinear dynamics.