Comment on “Bilinear Bäcklund transformation, soliton and periodic wave solutions for a (3+1)-dimensional variable-coefficient generalized shallow water wave equation” (Nonlinear Dyn. 87, 2529, 2017)

Abstract

In this Comment, several enhancements on the results in the paper “Bilinear Bäcklund transformation, soliton and periodic wave solutions for a (3+1)-dimensional variable-coefficient generalized shallow water wave equation” (Nonlinear Dyn. 87, 2529, 2017) are described. With respect to the stream under a pressure surface in the water, for the same equation, using the Hirota method and symbolic computation, we are able to build a set of the bilinear forms, two sets of the bilinear auto-Bäcklund transformations along with some analytic solutions, as well as a set of the similarity reductions. Beyond those in the paper (Nonlinear Dyn. 87, 2529, 2017), our results are dependent on the variable coefficients in the equation, while those coefficients respectively represent the perturbed effects, dispersion and nonlinearity.

1 Introduction

Fluids have been actively studied [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42], e.g., recent investigations on the nonlinear dynamics of certain marine inertial particles [1], triadic-interaction energy transfer in the fluid flow [2], nonlinear vibrations of a fluid-filled circular shell [3], shallow water waves [6, 9], incompressible fluids [10, 30], motion of a rigid plate in a Newtonian fluid [11], heat-conducting fluids [12], capillary fluids [13], fluids confined in the cylindrical and slit pores [14], shallow water in an open sea [15], oceans in the Solar System [16,17,18] and liquids with the gas bubbles [26]. Nowadays, such models have been proposed to describe the fluids [8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42], as different Navier–Stokes systems [10, 12, 13], a fractional Bagley–Torvik system [11], an extended Peng-Robinson system [14], a generalized (2+1)-dimensional dispersive long-wave system [15, 38], a variable-coefficient nonlinear dispersive-wave system [16, 17], a higher-order Boussinesq-Burgers system [18, 19], different extended (2+1)-dimensional coupled Burgers systems [20, 34], an Ablowitz–Kaup–Newell–Segur system [21,22,23,24], a generalized Konopelchenko–Dubrovsky–Kaup–Kupershmidt system [25], a (3+1)-dimensional nonlinear wave equation [26], different (3+1)-dimensional generalized Kadomtsev-Petviash-vili-type systems [9, 27, 36, 39, 41], a (2+1)-dimensional generalized Caudrey–Dodd–Gibbon–Kotera–Sawada equation [8], a modified Korteweg–de Vries–Calogero–Bogoyavlenskii-Schiff equation [28, 29], a (2+1)-dimensional generalized Boiti–Leon–Manna–Pem-pinelli equation [30], a (2+1)-dimensional reduced Yu–Toda–Sasa–Fukuyama equation [31], a (2+1)-dimensional generalized Bogoyavlensky-Konopel-chenko equation [32], a (2+1)-dimensional generalized Hirota-Satsuma-Ito equation [33], a Sharma-Tasso-Olver-Burgers equation [35], a (3+1)-dimensional generalized Yu-Toda-Sasa-Fukuyama equation [37], and a (3+1)-dimensional generalized Konopelchenko–Dubrovsky–Kaup–Kupershmid equation [40, 42].

Currently interesting, Ref. [43], i.e., the paper (Nonlinear Dyn. 87, 2529, 2017), has studied the following (3+1)-dimensional variable-coefficient generalized shallow water wave equation for the stream under a pressure surface in the water:

$$\begin{aligned}&\Upsilon _1(t) u_{yt}+\Upsilon _2(t) u_{xxxy}+\Upsilon _3(t) u_{x} u_{xy}\nonumber \\&\quad +\Upsilon _3(t) u_{y} u_{xx}+\Upsilon _4(t) u_{xz}=0 , \end{aligned}$$

(1)

with u(x, y, z, t) being the real differentiable function of the variables x, y, z and t, the real functions $\Upsilon _1(t)$ and $\Upsilon _4(t)$ denoting the perturbed effects, $\Upsilon _2(t)$ implying the dispersion, $\Upsilon _3(t)$ representing the nonlinearity, while the subscripts meaning the partial derivatives [43, 44]. For Eq. (1), Ref. [43] has obtained certain bilinear form, bilinear Bäcklund transformation, Lax pair, soliton and periodic wave solutions.

Also for Eq. (1), Ref. [45] has worked out certain lump-solution characteristics, Ref. [44] has got certain breathers, Ref. [47] has investigated a Kadomtsev–Petviashvili hierarchy reduction, some soliton and semi-rational solutions, while Ref. [50] has found some nonautonomous lump solutions and an interaction between a lump wave and a kink soliton. Special cases of Eq. (1) have been a (3+1)-dimensional generalized shallow water equation [for $\Upsilon _1(t)=\Upsilon _2(t)=1$, $\Upsilon _3(t)=-3$ and $\Upsilon _4(t)=-1$] applied in the weather simulations, tidal waves, irrigation and tsunami prediction [45,46,47] (and references therein), and a (3+1)-dimensional Jimbo-Miwa equation [for $\Upsilon _1(t)=2$, $\Upsilon _2(t)=1$, $\Upsilon _3(t)=3$ and $\Upsilon _4(t)=-3$] modelling some wave phenomena [27, 47] (and references therein).

This Comment will be to enhance the issues published in Ref. [43], in order to make them more complete. Results in this Comment, to be seen below, will also be different from those in Refs. [44, 45, 47, 50].

In Sect. 2 of this Comment, making use of symbolic computation [48, 49], we will construct a set of the bilinear forms for Eq. (1), which is different from and beyond that in Ref. [43], while in Sect. 3, two sets of the bilinear auto-Bäcklund transformations for Eq. (1), different from and beyond that in Ref. [43]. In addition, using symbolic computation, we will find a set of the similarity reductions for Eq. (1) in Sect. 4. Section 5 will be our conclusions.

2 Bilinear forms for Eq. (1)

Making use of the Hirota method [51] and symbolic computation, we assume that

$$\begin{aligned}&u(x,y,z,t)=\gamma \left[ \ln f(x,y,z,t)\right] _{x}\nonumber \\&\quad -\phi (y)-\psi (z)-\alpha (y) \beta (z) , \end{aligned}$$

(2)

with f(x, y, z, t) being a real differentiable function of x, y, z and t, $\phi (y)$, $\psi (z)$, $\alpha (y)$ and $\beta (z)$ denoting the real differentiable functions, while $\gamma$ meaning a real non-zero constant.

Substituting Assumption (2) into Eq. (1) and integrating the outcome once as for x with the integration function vanishing bring about

$$\begin{aligned}&\Upsilon _1(t) \left( \ln f\right) _{yt}+\Upsilon _2(t) \left( \ln f\right) _{xxxy}\nonumber \\&\quad +\gamma \Upsilon _3(t) \left( \ln f\right) _{xx} \left( \ln f\right) _{xy}\nonumber \\&\quad -\Upsilon _3(t) \left[ \phi '(y)+\alpha '(y) \beta (z)\right] \left( \ln f\right) _{xx}\nonumber \\&\quad +\Upsilon _4(t) \left( \ln f\right) _{xz}=0 , \end{aligned}$$

(3)

in which $\phi '(y)=\frac{\mathrm{d}}{\mathrm{d}y} \, \phi (y)$ and $\alpha '(y)=\frac{\mathrm{d}}{\mathrm{d}y} \, \alpha (y)$.

On account of the formulae [51]

$$\begin{aligned}&2 \left( \ln f\right) _{yt}\quad =\frac{D_y D_t f\cdot f}{f^2} ,\\&2 \left( \ln f\right) _{xxxy}=\frac{D_x^3 D_y f\cdot f}{f^2}\\&-3 \frac{D_x^2 f\cdot f}{f^2} \frac{D_x D_y f\cdot f}{f^2} , \\&2 \left( \ln f\right) _{xx}=\frac{D_x^2 f\cdot f}{f^2} ,\\&2 \left( \ln f\right) _{xy}=\frac{D_x D_y f\cdot f}{f^2} ,\\&2 \left( \ln f\right) _{xz}=\frac{D_x D_z f\cdot f}{f^2} , \end{aligned}$$

for the sake of transforming Eq. (1) into certain bilinear forms, we choose

$$\begin{aligned} \gamma =6 \frac{\Upsilon _2(t)}{\Upsilon _3(t)} , \end{aligned}$$

to obtain

$$\begin{aligned}&\left\{ \Upsilon _1(t) D_y D_t+\Upsilon _2(t) D^3_x D_y\right. \nonumber \\&\left. \quad -\Upsilon _3(t) \left[ \phi '(y)+\alpha '(y) \beta (z)\right] D^2_x\right. \nonumber \\&\left. \quad +\Upsilon _4(t) D_x D_z\right\} f\cdot f=0 , \end{aligned}$$

(4)

with $D_{x}$, $D_{y}$, $D_{z}$ and $D_{t}$ given by [51]

$$\begin{aligned}&D_{x}^{m_1}D_{y}^{m_2}D_{z}^{m_3}D_{t}^{m_4} H(x,y,z,t)\cdot G(x,y,z,t)\\&\quad \equiv \left( \frac{\partial }{\partial x}-\frac{\partial }{\partial x_0}\right) ^{m_1}\,\left( \frac{\partial }{\partial y}-\frac{\partial }{\partial y_0}\right) ^{m_2}\, \\&\quad \left( \frac{\partial }{\partial z}-\frac{\partial }{\partial z_0}\right) ^{m_3}\, \left( \frac{\partial }{\partial t}-\frac{\partial }{\partial t_0}\right) ^{m_4}\\&\quad H(x,y,z,t)\,G(x_0,y_0,z_0,t_0) \bigg |_{x_0=x,\,y_0=y,\,z_0=z,\,t_0=t}, \end{aligned}$$

$x_0$, $y_0$, $z_0$ and $t_0$ meaning the formal variables, H(x, y, z, t) representing a $C^{\infty }$ function of x, y, z and t, $G(x_0,y_0,z_0,t_0)$ representing a $C^{\infty }$ function of $x_0$, $y_0$, $z_0$ and $t_0$, while $m_1$, $m_2$, $m_3$ and $m_4$ being the non-negative integers [51].

In short, under the variable-coefficient constraint

$$\begin{aligned} \Upsilon _3(t)=\Upsilon _0 \Upsilon _2(t) , \end{aligned}$$

(5)

choosing $\gamma =\frac{6}{\Upsilon _0}$, we find a set of the bilinear forms for Eq. (1), i.e.,

$$\begin{aligned}&\left\{ \Upsilon _1(t) D_y D_t+\Upsilon _2(t) D^3_x D_y\right. \nonumber \\&\left. \quad -\Upsilon _0 \Upsilon _2(t) \left[ \phi '(y)+\alpha '(y) \beta (z)\right] D^2_x\right. \nonumber \\&\left. \quad +\Upsilon _4(t) D_x D_z\right\} f\cdot f=0 , \end{aligned}$$

(6)

with $\Upsilon _0$ implying a real non-zero constant.

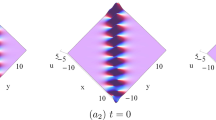
With respect to the stream under a pressure surface in the water, under Variable-Coefficient Constraint (5) and Assumption (2), Bilinear Forms (6) for Eq. (1) are dependent on the dispersion coefficient $\Upsilon _2(t)$ as well as perturbed-effect coefficients $\Upsilon _1(t)$ and $\Upsilon _4(t)$ in Eq. (1). Bilinear Forms (6) are different from the one presented in Ref. [43].

Bilinear Forms (6) are useful, e.g., for us to build some bilinear auto-Bäcklund transformations, to be seen below.

3 Bilinear auto-Bäcklund transformations with analytic solutions for Eq. (1)

Based on Bilinear Forms (6), with the Hirota method, motivated by Ref. [27], assuming that g (x, y, z, t) be another solution of Bilinear Forms (6), we take into account the expression

$$\begin{aligned}&f^2 \Big \{ \Big \{\,\Upsilon _1(t) D_y D_t +\Upsilon _2(t) D^3_x D_y\nonumber \\&\quad -\Upsilon _0 \Upsilon _2(t) \left[ \phi '(y)+\alpha '(y) \beta (z)\right] D^2_x\nonumber \\&\quad +\Upsilon _4(t) D_x D_z\,\Big \} g\cdot g \Big \} \nonumber \\&\quad - g^2 \Big \{ \Big \{\,\Upsilon _1(t) D_y D_t +\Upsilon _2(t) D^3_x D_y\nonumber \\&\quad -\Upsilon _0 \Upsilon _2(t) \left[ \phi '(y)+\alpha '(y) \beta (z)\right] D^2_x \nonumber \\&\quad +\Upsilon _4(t) D_x D_z\,\Big \} f\cdot f \Big \} , \end{aligned}$$

(7)

and make use of the exchange formulae [51]

$$\begin{aligned}&G^2 \left( D_y D_t \, H \cdot H\right) -H^2 \left( D_y D_t \, G \cdot G\right) \nonumber \\&\quad =2 \, D_y \left( D_t \, H \cdot G\right) \cdot \left( G H\right) , \end{aligned}$$

(8a)

$$\begin{aligned}&G^2 \left( D^2_x \, H \cdot H\right) -H^2 \left( D^2_x \, G \cdot G\right) \nonumber \\&\quad =2 \, D_x \left( D_x \, H \cdot G\right) \cdot \left( G H\right) , \end{aligned}$$

(8b)

$$\begin{aligned}&G^2 \left( D_x D_z \, H \cdot H\right) -H^2 \left( D_x D_z \, G \cdot G\right) \nonumber \\&\quad =2 \, D_x \left( D_z \, H \cdot G\right) \cdot \left( G H\right) , \end{aligned}$$

(8c)

$$\begin{aligned}&G^2 \left( D^3_x D_y \, H \cdot H\right) -H^2 \left( D^3_x D_y \, G \cdot G\right) \nonumber \\&\quad =\frac{3}{2} \, D_x \left( D^2_x D_y \, H \cdot G\right) \cdot \left( G H\right) \nonumber \\&\qquad +\frac{1}{2} \, D_y \left( D^3_x \, H \cdot G\right) \cdot \left( G H\right) \nonumber \\&\qquad -3 \, D_x \left( D_x D_y \, H \cdot G\right) \cdot \left( D_x \, H \cdot G\right) \nonumber \\&\qquad -\frac{3}{2} \, D_x \left( D^2_x \, H \cdot G\right) \cdot \left( D_y \, H \cdot G\right) \nonumber \\&\qquad -\frac{3}{2} \, D_y \left( D^2_x \, H \cdot G\right) \cdot \left( D_x \, H \cdot G\right) , \end{aligned}$$

(8d)

to get

$$\begin{aligned}&f^2 \Big \{ \left\{ \,\Upsilon _1(t) D_y D_t +\Upsilon _2(t) D^3_x D_y\right. \nonumber \\&\left. \qquad -\Upsilon _0 \Upsilon _2(t) \left[ \phi '(y)+\alpha '(y) \beta (z)\right] D^2_x\right. \nonumber \\&\left. \qquad +\Upsilon _4(t) D_x D_z\,\right\} g\cdot g \Big \} \nonumber \\&\qquad - g^2 \Big \{ \left\{ \,\Upsilon _1(t) D_y D_t +\Upsilon _2(t) D^3_x D_y\right. \nonumber \\&\left. \qquad -\Upsilon _0 \Upsilon _2(t) \left[ \phi '(y)+\alpha '(y) \beta (z)\right] D^2_x\right. \nonumber \\&\left. \qquad +\Upsilon _4(t) D_x D_z\,\right\} f\cdot f \Big \} \nonumber \\&\quad =\Upsilon _1(t) \left[ \, f^2 \left( D_y D_t g\cdot g\right) -g^2 \left( D_y D_t f\cdot f\right) \,\right] \nonumber \\&\qquad +\Upsilon _2(t) \left[ \, f^2 \left( D^3_x D_y g\cdot g\right) \right. \nonumber \\&\qquad \left. -g^2 \left( D^3_x D_y f\cdot f\right) \,\right] \nonumber \\&\qquad -\Upsilon _0 \Upsilon _2(t) \left[ \phi '(y)+\alpha '(y) \beta (z)\right] \nonumber \\&\qquad \left[ \, f^2 \left( D^2_x g\cdot g\right) -g^2 \left( D^2_x f\cdot f\right) \,\right] \nonumber \\&\qquad +\Upsilon _4(t) \left[ \, f^2 \left( D_x D_z g\cdot g\right) \right. \nonumber \\&\qquad \left. -g^2 \left( D_x D_z f\cdot f\right) \,\right] \nonumber \\&\quad =2 \, \Upsilon _1(t) \, D_y \left( D_t \, g \cdot f\right) \cdot \left( f g\right) \nonumber \\&\qquad -2 \, \Upsilon _0 \Upsilon _2(t) \left[ \phi '(y)+\alpha '(y) \beta (z)\right] \, \nonumber \\&\qquad D_x \left( D_x \, g \cdot f\right) \cdot \left( f g\right) \nonumber \\&\qquad +\Upsilon _2(t) \left[ \, \frac{3}{2} \, D_x \left( D^2_x D_y \, g \cdot f\right) \cdot \left( f g\right) \right. \nonumber \\&\qquad \left. +\frac{1}{2} \, D_y \left( D^3_x \, g \cdot f\right) \cdot \left( f g\right) \right. \nonumber \\&\qquad \left. -\frac{3}{2} \, D_y \left( D^2_x \, g \cdot f\right) \cdot \left( D_x \, g \cdot f\right) \right. \nonumber \\&\qquad \left. -3 \, D_x \left( D_x D_y \, g \cdot f\right) \cdot \left( D_x \, g \cdot f\right) \right. \nonumber \\&\qquad \left. -\frac{3}{2} \, D_x \left( D^2_x \, g \cdot f\right) \cdot \left( D_y \, g \cdot f\right) \right] \nonumber \\&\qquad +2 \, \Upsilon _4(t) \, D_x \left( D_z \, g \cdot f\right) \cdot \left( f g\right) \nonumber \\&\quad =\frac{1}{2} \, D_x \Big \{\left\{ 3 \, \Upsilon _2(t) D^2_x D_y -4 \, \Upsilon _0 \Upsilon _2(t)\right. \nonumber \\&\left. \qquad \left[ \phi '(y)\!+\!\alpha '(y) \beta (z)\right] D_x\!+\!4 \, \Upsilon _4(t) D_z\right\} g \cdot f \Big \} \cdot \left( f g\right) \nonumber \\&\qquad +\frac{1}{2} \, D_y \left\{ \left[ 4 \, \Upsilon _1(t) D_t +\Upsilon _2(t) D^3_x\right] g \cdot f \right\} \cdot \left( f g\right) \nonumber \\&\qquad -3 \, \Upsilon _2(t) D_x \left( D_x D_y \, g \cdot f\right) \cdot \left( D_x \, g \cdot f\right) \nonumber \\&\qquad -\frac{3}{2} \, \Upsilon _2(t) D_x \left( D^2_x \, g \cdot f\right) \cdot \left( D_y \, g \cdot f\right) \nonumber \\&\qquad -\frac{3}{2} \, \Upsilon _2(t) D_y \left( D^2_x \, g \cdot f\right) \cdot \left( D_x \, g \cdot f\right) \;\; . \end{aligned}$$

(9)

Making the assumptions that

$$\begin{aligned}&D_x \Big \{\left\{ 3 \, \Upsilon _2(t) D^2_x D_y-4 \, \Upsilon _0 \Upsilon _2(t) \right. \nonumber \\&\left. \quad \left[ \phi '(y)+\alpha '(y) \beta (z)\right] D_x\right. \nonumber \\&\left. \quad +4 \, \Upsilon _4(t)D_z \right\} g \cdot f \Big \} \cdot \left( f g\right) =0,\end{aligned}$$

(10a)

$$\begin{aligned}&D_y \left\{ \left[ 4 \, \Upsilon _1(t) D_t+\Upsilon _2(t) D^3_x\right] g \cdot f\right\} \cdot \left( f g\right) =0,\end{aligned}$$

(10b)

$$\begin{aligned}&D_x \left( D_x D_y \, g \cdot f\right) \cdot \left( D_x \, g \cdot f\right) =0, \end{aligned}$$

(10c)

$$\begin{aligned}&D_x \left( D^2_x \, g \cdot f\right) \cdot \left( D_y \, g \cdot f\right) =0, \end{aligned}$$

(10d)

$$\begin{aligned}&D_y \left( D^2_x \, g \cdot f\right) \cdot \left( D_x \, g \cdot f\right) =0, \end{aligned}$$

(10e)

we can obtain two sets of the bilinear auto-Bäcklund transformations for Eq. (1) in the following:

Set 1: $D^2_x \, g \cdot f \ne 0$ and $D_x D_y \, g \cdot f \ne 0$

We work out the following set of the bilinear auto-Bäcklund transformations for Eq. (1):

$$\begin{aligned}&u(x,y,z,t)=\frac{6}{\Upsilon _0} \left[ \ln f(x,y,z,t)\right] _{x}\nonumber \\&\quad -\phi (y)-\psi (z)-\alpha (y) \beta (z) , \end{aligned}$$

(11a)

$$\begin{aligned}&v(x,y,z,t)=\frac{6}{\Upsilon _0} \left[ \ln g(x,y,z,t)\right] _{x}\nonumber \\&\quad -\phi (y)-\psi (z)-\alpha (y) \beta (z) , \end{aligned}$$

(11b)

$$\begin{aligned}&\left\{ 3 \, \Upsilon _2(t) D^2_x D_y -4 \, \Upsilon _0 \Upsilon _2(t) \left[ \phi '(y)+\alpha '(y) \beta (z)\right] D_x\right. \nonumber \\&\left. \quad +4 \, \Upsilon _4(t) D_z\right\} g \cdot f=0 , \end{aligned}$$

(11c)

$$\begin{aligned}&\left[ 4 \, \Upsilon _1(t) D_t +\Upsilon _2(t) D^3_x\right] g \cdot f=0 , \end{aligned}$$

(11d)

$$\begin{aligned}&D_x D_y \, g \cdot f =\lambda _1(t) \, D_x \, g \cdot f , \end{aligned}$$

(11e)

$$\begin{aligned}&D^2_x \, g \cdot f =\lambda _2(t) \, D_y \, g \cdot f , \end{aligned}$$

(11f)

$$\begin{aligned}&D^2_x \, g \cdot f =\lambda _3(t) \, D_x \, g \cdot f , \end{aligned}$$

(11g)

in which $\lambda _1(t)$, $\lambda _2(t)$ and $\lambda _3(t)$ denote the real non-zero differentiable functions of t, while v (x, y, z, t) represents another solution of Eq. (1).

With respect to the stream under a pressure surface in the water, under Variable-Coefficient Constraint (5), mutually consistent (as seen right below), Bilinear Auto-Bäcklund Transformations (11) for Eq. (1) are dependent on the dispersion coefficient $\Upsilon _2(t)$ as well as perturbed-effect coefficients $\Upsilon _1(t)$ and $\Upsilon _4(t)$ in Eq. (1). Bilinear Auto-Bäcklund Transformations (11) are different from the one given in Ref. [43].

Bilinear Auto-Bäcklund Transformations (11) denote a system of the equations which connects a set of the solutions of Eq. (1) to another set of the solutions of Eq. (1) itself. Hence, we might, in principle at least, be capable of progressively finding more and more complicated solutions of Eq. (1).

Next, for the mutual consistency, or explicit solvability in relation to f and g, we will construct some analytic solutions for Eq. (1) via Bilinear Auto-Bäcklund Transformations (11).

Under the variable-coefficient constraint

$$\begin{aligned} \Upsilon _4(t)=\mu _0 \, \Upsilon _2(t) , \end{aligned}$$

(12)

with the choices of

$$\begin{aligned}&\lambda _1(t)=\sigma _2 \, \Upsilon _2(t) , \nonumber \\&\lambda _2(t)=\frac{\sigma _1^2}{\sigma _2} \, \Upsilon _2(t), \nonumber \\&\lambda _3(t)=\sigma _1 \, \Upsilon _2(t) ,\nonumber \\&\phi (y)=\zeta _1 \, y+\zeta _2 , \nonumber \\&\alpha (y)=\zeta _3 \, y+\zeta _4 , \nonumber \\&\beta (z)=\beta \quad \mathrm{only}, \end{aligned}$$

(13)

we construct out the following analytic solutions for Eq. (1) via Bilinear Auto-Bäcklund Transformations (11):

$$\begin{aligned}&u(x,y,z,t)=\frac{6}{\Upsilon _0} \left[ \ln f(x,y,z,t)\right] _{x} -\left( \zeta _1 \, y+\zeta _2\right) \nonumber \\&\quad -\psi (z)-\beta \left( \zeta _3 \, y+\zeta _4\right) , \end{aligned}$$

(14a)

$$\begin{aligned}&v(x,y,z,t)=\frac{6}{\Upsilon _0} \left[ \ln g(x,y,z,t)\right] _{x}\nonumber \\&\quad -\left( \zeta _1 \, y+\zeta _2\right) -\psi (z)-\beta \left( \zeta _3 \, y+\zeta _4\right) , \end{aligned}$$

(14b)

$$\begin{aligned}&f(x, y, z, t)=1 , \end{aligned}$$

(14c)

$$\begin{aligned}&g(x, y, z, t)=1+\epsilon _1 \, \mathrm {exp} \bigg \{\sigma _1 \, x+\sigma _2 \, y \nonumber \\&\quad -\frac{\sigma _1 \left[ 3 \, \sigma _1 \, \sigma _2 +4 \, \Upsilon _0 \, \left( \zeta _1+\beta \zeta _3\right) \right] }{4 \, \mu _0} z\nonumber \\&\qquad -\frac{\sigma _1^3}{4} \! \int \! \frac{\Upsilon _2(t)}{\Upsilon _1(t)} \, \mathrm{d}t\bigg \} , \end{aligned}$$

(14d)

with $\mu _0$, $\sigma _1$, $\sigma _2$ and $\epsilon _1$ as the real non-zero constants, while $\zeta _1$, $\zeta _2$, $\zeta _3$ and $\zeta _4$ as the real constants.

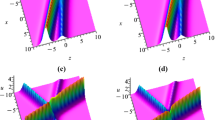
With respect to the stream under a pressure surface in the water, under Variable-Coefficient Constraints (5) and (12), Analytic Solutions (14) are dependent on the dispersion coefficient $\Upsilon _2(t)$ as well as perturbed-effect coefficient $\Upsilon _1(t)$ in Eq. (1).

Set 2: $D^2_x \, g \cdot f = 0$ and $D_x D_y \, g \cdot f = 0$

Similarly, we find the second set of the bilinear auto-Bäcklund transformations for Eq. (1):

$$\begin{aligned}&u(x,y,z,t)=\frac{6}{\Upsilon _0} \left[ \ln f(x,y,z,t)\right] _{x}\nonumber \\&\quad -\phi (y)-\psi (z)-\alpha (y) \beta (z) , \end{aligned}$$

(15a)

$$\begin{aligned}&v(x,y,z,t)=\frac{6}{\Upsilon _0} \left[ \ln g(x,y,z,t)\right] _{x}\nonumber \\&\quad -\phi (y)-\psi (z)-\alpha (y) \beta (z) , \end{aligned}$$

(15b)

$$\begin{aligned}&\bigg \{3 \, \Upsilon _2(t) D^2_x D_y -4 \, \Upsilon _0 \Upsilon _2(t) \left[ \phi '(y)+\alpha '(y) \beta (z)\right] D_x\nonumber \\&\quad +4 \, \Upsilon _4(t) D_z\bigg \} g \cdot f=0 , \end{aligned}$$

(15c)

$$\begin{aligned}&\left[ 4 \, \Upsilon _1(t) D_t +\Upsilon _2(t) D^3_x\right] g \cdot f=0 , \end{aligned}$$

(15d)

$$\begin{aligned}&D_x D_y \, g \cdot f=0 , \end{aligned}$$

(15e)

$$\begin{aligned}&D^2_x \, g \cdot f=0 \;\;. \end{aligned}$$

(15f)

With respect to the stream under a pressure surface in the water, under Variable-Coefficient Constraint (5), Bilinear Auto-Bäcklund Transformations (15) rely on the dispersion coefficient $\Upsilon _2(t)$ as well as perturbed-effect coefficients $\Upsilon _1(t)$ and $\Upsilon _4(t)$ in Eq. (1). Bilinear Auto-Bäcklund Transformations (15) are different from the one reported in Ref. [43].

Bilinear Auto-Bäcklund Transformations (15) denote a system of the equations which connects a set of the solutions of Eq. (1) to another set of the solutions of Eq. (1) itself. Hence, we might, in principle at least, be capable of progressively finding more and more complicated solutions of Eq. (1).

Next, for the mutual consistency, or explicit solvability in relation to f and g, we will construct some analytic solutions for Eq. (1) via Bilinear Auto-Bäcklund Transformations (15).

Via Bilinear Auto-Bäcklund Transformations (15), under Variable-Coefficient Constraints (5) and (12), with the choices of

$$\begin{aligned}&\phi (y)=\zeta _1 \, y+\zeta _2 , \nonumber \\&\alpha (y)=\zeta _3 \, y+\zeta _4 , \nonumber \\&\beta (z)=\beta \quad \mathrm{only}, \end{aligned}$$

(16)

we also construct out the following analytic solutions for Eq. (1):

$$\begin{aligned}&u(x,y,z,t)=\frac{6}{\Upsilon _0} \left[ \ln f(x,y,z,t)\right] _{x}\nonumber \\&\quad -\left( \zeta _1 \, y+\zeta _2\right) -\psi (z)-\beta \left( \zeta _3 \, y+\zeta _4\right) , \end{aligned}$$

(17a)

$$\begin{aligned}&v(x,y,z,t)=\frac{6}{\Upsilon _0} \left[ \ln g(x,y,z,t)\right] _{x}\nonumber \\&\quad -\left( \zeta _1 \, y+\zeta _2\right) -\psi (z)-\beta \left( \zeta _3 \, y+\zeta _4\right) , \end{aligned}$$

(17b)

$$\begin{aligned}&f(x, y, z, t)=1-\epsilon _2 \, \mathrm {exp}\bigg \{\sigma _1 \, x+\sigma _2 \, y \nonumber \\&\quad -\frac{\sigma _1 \left[ 3 \, \sigma _1 \, \sigma _2 +4 \, \Upsilon _0 \, \left( \zeta _1+\beta \zeta _3\right) \right] }{4 \, \mu _0} z\nonumber \\&\quad -\frac{\sigma _1^3}{4} \! \int \! \frac{\Upsilon _2(t)}{\Upsilon _1(t)} \, \mathrm{d}t\bigg \} , \qquad \end{aligned}$$

(17c)

$$\begin{aligned}&g(x, y, z, t)=1+\epsilon _2 \, \mathrm {exp} \bigg \{\sigma _1 \, x+\sigma _2 \, y \nonumber \\&\quad -\frac{\sigma _1 \left[ 3 \, \sigma _1 \, \sigma _2 +4 \, \Upsilon _0 \, \left( \zeta _1+\beta \zeta _3\right) \right] }{4 \, \mu _0} z\nonumber \\&\quad -\frac{\sigma _1^3}{4} \! \int \! \frac{\Upsilon _2(t)}{\Upsilon _1(t)} \, \mathrm{d}t\bigg \} , \end{aligned}$$

(17d)

with $\epsilon _2$ as the real non-zero constant.

With respect to the stream under a pressure surface in the water, under Variable-Coefficient Constraints (5) and (12), Analytic Solutions (17) are dependent on the dispersion coefficient $\Upsilon _2(t)$ as well as perturbed-effect coefficient $\Upsilon _1(t)$ in Eq. (1).

4 Similarity reductions for Eq. (1)

To start with, similar to those in Refs. [52,53,54,55], the form we assume, i.e.,

$$\begin{aligned}&u(x,y,z,t)=\theta (x,y,z,t)\nonumber \\&\quad +\kappa (x,y,z,t) p[r(x,y,z,t)] , \end{aligned}$$

(18)

could help us seek certain similarity reductions for Eq. (1), in which $\theta (x,y,z,t)$, $\kappa (x,y,z,t) \ne 0$ and $r(x,y,z,t) \ne 0$ represent the real to-be-determined differentiable functions of x, y, z and t, while p(r) implies a real differentiable function as for r.

Taking into account $r(x,y,z,t)=r(t)$ only, using symbolic computation¹ and substituting Assumption (18) into Eq. (1), we obtain

$$\begin{aligned}&\Upsilon _1(t) \kappa _{y} r'(t) p' +\Upsilon _3(t) \left( \kappa _{x} \kappa _{xy} +\kappa _{y} \kappa _{xx}\right) p^2 \nonumber \\&\quad +\left[ \Upsilon _1(t) \kappa _{yt} +\Upsilon _2(t) \kappa _{xxxy}+\Upsilon _4(t) \kappa _{xz}\right. \nonumber \\&\quad \left. +\Upsilon _3(t) \left( \kappa _{x} \theta _{xy} +\kappa _{xy} \theta _{x}+\kappa _{y} \theta _{xx} +\kappa _{xx} \theta _{y}\right) \right] p \nonumber \\&\quad +\left[ \Upsilon _1(t) \theta _{yt}+\Upsilon _2(t) \theta _{xxxy} +\Upsilon _4(t) \theta _{xz}\right. \nonumber \\&\quad \left. +\Upsilon _3(t) \left( \theta _{x} \theta _{xy} +\theta _{y} \theta _{xx}\right) \right] =0 , \end{aligned}$$

(19)

where $r'(t)=\frac{\mathrm{d}}{\mathrm{d}t} \, r(t)$ and $p'=\frac{\mathrm{d}}{\mathrm{d}r} \, p(r)$.

To represent a real ordinary differential equation (ODE), Eq. (19), for which we require that the ratios of the coefficients of different derivatives and powers of p(r) denote some functions with respect to r only, turns into

$$\begin{aligned}&\Upsilon _1(t) \kappa _{y} r'(t) \Omega _1(r) =\Upsilon _3(t) \left( \kappa _{x} \kappa _{xy} +\kappa _{y} \kappa _{xx}\right) , \end{aligned}$$

(20a)

$$\begin{aligned}&\Upsilon _1(t) \kappa _{y} r'(t) \Omega _2(r) =\nonumber \\&\quad \Upsilon _1(t) \kappa _{yt} +\Upsilon _2(t) \kappa _{xxxy}+\Upsilon _4(t) \kappa _{xz} \nonumber \\ {}&\quad +\Upsilon _3(t) \left( \kappa _{x} \theta _{xy} +\kappa _{xy} \theta _{x}+\kappa _{y} \theta _{xx} +\kappa _{xx} \theta _{y}\right) ,\nonumber \\ \end{aligned}$$

(20b)

$$\begin{aligned}&\Upsilon _1(t) \kappa _{y} r'(t) \Omega _3(r) =\Upsilon _1(t) \theta _{yt}+\Upsilon _2(t) \theta _{xxxy}\nonumber \\&\quad +\Upsilon _4(t) \theta _{xz} +\Upsilon _3(t) \left( \theta _{x} \theta _{xy} +\theta _{y} \theta _{xx}\right) , \end{aligned}$$

(20c)

with $\Omega _1(r)$, $\Omega _2(r)$ and $\Omega _3(r)$ as three real to-be-determined differentiable functions of r.

Seeing that the second freedom in Remark 2 in Ref. [52] helps us simplify Eq. (20a) into

$$\begin{aligned}&\kappa (x,y,z,t){=}\frac{1}{2} \phi _1^2 x^2 {+}\phi _2 x {+}\phi _3(y)+\phi _4(z){+}\phi _5(t) , \qquad \end{aligned}$$

(21a)

$$\begin{aligned}&r(t)=\phi _1 \! \int \! \frac{\Upsilon _3(t)}{\Upsilon _1(t)} \mathrm{d}t , \qquad \Omega _{1}(r)=0 , \end{aligned}$$

(21b)

and that based on the first freedom in Remark 2 in Ref. [52], Eq. (20c) leads to

$$\begin{aligned}&\theta (x,y,z,t)=\theta _1 x+\theta _2(z)+\theta _3(t) ,\nonumber \\&\Omega _{3}(r)=0 , \end{aligned}$$

(22)

we can transform Eq. (20b) into

$$\begin{aligned} \Omega _{2}(r)=0 , \end{aligned}$$

(23)

in which $\phi _1 \ne 0$, $\phi _2$ and $\theta _1$ denote the real constants, while $\phi _3(y)$, $\phi _4(z)$, $\phi _5(t)$, $\theta _2(z)$ and $\theta _3(t)$ imply the real differentiable functions.

In short, making use of symbolic computation, we end up with a set of the similarity reductions for Eq. (1), i.e.,

$$\begin{aligned}&u(x,y,z,t)=\theta _1 x+\theta _2(z) +\theta _3(t)\nonumber \\&\quad +\left[ \frac{1}{2} \phi _1^2 x^2 \!+\!\phi _2 x\!+\!\phi _3(y)\!+\!\phi _4(z)\!+\!\phi _5(t)\right] p[r(t)], \end{aligned}$$

(24a)

$$\begin{aligned}&r(t)=\phi _1 \! \int \! \frac{\Upsilon _3(t)}{\Upsilon _1(t)} \mathrm{d}t , \end{aligned}$$

(24b)

$$\begin{aligned}&p'+p^2=0 , \end{aligned}$$

(24c)

in which ODE (24c) represents a known ODE, the properties of which can be found, e.g., in Ref. [63], and some non-trivial solutions of which can be written as

$$\begin{aligned} p(r)=\frac{1}{r+\eta } , \end{aligned}$$

(25)

with $\eta$ as a real constant.

With respect to the stream under a pressure surface in the water, Similarity Reductions (24) are dependent on the perturbed-effect coefficient $\Upsilon _1(t)$ as well as nonlinearity coefficient $\Upsilon _3(t)$ in Eq. (1).

What we can see is that Similarity Reductions (24) transform Eq. (1) into a known ODE, i.e. ODE (24c).

5 Conclusions

Currently interesting, Ref. [43], i.e., the paper (Nonlinear Dyn. 87, 2529, 2017), has investigated Eq. (1), a (3+1)-dimensional variable-coefficient generalized shallow water wave equation.

In this Comment, with respect to the stream under a pressure surface in the water, several enhancements on Ref. [43] for Eq. (1) have been described, with the aid of the Hirota method and symbolic computation, as follows:

• Bilinear Forms (6), under Variable-Coefficient Constraint (5), via Assumption (2);

• Bilinear Auto-Bäcklund Transformations (11), under Variable-Coefficient Constraint (5), with Analytic Solutions (14), under Variable-Coefficient Constraints (5) and (12);

• Bilinear Auto-Bäcklund Transformations (15), under Variable-Coefficient Constraint (5), with Analytic Solutions (17), under Variable-Coefficient Constraints (5) and (12);

• Similarity Reductions (24), to a known ODE, i.e., ODE (24c).

We have known that (A) Bilinear Forms (6) are useful for us to build some bilinear auto-Bäcklund transformations, (B) each of Bilinear Auto-Bäcklund Transformations (11) and Bilinear Auto-Bäcklund Transformations (15), denoting a system of the equations which connects a set of the solutions of Eq. (1) to another set of the solutions of Eq. (1) itself, might lead to more and more complicated solutions of Eq. (1), and (C) Similarity Reductions (24) transform Eq. (1) into a known ODE, i.e. ODE (24c).

Beyond those in Ref. [43], our results have been shown to be dependent on the variable coefficients in Eq. (1), while those coefficients have respectively represented the perturbed effects, dispersion and nonlinearity.