A magnetic control method for large-deformation vibration of cantilevered pipe conveying fluid

Abstract

Soft active materials have the ability to undergo large deformation in response to stimuli such as light, heat, magnetic, and electric fields. Due to their promising applications in the fields of soft robots, flexible electronics, and biomedicine engineering, they have attracted tremendous attention from different disciplines and developed rapidly in the past decades basing on mutual efforts. Recently, a new class of soft active materials, known as hard-magnetic soft (HMS) materials is successfully developed. By applying magnetic fields, unprecedented mechanical behaviors of HMS structures have been observed. To further explore the potential applications of HMS materials, this work will investigate the dynamical behaviors of fluid-conveying pipes made of HMS materials for the first time. By considering the exactly geometric nonlinearities due to the bending deformation of the pipe, the governing equation of a cantilevered HMS pipe conveying fluid is derived based on Hamilton’s principle. The analyses of the stability, static deformation, and nonlinear vibration of the HMS pipe are conducted by solving the obtained governing equation. It is found that there is a critical flow velocity for the dynamic instability of the pipe. When the flow velocity is below this value, the HMS pipe may undergo a large static deformation in a stable state. However, the pipe would periodically oscillate with a large amplitude when the flow velocity is beyond the critical flow velocity. Results also indicate the mechanical responses including static deformation, loss of stability, and vibration of the HMS pipe conveying fluid can be effectively controlled by applying an external magnetic field.

1 Introduction

The phenomena of flow-induced vibrations (FIVs) are very common in engineering structures or systems, which may result in dramatic failure [1,2,3]. The FIVs of various fluid–structure interaction (FSI) systems including pipes conveying fluid have been intensively investigated due to their important engineering application and academic significance [4,5,6].

According to different classification standards, the dynamical system of fluid-conveying pipes can be classified into different types. For example, the fluid-conveying pipes can be differentiated by their boundary constraints, such as cantilevered pipes [7], pipes supported at both ends [8], pipes with additional spring support [9], motion-limiting constraint [10], or tip-end mass [11]. It is widely accepted that a supported pipe conveying fluid becomes unstable due to static buckling while a cantilevered pipe conveying fluid loses stability due to flutter. Another classification principle is based on the time-varying feature of the internal fluid flow, i.e., pipes conveying steady flow [8,9,10,11] and pipes conveying unsteady flow [12, 13]. When the internal fluid flow is unsteady, the dynamic responses of the pipe system become more complex. Specifically, a pipe conveying steady fluid is a simple self-excited system, while a pipe conveying pulsating flow could generate parametric resonance. Additionally, the fluid-conveying pipe systems could be divided into macroscopic and micro-/nanopipes. For micro-/nanopipes conveying fluid, their vibration characteristics are size-dependent [14, 15]. Besides, the dynamical system of a fluid-conveying pipe could be two-dimensional or three-dimensional depending on whether the movement of the pipe is planar or spatial.

The earliest works on the dynamical system of fluid-conveying pipes mainly focused on the linear stability. In 1939, Bourrières [16] derived the governing equation for the dynamical behaviors of the fluid-conveying pipe and studied the stability of a cantilevered pipe system, which was regarded as the first scientific study in this field. The famous benchmark works about the dynamics of fluid-conveying pipes supported at both ends were conducted by Feodos’ev [17], Huosner [18] and Niodson [19]. Since then, the cantilevered and supported systems gained continuous attentions [20,21,22] and more complicated pipe systems [23, 24] were also studied. Based on both experimental [25, 26] and theoretical [27, 28] investigations, it was found that the dynamics of a cantilevered pipe and a supported pipe are fundamentally different. The cantilevered pipe is subjected to flutter when the flow velocity of the transported fluid becomes sufficiently high. However, the fluid-conveying pipe with both ends supported would undergo buckling instability once the flow velocity exceeds a critical value.

In the past decades, the investigations on the nonlinear dynamics of fluid-conveying pipes increase rapidly [29,30,31,32,33]. Due to their interesting and complicated nonlinear dynamical behaviors, the fluid-conveying pipes were regarded as a class of representative dynamical system and can be used to develop or validate modern dynamics theory. In several early works on nonlinear dynamics of fluid-conveying pipes [31, 34,35,36,37], the governing equations were derived independently with different forms. In 1994, Semler et al. [38] undertook a systematic comparison of these nonlinear governing equations and unify the different forms. As a result, Semler et al.’s governing equation was commonly used in later studies of the planar oscillations of fluid-conveying pipes [39,40,41]. In 2007, Wadham-Gagnon et al. [42] further derived the governing equations for three-dimensional vibrations of fluid-conveying pipes. Since then, Wadham-Gagnon et al.’s equations were widely adopted in the investigations of nonplanar dynamical behaviors of fluid-conveying pipes [11, 43, 44]. It is noted that the nonlinear behaviors of the fluid-conveying pipes with cantilevered or supported boundaries are also fundamentally different. For a cantilevered pipe, the nonlinearities of the pipe mainly come from the curvature variation of the pipe centerline, with the centerline being always assumed to be inextensible. However, the nonlinearities of a supported pipe are mainly induced by the extension/compression of the centerline. Many interesting dynamical behaviors of the fluid-conveying pipe, e.g., limit-cycle oscillations [39], quasiperiodic vibrations [45], and chaotic motions [10, 46], were reported in existing works. Nevertheless, the vibration amplitudes of the pipe were always assumed to be relatively small in these works, and the geometric nonlinearities of the pipe were approximated by using Maclaurin series. When the pipe undergoes large-amplitude oscillations, the theoretical models proposed in these works are no longer applicable.

In order to satisfy the potential applications of soft pipes conveying fluid, it is necessary to develop efficient theoretical models for large-deformation vibrations. Recently, Chen et al. [47] proposed a novel geometrically exact model for cantilevered pipes conveying fluid. The governing equation of this new model has a very simple form and can be reduced to the relatively small-amplitude models by using Taylor expansion. The advantages of the geometrically exact model were further demonstrated in the studies of the pipe’s vibrations when the flow velocity is sufficiently high or the vibration amplitude is large enough [48]. However, it is still a great challenge to adjust/control the large-deformation vibrations of cantilevered pipes conveying fluid.

The motion control of fluid-conveying pipes is very important in practical applications including the propulsion and swerve of underwater soft robots, targeted transport of fluids, etc. For example, a soft pipe at microscale can be used to clear diseased regions and has potential applications for the treatment of thrombus [49]. A soft pipe conveying fluid can also be used as a component of soft robotics and can realize propulsion and swerve [50]. Since soft pipes conveying fluid are able to deform in a large range of space, they may play an important role in the 3D printing and matter transport in a narrow space. In these new applications, the deformation and oscillation of soft pipes need to be controlled.

It is noted that to control the dynamics of fluid-conveying pipes, most control methods were designed to suppress the deformations/vibrations of the pipe. Conventionally, absorbers are utilized for control purpose, which are composed of mass blocks, dampers, and springs [41, 51, 52]. Since the mass and flexural stiffness of the soft pipe are generally small, additional absorbers attached to the pipe may significantly change the natural frequency of the pipe. Therefore, the control method using additional absorbers is not an ideal choice. With this consideration, developing other novel and effective control methods for soft pipes conveying fluid is necessary and the aim of the current study.

The rapidly developed soft active materials that are responsive to external fields, such as magnetic, electric, thermal, and light fields, could be adopted to efficiently and precisely control the motion of dynamical systems. In this work, the recently developed hard-magnetic soft (HMS) materials [53] that have rapid responses under external magnetic actuations are utilized to adjust the dynamical behaviors of fluid-conveying pipes for the first time. When a HMS pipe is used to convey fluid, it is expected that the mechanical behaviors of the pipe system can be efficiently controlled by changing the external magnetic field.

The HMS materials were manufactured by embedding some hard-magnetic particles (e.g., the neodymium-iron-boron particles) into the soft materials [53]. Due to the important applications of the HMS materials in the areas of soft robots [54], biomedicine [49], etc., the mechanical responses of HMS structures have been investigated [55,56,57,58,59]. For example, the static deformations of a HMS beam with uniform magnetization have been analytically investigated [55, 56]. Chen et al. [57] designed the residual magnetic flux density of HMS beam to realize various functional deformations. Moreover, the deformations of a functionally graded HMS beam with the volume fraction of the embedding particles continuously varying were studied [58]. Very recently, the theoretical modeling on the three-dimensional large deformations of a HMS beam was realized by introducing three Euler angles [59]. The above-mentioned works provide a solid foundation for the theoretical studies of HMS structures.

In this work, the dynamical behaviors of a cantilevered pipe conveying fluid are adjusted by using HMS materials and external magnetic field. The theoretical investigations on the dynamics of such a pipe system are complicated due to magneto-mechanical coupling, fluid–structure coupling, and strong geometric nonlinearities. Based on Hamilton’s principle, the governing equation of the large-deformation vibrations of the HMS pipe conveying fluid will be derived. The analyses of the pipe system consist of three parts: statics, stability, and nonlinear vibration. The controlled motion of the pipe system will be studied. The underlying mechanisms of the dynamical adjustments of the fluid-conveying pipe will be explored.

2 Formulation

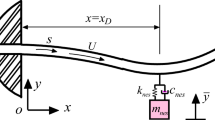
As shown in Fig. 1a, the hard-magnetic soft (HMS) pipe under consideration is a tubular beam with length L, cross-section area A, elastic modulus E, and mass per unit length m, conveying the fluid with flow velocity U and mass per unit length M, under the actuation of an external magnetic field with magnetic flux density B^a. The magnetic flux density of the applied magnetic field is assumed to be uniform. The magnitude of B^a is B^a, and the angle between the directions of B^a and the axis x₀ is α. We denote the residual magnetic flux density of the considered HMS pipe in the reference and the current configurations as ${\mathbf{B}}_{0}^{{\mathbf{r}}}$ and B^r, respectively. A nonuniform magnetization of the HMS pipe is considered in this work. Due to the difficulties of manufacturing the nonuniformly magnetized HMS pipe with continuously varying ${\mathbf{B}}_{0}^{{\mathbf{r}}}$, we assume that the residual magnetic flux density of the HMS pipe has a constant magnitude but may change directions. The considered type of the HMS pipe can be fabricated by 3D printing [53, 60].

Fig. 1

A cantilevered HMS pipe conveying fluid under a uniform external magnetic field: a the schematic diagram; b the coordinate system

For simplicity, we make the following assumptions: (i) the centerline of the cantilevered HMS pipe is inextensible; (ii) the HMS pipe is slender, and hence the Euler–Bernoulli beam model is applicable; (iii) the motion of the pipe is restricted to be planar; (iv) the flow of the transported fluid is a plug one; (v) ${\mathbf{B}}_{0}^{{\mathbf{r}}}$ has a constant magnitude B^r and is evenly divided into S parts, where ${\mathbf{B}}_{0}^{{\mathbf{r}}}$ is uniform in each part. From the clamped end of the pipe to the free end, the direction of ${\mathbf{B}}_{0}^{{\mathbf{r}}}$ is either along the positive direction x₀-axis or the reverse direction, as shown in Fig. 1a.

2.1 Derivation of the governing equation

In this subsection, the governing equation for the large-deformation vibrations of the HMS pipe conveying fluid under the actuation of an external magnetic field will be derived by a Hamiltonian approach. As Fig. 1a shows, the pipe will deform from a straight line to a curved line due to the flow-induced force and the magnetic force. The geometric relationship between the undeformed pipe element and the deformed one is given by [47, 48]

$$ {\rm{d}}u = \cos \theta {\rm{d}}s - {\rm{d}}x_{0} ,{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{d}}v = \sin \theta {\rm{d}}s, $$

(1)

where u is the longitudinal displacement, v is the transverse displacement, and θ is the rotational angle of the deformed pipe centerline; dx₀ and ds are the centerline lengths of the undeformed and deformed pipe elements, respectively. According to the inextensibility assumption, we have ds = dx₀. Hence, the centerline displacements can be expressed as

$$ u = \int_{0}^{{x_{0} }} {\cos \theta {\rm{d}}x_{0} } - x_{0} ,{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} v = \int_{0}^{{x_{0} }} {\sin \theta {\rm{d}}x_{0} } , $$

(2)

with the consideration of the displacement constraints of the cantilevered pipe, i.e. u(x₀ = 0) = 0 and v(x₀ = 0) = 0. Besides, the coordinates (x, y) of the deformed pipe centerline are

$$ x = u + x_{0} = \int_{0}^{{x_{0} }} {\cos \theta {\rm{d}}x_{0} } ,{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} y = v = \int_{0}^{{x_{0} }} {\sin \theta {\rm{d}}x_{0} } . $$

(3)

The velocity of the HMS pipe is given by [38]

$$ {\mathbf{V}}_{p} = \dot{x}{\mathbf{i}} + \dot{y}{\text{j}}\rm{,} $$

(4)

where the overdot denotes the differential operator with respect to time t. The velocity of the conveyed fluid consists of two parts and can be written as [38]

$$ {\mathbf{V}}_{f} = \left( {\dot{x}{\mathbf{i}} + \dot{y}{{\mathbf j}}} \right) + U\left( {x^{\prime}{\mathbf{i}} + y^{\prime}{{\mathbf j}}} \right), $$

(5)

where the prime represents the differential with respective to x₀. Combing Eq. (4) and Eq. (5), the total kinetic energy of the fluid-conveying pipe system is

$$ T = \frac{1}{2}m\int_{0}^{L} {\left( {\dot{x}^{2} + \dot{y}^{2} } \right){\rm{d}}x_{0} } + \frac{1}{2}M\int_{0}^{L} {\left[ {\left( {\dot{x} + Ux^{\prime}} \right)^{2} + \left( {\dot{y} + Uy^{\prime}} \right)^{2} } \right]{\rm{d}}x_{0} } . $$

(6)

Taking the variation of Eq. (6), we obtain

$$ \begin{aligned} \delta \int_{{t_{1} }}^{{t_{2} }} {T{\text{d}}t} & = \int_{{t_{1} }}^{{t_{2} }} {\int_{0}^{L} {\left\{ {\int_{{x_{0} }}^{L} {\left[ {\left( {m + M} \right)\ddot{u} + M\dot{U}\left( {u^{\prime } + 1} \right) + 2MU\dot{u}^{\prime } } \right]{\text{d}}x_{{\text{0}}} } } \right\}\sin \theta \delta \theta {\text{d}}x_{{\text{0}}} } {\text{d}}t} \\ & \quad - \int_{{t_{1} }}^{{t_{2} }} {\int_{0}^{L} {\left\{ {\int_{{x_{0} }}^{L} {\left[ {\left( {m + M} \right)\ddot{v} + M\dot{U}v^{\prime } + 2MU\dot{v}^{\prime } } \right]{\text{d}}x_{{\text{0}}} } } \right\}\cos \theta \delta \theta {\text{d}}x_{{\text{0}}} } {\text{d}}t} \\ & \quad + MU\int_{{t_{1} }}^{{t_{2} }} {\left( {\dot{x}_{L} \delta x_{L} + \dot{y}_{L} \delta y_{L} } \right){\text{d}}t} , \\ \end{aligned} $$

(7)

by utilizing Eq. (2). The subscripts L in Eq. (7) denote the values at x₀ = L.

The variation of the strain energy of the cantilevered HMS pipe is given by [61]

$$ \begin{aligned} \delta \int_{{t_{1} }}^{{t_{2} }} {{\mathcal{V}}_{s} {\rm{d}}t} & = \delta \left( {\int_{{t_{1} }}^{{t_{2} }} {\int_{0}^{L} {\frac{1}{2}EI\theta ^{\prime2} {\rm{d}}x_{0} } {\rm{d}}t} } \right) \\& \quad = EI\int_{{t_{1} }}^{{t_{2} }} {\left. {\theta ^{\prime}\delta \theta } \right|_{0}^{L} {\rm{d}}t} - EI\int_{{t_{1} }}^{{t_{2} }} {\int_{0}^{L} {\theta ^{\prime\prime}\delta \theta {\rm{d}}x_{0} } {\rm{d}}t} , \\ \end{aligned} $$

(8)

where $I = \int_{A} {y^{2} {\rm{d}}A}$ is the moment of inertia. For such a soft pipe, the gravity force plays an important role. The variation of the gravitational potential of the system is

$$ \begin{aligned} \delta \int_{{t_{1} }}^{{t_{2} }} {{\mathcal{G}{\rm d}}t} & = - \left( {m + M} \right)g\int_{{t_{1} }}^{{t_{2} }} {\int_{0}^{L} {\delta u{\rm{d}}x_{0} } {\rm{d}}t} \\ & \quad = \int_{{t_{1} }}^{{t_{2} }} {\left[ {\int_{0}^{L} {\left( {m + M} \right)g\left( {L - x_{0} } \right)\sin \theta \delta \theta {\rm{d}}x_{0} } } \right]{\rm{d}}t} , \\ \end{aligned} $$

(9)

where g is the gravitational acceleration.

In this work, the nonuniform ${\mathbf{B}}_{0}^{{\mathbf{r}}}$ of the considered HMS pipe is assumed to be uniform in each part. Figure 1a shows that the residual magnetic flux density in the deformed configuration can be expressed as [57]

$$ {\mathbf{B}}^{{\mathbf{r}}} = \chi B^{\rm r} {\rm cos}\theta {\mathbf{i}}{\kern 1pt} {\kern 1pt} + \chi B^{\rm r} \sin \theta {\mathbf{j}}, $$

(10)

where χ = χ(x₀) is a sign function that is introduced to describe the nonuniform magnetization. Based on the assumption (v), the expression of the sign function χ is

$\chi = \left( { - 1} \right)^{{r - 1}}$ when $\frac{{r - 1}}{S}L \le x_{0} < \frac{r}{S}L$ for r = 1, 2, …, S. (11).

The magnetization of the pipe is uniform when S = 1. Figure 1 shows that the magnetic flux density of the applied magnetic field can be expressed as

$$ {\mathbf{B}}^{{\mathbf{a}}} = B^{\rm a} {\rm cos}\alpha {\mathbf{i}}{\kern 1pt} {\kern 1pt} + B^{\rm a} \sin \alpha {\mathbf{j}}. $$

(12)

Consequently, the magnetic potential energy per volume at the current configuration of the HMS pipe is [53, 62]

$$ \phi _{m} = - \frac{1}{{\mu _{0} }}{\mathbf{B}}^{{\mathbf{r}}} \cdot {\mathbf{B}}^{{\mathbf{a}}} = - \frac{\chi }{{\mu _{0} }}B^{\mathbf r} B^{\mathbf a} \cos \left( {\theta - \alpha } \right), $$

(13)

where μ₀ is the air (or vacuum) permeability. Integrating Eq. (13) in the whole deformed configuration, then we can obtain the variation of the magnetic potential energy of the HMS pipe as

$$ \delta \int_{{t_{1} }}^{{t_{2} }} {{\mathcal{V}}_{m} {\rm{d}}t} = \frac{A}{{\mu _{0} }}\int_{{t_{1} }}^{{t_{2} }} {\int_{0}^{L} {\chi B^{\rm r} B^{\rm a} \sin \left( {\theta - \alpha } \right)\delta \theta {\rm{d}}x} {\rm{d}}t} . $$

(14)

The considered system of the cantilevered HMS pipe conveying fluid is non-conservative, and the corresponding Hamilton’s principle is [27]

$$ \delta \int_{{t_{1} }}^{{t_{2} }} {{\mathcal{L}{\rm d}}t} = \int_{{t_{1} }}^{{t_{2} }} {\left( {MU\left( {\partial {\mathbf{\dot{r}}}_{L} + U{\mathbf{\tau }}_{L} } \right) \cdot \delta {\mathbf{r}}_{L} } \right){\rm{d}}t} , $$

(15)

where ${\mathcal{L}} = T - {\mathcal{V}}_{s} - {\mathcal{V}}_{m} - {\mathcal{G}}$ is the Lagrangian of the system, r = xi + yj is the position vector, and $\uptau = \frac{1}{{\sqrt {x^{{\prime 2}} + y^{{\prime 2}} } }}\left( {x^{\prime } {\mathbf{i}} + y^{\prime } {\mathbf{j}}} \right)$ is the unit vector tangential to the centerline of the pipe. Substituting the expressions of r and $\mathbf \tau$ into Eq. (15), the right-hand side (rhs) of Eq. (15) can be expressed as

$$ \text{rhs} = {\kern 1pt} {\kern 1pt} MU\int_{{t_{1} }}^{{t_{2} }} {\left( {\dot{x}_{L} \delta x_{L} + \dot{y}_{L} \delta y_{L} } \right){\rm{d}}t} + MU^{2} \int_{{t_{1} }}^{{t_{2} }} {\left( {x^{\prime}_{L} \delta x_{L} + y^{\prime}_{L} \delta y_{L} } \right){\rm{d}}t} . $$

(16)

It is worth mentioning that the first term of Eq. (16) cancels out the last term of Eq. (7). The substitution of Eq. (3) into the second term in Eq. (16) leads to

$$ MU^{2} \int_{{t_{1} }}^{{t_{2} }} {\left( {x^{\prime}_{L} \delta x_{L} + y^{\prime}_{L} \delta y_{L} } \right){\rm{d}}t} = MU^{2} \int_{{t_{1} }}^{{t_{2} }} {\int_{0}^{L} {\sin \left( {\theta _{L} - \theta } \right)\delta \theta {\rm{d}}x_{0} } {\rm{d}}t} . $$

(17)

Combining Eqs. (7), (8), (9), (14), and (17) into Eq. (15) yields the governing equation of the large-amplitude oscillations of the cantilevered HMS pipe conveying fluid and the corresponding boundary conditions as

$$ \begin{aligned} & - \left\{ {\int_{{x_{0} }}^{L} {\left[ {\left( {m + M} \right)\int_{0}^{{x_{0} }} {\left( {\ddot{\theta }\sin \theta + \dot{\theta }^{2} \cos \theta } \right){\rm{d}}x_{0} } - M\dot{U}\cos \theta + 2MU\dot{\theta }\sin \theta } \right]{\rm{d}}x_{0} } } \right\}\sin \theta \\ & - \left\{ {\int_{{x_{0} }}^{L} {\left[ {\left( {m + M} \right)\int_{0}^{{x_{0} }} {\left( {\ddot{\theta }\cos \theta - \dot{\theta }^{2} \sin \theta } \right){\rm{d}}x_{0} } + M\dot{U}\sin \theta + 2MU\dot{\theta }\cos \theta } \right]{\rm{d}}x_{0} } } \right\}\cos \theta \\ & + EI\theta ^{\prime\prime} + aEI\dot{\theta ^{\prime\prime}} - \frac{A}{{\mu _{0} }}\chi B^{r} B^{a} \sin \left( {\theta - \alpha } \right) - \left( {m + M} \right)g\left( {L - x_{0} } \right)\sin \theta + MU^{2} \sin \left( {\theta - \theta _{L} } \right) = 0, \\ \end{aligned} $$

(18)

and

$$ \theta \left( {x_{0} = 0} \right) = 0,{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \theta ^{\prime}\left( {x_{0} = L} \right) = 0, $$

(19)

where E is replaced by E[1 + a(∂/∂t)] to account for the viscoelasticity of the pipe based on the Kelvin–Voigt model [61, 63].

2.2 Nondimensionalization

In order to reduce the number of system parameters and rewrite the governing equation in a simpler form, the following dimensionless quantities are introduced:

$$ \begin{aligned} {\kern 1pt} & \tau = \left( {\frac{{EI}}{{m + M}}} \right)^{{1/2}} \frac{t}{{L^{2} }},{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \mu = \left( {\frac{{EI}}{{m + M}}} \right)^{{1/2}} \frac{a}{{L^{2} }},{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \upsilon = \left( {\frac{M}{{EI}}} \right)^{{1/2}} UL,{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \gamma = \frac{{m + M}}{{EI}}L^{3} g,{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \\ & \beta = \frac{M}{{m + M}},{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} P = \frac{{AL^{2} B^{r} B^{a} }}{{EI\mu _{0} }},{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \xi = \frac{{x_{0} }}{L},{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \varsigma = \frac{u}{L},{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \eta = \frac{v}{L}{\kern 1pt} ,{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} X = \frac{x}{L},{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} Y = \frac{y}{L}{\kern 1pt} {\kern 1pt} {\kern 1pt} , \\ \end{aligned} $$

(20)

where μ is the dimensionless viscoelastic coefficient, υ is the dimensionless velocity of fluid, γ is the gravity parameter, β is the mass ratio, P is the dimensionless magnitude of the magnetic load, ζ and η are the dimensionless displacements, ξ is the dimensionless space variable, and τ is the dimensionless time variable. By using these dimensionless quantities, we can rewrite the governing equation as

$$ \begin{aligned} & \sin \theta \int_{\xi }^{1} {\int_{0}^{\xi } {\left[ {\frac{{\partial ^{2} \theta }}{{\partial \tau ^{2} }}\sin \theta + \left( {\frac{{\partial \theta }}{{\partial \tau }}} \right)^{2} \cos \theta } \right]\rm{d}\xi } \rm{d}\xi }\\&\quad + \sin \theta \int_{\xi }^{1} {\left( { - \frac{{\partial \upsilon }}{{\partial \tau }}\sqrt \beta \cos \theta + 2\upsilon \sqrt \beta \frac{{\partial \theta }}{{\partial \tau }}\sin \theta } \right)\rm{d}\xi } \\ & \quad + \cos \theta \int_{\xi }^{1} {\int_{0}^{\xi } {\left[ {\frac{{\partial ^{2} \theta }}{{\partial \tau ^{2} }}\cos \theta - \left( {\frac{{\partial \theta }}{{\partial \tau }}} \right)^{2} \sin \theta } \right]\rm{d}\xi } \rm{d}\xi }\\ & \quad + \cos \theta \int_{\xi }^{1} {\left( {\frac{{\partial \upsilon }}{{\partial \tau }}\sqrt \beta \sin \theta + 2\upsilon \sqrt \beta \frac{{\partial \theta }}{{\partial \tau }}\cos \theta } \right)\rm{d}\xi } \\ & \quad - \frac{{\partial ^{2} \theta }}{{\partial \xi ^{2} }} - \mu \frac{{\partial ^{3} \theta }}{{\partial \xi ^{2} \partial \tau }} + \chi P\sin \left( {\theta - \alpha } \right) + \gamma \left( {1 - \xi } \right)\sin \theta \\&\quad+ \upsilon ^{2} \sin \left( {\theta _{1} - \theta } \right) = 0, \\ \end{aligned} $$

(21)

where the subscript 1 denotes the value at ξ = 1. Furthermore, the dimensionless boundary conditions for this cantilevered pipe are given by

$$ \theta _{0} = 0,{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \frac{{\partial \theta _{1} }}{{\partial \xi }} = 0, $$

(22)

and the subscript 0 in Eq. (22) denotes the value at ξ = 0.

2.3 Numerical solution procedure

Since the HMS pipe may undergo large static deformations, the investigation of the nonlinear dynamics of the fluid-conveying HMS pipe includes three parts: stability analysis, statics analysis, and nonlinear vibration analysis. The stability analysis can determine whether the pipe will vibrate under the given system parameters. If the pipe does not oscillate, the statics analysis can give the real response of the pipe centerline. However, if the pipe vibrates, the nonlinear vibration analysis is required.

To carry out these three analyses, the infinite-dimensional model is discretized into a finite one. The Galerkin’s method will be employed to realize the spatial discretization. Therefore, the field variable θ can be expressed as

$$ \theta \left( {\xi ,\tau } \right) = \sum\limits_{{r = 1}}^{N} {\phi _{r} \left( \xi \right)q_{r} \left( \tau \right)} , $$

(23)

where $\phi _{r} \left( \xi \right)$ is a set of base functions, $q_{r} \left( \tau \right)$ is the corresponding generalized coordinates, and N is the number of employed base functions. The base functions that satisfy the boundary conditions of Eq. (22) can be given by [47, 48, 57, 58]

$$ \phi _{r} \left( \xi \right) = \sin \left( {\frac{{2r - 1}}{2}\pi \xi } \right){\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \left( {r = 1,{\kern 1pt} {\kern 1pt} 2,{\kern 1pt} {\kern 1pt} 3,{\kern 1pt} {\kern 1pt} \ldots } \right). $$

(24)

2.3.1 Static deformation

The static deformations can be predicted by the statics governing equation, which can be obtained by dropping the dynamical terms in Eq. (21), i.e.

$$ - \frac{{\partial ^{2} \theta ^{s} }}{{\partial \xi ^{2} }} + \chi P\sin \left( {\theta ^{s} - \alpha } \right) + \gamma \left( {1 - \xi } \right)\sin \theta ^{s} + \upsilon ^{2} \sin \left( {\theta _{1}^{s} - \theta ^{s} } \right) = 0. $$

(25)

Substituting Eq. (23) into Eq. (25), then multiplying $\phi _{i}$, and finally integrating from 0 to 1, yield

$$ \begin{aligned} & - \int_{0}^{1} {\phi _{i} \sum\limits_{{j = 1}}^{N} {\phi _{j} ^{{\prime \prime }} q_{j}^{s} } \rm{d}\xi } + P\int_{0}^{1} {\chi \sin \left( {\sum\limits_{{j = 1}}^{N} {\phi _{j} q_{j}^{s} } - \alpha } \right)\rm{d}\xi } \\&\quad+ \gamma \left[ {\int_{0}^{1} {\phi _{i} \left( {1 - \xi } \right)\sin \left( {\sum\limits_{{j = 1}}^{N} {\phi _{j} q_{j}^{s} } } \right)\rm{d}\xi } } \right] \\ {\kern 1pt} & \quad + \upsilon ^{2} \left\{ {\int_{0}^{1} {\phi _{i} \sin \left[ {\left( {\sum\limits_{{j = 1}}^{N} {\phi _{j} \left( 1 \right)q_{j}^{s} } } \right) - \left( {\sum\limits_{{j = 1}}^{N} {\phi _{j} q_{j}^{s} } } \right)} \right]\rm{d}\xi } } \right\} = 0. \\ \end{aligned} $$

(26)

The discretized equations can be solved by an iterative algorithm. By solving Eq. (26), we can obtain the expression of the rotational angle θ. Then the displacements and position of the deformed pipe can be determined by Eqs. (2) and (3), respectively. Numerical examples are provided in Sect. 3.2.

2.3.2 Stability

As mentioned above, it is important to know whether the deformed configurations studied in Sect. 2.3.1 are stable or not. To conduct the stability analysis, we need to introduce a perturbation θ^d(ξ, τ) in additional to the static deformation θ^s(ξ), i.e.,

$$ \theta \left( {\xi ,\tau } \right) = \theta ^{s} \left( \xi \right) + \theta ^{d} \left( {\xi ,\tau } \right). $$

(27)

Substituting Eq. (27) into Eq. (21) and keeping the linear terms of θ^d, we can obtain the static governing Eq. (25) and the following stability governing equation

$$ \begin{aligned} & \sin \theta ^{s} \int_{\xi }^{1} {\int_{0}^{\xi } {\left( {\sin \theta ^{s} \frac{{\partial ^{2} \theta ^{d} }}{{\partial \tau ^{2} }}} \right)\rm{d}\xi } \rm{d}\xi } + \sin \theta ^{s} \int_{\xi }^{1} {\left( {2\upsilon \sqrt \beta \sin \theta ^{s} \frac{{\partial \theta ^{d} }}{{\partial \tau }}} \right)\rm{d}\xi } \\ & \quad + \cos \theta ^{s} \int_{\xi }^{1} {\int_{0}^{\xi } {\left( {\cos \theta ^{s} \frac{{\partial ^{2} \theta ^{d} }}{{\partial \tau ^{2} }}} \right)\rm{d}\xi } \rm{d}\xi } + \cos \theta ^{s} \int_{\xi }^{1} {\left( {2\upsilon \sqrt \beta \cos \theta ^{s} \frac{{\partial \theta ^{d} }}{{\partial \tau }}} \right)\rm{d}\xi } \\ & \quad - \frac{{\partial ^{2} \theta ^{d} }}{{\partial \xi ^{2} }} - \mu \frac{{\partial ^{3} \theta ^{d} }}{{\partial \xi ^{2} \partial \tau }} + \chi P\cos \left( {\theta ^{s} - \alpha } \right)\theta ^{d} + \gamma \left[ {\left( {1 - \xi } \right)\cos \theta ^{s} } \right]\theta ^{d} \\ {\kern 1pt} & \quad + \upsilon ^{2} \left( {\theta _{1}^{d} - \theta ^{d} } \right)\cos \left( {\theta _{1}^{s} - \theta ^{s} } \right) = 0, \\ \end{aligned} $$

(28)

where the constant plug flow is considered, i.e. ∂υ/∂t = 0. Again, substituting Eq. (23) into Eq. (28), multiplying $\phi _{i}$, and integrating from 0 to 1, the following discretized equations are obtained as

$$ \left[ {{\mathbf{M}}^{{\mathbf{d}}} } \right]\left\{ {\frac{{\text{d} ^{2} {\mathbf{q}}^{{\mathbf{d}}} }}{{\mathbf{d} \tau ^{2} }}} \right\}{\mathbf{ + }}\left[ {{\mathbf{C}}^{{\mathbf{d}}} } \right]\left\{ {\frac{{\mathbf{d} {\mathbf{q}}^{{\mathbf{d}}} }}{{\mathbf{d} \tau }}} \right\}{\mathbf{ + }}\left[ {{\mathbf{K}}^{{\text{d}}} } \right]\left\{ {{\mathbf{q}}^{{\mathbf{d}}} } \right\}{\mathbf{ = 0}}, $$

(29)

where

$$ M_{{ij}}^{d} = \int_{0}^{1} {\left( {\phi _{i} \sin \theta ^{s} \int_{\xi }^{1} {\int_{0}^{\xi } {\phi _{j} \sin \theta ^{s} \rm{d}\xi } \rm{d}\xi } } \right)\rm{d}\xi } + \int_{0}^{1} {\left( {\phi _{i} \cos \theta ^{s} \int_{\xi }^{1} {\int_{0}^{\xi } {\phi _{j} \cos \theta ^{s} \rm{d}\xi } \rm{d}\xi } } \right)\rm{d}\xi } , $$

(30a)

$$ C_{{ij}}^{d} = 2\upsilon \sqrt \beta \int_{0}^{1} {\left( {\phi _{i} \sin \theta ^{s} \int_{\xi }^{1} {\phi _{j} \sin \theta ^{s} \rm{d}\xi } } \right)\rm{d}\xi } + 2\upsilon \sqrt \beta \int_{0}^{1} {\left( {\phi _{i} \cos \theta ^{s} \int_{\xi }^{1} {\phi _{j} \cos \theta ^{s} \rm{d}\xi } } \right)\rm{d}\xi } - \mu \left( {\int_{0}^{1} {\phi _{i} \phi _{j} ^{{\prime \prime }} \rm{d}\xi } } \right), $$

(30b)

$$ \begin{aligned} K_{{ij}}^{d} & = - \left( {\int_{0}^{1} {\phi _{i} \phi _{j} ^{{\prime \prime }} \rm{d}\xi } } \right) + P\int_{0}^{1} {\chi \cos \left( {\theta ^{s} - \alpha } \right)\phi _{i} \phi _{j} \rm{d}\xi } \\&\quad + \gamma \int_{0}^{1} {\left[ {\left( {1 - \xi } \right)\cos \theta ^{s} \phi _{i} \phi _{j} } \right]\rm{d}\xi } \\ & \quad {\kern 1pt} + \upsilon ^{2} \int_{0}^{1} {\phi _{i} \left[ {\phi _{j} \left( 1 \right) - \phi _{j} } \right]\cos \left( {\theta _{1}^{s} - \theta ^{s} } \right)\rm{d}\xi } . \\ \end{aligned} $$

(30c)

Equation (29) is reduced to a first-order form by introducing p^d = dq^d/dτ, and then the stability can be analyzed by solving the eigenvalue of the reduced first-order equations. As seen from Eq. (28), before carrying out stability analysis, the static deformation of the pipe needs to be determined.

2.3.3 Nonlinear vibration

To quantitatively predict the mechanical responses of the HMS pipe, it is necessary to carry out the nonlinear vibration analysis, i.e., to solve Eq. (21). Similar to the discretization process in Sects. 2.3.1 and 2.3.2, substituting Eq. (23) into Eq. (21), multiplying $\phi _{i}$, and integrating from 0 to 1, we can obtain the discretized form of Eq. (21) as

$$ {\mathbf{M}}\left\{ {\frac{{\rm{d}^{2} {\mathbf{q}}}}{{\rm{d}\tau ^{2} }}} \right\} + \left\{ {{{\mathbf{N}}}\left( {{\mathbf{q}},{\kern 1pt} {\kern 1pt} {\kern 1pt} \frac{{\rm{d}{\mathbf{q}}}}{{\rm{d}\tau }}} \right)} \right\} = 0, $$

(31)

where

$$ M_{{ij}} = \int_{0}^{1} {\phi _{i} \left( {\sin \theta \int_{\xi }^{1} {\int_{0}^{\xi } {\phi _{j} \sin \theta \rm{d}\xi } \rm{d}\xi } } \right)\rm{d}\xi } + \int_{0}^{1} {\phi _{i} \left( {\cos \theta \int_{\xi }^{1} {\int_{0}^{\xi } {\phi _{j} \cos \theta \rm{d}\xi } \rm{d}\xi } } \right)\rm{d}\xi } , $$

(32a)

$$ \begin{aligned} &{\mathcal{N}}_{i} = \int_{0}^{1} {\phi _{i} \sin \theta \int_{\xi }^{1} {\int_{0}^{\xi } {\left( {\frac{{\partial \theta }}{{\partial \tau }}} \right)^{2} \cos \theta \rm{d}\xi } \rm{d}\xi } \rm{d}\xi } - \int_{0}^{1} {\phi _{i} \cos \theta \int_{\xi }^{1} {\int_{0}^{\xi } {\left( {\frac{{\partial \theta }}{{\partial \tau }}} \right)^{2} \sin \theta \rm{d}\xi } \rm{d}\xi } \rm{d}\xi } \\ & \quad {\kern 1pt} + 2\upsilon \sqrt \beta \int_{0}^{1} {\phi _{i} \left( {\sin \theta \int_{\xi }^{1} {\frac{{\partial \theta }}{{\partial \tau }}\sin \theta \rm{d}\xi } + \cos \theta \int_{\xi }^{1} {\frac{{\partial \theta }}{{\partial \tau }}\cos \theta \rm{d}\xi } } \right)\rm{d}\xi } - \int_{0}^{1} {\phi _{i} \frac{{\partial ^{2} \theta }}{{\partial \xi ^{2} }}\rm{d}\xi } - \mu \int_{0}^{1} {\phi _{i} \frac{{\partial ^{3} \theta }}{{\partial \xi ^{2} \partial \tau }}\rm{d}\xi } \\ & \quad {\kern 1pt} + P\int_{0}^{1} {\phi _{i} \chi \sin \left( {\theta - \alpha } \right)\rm{d}\xi } + \gamma \int_{0}^{1} {\phi _{i} \left( {1 - \xi } \right)\sin \theta \rm{d}\xi } + \upsilon ^{2} \int_{0}^{1} {\phi _{i} \sin \left( {\theta _{1} - \theta } \right)\rm{d}\xi } , \\ \end{aligned} $$

(32b)

with

$$ \theta = \sum\limits_{{r = 1}}^{N} {\phi _{r} \left( \xi \right)q_{r} \left( \tau \right)} ,{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \frac{{\partial \theta }}{{\partial \tau }} = \sum\limits_{{r = 1}}^{N} {\phi _{r} \left( \xi \right)p_{r} \left( \tau \right)} ,{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \frac{{\partial ^{2} \theta }}{{\partial \xi ^{2} }} = \sum\limits_{{r = 1}}^{N} {\phi _{r} ^{{\prime \prime }} \left( \xi \right)q_{r} \left( \tau \right)} ,{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \frac{{\partial ^{3} \theta }}{{\partial \xi ^{2} \partial \tau }} = \sum\limits_{{r = 1}}^{N} {\phi _{r} ^{{\prime \prime }} \left( \xi \right)p_{r} \left( \tau \right)} , $$

(33)

and p = dq/dτ. Now we can rewrite Eq. (31) in a first-order form as

$$ \left\{ {\begin{array}{*{20}c} {\frac{{\rm{d}{\mathbf{q}}}}{{\rm{d}\tau }}} \\ {\frac{{\rm{d}{\mathbf{p}}}}{{\rm{d}\tau }}} \\ \end{array} } \right\} = \left[ {\begin{array}{*{20}c} {\mathbf{0}} & {\mathbf{I}} \\ {\mathbf{0}} & {\mathbf{0}} \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {\mathbf{q}} \\ {\mathbf{p}} \\ \end{array} } \right\} + \left\{ {\begin{array}{*{20}c} {\mathbf{0}} \\ { - {\mathbf{M}}^{{{\mathbf{ - 1}}}} {{\mathbf{N}}}} \\ \end{array} } \right\}. $$

(34)

By using a fourth-order Runge–Kutta integration algorithm, Eq. (34) is solved and θ(ξ, τ) can be determined. Once the expression of rotational angle is given, the displacements and position of pipe centerline can be obtained by Eqs. (2) and (3), respectively. As can be seen from Eq. (31), the nonlinear dynamic responses of the pipe can be directly determined based on Eq. (31). Thus, the nonlinear vibration analysis is independent of the analyses of static deformation and stability.

3 Results

Consistent with the numerical solution procedure given in Sect. 2.3, the presented results include three parts: stability, static deformations, and nonlinear vibrations. In the following subsections, we discuss the stability of the pipe system first, then the deformed configurations based on the statics model will be given, and the nonlinear dynamical results are provided at last.

The embedded hard-magnetic particles may affect the material properties of the pipe, including the density ρ and elastic modulus E. Both ρ and E of the HMS pipe are dependent on the volume fraction ψ of the embedded particles, and the expressions can be given by [49, 64]

$$ E = E_{0} \exp \left( {\frac{{2.5\psi }}{{1 - 1.35\psi }}} \right) $$

(35)

$$ \rho = \left( {1 - \psi } \right)\rho _{m} + \psi \rho _{p} $$

(36)

where E₀ denotes the elastic modulus of a pure rubber without magnetic particles, ρ_m is the density of the rubber matrix, and ρ_p is the density of the embedded particles.

In order to verify the effectiveness of the theoretical model and calculation procedure, the dimensionless parameters of the HMS pipe system are chosen to be the same as the parameters of a rubber pipe used in a previous experiment [39], i.e., β = 0.142, γ = 18.9. Although the embedded particles can significantly affect the material properties of the pipe, the same dimensionless parameter value β (or γ) can be achieved by adjusting the geometric dimension of the pipe. The viscoelastic damping coefficient μ = 5 × 10^–3 is taken without specifically indicated [10, 45].

In the following, the effects of υ (dimensionless flow velocity), P (dimensionless magnitude of magnetic load), S (number of the uniformly magnetized segments), and α (magnetic declination angle) on the mechanical responses of the pipe will be studied. The correctness of the present model and calculations will be validated by comparing with the Païdoussis and Semler’s results [39].

3.1 Stability

3.1.1 Variation of the eigenvalues

After determining the static deformation of the pipe via the method given in Sect. 2.3.1, the stability of the pipe system can be determined by carrying out the analysis procedure provided in Sect. 2.3.2. By solving Eq. (29), the eigenvalues Ω of the pipe system for various flow velocities are given in Figs. 2, 3 and 4. The imaginary part of the eigenvalue Im(Ω) is the frequency of the pipe system, while the real part of eigenvalue Re(Ω) is related to the system damping. The pipe system is stable provided that all Re(Ω) are no more than zero. For the case of Re(Ω) > 0, the pipe flutters if Im(Ω) > 0, while the pipe undergoes buckling instability if Im(Ω) = 0.

Fig. 2

The eigenvalue Ω of the pipe system for a α = 0, b α = π/3, c α = 2π/3 and d α = π, when S = 1, P = 10, β = 0.142, γ = 18.9 and μ = 5 × 10^–3, with various values of the flow velocity

In Fig. 2, the variations of the first-order and second-order eigenvalues with the increase of υ from 0 to 10 are given for different values of α when P = 10 and S = 1, i.e., the uniformly magnetized pipe is considered. As can be seen, there is a critical flow velocity υ_cr. When the flow velocity is below υ_cr, the HMS pipe is stable. If the flow velocity exceeds υ_cr, the HMS pipe will flutter in the second mode. Furthermore, Fig. 2 shows that the critical flow velocity υ_cr decreases with the increase of magnetic declination angle α.

To explore the influences of the strength of the magnetic load and the nonuniform magnetization on the system stability, the variations of the eigenvalue Ω for different values of P and S are shown in Figs. 3 and 4, respectively. It can be seen that there is a critical flow velocity υ_cr corresponding to the second-mode flutter for all cases. The pipe is stable when υ < υ_cr and will vibrate when υ ≥ υ_cr.

Fig. 3

The eigenvalue Ω of the pipe system for a P = 5, b P = 10, c P = 15 and d P = 20, when S = 1, α = π/3, β = 0.142, γ = 18.9 and μ = 5 × 10^–3, with various values of the flow velocity

Fig. 4

The eigenvalue Ω of the pipe system for a S = 1, b S = 2, c S = 3 and d S = 4, when P = 10, α = π/3, β = 0.142, γ = 18.9 and μ = 5 × 10^–3, with various values of the flow velocity

3.1.2 Variation of the critical flow velocity for flutter

As mentioned in Sect. 3.1.1, the critical flow velocity υ_cr plays a significant role in the stability analysis. The present subsection focuses on the values of υ_cr for various values of P, S and α. As shown in Fig. 5, by considering different types of magnetization and diverse magnetic declination angles, the evolutions of υ_cr with the strength of magnetic load P increasing from 0 to 15 are given. As shown in Fig. 5a–d, the critical velocity of the internal flow with the absence of the external magnetic field is 6.37, for μ = 5 × 10^–3. By setting μ = 0, the present work gives υ_cr = 6.17, which agrees very well with the experimental result υ_cr ≈ 6.0 and the theoretical result υ_cr = 6.15 in the previous work of [39]. It can be found that when the value of P, α, or S increases, the critical flow velocity may either increases or decreases. The complicated evolution of critical flow velocity is originated from the dependence of magnetic force vector on the values of P, α and S.

Fig. 5

The critical flow velocity for flutter of the pipe system for a S = 1, b S = 2, c S = 3 and d S = 4, when β = 0.142, γ = 18.9 and μ = 5 × 10^–3, with various values of P and α

The comparison of Fig. 5a–d shows that the influence of magnetic adjustments on the system stability decreases when the value of S increases. This is not surprising since the directions of the magnetic forces of the neighboring segments are opposite and the corresponding adjustment partly cancels each other. If the value of S approaches to infinity, the magnitude of the residual magnetic flux density would be zero macroscopically, and no adjustments can be achieved.

Figure 5 also shows that the critical flow velocity monotonously increases or decreases as the value of P increases, i.e., ∂υ_cr(P, S, α)/∂P ≥ 0 or ∂υ_cr(P, S, α)/∂P ≤ 0 when 0 ≤ P ≤ 15. When the value of α increases from 0 to π, ∂υ_cr/∂P ≥ 0 will gradually change to ∂υ_cr/∂P ≤ 0, (while ∂υ_cr/∂P ≤ 0 will gradually change to ∂υ_cr/∂P ≥ 0). This is due to the reversion of the magnetic force direction when α changes from 0 to π.

3.2 Static deformation

The evolutions of the deformed configurations of the pipe as the flow velocity increases from zero for different values of α, P and S are shown in Figs. 6, 7 and 8. In these figures, the blue solid lines represent the deformed configurations when υ < υ_cr, the red solid lines are the current configurations when υ = υ_cr, and the black chain lines are the deformed shapes when υ > υ_cr. In this subsection, all results are based on the statics model, i.e., the formulation in Sect. 2.3.1. According to the stability analysis given in Sect. 3.1, the deformed shapes of the pipe for υ < υ_cr are stable, while the deformed shapes of the pipe for υ > υ_cr are unstable. The stable configurations are the real mechanical responses of the HMS pipe. The unstable configurations are the unreal responses since the HMS pipe will vibrate in these cases.

Fig. 6

The static configurations of the pipe for a α = 0, b α = π/3, c α = 2π/3 and d α = π, when S = 1, P = 10, β = 0.142 and γ = 18.9, with various values of υ

The evaluations of the deformed shapes of the pipe as υ increases from zero when α = 0, π/3, 2π/3 and π are given in Fig. 6. As shown in this figure, the pipe keeps its initial configuration, i.e., a straight line, for arbitrary value of υ when α = 0. It is also found that the maximum deformation of the pipe occurs when υ = 0, and the pipe’s deformation increases as α increases. The underlying mechanism can be understood if we recall the governing equation of the pipe system. According to Eq. (21), the magnetic force of the pipe behaves as a tip-end force when S = 1, and its direction changes from the x₀-axis direction to the reverse-x₀-axis direction when α increases from 0 to π. As shown in Figs. 5a and 6, the increase in α leads to the decrease in υ_cr since the compressive force reduces the stiffness of the pipe system.

Figure 7 shows the deformed configurations of the pipe for various values of P and α when S = 1 and α = π/3. As expected, the increase of P leads to the larger deformation of the pipe. The deformed shape of the pipe tends to align with the direction of the applied magnetic field as P increases from 5 to 20 for υ = 0. When the value of υ increases from 0, the flow-induced force influences the pipe’s deformation and the pipe configuration will transform in a large space range. The deformed shapes of the pipe for various types of magnetization are given in Fig. 8. As can be seen, the value of S also has significant effect on the deformation of the pipe.

Fig. 7

The static configurations of the pipe for a P = 5, b P = 10, c P = 15 and d P = 20, when S = 1, α = π/3, β = 0.142 and γ = 18.9, with various values of υ

Fig. 8

The static configurations of the pipe for a S = 1, b S = 2, c S = 3 and d S = 4, when P = 10, α = π/3, β = 0.142 and γ = 18.9, with various values of υ

In summary, the static deformations of the fluid-conveying pipe have a strong dependence on the values of P, α and S. Therefore, the proposed magnetic adjustment method in this work is powerfully effective. It is interesting that the deformed configuration of the HMS pipe for υ = υ_cr is nearly the left-most one or the right-most one among the static configurations for various υ, as can be seen in Figs. 6, 7 and 8.

3.3 Nonlinear vibration

After the flow velocity exceeds the critical value of flutter, the deformed shapes of the pipe predicted by the statics model are unreal since the inertia effects cannot be ignored in the fluttering cases. To precisely predict the mechanical responses of the HMS pipe, it is necessary to carry out the nonlinear vibration analysis. In the following subsections, ξ = 1 is chosen as the observing point to show the bifurcation diagrams, time traces, and phases trajectories of the dynamics of the fluid-conveying HMS pipe.

Firstly, a comparison between the present and previous results of the dynamic responses of a cantilevered pipe when the fluid velocity becomes high is provided. It should be mentioned that the derived governing equation for the HMS pipe accounts for the exact geometric nonlinearities. However, in Païdoussis and Semler’s work [39], the geometric nonlinearities were approximated by using Taylor expansion, with third-order nonlinear terms being kept. As shown in Fig. 9, after using a Taylor expansion approximation, the present result agrees very well with Païdoussis and Semler’s result [39]. However, the geometrically exact model predicts a slightly smaller vibration magnitude when the dimensionless fluid velocity is less than 10. This difference shows the new feature of the geometrically exact model, especially when the large-amplitude oscillations of the pipe occur [47, 48].

Fig. 9

Comparison between the results based on geometrically-exact model and Taylor-expansion model [39], by plotting the transverse displacement amplitude of the pipe at ξ = 1, with β = 0.142, γ = 18.9 and μ = 0

3.3.1 Bifurcation diagrams

By considering different types of nonuniform magnetization, the motion amplitudes of θ₁ of the HMS pipe versus various flow velocities υ for P = 10 and α = π/3, i.e. the bifurcation diagrams, are shown in Fig. 10. It is seen that there is a critical value of flow velocity υ_cr. The HMS pipe undergoes static deformation when υ < υ_cr, while the periodic vibrations occur when υ ≥ υ_cr. In the presented bifurcation diagrams, the red dotted lines that represent the value of θ₁ based on the statics model are included for comparison. The results given in Fig. 10 agree well with the results of stability analysis in Sect. 3.1 and the static deformations in Sect. 3.2.

Fig. 10

Bifurcation diagrams for the rotation angle at the free end of the pipe for a S = 1, b S = 2, c S = 3 and d S = 4, when P = 10, α = π/3, β = 0.142, γ = 18.9 and μ = 5 × 10^–3, where the dotted lines represent the value of θ₁ based on the statics governing equation

To further show the nonlinear vibration behaviors of the HMS pipe, the bifurcation diagrams of the tip-end longitudinal displacement ζ₁ and the tip-end transverse displacement η₁ are given in Figs. 11 and 12, respectively. Again, the dotted lines denote the displacements obtained by the statics model. It can be observed that the HMS pipe will experience extremely large-amplitude vibration for a relatively large flow velocity υ. For examples, the vibration range of η₁ for υ = 10 in Fig. 12a is [−0.54, 0.56], and the vibration range of η₁ for υ = 10 in Fig. 12b is [−0.20, 0.72].

Fig. 11

Bifurcation diagrams for the longitudinal displacement at the free end of the pipe for a S = 1, b S = 2, c S = 3 and d S = 4, when P = 10, α = π/3, β = 0.142, γ = 18.9 and μ = 5 × 10^–3, where the dotted lines represent the value of ζ₁ based on the statics governing equation

Fig. 12

Bifurcation diagrams for the transverse displacement at the free end of the pipe for a S = 1, b S = 2, c S = 3 and d S = 4, when P = 10, α = π/3, β = 0.142, γ = 18.9 and μ = 5 × 10^–3, where the dotted lines represent the value of η₁ based on the statics governing equation

3.3.2 Time traces and phase trajectories

In this subsection, the time traces and the corresponding phase trajectories will be presented for several typical cases to show the details of the vibration characteristics of the pipe. In Fig. 13, the time traces of the displacements of the pipe centerline when υ = 10 are given for S = 1, 2, 3 and 4. Furthermore, the corresponding phase trajectories for the tip-end longitudinal displacement ζ₁ and the tip-end transverse displacement η₁ are shown in Figs. 14 and 15, respectively. As we can see, the fluid-conveying HMS pipe undergoes periodic large-deformation oscillations in these cases.

Fig. 13

Time traces for the tip-end displacements of the pipe when P = 10, α = π/3, β = 0.142, γ = 18.9, μ = 5 × 10^–3 and υ = 10, for a S = 1, b S = 2, c S = 3 and d S = 4

Fig. 14

Phase trajectories for the tip-end longitudinal displacement of the pipe when P = 10, α = π/3, β = 0.142, γ = 18.9, μ = 5 × 10^–3 and υ = 10, for a S = 1, b S = 2, c S = 3 and d S = 4

Fig. 15

Phase trajectories for the tip-end transverse displacement of the pipe when P = 10, α = π/3, β = 0.142, γ = 18.9, μ = 5 × 10^–3 and υ = 10, for a S = 1, b S = 2, c S = 3 and d S = 4

3.3.3 Oscillating shapes

The oscillating shapes of the HMS pipe will be presented in this subsection to clearly show the large-deformation vibrations. As shown in Fig. 16, the oscillating shapes of the pipe (see the blue lines) for S = 1, 2, 3 and 4 are given when P = 10, α = π/3 and υ = 10. Besides, the red line that represents the deformed configuration obtained by using the statics model is included for comparison. It is unexpected that the pipe does not rigorously vibrate around the statics model-based deformed shape. Especially for the case of S = 2 in Fig. 16b, the pipe almost oscillates on the right side of the red line.

Fig. 16

Oscillating shapes (the blue lines) of the HMS pipe when P = 10, α = π/3, β = 0.142, γ = 18.9, μ = 5 × 10^–3 and υ = 10, for a S = 1, b S = 2, c S = 3 and d S = 4, where the red line represents the deformed shape based on the statics governing equation

The oscillating shapes for the cases υ = 6, 7, 8 and 9 are given in Fig. 17. The other parameters in Fig. 17 are the same as those in Fig. 16b. As shown in Figs. 16b and 17, when the flow velocity is slightly above the critical value, the HMS pipe vibrates around the static deformed configuration, e.g., υ = 6 and 7. However, the HMS pipe may no longer oscillate around the static deformed configuration when the value of υ is relatively large, e.g. υ = 9 and 10. As can be seen from Eq. (21), the motion of the fluid-conveying pipe is odd symmetry about its initial shape, i.e., θ(ξ) = 0, without the consideration of the magnetic load. However, the term –χPsinαcosθ induced by the magnetic load can break the odd symmetry of pipe system. This effect is slight when υ is just above υ_cr, since (θ^d)² induced by –χPsinαcosθ can be neglected compared to θ^d induced by other terms. However, when the value of υ is sufficiently large, the effect of term –χPsinαcosθ is nontrivial, and the odd symmetry of the HMS pipe system will be broken.

Fig. 17

Oscillating shapes (the blue lines) of the HMS pipe when P = 10, α = π/3, S = 2, β = 0.142, γ = 18.9 and μ = 5 × 10^–3 for a υ = 6, b υ = 7, c υ = 8 and d υ = 9, where the red line represents the deformed shape based on the statics governing equation

4 Conclusions

In this work, a novel adjustment method for the mechanical responses of fluid-conveying pipes by using the HMS materials and an external magnetic field is proposed. Based on Hamilton’s principle, the governing equation for the large-deformation vibrations of a cantilevered HMS pipe conveying pipe is derived by considering the exact geometric nonlinearities due to curvature. The differential equation is discretized by using the Galerkin method and then solved via an iterative algorithm (for statics problem) or the fourth-order Runge–Kutta integration algorithm (for dynamical problem).

The analyses of the HMS pipe system consist of three parts: stability analysis, statics analysis, and nonlinear vibration analysis. Furthermore, the results of the nonlinear vibration analysis are consistent with the results of the stability and static analyses. Based on extensive calculations, the following conclusions can be drawn:

• (i) The static and dynamical behaviors of the fluid-conveying pipe can be well adjusted by using the HMS materials and applying an external magnetic field. By designing the magnetization of the HMS pipe, the strength, and the direction of the external magnetic field, we can efficiently adjust the stability, the deformed configuration and the vibrating shape of the pipe.

• (ii) There is a critical flow velocity υ_cr for the stability of the HMS pipe system. When υ < υ_cr, the HMS pipe undergoes a static deformation. However, when υ > υ_cr, the HMS pipe is subject to flutter in the second mode with a large oscillation amplitude. Besides, it is noted that the vibration of the pipe is periodic.

• (iii) After the value of υ exceeds the value of υ_cr, the fluid-conveying HMS pipe vibrates around the static deformed shape of the pipe for relatively small flow velocity. However, the pipe would no longer oscillate around the static deformed shape for sufficiently large flow velocity due to the even-symmetry term induced by the magnetic load.

Thus, the utilization of the HMS pipe to transport fluid provides a new efficient method to tune the deformation and the vibration of a fluid-conveying pipe by an external magnetic field. This magnetic adjustment method can be extended to the dynamical control of other flow-induced vibration systems. The developed large-deformation oscillation model is expected to be useful for further investigations on the nonlinear dynamics of various fluidic devices made of soft active materials.

Appendix 1

The convergence of the Galerkin discretization will be examined in this part. The evolution of the critical flow velocity υ_cr for various values of α as P increases from 0 to 15 is given in Fig. 

Fig. 18

Convergence test of the Galerkin discretization for a the critical flow velocity of stability analysis and b the bifurcation diagram of nonlinear vibration analysis of the fluid-conveying HMS pipe, where S = 1, P = 10, α = π/3, β = 0.142, γ = 18.9 and μ = 5 × 10^–3 are employed

18a. Note that the results of N = 3 and N = 4 are shown. It can be seen that the values of υ_cr obtained by using N = 3 agree very well with that obtained by using N = 4. Furthermore, Fig. 18b shows the bifurcation diagrams of θ₁ for N = 3 and 4 when S = 1, P = 10, α = π/3, β = 0.142, γ = 18.9 and μ = 5 × 10^–3. It can be found that there is a good agreement between the bifurcation diagram by using N = 3 and the counterpart by using N = 4. Therefore, the Galerkin discretization of N = 3 is valid for the problem at hand and all the results given in Sect. 3 are obtained by using N = 3.