1 Introduction

Composite laminated beams are common structures for load-bearing and strength enhancement in industries. In the critical environment, a primary concern of the structure is the vibration caused by external loads or self-motions, which may lead to the reduction of the system’s lifespan. Hence, the vibration suppression problem of composite laminated structures is significant.

Passive vibration absorption methods are widely used in engineering. In recent years, there has been great interest in nonlinear vibration suppression for composite beams and other structures. The common vibration control techniques are applying nonlinear passive control devices because they are simply designed, economical, and practical. The nonlinearity of these devices can increase the bandwidth of vibration suppression [1] and enhance the robustness of the system. To date, many studies have investigated the new design of passive nonlinear vibration absorbers and their applications. For example, nonlinear vibration absorbers and isolators based on saturation phenomenon [2, 3], magnetism [4], and inerter [5] were proposed and thoroughly investigated. Various kinds of impact dampers were designed and analyzed for resonance suppression [6, 7]. One of the most representative nonlinear vibration absorbers is the nonlinear energy sink which can realize the targeted energy transfer [8,9,10] and achieve vibration suppression at various temperatures and moisture levels [11]. The nonlinear energy sink was applied to many structures such as linear systems [12, 13], beams [14, 15], laminated plates [16,17,18], and trapezoidal wings [19]. Overall, these studies highlight the massive need for better vibration suppression devices and strategies for engineering structures. The requirement of new passive vibration absorbers still exists.

Shape memory alloys (SMA) have many extraordinary properties such as complete shape recovery after experiencing large strains and energy dissipation through hysteresis of response [20]. Paiva et al. discussed the constitutive modeling of SMAs including polynomial models, models with assumed phase transformation kinetics, and models with internal constraints [21]. Savi et al. investigated the nonlinear dynamics of SMA systems and observed periodic, quasi-periodic, and chaotic behaviors [22, 23]. SMAs attracted the interest of many researchers in vibration control and structural engineering over the past decades. Ghasemi et al. used the SMA pounding tuned mass damper to control the wave-induced vibrations of the offshore jacket platforms [24]. Kumbhar et al. proposed an adaptive tuned vibration absorber based on magnetorheological elastomer-shape memory alloy composite and studied the dynamic response of the system with this absorber [25]. Huang et al. applied an SMA-based tuned mass damper to a timber floor system for semi-active control [26]. Qian et al. experimentally investigate structural vibration suppression under strong seismic excitation with a new super-elastic shape memory alloy friction damper [27]. The integration of SMAs into composite structures has resulted in many benefits, which include actuation, vibration control, damping, sensing, and self-healing [28]. Alebrahim et al. studied the thermomechanical properties of a hybrid composite beam with carbon fibers and SMA wires numerically and experimentally [29]. Bayat and EkhteraeiToussi analyzed the vibrations of a composite beam with SMA wires using the Panico–Brinson model and differential quadrature-integral quadrature combined method [30, 31]. Soltanieh et al. investigated SMA wires embedded in composite plates with nonlinear finite element method and reported that SMA wires cannot always strengthen the plates [32]. Previous studies demonstrated that SMAs are great materials for new vibration absorbers. Short ropes can also dissipate energy when forced to deform bending due to the interwire friction. They have been widely used for vibration isolation [33] and tuned mass damper [34]. A new nonlinear vibration absorber made of assemblies of nickel titanium-Naval Ordnance Laboratory (NiTiNOL) strands, wires, and steel wire ropes was proposed by Carboni et al. [35]. The NiTiNOL-steel wire ropes (NiTi-ST) with multiple configurations were theoretically and experimentally analyzed, and the hysteresis was described with a modified Bouc–Wen model [36]. There are mainly two methods for modeling hysteresis: one is based on physical hysteresis characters, and the other is based on hysteresis phenomenology [37]. The phenomenological models are merely mathematical models, and they can describe different hysteresis loops more generally. There are operator-based models and differential-based models [38]. Bouc–Wen model is one of the most popular differential-based models with a strong ability in describing hysteresis loops with different trigonometric features [39]. Bouc–Wen model has widespread applications in structural elements, mechanical systems, energy dissipation systems, and so on. The modified Bouc–Wen model proposed by Carboni et al. [36] took account of the pinching behavior of NiTi-ST. The nonlinear dynamic behavior character of NiTi-ST was investigated in the frequency domain and time domain, and the absorber properties were optimized [40]. The NiTi-ST can be used for multiple purposes. Carboni et al. evaluated the NiTi-ST in a structure of multistory steel building model which demonstrated a good performance within designed frequency bandwidth [41]. Zhang et al. [42] developed a novel NES with NiTi-ST for whole-spacecraft vibration isolation.

Despite the rich dynamic behavior of the device, the NiTi-ST still requires robust mechanic models for analysis. The nonlinear parametric identification of NiTi-ST poses a considerable challenge to the research community. Carboni et al. [43] identified the parameters of the modified hysteretic restoring force model to minimize the difference between numerical and experimental results. Brewick et al. [44] employed data-driven methodologies to create a generalized model for NiTi-ST. The experiment data were identified with Volterra/Wiener neural network, polynomial basis methods, and artificial neural networks. The results indicated that the polynomial model can represent the nonlinear behaviors of NiTi-ST. Combined with naïve elastic net regularization, Brewick et al. reduced the order of the polynomial model and obtained comparable results of traditional methods [45]. Currently, most researchers are dedicated to parametric identification of NiTi-ST. The applications on composite structures are rarely presented, and the strong ability to suppress vibration of composite beams is rarely reported, to the authors’ best knowledge.

With the reduced-order polynomial model for NiTi-ST proved to be suitable for reporting the dynamic behavior briefly, in the present paper, the NiTi-ST coupled to a composite laminated beam is studied via semi-analytical and numerical methods for the first time. The nonlinear restoring and damping forces of NiTi-ST are converted into reduced-order polynomial models. It is noted that the real SMA devices exhibit strong thermomechanical coupling [46]. The difference between nonisothermal and isothermal behavior can be pronounced when the mechanical load is changing rapidly [47]. In the present paper, to simplify modeling, the composite beam embedded with NiTi-ST is investigated under the isothermal condition and the thermomechanical behavior is ignored. The nonlinear responses of the beam are obtained, and the vibration suppression effects of the NiTi-ST are examined. The rest of the paper is arranged as follows: In Sect. 2, a 1-DOF system with NiTi-ST is presented for polynomial model fitting. The composite beam model is established, and the polynomial model is coupled as the nonlinear restoring and damping force. In Sect. 3, the Galerkin truncation method is used to discretize the nonlinear governing equation of the beam and the HBM [48] combined with the presto-arc length method [49] is used to obtain the semi-analytical results. In Sect. 4, a modified variational approach [50, 51] is developed to establish the discretized beam model. The Newmark-β method is employed for nonlinear time-domain responses. The Runge–Kutta method is carried out to verify the results in Sects. 3 and 4. It is found that the NiTi-ST is a promising vibration absorber for the composite beam. The NiTi-ST may have a bright future in engineering applications.

2 Modeling of the system

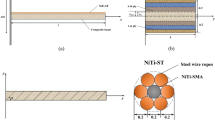
The coupled system is made of a slender laminated beam with length L, width B, and height h and NiTi-ST damper. The NiTi-ST is glued onto the composite beam with composite adhesive and fully fixed to the upper surface of the beam, as shown in Fig. 1. The beam is simply supported at the end of both sides.

Fig. 1
figure 1

Composite beam embedded with NiTi-ST

Full size image

2.1 Restoring and damping force model of NiTi-ST with validation

Considering the transverse vibration of the beam, the restoring and damping force \(f_{st}\) provided by NiTi-ST [36] can be expressed as

$$ f_{st} = (1 - r)k_{c} w^{3} + r(k_{e} w + z_{h} ) $$
(1)

where w is the generalized displacement field at the middle surface of the beam. The nonlinear restoring and damping force \(f_{st}\) is related to the displacement field of the beam. r, \(k_{c}\), \(k_{e}\) are parameters obtained by experiments. \(z_{h}\) is a hysteresis damping force described as a modified Bouc–Wen model:

$$ \left\{ {\begin{array}{*{20}l} {\dot{z}_{h} = \left\{ {k_{d} h(x) - (\gamma + \beta {\text{sgn}} (z_{h} \dot{w}))\left| {z_{h} } \right|^{n} } \right\}\dot{w}} \hfill \\ {h(x) = 1 - \xi e^{{ - \frac{{w^{2} }}{{w_{c} }}}} } \hfill \\ \end{array} } \right. $$
(2)

where \(k_{d}\), \(\gamma\), \(\beta\), n, \(\xi\), \(w_{c}\) are material parameters, \(\dot{z}_{h}\) is the first-order differentiation of \(z_{h}\) concerning time, \(h(x)\) is the pinching function for modulating the tangent stiffness at the origin. Table 1 lists the parameter values of different NiTi-ST configurations.

Table 1 Parameter values of different NiTi-ST configurations Snj [40]
Full size table

The restoring and damping force \(f_{st}\) is distributed at the middle surface of the beam with the form of differential equations, which are hard to be dealt with. Hence, based on the thought of restoring force surface method, the force \(f_{st}\) is identified into a polynomial function. To start polynomial fitting, the force–displacement–velocity data of NiTi-ST are essential, which can be obtained from the modified Bouc–Wen models. Therefore, a lumped-mass 1-DOF system shown in Fig. 2 is proposed to provide polynomial fitting data. Assuming that the force \(f_{st}\) is proportional to the force provided by NiTi-ST of a 1-DOF system. The force \(f_{st}\) is proportional to the force provided by NiTi-ST of a 1-DOF system. The rigid mass m moves along the vertical direction. The excitation force is expressed as \(F_{0} \sin (2\pi f_{0} t)\). Engorging the gravity effect of the mass m and the NiTi-ST, the governing equation is given as:

$$ m\ddot{w}_{m} = F_{0} \sin (2\pi f_{0} t) - f_{st} $$
(3)
Fig. 2
figure 2

A 1-DOF system restricted with NiTi-ST

Full size image

where wm represents the displacement of the mass m. It should be noted that the displacement wm is different with the displacement field of the composite beam. The displacement field of the beam is related to the position of the beam. Substituting Eqs. (1) (2) into Eq. (3), the dynamic equation can be solved with Runge–Kutta method. After obtaining the time-domain response of the 1-DOF system, the data of the last five periods are chosen for fitting.

The data obtained above are imported into the curve fitting toolbox of MATLAB. A polynomial function is proposed to capture the nonlinearity of the restoring and damping force. The polynomial function is of the displacement w and the velocity \(\dot{w}\) of the system. While polynomial-based models are moderately accurate, they are simple to implement and allowed for reduced-order modeling [44]. Since the analytical results of the responses are required next, polynomial models are necessary.

In an attempt to simplify the expression of the restoring and damping force model as much as possible, the maximum order of nonlinear terms is set to be 3. After removing several terms with little influence on the fitting results, a polynomial function basis with no more than five terms is used for fitting, which can be expressed as

$$ f_{st} = k_{1} w + k_{3} w^{3} + c_{1} \dot{w} + r_{21} w^{2} \dot{w} + r_{12} w\dot{w}^{2} $$
(4)

where \(k_{1}\), \(k_{3}\), \(c_{1}\), \(r_{21}\), and \(r_{12}\) are stiffness coefficient and nonlinear damping coefficients. The curve fitting results are listed in Table 2.

Table 2 Parameter values of identified restoring and damping force model
Full size table

Next, validation of the identified model is carried out. The force of the Bouc–Wen model in the 1-DOF system is replaced with the restoring and damping force of the polynomial fitting model. The restoring and damping force behavior is obtained, as presented in Fig. 3. The identified model reports acceptable results for all configurations. For configuration S1a, the polynomial model managed to capture the nonlinear cubic stiffness. The restoring and damping forces of configuration S2a and S2b are not accurately identified. The sharp corners of the hysteresis loops cannot be described with reduced-order polynomial models because the hysteresis damping is replaced with polynomial damping terms in the identified model. Higher order damping terms are required for more accurate descriptions. For the rest of the configurations, the identified polynomial model performs relatively better than S2a and S2b. The identified restoring and damping force model is applied for the rest of the modeling.

Fig. 3
figure 3

Force–displacement loops for different NiTi-ST configurations: a S1a, b S2a, c S2b, d S3a, e S3b and f S3c

Full size image

2.2 Composite beam model

The composite laminated beam with \(N_{l}\) layers is studied. The coordinates of kth lamina on the z-axis are \(z_{k}\) and \(z_{k + 1}\). Based on the Euler–Bernoulli beam model, displacement functions of an arbitrary point in the beam can be written as

$$ \left\{ {\begin{array}{*{20}l} {\tilde{u}(x,z,t) = - z\frac{\partial w}{{\partial x}}} \hfill \\ {\tilde{w}(x,z,t) = w(x,t)} \hfill \\ \end{array} } \right. $$
(5)

where \(\tilde{u}\) and \(\tilde{w}\) are the displacement of the arbitrary point in x- and z-directions, respectively. w is the generalized displacement at the middle surface of the beam. The generalized displacement field w differs from the displacement wm of the lumped-mass system in Fig. 2. It is related to the position x of the beam.

The normal strain of the composite laminated beam can be expressed as

$$ \varepsilon_{xx} = - z\frac{{\partial^{2} w}}{{\partial x^{2} }} $$
(6)

The constitutive equation of the kth layer can be expressed as follows

$$ \left[ {\begin{array}{*{20}c} {\sigma_{xx} } \\ {\sigma_{yy} } \\ {\sigma_{xy} } \\ \end{array} } \right]^{(k)} = \left[ {\begin{array}{*{20}c} {\overline{Q}_{11}^{(k)} } & {\overline{Q}_{12}^{(k)} } & {\overline{Q}_{16}^{(k)} } \\ {\overline{Q}_{12}^{(k)} } & {\overline{Q}_{22}^{(k)} } & {\overline{Q}_{26}^{(k)} } \\ {\overline{Q}_{16}^{(k)} } & {\overline{Q}_{26}^{(k)} } & {\overline{Q}_{66}^{(k)} } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {\varepsilon_{xx} } \\ {\varepsilon_{yy} } \\ {\gamma_{xy} } \\ \end{array} } \right]^{(k)} $$
(7)

where \(\overline{Q}_{i,j}^{(k)} (i,j = 1,2,6)\) denotes the transformed elastic coefficient related to the kth lamina elastic constants \(Q_{i,j}^{(k)}\) and the angle \(\theta^{(k)}\) between the x-axis and the principal material directions. It can be calculated with the following expression:

$$ \begin{aligned} \overline{Q}_{11}^{(k)} & = Q_{11}^{(k)} \cos^{4} \theta^{(k)} + 2\left( {Q_{12}^{(k)} + 2Q_{66}^{(k)} } \right)\sin^{2} \theta^{(k)} \cos^{2} \theta^{(k)} + Q_{22}^{(k)} \sin^{4} \theta^{(k)} \\ \overline{Q}_{12}^{(k)} & = \left( {Q_{11}^{(k)} + Q_{22}^{(k)} - 4Q_{66}^{(k)} } \right)\sin^{2} \theta^{(k)} \cos^{2} \theta^{(k)} + Q_{12}^{(k)} \left( {\sin^{4} \theta^{(k)} + \cos^{4} \theta^{(k)} } \right) \\ \overline{Q}_{22}^{(k)} & = Q_{11}^{(k)} \sin^{4} \theta^{(k)} + 2\left( {Q_{12}^{(k)} + 2Q_{66}^{(k)} } \right)\sin^{2} \theta^{(k)} \cos^{2} \theta^{(k)} + Q_{22}^{(k)} \cos^{4} \theta^{(k)} \\ \overline{Q}_{16}^{(k)} & = \left( {Q_{11}^{(k)} - Q_{12}^{(k)} - 2Q_{66}^{(k)} } \right)\sin \theta^{(k)} \cos^{3} \theta^{(k)} + \left( {Q_{12}^{(k)} - Q_{22}^{(k)} + 2Q_{66}^{(k)} } \right)\sin^{3} \theta^{(k)} \cos \theta^{(k)} \\ \overline{Q}_{26}^{(k)} & = \left( {Q_{11}^{(k)} - Q_{12}^{(k)} - 2Q_{66}^{(k)} } \right)\sin^{3} \theta^{(k)} \cos \theta^{(k)} + \left( {Q_{12}^{(k)} - Q_{22}^{(k)} + 2Q_{66}^{(k)} } \right)\sin \theta^{(k)} \cos^{3} \theta^{(k)} \\ \overline{Q}_{66}^{(k)} & = \left( {Q_{11}^{(k)} + Q_{22}^{(k)} - 2Q_{12}^{(k)} - 2Q_{66}^{(k)} } \right)\sin^{2} \theta^{(k)} + Q_{66}^{(k)} \left( {\sin^{4} \theta^{(k)} + \cos^{4} \theta^{(k)} } \right) \\ \end{aligned} $$
(8)

The elastic constants \(Q_{i,j}^{(k)}\) can be expressed from the engineering elastic parameters of the kth material:

$$ Q_{11}^{(k)} = \frac{{E_{1}^{(k)} }}{{1 - \mu_{12}^{(k)} \mu_{21}^{(k)} }},\quad Q_{12}^{(k)} = \frac{{\mu_{12}^{(k)} E_{2}^{(k)} }}{{1 - \mu_{12}^{(k)} \mu_{21}^{(k)} }},\quad Q_{22}^{(k)} = \frac{{E_{2}^{(k)} }}{{1 - \mu_{12}^{(k)} \mu_{21}^{(k)} }},\quad Q_{66}^{(k)} = G_{12}^{(k)} $$
(9)

The external load is uniformly distributed over an area with \(x_{1} = L/4\) and \(x_{2} = L/2\) on the upper surface of the beam, seeing Fig. 4.

Fig. 4
figure 4

Excitation applied on the beam

Full size image

According to the generalized Hamilton’s principle, the governing equation of the composite beam can be obtained by

$$ \delta \int_{{t_{1} }}^{{t_{2} }} {\left( {T - U + W_{f} + W_{st} } \right){\text{d}}t} = 0 $$
(10)

where \(T\), \(U\), \(W_{f}\), and \(W_{st}\) are the potential energy, the kinetic energy, the work done by the restoring and damping force provided by NiTi-ST, and the work done by external loads, respectively, given as:

$$ \left\{ {\begin{array}{*{20}l} {T = \frac{1}{2}\sum\limits_{k = 1}^{{N_{l} }} {\int_{{z_{k} }}^{{z_{k + 1} }} {\int_{S} {\rho^{(k)} \dot{w}^{2} } } } B\,{\text{d}}x\,{\text{d}}z} \hfill \\ {U = \frac{1}{2}\int_{0}^{L} {N_{x} } \frac{{\partial^{2} w}}{{\partial x^{2} }}B\,{\text{d}}x} \hfill \\ {W_{f} = \int_{0}^{L} {Bf_{w} } (x)w\,{\text{d}}x} \hfill \\ {W_{st} = \int_{0}^{L} { - \chi f_{st} w} \,{\text{d}}x} \hfill \\ \end{array} } \right. $$
(11)

with \(\rho^{(k)}\), \(N_{x}\), \(f_{w}\), \(\chi\) representing the density of kth lamina, the generalized force resultant of the beam, the external loads distributed on the x-axis, and the parameter modifying the restoring and damping force. \(N_{x}\) can be written as:

$$ N_{x} = \sum\limits_{k = 1}^{{N_{l} }} {\int_{{z_{k} }}^{{z_{k + 1} }} { - z\sigma_{xx} } } {\text{d}}z $$
(12)

Substituting Eqs. (4) and (11) into Eq. (10) and setting the coefficients of virtual displacements to zero yield

$$ \rho Bh\ddot{w} + B\frac{{\partial^{2} N_{x} }}{{\partial x^{2} }} + \eta B\frac{{\partial^{3} N_{x} }}{{\partial x^{2} \partial t}} = Bf_{w} - \chi \left( {k_{1} w + k_{3} w^{3} + c_{1} \dot{w} + r_{21} w^{2} \dot{w} + r_{12} w\dot{w}^{2} } \right) $$
(13)

Equation (13) is reduced by assuming that the thickness, density, and strain of every lamina are the same, respectively. The layers of the laminated beam are cross-ply (0°/90°/0°/90°). The geometry dimensions of the beam are length L = 0.462 m, width B = L/15, height h = L/50, and the material properties are \(E_{1}\) = 152.4 GPa, \(E_{2}\) = 10.16 GPa, \(G_{12} = G_{13} =\) 4.36 GPa, \(G_{23}\) = 3.75 GPa, \(\gamma_{12}\) = 0.3 and \(\rho\) = 1461.73 kg/m3. The damping coefficient \(\eta\) = 10–5, and the parameter modifying the restoring and damping force \(\chi\) = 0.2.

3 Analytical solutions

3.1 Galerkin truncation

The Galerkin method is one of the most common procedures for truncating the partial differential equation. Based on the simply supported boundary conditions, the solution of Eq. (13) is written as:

$$ w(x,t) = \sum\limits_{i = 1}^{n} {q_{i} (t) \cdot \sin \frac{i\pi x}{L}} $$
(14)

where \(i\) is the order of the modal shape function. Once substituting Eq. (14) into Eq. (13), according to the Galerkin method with four modes, the equation can be transformed into Eq. (15):

$$ \begin{aligned} & \int_{0}^{L} {\sum\limits_{i = 1}^{n} {\left( {\rho Bh\ddot{w} + B\frac{{\partial^{2} N_{x} }}{{\partial x^{2} }} + \eta B\frac{{\partial^{3} N_{x} }}{{\partial x^{2} \partial t}}} \right) \cdot \sin \frac{i\pi x}{L}{\text{d}}x} } \\ & \quad - \int_{0}^{L} {\sum\limits_{i = 1}^{n} {\left( {Bf_{w} - \chi \left( {k_{1} w + k_{3} w^{3} + c_{1} \dot{w} + r_{21} w^{2} \dot{w} + r_{12} w\dot{w}^{2} } \right)} \right) \cdot \sin \frac{i\pi x}{L}{\text{d}}x} } = 0 \\ \end{aligned} $$
(15)

Expanding Eq. (15) yields a set of ordinary differential equations:

$$ \begin{aligned} & \eta_{1,i} \ddot{q}_{i} + \eta_{2,i} \dot{q}_{i} + \eta_{3,i} q_{i} - \eta_{4,i} f_{w} + \eta_{5,i} \\ & \quad \cdot \int_{0}^{L} {\sum\limits_{i = 1}^{n} {\chi \left( {k_{1} w + \overline{k}_{3} w^{3} + c_{1} \dot{w} + r_{21} w^{2} \dot{w} + r_{12} w\dot{w}^{2} } \right) \cdot \sin \frac{i\pi x}{L}{\text{d}}x} } = 0 \\ \end{aligned} $$
(16)

where \(\eta_{j,i}\) are the coefficients of the ODEs.

3.2 Harmonic balance method

The harmonic balance method combined with the presto-arc length method is adopted for the approximately analytical results. With the thought of harmonic balance, the displacement response can be expanded as

$$ q_{i} (t) = A_{i,0} + \sum\limits_{j = 1}^{{\hat{n}}} {\cos (j\omega t) \cdot C_{i,j} } + \sum\limits_{j = 1}^{{\hat{n}}} {\sin (j\omega t) \cdot S_{i,j} } $$
(17)

with j as the harmonic order. The \(A_{i,0}\), \(C_{i,j},\) and \(S_{i,j}\) are the constant terms, the coefficients of cosine and sine terms, respectively. The velocity and acceleration responses are given as

$$ \begin{aligned} \dot{q}_{i} (t) & = - \sum\limits_{j = 1}^{{\hat{n}}} {j\omega \sin (j\omega t) \cdot C_{i,j} } + \sum\limits_{j = 1}^{{\hat{n}}} {j\omega \cos (j\omega t) \cdot S_{i,j} } \\ \ddot{q}_{i} (t) & = - \sum\limits_{j = 1}^{{\hat{n}}} {j^{2} \omega^{2} \cos (j\omega t) \cdot C_{i,j} } - \sum\limits_{j = 1}^{{\hat{n}}} {j^{2} \omega^{2} \sin (j\omega t) \cdot S_{i,j} } \\ \end{aligned} $$
(18)

Since the order of the nonlinear restoring and damping force is 3, the constant terms and the second-order terms are omitted. The harmonic terms with j = 1,3 remain and are substituted into Eq. (16). After balancing the coefficients of all the harmonic terms, a set of nonlinear algebraic equations related to the coefficients are obtained. Following the presto-arc length method, the amplitude–frequency response curve can be easily obtained.

3.3 Analytical results

The response is measured at the position of 3/4L on the x-axis. Figure 5 demonstrates the amplitude response of the composite beam. The natural frequency of the composite laminated beam is 146.3 Hz. As illustrated in Fig. 5a, the NiTi-ST successfully reduced the vibration amplitude around the natural frequency. The S3b configuration demonstrates the best result and the resonance frequency is hardly changed. The S1a and S3a configurations show slightly softening behavior. The softening behavior is caused by the quasi-zero stiffness of S1a and S3a around the origin. The restoring force provided by S1a configuration mainly consists of cubic stiffness restoring force, and the S3a is affected by the pinching effect. When the excitation increases, as shown in Fig. 5b, S1a and S3a present jump phenomenon, while other configurations show softening behaviors which might be the contribution of hysteresis. Figure 6 presents the progress with the increment of the external load.

Fig. 5
figure 5

Vibration suppression effect of different NiTi-ST configurations under small and large external loads: a fw = 4 kPa, b fw = 16 kPa. Legend ‘Null’ represents the response of composite beam without NiTi-ST

Full size image
Fig. 6
figure 6

Softening and unstable behavior of configurations with the increment of external load form 4 to 16 kPa: a S1a, b S3b

Full size image

A parametric study is carried out for avoiding the jump phenomenon. In Fig. 7, the minus cubic term \(r_{12}\) is changed for S1a and S3b. As the absolute value of \(r_{12}\) decreased, the S1a configuration recovered. On the contrary, while increasing the absolute value of \(r_{12}\) for S3b, the jump phenomenon appears. It seems that the sudden increments of amplitude are caused by the flaws of reduced-order polynomial model rather than the nonlinearity of NiTi-ST. The polynomial models are only suitable for reporting nonlinear responses under reasonable excitation.

Fig. 7
figure 7

Amplitudes at resonance frequency with various parameters of r12: a S1a and b S3b

Full size image

The equivalent linear damping c1 is also studied as shown in Fig. 8. With the increment of c1, the ability of vibration reduction is enhanced, while the resonance frequency remains unchanged. The polynomial model contains many terms related to the velocity, while the equivalent damping term plays a major role in dissipating energy. Hysteresis damping features of NiTi-ST are described with other high-order terms, which contribute to energy dissipation less than linear damping c1.

Fig. 8
figure 8

Amplitudes at resonance frequency with various parameters of c1 for S2b configuration

Full size image

4 Numerical analysis

4.1 Domain decomposition

The domain decomposition approach is a truncation method based on the modified variational principle (MVP) and the least-square weight residual method (LSWRM). With the adoption of MVP, the enforcement of the interface and boundary constraints is released. What’s more, the discretized equations are convenient for numerical simulation. To obtain the time-domain response of the beam embedded with NiTi-ST, the domain decomposition is applied. The beam is decomposed into N subdomains on the x-direction, as shown in Fig. 9. Sub-coordinate \(o^{\prime} - \overline{x}\) is established in each subdomain.

Fig. 9
figure 9

Beam model discretized in the space domain

Full size image

The modified variational function \(\Pi\) is constructed as:

$$ \Pi = \sum\limits_{i = 1}^{N} {\left( {T_{i} - U_{i} + W_{f,i} + W_{st,i} } \right)} + \sum\limits_{i = 1}^{N - 1} {\left( {P_{\lambda }^{i,i + 1} - P_{\kappa }^{i,i + 1} } \right)} $$
(19)

where \(T_{i}\), \(U_{i}\), \(W_{f,i}\), and \(W_{st,i}\) are the kinetic energy, the strain energy, the work done by external loads, and the work done by the restoring and damping force provided by NiTi-ST, respectively. They can be easily obtained by replacing the general displacement w with the displacement of each segment \(w_{i}\) in Eq. (11). The subscript i represents the segment number. \(P_{\lambda }^{i,i + 1}\) and \(P_{\kappa }^{i,i + 1}\) are the potential energy of the virtual boundaries between the i and i + 1 segment, given as

$$ P_{\lambda }^{i,i + 1} = \left. {\left( {\xi_{w} \sigma_{w} \Theta_{w} + \xi_{r} \sigma_{r} \Theta_{r} } \right)} \right|_{{x = x_{i + 1} }} $$
(20)
$$ P_{\kappa }^{i,i + 1} = \frac{1}{2}\left. {\left( {\xi_{w} \kappa_{w} \Theta_{w}^{2} + \xi_{r} \kappa_{r} \Theta_{r}^{2} } \right)} \right|_{{x = x_{i + 1} }} $$
(21)

where \(\Theta_{w}\) and \(\Theta_{r}\) are the relevant continuity equations coordinating the displacements of two adjacent subdomains, written as:

$$ \Theta_{w} = w_{i} - w_{i + 1} ,\quad \Theta_{r} = \frac{{\partial w_{i} }}{\partial x} - \frac{{\partial w_{i + 1} }}{\partial x} $$
(22)

\(\sigma_{w}\) and \(\sigma_{r}\) are the Lagrange multipliers which can be recognized by setting the variation of Eq. (19) to zero:

$$ \sigma_{w} = - \frac{{\partial N_{x} }}{\partial x},\quad \sigma_{r} = N_{x} $$
(23)

\(\xi_{w}\) and \(\xi_{r}\) are the parameters controlling the boundary conditions. For two adjacent subdomains, the values of these parameters are set to be 1. For the real boundaries of the beam, the values are listed in Table 3.

Table 3 Values of boundary controlling parameters for beam boundary conditions
Full size table

To obtain the discretized governing equation of motion, the generalized displacement of each beam segment \(w_{i}\) is expanded with the Chebyshev orthogonal polynomial of the first kind (COPFK). The COPFK is given as

$$ \psi_{0} (\overline{x}) = 1,\quad \psi_{1} (\overline{x}) = \overline{x},\quad \psi_{i} (\overline{x}) = 2\overline{x}\psi_{i} (\overline{x}) - \psi_{i - 1} (\overline{x}) $$
(24)

where \(\overline{x}\) is the local displacement of ith segment, given as \(x = a_{0} \overline{x} + a_{1}\) with \(a_{0} = \left( {x_{i + 1} - x_{i} } \right)/2\) and \(a_{1} = \left( {x_{i + 1} + x_{i} } \right)/2\). Then, the displacement \(w_{i}\) can be written as

$$ w_{i} (\overline{x},t) = \sum\limits_{j = 0}^{P} {\psi_{i} (\overline{x})w_{j,i} (t)} = {\varvec{\psi}}(x){\varvec{w}}_{i} (t) $$
(25)

with P being the maximum number of COPFK terms. Substituting Eqs. (20), (21) and (25) into Eq. (19) and performing the variational operation with respect to the generalized coordinate vector w, one obtains the discretized governing equations of the composite beam embedded with NiTi-ST:

$$ {\mathbf{M}}{\ddot{\varvec{q}}} + {\mathbf{C}}{\dot{\varvec{q}}} + ({\mathbf{K}} - {\mathbf{K}}_{{{\varvec{\uplambda}}}} + {\mathbf{K}}_{\upkappa } ){\varvec{q}} = {\mathbf{F}}_{w} + {\mathbf{F}}_{st} $$
(26)

where q is the global generalized coordinate vector. M and K are, respectively, the disjoint generalized mass and stiffness matrices. C is the structural damping matrix of the composite beam, which is defined a s \(\eta {\mathbf{K}}\), \({\mathbf{K}}_{\lambda }\) and \({\mathbf{K}}_{\kappa }\) are the generalized stiffness matrices introduced by the MVP and LSWRM, respectively. \({\mathbf{F}}_{w}\) and \({\mathbf{F}}_{st}\) are the generalized force vector of external loads and the nonlinear restoring and damping force provided by NiTi-ST. Setting the truncation order N = 4 and P = 4, the visualized patterns of M, K, \({\mathbf{K}}_{\lambda }\) and \({\mathbf{K}}_{\kappa }\) are presented in Fig. 10.

Fig. 10
figure 10

Visualized pattern of matrices in Eq. (26): a M, b K, c \({\mathbf{K}}_{\lambda }\) and d \({\mathbf{K}}_{\kappa }\)

Full size image

4.2 Numerical results in the time domain

Since Eq. (26) is a set of nonlinear ODEs, the Newmark-β method combined with direct iteration procedures is applied to obtain the time-domain responses. The parameters for Newmark-β method are: α = 0.25, β = 0.5 and Δt = 10−4 s. The initial generalized displacement velocity and acceleration vectors are set to be zero vectors.

The Newmark-β method with direct iteration procedure can be expressed as follows:

  1. 1.

    Ignore the nonlinear restoring and damping force vector. Start the Newmark-β procedure with the governing equation \({\mathbf{M}}{\ddot{\varvec{q}}} + {\mathbf{C}}{\dot{\varvec{q}} + }({\mathbf{K - K}}_{{{\varvec{\uplambda}}}} +{\mathbf{K}}_{\upkappa } ){\varvec{q}} = {\mathbf{F}}_{w}\). Calculate the generalized coordinate vector \({\varvec{q}}_{t + \Delta t}^{i}\) (\(i \ge 1\)) of the next Newmark step;

  2. 2.

    Start the direct iteration procedure. The nonlinear restoring and damping force \({\mathbf{F}}_{st}^{i}\) is related to \({\varvec{q}}^{i}\). Calculate \({\mathbf{F}}_{st}^{i}\) with \({\varvec{q}}^{i}\) from the previous step. Replace the governing equation with \({\mathbf{M}}{\ddot{\varvec{q}}}^{i + 1} + {\mathbf{C}}\dot{\varvec{q}}^{i + 1} +({\mathbf{K - K}}_{{{\varvec{\uplambda}}}} +{\mathbf{K}}_{\upkappa } ){\varvec{q}}^{i + 1} ={\mathbf{F}}_{w} + {\mathbf{F}}_{st}^{i},\) and start the Newmark-β procedure again. The first nonlinear coordinate vector \({\varvec{q}}^{i + 1}\) can be obtained;

  3. 3.

    Repeat the iteration i times until \(\left| {{\varvec{q}}^{i + 1} - {\varvec{q}}^{i} } \right| < \varepsilon\). While the difference of the response in two adjacent iteration steps is smaller than the tolerance value, the response is considered to be the real nonlinear response of the step of the Newmark procedure.

  4. 4.

    Calculate the next Newmark step based on the previous nonlinear response until the whole procedure is over.

Figure 11 demonstrates the time history response of the composite beam embedded with different NiTi-ST and excited with 146.3 Hz harmonic load. The size of the excitation is 4 kPa, which is the same as the external load of Fig. 5a. The response is measured at the position of 3/4L on the x-axis. The results indicated that S1a and S3b configuration strongly reduced the amplitude of vibration to 11.93% and 12.20% near the resonance frequency. The S2b performs worst among all the NiTi-ST configurations with a suppression rate of 44.39%. Figure 12 shows the vibration suppression effect of the beam excited with 1000 Hz load. The NiTi-ST can suppress the vibration rapidly at a higher frequency.

Fig. 11
figure 11

Time-domain responses with excitations at 146.3 Hz of different configurations: a S1a, b S2a, c S2b, d S3a, e S3b and f S3c

Full size image
Fig. 12
figure 12

Time-domain responses with excitations at 1000 Hz of different NiTi-ST configurations: a S1a, b S2a, c S2b, d S3a, e S3b and f S3c

Full size image

4.3 Verifications of semi-analytical and numerical results

The verifications are obtained via the Runge–Kutta method with a simulation time set to be long enough for a steady-state response. The amplitude is determined as the maximum absolute displacement in the last several periods of the time history. The numerical solutions are compared with the analytical results in Fig. 5b and yield good agreements, as shown in Fig. 13.

Fig. 13
figure 13

Verifications of semi-analytical results presented in Fig. 5b

Full size image

Good agreements of the numerical results can also be observed from Fig. 14. The domain decomposition method combined with the Newmark-beta method is proved to be a promising approach for nonlinear vibration analysis of continuum.

Fig. 14
figure 14

Verification of time-domain numerical results with and without NiTi-ST: a at 143 Hz without NiTi-ST, b at 143 Hz with NiTi-ST, c at 760 Hz without NiTi-ST and d at 760 Hz with NiTi-ST

Full size image

5 Conclusion

The present study was designed to determine the vibration suppression effect and nonlinear behavior of NiTi-ST coupled to a composite beam. According to the semi-analytical and numerical results, the NiTi-ST can greatly reduce the vibration of the composite beam under harmonic excitations. Differences between NiTi-ST configurations are revealed by the polynomial model. The minus cubic term of the model determines the softening behavior and can lead to instability. The polynomial models are suitable for reporting nonlinear responses under reasonable excitation. The linear damping term contributes to the ability of vibration suppression. What’s more, the ability of the domain decomposition method dealing with nonlinear vibration problems is proved. The numerical results achieved good agreements with the Runge–Kutta method. The domain decomposition method combined with the Newmark-β method shows great convenience in composite structures. Other structures such as plates, cylinder shells, and conical shells embedded with NiTi-ST may also be analyzed with this method.

This work is just the beginning of vibration suppression using NiTi-ST. Unfortunately, the study carried out numerical verifications only. The thermomechanical coupling behavior of NiTi-ST is ignored. Further researches and experiments are required to determine the accuracy of this coupled model and explore the practical vibration suppression application for more structures.