1 Introduction

As a kind of designable material structure, composite laminated shells are widely used in aerospace engineering. One representative application is the fairing shell of a rocket launcher. The fairing shell consists of a cylindrical section, a frustoconical section, and a nose. The complex working environment requires fairing with high strength, lightweight, corrosion resistance, and impact resistance. However, although the composite laminated shells can meet the strength requirement, low-frequency longitudinal coupled vibration often occurs during rocket launching. The vibration not only damages the interior spacecraft but also causes extreme discomfort to the astronauts, the understanding and reductions in layered and composite shells vibration have become a significant issue in the aerospace field.

Although the vibrations of composite laminated plates and shells have been widely investigated, as comprehensively reviewed by Sayyad et al. [1, 2] and Kumar et al. [3], the investigations on vibration reduction in composite shells are somewhat limited. All available works on composite laminated plates are active vibration control. In many practical circumstances including spacecraft launching, passive vibration reductions are feasible and reliable. Caresta et al. [4] proposed a passive vibration isolation method to reduce the radiated sound pressure of a submarine modeled as a reinforced cylindrical hull and revealed the effectiveness of the passive isolation of the end cap from the main hull. Gao et al. [5] proposed a passive vibration reduction method by depositing a hard coating on both sides of a composite laminated cylindrical shell. Cao et al. [6] investigated the free vibration of a cylindrical shell with passive damping layers and the influence of damping layer thickness on frequency parameters and loss factors. Zheng et al. [7] investigated the passive vibration reduction and the layout optimization of cylindrical shells embedded with passive constrained damping layer (PCDL) under broadband transverse excitation. Zheng et al. [8] investigated the dynamic characteristics of a cylindrical shell embedded with multiple passive damping layers (MPCDL) and demonstrated the improvement of vibration suppression due to the increased layers. Niu et al. [9] investigated the mixed vibration control of cylindrical shells by electromagnetic confinement layer damping (EMCLD) consisting of an electromagnet layer, permanent magnet layer, and viscoelastic damping layer. They demonstrated the apparent energy dissipation in the passive mode of the EMCLD. Plattenburg et al. [10] designed a dimensionless performance index to compare the responses of the same thin cylindrical shell under active vibration reduction and passive vibration reduction, respectively, and proposed a vibration control design scheme finally. Huang et al. [11] introduced the curved beam periodic structure into the transmission path of the internal vibration isolation system to reduce the vibration of the receiving column shell structure in a passive broadband manner. Abdoun et al. [12] investigated the passive vibration control, response curve and equivalent damping characteristics of a sandwich viscoelastic shell in a large frequency range. Jin et al. [13] established a three-layer passive constrained damping layer (PCDL) cylindrical shell with a general elastic constrained boundary and investigated its passive vibration reduction characteristics. Finally, the effects of layer thickness and shear parameters on natural frequency and loss factor were explained in detail. Deng et al. [14] verified that the acoustic black hole (ABH) is a very effective passive vibration reduction method for cylindrical shells. Actually, the passive control of cylindrical shells is rare. No research has been reported on the passive control of composite laminated cylindrical shells.

Among various passive vibration reduction approaches, shape memory alloy (SMA) can serve as a nonlinear damper. NiTiNOL-steel wire ropes belong to novel SMA. It is made of multiple wire ropes twisted together. Different wire numbers and twisting methods can form different types of wire ropes. They all have shape memory properties, high strength, pseudoelasticity, and high damping provided by mutual frictions among the wires [15,16,17]. Generally, the investigation on shape memory alloy are based on various constitutive models reflecting its super elasticity and hysteresis. For example, Pariza et al. [18] developed the Brinson model to express its constitutive relation to investigate the buckling problem of shape memory alloy plates subjected to uniform and linearly distributed in-plane loads. Nekouei et al. [19, 20] used Brinson's one-dimensional constitutive law to explore the dynamic behavior of shape memory carbon fiber reinforced laminated composite cylindrical shells and conical shells under uniform temperature change, and found that a small amount of carbon fiber could improve the Fundamental frequency and vibration control. However, a NiTiNOL-steel wire rope is usually regarded as a nonlinear damping device, with constitutive models yielding the restoring and damping forces that are experimental defined. Carboni et al. [21, 22] proposed a new absorber based on the restoring and damping force of NiTiNOL-steel wire rope, designed a set of devices to extend the Bouc-Wen model through experiments, and obtained the restoring and damping force model of NiTiNOL-steel wire rope. Carboni et al. [23, 24] established a nonlinear hysteresis beam model based on geometrically accurate plane beam theory, combined it with the Bouc-Wen model, and finally added the hysteresis behavior to the restoring and damping force model of NiTiNOL-steel wire rope. Niu et al. [25] proposed a nonlinear vibration isolator composed of a compliant mechanism with negative stiffness and a wire rope with hysteresis damping. Zhang et al. [26] proposed a novel nonlinear energy sink device for spacecraft, and the damping is produced by NiTiNOL-steel wire ropes. The generalized vibration transmissibility is used to describe the vibration isolation effect of the device, and the research shows that the device can effectively reduce the excessive vibration of the spacecraft. Zheng et al. [27] coupled NiTiNOL-steel wire rope as a nonlinear damper with the composite laminated beam model to suppress the vibration of the laminated composite beams. The amplitude-frequency responses curve obtained by the Galerkin method and the harmonic balance method demonstrated the vibration reduction effectiveness of the NiTiNOL-steel wire rope. As a nonlinear damping, NiTiNOL-steel wire ropes are limited to reduce vibration of composite laminated beams. It is not clear if NiTiNOL-steel wire ropes can work more sophisticated models such as a composite laminated shell. To explore the possibility, the present investigation focuses on the passive vibration reduction in a composite laminated cylindrical shell with embedded NiTiNOL-steel wire ropes.

The organization of this manuscript is as follows. Section 2 develops the dynamic model of a composite laminated cylindrical shell embedded with the NiTiNOL-steel wire ropes. Section 3 solves the Galerkin truncated governing equations with the finite element validations and examines the effects of different NiTiNOL-steel wire ropes parameters on vibration reduction. Section 4 ends the manuscript with concluding remarks.

2 Formulations

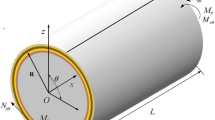
Consider a composite laminated cylindrical shell (CLCS) with the length \(L\), the radius \(R\), and the thickness \(h\), and four NiTiNOL-steel steel wire ropes. Four NiTiNOL-steel wire ropes are distributed on the mid-surface of the CLCS in a 90-ring array.

As shown in Fig. 1a, a cylindrical coordinate system is located at the center of the CLCS, where \(x = 0\). The structure is axisymmetric, but its deformation is asymmetric because its vibration mode has both beam bending mode and shell breathing mode. The displacements of arbitrary points on the shell are determined by three independent coordinate components \(x\), \(\theta\), and \(z\). The coordinates \(x\), \(\theta\), and \(z\) represent the axial, circumferential and radial directions of the cylindrical coordinate system, respectively. Internal forces of the CLCS are axial force \(N_{xx}\), bending moment \(M_{xx}\) and \(M_{\theta \theta }\), transverse shear force \(Q_{x}\) and \(Q_{\theta }\), circumferential shear force \(N_{x\theta }\), torsional moment \(M_{x\theta }\). Displacements \(u\), \(v\), \(w\) of arbitrary points on the CLCS are in the axial, the circumferential and the radial directions, respectively. As shown in Fig. 1b, four NiTiNOL-steel wire ropes are located on the mid-surface of the CLCS symmetrically along the axial direction.

Fig. 1
figure 1

Composite laminated cylindrical shell embedded with NiTiNOL-steel ropes; a Composite laminated cylindrical shell b The NiTiNOL-steel wire ropes layout

Full size image

2.1 Coordinating equation and constitutive equation

According to Donnell’s first-order shear deformation theory, the displacement of an arbitrary point on the CLCS can be assumed to be

$$ u\left( {x,\theta ,z,t} \right) = u_{0} \left( {x,\theta ,t} \right) + z\varphi_{x} \left( {x,\theta ,t} \right), $$
(1a)
$$ v\left( {x,\theta ,z,t} \right) = v_{0} \left( {x,\theta ,t} \right) + z\varphi_{\theta } \left( {x,\theta ,t} \right), $$
(1b)
$$ w\left( {x,\theta ,z,t} \right) = w_{0} \left( {x,\theta ,t} \right) $$
(1c)

where \(u_{0}\), \(v_{0}\), \(w_{0}\) are the axial, the circumferential and the radial displacements of arbitrary points on the mid-surface of the CLCS, \(\varphi_{x}\) and \(\varphi_{\theta }\) represent the rotation angles of the transverse normal respect to the \(x\)-axis and \(\theta\)-axis.

Similarly, the strain at an arbitrary point on the CLCS obeys the following relationship with the strain at an arbitrary point on the mid-surface of the CLCS

$$ \varepsilon_{xx} = \varepsilon_{xx,0} + z\chi_{xx} , $$
(2a)
$$ \varepsilon_{\theta \theta } = \varepsilon_{\theta \theta ,0} + z\chi_{\theta \theta } , $$
(2b)
$$ \gamma_{x\theta } = \gamma_{x\theta ,0} + z\chi_{x\theta } $$
(2c)

where \(\varepsilon_{xx,0}\), \(\varepsilon_{\theta \theta ,0}\) and \(\gamma_{x\theta ,0}\) are the strain at an arbitrary point on the mid-surface, \(\chi_{xx}\), \(\chi_{\theta \theta }\), and \(\chi_{x\theta }\) are the curvature changes and satisfying

$$ \chi_{xx} = \frac{{\partial \varphi_{x} }}{\partial x} = - \frac{{\partial^{2} w}}{{\partial x^{2} }}, $$
(3a)
$$ \chi_{\theta \theta } = \frac{{\partial \varphi_{\theta } }}{R\partial \theta } = - \frac{{\partial^{2} w}}{{R^{2} \partial \theta^{2} }}, $$
(3b)
$$ \chi_{x\theta } = \frac{{\partial \varphi_{x} }}{R\partial \theta } + \frac{{\partial \varphi_{\theta } }}{\partial x} = - \frac{{2\partial^{2} w}}{R\partial x\partial \theta } $$
(3c)

For small deformations, the coordination equation of arbitrary points on the mid-surface of the CLCS can be simplified as

$$ \varepsilon_{xx,0} = \frac{{\partial u_{0} }}{\partial x}, $$
(4a)
$$ \varepsilon_{\theta \theta ,0} = \frac{{\partial v_{0} }}{R\partial \theta } + \frac{{w_{0} }}{R}, $$
(4b)
$$ \gamma_{x\theta ,0} = \frac{{\partial v_{0} }}{\partial x} + \frac{{\partial u_{0} }}{R\partial \theta } $$
(4c)

The constitutive relationship of a single layer \(z_{k} < z < z_{k + 1}\) is considered. The generalized Hooke's law leads to the stress–strain relationship

$$ \left\{ {\begin{array}{*{20}c} {\sigma_{xx} } \\ {\sigma_{\theta \theta } } \\ {\tau_{x\theta } } \\ \end{array} } \right\}^{\left( k \right)} = \left[ {\begin{array}{*{20}c} {\overline{Q}_{11} } & {\overline{Q}_{12} } & {\overline{Q}_{16} } \\ {\overline{Q}_{21} } & {\overline{Q}_{22} } & {\overline{Q}_{26} } \\ {\overline{Q}_{61} } & {\overline{Q}_{62} } & {\overline{Q}_{66} } \\ \end{array} } \right]^{\left( k \right)} \left\{ {\begin{array}{*{20}c} {\varepsilon_{xx} } \\ {\varepsilon_{\theta \theta } } \\ {\gamma_{x\theta } } \\ \end{array} } \right\}^{\left( k \right)} $$
(5)

where \(k\) represents the \(k{\text{th}}\) layer, \({\overline{\mathbf{Q}}}^{{\left( {\text{k}} \right)}}\) is the transformation stiffness matrix for the stress–strain relationship of the \(k{\text{th}}\) layer. For orthotropic materials, the transformation stiffness matrix can be expressed as [28]

$$ \left[ {\begin{array}{*{20}c} {\overline{Q}_{11} } & {\overline{Q}_{12} } & {\overline{Q}_{16} } \\ {\overline{Q}_{21} } & {\overline{Q}_{22} } & {\overline{Q}_{26} } \\ {\overline{Q}_{61} } & {\overline{Q}_{62} } & {\overline{Q}_{66} } \\ \end{array} } \right]^{\left( k \right)} = {\mathbf{T}}\left[ {\begin{array}{*{20}c} {Q_{11} } & {Q_{12} } & 0 \\ {Q_{21} } & {Q_{22} } & 0 \\ 0 & 0 & {\overline{Q}_{66} } \\ \end{array} } \right]^{\left( k \right)} {\mathbf{T}}^{{\text{T}}} $$
(6)

where \({\mathbf{Q}}^{{\left( {\text{k}} \right)}}\) is the stiffness matrix, \({\mathbf{T}}\) is the transformation matrix. \({\mathbf{T}}\) can be written as

$$ T = \left[ {\begin{array}{*{20}c} {\cos^{2} \left( \alpha \right)} & {\sin^{2} \left( \alpha \right)} & { - 2\cos \left( \alpha \right)\sin \left( \alpha \right)} \\ {\sin^{2} \left( \alpha \right)} & {\cos^{2} \left( \alpha \right)} & {2\cos \left( \alpha \right)\sin \left( \alpha \right)} \\ {\cos \left( \alpha \right)\sin \left( \alpha \right)} & { - \cos \left( \alpha \right)\sin \left( \alpha \right)} & {\cos^{2} \left( \alpha \right) - \sin^{2} \left( \alpha \right)} \\ \end{array} } \right] $$
(7)

where \(\alpha\) is the angle between the principle direction of a layer of the CLCS and the \(x\)-axis. The coefficients \(Q_{ij}^{\left( k \right)}\) in the stiffness matrix can be expressed as

$$ Q_{11}^{\left( k \right)} = \frac{{E_{1} }}{{1 - \mu_{12} \mu_{21} }},Q_{12}^{\left( k \right)} = Q_{21}^{(k)} = \frac{{\mu_{12} E_{2} }}{{1 - \mu_{12} \mu_{21} }},Q_{22}^{\left( k \right)} = \frac{{E_{2} }}{{1 - \mu_{12} \mu_{21} }},Q_{66}^{\left( k \right)} = G_{12} $$
(8)

Among them, \(E_{1}\) and \(E_{2}\) represent the Young's elasticity modulus of a layer of materials in the principle direction, and \(\mu_{21}\) and \(\mu_{21}\) are the corresponding Poisson ratios, and \(G_{12}\) is the moduli of rigidity. It is worth noting that \(E_{1} \ne E_{2}\) for anisotropic materials, but \(E_{1} \mu_{21} = E_{2} \mu_{12}\).

2.2 Internal force equation

By integrating the stress in Eq. (5) on the section of the cylindrical shell and in the thickness direction, the internal forces and moments on the mid-surface of the CLCS are

$$ \left\{ {\begin{array}{*{20}c} {N_{xx} } \\ {N_{\theta \theta } } \\ {N_{x\theta } } \\ {M_{xx} } \\ {M_{\theta \theta } } \\ {M_{x\theta } } \\ \end{array} } \right\} = \left[ {\begin{array}{*{20}c} {A_{11} } & {A_{12} } & 0 & {B_{11} } & {B_{12} } & 0 \\ {A_{21} } & {A_{22} } & 0 & {B_{21} } & {B_{22} } & 0 \\ 0 & 0 & {A_{66} } & 0 & 0 & {B_{66} } \\ {B_{11} } & {B_{12} } & 0 & {D_{11} } & {D_{12} } & 0 \\ {B_{21} } & {B_{22} } & 0 & {D_{21} } & {D_{22} } & 0 \\ 0 & 0 & {B_{66} } & 0 & 0 & {D_{66} } \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {\varepsilon_{xx,0} } \\ {\varepsilon_{\theta \theta ,0} } \\ {\gamma_{x\theta ,0} } \\ {\chi_{xx} } \\ {\chi_{\theta \theta } } \\ {\chi_{x\theta } } \\ \end{array} } \right\} $$
(9)

\(A_{ij}\), \(B_{ij}\) and \(D_{ij}\) are, respectively, the stretch, the coupling and the bending stiffness coefficients with

$$ A_{ij} = \sum\limits_{k = 1}^{N} {\overline{Q}_{ij}^{k} } \left( {z_{k + 1} - z_{k} } \right),B_{ij} = \frac{1}{2}\sum\limits_{k = 1}^{N} {\overline{Q}_{ij}^{k} } \left( {z_{k + 1}^{2} - z_{k}^{2} } \right),D_{ij} = \frac{1}{3}\sum\limits_{k = 1}^{N} {\overline{Q}_{ij}^{k} } \left( {z_{k + 1}^{3} - z_{k}^{3} } \right) $$
(10)

where \(N\) is the total number of layers. Substituting Eqs. (4a–4c) and (3a–3c) into Eq. (9) yields the internal force equation

$$ N_{xx} = A_{11} \frac{{\partial u_{0} }}{\partial x} + A_{12} \left( {\frac{{\partial v_{0} }}{R\partial \theta } + \frac{{w_{0} }}{R}} \right) + B_{11} \frac{{\partial \varphi_{x} }}{\partial x} + B_{12} \frac{{\partial \varphi_{\theta } }}{R\partial \theta }, $$
(11a)
$$ N_{\theta \theta } = A_{12} \frac{{\partial u_{0} }}{\partial x} + A_{22} \left( {\frac{{\partial v_{0} }}{R\partial \theta } + \frac{{w_{0} }}{R}} \right) + B_{12} \frac{{\partial \varphi_{x} }}{\partial x} + B_{22} \frac{{\partial \varphi_{\theta } }}{R\partial \theta }, $$
(11b)
$$ N_{x\theta } = A_{66} \left( {\frac{{\partial v_{0} }}{\partial x} + \frac{{\partial u_{0} }}{R\partial \theta }} \right) + B_{66} \left( {\frac{{\partial \varphi_{x} }}{R\partial \theta } + \frac{{\partial \varphi_{\theta } }}{\partial x}} \right), $$
(11c)
$$ M_{xx} = B_{11} \frac{{\partial u_{0} }}{\partial x} + B_{12} \left( {\frac{{\partial v_{0} }}{R\partial \theta } + \frac{{w_{0} }}{R}} \right) + D_{11} \frac{{\partial \varphi_{x} }}{\partial x} + D_{12} \frac{{\partial \varphi_{\theta } }}{R\partial \theta }, $$
(11d)
$$ M_{\theta \theta } = B_{12} \frac{{\partial u_{0} }}{\partial x} + B_{22} \left( {\frac{{\partial v_{0} }}{R\partial \theta } + \frac{{w_{0} }}{R}} \right) + D_{12} \frac{{\partial \varphi_{x} }}{\partial x} + D_{22} \frac{{\partial \varphi_{\theta } }}{R\partial \theta }, $$
(11e)
$$ M_{x\theta } = B_{66} \left( {\frac{{\partial v_{0} }}{\partial x} + \frac{{\partial u_{0} }}{R\partial \theta }} \right) + D_{66} \left( {\frac{{\partial \varphi_{x} }}{R\partial \theta } + \frac{{\partial \varphi_{\theta } }}{\partial x}} \right). $$
(11f)

2.3 Application of the generalized Hamilton’s principle

The high damping property of NiTiNOL-steel wire rope is the key to reduce the shell vibration. Its restoring and damping force model is necessary. A NiTiNOL-steel wire rope is treated as a nonlinear damping device. The restoring and damping force of the NiTiNOL-steel wire rope is constituted by the polynomial fitting of the extended Bouc-Wen model. The extended Bouc-Wen model reflects the loading and unloading process of the NiTiNOL-steel wire rope with different configurations under static force through experiments, and the parameters of the restoring force are determined via its hysteresis curve. Carboni et al. [18,19,20,21] revealed the nonlinear mechanical hysteresis characteristics of NiTiNOL-steel wire ropes by experimental investigations, and obtained the restoring and damping force equation of NiTiNOL-steel wire ropes via the extension of the Bouc-Wen model with identified parameters of various configurations of NiTiNOL-steel wire ropes. The restoring and damping force \(f_{{{\text{st}}}}\) is [21]

$$ f_{{{\text{st}}}} = \left( {1 - r} \right)k_{{\text{c}}} w^{3} + r\left( {k_{{\text{e}}} w + z} \right) $$
(12)

where \(z\) is the hysteresis

$$ \left\{ {\begin{array}{*{20}l} {\frac{{{\text{d}}z}}{{{\text{d}}x}} = \left[ {k_{{\text{d}}} h\left( x \right) - \left( {\gamma + \beta {\text{sgn}} \left( {z\frac{{{\text{d}}w}}{{{\text{d}}x}}} \right)} \right)\left| z \right|^{n} } \right]\frac{{{\text{d}}w}}{{{\text{d}}x}}} \hfill \\ {h\left( x \right) = 1 - \xi {\text{e}}^{{ - \frac{{{\text{w}}^{2} }}{{{\text{w}}_{{\text{c}}} }}}} } \hfill \\ \end{array} } \right. $$
(13)

To deal with transcendental functions in Eq. (12) with Eq. (13), the restoring and damping force \(f_{{\text{st}}}\) is fitted into a polynomial

$$ f_{{{\text{st}}}} = k_{1} w_{0} + k_{3} w_{0}^{3} + c_{1} \frac{{\partial w_{0} }}{\partial t} + r_{21} w_{0}^{2} + r_{12} w_{0} \left( {\frac{{\partial w_{0} }}{\partial t}} \right)^{2} $$
(14)

where \(k_{1}\), \(k_{3}\), \(c_{1}\), \(r_{21}\) and \(r_{12}\) are polynomial fitting coefficients. Table 1 shows the fitted coefficient values of several configurations of NiTiNOL-steel wire ropes.

Table 1 Fitting coefficient values of several NiTiNOL-steel configurations [29]
Full size table

To establish the equation of motion via the generalized Hamilton’s principle, it is necessary to obtain the strain energy, the kinetic energy and the work done by an external force. The total strain energy of the CLCS is

$$ U = \frac{1}{2}\int_{S} {\left( {N_{xx,0} \varepsilon_{xx,0} + N_{\theta \theta ,0} \varepsilon_{\theta \theta ,0} + N_{x\theta ,0} \varepsilon_{x\theta ,0} + M_{xx} \chi_{xx} + M_{\theta \theta } \chi_{\theta \theta } + M_{x\theta } \chi_{x\theta } } \right){\text{d}}S} $$
(15)

where \(S\) represents the area of the mid-surface. The total strain energy of the CLCS can be divided into stretch strain energy \(U_{{\text{s}}}\), bending strain energy \(U_{{\text{b}}}\) and coupling strain energy \(U_{{\text{c}}}\) [29]. Substituting Eqs. (11a–11f), (3a–3c) and (4a–4c) into Eq. (15) leads to

$$ \begin{aligned} U_{{\text{s}}} = & \frac{1}{2}\int_{0}^{2\pi } {\int_{0}^{L} {\int_{{ - \frac{h}{2}}}^{\frac{h}{2}} {\left[ {A_{11} \left( {\frac{{\partial u_{0} }}{\partial x}} \right)^{2} + 2A_{12} \left( {\frac{{\partial v_{0} }}{R\partial \theta } + \frac{{w_{0} }}{R}} \right)\frac{{\partial u_{0} }}{\partial x} + A_{22} \left( {\frac{{\partial v_{0} }}{R\partial \theta } + \frac{{w_{0} }}{R}} \right)^{2} } \right.} } } \\ & \left. { + \;A_{66} \left( {\frac{{\partial v_{0} }}{\partial x} + \frac{{\partial u_{0} }}{R\partial \theta }} \right)^{2} } \right]R{\text{d}}z{\text{d}}\theta {\text{d}}x, \\ \end{aligned} $$
(16a)
$$ \begin{aligned} U_{{\text{b}}} = & \frac{1}{2}\int_{0}^{2\pi } {\int_{0}^{L} {\int_{{ - \frac{h}{2}}}^{\frac{h}{2}} {\left[ {D_{11} \left[ {\left( {\frac{{\partial \varphi_{x} }}{\partial x}} \right)^{2} + \frac{{\partial \varphi_{x} }}{\partial x}\frac{{\partial \varphi_{\theta } }}{R\partial \theta }} \right] + \frac{{2D_{12} }}{R}\frac{{\partial \varphi_{\theta } }}{\partial \theta }\frac{{\partial \varphi_{x} }}{\partial x}} \right.} } } \\ & \left. { + \;\frac{{D_{22} }}{{R^{2} }}\left( {\frac{{\partial \varphi_{\theta } }}{\partial \theta }} \right)^{2} + D_{66} \left( {\frac{{\partial \varphi_{x} }}{R\partial \theta } + \frac{{\partial \varphi_{\theta } }}{\partial x}} \right)^{2} } \right]R{\text{d}}z{\text{d}}\theta {\text{d}}x, \\ \end{aligned} $$
(16b)
$$ \begin{aligned} U_{{\text{c}}} = & \frac{1}{2}\int_{0}^{2\pi } {\int_{0}^{L} {\int_{{ - \frac{h}{2}}}^{\frac{h}{2}} {\left[ {2B_{11} \frac{{\partial u_{0} }}{\partial x}\frac{{\partial \varphi_{x} }}{\partial x} + \frac{{2B_{22} }}{{R^{2} }}\left( {\frac{{\partial v_{0} }}{\partial \theta } + w_{0} } \right)\frac{{\partial \varphi_{\theta } }}{\partial \theta } + \frac{{2B_{12} }}{R}\frac{{\partial \varphi_{\theta } }}{\partial \theta }\frac{{\partial u_{0} }}{\partial x}} \right.} } } \\ & \left. { + \;\frac{{2B_{12} }}{R}\left( {\frac{{\partial v_{0} }}{\partial \theta } + w_{0} } \right)\frac{{\partial \varphi_{x} }}{\partial x} + 2B_{66} \left( {\frac{{\partial \varphi_{x} }}{R\partial \theta } + \frac{{\partial \varphi_{\theta } }}{\partial x}} \right)\left( {\frac{{\partial v_{0} }}{\partial x} + \frac{{\partial u_{0} }}{R\partial \theta }} \right)} \right]R{\text{d}}z{\text{d}}\theta {\text{d}}x. \\ \end{aligned} $$
(16c)

The total kinetic energy \(T\) of the CLCS can also be divided into three components: translational kinetic energy \(T_{{\text{t}}}\), rotational kinetic energy \(T_{{\text{r}}}\), and coupled kinetic energy \(T_{{\text{c}}}\) [29]. They can be expressed as

$$ T_{t} = \frac{1}{2}\int_{0}^{2\pi } {\int_{0}^{L} {\int_{{ - \frac{h}{2}}}^{\frac{h}{2}} {\left[ {\left( {\frac{{\partial u_{0} }}{\partial t}} \right)^{2} + \left( {\frac{{\partial v_{0} }}{\partial t}} \right)^{2} + \left( {\frac{{\partial w_{0} }}{\partial t}} \right)^{2} } \right]\left( {\sum\limits_{k = 1}^{N} {\int_{{z_{k} }}^{{z_{k + 1} }} {\rho_{k} } } } \right)R{\text{d}}z{\text{d}}\theta {\text{d}}x} } } , $$
(17a)
$$ T_{r} = \frac{1}{2}\int_{0}^{2\pi } {\int_{0}^{L} {\int_{{ - \frac{h}{2}}}^{\frac{h}{2}} {\left[ {\frac{{\partial \varphi_{x} }}{\partial t} + \frac{{\partial \varphi_{\theta } }}{\partial t}} \right]\left( {\sum\limits_{k = 1}^{N} {\int_{{z_{k} }}^{{z_{k + 1} }} {\rho_{k} z^{2} } } } \right)} } } R{\text{d}}z{\text{d}}\theta {\text{d}}x, $$
(17b)
$$ T_{c} = \frac{1}{2}\int_{0}^{2\pi } {\int_{0}^{L} {\int_{{ - \frac{h}{2}}}^{\frac{h}{2}} {\left[ {\frac{{\partial u_{0} }}{\partial t}\frac{{\partial \varphi_{x} }}{\partial t} + \frac{{\partial v_{0} }}{\partial t}\frac{{\partial \varphi_{\theta } }}{\partial t}} \right]\left( {\sum\limits_{k = 1}^{N} {\int_{{z_{k} }}^{{z_{k + 1} }} {\rho_{k} z} } } \right)} } } R{\text{d}}z{\text{d}}\theta {\text{d}}x. $$
(17c)

Potential energy \(V\) yielded by restoring and damping force of NiTiNOL-steel wire ropes is

$$ V = \int_{0}^{L} {4\eta f_{{{\text{st}}}} w_{0} } {\text{d}}x $$
(18)

where \(F_{0}\) is the amplitude of basic excitation, \(f_{0}\) is the frequency of basic excitation, and \(\eta = 0.2\) is the NiTiNOL-steel modifying parameter.

The boundary potential energy \(U_{{\text{p}}}\) of CLCS can also be defined as [39]

$$ \begin{aligned} U_{{\text{p}}} = & \frac{1}{2}\int_{0}^{2\pi } {\int_{{ - \frac{h}{2}}}^{\frac{h}{2}} {\left( {k_{u0} u_{0}^{2} + k_{v0} v_{0}^{2} + k_{w0} w_{0}^{2} + K_{x0} \varphi_{x}^{2} } \right.} } \\ & \left. { + \;k_{{{\text{uL}}}} u_{0}^{2} + k_{{{\text{vL}}}} v_{0}^{2} + k_{{{\text{wL}}}} w_{0}^{2} + K_{{{\text{xL}}}} \varphi_{\theta }^{2} } \right){\text{d}}z{\text{d}}\theta \\ \end{aligned} $$
(19)

where \(k_{{{\text{u0}}}}\) is the linear axial spring stiffness coefficient, \(k_{{{\text{v0}}}}\) is the linear circumferential spring stiffness coefficient, \(k_{{{\text{w0}}}}\) is the linear radial spring stiffness coefficient, and \(K_{{{\text{x0}}}}\) is the linear torsion spring stiffness coefficient where \(x = 0\). \(k_{{{\text{uL}}}}\) is the linear axial spring stiffness coefficient, \(k_{{{\text{vL}}}}\) is the linear circumferential spring stiffness coefficient, \(k_{{{\text{wL}}}}\) is the linear radial spring stiffness coefficient, and \(K_{{{\text{xL}}}}\) is the linear torsion spring stiffness coefficient where \(x = L\).

The work done by the external harmonic excitation \(f = F_{0} \sin \left( {2\pi f_{0} t} \right)\) on the bottom surface of the CLCS can be calculated as

$$ W_{f} = \int_{0}^{2\pi } {F_{0} \sin \left( {2\pi f_{0} t} \right)u_{0} R{\text{d}}\theta } $$
(20)

Simply supported at both ends (SS-SS), fixed at one end and free at the other (C-F) are investigated. According to the generalized Hamilton’s principle

$$ \int_{{t_{1} }}^{{t_{2} }} {\left[ {\delta \left( {T - V - U} \right) + \delta W} \right]} \;{\text{d}}t = 0 $$
(21)

Substituting Eqs. (16a–16c), (17a–17c), (18) and (20) into Eq. (21), the variation of the total kinetic energy of the CLCS is obtained

$$ \begin{aligned} \delta T = & \int_{0}^{2\pi } {\int_{0}^{L} {\int_{{ - \frac{h}{2}}}^{\frac{h}{2}} {\left\{ {\left[ {\frac{{\partial u_{0} }}{\partial t}\delta \left( {\frac{{\partial u_{0} }}{\partial t}} \right) + \frac{{\partial v_{0} }}{\partial t}\delta \left( {\frac{{\partial v_{0} }}{\partial t}} \right) + \frac{{\partial w_{0} }}{\partial t}\delta \left( {\frac{{\partial w_{0} }}{\partial t}} \right)} \right]I_{0} } \right.} } } \\ & + \;\frac{1}{2}\left[ {\left( {\frac{{\partial \varphi_{x} }}{\partial t}\delta \left( {\frac{{\partial u_{0} }}{\partial t}} \right) + \frac{{\partial u_{0} }}{\partial t}\delta \left( {\frac{{\partial \varphi_{x} }}{\partial t}} \right)} \right)} \right.\left. { + \left( {\frac{{\partial \varphi_{\theta } }}{\partial t}\delta \left( {\frac{{\partial v_{0} }}{\partial t}} \right) + \frac{{\partial v_{0} }}{\partial t}\delta \left( {\frac{{\partial \varphi_{\theta } }}{\partial t}} \right)} \right)} \right]I_{1} \\ & \left. { + \;\frac{1}{2}\left[ {\left( {\delta \left( {\frac{{\partial \varphi_{x} }}{\partial t}} \right) + \delta \left( {\frac{{\partial \varphi_{\theta } }}{\partial t}} \right)} \right)I_{2} } \right]} \right\}R{\text{d}}z{\text{d}}\theta {\text{d}}x \\ \end{aligned} $$
(22)

The variation of the total strain energy of the CLCS is obtained

$$ \delta U = \delta U_{{\text{s}}} + \delta U_{{\text{b}}} + \delta U_{{\text{c}}} $$
(23)

where

$$ \begin{aligned} \delta U_{s} = & \int_{0}^{2\pi } {\int_{0}^{L} {\int_{{ - \frac{h}{2}}}^{\frac{h}{2}} {\left[ {A_{11} \frac{{\partial u_{0} }}{\partial x}\delta \left( {\frac{{\partial u_{0} }}{\partial x}} \right) + A_{12} \left( {\frac{1}{R}\delta \left( {\frac{{\partial v_{0} }}{\partial \theta }} \right) + \frac{1}{R}\delta w_{0} } \right)\frac{{\partial u_{0} }}{\partial x}} \right.} } } \\ & + \;A_{12} \left( {\frac{{\partial v_{0} }}{R\partial \theta } + \frac{{w_{0} }}{R}} \right)\delta \left( {\frac{{\partial u_{0} }}{\partial x}} \right) + A_{22} \left( {\frac{{\partial v_{0} }}{R\partial \theta } + \frac{{w_{0} }}{R}} \right)\left( {\frac{1}{R}\delta \left( {\frac{{\partial v_{0} }}{\partial \theta }} \right) + \frac{1}{R}\delta w_{0} } \right) \\ & \left. { + \;A_{66} \left( {\frac{{\partial v_{0} }}{\partial x} + \frac{{\partial u_{0} }}{R\partial \theta }} \right)\left( {\delta \left( {\frac{{\partial v_{0} }}{\partial x}} \right) + \frac{1}{R}\delta \left( {\frac{{\partial u_{0} }}{\partial \theta }} \right)} \right)} \right]{\text{d}}z{\text{d}}\theta {\text{d}}x, \\ \end{aligned} $$
(24a)
$$ \begin{aligned} \delta U_{{\text{b}}} = & \int_{0}^{2\pi } {\int_{0}^{L} {\int_{{ - \frac{h}{2}}}^{\frac{h}{2}} {\left\{ {D_{11} \frac{{\partial \varphi_{x} }}{\partial x}\delta \left( {\frac{{\partial \varphi_{x} }}{\partial x}} \right) + \frac{{D_{11} }}{2}\left[ {\frac{{\partial \varphi_{\theta } }}{R\partial \theta }\delta \left( {\frac{{\partial \varphi_{x} }}{\partial x}} \right) + \frac{{\partial \varphi_{x} }}{\partial x}\frac{1}{R}\left( {\frac{{\partial \varphi_{\theta } }}{\partial x}} \right)} \right]} \right.} } } \\ & \left. { + \frac{{D_{22} }}{{R^{2} }}\frac{{\partial \varphi_{\theta } }}{\partial \theta }\delta \left( {\frac{{\partial \varphi_{\theta } }}{\partial \theta }} \right) + D_{66} \left( {\frac{{\partial \varphi_{x} }}{R\partial \theta } + \frac{{\partial \varphi_{\theta } }}{\partial x}} \right)\left[ {\frac{1}{R}\delta \left( {\frac{{\partial \varphi_{x} }}{\partial \theta }} \right) + \delta \left( {\frac{{\partial \varphi_{\theta } }}{\partial x}} \right)} \right]} \right\}{\text{d}}z{\text{d}}\theta {\text{d}}x, \\ \end{aligned} $$
(24b)
$$ \begin{aligned} \delta U_{{\text{c}}} = & \int_{0}^{2\pi } {\int_{0}^{L} {\int_{{ - \frac{h}{2}}}^{\frac{h}{2}} {\left\{ {B_{11} \left[ {\frac{{\partial \varphi_{x} }}{\partial x}\delta \left( {\frac{{\partial u_{0} }}{\partial x}} \right) + \frac{{\partial u_{0} }}{\partial x}\delta \left( {\frac{{\partial \varphi_{x} }}{\partial x}} \right)} \right] + \left[ {\left( {\delta \left( {\frac{{\partial v_{0} }}{\partial \theta }} \right) + \delta w_{0} } \right)} \right.} \right.} } } \\ & \left. {\frac{{\partial \varphi_{\theta } }}{\partial \theta } + \left( {\frac{{\partial v_{0} }}{\partial \theta } + w_{0} } \right)\delta \left( {\frac{{\partial \varphi_{\theta } }}{\partial \theta }} \right)} \right]\frac{{B_{22} }}{{R^{2} }} + \left[ {\frac{{\partial u_{0} }}{\partial x}\delta \left( {\frac{{\partial \varphi_{\theta } }}{\partial \theta }} \right) + \frac{{\partial \varphi_{\theta } }}{\partial \theta }\delta \left( {\frac{{\partial u_{0} }}{\partial x}} \right)} \right] \\ & \frac{{B_{12} }}{R} + \left[ {\frac{{\partial \varphi_{x} }}{\partial x}\left( {\delta \left( {\frac{{\partial v_{0} }}{\partial \theta }} \right)v_{0} + \delta w_{0} } \right) + \left( {\frac{{\partial v_{0} }}{\partial \theta } + w_{0} } \right)\delta \left( {\frac{{\partial \varphi_{x} }}{\partial x}} \right)} \right]\frac{{B_{12} }}{R} + B_{66} \\ & \left[ {\left( {\frac{1}{R}\delta \left( {\frac{{\partial \varphi_{x} }}{\partial \theta }} \right) + \delta \left( {\frac{{\partial \varphi_{\theta } }}{\partial \theta }} \right)} \right)\left( {\frac{{\partial v_{0} }}{\partial x} + \frac{{\partial u_{0} }}{R\partial \theta }} \right) + \left( {\frac{{\partial \varphi_{x} }}{R\partial \theta } + \frac{{\partial \varphi_{\theta } }}{\partial x}} \right)} \right. \\ & \left. {\left. {\left( {\delta \left( {\frac{{\partial v_{0} }}{\partial x}} \right) + \frac{1}{R}\delta \left( {\frac{{\partial u_{0} }}{\partial \theta }} \right)} \right)} \right]} \right\}{\text{d}}z{\text{d}}\theta {\text{d}}x \\ \end{aligned} $$
(24c)

The variation of the potential energy yielded by the four NiTiNOL-steel wire ropes is obtained

$$ \delta V = \int_{0}^{L} {4\eta f_{st} \delta w_{0} } {\text{d}}x $$
(25)

The total virtual work done by the external harmonic excitation \(f\) is calculated

$$ \delta W = \int_{0}^{2\pi } {F_{0} \sin \left( {2\pi f_{0} t} \right)\delta \left( {u_{0} } \right)R{\text{d}}\theta } $$
(26)

The nonlinear partial differential governing equations of the CLCS embedded with NiTiNOL-steel wire rope are given as

$$ \frac{{\partial N_{xx} }}{\partial x} + \frac{{\partial N_{x\theta } }}{R\partial \theta } - F_{0} \sin \left( {2\pi f_{0} t} \right) = I_{0} \frac{{\partial^{2} u_{0} }}{{\partial t^{2} }} - I_{1} \frac{{\partial^{3} w_{0} }}{{\partial x\partial t^{2} }}, $$
(27a)
$$ \frac{{\partial N_{x\theta } }}{R\partial x} + \frac{{\partial N_{\theta \theta } }}{R\partial \theta } = I_{0} \frac{{\partial^{2} v_{0} }}{{\partial t^{2} }} - I_{1} \frac{{\partial^{3} w_{0} }}{{R\partial \theta \partial t^{2} }}, $$
(27b)
$$ - \frac{{N_{\theta \theta } }}{R} + f_{st} = I_{1} \frac{{\partial^{2} w_{0} }}{{\partial t^{2} }}, $$
(27c)
$$ \frac{{\partial M_{xx} }}{\partial x} + \frac{{\partial M_{x\theta } }}{R\partial \theta } = I_{1} \frac{{\partial^{2} u_{0} }}{{\partial t^{2} }} - I_{2} \frac{{\partial^{3} w_{0} }}{{\partial x\partial t^{2} }}, $$
(27d)
$$ \frac{{\partial M_{x\theta } }}{\partial x} + \frac{{\partial M_{\theta \theta } }}{R\partial \theta } = I_{1} \frac{{\partial^{2} v_{0} }}{{\partial t^{2} }} - I_{2} \frac{{\partial^{3} w_{0} }}{{R\partial \theta \partial t^{2} }}. $$
(27e)

Substituting the internal force Eqs. (11a–11f) and the restoring and damping force Eq. (14) of the NiTiNOL-steel wire ropes into Eqs. (27a–27e) leads to the governing equations

$$ \begin{array}{*{20}l} {A_{{11}} \frac{{\partial ^{2} u_{0} }}{{\partial x^{2} }} + A_{{12}} \left( {\frac{{\partial ^{2} v_{0} }}{{R\partial x\partial \theta }} + \frac{{\partial w_{0} }}{{R\partial x}}} \right) - B_{{11}} \frac{{\partial ^{3} w_{0} }}{{\partial x^{3} }} - B_{{12}} \frac{{\partial ^{3} w_{0} }}{{R^{2} \partial x\partial \theta ^{2} }} + } \hfill \\ {A_{{66}} \left( {\frac{{\partial ^{2} v_{0} }}{{R\partial x\partial \theta }} + \frac{{\partial ^{2} u_{0} }}{{R^{2} \partial \theta ^{2} }}} \right) - B_{{66}} \left( {\frac{{2\partial ^{3} w_{0} }}{{R^{2} \partial x\partial \theta ^{2} }}} \right) - F_{0} \sin \left( {2\pi f_{0} t} \right) = I_{0} \frac{{\partial ^{2} u_{0} }}{{\partial t^{2} }} - I_{1} \frac{{\partial ^{3} w_{0} }}{{\partial x\partial t^{2} }},} \hfill \\ \end{array}$$
(28a)
$$ \begin{array}{*{20}l} {A_{{12}} \frac{{\partial ^{2} u_{0} }}{{R\partial x\partial \theta }} + A_{{22}} \left( {\frac{{\partial ^{2} v_{0} }}{{R^{2} \partial \theta ^{2} }} + \frac{{\partial w_{0} }}{{R^{2} \partial \theta }}} \right) - B_{{12}} \frac{{\partial ^{3} w_{0} }}{{R\partial x^{2} \partial \theta }} - B_{{22}} \frac{{\partial ^{3} w_{0} }}{{R^{3} \partial \theta ^{3} }}} \hfill \\ {\quad + \;A_{{66}} \left( {\frac{{\partial ^{2} v_{0} }}{{\partial x^{2} }} + \frac{{\partial ^{2} u_{0} }}{{R\partial x\partial \theta }}} \right) - B_{{66}} \left( {\frac{{2\partial ^{3} w_{0} }}{{R\partial x^{2} \partial \theta }}} \right) = I_{0} \frac{{\partial ^{2} v_{0} }}{{\partial t^{2} }} - I_{1} \frac{{\partial ^{3} w_{0} }}{{R\partial \theta \partial t^{2} }},} \hfill \\ \end{array} $$
(28b)
$$ - A_{12} \frac{{\partial u_{0} }}{R\partial x} - A_{22} \left( {\frac{{\partial v_{0} }}{{R^{2} \partial \theta }} + \frac{{w_{0} }}{{R^{2} }}} \right) + \frac{{B_{12} }}{R}\frac{{\partial^{2} w_{0} }}{{\partial x^{2} }} + \frac{{B_{22} }}{{R^{3} }}\frac{{\partial^{2} w_{0} }}{{\partial \theta^{2} }} + 4\eta f_{{{\text{st}}}} = I_{0} \frac{{\partial^{2} w_{0} }}{{\partial t^{2} }}, $$
(28c)
$$ \begin{array}{*{20}l} {B_{{11}} \frac{{\partial ^{2} u_{0} }}{{\partial x^{2} }} + B_{{12}} \left( {\frac{{\partial ^{2} v_{0} }}{{R\partial x\partial \theta }} + \frac{{\partial w_{0} }}{{R\partial x}}} \right) - D_{{11}} \frac{{\partial ^{3} w_{0} }}{{\partial x^{3} }} - D_{{12}} \frac{{\partial ^{3} w_{0} }}{{R^{2} \partial x\partial \theta ^{2} }}} \hfill \\ {\; - \;D_{{66}} \left( {\frac{{\partial ^{2} v_{0} }}{{R\partial x\partial \theta }} + \frac{{\partial ^{2} u_{0} }}{{R^{2} \partial \theta ^{2} }}} \right) - 2B_{{66}} \frac{{\partial ^{3} w_{0} }}{{R^{2} \partial x\partial \theta ^{2} }} = I_{1} \frac{{\partial ^{2} u_{0} }}{{\partial t^{2} }} - I_{2} \frac{{\partial ^{3} w_{0} }}{{\partial x\partial t^{2} }},} \hfill \\ \end{array} $$
(28d)
$$ \begin{array}{*{20}l} {B_{{12}} \frac{{\partial ^{2} u_{0} }}{{R\partial x\partial \theta }} + B_{{22}} \left( {\frac{{\partial ^{2} v_{0} }}{{R^{2} \partial \theta ^{2} }} + \frac{{\partial w_{0} }}{{R^{2} \partial \theta }}} \right) - D_{{12}} \frac{{\partial ^{3} w_{0} }}{{R\partial x^{2} \partial \theta }} - D_{{22}} \frac{{\partial ^{3} w_{0} }}{{R^{3} \partial \theta ^{3} }}} \hfill \\ {\; + \;D_{{66}} \left( {\frac{{\partial ^{2} v_{0} }}{{\partial x^{2} }} + \frac{{\partial ^{2} u_{0} }}{{R\partial x\partial \theta }}} \right) - 2B_{{66}} \frac{{\partial ^{3} w_{0} }}{{R\partial x^{2} \partial \theta }} = I_{1} \frac{{\partial ^{2} v_{0} }}{{\partial t^{2} }} - I_{2} \frac{{\partial ^{3} w_{0} }}{{R\partial \theta \partial t^{2} }}.} \hfill \\ \end{array} $$
(28e)

3 Solutions

Four-term Galerkin truncation transforms the governing equations into a set of ordinary differential equations. The displacement field of an arbitrary point on the mid-surface of the CLCS is assumed to be an approximate displacement function satisfying the following boundary conditions.

Simple support at both ends (SS–SS)

$$ \begin{array}{*{20}c} {u_{0} = v_{0} = w_{0} = 0} & {M_{xx} = N_{xx} = 0} & {\begin{array}{*{20}c} {x = 0} \\ {x = L} \\ \end{array} } \\ \end{array} $$
(29)

Fixed at one end and free at the other (C–F)

$$ \begin{array}{*{20}l} {u_{0} = v_{0} = w_{0} = \varphi _{x} = \varphi _{\theta } = 0} \hfill & {x = 0} \hfill \\ {N_{{xx}} = N_{{\theta \theta }} = N_{{x\theta }} = M_{{xx}} = M_{{\theta \theta }} = M_{{x\theta }} = 0} \hfill & {x = L} \hfill \\ \end{array} , $$
(30)

The assumed displacement functions \(u_{0}\), \(v_{0}\), \(w_{0}\), \(\varphi_{{\text{x}}}\) and \(\varphi_{{\uptheta }}\) are

$$ u_{0} = \sum\limits_{m = 1}^{M} {\sum\limits_{n = 1}^{N} {u_{{{\text{mn}}}} \left( \tau \right)\cos \left( {\frac{m\pi x}{L}} \right)} } \cos \left( {n\theta } \right), $$
(31a)
$$ v_{0} = \sum\limits_{m = 1}^{M} {\sum\limits_{n = 1}^{N} {v_{{{\text{mn}}}} \left( \tau \right)\sin \left( {\frac{m\pi x}{L}} \right)} } \sin \left( {n\theta } \right), $$
(31b)
$$ w_{0} = \sum\limits_{m = 1}^{M} {\sum\limits_{n = 1}^{N} {w_{{{\text{mn}}}} \left( \tau \right)\sin \left( {\frac{m\pi x}{L}} \right)} } \cos \left( {n\theta } \right), $$
(31c)
$$ \varphi_{x} = - \sum\limits_{m = 1}^{M} {\sum\limits_{n = 1}^{N} {\frac{m\pi }{L}w_{{{\text{mn}}}} \left( \tau \right)\cos \left( {\frac{m\pi x}{L}} \right)} } \cos \left( {n\theta } \right), $$
(31d)
$$ \varphi_{\theta } = \sum\limits_{m = 1}^{M} {\sum\limits_{n = 1}^{N} {\frac{n}{R}w_{{{\text{mn}}}} \left( \tau \right)\sin \left( {\frac{m\pi x}{L}} \right)} } \sin \left( {n\theta } \right) $$
(31e)

where \(u_{{{\text{mn}}}}\), \(v_{{{\text{mn}}}}\) and \(w_{{{\text{mn}}}}\) represent the displacement shape functions with unknown time \(\tau\) in the axial direction, circumferential direction and radial direction. \(m\) and \(n\) are the numbers of axial waves and circumferential waves. \(M\) and \(N\) are the determined terms of Galerkin truncation. The function satisfies the boundary conditions that are simply supported at both ends (SS–SS) as well as are free at one end and clamped at the other end (C–F). For other elastic or inelastic boundaries, the displacement function needs to be adjusted to meet the requirements of the corresponding boundary conditions.

Substituting Eqs. (31a–31e) into Eqs. (28a–28e) leads to a set of ordinary differential equations when \(M = N = 4\)

$$ \begin{aligned} & \sum\limits_{\begin{subarray}{l} m = 1 \\ n = 1 \end{subarray} }^{4} {\left\{ {\left( { - \frac{{A_{11} m^{2} \pi^{2} }}{{L^{2} }} - \frac{{A_{66} n^{2} }}{{R^{2} }}} \right)u_{{{\text{mn}}}} \left( \tau \right) + \left( {\frac{{A_{12} mn\pi }}{{{\text{RL}}}} + \frac{{A_{66} mn\pi }}{{{\text{RL}}}}} \right)v_{{{\text{mn}}}} \left( \tau \right)} \right.} \\ & \left. { + \;\left( {\frac{{A_{12} m\pi }}{{{\text{RL}}}} + \frac{{B_{11} m^{3} \pi^{3} }}{{L^{3} }} + \frac{{B_{12} mn\pi^{2} }}{{R^{2} L}} + \frac{{B_{66} 2m\pi n^{2} }}{{R^{2} L}}} \right)} \right\} \\ = & \sum\limits_{\begin{subarray}{l} m = 1 \\ n = 1 \end{subarray} }^{4} {\left\{ {f + \frac{{I_{0} {\text{d}}^{2} u_{{{\text{mn}}}} }}{{{\text{d}}\tau^{2} }} - \left( {\frac{{I_{1} m\pi }}{L}} \right)\frac{{{\text{d}}^{2} w_{{{\text{mn}}}} }}{{{\text{d}}\tau^{2} }}} \right\}} , \\ \end{aligned} $$
(32a)
$$ \begin{aligned} & \sum\limits_{\begin{subarray}{l} m = 1 \\ n = 1 \end{subarray} }^{4} {\left\{ {\left( {A_{12} \frac{mn\pi }{{{\text{RL}}}} + A_{66} \frac{mn\pi }{{{\text{RL}}}}} \right)u_{{{\text{mn}}}} \left( \tau \right) + \left( { - A_{22} \frac{{n^{2} }}{{R^{2} }} - A_{66} \frac{{m^{2} \pi^{2} }}{{L^{2} }}} \right)v_{{{\text{mn}}}} \left( \tau \right)} \right.} \\ & \left. { + \;\left( { - A_{22} \frac{{n^{2} }}{{R^{2} }} - B_{12} \frac{{m^{2} \pi^{2} n}}{{L^{2} R}} - B_{22} \frac{{n^{3} }}{{R^{3} }} - B_{66} \frac{{2m^{2} \pi^{2} }}{{{\text{RL}}^{2} }}} \right)w_{{{\text{mn}}}} \left( \tau \right)} \right\} \\ = & \sum\limits_{\begin{subarray}{l} m = 1 \\ n = 1 \end{subarray} }^{4} {\left\{ {I_{0} \frac{{{\text{d}}^{2} v_{{{\text{mn}}}} }}{{{\text{d}}\tau^{2} }} + nI_{1} \frac{{{\text{d}}^{2} w_{{{\text{mn}}}} }}{{{\text{d}}\tau^{2} }}} \right\}} , \\ \end{aligned} $$
(32b)
$$ \begin{aligned} & \sum\limits_{\begin{subarray}{l} m = 1 \\ n = 1 \end{subarray} }^{4} {\left\{ {\left( {A_{12} \frac{m\pi }{{{\text{RL}}}}} \right)u_{{{\text{mn}}}} \left( \tau \right) + \left( { - A_{22} \frac{n}{{R^{2} }}} \right)v_{{{\text{mn}}}} \left( \tau \right)} \right.} \\ & \left. { + \;\left( { - A_{22} \frac{1}{{R^{2} }} - B_{12} \frac{{m^{2} \pi^{2} }}{{L^{2} R}} - B_{22} \frac{{n^{2} }}{{R^{3} }}} \right)w_{{{\text{mn}}}} \left( \tau \right)} \right\} \\ = & \sum\limits_{\begin{subarray}{l} m = 1 \\ n = 1 \end{subarray} }^{4} {\left\{ { - 4\eta f_{st} + I_{0} \frac{{{\text{d}}^{2} w_{{{\text{mn}}}} }}{{{\text{d}}\tau^{2} }}} \right\}} , \\ \end{aligned} $$
(32c)
$$ \begin{aligned} & \sum\limits_{\begin{subarray}{l} m = 1 \\ n = 1 \end{subarray} }^{4} {\left\{ {\left( { - B_{11} \frac{{m^{2} \pi^{2} }}{{L^{2} }} - D_{66} \frac{{n^{2} }}{{R^{2} }}} \right)u_{{{\text{mn}}}} \left( \tau \right) + \left( {B_{12} \frac{mn\pi }{{{\text{RL}}}} + D_{66} \frac{mn\pi }{{{\text{RL}}}}} \right)v_{{{\text{mn}}}} \left( \tau \right)} \right.} \\ & \left. { + \;\left( {B_{12} \frac{m\pi }{{{\text{RL}}}} + D_{11} \frac{{m^{3} \pi^{3} }}{{L^{3} }} + D_{12} \frac{{mn^{2} \pi }}{{{\text{LR}}^{2} }} + 2B_{66} \frac{{mn^{2} \pi }}{{{\text{LR}}^{2} }}} \right)w_{{{\text{mn}}}} \left( \tau \right)} \right\} \\ = & \sum\limits_{\begin{subarray}{l} m = 1 \\ n = 1 \end{subarray} }^{4} {\left\{ {I_{1} \frac{{{\text{d}}^{2} u_{{{\text{mn}}}} }}{{{\text{d}}\tau^{2} }} + \left( {\frac{m\pi }{L}} \right)I_{2} \frac{{{\text{d}}^{2} w_{{{\text{mn}}}} }}{{{\text{d}}\tau^{2} }}} \right\}} , \\ \end{aligned} $$
(32d)
$$ \begin{aligned} & \sum\limits_{\begin{subarray}{l} m = 1 \\ n = 1 \end{subarray} }^{4} {\left\{ {\left( {B_{12} \frac{mn\pi }{{{\text{RL}}}} + D_{66} \frac{{m^{2} \pi^{2} }}{{L^{2} }}} \right)u_{{{\text{mn}}}} \left( \tau \right) + \left( { - B_{22} \frac{{n^{2} }}{{R^{2} }} - D_{66} \frac{{m^{2} \pi^{2} }}{{L^{2} }}} \right)v_{{{\text{mn}}}} \left( \tau \right)} \right.} \\ & \left. { + \;\left( { - B_{22} \frac{n}{{R^{2} }} - D_{12} \frac{{m^{2} \pi^{2} n}}{{{\text{RL}}^{2} }} - D_{22} \frac{{n^{3} }}{{R^{3} }} - 2B_{66} \frac{{m^{2} n\pi^{2} }}{{{\text{LR}}}}} \right)w_{{{\text{mn}}}} \left( \tau \right)} \right\} \\ = & \sum\limits_{\begin{subarray}{l} m = 1 \\ n = 1 \end{subarray} }^{4} {\left\{ {I_{1} \frac{{{\text{d}}^{2} v_{{{\text{mn}}}} }}{{{\text{d}}\tau^{2} }} + nI_{2} \frac{{{\text{d}}^{2} w_{{{\text{mn}}}} }}{{{\text{d}}\tau^{2} }}} \right\}} . \\ \end{aligned} $$
(32e)

The standard nonlinear dynamic equations involving an inertia term, a damping term, a stiffness term, and a nonlinear term due to the restoring and damping force of the NiTiNOL-steel wire ropes are established

$$ \frac{{{\text{d}}^{2} {\mathbf{W}}}}{{{\text{d}}\tau^{2} }} + {\mathbf{C}}\frac{{{\text{d}}{\mathbf{W}}}}{{{\text{d}}\tau }} + {\mathbf{KW}} + {\mathbf{A}}\left( {{\mathbf{W}},\frac{{{\text{d}}{\mathbf{W}}}}{{{\text{d}}\tau }}} \right) = {\mathbf{F}} $$
(33)

where \({\mathbf{C}}\) is the damping matrix, \({\mathbf{K}}\) is the stiffness matrix, \({\mathbf{A}}\) is the nonlinear coefficient matrix, \({\mathbf{F}}\) is the external force column vector.

3.1 Modal analysis on the shell without the NiTiNOL-steel wire ropes and the finite element validations

According to the CLCS parameters given in Table 2, the frequency analysis and the modal analysis of the composite laminated cylindrical shell without NiTiNOL-steel wire ropes are carried out by the discrete reduced model after Galerkin truncation and validated by the finite element method. The natural frequencies are obtained via the two methods and are shown in Table 3. It demonstrates the results obtained by the two methods are relatively close, and the relative errors of the frequencies under the two boundaries are around 1%.

Table 2 The parameters of composite laminated cylindrical shell embedded with four NiTiNOL-steel wire ropes
Full size table
Table 3 Comparison of the natural frequencies and the relative errors obtained via the numerical method based on the Galerkin truncation and the finite element method
Full size table

Figure 2 shows the first four-term vibration modes of the composite laminated cylindrical shell without the NiTiNOL-steel wire ropes under SS-SS and C-F boundaries. They are both manifested as breathing modes.

Fig. 2
figure 2

The first four-term vibration modes of the composite laminated cylindrical shell without NiTiNOL-steel wire ropes: a SS-SS boundary; b C–F boundary

Full size image

3.2 Forced responses analysis on the shell embedded with the NiTiNOL-steel wire ropes and the finite element validations

Figure 3 depicts the amplitude-frequency responses of the composite laminated cylindrical shell without NiTiNOL-steel wire ropes and composite laminated cylindrical shell embedded with four NiTiNOL-steel wire ropes under the axial harmonic excitation \(F = F_{0} \sin \left( {2\pi f_{0} \tau } \right)\), the excitation amplitude \(F_{0} = 20\;{\text{kN}}\), and the frequency sweep range is \(\left[ {20\;{\text{Hz}},\;200\;{\text{Hz}}} \right]\). The response point is located at the upper vertex of the mid-surface of the composite laminated cylindrical shell where \(x = L/2\). Figure 3 illustrates the good consistency between the numerical results based on the Galerkin truncation and the finite element method, and the peak of amplitude-frequency responses of CLCS embedded with S1a NiTiNOL-steel wire ropes is much lower than the CLCS without NiTiNOL-steel wire ropes under SS–SS boundary and C–F boundary. Figure 3 demonstrates the damping effectiveness of S1a NiTiNOL-steel wire ropes.

Fig. 3
figure 3

Amplitude-frequency responses of CLCS and CLCS embedded with four NiTiNOL-steel wire ropes under axial harmonic excitation: a SS–SS boundary; b C–F boundary

Full size image

Figure 4 compares the time history responses and amplitude-frequency responses of CLCS without NiTiNOL-steel wire ropes and CLCS embedded with different configurations of NiTiNOL-steel wire ropes under the axial harmonic excitation, and the amplitude reduction rate is exploited to evaluate the vibration reduction in different configurations of NiTiNOL-steel wire ropes. In Fig. 4b, Under the SS–SS boundary, the peak of the amplitude-frequency responses of CLCS without NiTiNOL-steel wire ropes is 7.487 mm, the peak of the amplitude-frequency responses of CLCS embedded with S3b NiTiNOL-steel wire ropes is 0.908 mm, and the ARR is 87.87%. In Fig. 4d, under the C–F boundary, the peak of the amplitude-frequency responses of CLCS is 9.372 mm, the peak of the amplitude-frequency responses of CLCS embedded with S3b NiTiNOL-steel wire ropes is 1.168 mm, and the amplitude reduction rate is 87.54%. Obviously, Fig. 4 reveal the different vibration reduction performance of different configurations of NiTiNOL-steel wire ropes under the SS-SS boundary and the C–F boundary. Among them, S3b performs best in low-frequency passive vibration reduction, followed by S3c, S1a, S3a, S2a and S2b via the contrast of ARR.

Fig. 4
figure 4

Responses of CLCS system and CLCS system embedded with different configurations of NiTiNOL-steel wire ropes under axial harmonic excitation: a T–S responses under SS–SS boundary; b A–F responses under SS-SS boundary; c T–S responses under C–F boundary; d A–F responses under C–F boundary

Full size image

3.3 Vibration reduction performance for different parameters

In order to research the influencing factors of the vibration reduction in the NiTiNOL-steel wire ropes, this manuscript focuses on the influence of the amplitude of the harmonic excitation \(F_{0}\), the ratio of the length to the radius of the CLCS \(\varepsilon\), and the layer method (layer angle and layer order) of the CLCS. Of course, there are other influencing factors, such as the working environment temperature \(T\). As a shape memory alloy, the NiTiNOL-steel wire ropes are temperature-independent. However, the damping of NiTiNOL-steel wire rope is produced by the internal frictions among the wires instead of the shape memory properties. Therefore, the based experimental works [21] does not reveal the effects of the temperature. The present investigation does not account for the effects of the temperature.

The amplitude of the harmonic excitation is the reflection of its excitation strength. Whether the NiTiNOL-steel wire ropes can still maintain good vibration reduction performance under high-intensity excitation is worth investigated. This manuscript sets the excitation amplitude range from 2 to 20 kN. The relationship between the peak of amplitude-frequency responses of CLCS without NiTiNOL-steel wire ropes and varying harmonic excitation amplitude is presented in Fig. 5. As showed in Fig. 5, with the increasing of the external excitation amplitude, the peak value of the amplitude-frequency responses of the CLCS without NiTiNOL-steel wire ropes also increases drastically. When the excitation amplitude is 2 kN, the peak value is 3.744 mm; When the excitation amplitude is 20 kN, the peak value is 37.437 mm.

Fig. 5
figure 5

Amplitude-frequency responses of CLCS without NiTiNOL-steel wire ropes

Full size image

Figure 6 depicts the amplitude-frequency responses of CLCS embedded with different configurations of NiTiNOL-steel wire ropes with the variable amplitudes of the harmonic excitation. Figure 6 reveals the reduced growth rate of the peak of the amplitude-frequency responses of different configurations of NiTiNOL-steel wire ropes. The peaks of the amplitude-frequency responses of the CLCS embedded with S1a, S2a, S2b, S3a, S3b and S3c NiTiNOL-steel wire ropes are 4.186 mm, 11.494 mm, 13.805 mm, 8.707 mm, 1.925 mm and 1.977 mm when the excitation amplitude is 20 kN. The ARR of CLCS embedded with S3b NiTiNOL-steel wire ropes is 94.86%. The ARR of CLCS embedded with S2b NiTiNOL-steel wire ropes is 63.12%. Figure 6 presents the increasing trend of ARR about different configurations NiTiNOL-steel wire ropes with the increase in the amplitude of the harmonic excitation. Figure 6 reveals better vibration reduction with a larger amplitude of harmonic excitation, if the structure is not damaged.

Fig. 6
figure 6

Amplitude-frequency responses curve of CLCS system embedded with NiTiNOL-steel wire ropes under different F0: a S1a; b S2a; c S2b; d S3a; e S3b; f S3c

Full size image

The ratio of the length to the radius of the CLCS determines the characteristics of the low-frequency vibration modes of the CLCS. Low-frequency vibration modes are more prone to transverse and longitudinal bending vibration modes with larger \(\varepsilon\), and the low-frequency vibration modes are more toward the breathing vibration with the smaller \(\varepsilon\). Figure 7 depicts the amplitude-frequency responses of the CLCS without NiTiNOL-steel wire ropes and the CLCS embedded with different configurations of NiTiNOL-steel wire ropes under different \(\varepsilon\). Figure 7 presents the increasing ARR with the increasing \(\varepsilon\).When the \(\varepsilon = 5\), the ARR of CLCS embedded with S3b NiTiNOL-steel wire ropes is 93.91%, while the ARR of CLCS embedded with S2b NiTiNOL-steel wire ropes is 58.34%.

Fig. 7
figure 7

Amplitude-frequency responses curve of CLCS system with different ε embedded with NiTiNOL-steel wire ropes: a S1a; b S2a; c S2b; d S3a; e S3b; f S3c

Full size image

This manuscript investigates a 4-layer CLCS with the same material, so the layer method is determined by the layer angle and layer order. The symmetrical layer method of \(\left[ {0^{ \circ } ,90^{ \circ } ,90^{ \circ } ,0^{ \circ } } \right]\), the cross layer method of \(\left[ {0^{ \circ } ,90^{ \circ } ,0^{ \circ } ,90^{ \circ } } \right]\), the symmetrical layer method of \(\left[ {0^{ \circ } ,45^{ \circ } ,45^{ \circ } ,0^{ \circ } } \right]\) and the crossed layer method of \(\left[ {0^{ \circ } ,45^{ \circ } ,0^{ \circ } ,45^{ \circ } } \right]\) are investigated, respectively.

Figure 8 compares the amplitude-frequency responses of CLCS embedded with different configurations of NiTiNOL-steel wire ropes under different layer methods. Figure 8 demonstrates the little influence of the layer angle to vibration reduction under the symmetrical layer, the larger influence to vibration reduction under the crossed layer. Combining the layer angle and layer order, Fig. 8 reveal that \(\left[ {0^{ \circ } ,45^{ \circ } ,0^{ \circ } ,45^{ \circ } } \right]\) layer method can maximize the vibration reduction. In this layer method, the ARR of the CLCS embedded with S3b NiTiNOL-steel wire ropes is 90.98%.

Fig. 8
figure 8

Amplitude-frequency responses curve of CLCS system with different layup methods embedded with NiTiNOL-steel wire ropes: a S1a; b S2a; c S2b; d S3a; e S3b; f S3c

Full size image

4 Conclusions

A composite laminated cylindrical shell embedded with four NiTiNOL-steel wire ropes is investigated. The NiTiNOL-steel wire ropes are located on the middle surface of the cylindrical shell in a 90° annular array along the axial direction. Donnell’s theory based on first-order shear deformation theory is utilized to model the shell. The restoring and damping force of the NiTiNOL-steel wire ropes based on the Bouc-Wen model and is fitted by a polynomial and coupled into the governing equations of the shell. The fourth-term Galerkin truncation transforms the governing equations into a set of ordinary differential equations. Numerical results based on the Galerkin truncation yield the natural frequencies, the vibrating modes and the responses to harmonic excitations, and the outcomes are verified by the finite element method.

The amplitude reduction rate of the first-order resonance peak under the amplitude-frequency responses is used to evaluate the vibration reduction performance. For different configurations of NiTiNOL-steel wire ropes embedded in composite laminated cylindrical shell and various related parameters, the following conclusions are yielded: (1) Under the simply supported (SS–SS) at both ends condition and one end is fixed and the other end is free (C-F), S3b NiTiNOL-steel wire ropes perform best in low-frequency passive vibration reduction, followed by S3c, S1a, S3a, S2a and S2b. (2) The larger external excitation amplitude, the better vibration reduction performance of the NiTiNOL-steel wire ropes. (3) The NiTiNOL-steel wire ropes become more effective with the increasing ratio of the shell length to the shell radius. (4) The best layer method of the composite laminated cylindrical shell is \(\left[ {0^{ \circ } ,45^{ \circ } ,0^{ \circ } ,45^{ \circ } } \right]\), for the embedded S3b NiTiNOL-steel wire ropes.

In short, vibration reduction can be achieved by using NiTiNOL-steel wire ropes as passive vibration absorbers embedded in composite laminated cylindrical shells. The investigation reveals a new possibility to passively reduce vibration of composite laminated shells.