Abstract
This paper presents the extended Kalman filter (EKF) and moving horizon estimation (MHE) approach-based nonlinear stochastic filtering of fractional-order complementary metal oxide semiconductor (CMOS) circuit. The fractional-order calculus is used to get better reliability of the circuit. The two metal oxide semiconductor field-effect transistors of CMOS circuit are modeled using Enz–Krummenacher–Vittoz (EKV) model, and Kirchhoff’s current law (KCL) is then applied to obtain the state-space model. Ornstein–Uhlenbeck (O.U.) process is used to model the input source, which is a white Gaussian noise and Brownian process. Following are the advantages of the proposed method: (1) State estimation using EKF and MHE is real-time and can be used for the estimation purpose when parameters are slowly varying with time. (2) Fractional-order calculus leads to better flexibility in circuits. (3) Application of Kronecker product gives better and more accurate nonlinear mathematical representation. The estimated output values obtained using the proposed techniques have been compared with the wavelet transform (WT) method when nonlinear dynamics are represented using Kronecker product-based representation. The estimated output voltage using estimation algorithms is then compared with PSPICE simulated values. Simulation results validate the better disturbance rejection ability of the proposed methods.
Similar content being viewed by others
Explore related subjects
Discover the latest articles, news and stories from top researchers in related subjects.Avoid common mistakes on your manuscript.
1 Introduction
Complementary metal oxide semiconductor (CMOS) circuit is basic building block component and used in many complex circuit as it override the power dissipation and speed constraints. They are widely use in field of biomedical engineering [1, 2], wireless communication [3], low power high frequency generators [4, 5], converters [6, 7], digital circuits [8, 9]. Well-known Enz–Krummenacher–Vittoz (EKV) model is used to model the MOSFETs of CMOS due to its desirable merits such as low power design and flexibility to use in any mode of inversion, i.e., weak, moderate and strong inversion [10,11,12].
In the last few decades, fractional-order calculus have attracted amongst the researchers in the arena of mathematical analysis in classical and modern physics, relative to their integer-order counterparts. Fractional-order calculus has several advantages over conventional calculus; therefore, it became popular amongst researchers over a few decades. Several phenomena are better explained using fractional-order calculus for many systems. Moreover, estimation of the states in many electrical systems are investigated in a better way using fractional-order differential equations due to its property of huge global memory. Recently, significant progress can be seen due to its importance in engineering science [13,14,15]. Several variants of fractional-order calculus have been used in a wide range of applications. Radwan et al. [16] generalized the fundamental resistor–capacitor (RC) circuit and resistor-inductor (RL) circuit. In [17], Nezzari et al. used fractional-order sinusoidal functions for analog circuits. Radwan [18] analyzed the series fractional-order circuit which has the advantage of an improved degree of freedom. Fractional-order capacitor was first introduced by Carlson and halijak [19] followed by Roy [20]. They considered impedance using a capacitor as semi-infinite self-similar RC trees which is expressed as \(Z=\frac{1}{C}s^{\frac{1}{2}}\), where s is the complex variable. This was further modified as \(Z=\frac{1}{C}s^{\alpha }\) for more flexibility and reliability [21]. Moreover, novel fractional calculus-based Atangana–Baleanu approach have been proposed by researchers for different applications [22,23,24,25]. The recent applications of fractional-order calculus in circuits are shown in Table 1.
In the literature, several techniques has been employed for state estimation, each having its pros and cons [41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58]. Broadly, we classify the state estimation as static state estimation (SSE) and dynamical state estimation (DSE). Summary of different state estimation methods and their applications in circuits and systems are discussed in Table 2. SSE is employed when the estimated state is at a quasi-steady state in terms of magnitude and phase. Weighted least squares (WLS) method is the most commonly used SSE method [41, 42]. However, this method is limited to static-state estimation only, but when states are dynamical, DSE is preferred. DSE method includes variants of the Kalman filtering method, H\(_\infty \) filtering method, particle filtering (PF) method. For the state and parameter estimation of linear systems, Kalman filter (KF) is employed [43,44,45,46,47]. Though, KF method has the advantages as: (1) It takes both, measurement noise and process noise into consideration, therefore, gives better accuracy. The process noise and the measurement noise are assumed as Gaussian distribution. (2) It is a real-time algorithm, so it can be implemented using hardware. (3) It has less complexity, thus requires less time and memory to process. However, it has several disadvantages also: (1) KF method is only applicable for linear dynamical systems; it fails for estimation of nonlinear dynamical systems. (2) The external noise is assumed to be stationary Gaussian in KF method. To overcome these disadvantage, several other nonlinear dynamical state estimation methods are used. H\(_\infty \) filters have a wide range of applications for the state and parameter estimation in different nonlinear dynamical systems. Tang et al. [48] proposed model switching algorithm for the state of charge (SOC) estimation based on H-infinity filter. In [49], Chen et al. presented H-infinity filtering-based SOC estimation in varying environmental temperature and battery current. Song et al. [51] proposed PF-based state estimation of joint lithium-ion battery taking advantage of least square support vector machine (SVM). The main advantage of H\(_\infty \) filter is that it gives more accurate output estimation even when the system is highly nonlinear, i.e., process and measurement noises are non-Gaussian. Besides these advantages, it has some limitations, too: (1) implementation of H\(_\infty \) has significant difficulty when resources are constraints. (2) Fundamental time-domain is not addressed when dealing with the frequency-domain process. Recently, PF has also been used for the state/parameter estimation of the nonlinear system. For non-Gaussian signals, Bayesian conditional probabilities using non-Gaussian probability density functions (PDFs) have been used for updating the weights involved in state estimation. This method can be applied for Markovian state dynamics, i.e., input is represented using Ornstein–Uhlenbeck (O.U.) process [52], and then it is added to the state process to obtain a greater size non-Gaussian Markov process. In [53], the authors presented a detailed SOC estimation and remaining discharge time estimation based on PF. Chen et al. [54] observed voltage-based SOC and open-circuit voltage (OCV) estimation using PF. In order to improve the convergence of error in the estimation, Ding et al. [55] proposed PF appended with output error model, which is advantageous to estimate the parameters for strongly nonlinear systems. However, PF method has the disadvantage that particle degradation leads to an increase in estimation error. Extended Kalman filter (EKF) is an extensively used state estimation method which can be used for nonlinear dynamical systems [56,57,58,59]. It is derived from the Kushner Kallainpur filter, which is a real-time estimator. The major advantage of EKF is that it considers the stochastic approach for estimation, i.e., it takes measurement noise and process noise into consideration; therefore, it gives less estimation error, and it is the real-time estimator. For non-Gaussian measurement noise also, the Bayesian method-based nonlinear EKF can be developed. Wavelet transform (WT) (block processing) method has been used for state, and parameter estimation of circuit and systems [60]. The main advantage of WT estimation method is that minimum and maximum frequencies are varied for different time slots. Also, we do not require all the wavelet coefficients as its resolution can be adjusted to get the best estimates, i.e., best estimates can be obtained using lesser data. However, WT has the disadvantage that estimation using WT is not real time. The computational complexity of Kronecker-based EKF algorithm is less, i.e., \(O(n_x^3)\), as compared to the computational burden of Kronecker-based WT, which is \(O(n_x^5)\), where \(n_x\) denotes the state vector per iteration size [57]. Recently, moving horizon estimation (MHE) approach has been used for state estimation of nonlinear systems [62,63,64,65]. This method has the advantage that the MHE method is less sensitive to the poor initial values and has faster convergence to the actual output values. But large value of horizon length leads to increase in the computational complexity.
In the literature, a very few of the Bayesian estimation methods used been applied to fractional-order circuits [26, 27] but none of the previous works have investigated the performance using fractional-order calculus based stochastic filtering methods by transforming the dynamical state equations using Kronecker product (tensor product) [66, 67] into a form, where the gradient algorithm can be applied. Moreover, fractional-order calculus-based block processing method has also not been used in the literature. The importance of these models lies in the fact that these models can accommodate conventional filtering method. Therefore, an investigation is essential in the estimation as fractional-order calculus leads to better flexibility in the parameter and state estimation. Motivated by the aforementioned merits of fractional-order systems, a detailed analysis of fractional-order calculus-based EKF, WT, and MHE methods have been performed for the output voltage estimation of fractional-order CMOS circuit.
We can summarize the key contributions of the paper as:
-
1.
EKF and MHE method-based output voltage estimation of fractional-order CMOS circuit is proposed. The main advantage of FOC based circuit representation is that it can be considered as a super set of integer-order calculus.
-
2.
To improve the accuracy of nonlinear dynamical systems, Kronecker product-based modeling of fractional-order circuit is presented.
-
3.
Estimated output using FOC-based EKF and MHE is then compared with estimation using FOC-based WT method. In the literature, wavelet-based parameter estimation (block processing) is usually applied to linear models. Here, we applied to a fractional-order nonlinear dynamical system where Kronecker products is used to represent nonlinear terms.
-
4.
This work presents fractional-order modeling method for CMOS circuit based on Grünwald–Letnikov fractional calculus definition. The proposed model is more accurate for fractional calculus method than the other integer-order modeling method in the literature. Moreover, the proposed fractional-order model is not only the simplified model structure, but the computational complexity is also reduced without affecting the accuracy of the model.
The remaining paper is organized as follows: A brief introduction to EKF and MHE methods has been presented in Sects. 2 and 3 respectively. Section 4 introduces the fundamentals of fractional-order calculus. In Sect. 5, EKV modeled Kronecker product-based fractional-order Modeling of CMOS circuit is illustrated in detail. Section 6 covers Kronecker product-based fractional-order system representation using WT method. Section 7 presents application of EKF to fractional-order-based CMOS circuit expressed in terms of Kronecker product. Finally, simulation results and conclusions are detailed in Sects. 8 and 9, respectively.
2 Extended Kalman filter
Following notations have been used throughout the paper:-
-
1.
Cap on letters denotes estimated value, e.g., \({\hat{{\mathbf{x }}}}\).
-
2.
Random variables (\({\mathbf{x }}_k, {\mathbf{z }}_k,{\mathbf{v }}_k, {\mathbf{w }}_k\)) are denoted using bold lower case letters.
-
3.
Bold italic lower case letters denote deterministic vectors \(({{\varvec{u}}}_k)\).
-
4.
Bold italic capital letters denote matrices (\({{\varvec{F}}}_k, {{{\varvec{H}}}}_k, {{\varvec{Q}}}_k, {{\varvec{R}}}_k, {{\varvec{B}}}_k\), \({{\varvec{P}}}_k\), \({{\varvec{L}}}_k\), \({{\varvec{M}}}_k\)).
EKF is widely used nonlinear filter used for parameter and state estimation of the nonlinear systems [56,57,58,59]. Block diagram representation of dynamical system is shown in Fig. 1. A nonlinear system has general form
where \(\mathbf{x }_{k}\) denotes the state vector, \(\mathbf{f }_{k}(.)\) and \(\mathbf{h }_{k}(.)\) are the deterministic nonlinear functions of input and noises. \({{\varvec{u}}}_{k}\) is the known input. \(\mathbf{z }_{k}\) is the measured output vector. \(\mathbf{v }_{k}\) and \(\mathbf{w }_{k}\) denote the process and measurement noise vector, respectively. They are Gaussian process with zero mean and covariance \({{\varvec{Q}}}_k\) and \({{\varvec{R}}}_k\), respectively. \(\mathbf{v }_{k}\) is the process noise, and it is zero mean white Gaussian noise with covariance matrix \({{\varvec{Q}}}_k\).
where \({\mathbb {E}}\) is the expectation taken. \(\delta (k-i)\) is dirac delta function. It has nonzero value at \(k=i\), otherwise zero everywhere, i.e.,
and
The two noises \(\mathbf{v }_{k}\) and \(\mathbf{w }_{k}\) are mutually uncorrelated and also uncorrelated with the state, and thus, we can formulate them as
Following steps are involved in the EKF algorithm:-
-
1.
Initialization:-
First, initialize the estimate of the state \({\hat{\mathbf{x }}}_{{k-1|k-1}}\), error covariance matrix \({{\varvec{P}}}_{k-1|k-1}\), \({{\varvec{Q}}}_k\) and \({{\varvec{R}}}_k\).
-
2.
Prediction step:-
The state vector is predicted as
$$\begin{aligned} {\hat{\mathbf{x }}}_{{k|k-1}}={\mathbb {E}}[\mathbf{x }_k|\mathbf{z }_{k-1}]. \end{aligned}$$(9)$$\begin{aligned} {\hat{\mathbf{x }}}_{{k|k-1}}&={\mathbb {E}}[\mathbf{f }_{k-1}(\mathbf{x }_{k-1}, {{\varvec{u}}}_{k-1}, \mathbf{v }_{k-1})|\mathbf{z }_{k-1}] \end{aligned}$$(10)$$\begin{aligned}&={\mathbb {E}}[\mathbf{f }_{k-1}(\mathbf{x }_{k-1}, {{\varvec{u}}}_{k-1}|\mathbf{z }_{k-1})] \end{aligned}$$(11)as \({\mathbb {E}}[{\mathbf{v }}_{k-1})|\mathbf{z }_{k-1}]=0\). Now, expanding nonlinear function \({\mathbf{f }}_{k-1}(.)\) using Taylor series expansion, we have
$$\begin{aligned} {\mathbf{f}}_{k-1}({{\mathbf{x}}}_{k-1}, {{\varvec{u}}}_{k-1})= & {} {{\mathbf{f}}}_{k-1}({{\hat{{\mathbf{x}}}}}_{k-1|k-1}, {{\varvec{u}}}_{k-1}) \nonumber \\&+\,{{\varvec{F}}}_{k-1}{{\tilde{{\mathbf{x}}}}}_{k-1}+\Delta {{\mathbf{f}}}({{\tilde{{\mathbf{x}}}}}_{k-1}^2),\nonumber \\ \end{aligned}$$(12)where \({{\varvec{F}}}_{k-1}\) is the Jacobian matrix obtained using
$$\begin{aligned} {{\varvec{F}}}_{k-1}&=\frac{\partial \mathbf{f }_{k-1}({{\hat{{\mathbf{x}}}}}_{k-1|k-1}, {{\varvec{u}}}_{k-1} )}{\partial \mathbf{x }_{k-1}} \end{aligned}$$(13)$$\begin{aligned}&=\left[ \begin{array}{cccc}\frac{\partial \mathbf{f }_{{k-1}}^{(1)}(.)}{\partial \mathbf{x }_1}&{} \frac{\partial \mathbf{f }_{{k-1}}^{(1)}(.)}{\partial \mathbf{x }_2}&{}\dots &{}\frac{\partial \mathbf{f }_{{k-1}}^{(1)}(.)}{\partial \mathbf{x }_n}\\ \frac{\partial \mathbf{f }_{{k-1}}^{(2)}(.)}{\partial \mathbf{x }_1}&{} \frac{\partial \mathbf{f }_{{k-1}}^{(2)}(.)}{\partial \mathbf{x }_2}&{}\dots &{}\frac{\partial \mathbf{f }_{{k-1}}^{(2)}(.)}{\partial \mathbf{x }_n}\\ \vdots &{} \vdots &{}\ddots &{}\vdots \\ \frac{\partial \mathbf{f }_{{k-1}}^{(n)}(.)}{\partial \mathbf{x }_1}&{} \frac{\partial \mathbf{f }_{{k-1}}^{(n)}(.)}{\partial \mathbf{x }_2}&{}\dots &{}\frac{\partial \mathbf{f }_{{k-1}}^{(n)}(.)}{\partial \mathbf{x }_n} \end{array}\right] , \end{aligned}$$(14)where \(\mathbf{f }_{{k-1}}(.)=\left[ \begin{array}{cccc}\mathbf{f }_{{k-1}}^{(1)}(.)&\mathbf{f }_{{k-1}}^{(2)}(.)&\dots&\mathbf{f }_{{k-1}}^{(n)}(.) \end{array}\right] ^T\), \({{\tilde{\mathbf{x }}}}_{k}={\mathbf{x }}_{k}-{\hat{\mathbf{x }}}_{k-1}\) and \(\Delta \mathbf{f }({{\tilde{\mathbf{x }}}}_{k-1}^2)\) is the higher order terms in Taylor series expansion.
$$\begin{aligned} {\mathbf{x}}_k= & {} {\mathbf{f}}_{k-1}({{\hat{{\mathbf{x}}}}}_{k-1|k-1}, {{\varvec{u}}}_{k-1}) +{{\varvec{F}}}_{k-1}{{\tilde{{\mathbf{x}}}}}_{k-1} \nonumber \\&+\,\Delta {\mathbf{f}}({{\tilde{{\mathbf{x}}}}}_{k-1}^2)+{\mathbf{v}}_{k-1}. \end{aligned}$$(15)Expected value of (12), by considering the higher-order terms equal to zero, is
$$\begin{aligned} {\mathbb {E}}[\mathbf{f }_{k-1}(\mathbf{x }_{k-1}, {{\varvec{u}}}_{k-1})]= & {} {\mathbb {E}}[\mathbf{f }_{k-1}({{\hat{{\mathbf{x}}}}}_{k-1|k-1}, {{\varvec{u}}}_{k-1})]\nonumber \\&+\,{{\varvec{F}}}_{k-1}\,{\mathbb {E}}[{{\tilde{\mathbf{x }}}}_{k-1}]. \end{aligned}$$(16)As \({\mathbb {E}}[{{\tilde{\mathbf{x }}}}_{k-1}]=0\), therefore, from (11) and (16), time updated state estimate is
$$\begin{aligned} {\hat{{\mathbf{x}}}}_{{k|k-1}}= {\mathbf{f }}_{k-1}({{\hat{{\mathbf{x}}}}}_{k-1|k-1}, {{{\varvec{u}}}}_{k-1}). \end{aligned}$$(17)Error in updated state estimate is
$$\begin{aligned} {{\tilde{\mathbf{x }}}}_{k|k-1}={\mathbf{x }}_{k}-{\hat{\mathbf{x }}}_{k|k-1}. \end{aligned}$$(18)Therefore, from (15) and (18), we have
$$\begin{aligned} {\tilde{\mathbf{x }}}_{k|k-1}&=\mathbf{f }_{k-1}({{\hat{{\mathbf{x}}}}}_{k-1|k-1}, {{\varvec{u}}}_{k-1})+{{\varvec{F}}}_{k-1}{\tilde{\mathbf{x }}}_{k-1} \nonumber \\&\quad +\,\mathbf{v }_{k-1}-\mathbf{f }_{k-1}({{\hat{{\mathbf{x}}}}}_{k-1|k-1}, {{\varvec{u}}}_{k-1}) \end{aligned}$$(19)$$\begin{aligned}&={{\varvec{F}}}_{k-1}{\tilde{\mathbf{x }}}_{k-1}+\mathbf{v }_{k-1}. \end{aligned}$$(20)Time updated error covariance is
$$\begin{aligned} {{\varvec{P}}}_{k|k-1}={\mathbb {E}}[({\tilde{\mathbf{x }}}_{k|k-1})({\tilde{\mathbf{x }}}_{k|k-1})^T]. \end{aligned}$$(21)$$\begin{aligned} {{\varvec{P}}}_{k|k-1}&= {{\varvec{F}}}_{k-1}\,{\mathbb {E}}[({\tilde{\mathbf{x }}}_{k-1}) ({\tilde{\mathbf{x }}}_{k-1})^T] {{\varvec{F}}}_{k-1}^T\nonumber \\&\quad +\,{\mathbb {E}}[(\mathbf{v }_{k-1})(\mathbf{v }_{k-1})^T] \end{aligned}$$(22)$$\begin{aligned}&= {{\varvec{F}}}_{k-1}{{\varvec{P}}}_{k-1|k-1}{{\varvec{F}}}_{k-1}^T +{{\varvec{L}}}_{k-1}{{\varvec{Q}}}_{k-1}{{\varvec{L}}}_{k-1}^T \end{aligned}$$(23)where
$$\begin{aligned} {{\varvec{L}}}_{k-1}=\frac{\partial \mathbf{f }_{k-1}({{\hat{{\mathbf{x}}}}}_{k-1|k-1} )}{\partial \mathbf{v }_{k-1}}. \end{aligned}$$(24) -
3.
Update step:-
The main objective is to obtained the best unbiased state. Consider
$$\begin{aligned} {{\hat{{\mathbf{x}}}}}_{k|k}=\mathbf{x }_k^a+{{\varvec{K}}}_k\mathbf{z }_k, \end{aligned}$$(25)where \({{\varvec{K}}}_k\) is the Kalman gain for EKF. From unbiasedness condition
$$\begin{aligned} {\mathbb {E}}[{\mathbf{x }}_{k}-{\hat{\mathbf{x }}}_{k|k}|\mathbf{z }_k]=0. \end{aligned}$$(26)Therefore, from (2), (18) and (26), we have
$$\begin{aligned}&{\mathbb {E}}[ ({\tilde{\mathbf{x }}}_{k|k-1}+{\hat{\mathbf{x }}}_{k|k-1})-(\mathbf{x }_k^a+{{\varvec{K}}}_k\,(\mathbf{h }_k(\mathbf{x }_{k})\nonumber \\&\quad +\mathbf{w }_{k}))\,|\mathbf{z }_k]=0, \end{aligned}$$(27)$$\begin{aligned}&{\mathbb {E}}[ ({\tilde{\mathbf{x }}}_{k|k-1}]+{\mathbb {E}}[{\hat{\mathbf{x }}}_{k|k-1})]-{\mathbb {E}}[\mathbf{x }_k^a +{{\varvec{K}}}_k\,(\mathbf{h }_k(\mathbf{x }_{k})]\nonumber \\&\quad -{\mathbb {E}}[ \mathbf{w }_{k}))|\mathbf{z }_k]=0. \end{aligned}$$(28)As \( {\mathbb {E}}[ ({\tilde{\mathbf{x }}}_{k|k-1}]=0\), \({\mathbb {E}}[\mathbf{w }_{k}]=0\), (28) yields
$$\begin{aligned}&{\hat{\mathbf{x }}}_{k|k-1}-\mathbf{x }_k^a-{\mathbb {E}}[{{\varvec{K}}}_k\, (\mathbf{h }_k(\mathbf{x }_{k})]=0, \end{aligned}$$(29)$$\begin{aligned}&\mathbf{x }_k^a={\hat{\mathbf{x }}}_{k|k-1}-{{\varvec{K}}}_k\,{\mathbb {E}} [(\mathbf{h }_k(\mathbf{x }_{k})]. \end{aligned}$$(30)Now, substituting the value of \(\mathbf{x }_k^a\) from (30) in (25), we get
$$\begin{aligned} {\hat{\mathbf{x }}}_{k|k}={\hat{\mathbf{x }}}_{k|k-1}+{{\varvec{K}}}_k\,(\mathbf{z }_k -{\mathbb {E}}[\mathbf{h }_k(\mathbf{x }_{k})]). \end{aligned}$$(31)Now, expanding \(\mathbf{h }_k(.)\) using Taylor series expansion, we get
$$\begin{aligned} \mathbf{h }_{k}(\mathbf{x }_{k}) = \mathbf{h }_{k}({{\hat{{\mathbf{x}}}}}_{k|k-1})+{{\varvec{H}}}_{k}{\tilde{\mathbf{x }}}_{k-1}+\Delta \mathbf{h }({\tilde{\mathbf{x }}}_{k-1}^2), \end{aligned}$$(32)where
$$\begin{aligned} {{\varvec{H}}}_{k}&=\frac{\partial \mathbf{h }_{k}(\mathbf{f }_{k-1}({{\hat{{\mathbf{x}}}}}_{k-1|k-1} ))}{\partial \mathbf{x }_{k}} \end{aligned}$$(33)$$\begin{aligned}&=\left[ \begin{array}{cccc}\frac{\partial \mathbf{h }_{k}(\mathbf{f }_{{k-1}}(.))}{\partial \mathbf{x }_1}&\frac{\partial \mathbf{h }_{k}(\mathbf{f }_{{k-1}}(.))}{\partial \mathbf{x }_2}&\dots&\frac{\partial \mathbf{h }_{k}(\mathbf{f }_{{k-1}}(.))}{\partial \mathbf{x }_n} \end{array}\right] \end{aligned}$$(34)and \(\Delta \mathbf{h }({\tilde{\mathbf{x }}}_{k-1}^2)\) is the higher-order term. Expected value of (32), by considering the higher-order terms equal to zero, is
$$\begin{aligned} {\mathbb {E}}[h_{k}(\mathbf{x }_{k})]= & {} {\mathbb {E}}[h_{k}({{\hat{{\mathbf{x}}}}}_{k|k-1})]+{{\varvec{H}}}_{k}\,{\mathbb {E}}[{\tilde{\mathbf{x }}}_{k-1}]\nonumber \\&+\,{\mathbb {E}}[\Delta \mathbf{h }({\tilde{\mathbf{x }}}_{k-1}^2)]. \end{aligned}$$(35)As \({\mathbb {E}}[{\tilde{\mathbf{x }}}_{k-1}]=0\), \({\mathbb {E}}[\Delta \mathbf{h }({\tilde{\mathbf{x }}}_{k-1}^2)]\), then (35) gives
$$\begin{aligned} {\mathbb {E}}[\mathbf{h }_{k}(\mathbf{x }_{k})] = \mathbf{h }_{k}({{\hat{{\mathbf{x}}}}}_{k|k-1}). \end{aligned}$$(36)Substituting the value of \({\mathbb {E}}[\mathbf{h }_{k}(\mathbf{x }_{k})]\) from (36) in (31), we get
$$\begin{aligned} {\hat{\mathbf{x }}}_{k|k}={\hat{\mathbf{x }}}_{k|k-1}+{{\varvec{K}}}_k\,(\mathbf{z }_k-\mathbf{h }_k({\hat{\mathbf{x }}}_{k|k-1})). \end{aligned}$$(37)The error in the updated measured value is
$$\begin{aligned} {\tilde{\mathbf{x }}}_{k|k}={\mathbf{x }}_{k}-{\hat{\mathbf{x }}}_{k|k}. \end{aligned}$$(38)From equations (2), (15) and (38), we have
$$\begin{aligned} {\tilde{\mathbf{x }}}_{k|k}&=\{\mathbf{f }_{k-1}({\hat{{\mathbf{x}}}}_{k-1|k-1}, {{\varvec{u}}}_{k-1})+{{\varvec{F}}}_{k-1}{\tilde{\mathbf{x }}}_{k-1}\nonumber \\&\quad +\,\Delta \mathbf{f }({\tilde{\mathbf{x }}}_{k-1}^2)+\mathbf{v }_{k-1}\}-\{\hat{\mathbf{x }}_{k|k-1} \nonumber \\&\quad +\,{{\varvec{K}}}_k\,((\mathbf{h }_k(\mathbf{x }_{k}) +\mathbf{w }_{k})-\mathbf{h }_k({\hat{\mathbf{x }}}_{k|k-1}))\}. \end{aligned}$$(39)Substituting the value of \({\hat{\mathbf{x }}}_{k|k-1}\) and \(h_{k}(\mathbf{x }_{k}) \)from (17) and (32), respectively, to (39), we get
$$\begin{aligned} {\tilde{\mathbf{x }}}_{k|k}&=\{\mathbf{f }_{k-1}({\hat{{\mathbf{x}}}}_{k-1|k-1}, {{\varvec{u}}}_{k-1})+{{\varvec{F}}}_{k-1}{\tilde{\mathbf{x }}}_{k-1}\nonumber \\&\quad +\,\Delta \mathbf{f }({\tilde{\mathbf{x }}}_{k-1}^2)+\mathbf{v }_{k-1}\}-\{\mathbf{f }_{k-1} ({\hat{{\mathbf{x}}}}_{k-1|k-1}, {{\varvec{u}}}_{k-1}) \nonumber \\&\quad +\,{{\varvec{K}}}_k\,(\mathbf{h }_{k}({\hat{{\mathbf{x}}}}_{k|k-1})+{{\varvec{H}}}_{k}{\tilde{\mathbf{x }}}_{k|k-1}\nonumber \\&\quad +\,\Delta \mathbf{h }({\tilde{\mathbf{x }}}_{k-1}^2) +\mathbf{w }_{k}))-\mathbf{h }_k({\hat{\mathbf{x }}}_{k|k-1}))\}. \end{aligned}$$(40)Simplifying equation (40) and substituting \({\tilde{\mathbf{x }}}_{k|k-1}\) from (20) to (40), we get
$$\begin{aligned} {\tilde{\mathbf{x }}}_{k|k}&= {{\varvec{F}}}_{k-1}{\tilde{\mathbf{x }}}_{k-1}+\mathbf{v }_{k-1} -{{\varvec{K}}}_k{{\varvec{H}}}_k({{\varvec{F}}}_{k-1}{\tilde{\mathbf{x }}}_{k-1}+\mathbf{v }_{k-1}) \nonumber \\&\quad -\,{{\varvec{K}}}_k\mathbf{w }_{k} \end{aligned}$$(41)$$\begin{aligned}&=({{\varvec{I}}}-{{\varvec{K}}}_k\mathbf{H }_k){{\varvec{F}}}_{k-1}{\tilde{\mathbf{x }}}_{k-1}\nonumber \\&\quad +\,({{\varvec{I}}}-{{\varvec{K}}}_k\mathbf{H }_k)\mathbf{v }_{k-1}-{{\varvec{K}}}_k\mathbf{w }_{k}. \end{aligned}$$(42)Posteriori error covariance is
$$\begin{aligned} {{\varvec{P}}}_{k|k}={\mathbb {E}}[( {\tilde{\mathbf{x }}}_{k|k} )( {\tilde{\mathbf{x }}}_{k|k} )^T]. \end{aligned}$$(43)From (42)
$$\begin{aligned} {{\varvec{P}}}_{k|k}&={\mathbb {E}}[( ({{\varvec{I}}}-{{\varvec{K}}}_k{{\varvec{H}}}_k){{\varvec{F}}}_{k-1} {\tilde{\mathbf{x }}}_{k-1}+ ({{\varvec{I}}}-{{\varvec{K}}}_k{{\varvec{H}}}_k)\mathbf{v }_{k-1}\nonumber \\&\quad -\,{{\varvec{K}}}_k\mathbf{w }_{k} )(({{\varvec{I}}}-{{\varvec{K}}}_k{{\varvec{H}}}_k) \nonumber \\&\quad \times {{\varvec{F}}}_{k-1}{\tilde{\mathbf{x }}}_{k-1}+({{\varvec{I}}} -{{\varvec{K}}}_k{{\varvec{H}}}_k)\mathbf{v }_{k-1}-{{\varvec{K}}}_k \mathbf{w }_{k} )^T] \end{aligned}$$(44)$$\begin{aligned}&={{\varvec{P}}}_{k|k-1}-{{\varvec{K}}}_k{{\varvec{H}}}_k -{{\varvec{P}}}_{k|k-1}{{\varvec{H}}}_k^T{{\varvec{K}}}_k^T\nonumber \\&\quad +\, {{\varvec{K}}}_k{{\varvec{H}}}_k{{\varvec{P}}}_{k|k-1} \mathbf{H }_k^T{{\varvec{K}}}_k{^T} \nonumber \\&\quad +\, {{\varvec{K}}}_k{{\varvec{M}}}_k{{\varvec{R}}}_k {{\varvec{M}}}_k^T{{\varvec{K}}}_k^{T}, \end{aligned}$$(45)where
$$\begin{aligned} {{\varvec{M}}}_{k-1}=\frac{\partial \mathbf{f }_{k-1}({\hat{{\mathbf{x}}}}_{k-1|k-1} )}{\partial \mathbf{w }_{k-1}}. \end{aligned}$$(46)Kalman gain is optimized by minimizing \(tr({{\varvec{P}}}_{k|k})\) with respect to \({{\varvec{K}}}_k\), i.e.,
$$\begin{aligned}&\frac{\partial {{\varvec{P}}}_{k|k} }{\partial {{\varvec{K}}}_k} =0 \end{aligned}$$(47)$$\begin{aligned}&({{\varvec{H}}}_k{{\varvec{P}}}_{k|k-1})^T -{{\varvec{P}}}_{k|k-1}{{\varvec{H}}}_k^T+2\,{{\varvec{K}}}_k {{\varvec{H}}}_k{{\varvec{P}}}_{k|k-1}{{\varvec{H}}}_k^T \nonumber \\&\quad +\, 2\,{{\varvec{K}}}_k{{\varvec{M}}}_k{{\varvec{\textit{R}}}}_k {{\varvec{M}}}_k^T =0. \end{aligned}$$(48)Thus, the Kalman gain is
$$\begin{aligned} {{\varvec{K}}}_k={{\varvec{P}}}_{k|k-1}{{\varvec{H}}}_k^T({{\varvec{H}}}_k{{\varvec{P}}}_{k|k-1} {{\varvec{H}}}_k^T +{{\varvec{M}}}_k{{\varvec{R}}}_k{{\varvec{M}}}_k^T)^{-1}.\nonumber \\ \end{aligned}$$(49)$$\begin{aligned} { {{\varvec{P}}}_{k|k} }&=({{\varvec{I}}}-{{\varvec{K}}}_k{{\varvec{H}}}_k){{\varvec{P}}}_{k|k-1}-({{\varvec{I}}}-{{\varvec{K}}}_k{{\varvec{H}}}_k) {{\varvec{P}}}_{k|k-1} \nonumber \\&\quad {{\varvec{H}}}_k^T{{\varvec{K}}}_k^{T}+\,{{\varvec{K}}}_k{{\varvec{M}}}_k{{\varvec{R}}}_k{{\varvec{M}}}_k^T{{\varvec{K}}}_k^{T} \end{aligned}$$(50)$$\begin{aligned}&=({{\varvec{I}}}-{{\varvec{K}}}_k{{\varvec{H}}}_k){{\varvec{P}}}_{k|k-1}-({{\varvec{P}}}_{k|k-1} {{\varvec{H}}}_k^T \nonumber \\&\quad -\,{{\varvec{P}}}_{k|k-1}{{\varvec{H}}}_k^T){{\varvec{K}}}_k{^T} \end{aligned}$$(51)$$\begin{aligned}&=({{\varvec{I}}}-{{\varvec{K}}}_k{{\varvec{H}}}_k){{\varvec{P}}}_{k|k-1}. \end{aligned}$$(52)
Summary of the steps involved in EKF algorithm is given in Table 3. \((k|k-1)\) denotes prior estimate and (k|k) is the post estimate. \({{\varvec{I}}}\) denotes identity matrix. Figure 2 shows the block diagram representation of the steps involve in EKF algorithm.
3 Moving horizon estimation
MHE is widely used estimation method for linear and nonlinear systems. In this method, the computational burden is reduced by considering finite horizon of measurement data. Also, it is non-trivial to summarize the effect of discarded data on the current states, which is so called arrival cost. As real-time implementation of full information estimation is not feasible. To get over infinite dimensionality, data size is bounded using moving horizon approach. Formalism of MHE has following form
where M denotes the horizon length. When (53) is subjected to (1) and (2), it gives the solution of (2) i.e., \(\mathbf{x }_k:=\mathbf{x }(k;{\mathbf{z }}\) at time k, \(\{{\mathbf{v }}_k\}_{k=\tau -M}^{k-1})\), \({\mathbf{v }}_k\) is the process noise vector which is varied from time \(\tau -M\) to \({k-1}\). \(\theta _{\tau -M}(\mathbf{z })\) is the arrival cost, that summarizes the output data \(\mathbf{z }_{k=0}^{\tau -m-1}\) which is a function of the state \(\mathbf{x }_{\tau -M}\). M is the key parameter in MHE. Lower value of M leads to large estimation error and larger value of horizon length, on the other hand, corresponds to high computational burden. Problem formulation for MHE is approximated by the above filtering scheme and its posteriori states and covariance matrix are recursively updated by EKF method to obtain the optimal estimates.
4 Fractional-order calculus
Fractional-order modeling of the systems deals with the modeling of the systems using fractional-order derivative (FOD) of the state functions. FOC was first introduced in 1695 by Leibniz, but it got attention amongst the researchers recently. In the literature, mainly, Grünwald–Letnikov, Riemann–Liouville and Caputo defined FOC in the form of integer-order derivatives [68]. Among these three, Grünwald–Letnikov definition for FOD can be utilized for state estimation of any system due to its compatibility with Kalman filter and its variants [69]. Mathematically, it can be formulated as
where \({\mathcal {D}}^\alpha \) and \(\alpha \) are the integral-differential operator and integral–differential-order, respectively. \(\frac{t}{T}\) is the memory length. \(\langle \alpha , j\rangle \) is the Newton binomial coefficient which is formulated as
where \(\Gamma (.)\) is the Gamma function. Mathematically, it is expressed as
Continuous time Grünwald–Letnikov FOD has the disadvantage that it can not be operated and implemented on computer software as it is infinite dimensional. To get over infinite dimensionality, Grünwald–Letnikov FOD is converted to discrete form and truncated to finite dimensional. Therefore, equation (54) is represented as
5 Kronecker product-based fractional-order modeling of CMOS circuit
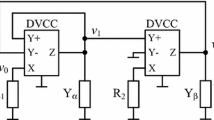
Figures 3 and 4 show the CMOS circuit and its equivalent EKV model, respectively. Applying Kirchhoff’s voltage law (KVL) and Kirchhoff’s current law (KCL) and replacing the MOS transistor by EKV model, we have
where \(x_1\), \(x_2{\ldots }x_6\) are the state variables such that \(x_1=v_G\), \(x_2=v_B^{(1)}\), \(x_3=v_S^{(1)}\), \(x_4=v_B^{(2)}\), \(x_5=v_S^{(2)}\) and \(x_6=v_D\). \(C_{GD}\), \(C_{GS}\) and \(C_{GB}\) denote the drain to channel capacitance, source to channel capacitance and base to channel capacitance for MOSFETs used in CMOS. \(C_{OX}\) is oxide capacitance. Drain currents \(I_D^{(1)}\) and \(I_D^{(2)}\) for n-type and p-type MOSFET are
As \(I_{DB}^{(1)}\cong 0\), \(I_{DB}^{(2)}\cong 0\), therefore \(I_D^{(1)} \cong I_{DS}^{(1)}\), \(I_D^{(2)} \cong I_{DS}^{(2)}\). Expression of drain current in weak inversion using EKV model [10,11,12] for n-type and p-type MOSFETs are
where \(\frac{W^{(1)}}{L^{(1)}}\) and \(\frac{W^{(2)}}{L^{(2)}}\) represent the aspect ratio, \(V_{T_0}\) is the equilibrium threshold voltage and \(V_T\) denotes the thermal voltage, respectively. \(I_0\) and \(\eta \) are the unary specific current and subthreshold slope factor, respectively.
Equations (67) and (68) are expanded using Maclaurin series while keeping the quadratic terms as
Now, the input is modeled as O.U. process [52] as
where \(\gamma _j\), \(\sigma _j\) and \(\rho _j\) are the constants values. \(N_j\) denotes the Gaussian process with zero mean and variance is equal to unity. The input is modeled such that it accounts the Gaussian process and the Brownian process. Thus,
where \(\beta _j(t)\) is the Brownian motion process. Using \(C_{GS}^{(1)}+C_{{GS}_0}^{(1)}=C_S^{(1)}\), \(C_{GD}^{(1)}+C_{{GD}_0}^{(1)}=C_D^{(1)}\), \(C_{GB}^{(1)}+C_{{GB}_0}^{(1)}=C_B^{(1)}\), \(C_{GS}^{(2)}+C_{{GS}_0}^{(2)}=C_S^{(2)}\), \(C_{GD}^{(2)}+C_{{GD}_0}^{(2)}=C_D^{(2)}\), \(C_{GB}^{(2)}+C_{{GB}_0}^{(2)}=C_B^{(2)}\). Now, the differential equations (58)–(64) are converted to fractional-order stochastic differential equations (SDE) as
where
Vector form are obtained using Taylor series expansion to retain the quadratic terms from the nonlinear function \(\mathbf{f }(.)\) to give
where \( \mathbf{x }{(t)}=\left[ {\begin{array}{cccccc} x_1&x_2&x_3&x_4&x_5&x_6\end{array}}\right] ^T\),
and \({{\varvec{A}}}_7=0\). Input source \({{\varvec{u}}}_1=v_{in}\), \({{\varvec{u}}}_2=V_{IN}\).
6 Kronecker product-based fractional-order system representation using WT method
The measurement model is expressed as:
where
\(\sigma \) is the nonzero constant value and \(\mathbf{N }(t)\) denotes the zero mean white Gaussian process. \(\mathbf{x }(t)\) is represented using wavelet basis and selecting minimum and maximum frequency of operation. The wavelet method is applied either directly to estimate the entire set of the state variables or another way is to formulate a square non-singular matrix. Representing \(\frac{d^\alpha (.)}{dt^\alpha }={\mathcal {D}}^\alpha (.)\), thus, the latter case is formulated as
and so
The signals \({\mathcal {D}}^\alpha \mathbf {y} (t)\) and \({\mathcal {D}}^{2\alpha }{} \mathbf {y} (t)\) are expressed using wavelets as
Substituting (84) and (85) into (83) and omitting noise terms, we have
where
Now, the inner product is computed with \(\Psi _{p, q}\) on (86) as
where the input \({{\varvec{u}}}(t)=\sum {{\varvec{u}}}[i, k]\Psi _{i, k}(t)\), i.e., \({{\varvec{u}}}[i, k]=<{{\varvec{u}}}, \Psi _{i, k}>\). Equation (88) can be formulated as
where \(m_1\), \(m_2\) and \(m_3\) are formulated in terms of \({\mathcal {G}}\), \({{\varvec{A}}}_1,\ldots ,{{\varvec{A}}}_5\). \(m_1\), \(m_2\) depend on \(\varvec{\Theta }\), so we write
Now, the perturbation method is applied and \({\mathcal {O}}(\delta ^2)\) terms are retained as
Comparing the coefficients of \(\delta ^{(0)}\), \(\delta ^{(1)}\), \(\delta ^{(2)}\) respectively gives
where \(c_{{\mathcal {D}}^\alpha \mathbf {y} }^{(0)}[i, k]\), \(c_{{\mathcal {D}}^\alpha \mathbf {y} }^{(1)}[i, k]\) and \(c_{{\mathcal {D}}^\alpha \mathbf {y} }^{(2)}[i, k]\) are obtained from WT of \({{\mathcal {D}}^\alpha \mathbf {y} }^{(0)}[i, k]\), \({{\mathcal {D}}^\alpha \mathbf {y} }^{(1)}[i, k]\) and \({{\mathcal {D}}^\alpha \mathbf {y} }^{(2)}[i, k]\), respectively, by equating \({\mathcal {O}}(\delta ^0)\), \({\mathcal {O}}(\delta ^1)\) and \({\mathcal {O}}(\delta ^2)\) variations expressed in \(\mathbf{y }(t)\).
The gradient search algorithm can also be used estimate \(\varvec{\Theta }\) to minimize
7 Applying EKF to MOSFET circuit
Discrete time equations of (73)–(79) in the form of state space model can be formulated as
Kronecker product-based representation of the equation (96) in terms of fractional-order CMOS model is represented as
where
where \(T_s\) is sampling time period. \(\beta _{k}\) is the Brownian motion noise which is expressed as
and \(\Phi _l^\alpha =diag[\langle \alpha , l\rangle , \langle \alpha , l\rangle , \langle \alpha , l\rangle , \langle \alpha , l\rangle , \langle \alpha , l\rangle , \langle \alpha , l\rangle ]\).
Measurement model is
where
EKF method has been applied to the equations by introducing process noise \({\mathbf{v }_k}\) and measurement noise \(\mathbf{w }{_k}\) to (98) and (106), respectively, which can be expressed as
8 Results and discussion
In this paper, output voltage of CMOS circuit has been estimated using EKF in MATLAB software when nonlinear dynamics are represented using Kronecker product. The estimated output using EKF has been compared with WT method which is based on Kronecker product. For this, the least mean squares method is used for the estimation using Kronecker product-based WT method. In both the cases, CMOS circuit is modeled using fractional-order calculus. Maximum input voltage is 10 mV. Following are the parameters which has been used for PSPICE simulations: \(V_T=0.0256V\), \(V_{T_0}=0.5V\), \(R_{IN}=3\,k\Omega \), \(C_{GX}=1.0 \times 10^{-11}\), \(C_S^{(1)}=C_S^{(2)}=1.5 \times 10^{-10}F\), \(C_D^{(1)}=C_D^{(2)}=1.5 \times 10^{-10}F\), \(C_B^{(1)}=C_B^{(2)}=4 \times 10^{-10}F\), \(C_{BS}^{(1)}=C_{BS}^{(2)}=0.99 \times 10^{-11}F\), \(C_{BD}^{(1)}=C_{BD}^{(1)}=1.0 \times 10^{-11}F\), \(I_0=1.0 \times 10^{-9}A\), \(\eta _1=\eta _2=1\), \(\rho _j=1\) and \(\gamma _j=1\). The covariance of process noise, \({{\varvec{Q}}}_k=\text {diag}[ 10^{-8}\quad 10^{-6}\quad 10^{-8}\quad 10^{-6}\quad 10^{-8}\quad 10^{-5}]\), the covariance of measurement noise, \({{\varvec{R}}}_k=0.5\times 10^{-6}\). Covariance matrix \({{\varvec{P}}}_{k|k}\) should not be singular as it will affect the convergence. Covariance matrix \({{\varvec{P}}}_{0|0} =Cov(\mathbf{x }(0))={{\varvec{Q}}}_k\). Initial state estimate \(\mathbf{x }_{0|0}=0\).
From Figs. 5 and 6, it can be seen that Kronecker product-based EKF smoothens better when compared with WT method based on Kronecker product-based representation for different value of fractional-order parameter \(\alpha \) and white Gaussian noise with \(\mu =0\), \(\sigma ^2=0.001\) is added with input. Figures 7 and 8 show the estimated output using MHE approach for different values of \(\alpha \). Their estimation error is compared in terms of root-mean-square error (RMSE). RMSE is computed using
where \(e{_k}\) denotes the estimation error. It is the difference between the actual output value (simulated output values) and the estimated output value. Total number of samples are N.
Table 4 shows the RMSE of estimated output using EKF and WT method when maximum CMOS input is 10 mV for different value of fractional parameter \(\alpha \). Table 5 shows the RMSE of estimated output using MHE approach for different values of fractional parameter \(\alpha \) and horizon length M. It can be observed that MHE method gives better estimation for larger value of horizon length M. Also, MHE is less sensitive to the poor initial values and has faster convergence to the actual output values as compared to EKF and WT method.
9 Remarks
-
1.
\(\mathbf{x }(t)\) can be expanded using wavelet basis as
$$\begin{aligned} \mathbf{x }(t)=\sum _{ N_1\le i\le N_2, k_{\text {min}}(i)\le k\le k_{\text {max}}(i)} c(i, k)\Psi _{i, k}(t),\nonumber \\ \end{aligned}$$(112)where resolution range \([N_1, N_2]\) depends on frequency of operation and the measured time duration and the mother wavelet \(\Psi _{i, k}(t)\) is given by
$$\begin{aligned} \Psi _{i\,, k}(t)=2^{\frac{i}{2}}\Psi (2^i\,t-k). \end{aligned}$$(113)The mother wavelet is oscillatory and has zero mean value which can be expressed as
$$\begin{aligned} \int _{-\infty }^{\infty }\psi (t)dt=0. \end{aligned}$$(114)Also, this function needs to satisfy the admissibility condition
$$\begin{aligned} \int _{-\infty }^{\infty }\frac{|{{\hat{\psi }}} (\omega )|^2}{|\omega |}d \omega =0. \end{aligned}$$(115)The admissibility condition allows the reconstruction of the original signal using inverse WT.
The wavelets can be classified as: (1) continuous wavelet transform (CWT) and (2) discrete wavelet transform (DWT). The CWT maps a function f(t) onto time scale space by
$$\begin{aligned} W_f\,<a,\,b>\,=&\, \int _{-\infty }^{\infty }\psi _{a,\,b}(t)\,f(t)dt \end{aligned}$$(116)$$\begin{aligned} =&<\psi _{a,\,b}(t),\,f(t)>. \end{aligned}$$(117)The CWT uses the translations and dilations of a prototype or mother function \(\psi (t)\). CWT is described by the following equation
$$\begin{aligned} X( \,a,\, b)= & {} \frac{1}{{|a|^{\frac{1}{2}}}}\int _{-\infty }^{\infty }x(t)\psi ^*\left( \frac{t-b}{a}\right) dt,\nonumber \\&\quad a>0, \,\, b\in {\mathbb {R}}, \end{aligned}$$(118)where \(\psi (t)\) is the mother wavelet. a is the scaling parameter. b is the translation parameter. \(*\) denotes the complex conjugate. \(a>1\) gives dilated wavelet. \(a<1\) gives contracted wavelet. \(\frac{1}{{|a|^{\frac{1}{2}}}}\) is the energy normalization factor. Wavelets are mathematical functions that decompose the data into different frequency components and then analyze each component with a resolution matched to its scale.
In DWT, scaling and translation parameters are discretized, \(a=2^n\), \(b=2^n\,\,k\). So the DWT is
$$\begin{aligned} \psi _{n,\,k}(t) =2^{\frac{-n}{2}}\psi (2^{-n}t-k),\quad j,\, k\in {\mathbb {Z}}. \end{aligned}$$(119)The orthonormal wavelets satisfy the condition:-
$$\begin{aligned}&\int _{-\infty }^{\infty } \psi _{n,\quad k}(t) \psi _{n', \quad k'}(t)dt\nonumber \\&=\left\{ \begin{array}{ll} 1, &{} {\text {if } n=n'\,\, \text { and } \,\,k=k';} \\ 0, &{} \hbox {Otherwise.} \end{array} \right. \end{aligned}$$(120)Mother wavelet \(\psi \) can be reconstructed from the ”scaling sequence” for different type of wavelets (Daubechies wavelet, Haar wavelet, Shannon wavelet etc.) which have specific properties required for specific kinds of applications. Daubechies wavelets are discrete time orthogonal wavelets. The scaling and wavelet functions of Daubechies wavelets have longer supports, which offers improved capability of these transformations. These transformations offer powerful tool for various signal processing such as compression, noise removal, and image enhancement.
-
2.
Consider that mother wavelet is concentrated on range [a, b]. Let \(\omega _{\text {min}}\) and \(\omega _{\text {max}}\) are the lowest and the highest operating frequency. Consider \([0, \tau ]\) is the measurement time span. Then, for a specified resolution index i, the extent of the transition index k is chosen such that \(a\le 2^i\,t-k\le b, t\in [0, \tau ]\). Therefore, \(2^i\,t-b\le k\le 2^i,t-a, t\in [0, \tau ]\) or \(-b\le k\le 2^i\,T-a, t\in [0, \tau ]\). Wavelet frequency \(\Psi _{n, k}(t)\) is mathematically expressed as
$$\begin{aligned}&\left| \frac{\frac{d\Psi _{n,k}(t)}{dt}}{\Psi _{n,k}(t)}\right| =\frac{2^n\left| \Psi '(2^nt-k)\right| }{\left| \Psi (2^nt-k)\right| }\nonumber \\&\times \in [2^n\lambda _{\text {min}}, 2^n\lambda _{\text {max}}], \end{aligned}$$(121)where
$$\begin{aligned}&\lambda _{\text {max}}=\max _{t}\frac{|\Psi '(t)|}{|\Psi (t)|}, \end{aligned}$$(122)$$\begin{aligned}&\lambda _{\text {min}}=\min _{t}\frac{|\Psi '(t)|}{|\Psi (t)|}, \end{aligned}$$(123)so the resolution indexes \(N_1\), \(N_2\) must be chosen such that
$$\begin{aligned}&2^{N_2}\lambda _{\text {max}}\approx \frac{\omega _{\text {max}}}{2\pi }, \end{aligned}$$(124)$$\begin{aligned}&2^{N_1}\lambda _{\text {min}}\approx \frac{\omega _{\text {min}}}{2\pi }, \end{aligned}$$(125)or
$$\begin{aligned}&{N_1}\approx \text {log}_2\left( \frac{\omega _{\text {min}}}{2\pi \lambda _{\text {min}}}\right) , \end{aligned}$$(126)$$\begin{aligned}&{N_2}\approx \text {log}_2\left( \frac{\omega _{\text {max}}}{2\pi \lambda _{\text {max}}}\right) . \end{aligned}$$(127)Now, resolution index range is selected using this method enables us to reserve lesser data for estimation purpose, i.e., estimation is done using compression.
-
3.
When the non-Gaussian distribution is added with Gaussian noise of measured output which is so called outlier. This can be considered into EKF formalism. As EKF is obtained from Kushner Kallainpur filter of infinite dimensional when the states are Markov process and the measurement noise considered as Gaussian process. However, for non-Gaussian measurement noise also, the nonlinear filter can be formulated which is based on the Bayesian method for computing the conditional probabilities using non-Gaussian PDFs. The method is based on the fact that, although the measurement noise is non-Gaussian, it is white and the state process is Markov process. Consider a discrete state model
$$\begin{aligned}&{\varvec{\theta }_{m+1}=\mathbf{f}( \varvec{\theta }_{m}, {{\varvec{u}}}_{m+1})+\mathbf{v }_{m+1}}, \end{aligned}$$(128)$$\begin{aligned}&{\mathbf{z }(m)=\mathbf{h }(\varvec{\theta }_{m})+\mathbf{w }_{m}}, \end{aligned}$$(129)$$\begin{aligned}&{\mathbf{z }_{m}=\mathbf{z }(m); \quad k\le m}. \end{aligned}$$(130)Bayesian arguments can help in developing nonlinear filter for non-Gaussian measurement noise for which states are Markov process.
$$\begin{aligned}&{p(\varvec{\theta }_{m+1}|\mathbf{z }_{m+1})=\frac{p(\varvec{\theta }_{m+1}, \mathbf{z }_{m+1})}{p(\mathbf{z }_{m+1})}=\frac{p(\mathbf{z }({m+1}), \mathbf{z }_{m}, \varvec{\theta }_{m+1})}{p(\mathbf{z }_{m+1})}} \end{aligned}$$(131)$$\begin{aligned}&\quad =\frac{\int p(\mathbf{z }({m+1})|\varvec{\theta }_{m+1})p(\varvec{\theta }_{m+1}|\varvec{\theta }_{m})p(\varvec{\theta }_{m}|\mathbf{z }_{m})d\varvec{\theta }_m}{\int p(\mathbf{z }({m+1})|\varvec{\theta }_{m+1})p(\varvec{\theta }_{m+1}| \mathbf{x }_{m})p(\varvec{\theta }_{m}|\mathbf{z }_{m})d\varvec{\theta }_md\varvec{\theta }_{m+1}} \end{aligned}$$(132)$$\begin{aligned}&\quad =\frac{\int p_{w_{m+1}}(\mathbf{z }({m+1})-h(\varvec{\theta }_{m+1}))p_{v_{m+1}}(\varvec{\theta }_{m+1} -f(\varvec{\theta }_{m}, {{\varvec{u}}}_{m+1}))p(\varvec{\theta }_{m}|\mathbf{z }_{m})d\varvec{\theta }_m}{\int p_{w_{m+1}}(\mathbf{z }({m+1})-h(\varvec{\theta }_{m+1}))p_{v_{m+1}}(\varvec{\theta }_{m+1}-\mathbf{f }(\varvec{\theta }_{m}, {{\varvec{u}}}_{m+1}))p(\varvec{\theta }_{m}|\mathbf{z }_{m})d\varvec{\theta }_md\varvec{\theta }_{m+1}} \end{aligned}$$(133)$$\begin{aligned}&{\hat{\varvec{\theta }}}_{{m+1}|{m+1}}=\underset{\varvec{\theta }}{{\text {argmax}}}\int p_{\mathbf{w }_{m+1}}(\mathbf{z }({m+1})-h(\varvec{\theta }))p_{\mathbf{v }_{m+1}}(\varvec{\theta }\nonumber \\&\qquad -\,\mathbf{f }(\varvec{\theta }_m, {{\varvec{u}}}_{m+1}))p(\varvec{\theta }_m|\mathbf{z }_m)d\varvec{\theta }_m. \end{aligned}$$(134)It should be noted that \(\mathbf{z }(m)\) denotes the instantaneous measurement at the time n, while \({\mathbf{z }}_m=\{{\mathbf{z }}_k: k\le m\}\) is the aggregate of all measurements taken up to time m.
On the other hand, joint conditional density in case of MHE is expressed using Bayesian rule as
$$\begin{aligned} p\left( \varvec{\theta }_{m}|\mathbf{z }_{m}\right) \propto p\left( \mathbf{z }_{m}|\varvec{\theta }_{m}\right) p\left( \varvec{\theta }_{m}|\mathbf{z }_{1:k-m}\right) , \end{aligned}$$(135)where \(\varvec{\theta }_m\) be the Markovian sequence. The joint conditional density for first and second orders are
$$\begin{aligned} p\left( \varvec{\theta }_{m}|\mathbf{z }_{m}\right)&=c_1\prod _{j=k-m+1}^{k} p(\mathbf{z }_j|\varvec{\theta }_{j})\nonumber \\&\quad \prod _{j=k-m+1}^{k} p(\varvec{\theta }_{j+1}|\varvec{\theta }_{j}) p(\varvec{\theta }_{k-m+1}|\mathbf{z }_{1:k-m}), \end{aligned}$$(136)$$\begin{aligned} p\left( \varvec{\theta }_{m}|\mathbf{z }_{m}\right) =&c_2\prod _{j=k-m+1}^{k} e^{\left( -\frac{1}{2}||\mathbf{z }_{j}-\mathbf{h }(\varvec{\theta }_j)||^2_{{{\varvec{R}}}^{-1}}\right) }\nonumber \\&\quad \prod _{j=k-m+1}^{k}e^{\left( -\frac{1}{2}||\varvec{\theta }_{j+1}- \mathbf{f }(\mathbf{x }_j)||^2_{{{\varvec{Q}}}^{-1}}\right) }\nonumber \\&\times p(\varvec{\theta }_{k-m+1}|\mathbf{z }_{1:k-m}), \end{aligned}$$(137)respectively, where \(c_1\) and \(c_2\) are the constants, \(p(\mathbf{z }_j|\varvec{\theta }_{j})\) is the likelihood function for each measured value around horizon. It should be noted that state transition density function \(p_\mathbf{w }(\varvec{\theta }_{k+1}-f(\varvec{\theta }_{k}))\) is \({\mathcal {N}}(0, {{\varvec{Q}}}_k)\) and likelihood function \(p_\mathbf{v }(\mathbf{z }_{k+1}-h(\varvec{\theta }_{k}))\) is \({\mathcal {N}}(0, {{\varvec{R}}}_k)\). The negative logarithmic form of (137) is
$$\begin{aligned}&\min _{\varvec{\theta }_{m}}\prod _{j=k-m+1}^{k}||\mathbf{z }_{j}-\mathbf{h } (\varvec{\theta }_j)||^2_{{{\varvec{R}}}^{-1}}\nonumber \\&\quad +\, \prod _{j=k-m+1}^{k}||\varvec{\theta }_{j+1}- \mathbf{f }(\mathbf{x }_j)||^2_{{{\varvec{Q}}}^{-1}} \nonumber \\&\quad -\,\text {ln}\,p(\varvec{\theta }_{k-m+1} |\mathbf{z }_{1:k-m}). \end{aligned}$$(138)To obtain the optimal estimates, (138) is minimized.
-
4.
Stability of EKF depends on selection of measurement noise variance \({{\varvec{R}}}_k\). If \({{\varvec{R}}}_k\) is taken very small with respect to some matrix norm, then corresponding \({{\varvec{R}}}_k^{-1}\) will be very large and will cause numerical instability. Thus, \({{\varvec{R}}}_k\) is chosen such that system remains stable.
10 Conclusions
In this paper, output voltage of CMOS circuit is estimated using MHE, EKF and WT method. For this, MOSFET used in CMOS circuit are modeled using the EKV model. Fractional-order calculus is used to get better reliability of the circuit. To get better estimates, the nonlinear dynamical system is mathematically expressed in terms of Kronecker-based representation. The estimated output voltage using MHE approach and Kronecker product-based EKF method has been compared with the Kronecker product-based WT method for the nonlinear dynamical system, for which least mean squares has been used for state estimation. RMSE is computed for different value of fractional-order parameter \(\alpha \). The simulation results validate the better performance of MHE and EKF method as compared to WT method and compared to the EKF, the MHE is less sensitive to the poor initial values and has faster convergence to the actual output values. Replacement of integer-order by fractional-order element leads to several precedences since more parameters are included. These parameters help to improve the performance and intensify the novel behavior which lead to circuit design and control with better flexibility. The proposed method is valid to any type of fractional-order nonlinear system for the estimation purpose. It should be noted that proposed algorithm should be analyzed by uncertainties and non-Gaussian noise often peculiar to applications. Although, error divergence in estimation using Kronecker product-based representation in EKF algorithm needs further investigations. We are planning to report the these results also in near future. Also, investigation of the non-Gaussian noise effect in the process and measurement model of fractional-order circuit and application of Monte Carlo particle filters to obtain the optimal estimates is another scope for future research.
References
Saadi, H., Attari, M., Escid, H.: Noise optimization of CMOS front-end amplifier for embedded biomedical recording. Arab. J. Sci. Eng. 45(3), 1961–1968 (2020)
Nagulapalli, R., Hayatleh, K., Barker, S., Georgiou, P., Lidgey, F.J.: A high value, linear and tunable cmos pseudo-resistor for biomedical applications. J. Circuits Syst. Comput. 28(6), 1950096 (2019)
Lee, S., Hara, S., Yoshida, T., Amakawa, S., Dong, R., Kasamatsu, A., Sato, J., Fujishima, M.: An 80-Gb/s 300-GHz-band single-chip CMOS transceiver. IEEE J. Solid-State Circuits 54(12), 3577–3588 (2019)
Jangra, V., Kumar, M.: A wide tuning range VCO design using multi-pass loop complementary current control with IMOS varactor for low power applications. Int. J. Eng. Sci. Technol. 22(4), 1077–1086 (2019)
Dastgerdi, M.A., Habibi, M., Dolatshahi, M.: A novel two stage cross coupled architecture for low voltage low power voltage reference generator. Analog Integr. Circuits Signal Process. 99(2), 393–402 (2019)
Lei, T., Shao, L.L., Zheng, Y.Q., Pitner, G., Fang, G., Zhu, C., Li, S., Beausoleil, R., Wong, H.S., Huang, T.C., Cheng, K.T.: Low-voltage high-performance flexible digital and analog circuits based on ultrahigh-purity semiconducting carbon nanotubes. Nat. Commun. 10(1), 1 (2019)
Gonen, B., Karmakar, S., van Veldhoven, R., Makinwa, K.A.: A continuous-time zoom ADC for low-power audio applications. IEEE J. Solid-State Circuits 55(4), 1023–1031 (2019)
Zhang, H., Li, C., Wang, J., Hu, W., Zhang, D.W., Zhou, P.: Complementary logic with voltage zero loss and nano watt power via configurable MoS2/WSe2 gate. Adv. Funct. Mater. 28(44), 1805171 (2018)
Kalra, S., Bhattacharyya, A.B.: A unified analytical transregional MOSFET model for nanoscale CMOS digital technologies. Int. J. Numer. Model. Electron. Netw. Device Fields 33(1), e2700 (2020)
Enz, C.C., Krummenacher, F., Vittoz, E.A.: An analytical MOS transistor model valid in all regions of operation and dedicated to low-voltage and low-current applications. Analog Int. Circuits Signal Process. 8(1), 83–114 (1995)
Enz, C., Chicco, F., Pezzotta, A.: Nanoscale MOSFET modeling: Part 1: the simplified EKV model for the design of low-Power analog circuits. IEEE Solid-State Circuits Mag. 9(3), 26–35 (2017)
Enz, C., Chicco, F., Pezzotta, A.: Nanoscale MOSFET modeling: Part 2: using the inversion coefficient as the primary design parameter. IEEE Solid-State Circuits Mag. 9(4), 73–81 (2017)
Petras, I., Podlubny, I., O’Leary, P., Dorcak, L., Vinagre, B.M.: Analogue Realization of Fractional Order Controllers. Fakulta Berg, Kosice (2002)
Sabatier, J.: Advances in Fractional Calculus: Theoretical Development and Applications in Physics and Engineering. Springer, Amsterdam (2007)
Magin, R.L.: Fractional Calculus in Bioengineering. Begell House, Redding (2006)
Radwan, A.G., Salama, K.N.: Fractional-order RC and RL circuits. Circuits Syst. Signal Process. 31(6), 1901–1915 (2012)
Nezzari, H., Charef, A., Boucherma, D.: Analog circuit implementation of fractional order damped sine and cosine functions. IEEE Trans. Emerg. Sel. Topics Circuits Syst. 3(3), 386–393 (2013)
Radwan, A.G.: Stability analysis of the fractional-order RL\(_\beta \)C\(_\alpha \) circuit. J. Fract. Calc. Appl. 3(1), 1–5 (2012)
Carlson, G., Halijak, C.: Approximation of fractional capacitors \((\frac{1}{s})^{\frac{1}{n}}\) by a regular Newton process. IEEE Trans. Circuits Syst. 11(2), 210–213 (1964)
Roy, S.: On the realization of a constant-argument immittance or fractional operator. IEEE Trans. Circuits Syst. 14(3), 264–274 (1967)
Nakagawa, M., Sorimachi, K.: Basic characteristics of a fractance device. IEICE Trans. Fundam. Electron. Commun. Comput. Sci. E. 75(12), 1814–1819 (2019)
Arqub, O.A., Al-Smadi, M.: Atangana–Baleanu fractional approach to the solutions of Bagley–Torvik and Painleve equations in Hilbert space. Chaos Solitons Fractals 117, 161–167 (2018)
Arqub, O.A., Maayah, B.: Numerical solutions of integrodifferential equations of Fredholm operator type in the sense of the Atangana–Baleanu fractional operator. Chaos Solitons Fractals 117, 117–124 (2018)
Arqub, O.A., Maayah, B.: Fitted fractional reproducing kernel algorithm for the numerical solutions of ABC-Fractional Volterra integro-differential equations. Chaos Solitons Fractals 126, 394–402 (2019)
Arqub, O.A., Maayah, B.: Modulation of reproducing kernel Hilbert space method for numerical solutions of Riccati and Bernoulli equations in the Atangana-Baleanu fractional sense. Chaos Solitons Fractals 125, 163–170 (2019)
Mawonou, K.S., Eddahech, A., Dumur, D., Beauvois, D., Godoy, E.: Improved state of charge estimation for Li-ion batteries using fractional order extended Kalman filter. J. Power Sources 435, 226710 (2019)
Hidalgo-Reyes, J.I., Gomez-Aguilar, J.F., Alvarado-Martinez, V.M., Lopez-Lopez, M.G., Escobar-Jimenez, R.F.: Battery state-of-charge estimation using fractional extended Kalman filter with Mittag–Leffler memory. Alex. Eng. J. 59(4), 1919–1929 (2020)
Wang, Y., Gao, G., Li, X., Chen, Z.: A fractional-order model-based state estimation approach for lithium-ion battery and ultra-capacitor hybrid power source system considering load trajectory. J. Power Sources 449, 227543 (2020)
Huang, X., Gao, Z., Yang, C., Liu, F.: State estimation of continuous-time linear fractional-order systems disturbed by correlated colored noises via Tustin generating function. IEEE Access 8, 18362–18373 (2020)
Elwy, O., Said, L.A., Madian, A.H., Radwan, A.G.: All possible topologies of the fractional-order Wien oscillator family using different approximation techniques. Circuits Syst. Signal Process. 38(9), 3931–3951 (2019)
Said, L.A., Radwan, A.G., Madian, A.H., Soliman, A.M.: Two-port two impedances fractional order oscillators. Microelectron. J. 55, 40–52 (2016)
Radwan, A.G., Elwakil, A.S., Soliman, A.M.: Fractional-order sinusoidal oscillators: design procedure and practical examples. IEEE Trans. Circuits Syst. I Regul. Pap. 55(7), 2051–2063 (2008)
Kavyanpoor, M., Shokrollahi, S.: Dynamic behaviors of a fractional order nonlinear oscillator. J. King Saud Univ. Sci. 31(1), 14–20 (2019)
AbdelAty, A.M., Soltan, A., Ahmed, W.A., Radwan, A.G.: Fractional order Chebyshev-like low-pass filters based on integer order poles. Microelectron. J. 90, 72–81 (2019)
Hamed, E.M., Said, L.A., Madian, A.H., Radwan, A.G.: On the approximations of cfoa-based fractional-order inverse filters. Circuits Syst. Signal Process. 39(1), 2–9 (2020)
Tolba, M.F., AboAlNaga, B.M., Said, L.A., Madian, A.H., Radwan, A.G.: Fractional order integrator/differentiator: FPGA implementation and FOPID controller application. AEU Int. J. Electron. Commun. 98, 220–229 (2019)
Bertsias, P., Psychalinos, C., Maundy, B.J., Elwakil, A.S., Radwan, A.G.: Partial fraction expansion-based realizations of fractional order differentiators and integrators using active filters. Int. J. Circuit Theory Appl. 47(4), 513–531 (2019)
Radwan, A.G., Emira, A.A., AbdelAty, A.M., Azar, A.T.: Modeling and analysis of fractional order DC–DC converter. ISA Trans. 82, 184–199 (2018)
Wei, Z., Zhang, B., Jiang, Y.: Analysis and modeling of fractional-order buck converter based on Riemann–Liouville derivative. IEEE Access 7, 162768–16277 (2019)
Kumar, V., Ali, I.: Fractional order sliding mode approach for chattering free direct power control of DC/AC converter. IET Power Electron. 12(13), 3600–3610 (2019)
Monticelli, A.: State Estimation in Electric Power Systems: A Generalized Approach. Springer, Berlin (2012)
Wu, Y., Xiao, Y., Hohn, F., Nordstrom, L., Wang, J., Zhao, W.: Bad data detection using linear WLS and sampled values in digital substations. IEEE Trans. Power Deliv. 33(1), 150–157 (2017)
Shrivastava, P., Soon, T.K., Idris, M.Y., Mekhilef, S.: Overview of model-based online state-of-charge estimation using Kalman filter family for lithium-ion batteries. Renew. Sustain. Energ. Rev. 113, 109233 (2019)
Bansal, R., Majumdar, S., Parthasarthy, H.: Stochastic filtering in electromagnetics. IEEE Trans. Antennas Propag. (2020). https://doi.org/10.1109/TAP.2020.3027054
Diouf, M.L., Iggidr, A., Souza, M.O.: Stability and estimation problems related to a stage-structured epidemic model. Math. Biosci. Eng. 16(5), 4415–4432 (2019)
Zhao, D., Ding, S.X., Karimi, H.R., Li, Y., Wang, Y.: On robust Kalman filter for two-dimensional uncertain linear discrete time-varying systems: a least squares method. Automatica 99, 203–212 (2019)
Netto, M., Mili, L.: A robust data-driven Koopman Kalman filter for power systems dynamic state estimation. IEEE Trans. Power Syst. 33(6), 7228–7237 (2018)
Tang, X., Gao, F., Zou, C., Yao, K.E., Hu, W., Wik, T.: Load-responsive model switching estimation for state of charge of lithium-ion batteries. Appl. Energy 238, 423–434 (2019)
Chen, N., Zhang, P., Dai, J., Gui, W.: Estimating the state-of-charge of lithium-ion battery using an H-infinity observer based on electrochemical impedance model. IEEE Access 8, 26872–26884 (2020)
Rigatos, G., Siano, P., Raffo, G.: A nonlinear H-infinity control method for multi-DOF robotic manipulators. Nonlinear Dyn. 88(1), 329–348 (2017)
Song, Y., Liu, D., Liao, H., Peng, Y.: A hybrid statistical data-driven method for on-line joint state estimation of lithium-ion batteries. Appl. Energy 261, 114408 (2020)
Jazwinski, A.H.: Stochastic Processes and Filtering Theory. Academic Press, New York (1970)
Wang, Y., Chen, Z.: A framework for state-of-charge and remaining discharge time prediction using unscented particle filter. Appl. Energy 260, 114324 (2020)
Chen, Z., Sun, H., Dog, G., Wei, J., Wu, J.I.: Particle filter-based state-of-charge estimation and remaining-dischargeable-time prediction method for lithium-ion batteries. J. Power Sources 414, 158–166 (2019)
Ding, J., Chen, J., Lin, J., Wan, L.: Particle filtering based parameter estimation for systems with output-error type model structures. J. Frankl. Inst. 356(10), 5521–5540 (2019)
Feng, L., Ding, J., Han, Y.: Improved sliding mode based 1109 EKF for the SOC estimation of lithium-ion batteries. Ionics 26, 2875–2882 (2020)
Bansal, R., Majumdar, S., Parthasarathy, H.: Extended Kalman filter based nonlinear system identification described in terms of Kronecker product. AEU Int. J. Electron. Commun. 108, 107–117 (2019)
Hu, G., Zhang, Z., Armaou, A., Yan, Z.: Robust extended Kalman filter based state estimation for nonlinear dynamic processes with measurements corrupted by gross errors. J. Taiwan Inst. Chem. Eng. 106, 20–33 (2020)
Haykin, S.: Kalman Filtering and Neural Networks. Wiley, New York (2001)
Majumdar, S., Parthasarathy, H.: Wavelet-based transistor parameter estimation. Circuits Syst. Signal Process. 29(5), 953–970 (2010)
Song, P., Tan, Y., Geng, X., Zhao, T.: Noise reduction on received signals in wireless ultraviolet communications using wavelet transform. IEEE Access 8, 131626–131635 (2020)
Shen, J.N., He, Y.J., Ma, Z.F., Luo, H.B., Zhang, Z.F.: Online state of charge estimation of lithium-ion batteries: a moving horizon estimation approach. Chem. Eng. Sci. 154, 42–53 (2016)
Shen, J.N., Shen, J.J., He, Y.J., Ma, Z.F.: Accurate state of charge estimation with model mismatch for li-ion batteries: a joint moving horizon estimation approach. IEEE Trans. Power Electron. 34(5), 4329–4342 (2018)
Zou, L., Wang, Z., Han, Q.L., Zhou, D.: Moving horizon estimation for networked time-delay systems under Round-Robin protocol. IEEE Trans. Automat. Control 64(12), 5191–5198 (2019)
Rawlings, J.B., Bakshi, B.R.: Particle filtering and moving horizon estimation. Comput. Chem. Eng. 30(10–12), 1529–1541 (2006)
Brewer, J.: Kronecker products and matrix calculus in system theory. IEEE Trans. Circuits Syst. 25(9), 772–781 (1978)
Greub, W.H.: Multilinear Algebra. Springer, Berlin (1967)
Baleanu, D., Diethelm, K., Scalas, E., Trujillo, J.J.: Fractional Calculus: Models and Numerical Methods. World Scientific, Singapore (2010)
Hu, X., Yuan, H., Zou, C., Li, Z., Zhang, L.: Co-estimation of state of charge and state of health for lithium-ion batteries based on fractional-order calculus. IEEE Trans. Veh. Technol. 67(11), 10319–10329 (2018)
Acknowledgements
The author would like to express his gratitude to the unknown referees for carefully reading the paper and giving valuable suggestions.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The author declares that there are no conflicts of interests regarding the publication of this manuscript.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
About this article
Cite this article
Bansal, R. Stochastic filtering in fractional-order circuits. Nonlinear Dyn 103, 1117–1138 (2021). https://doi.org/10.1007/s11071-020-06152-x
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11071-020-06152-x