1 Introduction

Fractional-order calculus is nowadays widespread in many fields of our (not only scientific) world, such as in biology, chemistry, medicine, mechanics, thermodynamics, control theory, finances, and nanotechnologies. It is mainly thanks to the fact that differential equations whose order is a non-integer number better describe many dynamic systems around us and that this topic is mathematically very well worked out. Today fractional-order systems are an emerging area of multidisciplinary research which has given rise to many new potential applications [3]. Also, designers of analog circuits are recently getting on this research although a solid-state fractional-order element has not been commercially available yet. Nevertheless, a number of circuits with fractional elements have been published, such as filters [5, 10, 17, 19, 22, 25–28], oscillators [11, 16, 18], controllers [14], and differentiators [13, 29]; also, various methods to implement the fractional impedance have been presented [1, 2, 9, 12, 15, 18, 20, 23, 24, 26].

Let us consider a fractional-order admittance \(Y_{\alpha }\) at the general frequency \(\omega \) which is characterized by the following relation

$$\begin{aligned} Y_{\alpha } =\frac{\left| Y_{\alpha 0}\right| }{\omega _{0}^{\alpha }}(j\omega )^{\alpha } =C_{\alpha } (j\omega )^{\alpha }. \end{aligned}$$
(1)

Here \(|Y_{\alpha 0}|\) is the magnitude of the admittance at a reference frequency \(\omega _{0}\), while \(\alpha \) is the order of the admittance which lies in the range \(0<\alpha <1\). The variable \(C_{\alpha }=|Y_{\alpha 0}|/\omega _{0}^{\alpha }\) is usually considered as pseudo-capacitance, and it should be noted that the physical meaning of this quantity depends on the value of \(\alpha \). If \(\alpha \) converges to one, \(C_{\alpha }\) represents capacitance as apparent from (1). However, if \(\alpha \) tends to zero, \(C_{\alpha }\) has the meaning of conductance. The unit of \(C_{\alpha }\) is also somehow changeable—it shifts between F (Farad) when \(\alpha \) is one and \(\Omega ^{-1}\) when it is zero. Considering arbitrary value of \(\alpha \), the \(C_{\alpha }\) unit should be F s\(^{\alpha -1}\) [30].

Moreover, the value of \(C_{\alpha }\) does not provide us with quick information about the magnitude of the fractional-order admittance at an important frequency, such as oscillation or cutoff frequency. We must always compute it taking care of the value of \(\alpha \). When \(\alpha \) is close to zero, \(Y_{\alpha }\) is approximately equal to \(C_{\alpha }\), and almost independent of frequency. But on the contrary when \(\alpha \) is higher, the magnitude of the admittance is frequency dependent, and this dependency is not so clear due to the non-integer exponent \(\alpha \). Thus, it seems more suitable to use the values \(|Y_{\alpha 0}|\) and \(\omega _{0}\) instead of \(C_{\alpha }\) to describe fractional admittance. (Of course knowing \(\alpha \) is also necessary in both cases.) These values will be also used later in the description of the designed oscillator, whereas \(\omega _{0}\) will be the oscillation frequency.

The magnitude of the admittance \(Y_{\alpha }\) varies with frequency with a slope of \(20 \alpha \) dB/dec. Its phase is constant vs frequency and is equal to \((\pi /2) \alpha \). Thus one-port circuits with fractional-order immittance are also called constant phase elements (CPE).

Our work deals with the design, analysis, computer simulation, and experimental measurement of a sinusoidal oscillator with two current conveyors and two fractional immittance elements. Although several previously published papers offer a detailed look on the general principles of fractional oscillators [11, 16, 18] and verify selected ones by PSpice simulation, we aimed at the design, properties, and verification of one particular circuit and refer to its special properties that are not present at integer-order oscillators. Utilization of fractional elements brings the benefits of tunability through the order of the employed elements, availability of arbitrary/variable phase shift between the outputs of oscillator, and setting the slope of the oscillation frequency while tuning it by resistances.

The employment of current conveyors as active elements offers the following advantages, with regards to the corresponding discrete component op-amp RC implementations: only grounded resistors and capacitors, reduced active component count, and significantly lower power supply voltage. In comparison with the fractional oscillators in [11, 16, 18], our circuit employs less passive elements which are all grounded. The circuits in [11] contain also more active elements. The previously published fractional oscillators do not provide three outputs with arbitrary phase shift proportional to the orders of two fractances.

Moreover, we utilized a recent sample of low-voltage and low-power current conveyor, and thus this oscillator can be suitable for biomedical, portable, battery-powered, and other applications where the low-power consumption is necessary. Unlike the conventional conveyor, the used one utilizes the bulk-driven quasi-floating-gate (BD-QFG) technique in order to offer high threshold-to-supply voltage ratio \((V_{\mathrm{TH}}/V_{\mathrm{DD}})\) and maximum input-to-supply voltage ratio \((V_{\mathrm{in.max}}/V_{\mathrm{DD}})\) [8]. The BD-QFG technique is well described in [7, 8].

This paper is organized as follows: The oscillator design is presented in Sect. 2, while in Sect. 3 the tuning possibilities along with theoretical graphs are demonstrated. In Sect. 4 Cadence simulation and experimental results are illustrated and finally the paper is concluded in Sect. 5.

2 Fractional-Order Oscillator Design

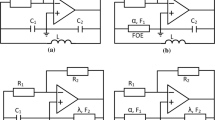
The basic circuit for the fractional-order oscillator design is shown in Fig. 1. Two differential voltage current conveyors (DVCC) [4] were employed as active elements. DVCC is a very versatile active element that was previously used also for designing integer-order oscillators [21]. The terminal currents and voltages of DVCC are described by the following relations: \(I_{Y+}=I_{Y-}=0\), \(V_{X}=V_{Y+}-V_{Y-}\), and \(I_{Z}=I_{X}\). Voltages are referenced to ground, and currents are considered positive when flowing into the block. Two grounded fractional-order admittances \((Y_{\alpha },~Y_{\beta })\) are connected to Z terminals of conveyors.

It should be noted here that the circuit can also operate as oscillator only with one fractional-order admittance, while the second one is replaced by a classic (i.e., integer-order) capacitor. But it can be shown that this solution leads to very different values of passive elements which are not suitable from the integration point of view.

Fig. 1
figure 1

Oscillator with current conveyors and fractional-order admittances

Full size image

The characteristic equation of the circuit is

$$\begin{aligned} Y_{\alpha } Y_{\beta } R_{1} R_{2} -Y_\beta R_2 +1=0. \end{aligned}$$
(2)

Assuming that \(\omega _{0}\) is the oscillation frequency, the formula in (1) for the fractional admittance \(Y_{\alpha }\) will be simplified at this frequency to \(Y_{\alpha }=|Y_{\alpha 0}|j^{\alpha }\), and similarly \(Y_{\beta }=|Y_{\beta 0}|j^{\beta }\). After substituting these relations into (2), rearranging terms in order to separate real and imaginary parts and equating them to zero, we can derive the following relations

$$\begin{aligned} R_{1}= & {} \frac{\sin \left( \frac{\pi }{2}\beta \right) }{\left| {Y_{\alpha 0}}\right| \sin \left[ \frac{\pi }{2}\left( {\alpha +\beta }\right) \right] }, \end{aligned}$$
(3)
$$\begin{aligned} R_{2}= & {} \frac{\sin \left[ \frac{\pi }{2}\left( \alpha +\beta \right) \right] }{\left| {Y_{\beta 0}}\right| \sin \left( {\frac{\pi }{2}\alpha }\right) }. \end{aligned}$$
(4)

The expressions in (3)–(4) are used for computing the values of the resistances \(R_{1}\) and \(R_{2}\) in order the circuit to oscillate at the frequency \(\omega _{0}\). In other words, the values described by (3) and (4) fulfill the condition of oscillation. We do not show any relation for oscillation frequency as in fact it does not exist. It is due to the mathematical description of fractional admittances (1) chosen in the oscillator design. The oscillation frequency is simply \(\omega _{0}\), i.e., the value of frequency where the fractional admittances used in the oscillator have their magnitudes \(|Y_{\alpha 0}|\) and \(|Y_{\beta 0}|\).

Unfortunately, the oscillation frequency and condition cannot be set independently, but this problem seems to be common to this class of fractional-order oscillators.

To tune the oscillation frequency to a new value \(\omega _{0}^{\prime }\), the following formulas can be used

$$\begin{aligned} \frac{\omega _{0}^{\prime }}{\omega _0}=\left\{ {\frac{\sin \left( {\frac{\pi }{2}{\beta }'}\right) }{\left| {Y_{\alpha 0}}\right| R_1 ^{\prime }\sin \left[ {\frac{\pi }{2}\left( {{\alpha }'+{\beta }'} \right) }\right] }}\right\} ^{\frac{1}{{\alpha }'}}=\left\{ {\frac{\sin \left[ {\frac{\pi }{2}\left( {{\alpha }'+{\beta }'} \right) }\right] }{\left| {Y_{\beta 0}}\right| R_2^{\prime }\sin \left( {\frac{\pi }{2}{\alpha }'}\right) }}\right\} ^{\frac{1}{{\beta }'}}. \end{aligned}$$
(5)

Here \(|Y_{\alpha 0}|\) and \(|Y_{\beta 0}|\) are still the admittance magnitudes at the original oscillation frequency \(\omega _{0}\) and the single quotes at \(R_{1}\), \(R_{2}\), \(\alpha \), and \(\beta \) mean that their values are going to be modified in order to tune. The whole relation (5) must be valid to keep the circuit at the oscillation boundary, i.e., it represents the oscillation condition. Obtaining the relation (5) is similar to deriving (3) and (4) from the characteristic equation (2) with the difference in the substitution of fractional admittances by the relations

$$\begin{aligned} Y_\alpha ={\left| {Y_{\alpha 0}}\right| \left( {j\omega _{0}^{\prime }} \right) ^{{\alpha }'}}/{\omega _0^{{\alpha }'}}\hbox { and } Y_\beta ={\left| {Y_{\beta 0}}\right| \left( {j\omega _0^{\prime }} \right) ^{{\beta }'}}\Big /{\omega _0^{{\beta }'}}. \end{aligned}$$

It is apparent that the oscillation frequency and condition are influenced not only by resistances and magnitudes of admittances as in the case of classic oscillators but also by the admittance orders \(\alpha \) and \(\beta \). This increases the degree of freedom and brings other interesting properties that will be shown below.

Three voltage outputs (\(v_{0}\), \(v_{1}\), and \(v_{2}\)) are available as indicated in Fig. 1. Their voltages are related in the following way

$$\begin{aligned} v_{0}= & {} v_1 \left| Y_{\alpha 0}\right| R_1 e^{j\frac{\pi }{2}\alpha }, \end{aligned}$$
(6)
$$\begin{aligned} v_{2}= & {} \frac{v_1}{\left| Y_{\beta 0}\right| R_2}e^{-j\frac{\pi }{2}\beta }. \end{aligned}$$
(7)

It is seen that the phase shift between \(v_{0}\) and \(v_{1}\) is \(\alpha \pi /2\), between \(v_{2}\) and \(v_{1}\) is -\(\beta \pi /2\), and between \(v_{0}\) and \(v_{2}\) is \((\alpha +\beta ) \pi /2\). The phase difference between the output voltages can be set continuously depending on the parameters \(\alpha \) and \(\beta \). This property is unique and is not available at integer-order oscillators.

It is also interesting to determine sensitivities of the normalized oscillation frequency \((\omega _{0}'/\omega _{0})\) to the passive element parameters:

$$\begin{aligned}&S_{\left| Y_{\alpha 0}\right| }^{\frac{\omega _{0}^{\prime }}{\omega _{0}}}=S_{R_1}^{\frac{\omega _{0}^{\prime }}{\omega _0}} =-\frac{1}{\alpha }, \end{aligned}$$
(8)
$$\begin{aligned}&S_{\left| Y_{\beta 0}\right| }^{\frac{\omega _{0}^{\prime }}{\omega _0}} =S_{R_2}^{\frac{\omega _0 ^{\prime }}{\omega _0 }} =-\frac{1}{\beta }. \end{aligned}$$
(9)

The sensitivities increase in their absolute values with decreasing coefficients \(\alpha \) and \(\beta \). The oscillation frequency can be controlled by setting \(\alpha \) and \(\beta \) as seen in (5), but one must consider that in particular for low values of \(\alpha \) and \(\beta \), the oscillation frequency could be very sensitive to tolerances of passive element parameters.

3 Tuning of the Oscillation Frequency

Equation (5) suggests the possibilities of tuning the oscillation frequency. The first option is to modify the order (\(\alpha '\) and \(\beta '\)) of the admittances. This requires a controllable fractional-order element which can be based on principles described in [6]. The authors introduced an electronically controllable RC element with distributed parameters in bipolar technology. The second tuning possibility is varying resistances \(R_{1}\) and \(R_{2}\). This section analyzes both these tuning options and brings several characteristics that graphically illustrate the theoretical relations.

3.1 Tuning Through the Order of the Fractional Admittances

Let us aim at the tuning by the coefficients \(\alpha '\) and \(\beta '\). To simplify the analysis, both these coefficients will be considered equal \((\alpha '=\beta ')\) and, thus, (5) is transformed to

$$\begin{aligned} \frac{\omega _{0}^{\prime }}{\omega _0}=\left[ {\frac{1}{\left| {Y_{\alpha 0}}\right| 2R_{1}^{\prime }\cos \left( {\frac{\pi }{2}{\alpha }'}\right) }}\right] ^{\frac{1}{{\alpha }'}}=\left[ {\frac{2\cos \left( {\frac{\pi }{2}{\alpha }'}\right) }{\left| {Y_{\beta 0}}\right| R_2^{\prime }}} \right] ^{\frac{1}{{\alpha }'}}=\left( {\frac{1}{\left| {Y_{\alpha 0}}\right| \left| {Y_{\beta 0}}\right| R_1 ^{\prime }R_2^{\prime }}}\right) ^{\frac{1}{2{\alpha }'}}\!.\qquad \end{aligned}$$
(10)

Let us choose the initial magnitudes of fractional-order admittances \(|Y_{\alpha 0}|=|Y_{\beta 0}|=1/17{,}000\,\Omega ^{-1}\) and the fractional orders \(\alpha =\beta =0.5\). As already mentioned, if the admittances \(Y_{\alpha }\) and \(Y_{\beta }\) had these properties at a chosen frequency \(\omega _{0}\) and the resistances \(R_{1}\) and \(R_{2}\) are computed by (3) and (4), \(\omega _{0}\) would be the oscillation frequency. The calculated resistance values are \(R_{1}=12{,}021\,\Omega \), \(R_{2}=24{,}042\,\Omega \). The effect of increasing or decreasing the value of \(\alpha '\) compared to the initial value of 0.5 on the normalized oscillation frequency is presented in Fig. 2a. It should be noted that the resistance \(R_{1}\) remained constant during this tuning \((R_{1}=R_{1}'=12{,}021\,\Omega )\), and \(R_{2}\) was computed as a new value \(R_{2}'\) by \(R_{2}'=4R_{1}'\hbox {cos}^{2}(\pi \alpha '/2)\) in order to keep the whole relation (10) valid and thus to meet the oscillation condition. The computed values of \(R_{2}'\) vs \(\alpha '\) are depicted in Fig. 2b.

Fig. 2
figure 2

a Tuning of normalized oscillation frequency \((\omega _{0}'/\omega _{0})\) by changing the order of both fractional elements (\(R_{1}=\hbox {const.}\)), and b computed values of \(R_{2}'\) as a function of the order

Full size image

Another possibility is to set \(R_{2}\) constant \((R_{2}=R_{2}'= 24{,}042\,\Omega )\) and to compute \(R_{1}'\). This variant is presented in Fig. 3.

Fig. 3
figure 3

a Tuning of normalized oscillation frequency \((\omega _{0}'/\omega _{0})\) by changing the order of both fractional elements \((R_{2} = \hbox {const.})\); b computed values of \(R_{1}'\) as a function of the order

Full size image

The curve of the normalized oscillation frequency in Fig. 3a has inverse slope compared to the one in Fig. 2a, i.e., the frequency decreases with increasing \(\alpha '\). Figure 3b shows that the range of the computed resistance \(R_{1}'\) is high and \(R_{1}'\) rises dramatically at values of \(\alpha '\) close to one.

3.2 Tuning Through the Resistances \(R_{1}\) and \(R_{2}\)

Another possibility of setting the oscillation frequency resulting from (5) or (10) is changing resistances \(R_{1}'\) and \(R_{2}'\) while keeping constant the properties of fractional elements. Choosing \(|Y_{\alpha 0}|=Y_{\beta 0}|= 1/17{,}000\,\Omega ^{-1}\) and \(\alpha =\beta =\hbox {const}\)., the relation between \(R_{1}'\) and \(R_{2}'\) is similar to the previous subsection \(R_{2}'=4R_{1}'\hbox {cos}^{2}(\pi \alpha /2)\). Figure 4 depicts the tuning of the oscillator frequency by the resistances \(R_{1}'\) and \(R_{2}'\) for various values of \(\alpha =\beta =\hbox {const}\).

Fig. 4
figure 4

Tuning of normalized oscillation frequency \((\omega _{0}'/\omega _{0})\) by changing \(R_{1}'\) (and \(R_{2}'\)) for various values of \(\alpha = \beta \)

Full size image

It is obvious from the figure above that the slope of the oscillation frequency vs \(R_{1}'\) can be modified by \(\alpha =\beta \). Of particular interest is the increased range of the oscillation frequency at lower values of \(\alpha \). For example, with \(\alpha =0.2\) the oscillation frequency changes by five decades when the resistances \(R_{1}'\) and \(R_{2}'\) change by one decade. Thus, it is possible to obtain high oscillation frequencies when resistances and capacitances are relatively large compared to their values in classic oscillators. Similarly very low oscillation frequencies can be reached without necessity to increase R and C excessively. Of course one should again remember that sensitivities rise in this case as mentioned in the end of the Sect. 2.

4 Simulation and Experimental Measurement

The used BD-QFG DVCC was designed and fabricated in Cadence platform using \(0.35\,\upmu \hbox {m}\) CMOS AMIS process with total chip area of \(213 \times 266\,\upmu \hbox {m}\) [8]. The parameters of fractional elements are \(\alpha =\beta =0.5, |Y_{\alpha 0}|=|Y_{\beta 0}|= 1/17{,}000\,\Omega ^{-1}\) at \(\omega _{0}= 10{,}000\,\hbox {rad/s}\) \((f_{0}=1592\;\hbox {Hz})\). The resistances computed from (3) and (4) are again \(R_{1}=12{,}021\,\Omega \), \(R_{2}=24{,}042\,\Omega \). The value of oscillation frequency was chosen with respect to the properties of the BD-QFG conveyors and to the possible application of the oscillator in biomedical and/or other low-power applications.

The fractional elements were designed as RC circuits whose parameters were computed by a method that uses elliptic functions and results in an equal ripple approximation of the constant-argument characteristic [24]. The schematic of the RC circuit is illustrated in Fig. 5.

Fig. 5
figure 5

RC circuit approximating fractional admittance (resistances in Ohms, capacitances in Farads)

Full size image
Fig. 6
figure 6

Magnitude and phase frequency characteristics of impedance of RC circuit in Fig. 6 (thick lines) and their most deviated values from Monte Carlo analysis with 10 % R and C tolerances (thin lines)

Full size image

Structure with 10 resistors and nine capacitors was chosen in order to approximate the fractional admittance more accurately in a wider frequency range for the purpose of tuning verification. Approximation with a simpler structure can be sufficient if frequency tuning is not necessary or is limited to a narrow band. The impedance magnitude and phase frequency characteristics of the approximation RC circuit are shown by thick lines in Fig. 6. The effect of resistor and capacitor tolerances on the impedance magnitude and phase variations of the circuit in Fig. 5 has been studied. Monte Carlo analysis with 500 runs and 10 % tolerances of passive elements has been carried out. The most deviated magnitude and phase values from all the runs are presented by thin lines in Fig. 6. The standard deviations of the impedance magnitude and phase at the theoretical oscillation frequency 1592 Hz are 400 \(\Omega \) and 0.88\(^{\circ }\), respectively. With regard to the 10 % deviations of the passive elements, the approximating circuit offers satisfactory tolerances.

Cadence simulations of the designed oscillator have been carried out and the obtained output voltage waveforms of the oscillator are presented in Fig. 7.

Fig. 7
figure 7

Simulated output voltages of the designed oscillator versus time

Full size image

The simulated oscillation frequency is 1560 Hz which is near to the theoretically expected value 1592 Hz. The amplitudes are \(V_{0}=85\hbox { mV}\), \(V_{1}=120\hbox { mV}\), \(V_{2}=86\hbox { mV}\) and phase shifts are 45\(^{\circ }\).

In order to verify the tuning capability of the oscillator, the plot of the simulated oscillation frequency, setting \(\alpha '=\beta '\) and keeping \(R_{1}\) constant, as a function of the order is presented in Fig. 8.

Fig. 8
figure 8

Simulated oscillation frequency versus \(\alpha ' = \beta ' (R_{1}=\hbox {const.})\)

Full size image

The second considered possibility of tuning—by changing \(R_{1}'\) (while keeping \(\alpha =\beta =0.5\) and maintaining oscillation condition \(R_{2}' \approx 2R_{1}'\)) is shown in Fig. 9.

Fig. 9
figure 9

Simulated oscillation frequency versus \(R_{1}' (\alpha = \beta = 0.5)\)

Full size image

The oscillator was also implemented with samples of BD-QFG DVCC and passive element parameters mentioned at the beginning of this section. The experimental circuit is shown in Fig. 10, and the measured waveforms are presented in Fig. 11.

Fig. 10
figure 10

The experimental sample of the measured oscillator using BD-QFG DVCC. a Top side. b Bottom side

Full size image
Fig. 11
figure 11

Measured output voltages of the designed oscillator versus time

Full size image

The measured oscillation frequency is 1600 Hz which is almost equal to the theoretical one. Also the phase shifts between outputs (45.6 and 46.2\(^{\circ }\)) and amplitudes are in accordance with expectations.

The spectrum of the first output signal is shown in Fig. 12. The basic harmonic component is at least 40 dB larger than the higher ones. The value of THD computed from measured spectral components is approximately 1 %.

Fig. 12
figure 12

Measured spectrum of the first output voltage (vertical scale 20 dB/div, horizontal 2 kHz/div)

Full size image

Tuning the oscillation frequency by changing \(R_{1}'\) was also carried out with the experimental circuit. With \(R_{1}'=24\,\hbox {k}\Omega \) the oscillation frequency was 416 Hz (theoretically 399 Hz) and with \(R_{1}'=6.2\,\hbox {k}\Omega \) the oscillation frequency was 6 kHz (theoretically 5.98 kHz).

5 Conclusion

The aim of this paper was to present design and evaluation of fractional-order oscillator from the practical point of view. We have chosen a particular basic circuit with two current conveyors (employed in simulation and measurement by low-voltage low-power BD-QFG DVCCs), two grounded resistors, and two grounded fractional immittance elements (employed in simulation and measurement by RC ladder circuits). The theoretical analysis showed design rules for passive elements and possibilities of tuning which is possible also by setting orders of fractional elements. An arbitrary phase shift of output signals is another unique property which is not present in common integer-order oscillators. Simulation and the experimental results are very close to the theoretical ones and prove the attractive features of the designed oscillator.