1 Introduction

Fractional-order and classical integer-order calculus were proposed almost in the same period. However, in the early stage, fractional calculus was not well applied in engineering due to its imperfections in theory. Liouville made the first major study on fractional calculus in 1832, where he applied his definition to solve some problems in theory. After that, fractional calculus has been well applied and studied. Caputo and Mainardi [1] proposed a new dissipation model based on the memory effect of fractional derivative. Podlubny [2, 3] proved the convergence relation of the error between short and long memory and introduced the fractional-order PID controllers. Through the research by Shen et al. [4], Niu et al. [5], Yang et al. [6], Yaghi and Efe [7], it was found that the fractional-order PID controllers are indeed superior to the conventional PID controllers in performances. Moreover, the numerical calculation methods of fractional differential equation had been continuously improved. Lubich [8] proposed the fractional linear multistep method and showed numerical examples by Abel integral equation, diffusion problem and special functions in 1986. Diethelm et al. [9, 10] studied the fractional Adams method for the numerical solution of fractional differential equation. Zhu et al. [11], Kumar and Agrawal [12], Cao and Xu [13] also proposed some efficient numerical calculation methods.

The improvement of numerical calculation methods makes it easier for researchers to study the dynamic phenomena of fractional-order nonlinear systems such as bifurcation, chaos and synchronization. Cermak and Nechvatal [14] theoretically analyzed some local bifurcations in the fractional Chen system and discussed the chaotic behavior of the system with low-order derivatives. Lei et al. [15] used Melnikov method to study the chaotic behavior of a generalized Duffing-type oscillator with fractional-order deflection under dichotomous noise excitation. Niu et al. [16] investigated the chaos of the fractional-order Duffing system by the Melnikov method. Leung et al. [17, 18] proposed the residue harmonic balance method and studied the periodic bifurcation of Duffing–van der Pol oscillators with fractional derivatives and time delay by this method. He et al. [19], Eshaghi et al. [20, 21] and Du et al. [22] studied the chaos control of fractional-order dynamical systems and found some important phenomena.

Analytical research was also an important subject, and there were some important works on the resonance of fractional-order dynamic systems. Shen et al. [23, 24] studied the primary resonance of fractional-order Duffing oscillator and van der Pol oscillator by the averaging method and analyzed the effects of the fractional-order derivative on the amplitude–frequency response of these oscillator. Van Khang and Chien [25] studied the subharmonic resonance of Duffing oscillator with fractional-order derivative by the averaging method. For the conventional Duffing oscillators excited by multiple-term frequency, they may exhibit complex resonance phenomena, such as simultaneous resonance and combination resonance. Nayfeh and Yang [26, 27] studied the combination resonance and simultaneous resonance of some conventional Duffing oscillators under multiple-term frequency excitation. Moreover, Kacem et al. [28], Leung et al. [29] and Zhao [30] studied the resonance control of some conventional Duffing oscillators. However, the analytical research on the resonance of the fractional-order Duffing oscillator excited by multiple-term frequency is relatively few at present.

Duffing-type equations can describe many issues in engineering vibration, such as the forced vibration of viscoelastic beam [31, 32], the response of rotating machine [33] and the response of coupled pitch-roll ship [34]. Accordingly, the study on the primary and subharmonic simultaneous resonance of fractional-order Duffing oscillator is necessary. In this paper, the primary and subharmonic simultaneous resonance of fractional-order Duffing oscillator is studied analytically. In Sect. 2, an important formula is derived based on the Caputo’s definition, and the approximately analytical solution of the simultaneous resonance is obtained by the method of multiple scales. Section 3 presents the analysis on the steady-state response and its stability, multi-value characteristic and frequency response. In Sect. 4, the effects of nonlinear factor and fractional-order term on the steady-state response are analyzed by numerical simulation, and the results are discussed in depth.

2 The approximately analytical solution of Duffing oscillator with fractional-order derivative

The following Duffing oscillator with fractional-order derivative is considered

$$ m\ddot{u}\left( t \right) + c\dot{u}\left( t \right) + ku\left( t \right) + \alpha_{1} u^{3} \left( t \right) + \beta_{1} D^{p} u\left( t \right) = \bar{F}_{1} \cos \omega_{1} t + \bar{F}_{2} \cos \omega_{2} t , $$
(1)

where \( m \), \( c \), \( k \), \( \alpha_{1} \), \( \bar{F}_{i} \) and \( \omega_{i} \) (\( i = 1,\,2 \)) are the system mass, linear damping coefficient, linear stiffness coefficient, nonlinear stiffness coefficient, excitation amplitude and excitation frequency, respectively, and \( D^{p} u\left( t \right) \) is the p-order derivative of \( u\left( t \right) \) to \( t \) with the fractional coefficient \( \beta_{1} \) (\( \beta_{1} > 0 \)) and fractional order \( p \) (\( 0 \le p \le 1 \)). The fractional-order term is introduced in Eq. (1) due to the fact that many materials or devices in engineering exhibit obvious viscoelasticity, which could be accurately described by fractional-order derivative. There are several definitions for fractional-order derivative, such as Grünwald–Letnikov, Riemann–Liouville and Caputo definitions, and they are equivalent under some conditions for a wide class of functions [2]. However, one subtle difference is that the initial conditions for the fractional-order differential equations with the Caputo derivatives are in the same form as for the integer-order differential equations [35]. Therefore, Caputo’s definition is adopted

$$ D_{t}^{p} \left[ {u\left( t \right)} \right]\,: = \frac{1}{{\Gamma \left( {1 - p} \right)}}\int_{0}^{t} {\left( {t - s} \right)^{ - p} u^{\prime}\left( s \right)\;} {\text{d}}s, $$
(2)

where \( \Gamma \left( z \right) \) is Gamma function satisfying \( \Gamma \left( {z + 1} \right) = z\Gamma \left( z \right) \).

In order to make Eq. (1) satisfy the requirements for the method of multiple scales formally, one can set

$$ \begin{aligned} 2\varepsilon \mu & = \frac{c}{m},\quad \omega_{0}^{2} = \frac{k}{m},\quad \varepsilon \alpha = \frac{{\alpha_{1} }}{m},\quad \\ \varepsilon \beta & = \frac{{\beta_{1} }}{m},\quad F_{1} = \frac{{\bar{F}_{1} }}{m},\quad F_{2} = \frac{{\bar{F}_{2} }}{m}, \\ \end{aligned} $$

so that Eq. (1) becomes into

$$ \ddot{u}\left( t \right) + 2\varepsilon \mu \,\dot{u}\left( t \right) + \omega_{0}^{2} u\left( t \right) + \varepsilon \alpha {\kern 1pt} u^{3} \left( t \right) + \varepsilon \beta {\kern 1pt} D^{p} u\left( t \right) = F_{1} \cos \omega_{1} t + F_{2} \cos \omega_{2} t , $$
(3)

where \( \omega_{0} \) is natural frequency of linearized Eq. (1).

The primary and subharmonic simultaneous resonance (PSSR) means that \( \omega_{1} \) and \( \omega_{2} \) are close to \( \omega_{0} \) and \( 3\omega_{0} \), respectively, and \( F_{1} \) is enough small, i.e.,

$$ \begin{aligned} F_{1} & = \varepsilon f,\,\omega_{1} = \omega_{0} + \varepsilon \sigma_{1} ,\omega_{2} = 3\omega_{0} + \varepsilon \sigma_{2} , \\ f & = O\left( 1 \right),\sigma_{1} = O\left( 1 \right),\sigma_{2} = O\left( 1 \right), \\ \end{aligned} $$

where \( \sigma_{1} \) and \( \sigma_{2} \) are detuning factors. Accordingly, Eq. (3) can be transformed into

$$ \begin{aligned} \ddot{u}\left( t \right) + \omega_{0}^{2} u\left( t \right) & = \varepsilon [f\cos \left( {\omega_{0} t + \varepsilon \sigma_{1} t} \right) - 2\mu \,\dot{u}\left( t \right) \\ & \quad - \;\alpha {\kern 1pt} u^{3} \left( t \right) - \beta {\kern 1pt} D^{p} u\left( t \right)] + F_{2} \cos \left( {3\omega_{0} t + \varepsilon \sigma_{2} t} \right). \\ \end{aligned} $$
(4)

Here, we use the method of multiple scales to find the approximate solution of Eq. (4). The solution expressed in two different time scales is

$$ u\left( {t\,;\,\varepsilon } \right) = u_{0} \left( {T_{0} ,T_{1} } \right) + \varepsilon u_{1} \left( {T_{0} ,T_{1} } \right), $$
(5)

where \( T_{0} = t \) and \( T_{1} = \varepsilon t \).

Substituting Eq. (5) into Eq. (4) and equating the coefficients of \( \varepsilon^{0} \) and \( \varepsilon^{1} \) on both sides, one could obtain

$$ D_{0}^{2} u_{0} + \omega_{0}^{2} u_{0} = F_{2} \cos \left( {3\omega_{0} T_{0} + \sigma_{2} T_{1} } \right), $$
(6a)
$$ \begin{aligned} D_{0}^{2} u_{1} + \omega_{0}^{2} u_{1} & = - 2D_{0} D_{1} u_{0} + f\cos \left( {\omega_{0} T_{0} + \sigma_{1} T_{1} } \right) \\ & \quad - \;2\mu D_{0} u_{0} - \alpha u_{0}^{3} - \beta D_{{T_{0} }}^{p} u_{0} . \\ \end{aligned} $$
(6b)

The general solution of Eq. (6a) can be written as

$$ \begin{aligned} u_{0} \left( {T_{0} ,T_{1} } \right) & = a\left( {T_{1} } \right)\cos \left[ {\omega_{0} T_{0} + \theta \left( {T_{1} } \right)} \right] \\ & \quad + \;\frac{{F_{2} }}{{\omega_{0}^{2} - \omega_{2}^{2} }}\cos \left( {3\omega_{0} T_{0} + \sigma_{2} T_{1} } \right), \\ \end{aligned} $$
(7)

and it can also be written in the following form

$$ u_{0} \left( {T_{0} ,T_{1} } \right) = A\left( {T_{1} } \right)e^{{j\omega_{0} T_{0} }} + Be^{{j\left( {3\omega_{0} T_{0} + \sigma_{2} T_{1} } \right)}} + cc, $$
(8)

where \( A\left( {T_{1} } \right) = \frac{{a\left( {T_{1} } \right)}}{2}e^{{j\theta \left( {T_{1} } \right)}} \), \( B = \frac{{F_{2} }}{{2\left( {\omega_{0}^{2} - \omega_{2}^{2} } \right)}} \), \( j \) is the imaginary unit, and \( cc \) stands for the complex conjugate of the preceding terms.

An approximate formula should be derived before proceeding to the next step. According to Caputo’s definition, the p-order (\( 0 \le p \le 1 \)) derivative of \( e^{j\varOmega t} \) can be expressed as

$$ \begin{aligned} D_{t}^{p} e^{j\varOmega \,t} & = \frac{1}{{\Gamma \left( {1 - p} \right)}}\int_{0}^{t} {\left( {t - s} \right)^{ - p} j\varOmega {\kern 1pt} e^{{j\varOmega {\kern 1pt} s}} {\text{d}}s} \\ & = \frac{1}{{\Gamma \left( {1 - p} \right)}}\int_{0}^{t} {v^{ - p} j\varOmega {\kern 1pt} e^{{j\varOmega \left( {t - v} \right)}} {\text{d}}v} \\ & = \frac{{j\varOmega {\kern 1pt} e^{{j\varOmega {\kern 1pt} t}} }}{{\Gamma \left( {1 - p} \right)}}\int_{0}^{t} {v^{ - p} e^{{ - j\varOmega {\kern 1pt} v}} dv} \\ & = \frac{{j\varOmega {\kern 1pt} e^{{j\varOmega {\kern 1pt} t}} }}{{\Gamma \left( {1 - p} \right)}}\int_{0}^{t} {v^{ - p} \left( {\cos \varOmega v - j\sin \varOmega v} \right){\text{d}}v} \\ & = \frac{{\varOmega {\kern 1pt} e^{{j\varOmega {\kern 1pt} t}} }}{{\Gamma \left( {1 - p} \right)}}\left( {jI_{c} + I_{s} } \right), \\ \end{aligned} $$

where \( I_{c} = \int_{0}^{t} {v^{ - p} \cos \varOmega {\kern 1pt} v{\text{d}}v} \), \( I_{s} = \int_{0}^{t} {v^{ - p} \sin \varOmega {\kern 1pt} v{\text{d}}v} \). When \( t \to \infty \), there are the following approximate results

$$ I_{c} \approx \tilde{I}_{c} = \mathop {\lim }\limits_{t \to \infty } \int_{0}^{t} {v^{ - p} \cos \varOmega {\kern 1pt} v{\text{d}}v} = \varOmega^{p - 1} \Gamma \left( {1 - p} \right)\sin \left( {\frac{p\pi }{2}} \right), $$
(9a)
$$ I_{s} \approx \tilde{I}_{s} = \mathop {\lim }\limits_{t \to \infty } \int_{0}^{t} {v^{ - p} \sin \varOmega {\kern 1pt} v{\text{d}}v} = \varOmega^{p - 1} \Gamma \left( {1 - p} \right)\cos \left( {\frac{p\pi }{2}} \right). $$
(9b)

Therefore, the p-order derivative of \( e^{j\varOmega t} \) can be approximately written as

$$ D_{t}^{p} e^{{j\varOmega {\kern 1pt} t}} \approx \varOmega^{p} e^{{j\left( {\varOmega {\kern 1pt} t + \frac{p\pi }{2}} \right)}} . $$
(10)

Substituting Eq. (8) into Eq. (6b), where \( \beta D_{{T_{0} }}^{p} u_{0} \) can be calculated using Eq. (10), one could obtain the following condition to eliminate secular terms from \( u_{1} \)

$$ \begin{aligned} & - 2j\omega_{0} D_{1} A - 3\alpha A^{2} \bar{A} - 6\alpha AB^{2} - \beta \omega_{0}^{p} Ae^{{j\frac{p\pi }{2}}} \\ & \quad - \;2j\mu \omega_{0} A - 3\alpha \bar{A}^{2} Be^{{j\sigma_{2} T_{1} }} + \frac{f}{2}e^{{j\sigma_{1} T_{1} }} = 0. \\ \end{aligned} $$
(11)

By substituting \( A\left( {T_{1} } \right) = \frac{{a\left( {T_{1} } \right)}}{2}e^{{j\theta \left( {T_{1} } \right)}} \) into Eq. (11) and separating the real and imaginary parts, the differential equations about slowly varying amplitude \( a\left( {T_{1} } \right) \) and phase \( \theta \left( {T_{1} } \right) \) are obtained as follows:

$$ \begin{aligned} D_{1} a & = - \mu {\kern 1pt} a + \frac{{3\alpha \,a^{2} B}}{{4\omega_{0} }}\sin \left( {3\theta - \sigma_{2} T_{1} } \right) - \frac{f}{{2\omega_{0} }}\sin \left( {\theta - \sigma_{1} T_{1} } \right) \\ & \quad - \;\frac{a}{2}\beta \,\omega_{0}^{p - 1} \sin \left( {\frac{p\pi }{2}} \right), \\ \end{aligned} $$
(12a)
$$ \begin{aligned} aD_{1} \theta & = \frac{{3\alpha {\kern 1pt} a{\kern 1pt} B^{2} }}{{\omega_{0} }} + \frac{{3\alpha {\kern 1pt} a^{3} }}{{8\omega_{0} }} + \frac{{3\alpha {\kern 1pt} a^{2} B}}{{4\omega_{0} }}\cos \left( {3\theta - \sigma_{2} T_{1} } \right) \\ & \quad - \;\frac{f}{{2\omega_{0} }}\cos \left( {\theta - \sigma_{1} T_{1} } \right) + \frac{a}{2}\beta \,\omega_{0}^{p - 1} \cos \left( {\frac{p\pi }{2}} \right). \\ \end{aligned} $$
(12b)

Then, the first-order approximately analytical solution of Eq. (3) can be expressed as

$$ u\left( t \right) = a\cos \left( {\omega_{0} t + \theta } \right) + 2B\cos \omega_{2} t, $$
(13)

where \( a \) and \( \theta \) are functions in slow time scale \( T_{1} \), and determined by Eq. (12).

3 The steady-state response and its stability

The system stability, especially the stability of steady-state response, is an important issue in engineering vibration, so that the steady-state response and system stability are considered in this section. Observing Eq. (12), it can be found that steady-state motions (i.e., \( D_{1} a = 0 \) and \( D_{1} \theta = 0 \)) exist if, and only if, both \( \theta - \sigma_{1} T_{1} \) and \( 3\theta - \sigma_{2} T_{1} \) are constants, that means \( D_{1} \theta = \sigma_{1} = \sigma_{2} /3 \). Therefore steady-state motions exist only when \( \omega_{1} = \omega_{2} /3 \) is strictly satisfied. Letting \( \sigma_{1} = \sigma_{2} /3 = \sigma \) and \( \theta - \sigma T_{1} = \varphi \) in Eq. (12), it will become into the following autonomous form

$$ D_{1} a = - \mu {\kern 1pt} a + \frac{{3\alpha \,a^{2} B}}{{4\omega_{0} }}\sin 3\varphi - \frac{f}{{2\omega_{0} }}\sin \varphi - \frac{a}{2}\beta \,\omega_{0}^{p - 1} \sin \left( {\frac{p\pi }{2}} \right), $$
(14a)
$$ \begin{aligned} aD_{1} \varphi & = - \sigma a + \frac{{3\alpha {\kern 1pt} a{\kern 1pt} B^{2} }}{{\omega_{0} }} + \frac{{3\alpha {\kern 1pt} a^{3} }}{{8\omega_{0} }} + \frac{{3\alpha {\kern 1pt} a^{2} B}}{{4\omega_{0} }}\cos 3\varphi \\ & \quad - \;\frac{f}{{2\omega_{0} }}\cos \varphi + \frac{a}{2}\beta \,\omega_{0}^{p - 1} \cos \left( {\frac{p\pi }{2}} \right). \\ \end{aligned} $$
(14b)

Correspondingly, the approximately analytical solution becomes into

$$ u\left( t \right) = a\cos \left( {\omega_{1} t + \varphi } \right) + 2B\cos \omega_{2} t, $$
(15)

where \( a \) and \( \varphi \) are determined by Eq. (14).

In order to verify the correctness and precision of the analytical solution, the obtained result is compared with numerical solution, where the analytical solution and the numerical solution are calculated by Eqs. (15) and (3), respectively. The numerical calculation method introduced in Ref. [35] is used to calculate the numerical solution, and the calculation scheme is as follows:

$$ x\left( {t_{k} } \right) = y\left( {t_{k - 1} } \right)h^{{q_{1} }} - \sum\limits_{n = 1}^{k} {c_{n}^{{\left( {q_{1} } \right)}} x\left( {t_{k - 1} } \right)} , $$
(16a)
$$ \begin{aligned} y\left( {t_{k} } \right) & = [F_{1} \cos \omega_{1} t_{k} + F_{2} \cos \omega_{2} t_{k} - 2\varepsilon \mu y\left( {t_{k - 1} } \right) \\ & \quad - \omega_{0}^{2} x\left( {t_{k} } \right) - \varepsilon \alpha x^{3} \left( {t_{k} } \right) - \varepsilon \beta z\left( {t_{k - 1} } \right)]h^{{q_{2} }} \\ & \quad - \sum\limits_{n = 1}^{k} {c_{n}^{{\left( {q_{2} } \right)}} y\left( {t_{k - 1} } \right)} , \\ \end{aligned} $$
(16b)
$$ z\left( {t_{k} } \right) = y\left( {t_{k} } \right)h^{{q_{3} }} - \sum\limits_{n = 1}^{k} {c_{n}^{{\left( {q_{3} } \right)}} z\left( {t_{k - 1} } \right)} , $$
(16c)

where \( q_{1} = q_{2} = 1 \), \( q_{3} = 1 - p \), and \( c_{n}^{\left( q \right)} \) is the fractional binomial coefficient with the iterative relationship as \( c_{0}^{\left( q \right)} = 1 \) and \( c_{n}^{\left( q \right)} = \left( {1 - \frac{1 + q}{n}} \right)c_{n - 1}^{\left( q \right)} \). According to Eq. (10), the initial value of fractional-order term is given by

$$ D_{t}^{p} \left[ {u\left( t \right)} \right]\left| {_{t = 0} } \right. = u\left( 0 \right)\omega_{0}^{p} \cos \left( {\frac{p\pi }{2}} \right). $$
(17)

A set of basic parameters of the demonstrated system are defined as \( \varepsilon { = 0} . 1 \), \( \mu { = 0} . 1 \), \( \omega_{0} = 2 \), \( \alpha = 5 \), \( \beta = 1 \), \( p = 0.6 \), \( F_{1} = 0.1 \), \( F_{2} = 24 \), and \( \omega_{2} = 3\omega_{1} \). For each given \( \omega_{1} \), the system is simulated for 300 time units, and the time-step is set to \( 0.001 \) (the same below). Taking the maximum amplitude after 270 time units as the steady-state amplitude \( \bar{u} \), the amplitude–frequency curves of the system can be obtained as shown in Fig. 1. Moreover, setting \( \omega_{1} = 2.2 \), \( \left( {a_{0} \,,\,\varphi_{0} } \right) = \left( {2\,,\,0} \right) \), and the corresponding initial values of the numerical solution calculated by Eqs. (15) and (17) is \( \left( {u_{0} \;,\;\dot{u}_{0} \;,\;D^{p} u_{0} } \right) = \left( { 1. 3 9 3 3\;,\; 0. 0 1 6 7\; ,\; 1. 2 4 1 3} \right) \). Then, the comparison of the displacement time history between the analytical and the numerical solution can be plotted in Fig. 2.

Fig. 1
figure 1

Comparison of amplitude–frequency curves by the approximately analytical solution (the solid line) and the numerical solution (the circles): a system response to \( \omega_{1} \); b system response to \( \omega_{2} \)

Full size image
Fig. 2
figure 2

Comparison of displacement time histories by the approximately analytical solution (the solid line) and the numerical solution (the circles), where \( \omega_{1} = 2.2 \), \( \omega_{2} = 3\omega_{1} \): a transient response; b steady-state response

Full size image

Figure 1 shows that the error of analytical solution is low in a wide range of frequency, and it can be seen from Fig. 2 that both the transient and steady-state response of analytical solution are relatively accurate in the resonance range.

In addition, it can be found that the steady-state response is multi-value in a certain range of frequency. In fact, other branches can also be obtained, and they are stable, if the initial value of the simulation is changed suitably. The reason for the above phenomenon can be revealed from Eq. (15), i.e., the multi-value characteristic and stability of the steady-state response are subjected to the first part (i.e., \( a\cos \left( {\omega_{1} t + \varphi } \right) \)) in the analytical solution. Therefore, we will only focus on this part in the stability analysis of the steady-state response.

Letting \( D_{ 1} a = 0 \), \( D_{1} \varphi = 0 \), and marking steady-state amplitude as \( \bar{a} \) and steady-state phase as \( \bar{\varphi } \), one could obtain

$$ \frac{{3\alpha \,\bar{a}^{2} B}}{{4\omega_{0} }}\sin 3\bar{\varphi } - \frac{f}{{2\omega_{0} }}\sin \bar{\varphi } = \mu {\kern 1pt} \bar{a} + \frac{{\bar{a}}}{2}\beta \,\omega_{0}^{p - 1} \sin \left( {\frac{p\pi }{2}} \right), $$
(18a)
$$ \begin{aligned} & \frac{{3\alpha {\kern 1pt} \bar{a}^{2} B}}{{4\omega_{0} }}\cos 3\bar{\varphi } - \frac{f}{{2\omega_{0} }}\cos \bar{\varphi } \\ & \quad = \sigma \bar{a} - \frac{{3\alpha {\kern 1pt} \bar{a}{\kern 1pt} B^{2} }}{{\omega_{0} }} - \frac{{3\alpha {\kern 1pt} \bar{a}^{3} }}{{8\omega_{0} }} - \frac{{\bar{a}}}{2}\beta \,\omega_{0}^{p - 1} \cos \left( {\frac{p\pi }{2}} \right). \\ \end{aligned} $$
(18b)

Furthermore, the amplitude–frequency equation and phase–frequency equation of steady-state response can be obtained as follows:

$$ \begin{aligned} & \left[ {24\alpha \beta \omega_{0}^{p} \left( {\bar{a}^{2} + 8B^{2} } \right)\cos \frac{p\pi }{2} - 48\sigma \alpha \omega_{0} \left( {\bar{a}^{2} + 8B^{2} } \right) + 3\alpha \left( {3\alpha \bar{a}^{4} + 36\alpha \bar{a}^{2} B^{2} + 192\alpha B^{4} - 8Bf} \right)} \right. \\ & \left. { + 16\beta^{2} \omega_{0}^{2p} - 64\beta \omega_{0}^{p + 1} \left( {\sigma \cos \frac{p\pi }{2} - \mu \sin \frac{p\pi }{2}} \right) + 64\omega_{0}^{2} \left( {\sigma^{2} + \mu^{2} } \right)} \right]^{2} \left[ {9\alpha^{2} \bar{a}^{6} + 108\alpha^{2} \bar{a}^{4} B^{2} } \right. \\ & + 48\alpha \bar{a}^{2} B\left( {12\alpha B^{3} + f} \right) + 24\alpha \bar{a}^{2} \beta \omega_{0}^{p} \left( {\bar{a}^{2} + 8B^{2} } \right)\cos \frac{p\pi }{2} - 48\alpha \bar{a}^{2} \sigma \omega_{0} \left( {\bar{a}^{2} + 8B^{2} } \right) + 16\bar{a}^{2} \beta^{2} \omega_{0}^{2p} \\ & \left. { - 64\bar{a}^{2} \beta \omega_{0}^{p + 1} \left( {\sigma \cos \frac{p\pi }{2} - \mu \sin \frac{p\pi }{2}} \right) + 64\bar{a}^{2} \omega_{0}^{2} \left( {\sigma^{2} + \mu^{2} } \right) - 16f^{2} } \right] \\ & = 98304\alpha B\omega_{0}^{2} f^{3} \left( {\mu + \frac{1}{2}\beta \omega_{0}^{p - 1} \sin \frac{p\pi }{2}} \right)^{2} \\ \end{aligned} $$
(19a)
$$ \begin{aligned} & 4\left( {9\bar{a}^{4} \alpha^{2} B^{2} - 12\bar{a}^{2} \alpha Bf\cos 2\bar{\varphi } + 4f^{2} } \right) \\ & \quad - \;\bar{a}^{2} \left[ {9\alpha^{2} \left( {\bar{a}^{2} + 8B^{2} } \right)^{2} + 24\alpha \beta \omega_{0}^{p} \left( {\bar{a}^{2} + 8B^{2} } \right)} \right.\cos \frac{p\pi }{2} \\ & \quad - \;48\sigma \alpha \omega_{0} \left( {\bar{a}^{2} + 8B^{2} } \right) + 16\beta^{2} \omega_{0}^{2p} \\ & \quad \left. { - \;64\beta \omega_{0}^{p + 1} \left( {\sigma \cos \frac{p\pi }{2} - \mu \sin \frac{p\pi }{2}} \right) + 64\omega_{0}^{2} \left( {\mu^{2} + \sigma^{2} } \right)} \right] = 0. \\ \end{aligned} $$
(19b)

Next, the stability condition of the steady-state response will be derived by Lyapunov’s first method. Defining a state vector \( {\mathbf{V}} = \left[ {a\;,\;\varphi } \right]^{\text{T}} \), a vector function is generated as

$$ F\left( {\mathbf{V}} \right) = {\dot{\mathbf{V}}} = \left[ {\begin{array}{*{20}c} { - \mu {\kern 1pt} a + \frac{{3\alpha \,a^{2} B}}{{4\omega_{0} }}\sin 3\varphi - \frac{f}{{2\omega_{0} }}\sin \varphi - \frac{a}{2}\beta \,\omega_{0}^{p - 1} \sin \left( {\frac{p\pi }{2}} \right)} \\ { - \sigma + \frac{{3\alpha {\kern 1pt} {\kern 1pt} B^{2} }}{{\omega_{0} }} + \frac{{3\alpha {\kern 1pt} a^{2} }}{{8\omega_{0} }} + \frac{{3\alpha {\kern 1pt} aB}}{{4\omega_{0} }}\cos 3\varphi - \frac{f}{{2a\omega_{0} }}\cos \varphi + \frac{1}{2}\beta \,\omega_{0}^{p - 1} \cos \left( {\frac{p\pi }{2}} \right)} \\ \end{array} } \right]. $$
(20)

The Jacobi matrix and the characteristic equation of \( F\left( {\mathbf{V}} \right) \) at the steady-state response are as follows:

$$ {\mathbf{J}} = \left[ {\begin{array}{*{20}c} {\frac{{3\bar{a}\alpha B\sin 3\bar{\varphi }}}{{2\omega_{0} }} - \frac{1}{2}\beta \omega_{0}^{p - 1} \sin \frac{p\pi }{2} - \mu \quad } & {\frac{{9\bar{a}^{2} \alpha B\cos 3\bar{\varphi }}}{{4\omega_{0} }} - \frac{{f\cos \bar{\varphi }}}{{2\omega_{0} }}} \\ {\frac{{f\cos \bar{\varphi }}}{{2\bar{a}^{2} \omega_{0} }}{ + }\frac{{3\bar{a}\alpha }}{{ 4\omega_{0} }} + \frac{{3\alpha B\cos 3\bar{\varphi }}}{{ 4\omega_{0} }}} & {\frac{{f\sin \bar{\varphi }}}{{2\bar{a}\omega_{0} }} - \frac{{9\bar{a}\alpha B\sin 3\bar{\varphi }}}{{4\omega_{0} }}} \\ \end{array} } \right], , $$
(21a)

and

$$ \lambda^{2} - P\lambda + Q = 0, $$
(21b)

where \( P = {\text{tr}}{\mathbf{J}} \), \( Q = \det \left[ {\mathbf{J}} \right] \).

According to Lyapunov’s theory, the stability condition of steady-state response is \( P < 0 \) and \( Q > 0 \). For the damped system, there is always \( P < 0 \). Accordingly, the stability condition of the researched system is Q > 0, i.e.,

$$ \begin{aligned} & 27\bar{a}^{6} \alpha^{2} - 1728\bar{a}^{2} \alpha^{2} B^{4} + 48\bar{a}\alpha f\left( {\bar{a}^{2} + 16B^{2} } \right)\cos \bar{\varphi } \\ & \quad - \;48\bar{a}^{2} \beta^{2} \omega_{0}^{2p} + 192\bar{a}^{2} \beta \omega_{0}^{p + 1} \left( {\sigma \cos \frac{p\pi }{2} - } \right.\left. {\mu \sin \frac{p\pi }{2}} \right) \\ & \quad - \;192\bar{a}^{2} \omega_{0}^{2} \left( {\sigma^{2} + \mu^{2} } \right) - 64\bar{a}\beta \omega_{0}^{p} \left[ {9\bar{a}\alpha B^{2} \cos \frac{p\pi }{2} - 2f\cos \left( {\bar{\varphi } + \frac{p\pi }{2}} \right)} \right] \\ & \quad + \;128\bar{a}\omega_{0} \left( {9\sigma \bar{a}\alpha B^{2} - } \right.\left. {2f\mu \sin \bar{\varphi } - 2f\sigma \cos \bar{\varphi }} \right) - 64f^{2} > 0. \\ \end{aligned} $$
(22)

Up to now, for each \( \sigma \) satisfying the aforementioned limit, all corresponding steady-state solutions \( \left( {\sigma_{i} {\kern 1pt} ,\bar{a}_{i} {\kern 1pt} ,\bar{\varphi }_{i} } \right) \) can be obtained from Eq. (19) and their stability can be determined by Eq. (22). The parameters of the demonstrated system are still defined as \( \varepsilon = 0.1 \), \( \mu = 0.1 \), \( \omega_{0} = 2 \), \( \alpha = 5 \), \( \beta = 1 \), \( p = 0.6 \), \( F_{1} = 0.1 \), and \( F_{2} = 24 \). In Figs. 3 and 4, the typical amplitude–frequency and phase–frequency curves are shown, respectively. It can be seen from Fig. 3 that there are as many as three bifurcation points in the amplitude–frequency response, namely \( H_{11} \), \( H_{12} \), and \( H_{13} \), which correspond to \( H_{21} \), \( H_{22} \), and \( H_{23} \) in the phase–frequency response, respectively. Furthermore, it can be found from Figs. 3 and 4 that there are as many as seven branches s1 ~ s7, which means that the whole responses of Eq. (3) also have up to seven branches S1 ~ S7 in a certain range of frequency. For instance, the corresponding four stable periodic orbits of S1, S3, S4 and S6 are as shown in Fig. 5, where \( \sigma = 2.5 \) (i.e., \( \omega_{1} = 2.25 \) and \( \omega_{2} = 3\omega_{1} \)),and the initial values \( \left( {u_{0} \;,\;\dot{u}_{0} \;,\;D^{p} u_{0} } \right) \) of the four groups are set as \( \left( { 1. 0 8 2 5\;,\; 0. 7 2 7 6\;,\;0.9644} \right) \), \( \left( {{ - 0} . 7 2 7 5\; ,\; 0. 3 4 8 2\; ,\;{ - 0} . 6 4 8 1} \right) \), \( \left( {{ - 1} . 4 8 9 5\; ,\; 3. 1 9 4 4\; ,\;{ - 1} . 3 2 7 1} \right) \), \( \left( {{ - 1} . 0 2 9 8\;,\;{ - 3} . 0 4 7 8\; ,\;{ - 0} . 9 1 7 4} \right) \), respectively.

Fig. 3
figure 3

Amplitude–frequency curves of steady-state resonance (the circles for stable solution and the asterisks for unstable one), and the three bifurcation points are \( H_{11} \left( { 1. 2 0 0 0\; ,\; 0. 3 9 9 4} \right) \), \( H_{12} \left( { 1. 8 0 0 0\; ,\; 1. 1 2 1 1} \right) \) and \( H_{13} \left( { 2. 0 0 0 0\; ,\; 0. 4 8 5 4} \right) \), respectively

Full size image
Fig. 4
figure 4

Phase–frequency curves of steady-state resonance (the circles for stable solution and the asterisks for unstable one), and the three bifurcation points are \( H_{21} \left( { 1. 2 0 0 0\; ,\;{ - 1} . 7 2 6 5} \right) \), \( H_{22} \left( { 1. 8 0 0 0\; ,\;{ - 2} . 8 0 1 2} \right) \) and \( H_{23} \left( { 2. 0 0 0 0\; ,\; 1. 6 2 5 0} \right) \), respectively

Full size image
Fig. 5
figure 5

Four stable periodic orbits of Eq. 3

Full size image

This multi-value characteristic can be used for system status switching, i.e., as long as the state variables (i.e., \( u \) and \( \dot{u} \)) of the oscillator are switched to another periodic orbit, the system will run stably in the new periodic orbit. It should be noted that in practice, it is necessary to ensure that the status switching process is smooth, which may involve the process control method, and the smoothness is not considered here. Just as an example, the case of \( \sigma = 2.5 \) is still considered, and two points \( O_{1} \left( { - 0.4859\,,\,0.1323} \right) \) and \( O_{2} \left( { - 1.018\,,\, - 3.502} \right) \) on S3 and S6 are marked, respectively, in the state space. Then, \( O_{1} \) is set to the initial value of Eq. (3). After running for 320 time units, one can let the oscillator switch to \( O_{2} \) and continue to run for 320 time units. The phase trajectory of Eq. (3) can be obtained as shown in Fig. 6. In addition, as previously stated, many engineering vibration issues are related to Duffing system. For the rotating machine, it may pass through the resonance regions during starting and/or stopping processes. At this time, the system response can be switched between multiple branches, and the amplitude will suddenly increase or decrease, which is called jump phenomenon. This phenomenon was observed in the experiment of Ref. [36].

Fig. 6
figure 6

Status switching from S3 to S6

Full size image

4 The effects of system parameters on amplitude–frequency curves

4.1 The effect of nonlinear factor \( \varvec{\alpha} \)

In order to reveal the effect of nonlinear factor on the system, the demonstrated system is simulated under different \( \alpha \), where other parameters are still defined as \( \varepsilon = 0.1 \), \( \mu = 0.1 \), \( \omega_{0} = 2 \), \( \beta = 1 \), \( p = 0.6 \), \( F_{1} = 0.1 \) and \( F_{2} = 24 \). The effects of nonlinear factor on stiffness hardening system (i.e., \( \alpha > 0 \)) and stiffness softening system (i.e., \( \alpha < 0 \)) are shown in Fig. 7. It can be seen that for the stiffness hardening system, the topologies of amplitude–frequency curves of primary and 1/3 subharmonic resonance are emerged simultaneously in the PSSR range. And \( \alpha \) mainly affects the amplitude in a certain range of frequency, i.e., the amplitude decreases due to the gradual hardening of the stiffness. However, for the stiffness softening system, the amplitude–frequency curves of PSSR shows special topologies, and \( \alpha \) affects the amplitude, multi-value characteristic and stability simultaneously. That means the resonance peak decreases and the system tends to be stable with the gradual softening of stiffness.

Fig. 7
figure 7

Effects of nonlinear factor (the circles for stable solution and the asterisks for the unstable one): a Stiffness hardening system; b Stiffness softening system

Full size image

4.2 The effect of fractional order \( {p} \)

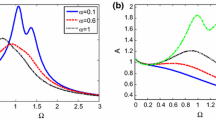
In this section, we investigate how the variation of fractional order \( p \) affects the system. The parameters of the demonstrated system are defined as \( \varepsilon = 0.1 \), \( \mu = 0.1 \), \( \omega_{0} = 2 \), \( \alpha = 5 \), \( \beta = 0.3 \), \( F_{1} = 0.1 \) and \( F_{2} = 24 \). Through numerical calculation, the amplitude–frequency curves of \( p = 0.2 \), \( p = 0.5 \), \( p = 0.7 \) and \( p = 1 \) can be obtained, respectively, as shown in Fig. 8a. In this demonstrated system, \( p \) mainly affects the feature of subharmonic resonance, but has a slight influence on the feature of primary resonance.

Fig. 8
figure 8

Effects of fractional order \( p \): a Stiffness hardening system; b Stiffness softening system

Full size image

Considering the particularity of the stiffness softening system, we do another numerical calculation for \( \alpha = - 8 \), and the result is shown in Fig. 8b. This result still shows that \( p \) mainly affects the feature of subharmonic resonance, which means that it is possible to change one of the resonance features independently by selecting appropriate parameters, even simultaneous resonance.

Furthermore, the jump phenomenon mentioned in Sect. 3 is also affected by the fractional order \( p \). The demonstration system and numerical conditions in Sect. 3 are still used, but the fractional order is defined as \( p = 0.2 \), \( p = 0.4 \) and \( p = 0.6 \), respectively. By repeating the simulation process in Fig. 1, the amplitude–frequency curves of the system with different \( p \) can be obtained, and it is shown in Fig. 9. In this figure, three jump points \( R_{1} \), \( R_{2} \) and \( R_{3} \) corresponding to different \( p \) are marked, respectively. It can be found that the frequency of jump point shifting to lower frequency with the increase in fractional order \( p \).

Fig. 9
figure 9

Effects of fractional order \( p \) on jump phenomenon, where the corresponding frequencies of \( R_{1} \), \( R_{2} \) and \( R_{3} \) are \( \omega_{1} = 3.48 \), \( \omega_{1} = 3.38 \) and \( \omega_{1} = 3.28 \), respectively: a panoramic view; b local view

Full size image

4.3 The effect of fractional coefficient \( {\beta} \)

Two cases of \( p \gg 0.5 \) and \( p \ll 0.5 \) is considered here. Considering the case of \( p \gg 0.5 \) firstly, the parameters of the demonstrated system are defined as \( p = 0.9 \), \( \varepsilon = 0.1 \), \( \mu { = 0} . 1 \), \( \omega_{ 0} { = 2} \), \( \alpha { = }5 \), \( F_{1} = 0.1 \) and \( F_{2} = 24 \). The evolutions of the amplitude–frequency curves due to the variation of the fractional coefficient \( \beta \) are shown in Fig. 10. Furthermore, for the ease of comparison, the evolutions of the amplitude–frequency curves due to the variation of linear damping coefficient \( \mu \) are also given for \( p = 0.6 \) and \( \beta = 1 \), which is shown in Fig. 11. From Figs. 10 and 11, it can be found that the effect of the fractional coefficient \( \beta \) is almost equivalent to the effect of the linear damping coefficient \( \mu \) when \( p \gg 0.5 \). With the increase in \( \beta \) and \( \mu \), the corresponding primary resonance is reduced significantly, and the existing region for subharmonic resonance is also decreased.

Fig. 10
figure 10

The evolutions of the amplitude–frequency curves due to the change of \( \beta \) when \( p \gg 0.5 \) (the circles for stable solution and the asterisks for unstable one): a \( \beta = 0.6 \); b \( \beta = 1 \); c \( \beta = 1.06 \); d \( \beta = 1.3 \)

Full size image
Fig. 11
figure 11

The evolutions of the amplitude–frequency curves due to the change of \( \mu \) (the circles for stable solution and the asterisks for unstable one): a \( \mu = 0.1 \); b \( \mu = 0.26 \); c \( \mu = 0.28 \); d \( \mu = 0.4 \)

Full size image

Next, considering the case of \( p \ll 0.5 \), the parameters of the previous demonstrated system are still used, but the fractional order is modified to \( p = 0.1 \). According to the previous conclusions, the peak and topology of the amplitude–frequency curves are mainly affected by nonlinear factors and linear damping, respectively. Therefore, \( \beta \) has almost no effect on the structure of the amplitude–frequency curve when \( p \ll 0.5 \), which is confirmed in Fig. 12. That means the increase in \( \beta \) only leads to the resonance regions shifting to high frequency.

Fig. 12
figure 12

The evolutions of the amplitude–frequency curves due to the change of \( \beta \) when \( p \ll 0.5 \) (the circles for stable solution and the asterisks for unstable one): a \( \beta = 0.5 \); b \( \beta = 2 \); c \( \beta = 3.5 \)

Full size image

In fact, \( \beta \) has different effects under different \( p \), and the reason for this phenomenon is that the fractional-order term in the system has the functions of linear stiffness and linear damping simultaneously. In other words, if \( p \gg 0.5 \), the linear damping effect of fractional-order term will be stronger, so that the effect on the system is almost equivalent to that of linear damping. However, if \( p \ll 0.5 \), the linear stiffness effect of fractional-order term will be stronger, and the increase in \( \beta \) leads to the increase in system stiffness, which increases the natural frequency of the system, so that the resonance regions shift to high frequency. Regarding the equivalent linear stiffness and equivalent linear damping of fractional-order term, their calculation methods have been given quantitatively in Ref. [23], and here we only discuss them qualitatively.

5 Conclusions

The primary and subharmonic simultaneous resonance of Duffing oscillator with fractional-order derivative is studied. Firstly, the fractional-order derivative for \( e^{j\varOmega t} \) is derived approximately based on Caputo’s definition, and the approximately analytical solution is obtained by the method of multiple scales. Then, the correctness and satisfactory precision of the analytical solution are verified by numerical simulation. Additionally, the stability and multi-value characteristic of the system are discussed. The stability condition of the steady-state response is derived by the Lyapunov’s first method, and the stability of steady-state response is analyzed based on this condition. It is found that there are at most seven branches in the steady-state response, including four stable branches and three unstable branches. Finally, the effects of system parameters are analyzed by numerical calculation, especially the effect of fractional-order term in the system, i.e., equivalent linear stiffness and equivalent linear damping. They are embodied simultaneously in the dynamic system, and the focus and intensity of the effects are determined by \( p \) and \( \beta \), respectively.