1 Introduction

In this work, the generalized Duffing-type differential equation with fractional-order deflection is considered:

$$\begin{aligned} \ddot{x}-ax+bx\left| x \right| ^{\alpha -1}=-\varepsilon \delta \dot{x}+\varepsilon \gamma \cos \, \omega t, \end{aligned}$$
(1)

where \(\ddot{x}\) is an inertial term with unit mass, \(-\varepsilon \delta \dot{x}\) represents linear damping, and \(\varepsilon \gamma \cos \, \omega t\) is an excitation with period \(T=\frac{2\pi }{\omega }\). To satisfy the Melnikov technique requirements, damping and excitation are assumed to be small-amplitude perturbations, that is, \(0<\varepsilon<<1\). The restitution force \(-ax+bx\left| x \right| ^{\alpha -1}(a>0,b>0\), and \(\alpha >1)\) is composed of a linear feedback term and a nonlinear feedback term with fractional-order deflection. Equation (1) can be used to model the oscillatory motion for the modal displacement \(x\left( t \right) \) of a buckled beam with simply supported or hinged ends [1]. The constant \(\alpha \) is an integer or a fraction which depends on the material and bending properties of the beam.

Many materials with elastic properties are not linear based on the value of \(\alpha \). For example, the elastic properties of aircraft materials, such as aluminum and titanium, are of Ramberg–Osgood type [2] where \(\alpha \) is a fraction higher than 1. For copper and copper alloys with Ludwick elastic properties [3, 4], \(\alpha \) is a rational number that is determined experimentally. The constitutive models of wood [5, 6], polymers [5, 7], and composite materials [5, 8] are presented in polynomial form where \(\alpha =3\), and the differential equation of a beam’s motion is of Duffing type with strong cubic nonlinearity. The vibrations of a piano hammer, which is a wooden beam coated with several layers of compressed wool felts, are described with dynamic system (1). The elastic force in the hammer is nonlinear, and the exponent \(\alpha \) has values that range from 2.2 to 3.5 for used hammers and 1.5 to 2.8 for new hammers [9]. A vibration model of an open-celled polyurethane foam automotive seat cushion [10, 11] has the form of Eq. (1) with the experimentally obtained value of exponent \(\alpha \) as 5.945. In addition, Eq. (1) is used to describe numerous electronic phenomena. The nonlinearity of restitution force has an important role in micro-electromechanical systems, such as micro-oscillators [12], micro-filters [13], and micro-actuators [14]. The optimal value of \(\alpha \) is given in [15]. Thus, system (1) is of great importance in practice.

In recent years, many studies have qualitatively and quantitatively analyzed dynamics and the control of system (1) in which \(\alpha \) is an integer. Wiggins [16] provided detailed descriptions of the mechanisms that give rise to chaos in nonlinear systems with harmonic periodic excitation and derived explicit techniques for the detection of chaos-inducing mechanisms by introducing the Melnikov method to investigate global bifurcation and chaos. Moreover, the Melnikov method is used to discuss the possibility of chaos suppression through a small resonant parametric perturbation by an analytical estimation, which is confirmed by numerical computations [17,18,19]. Fronzoni et al. [20] analyzed a large amount of actual data to find the control effect of laminar phases in suppressing chaos under parametric perturbation. Cicogna and Fronzoni [21, 22] obtained the same results as Fronzoni et al. by investigating experimental device models. Nonetheless, Cuadros and Chacón [23] pointed out the differences between Melnikov analysis and numerical calculation in the aforementioned results. Chacón showed that these differences resulted from an error in the calculation of the Melnikov distance instead of the perturbed nature of the method. In the above case, however, the effect of phase control on chaos suppression is not explicit. Qu et al. [24] and Yang et al. [25] utilized detailed numerical methods to describe the effect of phase control in a Duffing oscillator with a second external force term. Leung and Liu [26] further studied the effect of phase control on some nonlinear oscillators on the basis of [24, 25]. Furthermore, Chacón [27,28,29,30,31] derived the strict criteria by applying the Melnikov method for controlling homoclinic and heteroclinic chaos in a low-dimensional, non-autonomous, and dissipative Duffing oscillator, i.e., \(\alpha =3\). By comparing parametric excitation and external additional forcing terms as chaos-suppressing perturbations, Chacón [28] showed that the latter inhibits chaotic dynamics far more easily (i.e., for a larger interval of amplitudes) than the previous for small driving periods of the primary chaos-inducing excitation and vice versa. Then the critical parameter value for chaos with analytical methods is obtained and the issue of chaos control when \(\alpha \) is a fraction is investigated in references [5, 32, 33]. Beyond that, Lenci et al. comprehensively analyzed complex dynamical behaviors (including chaos, bifurcation and manifolds) in Duffing oscillators by using different theoretical techniques and numerical methods [34,35,36], and applied to a variety of systems in applications [37, 38]. However, few studies have addressed the issue of chaos suppression in system (1), where the order of deflection \(\alpha \) is a fraction. In particular, whether and how \(\alpha \) would influence the control effect of chaos-suppressing excitations should be considered.

In this work, we utilize the Melnikov technique and introduce additional periodic excitation to study the suppression of horseshoe chaos in a generalized Duffing oscillator with fractional-order deflection under an external excitation. The rest of the paper is organized as follows: Section 2 presents the condition for the chaos induction of dynamic system (1) by means of the Melnikov technique. In Sect. 3, we describe the application of the Melnikov technique in the inhibition of horseshoe chaos in system (1) by introducing external or parametric periodic excitation as a chaos-suppressing excitation. We find that the initial phase differences between the chaos-inducing and chaos-suppressing excitation has a key role in inhibiting chaos. Section 4 provides a discussion on the comparison of the effectiveness of chaos suppression by external periodic excitation and parametric excitation in the principal resonant case. Our primary conclusions are presented in Sect. 5.

2 Chaos in a generalized Duffing oscillator with fractional-order deflection

Melnikov analysis is a classical method for the measurement of the splitting distance between invariant manifolds for a wide variety of dynamic systems that are close to integrable systems. It is an approximate or limited method for the detection of chaos. If the Melnikov function has a simple zero point, then invariant manifolds will intersect transversely, indicating the persistence of homoclinic (or heteroclinic) orbits and the presence of homoclinic (or heteroclinic) chaos. Therefore, the equilibrium points and stability of the unperturbed system should be analyzed. To begin, by introducing \(\dot{x}_1 =x_2 \), system (1) can be written as the following first-order differential equations:

$$\begin{aligned} \left\{ {\begin{array}{l} \dot{x}_1 =x_2 , \\ \dot{x}_2 =ax_1 -bx_1 \left| {x_1 } \right| ^{\alpha -1}+\varepsilon \left( {-\delta x_2 +\gamma \cos \, \omega t} \right) . \\ \end{array}} \right. \end{aligned}$$
(2)

For \(\varepsilon =0\), Eq. (2) can be recast into an unperturbed system (3):

$$\begin{aligned} \left\{ {\begin{array}{l} \dot{x}_1 =x_2 , \\ \dot{x}_2 =ax_1 -bx_1 \left| {x_1 } \right| ^{\alpha -1}. \\ \end{array}} \right. \end{aligned}$$
(3)

System (3) is a Hamiltonian system that has three equilibrium points for \(\alpha \!>\!1\): \(\left( {x_1 ,x_2 } \right) _{1,2} \!=\!( {\pm ( {\frac{a}{b}} )^{\frac{1}{\alpha -1}}\!,0} )\) and \(o=\left( {0,0} \right) \). The point o is a hyperbolic saddle point which is connected to itself by two homoclinic orbits \(\Gamma ^{+}\left( t \right) \) and \(\Gamma ^{-}\left( t \right) \) when the initial condition \(( {x_1^0 \left( t \right) ,x_2^0 \left( t \right) } )=( {\pm \left( {\frac{\alpha +1}{2}} \right) ^{\frac{1}{\alpha -1}},0} )\) is satisfied.

It is known that the solutions of Eq. (2) for the homoclinic orbits are provided in explicit forms by

$$\begin{aligned} x_1 ^{\pm }\left( t \right)= & {} \pm \left( {\frac{a\left( {\alpha +1} \right) }{2b}} \right) ^{\frac{1}{\alpha -1}}\\&\times \left( {\hbox {sech}\left( {\frac{\sqrt{a}\left( {\alpha -1} \right) }{2}t} \right) } \right) ^{\frac{2}{\alpha -1}}, \\ x_2 ^{\pm }\left( t \right)= & {} \mp \sqrt{a}\left( {\frac{a\left( {\alpha +1} \right) }{2b}} \right) ^{\frac{1}{\alpha -1}}\\&\times \,\left( {\hbox {sech}\left( {\frac{\sqrt{a}\left( {\alpha -1} \right) }{2}t} \right) } \right) ^{\frac{2}{\alpha -1}}\\&\times \tanh \,\left( {\frac{\sqrt{a}\left( {\alpha -1} \right) }{2}t} \right) . \end{aligned}$$

For the sake of simplicity, let

$$\begin{aligned} A=\left( {\frac{a\left( {\alpha +1} \right) }{2b}} \right) ^{\frac{1}{\alpha -1}}, \quad B=\frac{\sqrt{a}\left( {\alpha -1} \right) }{2}. \end{aligned}$$
(4)

Then, the homoclinic orbits can be written as the following forms:

$$\begin{aligned} x_1 ^{\pm }\left( t \right)= & {} \pm A\left( {\hbox {sech }\left( {Bt} \right) } \right) ^{\frac{2}{\alpha -1}}, \nonumber \\ x_2 ^{\pm }\left( t \right)= & {} \mp \sqrt{a}A\left( {\hbox {sech }\left( {Bt} \right) } \right) ^{\frac{2}{\alpha -1}}\left( {\tanh \, \left( {Bt} \right) } \right) , \end{aligned}$$
(5)

where \(\sec h(\cdot )\) and \(\tanh \, (\cdot )\) are hyperbolic functions. Relations (5) are the general forms of the homoclinic orbits for Eq. (2) and are valid for any value, either as an integer or as a fraction, of the order of deflection \(\alpha \) as long as \(\alpha >1\). The positive or negative sign refers to the top or bottom homoclinic orbit of system (3).

The homoclinic orbits are obtained on the basis of the above equations. When the weak damped term \(\varepsilon \delta x_2 \) and the external periodical excitation term \(\varepsilon \gamma \cos \, \left( {\omega t} \right) \) participate in the unperturbed system, the homoclinic orbits will be broken, i.e., homoclinic chaos will occur. Therefore, we can discuss the conditions for generating chaos by applying the Melnikov technique to Eq. (2). The Melnikov function of system (2) is:

$$\begin{aligned} M^{\pm }\left( {t_0 } \right)= & {} \int _{-\infty }^{+\infty } {x_2 ^{\pm }\left( t \right) }\nonumber \\&\times \,\left[ {-\delta x_2 ^{\pm }\left( t \right) +\gamma \cos \, \omega \left( {t+t_0 } \right) } \right] \hbox {d}t. \end{aligned}$$
(6)

Given that \(x_2 ^{\pm }\left( t \right) \) is an odd function, Eq. (6) is transformed into the following form:

$$\begin{aligned} M^{\pm }\left( {t_0 } \right)= & {} -\delta \int _{-\infty }^{+\infty } {\left( {x_2 ^{\pm }\left( t \right) } \right) ^{2}} \hbox {d}t-\gamma \sin \, \left( {\omega t_0 } \right) \nonumber \\&\times \,\int _{-\infty }^\infty {\sin \, \left( {\omega t} \right) x_2 ^{\pm }\left( t \right) } \hbox {d}t. \end{aligned}$$
(7)

By substituting Eq. (5) into Melnikov function (7), the Melnikov function can be written as:

$$\begin{aligned} M^{\pm }\left( {t_0 } \right) =-C\pm D\sin \, \left( {\omega t_0 } \right) , \end{aligned}$$

where

$$\begin{aligned} C= & {} \delta \int _{-\infty }^{+\infty } {\left( {x_2 ^{\pm }\left( t \right) } \right) ^{2}} \hbox {d}t \nonumber \\= & {} \frac{4a\delta A^{2}}{\alpha +3}\int _0^{+\infty } {\left( {\cosh \left( {Bt} \right) } \right) } ^{-\frac{4}{\alpha -1}}\hbox {d}t, \end{aligned}$$
(8)

and

$$\begin{aligned} D= & {} \sqrt{a}\gamma A\int _{-\infty }^{+\infty } {\sin \, \left( {\omega t} \right) \left( {\hbox {sech}\left( {Bt} \right) } \right) ^{\frac{2}{\alpha -1}}\tanh \, \left( {Bt} \right) } \hbox {d}t \nonumber \\= & {} \frac{\omega \gamma A}{\sqrt{a}\left( {\alpha -1} \right) }\frac{2^{\frac{2}{\alpha -1}}}{\Gamma \left( {\frac{2}{\alpha -1}} \right) }\nonumber \\&\times \,\Gamma \left( {\frac{\sqrt{a}+i\omega }{\sqrt{a}\left( {\alpha -1} \right) }} \right) \Gamma \left( {\frac{\sqrt{a}-i\omega }{\sqrt{a}\left( {\alpha -1} \right) }} \right) . \end{aligned}$$
(9)

where Eqs. (8–9) are calculated through partial integration, and the exact analytical solution for \(\alpha >1\) is given in Ref. [5].

Thus, when the Melnikov function exists as a simple zero point, the necessary condition for horseshoe chaos for Eq. (2) and a sufficiently small \(\varepsilon \) is \(D-C\equiv r>0\).

3 Suppression of chaos with harmonic periodic excitation

Given that the existence of a simple zero point in the Melnikov function signifies horseshoe chaos, we consider the controlled system by introducing external and parametric harmonic periodic excitations, which can inhibit the occurrence of chaos in system (2). Then, Eq. (2) is rewritten as the following controlled system

$$\begin{aligned} \left\{ {\begin{array}{l} \dot{x}_1 =x_2 , \\ \dot{x}_2 =ax_1 -bx_1 \left| {x_1 } \right| ^{\alpha -1}\\ \quad \qquad +\,\varepsilon \left( {-\delta x_2 +\gamma \cos \, \omega t} \right) +e\left( t \right) . \\ \end{array}} \right. \end{aligned}$$
(10)

In this system, \(e\left( t \right) \) is the control excitation, which has two types:

$$\begin{aligned} a\left( t \right) =\varepsilon f\cos \, \left( {\Omega t+\varphi } \right) , \end{aligned}$$

or

$$\begin{aligned} p\left( t \right) =\varepsilon fx_1 \cos \, \left( {\Omega t+\varphi } \right) , \end{aligned}$$

where f, \(\Omega \), and \(\varphi \) are the dimensionless amplitude coefficient, frequency, and initial phase of control excitation, respectively. The former is an additional external excitation, whereas the latter is parametric excitation. In the following work, we will show the conditions of the parameters for chaos suppression by means of the Melnikov technique.

3.1 Suppression of chaos with external periodic excitation

To begin with, an external periodic excitation is taken as a chaos-suppressing perturbation to drive system (2), which gives rise to horseshoe chaos, i.e., \(e\left( t \right) =a\left( t \right) =\varepsilon f\cos \, \left( {\Omega t+\varphi } \right) \) in system (10). Then, system (10) can be transformed into the following form:

$$\begin{aligned} \left\{ {\begin{array}{l} \dot{x}_1 =x_2 , \\ \dot{x}_2 =ax_1 -bx_1 \left| {x_1 } \right| ^{\alpha -1}+\varepsilon \left( {-\delta x_2 +\gamma \cos \, \omega t} \right) \\ \qquad \quad +\,\varepsilon f\cos \, \left( {\Omega t+\varphi } \right) . \\ \end{array}} \right. \end{aligned}$$
(11)

Based on Eq. (11), the Melnikov control for this perturbed system will be designed to compel the chaotic system to follow a regular periodic trajectory. By subjecting Eq. (11) to Melnikov analyses, we obtain the following Melnikov function:

$$\begin{aligned} M^{\pm }\left( {t_0 } \right) =-C\pm D\sin \, \left( {\omega t_0 } \right) \pm E\sin \, \left( {\Omega t_0 +\varphi } \right) , \end{aligned}$$
(12)

where the positive or negative sign denotes the upper or lower homoclinic orbit associated with the unperturbed Hamilton oscillator system (3); C and D are given in formulae (8) and (9), and

$$\begin{aligned} E= & {} \sqrt{a}fA\int _{-\infty }^{+\infty } {\sin \, \left( {\Omega t} \right) \left( {\hbox {sech}\left( {Bt} \right) } \right) ^{\frac{2}{\alpha -1}}\tanh \, \left( {Bt} \right) } \hbox {d}t \nonumber \\= & {} \frac{\Omega fA}{\sqrt{a}\left( {\alpha -1} \right) }\frac{2^{\frac{2}{\alpha -1}}}{\Gamma \left( {\frac{2}{\alpha -1}} \right) }\nonumber \\&\Gamma \left( {\frac{\sqrt{a}+i\Omega }{\sqrt{a}\left( {\alpha -1} \right) }} \right) \Gamma \left( {\frac{\sqrt{a}-i\Omega }{\sqrt{a}\left( {\alpha -1} \right) }} \right) . \end{aligned}$$
(13)

The three constants can be calculated through partial integration, and the exact analytical solutions for \(\alpha >1\) are given in Ref. [5]. Therefore, \(C>0\), \(D>0\), \(E>0\) for all the parameters in the range of interest.

Given that the Melnikov function (12) measures the distance between the perturbed stable and unstable manifolds in the Poincaré section at \(t_0 \), the conditions of control can be deduced in detail. The cases \(M^{\pm }\left( {t_0 } \right) \) will be studied separately in the next section.

3.1.1 Inhibition of manifold transverse intersections near the upper homoclinic orbit

If the external periodical excitation acts on the system in such a way that provides a condition for \(M^{+}\left( {t_0 } \right) \) to retain its sign, then horseshoe chaos will be suppressed. Fortunately, the combination of \(D-C-E<0\) and \(-D-C+E<0\) provides a necessary condition for \(M^{+}\left( {t_0 } \right) \) to retain its sign, specifically, \(M^{+}\left( {t_0 } \right) <0\). Note that Chacón has discussed the first case in detail and the second case is omitted in Ref. [28].

First, the case

$$\begin{aligned} D-C-E<0, \end{aligned}$$
(14)

is considered. By substituting the parameters in Eq. (12) into Eq. (14), we obtain

$$\begin{aligned} f>\left( {1-\frac{C}{D}} \right) T, \end{aligned}$$
(15)

where

$$\begin{aligned} T=\frac{f D}{E}. \end{aligned}$$
(16)

However, Eq. (14) is only one possible condition for \(M^{+}\left( {t_0 } \right) \) to retain its sign, specifically, \(M^{+}\left( {t_0 } \right) <0\). To obtain the sufficient condition of \(M^{+}\left( {t_0 } \right) <0\), we will introduce the following lemmas [26] for \(M^{+}\left( {t_0 } \right) \) to be always negative.

Lemma 1

Suppose \(\Omega /\omega \) is irrational. Then, there exists a \(t_0^{\prime } \) such that

$$\begin{aligned} D\sin \, \left( {\omega t_0^{\prime } } \right) +E\sin \, \left( {\Omega t_0^{\prime } +\varphi } \right) >D-E. \end{aligned}$$

Lemma 2

Suppose \(\Omega /\omega =k/l\), where k, l are positive integers . Then, there exists a \(t_0^{\prime } \) such that \(\sin \, \left( {\omega t_0^{\prime } } \right) =-\sin \, \left( {\Omega t_0^{\prime } +\varphi } \right) =1\) if and only if

$$\begin{aligned} \frac{k}{l}=\frac{4j-1-2\varphi /\pi }{4i+1}, \end{aligned}$$

where i, j are some integers.

Lemma 3

Suppose

$$\begin{aligned} g\left( {t,k,l} \right) =\frac{1-\cos \, \left( {kt/l} \right) }{1-\cos \, \left( t \right) }, \end{aligned}$$

where t is any real number and k, l are two irreducible positive integers. Then, the function \(g\left( {t,k,l} \right) \) is finite if and only if \(l=1\). Moreover, if \(l=1\), we have \(0\le g\left( {t,k,1} \right) \le k^{2}\).

Theorem 1

Suppose \(\Omega /\omega =k\), where k is a positive integer, and integers i and j are such that

$$\begin{aligned} k=\frac{4j-1-2\varphi /\pi }{4i+1}. \end{aligned}$$

Then, we always have \(M^{+}\left( {t_0 } \right) <0\) if \(f_{\min }<f<f_{\max }\), where \(f_{\min } =\left( {1-\frac{C}{D}} \right) T\) and \(f_{\max } =\frac{T}{k^{2}}\).

Proof

Equation (15) is only one condition for \(M^{+}\left( {t_0 } \right) <0\). Hence, a sufficient condition is required to inhibit chaos. Supposing that Eq. (15) is a sufficient condition for \(M^{+}\left( {t_0 } \right) \) to be negative for all \(t_0 \), one must have

$$\begin{aligned} D\sin \, \left( {\omega t_0 } \right) +E\sin \, \left( {\Omega t_0 +\varphi } \right) <D-E, \quad \forall t_0 \in \mathbf{R}. \end{aligned}$$
(17)

Let \(k=\frac{4j-1-2\varphi /\pi }{4i+1}\). Then, from Lemma 2, Eq. (17) can be rewritten as \(\frac{1-\cos \, \left( {kt} \right) }{1-\cos \, \left( t \right) }<\frac{D}{E}\), where \(t=\omega t_0 -5\pi /2\). In fact, if \(f<f_{\max } \), then \(f<\frac{T}{k^{2}}\), that is, \(k^{2}<\frac{T}{f}=\frac{D}{E}\) given in Eq. (16). Fortunately, Lemma 3 provides the condition \(\frac{1-\cos \, \left( {kt} \right) }{1-\cos \, \left( t \right) }\le k^{2}\) to be fulfilled for all t. \(\frac{1-\cos \, \left( {kt} \right) }{1-\cos \, \left( t \right) }<\frac{D}{E}\) can be derived from the two facts. Therefore, Eq. (17) is always satisfied.

On the other hand, the second case

$$\begin{aligned} -D-C+E<0 \end{aligned}$$
(18)

is considered. Similarly, Eq. (18) can be transformed into the following equivalent condition:

$$\begin{aligned} f<\left( {1+\frac{C}{D}} \right) T, \end{aligned}$$
(19)

where T is given in Eq. (16).

However, Eq. (18) is also not a sufficient condition for \(M^{+}\left( {t_0 } \right) \) to remain negative for all \(t_0 \). Similar to Lemma 1 and Theorem 1, we can obtain the following lemma and theorem:

Lemma 4

Suppose \(\Omega /\omega \) is irrational. Then, there exists a \(t_0^{\prime } \) such that

$$\begin{aligned} D\sin \, \left( {\omega t_0^{\prime } } \right) +E\sin \, \left( {\Omega t_0^{\prime } +\varphi } \right) >-D+E. \end{aligned}$$

Theorem 2

Suppose \(\Omega /\omega =1/k\), where k is a positive integer, and integers i and j are such that

$$\begin{aligned} k=\frac{4i-1}{4j+1-2\varphi /\pi }. \end{aligned}$$

Then, we always have \(M^{+}\left( {t_0 } \right) <0\) if \(f_{\min } ^{{\prime }}<f<f_{\max } ^{{\prime }}\) is satisfied, where \(f_{\min } ^{{\prime }}=Tk^{2}\) and \(f_{\max } ^{{\prime }}=\left( {1+\frac{C}{D}} \right) T\).

According to Theorems 1 and 2, to inhibit transverse intersections between the stable and unstable manifolds near the upper homoclinic orbit \(\Gamma ^{+}\left( t \right) \) in system (10), we can introduce external excitation as the chaos-suppressing perturbation as long as its frequency satisfies the resonant condition \(\Omega /\omega =k\) or \(\Omega /\omega =1/k\); its initial phase is such that \(k=\frac{4j-1-2\varphi /\pi }{4i+1}\)or \(k=\frac{4i-1}{4j+1-2\varphi /\pi }\) where k, i, j are some integers, and \(f_{\min }<f<f_{\max } \) or \(f_{\min } ^{{\prime }}<f<f_{\max } ^{{\prime }}\). The conditions show that in addition to the frequency, the phase of the chaos-suppressing excitation has a key role in suppressing chaos. Clearly, if the parameters in system (10) satisfy the three requirements, we always have \(M^{+}\left( {t_0 } \right) <0\). Unfortunately, we cannot ensure that \(M^{+}\left( {t_0 } \right) >0\) with similar considerations and derivations.

3.1.2 Inhibition of manifold transverse intersections near the lower homoclinic orbit

The same approach holds for \(M^{-}\left( {t_0 } \right) <0\). The combination of Eqs. (14) and (18) provides a necessary condition for \(M^{-}\left( {t_0 } \right) \) to retain its sign. Specifically, \(M^{-}\left( {t_0 } \right) <0\). Therefore, we can obtain the following lemmas and theorems.

Lemma 5

Suppose \(\Omega /\omega \) is irrational. Then, there exists a \(t_0^{\prime } \) such that

$$\begin{aligned} -D\sin \, \left( {\omega t_0^{\prime } } \right) -E\sin \, \left( {\Omega t_0^{\prime } +\varphi } \right) >D-E. \end{aligned}$$

Lemma 6

Suppose \(\Omega /\omega =k/l\), where k, l are positive integers. Then, there exists a \(t_0^{\prime } \) such that \(-\sin \, \left( {\omega t_0^{\prime } } \right) =\sin \, \left( {\Omega t_0^{\prime } +\varphi } \right) =1\) if and only if

$$\begin{aligned} \frac{k}{l}=\frac{4j+1-2\varphi /\pi }{4i-1}, \end{aligned}$$

where i, j are integers.

Theorem 3

Suppose \(\Omega /\omega =k\), where k is a positive integer, and there are integers i, j such that

$$\begin{aligned} k=\frac{4j+1-2\varphi /\pi }{4i-1}. \end{aligned}$$

Then, we always have \(M^{-}\left( {t_0 } \right) <0\) if \(f_{\min }<f<f_{\max } \), where \(f_{\min } =\left( {1-\frac{C}{D}} \right) T\) and \(f_{\max } =\frac{T}{k^{2}}\).

Lemma 7

Suppose \(\Omega /\omega \) is irrational. Then, there exists a \(t_0^{\prime } \) such that

$$\begin{aligned} -D\sin \, \left( {\omega t_0^{\prime } } \right) -E\sin \, \left( {\Omega t_0^{\prime } +\varphi } \right) >-D+E. \end{aligned}$$

Theorem 4

Suppose \(\Omega /\omega =1/k\), where k is a positive integer, and there are integers i, j such that

$$\begin{aligned} k=\frac{4i+1}{4j-1-2\varphi /\pi }. \end{aligned}$$

Then, we always have \(M^{-}\left( {t_0 } \right) <0\) if \(f_{\min } ^{{\prime }}<f<f_{\max } ^{{\prime }}\) is satisfied, where \(f_{\min } ^{{\prime }}=Tk^{2}\) and \(f_{\max } ^{{\prime }}=\left( {1+\frac{C}{D}} \right) T\).

From Theorems 3 and 4, to inhibit transverse intersections between the stable and unstable manifolds near the lower homoclinic orbit \(\Gamma ^{-}\left( t \right) \) in system (10), we can introduce external excitation as the chaos-suppressing perturbation as long as its frequency satisfies the resonant condition \(\Omega /\omega =k\) or \(\Omega /\omega =1/k\); its initial phase is such that \(k=\frac{4j+1-2\varphi /\pi }{4i-1}\) or \(k=\frac{4i+1}{4j-1-2\varphi /\pi }\) where k, i, j are some integers, and \(f_{\min }<f<f_{\max } \) or \(f_{\min } ^{{\prime }}<f<f_{\max } ^{{\prime }}\). The conditions show that in addition to the frequency, the phase of the chaos-suppressing excitation has a key role in suppressing chaos. Clearly, if the parameters in system (10) satisfy the three requirements, we always have \(M^{-}\left( {t_0 } \right) <0\). Unfortunately, we cannot ensure that \(M^{-}\left( {t_0 } \right) >0\) with similar considerations and derivations.

Remark 1

In light of the arguments presented above, introducing the external resonant excitation as the chaos-suppressing perturbation can indeed inhibit transverse intersections between stable and unstable manifolds and thus suppress horseshoe chaos in system (10). For example, in suppressing horseshoe chaos near the upper (or lower) homoclinic orbit \(\Gamma ^{+}\left( t \right) \) or \(\Gamma ^{-}\left( t \right) \), we can employ the periodic perturbation with its frequency satisfying \(\Omega /\omega =k\) (where k is a positive integer) and \(f_{\min }<f<f_{\max } \). Note that at the same time, we have to select an suitable phase: \(\varphi =\frac{3\pi }{2}\) or \(\varphi =\frac{\pi }{2}\) for \(k=4m \), where m is a nonnegative integer; \(\varphi =\pi \) for \(k=4m+1\); \(\varphi =\frac{\pi }{2}\) or \(\varphi =\frac{3\pi }{2}\) for \(k=4m+2\); and \(\varphi =0\) for \(k=4m+3\). This shows that in chaos suppression, the initial phase of the chaos-suppressing excitation must be selected accordingly. Furthermore, we can observe that with the increase in resonance order k, the interval of amplitudes \(\left[ {f_{\min } ,\;f_{\max } } \right] \) for chaos suppression quickly contracts given the other parameters that satisfy the inhibition theorems. Alternatively, we can also utilize periodic perturbation with a frequency that satisfies \(\Omega /\omega =1/k\) (where k is a positive integer) and \(f_{\min }^{\prime }<f<f_{\max }^{\prime } \). In this case, we can select the phase \(\varphi =\pi \) if \(k=1\). However, if \(k\ge 2\), \(f_{\min }^{\prime } >f_{\max }^{\prime } \) always exists such that suppression of horseshoe chaos cannot be accomplished.

3.2 Suppression of chaos with parametric periodic excitation

For comparison with Sect. 3.1, we impose the parametric excitation \(p\left( t \right) \) on the control excitation in system (10). Then, the controlled system is rewritten as:

$$\begin{aligned} \left\{ {\begin{array}{l} \dot{x}_1 =x_2 , \\ \dot{x}_2 =ax_1 -bx_1 \left| {x_1 } \right| ^{\alpha -1}+\varepsilon \left( {-\delta x_2 +\gamma \cos \, \omega t} \right) \\ \quad +\varepsilon fx_1 \cos \, \left( {\Omega t+\varphi } \right) . \\ \end{array}} \right. \end{aligned}$$
(20)

The Melnikov function for this perturbed system can be indicated by the following form:

$$\begin{aligned} M^{\pm }\left( {t_0 } \right) =-C\pm D\sin \, \left( {\omega t_0 } \right) +F\sin \, \left( {\Omega t_0 +\varphi } \right) , \end{aligned}$$
(21)

where

$$\begin{aligned} F= & {} 2a^{\frac{3}{2}}A^{2}f\int _0^{+\infty } {\sin \, \left( {\Omega t} \right) \left( {\sec h\left( {Bt} \right) } \right) ^{\frac{4}{\alpha -1}}\tanh \, \left( {Bt} \right) } \hbox {d}t \nonumber \\= & {} \frac{\sqrt{a}f\Omega A^{2}}{2\left( {\alpha -1} \right) }\frac{2^{\frac{4}{\alpha -1}}}{\Gamma \left( {\frac{4}{\alpha -1}} \right) }\nonumber \\&\times \,\Gamma \left( {\frac{2\sqrt{a}+i\Omega }{\sqrt{a}\left( {\alpha -1} \right) }} \right) \Gamma \left( {\frac{2\sqrt{a}-i\Omega }{\sqrt{a}\left( {\alpha -1} \right) }} \right) , \end{aligned}$$
(22)

and \(F>0\) for the parameters in the range of interest.

3.2.1 Inhibition of manifold transverse intersections near the upper homoclinic orbit

Similar to the external periodic excitation case, the parametric excitation acts on system (10) in such a way that provide a condition for \(M^{+}\left( {t_0 } \right) \) to retain its sign, specifically \(M^{+}\left( {t_0 } \right) <0\). Then, horseshoe chaos will suppressed. The combination \(D-C-F<0\) and \(-D-C+F<0\) provides a necessary condition for \(M^{+}\left( {t_0 } \right) \) to retain its sign, specifically \(M^{+}\left( {t_0 } \right) <0\).

First, the case

$$\begin{aligned} D-C-F<0, \end{aligned}$$
(23)

is considered. This relationship provides half of the necessary condition for \(M^{+}\left( {t_0 } \right) \) to retain its sign, specifically \(M^{+}\left( {t_0 } \right) <0\). Now, by substituting the parameters in Eq. (21) into formula (23), we obtain

$$\begin{aligned} f>\left( {1-\frac{C}{D}} \right) T^{{\prime }}, \end{aligned}$$
(24)

where

$$\begin{aligned} T^{{\prime }}=\frac{f D}{F}. \end{aligned}$$
(25)

However, Eq. (24) is only one possible condition for \(M^{+}\left( {t_0 } \right) \) to maintain the same sign, specifically \(M^{+}\left( {t_0 } \right) <0\). To obtain a sufficient condition of \(M^{+}\left( {t_0 } \right) <0\), we will introduce the following lemmas [26] for the function \(M^{+}\left( {t_0 } \right) \) to be always negative.

Lemma 8

Suppose \(\Omega /\omega \) is irrational. Then, a \(t_0^{\prime } \) exists such that

$$\begin{aligned} D\sin \, \left( {\omega t_0^{\prime } } \right) +F\sin \, \left( {\Omega t_0^{\prime } +\varphi } \right) >D-F. \end{aligned}$$

Lemma 9

Suppose \(\Omega /\omega =k/l\) (where k, l are positive integers). Then, there exists a \(t_0^{\prime } \) such that \(\sin \, \left( {\omega t_0^{\prime } } \right) =-\sin \, \left( {\Omega t_0^{\prime } +\varphi } \right) =1\) if and only if

$$\begin{aligned} \frac{k}{l}=\frac{4j-1-2\varphi /\pi }{4i+1}, \end{aligned}$$

where i, j are integers.

Theorem 5

Suppose \(\Omega /\omega =k\), where k is a positive integer, and there are integers i,j such that

$$\begin{aligned} k=\frac{4j-1-2\varphi /\pi }{4i+1}. \end{aligned}$$

Then, we always have \(M^{+}\left( {t_0 } \right) <0\) if \(\overline{f} _{\min }<f<\overline{f} _{\max } \), where \(\overline{f} _{\min } =\left( {1-\frac{C}{D}} \right) T^{{\prime }}\),\(\overline{f} _{\max } =\frac{T^{{\prime }}}{k^{2}}\).

The second case

$$\begin{aligned} -D-C+F<0, \end{aligned}$$
(26)

is considered. Similar to the above derivation process, Eq. (26) can be transformed into the following equivalent condition:

$$\begin{aligned} f<\left( {1+\frac{C}{D}} \right) T^{{\prime }}, \end{aligned}$$
(27)

where \(T^{{\prime }}\) is given in Eq. (25).

However, Eq. (27) is not a sufficient condition for \(M^{+}\left( {t_0 } \right) \) to be negative for all \(t_0 \). Thus, we present the following lemma and theorem.

Lemma 10

Suppose \(\Omega /\omega \) is irrational. Then, there exists a \(t_0^{\prime } \) such that

$$\begin{aligned} D\sin \, \left( {\omega t_0^{\prime } } \right) +F\sin \, \left( {\Omega t_0^{\prime } +\varphi } \right) >-D+F. \end{aligned}$$

Theorem 6

Suppose \(\Omega /\omega =1/k\), where k is a positive integer, and there are integers i and j such that

$$\begin{aligned} k=\frac{4i-1}{4j+1-2\varphi /\pi }. \end{aligned}$$

Then, the objective of \(M^{+}\left( {t_0 } \right) <0\) can be achieved if \(\overline{f^{{\prime }}} _{\min }<f<\overline{f^{{\prime }}} _{\max } \), where \(\overline{f^{{\prime }}} _{\min } =k^{2}T^{{\prime }}\), \(\overline{f^{{\prime }}} _{\max } =\left( {1+\frac{C}{D}} \right) T^{{\prime }}\).

According to Theorems 5 and 6, to inhibit transverse intersections between the stable and unstable manifold near the upper homoclinic orbit \(\Gamma ^{+}\left( t \right) \) in system (20), we can introduce parametric excitation as the chaos-suppressing perturbation as long as its frequency satisfies the resonant condition \(\Omega /\omega =k\) or \(\Omega /\omega =1/k\); its initial phase is such that \(k=\frac{4j-1-2\varphi /\pi }{4i+1}\) or \(k=\frac{4i-1}{4j+1-2\varphi /\pi }\) where k, i, j are some integers; and \(\overline{f} _{\min }<f<\overline{f} _{\max } \) or \(\overline{f^{{\prime }}} _{\min }<f<\overline{f^{{\prime }}} _{\max } \). These conditions show that in addition to the frequency, the phase of the chaos-suppressing excitation plays a key role in chaos suppression. Clearly, if the parameters in system (20) satisfy the three requirements, we will always have \(M^{+}\left( {t_0 } \right) <0\). Unfortunately, we cannot ensure that \(M^{+}\left( {t_0 } \right) >0\) with similar considerations and derivations.

3.2.2 Inhibition of manifold transverse intersections near the lower homoclinic orbit

The same approach holds for \(M^{-}\left( {t_0 } \right) <0\). The combination of Eqs. (23) and (26) provides the necessary condition for \(M^{-}\left( {t_0 } \right) \) to retain its sign, specifically \(M^{-}\left( {t_0 } \right) <0\). Therefore, we can obtain the following lemmas and theorems.

Lemma 11

Suppose \(\Omega /\omega \) is irrational. Then, there exists a \(t_0^{\prime } \) such that

$$\begin{aligned} -D\sin \, \left( {\omega t_0^{\prime } } \right) +F\sin \, \left( {\Omega t_0^{\prime } +\varphi } \right) >D-F. \end{aligned}$$

Lemma 12

Suppose \(\Omega /\omega =k/l\), where k and l are positive integers. Then, there exists a \(t_0^{\prime } \) such that \(\sin \, \left( {\omega t_0^{\prime } } \right) =\sin \, \left( {\Omega t_0^{\prime } +\varphi } \right) =-1\) if and only if

$$\begin{aligned} \frac{k}{l}=\frac{4j-1-2\varphi /\pi }{4i-1}, \end{aligned}$$

where i, j are integers.

Theorem 7

Suppose \(\Omega /\omega =k\), where k is a positive integer, and there are integers i,j such that

$$\begin{aligned} k=\frac{4j-1-2\varphi /\pi }{4i-1}. \end{aligned}$$

Then, we will always have \(M^{-}\left( {t_0 } \right) <0\) if \(\overline{f} _{\min }<f<\overline{f} _{\max } \), where \(\overline{f} _{\min } =\left( {1-\frac{C}{D}} \right) T^{{\prime }}\) and \(\overline{f} _{\max } =\frac{T^{{\prime }}}{k^{2}}\).

Lemma 13

Suppose \(\Omega /\omega \) is irrational. Then, there exists a \(t_0^{\prime } \) such that

$$\begin{aligned} -D\sin \, \left( {\omega t_0^{\prime } } \right) +F\sin \, \left( {\Omega t_0^{\prime } +\varphi } \right) >-D+F. \end{aligned}$$

Theorem 8

Suppose \(\Omega /\omega =1/k\), where k is a positive integer, and there are integers i, j such that

$$\begin{aligned} k=\frac{4i+1}{4j+1-2\varphi /\pi }. \end{aligned}$$

Then, there always exists \(M^{-}\left( {t_0 } \right) <0\) if \(\overline{f^{{\prime }}} _{\min }<f<\overline{f^{{\prime }}} _{\max } \), where \(\overline{f^{{\prime }}} _{\min } =k^{2}T^{{\prime }}\) and \(\overline{f^{{\prime }}} _{\max } =\left( {1+\frac{C}{D}} \right) T^{{\prime }}\).

According to Theorems 7 and 8, to inhibit transverse intersections between the stable and unstable manifolds near the lower homoclinic orbit \(\Gamma ^{-}\left( t \right) \) in system (20), we can introduce parametric excitation as the chaos-suppressing perturbation as long as its frequency satisfies the resonant condition \(\Omega /\omega =k\) or \(\Omega /\omega =1/k\); its initial phase is such that \(k=\frac{4j-1-2\varphi /\pi }{4i-1}\) or \(k=\frac{4i+1}{4j+1-2\varphi /\pi }\) where k, i, j are integers, and \(\overline{f} _{\min }<f<\overline{f} _{\max } \) or \(\overline{f^{{\prime }}} _{\min }<f<\overline{f^{{\prime }}} _{\max } \). These conditions show that in addition to the frequency, the phase of the chaos-suppressing excitation has a key role in chaos suppression. Clearly, if the parameters in system (20) satisfy the three requirements, we will always have \(M^{-}\left( {t_0 } \right) <0\). Unfortunately, we cannot ensure \(M^{-}\left( {t_0 } \right) >0\) with similar considerations and derivations.

Fig. 1
figure 1

Bifurcation diagram (a) and the maximum Lyapunov exponent (b) of generalized Duffing equation under external periodic excitation with \(a=1\), \(b=1\), \(\alpha =5/3\), \(\delta =2\), \(\gamma =3\), \(\varepsilon =0.1\), \(\Omega =1\), \(\omega =1\), \(\varphi =\pi \)

Full size image

Remark 2

In light of the arguments presented above, introducing parametric resonant excitation as the chaos-suppressing perturbation can indeed inhibit transverse intersections between stable and unstable manifolds and thus suppress horseshoe chaos in system (20). For example, in suppressing horseshoe chaos near the upper (or lower) homoclinic orbit \(\Gamma ^{+}\left( t \right) \) (or \(\Gamma ^{-}\left( t \right) )\), we can employ periodic perturbation with frequency that satisfies \(\Omega /\omega =k\), where k is a positive integer, and \(\overline{f} _{\min }<f<\overline{f} _{\max } \). Note that at the same time we have to select a suitable phase: \(\varphi =\frac{3\pi }{2}\) for \(k=4m \), where m is a nonnegative integer; \(\varphi =\pi \) or \(\varphi =0\) for \(k=4m+1\); \(\varphi =\frac{\pi }{2}\) for \(k=4m+2\); and \(\varphi =0\) or \(\varphi =\pi \) for \(k=4m+3\). This shows that in chaos suppression, the initial phase of the chaos-suppressing excitation must be selected accordingly. Furthermore, we can observe that with the increase in resonance order k, the interval of amplitudes \([ {\bar{{f}}_{\min } ,\;\bar{{f}}_{\max } } ]\) for chaos suppression contracts quickly given the other parameters that satisfy the inhibition theorems. Alternatively, we can also utilize periodic perturbation with frequency that satisfies \(\Omega /\omega =1/k\) where k is a positive integer and \(\overline{f} _{\min }<f<\overline{f} _{\max } \). In this case, we can select the phase \(\varphi =\pi \) or \(\varphi =0\) if \(k=1\). However, if \(k\ge 2\), \(\overline{f^{{\prime }}} _{\min } >\overline{f^{{\prime }}} _{\max } \) exists such that horseshoe chaos cannot be suppressed.

3.3 Numerical simulation

In this part, we will provide numerical simulation to validate analytical results regarding the effect of chaos suppression with the addition of periodic excitations. The parameters of the generalized Duffing-type differential equation with fractional-order deflection (2) are set as \(a=1,b=1,\alpha =5/3,\delta =2,\gamma =3,\omega =1\). Then, according to the theoretical analysis in Sect. 2, the corresponding Melnikov function is in the form of Eq. (7), where \(C\approx 2.17,D\approx 3.9\) and \(A\approx 1.54,B\approx 0.33\), which satisfy the necessary condition for simple zero point of the Melnikov function and system (2) exhibits Smale horseshoe chaos.

Fig. 2
figure 2

(Color Online) The global dynamics of generalized Duffing equation under external periodic excitation. The parameters are \(a=1,b=1,\alpha =5/3,\delta =2,\gamma =3\), \(\varepsilon =0.1,\Omega =1,\omega =1,\varphi =\pi \). a \(f=0\), b \(f=2.0\)

Full size image
Fig. 3
figure 3

Bifurcation diagram and the maximum Lyapunov exponent of generalized Duffing equation under parametric periodic excitation with \(a=1,b=1,\alpha =5/3,\delta =2,\gamma =3\), \(\varepsilon =0.1,\Omega =1,\omega =1,\varphi =\pi \)

Full size image
Fig. 4
figure 4

Ratio for the largest inhibition interval of amplitudes between external and parametric excitations S versus principal resonance frequency \(\omega \) for different deflection orders

Full size image

On this basis, the Melnikov function of the system under external periodic excitation (11) is described in Eq. (12), where C, D are the same with the unperturbed cases and \(E\approx 2.74\) is computed through numerical integration by formula (13). For convenience, we consider a special case with \(\Omega =1,\omega =1\), so that \(k=1\). Thus, obtained from theorems and remarks in Sect. 3.1, the interval of amplitudes f for chaos suppression is \([ {( {1-\frac{C}{D}} )T,\frac{T}{k^{2}}} ]\approx [ {1.34,3.0} ]\) or \([ {Tk^{2},( {1+\frac{C}{D}} )T} ]\approx [ {3.0,4.66} ]\), where T is given in Eq. (16).

For the case of chaos suppression under parametric excitation (20), the Melnikov function is described in Eq. (21), where C, D are the same with the unperturbed cases and \(F=3.4245\) is computed by formula (22). The frequency of excitations is the same with \(\Omega =1,\omega =1\), so that \(k=1\). Thus, obtained from theorems and remarks in Sect. 3.2, the interval of amplitudes f for chaos suppression is \([ {( {1-\frac{C}{D}} ){T}^{\prime },\frac{{T}^{\prime }}{k^{2}}} ]\approx [ {1.07,2.40} ]\) or \([ {{T}^{\prime }k^{2},( {1+\frac{C}{D}} ){T}^{\prime }} ]\approx [ {2.40,3.73} ]\), where \({T}^{\prime }\) is given in Eq. (25).

In numerical simulations, using fourth-order Runge–Kutta method and Wolf algorithm, we calculate bifurcation diagram and the maximum Lyapunov exponent of generalized Duffing equation under external periodic excitation (11) by varying with the amplitude f of control excitation as shown in Fig. 1. Here, bifurcation diagrams show the system state \(x_1 \) for each value of f by using the stroboscopic sampling method with sampling period \(T=2\pi \). The Lyapunov exponent is a universal quantitative index to evaluate the divergence of nearby orbits in nonlinear dynamics. A positive maximum Lyapunov exponent indicates the chaotic behavior of the system. It can be observed that the bifurcation diagram is in agreement with the numerical results of the maximum Lyapunov exponent graph. The diagrams demonstrate that the chaotic attractor is suppressed to a stable state through the addition of an external periodic excitation in the range of \(f\in \left[ {0.27,5.73} \right] \), which contains the amplitude range of suppressing Smale horseshoe chaos, that is \(\left[ {1.07,2.40} \right] \) or \(\left[ {2.40,3.73} \right] \), theoretically.

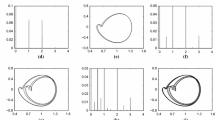
More exactly, to compare the effect of the control, we present the global behavior of manifolds obtained without and with the addition of the external periodic excitation by employing the generalized cell mapping methods [39, 40] in Fig. 2. The domain is chosen as \(D=\left\{ {-2\le x_1 \le 2,-2\le x_2 \le 2} \right\} \) with a cell structure of \(1000\times 1000.60\times 60\) points are evenly selected within each cell. When the system is not suppressed with \(f=0\) (Fig. 2a), there is a chaotic attractor in the region A and region B is the basin of attraction, while the chaotic attractor becomes two stable periodic-1 attractors denoted by \(\mathbf{A}_{1}\) and \(\mathbf{A}_{2}\) under the external periodic excitation with \(f=2.0\) as shown in Fig. 2b. Here, \(\mathbf{B}_{1 }\) and \(\mathbf{B}_{2 }\) are the basins of attraction corresponding to the two attractors \(\mathbf{A}_{1}\) and \(\mathbf{A}_{2}\), respectively. \(\mathbf{B}_{12}\) is the basin boundary between basins of attraction \(\mathbf{B}_{1 }\) and \(\mathbf{B}_{2}\). \(\mathbf{S}_{12 }\) is the periodic saddle on the basin boundary \(\mathbf{B}_{12}\). UM is the unstable manifold of periodic saddle \(\mathbf{S}_{12}\).

Similar results are given in Fig. 3 for the system under parameter periodic excitation (20). The chaotic attractor can also be suppressed to a stable periodic state under parametric excitation within the range of suppressing Smale horseshoe chaos theoretically. Numerical simulations typically verify the correctness of the analytical results presented above.

4 Comparison between external and parametric periodic perturbations

We now compare the inhibition efficiencies of the external and parametric periodic perturbations for the principal resonance case \(k=1\) because this case permits the largest interval of amplitudes for chaos suppression. If \(k=1\) and given the optimum phase \(\varphi \) that satisfies the inhibition theorems, we can observe that in the external perturbation case, the inhibition interval of amplitudes is \(( {f_{\min } ,f_{\max }^{\prime } } )\) and its width can be defined as \(\Delta \overline{f} \triangleq f_{\max }^{\prime } -f_{\min } =\frac{2C}{D}T\), where C, D, T are given in Eqs. (8), (9), and (16). By comparison, in the parametric perturbation case, the inhibition interval of amplitudes is \(( {\bar{{f}}_{\min } ,\bar{{f}}_{\max }^{\prime } } )\) and its width can be defined as \(\Delta \overline{f} \triangleq \bar{{f}}_{\max }^{\prime } -\bar{{f}}_{\min } =\frac{2C}{D}{T}^{\prime }\), where \({T}^{\prime }\) satisfies Eq. (25). We then obtain the ratio between the two interval widths

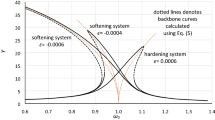
$$\begin{aligned} S=\frac{\Delta f}{\Delta \bar{{f}}}=\frac{T}{{T}^{\prime }}=\frac{F}{E}. \end{aligned}$$
(28)

For the restitution force coefficients \(a=1\), \(b=1\), Fig. 4 shows the proportion of parametric extent between the two periodical excitations versus \(\omega \) for different deflection orders where \(\alpha >1\). The ratio for the largest inhibition interval of amplitudes between the two excitations S increases as \(\omega \) increases. For \(\alpha =\frac{3}{2}\) above (below) a critical value of frequency \(\omega _c \approx 0.72\), external (parametric) excitation more effectively suppresses homoclinic chaos because it provides a wider amplitude range than parametric (external) excitation. Similar results hold for other deflection orders, \(\alpha =\frac{5}{3}\), 2, 3 or \(\frac{17}{3}\), that are integers or fractions. Moreover, the critical value \(\omega _c \) will shift to a larger frequency value with the increase in \(\alpha \).

5 Conclusions

We have provided the analytical expressions of chaos suppression in a generalized Duffing oscillator with fractional-order deflection by introducing an external periodic resonant excitation and parametric excitation as chaos-suppressing perturbation. Melnikov technique is employed to show that to inhibit homoclinic chaos, the amplitude of the chaos-suppressing perturbation must be selected from a fixed range as long as its frequency satisfies a resonant condition with the chaos-inducing excitation. Note that the necessary condition for Melnikov functions retains their signs, which is omitted in Ref. [28]. Thus, we obtain a wider range for the amplitude of suppression. We observed that as resonance order increases, this range quickly contracts and the principal resonance case admits the largest amplitude interval for chaos suppression. Numerical results typically indicate that the chaotic attractor can be suppressed to a stable state within the range of theoretical analysis of excitation amplitude. Remarkably, the initial phase of the chaos-suppressing excitation has a key role in suppressing chaos because it depends on the resonant condition and must be selected accordingly. Thus, to compare the chaos-suppressing efficiency between the external and parametric periodic perturbations, we select the optimum phase that satisfies the inhibition theorems for the principal resonance case. In this case, external (parametric) excitation with a frequency above (below) a critical value is more effective in suppressing homoclinic chaos, for it provides a wider amplitude range than parametric (external) excitation. These results hold for an arbitrary deflection order either as an integer or as a fraction as long as it is larger than 1 depending on the material and bending properties of the beam. Moreover, the critical value of the frequency will shift to a larger value as the deflection order increases.