1 Introduction

Research in area of chaotic systems and their analysis has quite a long tradition. Recently a new type of electrical circuits which exhibit chaos have been investigated. Such oscillators are represented by simple electrical circuits consist of new electrical elements, such as memristor, memcapacitor, and meminductor. It opens a new area of chaotic systems, for example, see [1,2,3,4].

On the other hand, the subject of fractional calculus has reached popularity and importance during the past few decades. The basic symptoms, which should be presented in the system in order to the fractional calculus should be used are: recursion, fractality, roughness, heredity, (long) memory. Fractional calculus, a.k.a. non-integer calculus, is known since the classical calculus with the first written reference dated September 1695 in the letters between Leibniz and L’Hospital. Nowadays, the fractional calculus has a wide area of applications in various fields as well as in the chaotic systems [5].

Taking into account above considerations, we may combine the fractional calculus technique and modeling of the chaotic oscillators, where the new concept of electrical circuits with memristive elements is used [6,7,8].

This brief comment is organized as follows. Section 1 introduces the problem and main motivation. In Sect. 2 the fractional calculus fundamentals are described. In Sect. 3 the memristive systems are discussed. Section 4 presents a new model of the fractional-order chaotic system. In Sect. 5 the simulation results are presented. In Sect. 6 the conclusions of this comment and further possible research in this area are discussed.

2 Preliminaries

2.1 Definition of fractional-order derivative/integral

Fractional calculus is a generalization of integration and differentiation to joint non-integer \(\gamma \)-order operator \(_{a}D^{\gamma }_{b}\), where a and b are the bounds of the operation. The standard notation for denoting the common left-sided integro-differential operator of a function f(t) defined within the interval [a, t] is \(_{a}D^{\gamma }_{t} f(t)\), with \(\gamma \in \hbox {R}\).

There exist many definitions for the fractional-order operator (fractional-order integrals for \(\gamma <0\) and derivatives for \(\gamma >0\)) but in this article, we will restrict only on the Caputo’s definition (CD) and the Grünwald-Letnikov definition (GLD), respectively.

The CD, for \(n-1< \gamma <n\), can be written as [9]:

$$\begin{aligned} {}_{a}D_{t}^{\gamma }f(t)= \frac{1}{\varGamma (n- \gamma )} \int _{a}^{t} \frac{f^{(n)}(\tau )}{(t-\tau )^{\gamma - n + 1}}d\tau . \end{aligned}$$
(1)

In case of electrical circuits, where the fractional derivative is used in fractional-order model of circuit elements, the Caputo’s definition can be used because the initial conditions for the fractional differential equations with the Caputo derivatives are in the same form as for ordinary differential equations, i.e., \(f^{(n)}(0)=c_n\), \(\forall n \in \hbox {N}\).

The GLD is given as follows [9, 10]:

$$\begin{aligned} {}_{a}D^{\gamma }_{t}f(t)=\lim _{h_s \rightarrow 0}\frac{1}{h_s^{\gamma }} \sum _{i=0}^{\left\lfloor \frac{t-a}{h_s}\right\rfloor }(-1)^i {\gamma \atopwithdelims ()i} f(t-ih_s), \end{aligned}$$
(2)

where \(\lfloor z\rfloor \) is the floor function, i.e., the greatest integer smaller than z, and

$$\begin{aligned} {\gamma \atopwithdelims ()i} =\frac{\varGamma (\gamma +1)}{\varGamma (i+1)\,\varGamma (\gamma -i+1)} \end{aligned}$$
(3)

are the binomial coefficients for \({\gamma \atopwithdelims ()0} = 1.\) This form of the derivative definition is very helpful for obtaining a numerical solution of fractional differential equation.

2.2 Numerical solution of fractional differential equation

Since the both definitions CD and GLD are equivalent for a wide class of the functions, for numerical calculation of fractional-order derivative we can use the relation (4) derived from the GLD (2). The relation for the numerical approximation of \({\gamma }\)-th derivative at the points \(kh_s,\, (k = 1, 2, 3, \dots )\) has the following form [9]:

$$\begin{aligned} {}_{(k-L_m/h_s)}D^{\gamma }_{t_k} f(t) \approx h_s^{-\gamma } \sum _{i=0}^{k} c_i^{(\gamma )} f(t_{k-i}), \end{aligned}$$
(4)

where \(L_m\) is the “memory length”, \(t_k=kh_s\), \(h_s\) is the time step of calculation (definition (4) is valid only as \(h_s\) tends toward 0 and that the accuracy of the simulation depends on the value of \(h_s\)) and \(c_i^{(\gamma )} \,(i=0, 1, 2, \dots )\) are the binomial coefficients. For their calculation we may use the following expression:

$$\begin{aligned} c_0^{(\gamma )} = 1, \qquad c_i^{(\gamma )} = \left( 1 - \frac{1+ \gamma }{i}\right) c_{i-1}^{(\gamma )}. \end{aligned}$$
(5)

Thus, general numerical solution of the fractional differential equation (initial value problem)

$$\begin{aligned} {{}_{0}}{{D}_{t}^{\gamma }} x(t) = f(x(t),t), \end{aligned}$$

can be expressed as follows [5, 11]:

$$\begin{aligned} x(t_k) = f\left( x(t_k), t_k \right) h_s^{\gamma } - \sum _{i=0}^{k} c_i^{(\gamma )} x(t_{k-i}). \end{aligned}$$
(6)

For the memory term expressed by the sum, a “short memory” principle for various length \(L_m\) can be used.

An evaluation of the short memory effect and convergence relation of the error between short and long memory were very clearly described and proved in [9].

3 Fractional-order memristive systems

There are a huge number of electrical circuit where the fractional calculus can be used (e.g., [12,13,14], etc.); however, the classical circuit theory is limited to the variables v, i, q, and \(\phi \), which are used for description of all four basic devices (resistor, capacitor, inductor, and memristor). The memristor was postulated by Leon Chua in 1971 [15] and manufactured by HP in 2008 [16]. Moreover, other devices (memcapacitor, meninductor) recently introduced in [17] are located beyond these limits. Certain circuit elements, memcapacitor and meninductor, involve not only those four variables but also the time-integrals of the charge and the flux [18]. These new state variables lead to the so-called “mem” systems, which are a class of higher-order devices. These memory elements are a general term and belong to group of memristive systems [19]. Such memristive systems can be described by fractional-order models [6, 7, 20,21,22]. This notion is also based on the fact, that there is not ideal electrical element and the real elements lie in between two ideal, e.g., fractor or fractductor [5, 13, 23].

Since, the real capacitor and the real inductor have been investigated by many authors and the experimental evidences of their real orders of the models were confirmed [14, 24, 25], real memristor, memcapacitor, and meminductor, were not investigated experimentally yet, just by simulation models or by the emulators [26,27,28].

However, there are many electrical circuits, mainly oscillators, where memristor, memcapacitors, and meminductors, have been used [29, 30]. Nowadays, application of such elements also in other type of circuits rapidly grows, for instance, new kind of PID controller [31], neuron network model [32], and so on.

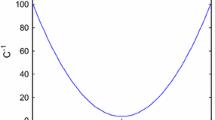
Le us recall to a linear capacitor model proposed in 1994 by Westerlund and Ekstam [24]. For a general input voltage v(t), applied at \(t=0\), the current is

$$\begin{aligned} i(t)=C {{}_0}D^{\alpha }_{t}\, v(t), \quad 0 < \alpha \le 1, \quad \hbox {for}\quad t > 0, \end{aligned}$$
(7)

where C is the capacitance of the capacitor with unit [F/s\(^{1-\alpha }\)]. It is related to the kind of dielectric. Another constant \(\alpha \) (order),  \(\alpha \in \hbox {R}\), is related to the losses of the capacitor. Westerlund and Ekstam provided in their work the table of various capacitor dielectrics with appropriate constant \(\alpha \) which has been obtained experimentally by measurements on the real capacitors.

By using the relations, described in [18], for memcapacitor and meminductor and well-known relations between four basic elements (resistor, capacitor, inductor, memristor), we can obtain another floor of the four square symmetry, which is depicted in Fig. 1.

Fig. 1
figure 1

Connection of known electrical elements (Inspired by Refs. [8, 18])

Full size image

As we can observe in Fig. 1, some additional electrical elements, were not discovered so far.

4 Model of the fractional-order chaotic system

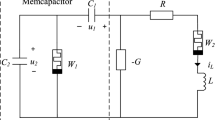
In paper [30], the chaotic oscillator circuit based on the resistor, capacitor, negative resistor, memcapacitor and meminductor was introduced. According to Kirchhoff laws and additional scale transformation the chaotic system can be presented as the following dimensionless dynamical system:

$$\begin{aligned} \frac{\mathrm{d} x(t)}{\mathrm{d}t}= & {} a z(t) + b z(t) w (t) - x(t),\nonumber \\ \frac{\mathrm{d} y(t)}{\mathrm{d}t}= & {} d y(t) + e y(t) v^2(t) - f z(t) - gz(t)w(t), \nonumber \\ \frac{\mathrm{d} z(t)}{\mathrm{d}t}= & {} h y(t) + j y(t) v^2(t) - k x(t),\nonumber \\ \frac{\mathrm{d} w(t)}{\mathrm{d}t}= & {} n_1 z(t),\nonumber \\ \frac{\mathrm{d} v(t)}{\mathrm{d}t}= & {} n_2 y(t), \end{aligned}$$
(8)

where for the parameters: \(a = 1.73\), \(b = -2.04\), \(d = 0.46\), \(e = 0.04\), \(f = 0.67\), \(g = 0.19\), \(h = 0.48\), \(j = 0.52\), \(k = n_1 = n_2 = 0.21\), the initial values setting: \(x(0)=0.2\), \(y(0)=0.5\), \(z(0)=0.45\), \(w(0)=0.1\), \(v(0)=0.5\), the chaotic attractor was obtained.

Taking into account the consideration described in previous section, the fractional-order models of the elements used in the chaotic oscillator (Fig. 5 in [30]) could be applied to Kirchhoff laws. Then, instead of the system (8), we obtain the following set of fractional differential equations:

$$\begin{aligned} {}_0D_t^{\gamma _1} x(t)= & {} a z(t) + b z(t) w (t) - x(t),\nonumber \\ {}_0D_t^{\gamma _2} y(t)= & {} d y(t) + e y(t) v^2(t) - f z(t) - gz(t)w(t), \nonumber \\ {}_0D_t^{\gamma _3} z(t)= & {} h y(t) + j y(t) v^2(t) - k x(t),\nonumber \\ {}_0D_t^{\gamma _4} w(t)= & {} n_1 z(t),\nonumber \\ {}_0D_t^{\gamma _5} v(t)= & {} n_2 y(t), \end{aligned}$$
(9)

where \(\gamma _1\), \(\gamma _2\), \(\gamma _3\), \(\gamma _4\), and \(\gamma _5\) are the real orders of the elements used in the chaotic oscillator, described in [30].

For simulation purposes we will use a numerical solution of the fractional deferential equations (9) obtained by using the relationships (4) and (5) as well as the principle (6), which lead to equations in the form:

$$\begin{aligned} {x}(t_{k})= & {} [ a z(t_{k-1}) + b z(t_{k-1})w(t_{k-1})-x(t_{k-1}) ] h_s^{\gamma _1} \nonumber \\&- \sum _{i=0}^k c_i^{(\gamma _1)} {x}(t_{k-i}), \nonumber \\ {y}(t_k)= & {} [ d y(t_{k-1}) + e y(t_{k-1}) v(t_{k-1})^2 -f z(t_{k-1}) \nonumber \\&-g z(t_{k-1}) w(t_{k-1})] h_s^{\gamma _2} - \sum _{i=0}^k c_i^{(\gamma _2)} {y}(t_{k-i}), \nonumber \\ {z}(t_k)= & {} [h y(t_{k-1}) + j y(t_{k-1})v(t_{k-1})^2 - k x(t_{k-1}) ] h_s^{\gamma _3} \nonumber \\&- \sum _{i=0}^k c_i^{(\gamma _3)} {z}(t_{k-i}), \nonumber \\ {w}(t_{k})= & {} [ n_1 z(t_{k-1})] h_s^{\gamma _4} - \sum _{i=0}^k c_i^{(\gamma _4)} {w}(t_{k-i}), \nonumber \\ {v}(t_{k})= & {} [ n_2 y(t_{k-1})] h_s^{\gamma _5} - \sum _{i=0}^k c_i^{(\gamma _5)} {v}(t_{k-i}), \end{aligned}$$
(10)

where \(T_{sim}\) is the simulation time, \(k=1,2,3 \dots , N\), for \(N = [ T_{sim}/h_s ]\), and (x(0), y(0), z(0), w(0), v(0)) is the start point (initial conditions). The binomial coefficients \(c_i^{(\gamma _1)}\), \(c_i^{(\gamma _2)}\), \(c_i^{(\gamma _3)}\), \(c_i^{(\gamma _4)}\), and \(c_i^{(\gamma _5)}\) are calculated according to relation (5), respectively.

For further simulations and analysis the numerical solution (10) of the system (9) was coded in MATLAB.

5 Simulation results

Let us use proposed numerical solution (10) to simulate chaotic system (9) for the same parameters and initial conditions setting as they were defined for chaotic system (8), for simulation time \(T_{\mathrm{sim}}=1000\) s, time step \(h_s=0.005\), derivative orders \(\gamma _1=0.9\), \(\gamma _2=1\), \(\gamma _3=1\), \(\gamma _4=1\), and \(\gamma _5=1\). Let us assume \(\gamma _1=0.9\), which corresponds to the real order of many capacitors as well as the capacitor \(C_1\) used in the chaotic oscillator circuit (Fig. 5 in [30]). Obviously, for a real oscillator circuit with the real capacitor \(C_1\) the order \(\gamma _1\) should be experimentally measured. However, in [30] was not built the real circuit and therefore is unknown the capacitor model number. Moreover, other elements, namely memcapacitor \(C_M\) and meminductor \(L_M\), in circuit are just artificial and were not manufactured yet.

Fig. 2
figure 2

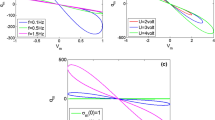
Chaotic attractor in \(x-y\) state plane of system (9)

Full size image
Fig. 3
figure 3

Chaotic attractor in \(x-w\) state plane of system (9)

Full size image
Fig. 4
figure 4

Chaotic attractor in \(y-w\) state plane of system (9)

Full size image
Fig. 5
figure 5

Chaotic attractor in \(z-w\) state plane of system (9)

Full size image
Fig. 6
figure 6

Chaotic attractor in \(z-v\) state plane of system (9)

Full size image
Fig. 7
figure 7

Chaotic attractor in \(w-v\) state plane of system (9)

Full size image

In Figs. 2, 3, 4, 5, 6 and 7 are depicted chaotic behavior (one-scroll attractor) of the system (9) for the parameters the initial conditions setting as in (8), and \(\gamma _1=0.9\), \(\gamma _2=\gamma _3=\gamma _4=\gamma _5=1\), in various state planes, respectively.

The Lyapunov exponents of the system (9), computed according to method described in [33], for the parameters as in (8), and orders \(\gamma _1=0.9\), \(\gamma _2=\gamma _3=\gamma _4=\gamma _5=1\), have the following values: 0.5807, \(-\,0.1683\), \(-\,0.0047\), \(-\,0.9647\), \(-\,1.0267\), which confirm the chaotic behavior because at least one exponent is positive.

6 Conclusions

In this comment, we mentioned that the results presented in paper [30] can be enhanced. Proposed chaotic oscillator consists of meminductor and memcapacitor as well as resistor, capacitor and negative resistor, can be described by fractional differential equations. Applying fractional-order derivative into the mathematical model of the oscillator elements, a memory effect and other dynamical properties are caught. Moreover, we obtain more degree of freedom due to the derivative orders.

Since, the orders of the real capacitors and inductors models have been investigated and experimentally confirmed, there is not an experimental evidence of real orders in model of memristors, meminductors and memcapacitors because they are not commercially produced and sold. However, proposed fractional-order model of the chaotic oscillator allows us to use the fractional orders, except for capacitor \(C_1\) order \(\gamma _1\), also for memcapacitor \(C_M\) order \(\gamma _2\) as well as for meminductor \(L_M\) order \(\gamma _3\). Even more, instead negative resistor G a memristor can be used. This is an idea for further research in this field of chaotic oscillator circuits. Moreover, it opens a new area for research of the chaotic systems dynamics.