Coexisting attractors in a memcapacitor-based chaotic oscillator

Abstract

In this paper, a smooth curve model of memcapacitor and its equivalent circuit are designed. Based on this memcapacitor, a novel memcapacitive chaotic circuit is presented. Dynamical behaviors of the circuit with various parameters are investigated both theoretically and experimentally. The numerical results indicate that the circuit displays complex nonlinear properties including coexisting and symmetrical bifurcations. The main characteristic of this memcapacitive chaotic circuit is the various coexisting attractors. Different kinds of coexisting attractors and their corresponding conditions are given. The equilibrium set, Lyapunov exponent spectrum and the basin of attraction are also analyzed. Besides, experimental results are given to confirm the correction of the numerical simulations.

1 Introduction

Memristor is postulated as the fourth basic circuit element by Chua [1] in 1971. However, the interest in memristive systems has not grown rapidly until a solid-state memristor was developed by Hewlett-Packard in 2008 [2]. Because of particular nonlinear characteristics of a memristor, it is widely employed to generate chaos by replacing nonlinear resistance elements in classic chaotic circuits, and some novel dynamic behaviors could be observed [3–6]. Recently, memristors are also used to compose and improve neural networks. Ref. [7] investigates the problem of exponential lag synchronization control of memristive neural networks (MNNs) via the fuzzy method and applications in pseudorandom number generators. Ref. [8] introduces a general class of memristive neural networks with time delays. And a general class of memristive neural networks with discrete and distributed delays is investigated in Ref. [9], where some Lagrange stability criteria dependent on the network parameters are derived via nonsmooth analysis and control theory.

Furthermore, Chua et al. proposed the concept of meminductor and memcapacitor generalized from the memristor in 2009 [10], whose properties depend on the history of the device. Although the actual solid-state memcapacitors are not fabricated until now, the potential values have attracted more and more attentions. Differing from a memristor’s hysteretic loop character between charge and voltage, a memcapacitor appears a hysteretic loop between current and voltage.

Previous researches of memcapacitors involved designing SPICE simulators in order to explore the behaviors of different memcapacitor models [11–13]. A mutator is also used to transform a memristor to a memcapacitor in Refs. [14, 15]. Ref. [16] proposes a memcapacitor emulator based on an analog model of a memristor, and Ref. [17] introduces a new memcapacitor emulator without using any memristor. Ref. [18] designs a floating memcapacitor emulator without grounded restriction that can be practically applied in electronic circuits, and Ref. [19] implements a memcapacitor emulator with off-the-shelf electronic devices. The analytical analysis of these two memcapacitors connected in series and in parallel is discussed in Ref. [20], which obtains the formulas of instantaneous memcapacitance for each memcapacitor. Recently, the researches of the memcapacitor-based circuits have gradually become a focus. Ref. [21] describes a memcapacitor-based chaotic circuit with a novel method to emulate a charge-controlled memcapacitor. In Ref. [22], a CMOS neural amplifier based on memcapacitor has been realized, where a performance comparison between memcapacitor-based realization and conventional integrated one has been introduced. Furthermore, a resistive-less memcapacitor-based relaxation oscillator is introduced in Ref. [23] and the boundary dynamics of the charge-controlled memcapacitor for Joglekar’s window function is discussed in Ref. [24].

In this paper, a new memcapacitive chaotic circuit is presented. Differing from other memcapacitor-based researches reported in Refs. [17–24], this circuit has special properties of coexisting bifurcations and coexisting attractors. It is remarkable that coexisting attractors generated in memcapacitor-based circuits are rare to be reported. In fact, the phenomenon of coexisting attractors is essentially multistability, which is a common occurrence in many nonlinear dynamical systems, corresponding to the coexistence of more than one stable attractor for the same set of system parameters [25]. And many researchers have committed themselves to investigate the special dynamic behaviors of coexisting attractors over the past few years. Ref. [26] introduces a new 3D autonomous quadratic chaotic system which not only generates four-scroll chaotic attractors but also produces coexisting attractors. Ref. [27] investigates a special chaotic system with only one stable equilibrium but coexistence of point, periodic and chaotic attractors. Many researches are reported in order to explore the internal mechanism and potential engineering applications of coexisting attractors [28–30]. The research on coexisting attractors and extreme multistability might have important consequences in the reproducibility of certain experimental systems [31]. For example, some chemical reactions show a random long-term behavior for the same set of experimental conditions [32, 33]. The cause of this randomness is not known, whereas multistability offers a possible mechanism for the behavior [31].

To our best knowledge, the researches of the coexisting attractors in memcapacitive (or memristive) circuits are still relatively less. The main purpose of this paper is to investigate various coexisting attractors in the presented memcapacitor-based circuit and the corresponding conditions. The paper focuses on analysis of complex dynamics depended on the starting conditions, and it has some practical significance with respect to memcapacitor-based applications.

The rest of this paper is organized as follows. In Sect. 2, mathematical modeling of the memcapacitor and its equivalent circuit are performed by theoretical analysis and multisim simulations. A memcapacitor-based oscillator is presented, and its equilibrium points are analyzed. In Sect. 3, the dynamical behaviors of the circuit are described, including bifurcation diagrams, Lyapunov exponents, basins of attraction, coexisting bifurcations and coexisting attractors. In Sect. 4, the experimental verification is performed. The conclusions are summarized in the last section.

2 Memcapacitor model and a memcapacitor-based chaotic oscillator

2.1 Memcapacitor model and its equivalent circuit

The definition of a general memcapacitor is presented in Ref. [10]. According to the definition, an nth-order voltage-controlled memcapacitive system can be described by the equations

$$\begin{aligned}&q(t)=C(x,u_\mathrm{c} ,t)u_\mathrm{c} (t) \end{aligned}$$

(1)

$$\begin{aligned}&\dot{\sigma }=f(\sigma ,u_\mathrm{c} ,t) \end{aligned}$$

(2)

Fig. 1

The relationship of the inverse memcapacitance $C^{-1}$ and variable $\sigma$

Fig. 2

The equivalent circuit of the charge-controlled memcapacitor characterized by Eq. (7)

where q(t) is the charge goes through the memcapacitor at time t, $\sigma$ is the integral of q(t), $u_\mathrm{c}(t)$ is the voltage across the memcapatitor, and C is its corresponding memcapacitance at time t, which depends on the state of the system. Similarly, an nth-order charge-controlled memcapacitive system is defined as

$$\begin{aligned}&u_\mathrm{c} (t)=C^{-1}(\sigma ,q,t)q(t)\end{aligned}$$

(3)

$$\begin{aligned}&\dot{\sigma }=f(x,q,t) \end{aligned}$$

(4)

where $C^{-1}$ is an inverse memcapacitance.

In this paper, a charge-controlled memcapacitor is used to construct a chaotic oscillator, whose memcapacitance depends on the device’s charge and changes nonlinearly. The inverse memcapacitance is defined [21] as

$$\begin{aligned}&C^{-1}=a+b\sigma ^{2}\end{aligned}$$

(5)

$$\begin{aligned}&\sigma =\int _{t_0 }^t {q(t)\mathrm{d}t} \end{aligned}$$

(6)

Then, the nonlinear charge–voltage relationship of the memcapacitor can be defined as follows

$$\begin{aligned}&u_\mathrm{c} (t)=(a+b\sigma ^{2})q(t)\end{aligned}$$

(7)

$$\begin{aligned}&\dot{\sigma }=q(t) \end{aligned}$$

(8)

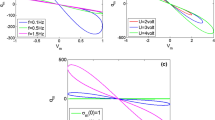
where a and b are constant coefficients. If we set $a=3.58$, $b=3.9$, the relationship between the inverse memcapacitance $C^{-1}$ and variable $\sigma$ is shown in Fig. 1.

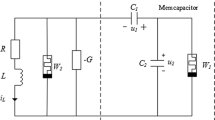
An equivalent circuit of a charge-controlled memcapacitor is designed according to Eq. (7), which is shown in Fig. 2. The input current is collected by R10 and the output of U5 is sent to integral circuits consisted by operational amplifiers U1 and U2, which are responsible to get the signs of $-q$ and $\sigma$. U3 works for the inversion of the sign of $-q$. The amplifier U4 works as inverting adder and its output is described as

$$\begin{aligned} u_c =-\left( \frac{R_9 }{R_7 }+\frac{R_9 }{R_8 }\sigma ^{2}\right) q(t) \end{aligned}$$

(9)

In order to better explore the property of this memcapacitor emulator, we set the applied current $u_i =5\sin (2\pi f)$ with f varying, and then, the simulation results are shown in Fig. 3.

Fig. 3

Multisim simulations to emulate q(t)–$u_\mathrm{c}$ hysteresis loop of the memcapacitor in conditions of $f=20\,\hbox {Hz}$, $f=40\,\hbox {Hz}$ and $f=80\,\hbox {Hz}$

2.2 Memcapacitor-based chaotic oscillator and typical chaotic attractors

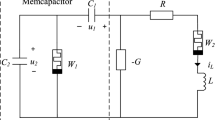
Based on memcapacitor model in Eq. (7), a new chaotic oscillator is designed as shown in Fig. 4.

Fig. 4

The presented oscillation circuit based on a memcapacitor model

From Fig. 4, we can obtain a set of four first-order differential equations, which define the relationship among the four circuit variables $(i_1 ,i_2 ,q,\sigma )$

$$\begin{aligned} \left\{ {\begin{array}{l} \frac{\mathrm{d}i_1 }{\mathrm{d}t}=\frac{1}{L_1 }(u_\mathrm{cm} -Ri_1 ) \\ \frac{\mathrm{d}i_2 }{\mathrm{d}t}=\frac{1}{L_2 }(Gi_2 -u_\mathrm{cm} ) \\ \frac{\mathrm{d}q}{\mathrm{d}t}=i_2 -i_1 \\ \frac{\mathrm{d}\sigma }{\mathrm{d}t}=q \\ \end{array}} \right. \end{aligned}$$

(10)

where $u_\mathrm{cm} =(a+b\sigma ^{2})q$. Let circuit parameters as Table 1. For initial condition as (0.01, 0, 0, 0), system (10) is chaotic and the chaotic attractors are shown in Fig. 6. In this case, the corresponding Lyapunov exponents are $\mathrm{LE}_{1}=0.015969$, $\mathrm{LE}_{2}=-0.00296$, $\mathrm{LE}_{3}=-0.013488$, $\mathrm{LE}_{4}=-0.21438$, and the Lyapunov dimension is $\hbox {d}L=2.964$.

2.3 Dissipativity and stability

To generate chaotic attractors, it is necessary for the system to be dissipative. The dissipativity of Eq. (10) is described as

$$\begin{aligned} \Delta V=\frac{\partial \dot{i}_1 }{i_1 }+\frac{\partial \dot{i}_2 }{i_2 }+\frac{\partial \dot{q}}{q}+\frac{\partial \dot{\sigma }}{\sigma }=-\frac{R}{L_1 }+\frac{G}{L_2 } \end{aligned}$$

(11)

When the circuit parameters are set as $a= 3.58$, $b= 3.9$, $1/L_{1}= 7.33\,\hbox {H}^{-1}$, $R =1.79\,\hbox {K}\Omega$, $G =1.78\,\hbox {mS}$ and $1/L_{2}=7.25\,\hbox {H}^{-1}$, the exponential constrain rate satisfies the following relation

$$\begin{aligned} \Delta V={-0.2157}<0 \end{aligned}$$

(12)

Obviously, the dissipativity of Eq. (10) is negative, implying that all trajectories are ultimately confined to a specific subset of zero volume [34].

Table 1 Circuit parameters for simulations and experiments

Fig. 5

Chaotic attractors and chaotic q–u hysteresis loops of memcapacitor in the chaotic oscillation circuit: a, b and c chaotic attractors; d chaotic q–u hysteresis loops

The equilibrium state of system (5) is given by an equilibrium set $E=\{(i_1 ,i_2 ,q,\sigma ){\vert } i_{1}=i_{2}=q=0,\sigma =c\}$, where c is a real constant. The Jacobian matrix J at this equilibrium set E is given as

$$\begin{aligned} J=\left[ {{\begin{array}{cccc} {-\frac{R}{L_1 }}&{} \quad 0&{} \quad {\frac{bc^{2}+a}{L_1 }}&{} \quad 0 \\ 0&{}\quad {\frac{G}{L_2 }}&{}\quad {\frac{-bc^{2}-a}{L_2 }}&{}\quad 0 \\ {-1}&{}\quad 1&{}\quad 0&{} \quad 0 \\ 0&{}\quad 0&{} \quad 1&{}\quad 0 \\ \end{array} }} \right] \end{aligned}$$

(13)

Fig. 6

The stable and unstable regions with the conditions varying

and its characteristic equation is given by

$$\begin{aligned}&\lambda ^{4}-\frac{GL_1 -L_2 R}{L_1 L_2 }\lambda ^{3}\nonumber \\&\quad -\frac{-L_1 bc^{2}-L_2 bc^{2}+GR-L_1 a-L_2 a}{L_1 L_2 }\lambda ^{2}\nonumber \\&\quad -\frac{Gbc-Rbc+Ga-Ra}{L_1 L_2 }\lambda =0 \end{aligned}$$

(14)

If we keep parameters b and c as variables and set other parameters in Table 1, Eq. (14) can be simplified as:

$$\begin{aligned}&\lambda \left[ \lambda ^{3}+\frac{1.79-12.905L_1 }{L_1 }\lambda ^{2}\right. \nonumber \\&\quad +\frac{3.9c^{2}-19.52+26L_1 +28.3L_1 c^{2}}{L_1 }\lambda \nonumber \\&\quad \left. +\frac{0.26+0.283c^{2}}{L_1 }\right] =0 \end{aligned}$$

(15)

Table 2 Different eigenvalues $\lambda _i (i =1, 2, 3)$ of the equilibrium set E

Table 3 Circuit parameters for coexisting bifurcations

Fig. 7

Dynamic characters of the oscillator (10) with respect to $1/L_{1}$: a bifurcation diagram and b Lyapunov spectrum

Since the coefficients of cubic polynomial equation in Eq. (15) are all nonzero values, according to Routh–Hurwitz condition, the necessary and sufficient conditions of the root’s real parts of this polynomial are negative is

$$\begin{aligned} \left\{ {\begin{array}{l} \frac{1.79-12.905L_1 }{L_1 }>0 \\ \frac{3.9c^{2}-19.52+26L_1 +28.3L_1 c^{2}}{L_1 }>0 \\ \frac{0.26+0.283c^{2}}{L_1 }>0 \\ \frac{1.79-12.905L_1 }{L_1 }\frac{3.9c^{2}-19.52+26L_1 +28.3L_1 c^{2}}{L_1 }\\ \quad -\,\frac{0.26+0.283c^{2}}{L_1 }>0 \\ \end{array}} \right. \end{aligned}$$

(16)

Then, we can obtain $0<L_1 <0.1387$. If we set $L_1 \in (0,0.2)$ and $\left| c \right| \in [0,3]$, the region satisfying the conditions of Eq. (16) is shown as blue color in Fig. 6, which means that the equilibrium set is stable. And the yellow color indicates the region of unstable.

Fig. 8

Coexisting attractors in different conditions of: a $1/L_{1}=7.31$, b $1/L_{1}=7.3267$, c $1/L_{1}=7.4$, d $1/L_{1}=7.46$, e $1/L_{1}=7.491$, f $1/L_{1}=7.6$

If we set $L_{1}=1/7.33\,\hbox {H}$, the three eigenvalues $\lambda _i (i=1, 2, 3)$ of the equilibrium set E are listed in Table 2 for typical values of constant c except for the zero eigenvalue, from which we can obtain the conclusion that the dynamical behaviors of this circuit are heavily depending on the initial state of the variable c. Being sensitive to the initial condition is similar to the memristive systems.

3 Dynamical behaviors of the oscillator

3.1 Coexisting bifurcation with $L_{1}$

When the inductor $L_{1}$ in Fig. 4 is varying and other circuit parameters are set in Table 3, the bifurcation diagram of the state variable $\sigma (t)$ is shown in Fig. 7a, where the orbit colored with red starts from the initial conditions of (−0.45, 0, 0, 0) and that colored with blue starts from the initial conditions of (0.45, 0, 0, 0). The corresponding Lyapunov exponent spectra are shown in Fig. 7b (for better clarity, the fourth Lyapunov exponents are presented partly and it has smaller negative values).

Table 4 Circuit parameters for symmetrical bifurcation

Fig. 9

Dynamic characters of the oscillator (10) with respect to $i_{1}(0)$: a bifurcation diagram and b Lyapunov spectrum

With reference to Fig. 7a, we can conclude that the dynamics of the memcapacitive circuit starts from periodic orbit and then enters into period-doubling orbit through chaotic orbit with the parameter $1/L_{1}$ increasing gradually. In Fig. 7b, the corresponding Lyapunov exponent spectra are presented in the region of $1/L_{1}\in (7.3,8)$, where we can observe several periodic windows in the chaotic region.

Fig. 10

Coexisting attractors in different conditions: a $i_{1}(0)=-1$, $i_{1}(0)=-0.75$, b $i_{1}(0)=-0.5$, $i_{1}(0)=-0.05$, c $i_{1}(0)=0.5$, $i_{1}(0)=0.05$, d $i_{1}(0)=1$ and $i_{1}(0)=0.75$

Table 5 Coexisting attractors for various parameters and conditions

The novel property of this bifurcation diagram is the coexisting bifurcation. The phenomenon of coexisting bifurcation results from the circuit existing coexisting attractors, which means that there are disparate attractors in the conditions of different initial values with the fixed circuit parameters. In this memcapacitive oscillation described by Eq. (10), if we fix circuit parameters in Table 3 and keep $L_{1}$ varying, we can observe several kinds of coexisting attractors with different initial conditions. Figure 8 shows the coexisting attractors in detail, where the blue attractor starts from the initial conditions of (0.45, 0, 0, 0) and the red one starts from (−0.45, 0, 0, 0). It can be found that the two coexisting attractors start from a symmetric pair of limit cycles and then evolve into a symmetric pair of single-scroll attractors and finally the single-scroll attractors develop double-scroll attractors. Since the state variable $\sigma (t)$ of the coexisting attractors are symmetrical about the origin, it is not difficult to get the conclusion that the coexisting bifurcations of $\sigma (t)$ are also symmetrical about straight line $\sigma =0$ as shown in Fig. 7a.

3.2 Symmetrical bifurcation with initial conditions

Different from coexisting bifurcation mentioned above, the proposed chaotic circuit also has other kind of symmetrical bifurcation. If we set circuit parameters in Table 4 and regard the initial conditions $(i_{1}(0), 0, 0,0)$ as bifurcation parameter, the bifurcation diagrams of the state variable $\sigma (t)$ and the corresponding Lyapunov exponent spectra are presented in Fig. 9. It is remarkable that the bifurcation diagram is symmetrical about the origin. As initial condition $i_{1}(0)$ increases gradually within the region [−1, 1], the orbit of the memcapacitive circuit starts from point attractors and turns into limit cycles at $i_{1}(0)=-0.75$, and the maximum Lyapunov exponents $\mathrm{LE}_{2}$ and $\mathrm{LE}_{3}$ increase from negative to zero along with $\mathrm{LE}_{1}$. Then, the system orbit goes to chaotic status via period-doubling bifurcations. There are several narrow period windows in the chaotic region. Correspondingly, the positive Lyapunov exponent $\mathrm{LE}_{1}$ descends into zero rapidly. Therefore, $\mathrm{LE}_{1}$ in chaotic region is presented burr shape as shown in Fig. 9b. Finally, the dynamics of the system settle down to periodic behaviors via reverse period-doubling bifurcations in the regions of [−1, 0], whereas the system has a reverse evolutionary process in the regions of [0, 1].

Dynamical behaviors of the symmetrical bifurcation also result from coexisting attractors and mainly occur in the regions of $i_{1}(0)\in [-1, 1]$. The whole evolutionary process of the system with respect to $i_{1}(0)$ is presented in Fig. 10, and the corresponding attractor types and their initial conditions are described in Table 5.

3.3 Multistability with coexisting attractors

As mentioned above, the oscillator (10) has different kinds of coexisting attractors. For the circuit parameters listed as Table 6, there are also other examples of multistability with coexisting attractor. Under different parameters, one system existing several kinds of coexisting attractors is not peculiar. However, it is novel for this proposed memcapacitive circuit that there exists twelve variant types of coexisting attractors in one parameter combination. All kinds of coexisting attractors are shown in Fig. 11, and the corresponding initial conditions are described in Table 7.

For more details, the main coexisting regimes are symmetric pairs of chaotic attractors, limit cycles and point attractors coexisting with each other. There are four forms of chaotic attractors, which are shown in Fig. 11b–d, and five types of limit cycle attractors are described in Fig. 11f–j. Besides, the point attractor and a symmetric pair of period-doubling cycles are also presented in Fig. 11a, k, l, respectively.

The basins of attraction for different coexisting attractors are indicated diverse colors which are shown in Fig. 12, where we can get the conclusion that the coexisting attractors transform from one to another roughly following the linear principles. Moreover, the complete transformation track is Fig. 11a $\rightarrow$ k $\rightarrow$ i $\rightarrow$ c $\rightarrow$ d $\rightarrow$ f $\rightarrow$ h $\rightarrow$ g $\rightarrow$ e $\rightarrow$ b $\rightarrow$ j $\rightarrow$ l $\rightarrow$ a, which means that the orbit of the system starts from point attractors and turns into limit cycles, then goes to chaotic status and settles down periodic behaviors via reverse period-doubling bifurcations. The transforming process is split in Fig. 11h into separate ports. The conversions from Fig. 11g to a are just the reverse process.

Table 6 Circuit parameters for symmetrical bifurcations

Fig. 11

Phase portrait of coexisting attractors in the $i_{1}$–$i_{2}$ plane: a point attractor, b, c a symmetric pair of strange attractors, d, e a symmetric pair of strange attractors, f, g a symmetric pair of limit cycles, h limit cycles, i, j a symmetric pair of limit cycles, k, l a symmetric pair of period-doubling cycles

Table 7 Coexisting attractors for various parameters and condition

4 Experimental verification

In this section, an experimental circuit is designed to realize the chaotic oscillator (10) based on a memcapacitor model. If we make timescale and amplitude scale transformations to Eq. (10) by setting time scaling factor as $\tau =100 {t}$ and amplitude scaling factor as $B=800b$ and then fixing circuit parameters in Table 1, Eq. (10) can be shown as

$$\begin{aligned} \left\{ {\begin{array}{l} \frac{\mathrm{d}i_1 }{\mathrm{d}\tau }=733 (3.58+\hbox {3120}\sigma ^{2})q-1312.07i_1 \\ \frac{\mathrm{d}i_2 }{\mathrm{d}\tau }=\hbox {1290.5}i_2 -725(3.58+\hbox {3120}\sigma ^{2})q \\ \frac{\mathrm{d}q}{\mathrm{d}\tau }=100i_2 -100i_1 \\ \frac{\mathrm{d}\sigma }{\mathrm{d}\tau }=100q \\ \end{array}} \right. \end{aligned}$$

(17)

The designed circuit of the experimental circuit is shown as Fig. 13, which can be described as

$$\begin{aligned} \left\{ {\begin{array}{l} \frac{\mathrm{d}i_1 }{\mathrm{d}t}=\frac{1}{R_1 C_4 }\left( \frac{R_4 }{R_3 }+\frac{R_4 }{R_2 }\sigma ^{2}\right) q-\frac{1}{R_7 C_4 }i_1 \\ \frac{\mathrm{d}i_2 }{\mathrm{d}t}=\frac{1}{R_{13} C_2 }i_2 -\frac{1}{R_{14} C_2 }\left( \frac{R_4 }{R_3 }+\frac{R_4 }{R_2 }\sigma ^{2}\right) q \\ \frac{\mathrm{d}q}{\mathrm{d}t}=\frac{1}{R_{15} C_3 }i_2 -\frac{1}{R_{16} C_3 }i_1 \\ \frac{\mathrm{d}\sigma }{\mathrm{d}t}=\frac{1}{R_{12} C_1 }q \\ \end{array}} \right. \end{aligned}$$

(18)

In Fig. 13, the operational amplifiers are chosen as LF347N type and the multipliers are selected as AD633 type. Comparing Eq. (17) with Eq. (18), and let the corresponding coefficients be equal, then we can obtain

$$\begin{aligned} \left\{ {{\begin{array}{lll} {\frac{1}{R_1 C_4 }=733}&{} {\frac{R_4}{R_3 }=3.58}&{} {\frac{R_4 }{R_2 }=3120} \\ {\frac{1}{R_7 C_4 }=1312.07}&{} {\frac{1}{R_{13} C_2 }=1290.5}&{} {\frac{1}{R_{14} C_2 }=725} \\ {\frac{1}{R_{15} C_3 }=100}&{} {\frac{1}{R_{16} C_3 }=100}&{} {\frac{1}{R_{12} C_3 }=100} \\ \end{array} }} \right. \end{aligned}$$

(19)

Fig. 12

Basins of attraction of coexisting attractors in the $i_{1}$–$i_{2}$ plane

When we set $C_1 =C_2 =C_3 =C_4 =10\,\hbox {nF}$, the resistance parameters can be obtained as: $R_1 \approx 137\,\hbox {k}\Omega$, $R_2 \approx 0.032\,\hbox {k}\Omega$, $R_3 \approx 27.93\,\hbox {k}\Omega$, $R_4 \approx 100\,\hbox {k}\Omega$, $R_7 \approx 76\,\hbox {k}\Omega$, $R_{12} \approx 1000\,\hbox {k}\Omega$, $R_{13} \approx 77.5\,\hbox {k}\Omega$, $R_{14} \approx 138\,\hbox {k}\Omega$, $R_{15} =1000\,\hbox {k}\Omega$, $R_{16} =1000\,\hbox {k}\Omega$.

The experimental results according to Fig. 13 are plotted in Fig. 14. Compared Fig. 5 with Fig. 14, it is obvious that the dynamical behaviors obtained in the experimental circuit match well with those presented by numerical simulations.

Fig. 13

The circuit schematic of Eq. (10)

Fig. 14

Chaotic attractors and chaotic hysteresis q–u loops observed by analog oscilloscope for memcapacitor-based oscillator from the experimental device: a, b, c, d, e chaotic attractors; f chaotic hysteresis loops

5 Conclusions

In this paper, a memcapacitor model and its equivalent circuit are presented. Besides, a chaotic oscillation based on this memcapacitor model is designed. The dynamical characteristics of this oscillation are investigated both theoretically and numerically. The results indicate that this oscillation possesses novel dynamical characteristics: coexisting and symmetrical bifurcations. Compared with other chaotic oscillations, this circuit has various kinds of coexisting attractors. The basin of attraction with respect to initial conditions is used to expound the coexisting attractors. Finally, an experimental circuit is designed to realize the proposed chaotic oscillator. The typical chaotic attractors and some coexisting attractors are captured experimentally. The obtained experimental results consist with the numerical simulations.