1 Introduction

In 1971, from the logical and axiomatic points of view, Chua postulated the existence of a fundamental two-terminal passive device, named memristor (a contraction of memory–resistor), for which a nonlinear relationship links charge and flux [1]. However, on April 30, 2008, Stan Williams et al. [2] announced that the missing circuit element has been found [3], which it took more than 30 years to show experimentally at HP laboratories that it is possible to realize a passive memristor-like device in nanotechnology [2, 3].

An important feature is that an ideal memristor can display nonvolatile memory and also has potential to reproduce the behavior of a biological synapse [4]. In 1976, a broader class of memristive systems including the memristor was presented by Kang and Chua [5]. Furthermore, the design of memristive systems requires a deep and clear understanding of the nonlinear dynamics of these memristive systems. Many studies and applications for the memristor have been done. In [6, 7], the authors have generalized the notion of memristor to memcapacitor and meminductor elements, and an artificial synapse can be realized by these elements. The combination of these elements in circuits can find applications in neuromorphic devices to simulate complex learning, adaptive, spontaneous behavior and associative memory. The three mutually coupled memristor oscillator circuits are constructed, and the stability of the multimode oscillation for such circuit is carefully analyzed in [8]. In [9], for recognizing and exploring the electrical activities in neurons, the research progresses for the biological Hodgkin–Huxley model and its simple versions are reviewed. The memristor-based FitzHugh–Nagumo model is designed, and the chaotic behaviors of the model under external stimuli have also been found. Furthermore, the synchronization of coupled memristor-based chaotic neurons with memristor synapse is studied [10]. In [11], an external current is injected into the Hindmarsh–Rose (HR) neuron model, an improved HR model has been proposed, and this results in the emergence of various dynamical behaviors such as hyperchaos, periodic bursters and so on. For implementing the spike Timing-Dependent Plasticity mechanism, a novel fully floating memristor-based circuit has been presented [12]. In the four-dimensional current–voltage phase space, the authors constructed the memristor canonical Chua’s circuit [13, 14]. In [15], the authors have further shown that the equations of dissipative memristor circuits can represented by Hamilton’s equations. In the above cases, a continuous piecewise-linear function is used to represent the flux–charge characteristic curve of these circuits in [15,16,17,18,19]. The simplest parallel memristor system based on a voltage-controlled memristor is designed, and its dynamical characteristics are numerically analyzed [20]. In [21], the authors have proposed an electronic model based on Duffing oscillator with a characteristic memristor nonlinear element, and for a certain range of circuit parameters the dynamical behaviors of this circuit such as bifurcations, chaos, three tori, transient chaos and intermittency are observed. By substituting Chua’s diode with a first-order memristive diode bridge in the classical Chua’s circuit, a novel memristive chaotic circuit is constructed [22]. In [23], the authors designed a second-order circuit employing an inductor, a capacitor, a resistor and a flux-controlled memristor, and analyzed local stability of equilibria, local and global bifurcations, and furthermore, derived necessary and sufficient conditions for the occurrence of a supercritical Hopf bifurcation. In particular, for the memristor-based canonical circuits many authors have applied a classical piecewise-linear function to describe the flux–charge characteristic curve [24,25,26,27].

However, the known analytic approaches are all for differentiable and smooth dynamical systems; frequently, nonlinear circuits are modeled by dynamical systems, i.e., their nonlinearities are assumed sufficiently smooth. In these analytic approaches, if one wants to find an evidence of the appearance of periodic oscillations, then the Hopf bifurcation Theorem [28,29,30] is one of the most practical and important results. However, in the real world, one has to employ piecewise-linear or discontinuous systems so as to get more precise models. In practical applications, such as in the field of nonlinear electronics and control, piecewise-linear or discontinuous systems are very common [31, 32].

Bifurcation analysis of piecewise-linear or discontinuous systems may be very difficult; up to now, no general theoretic results for this class of systems can be applied practically, and at the same time, we must consider the cumulative contribution of every phase space section to the system dynamics. In particular, the classical Hopf bifurcation theorems cannot directly be applied to piecewise-linear or discontinuous systems due to their non-differentiability or discontinuity. But, bifurcations may occur in piecewise-linear or discontinuous systems and they have similarities (but also discrepancies) with the Hopf bifurcation in differential and smooth dynamical systems [33].

In this paper, we design a simple memristor-based circuit by employing an inductor, a capacitor and a flux-controlled memristor, and use two kinds of nonlinear functions as the flux–charge characteristic curve. One is continuous piecewise-linear function, and another is discontinuous function. The analysis of memristor-based circuit with the flux–charge characteristic curve of continuous piecewise-linear function is studied by applying the point transformation method of Andronov [34], which is a very useful tool for analyzing piecewise-linear systems.

The analysis of the circuit with the flux–charge characteristic curve of discontinuous function is performed by applying Fourier series expansion and the multiple-scale method [35]. The underlying idea of the multiple-scale method is to consider the expansion representing the response to be a function of multiple independent variables, or scales, instead of a single variable. First, in this paper we expand the sign function into Fourier series, then using the multiple-scale method obtain the approximated period and amplitude of the limit cycle.

The remaining part of this paper is organized as follows. In Sect. 2, we design a simple memristor-based circuit with continuous piecewise-linear function. Section 3 will start with a short introduction of the point transformation method, and the whole point transformation is the product of some point transformations of a straight line into a straight line, these point transformations can be expressed in the form of parameters. In this problem, the fixed points corresponding to limit cycles will be determined by two transcendental equations and their stability is also studied. In Sect. 4, we will first expand the sign function into Fourier series, then using the multiple-scale method we obtain the period and the amplitude of the approximated periodic solution. In Sect. 5, numerical simulations support the validity of theoretical analysis. In the last section, some conclusions and future researches about the models will be presented.

2 A circuit with only one memristor

In this section, the circuit with a flux-controlled memristor, an inductor and a capacitor are shown in Fig. 1.

Fig. 1
figure 1

A circuit with an inductor, a capacitor and a memristor

Full size image

Assume that the values of L andC for the impedance and capacitance are positive constants, and apply Kirchhoff’s current law and Kirchhoff’s voltage law (see Fig. 1), we have

$$\begin{aligned} \left\{ {\begin{array}{l} i(t)-{\hat{i}}(t)-i_{m} (t)=0, \\ -v(t)-{\hat{v}}(t)=0, \\ {\hat{v}}(t)-v_M (t)=0. \\ \end{array}} \right. \end{aligned}$$
(1)

Integrating both sides of Eq. (1) from time instant \(t_{0}\) to time instant t, we get

$$\begin{aligned} \left\{ {\begin{array}{l} q(t)-{\hat{q}}(t)-q_m (t)=Q, \\ -\phi (t)-{\hat{\phi }}(t)=\phi , \\ {\hat{\phi }}(t)-\phi _M (t)=\phi . \\ \end{array}} \right. \end{aligned}$$
(2)

where \(Q=q(t_0 )-{\hat{q}}(t_0 )-q_m (t_0 ),\;\;\phi =-\phi (t_0 )-{\hat{\phi }}(t_0 ),\;\phi ={\hat{\phi }}(t_0 )-\phi _M (t_0 ).\)

For convenience, we let \(Q=0, \;\phi =0,\phi =0\), Eq. (2) have the following constitutive equations:

$$\begin{aligned}&\phi (t)= L\frac{\mathrm{d}q(t)}{\mathrm{d}t},\; {\hat{q}}(t)=C\frac{\mathrm{d}{\hat{\phi }}(t)}{\mathrm{d}t} \hbox { and } \\&q_m (t)= q_m (\phi _m (t))=q_m ({\hat{\phi }}(t)). \end{aligned}$$

Substituting the constitutive laws of bipoles into (2) yields

$$\begin{aligned} \left\{ {\begin{array}{l} \frac{\mathrm{d}{\hat{\phi }}(t)}{\mathrm{d}t}=\frac{q(t)}{C}-\frac{q_m ({\hat{\phi }}(t))}{C}, \\ \frac{\mathrm{d}q(t)}{\mathrm{d}t}=-\frac{{\hat{\phi }}(t)}{L}. \\ \end{array}} \right. \end{aligned}$$
(3)

Assume \(\alpha =1/C \hbox { and } \xi =1/L\) (note that the parameters \(\alpha \hbox { and } \xi \) are positive real values), and define state variables as \(x(t)={\hat{\phi }}(t) \hbox { and } y(t)=q(t)\), state equations of the circuit in Fig. 1 become as

$$\begin{aligned} \left\{ {\begin{array}{l} \frac{\mathrm{d}x(t)}{\mathrm{d}t}=\alpha y(t)-\alpha q_m (x(t)), \\ \frac{\mathrm{d}y(t)}{\mathrm{d}t}=-\xi x(t). \\ \end{array}} \right. \end{aligned}$$
(4)

We choose the following expression for the memristor charge–flux (i.e., \(q_{m}(t)-x(t)\) nonlinear relationship) [1, 5, 13, 23]:

$$\begin{aligned} q_m (x(t))=bx(t)+(a-b)\mathrm{sat}(x(t)), \end{aligned}$$
(5)

where nonlinear function sat(x(t)) is defined as

$$\begin{aligned} \mathrm{sat}(x(t))=\frac{1}{2}\left( \left| {x(t)+1} \right| -\left| {x(t)-1} \right| \right) . \end{aligned}$$
(6)

Equation (4) can become as

$$\begin{aligned} {\ddot{x}}(t)+[\alpha (a-b)H(1-\left| x \right| )+\alpha b]\dot{x}(t)+\alpha \xi x(t)=0,\nonumber \\ \end{aligned}$$
(7)

where

$$\begin{aligned} H(x)=\left\{ {\begin{array}{l} 0,\quad x<0, \\ 1,\quad x\ge 0. \\ \end{array}} \right. \end{aligned}$$

Equation (7) may rewrite as

$$\begin{aligned}&\ddot{x}(t)+\alpha b\dot{x}(t)+\alpha \xi x(t)=0,\quad \left| x \right| \ge 1, \end{aligned}$$
(8a)
$$\begin{aligned}&\ddot{x}(t)+\alpha a\dot{x}(t)+\alpha \xi x(t)=0,\quad \left| x \right| <1. \end{aligned}$$
(8b)

Let \(t=\tau /{\sqrt{\alpha \xi }},\) for convenience of our study, we still replace \(\tau \) with t, then Eq. (8) becomes

$$\begin{aligned}&\ddot{x}(t)+bd\dot{x}(t)+x(t)=0,\quad \left| x \right| \ge 1, \end{aligned}$$
(9a)
$$\begin{aligned}&\ddot{x}(t)+ad\dot{x}(t)+x(t)=0,\quad \left| x \right| <1, \end{aligned}$$
(9b)

where \(d=\sqrt{\alpha /\xi }\). Thus, the phase plane (x, y) (where \(y=\dot{x})\) is divided by the lines \(x=-\,1\) and \(x=+\,1\) into three linear regions: \(\hbox {(I)} x<-1,\;\hbox {(II)} \left| x \right| <1 \hbox { and } \hbox {(III)} x>+1\), in each of which the appropriate linear equation (9) holds (see Fig. 2 and Remark 1).

Fig. 2
figure 2

The phase plane (x, y) for Eq. (9)

Full size image

From the point of view of physics, the phase paths must be continuous on the phase plane as well as on the boundaries \(x=-\,1\) and \( x=+\,1\) (see Remark 1). Also, Eq. (9) is invariant under a change in the variables (x, y) into \((-x, -y)\). The same symmetry is also established for the paths in the upper and lower half of the region (I).

Remark 1

In Fig. 2, the phase paths are presented as spirals. This only takes place for \(\left| b \right|<2/d, \;\left| a \right| <2/d\).

The dynamical system (9) has a unique state of the equilibrium at the origin (0, 0) which is a node \((\left| a \right| \ge 2/d)\)or a focus \((\left| a \right| <2/d)\), stable for \( a>0\) and unstable for \(a<0\). In the following, we will mainly consider the self-excited circuit in which \(b>0\) and \(a<0\).

Remark 2

If \(b>0\) and \(a>0\), then all phase paths approach asymptotically the stable state of the equilibrium (0, 0); hence, the system will not oscillate (whatever the initial conditions).

3 The approximated periodic solution with continuous piecewise-linear function

3.1 Point transformation

The phase plane (x, y) for the system is filled with sections of paths, corresponding to the linear equation (9), these sections of paths are joined together at their ends on the straight lines \(x=-\,1\) and \(x=+\,1\), thus forming entire phase paths.

To find all limit cycles, we construct the point transformation of the half line into themselves and determine its fixed points.

Let \(\Omega \) be obviously the composite of four transformations \(\Omega _1 , \Omega _2 , \Omega _3 \hbox { and } \Omega _4 \), where we denote the transformation from the half lines S to \({S}'\) as \(\Omega _1 \), the transformation from \({S}'\) to \(S_{1}\) as \(\Omega _2 \), the transformation from \(S_{1}\) to \(S_1 ^{\prime }\) as \(\Omega _3 \), the transformation from \(S_1 ^{\prime }\) to S as \(\Omega _4 \), respectively. By the symmetry, we have

$$\begin{aligned} \Omega _3 \equiv \Omega _1 \;\hbox {and}\;\Omega _4 \equiv \Omega _2 . \end{aligned}$$
(10)

Therefore, the transformation \(\Omega \) is obtained by applying the transformation \({\Omega }'\) twice, i.e.,

$$\begin{aligned} {\Omega }'=\Omega _1 \bullet \Omega _2 ,\;\hbox {then}\;\Omega =({\Omega }')^{2}, \end{aligned}$$
(11)

relates S to \(S_{1}\).

In the region (I) (\(x<-1\)), the phase paths are determined by (9a), i.e., the solution of Eq. (9a) is

$$\begin{aligned} x(t)=A\mathrm{e}^{\lambda _1 t}+B\mathrm{e}^{\lambda _2 t}, \end{aligned}$$
(12)

where \(\lambda _1 \hbox { and } \lambda _2 \) are the roots of the quadratic equation:

$$\begin{aligned} \lambda ^{2}+bd\lambda +1=0. \end{aligned}$$
(13)

As is well known, for \(\left| b \right| >2/d\) these roots are real and for \(\left| b \right| <2/d\) they are complex. Accordingly, depending on the sign of \(b^{2}d^{2}-4\), we may obtain two types of solutions and two different processes: for \(\left| b \right| <2/d\), a damped oscillating process and for \(\left| b \right| >2/d\), a damped aperiodic process.

When \(\left| b \right| <2/d\), the roots of the characteristic Eq. (13) are:

$$\begin{aligned} \lambda _{1,2} =-h_1 \pm \hbox {j}\omega _1 , \end{aligned}$$
(14)

where \(0<h_1 ={bd}/2<1(b>0),\;\omega _1 =\sqrt{1-h_1^2 },\;\hbox {j}=\sqrt{-1},\) and the general solution of the equation (9a) is

$$\begin{aligned} x(t)=\mathrm{e}^{-h_1 t}(A\cos \omega _1 t+B\sin \omega _1 t), \end{aligned}$$
(15)

where A and B are determined by the initial conditions. And precisely, if \(x=x_{0}, y=y_{0}\) at \(t=0\), then its solution is

$$\begin{aligned} \left\{ {\begin{array}{l} x=\mathrm{e}^{-h_1 t}\left[ x_0 \cos \omega _1 t+\frac{y_0 +h_1 x_0 }{\omega _1 }\sin \omega _1 t\right] , \\ y=\dot{x}=\mathrm{e}^{-h_1 t}\left[ y_0 \cos \omega _1 t-\frac{x_0 +h_1 y_0 }{\omega _1 }\sin \omega _1 t\right] . \\ \end{array}} \right. \end{aligned}$$
(16)

Therefore, the equation of the path leaving S at \(t=0\)\((x_0 =-1, y_0 =-s, \hbox {where } s>0)\) is

$$\begin{aligned} \left\{ {\begin{array}{l} x=-\mathrm{e}^{-h_1 t}\left[ \cos \omega _1 t+\frac{s+h_1 }{\omega _1 }\sin \omega _1 t\right] , \\ y=\dot{x}=\mathrm{e}^{-h_1 t}\left[ -s\cos \omega _1 t+\frac{1+h_1 s}{\omega _1 }\sin \omega _1 t\right] . \\ \end{array}} \right. \end{aligned}$$
(17)

The representative point moving along the path (17) will reach at time \(t_1 ={\tau _1 }/{\omega _1 }\), the half line \({S}'\) at a point \({s}'\)\((x=-1, y={s}'>0)\) (see Fig. 2)

$$\begin{aligned} \left\{ {\begin{array}{l} {s}'=\mathrm{e}^{-h_1 \frac{\tau _1 }{\omega _1 }}\left[ -s\cos \tau _1 +\frac{1+sh_1 }{\omega _1 }\sin \tau _1\right] , \\ -1=-\mathrm{e}^{-h_1 \frac{\tau _1 }{\omega _1 }}\left[ \cos \tau _1 +\frac{s+h_1 }{\omega _1 }\sin \tau _1 \right] . \\ \end{array}} \right. \end{aligned}$$

Solving the above equations for s and \({s}'\), we obtain the correspondence or the sequence function (The function for the point transformation of a line into another line is called as the sequence function or the correspondence function) for the transformation \(\Omega _1 \)

$$\begin{aligned} \left\{ {\begin{array}{l} s=\frac{\mathrm{e}^{\gamma _1 \tau _1 }-\cos \tau _1 -\gamma _1 \sin \tau _1 }{\sqrt{1+\gamma _1^2 }\sin \tau _1 }, \\ {s}'=\frac{\mathrm{e}^{-\gamma _1 \tau _1 }-\cos \tau _1 +\gamma _1 \sin \tau _1 }{\sqrt{1+\gamma _1^2 }\sin \tau _1 }, \\ \end{array}} \right. \end{aligned}$$
(18)

where

$$\begin{aligned} \gamma _1 =\frac{h_1 }{\omega _1 }=\frac{h_1 }{\sqrt{1-h_1^2 }},\;\omega _1 =\frac{1}{\sqrt{1+\gamma _1^2 }}. \end{aligned}$$

(as \(h_{1}\) varies from 0 to + 1, \(\gamma _1 \) increases monotonically from 0 to \(+\infty )\).

We pass now to the point transformation \(\Omega _2 \), i.e., the transformation of the points of the half straight line \({S}'\)into point \((+1, s_{1})\) of the half straight line \(S_{1}\) as generated by paths in the region (II), limiting ourselves to the case \(-1<h_2 =\frac{ad}{2}<0,\;-\frac{2}{d}<a<0.\)

Similar to the above approach, if the initial value \(({x}'_0 , {y}'_0 )\), then the solution of (9b) is

$$\begin{aligned} \left\{ {\begin{array}{l} x=\mathrm{e}^{-h_2 t}\left[ {x}'_0 \cos \omega _2 t+\frac{{y}'_0 +h_2 {x}'_0 }{\omega _2 }\sin \omega _2 t\right] , \\ y=\dot{x}=\mathrm{e}^{-h_2 t}\left[ {y}'_0 \cos \omega _2 t-\frac{{x}'_0 +h_2 {y}'_0 }{\omega _2 }\sin \omega _2 t\right] , \\ \end{array}} \right. \end{aligned}$$
(19)

where

$$\begin{aligned} h_2 =\frac{ad}{2},\;\omega _2 =\sqrt{1-h_2^2 }. \end{aligned}$$

For the phase path leaving the point \((-1, {s}')\) of the half line \({S}'(x=-1, {s}'>0)\) at \(t=0\) and passing through the region (II), we have, according to (9b) for the case \(-1<h_2 <0.\)

$$\begin{aligned} \left\{ {\begin{array}{l} x=\mathrm{e}^{-h_2 t}\left[ -\cos \omega _2 t+\frac{{s}'-h_2 }{\omega _2 }\sin \omega _2 t\right] , \\ y=\dot{x}=\mathrm{e}^{-h_2 t}\left[ {s}'\cos \omega _2 t+\frac{1-{s}'h_2 }{\omega _2 }\sin \omega _2 t\right] . \\ \end{array}} \right. \end{aligned}$$
(20)

The parametric expressions for the transformation \(\Omega _2 \) can be obtained by assuming that \(S_{1}\) is reached at the point \(x=+\,1, y=s_1 >0\), at \(t_2 ={\tau _2 }/{\omega _2 }>0,\) and solving for \({s}'\) and \(s_{1}\)

$$\begin{aligned} \left\{ {\begin{array}{l} {s}'=\frac{\mathrm{e}^{\gamma _2 \tau _2 }+\cos \tau _2 +\gamma _2 \sin \tau _2 }{\sqrt{1+\gamma _2^2 }\sin \tau _2 }, \\ s_1 =\frac{\mathrm{e}^{-\gamma _2 \tau _2 }+\cos \tau _2 -\gamma _2 \sin \tau _2 }{\sqrt{1+\gamma _2^2 }\sin \tau _2 }, \\ \end{array}} \right. \end{aligned}$$
(21)

where

$$\begin{aligned} \gamma _2 =\frac{h_2 }{\omega _2 }=\frac{h_2 }{\sqrt{1-h_2^2 }}<0,\;\omega _2 =\frac{1}{\sqrt{1+\gamma _2^2 }}. \end{aligned}$$

3.2 Fixed point and stability of limit cycle

In the following, we will discuss some properties for (18). On differentiating (18), we get

$$\begin{aligned} \frac{\mathrm{d}s}{\mathrm{d}\tau _1 }=\frac{1-\mathrm{e}^{\gamma _1 \tau _1 }(\cos \tau _1 -\gamma _1 \sin \tau _1 )}{\sqrt{1+\gamma _1^2 }\sin ^{2}\tau _1 }, \end{aligned}$$

and

$$\begin{aligned} \frac{\mathrm{d}{s}'}{\mathrm{d}\tau _1 }=\frac{1-\mathrm{e}^{-\gamma _1 \tau _1 }(\cos \tau _1 +\gamma _1 \sin \tau _1 )}{\sqrt{1+\gamma _1^2 }\sin ^{2}\tau _1 }. \end{aligned}$$

Now we introduce the auxiliary function

$$\begin{aligned} \varphi (\tau ,\gamma )=1-\mathrm{e}^{\gamma \tau }(\cos \tau -\gamma \sin \tau ). \end{aligned}$$

Hence, the following Lemma 1 is immediate.

Lemma 1

The following three properties of the function \(\varphi (\tau ,\gamma )\) hold:

  1. (i)

    \(\varphi (\tau ,\gamma )=\varphi (-\tau ,-\gamma );\)

  2. (ii)

    \(\frac{\partial \varphi }{\partial \tau }=(1+\gamma ^{2})\mathrm{e}^{\gamma \tau }\sin \tau ;\)

  3. (iii)

    For \(\gamma >0\), there exists \(\tau =\tau ^{0}(\gamma ), \tau \in (0,\;2\pi )\) such that \(\varphi (\tau ^{0}, \gamma )=0\) and for \(\tau <\tau ^{0}, \varphi (\tau , \gamma ) >0.\)

By (ii), we can see that \(\varphi (\tau ,\gamma )\) with respect to \(\tau \) under \(\gamma >0\) is monotonically increased when \(\tau \in (0, \pi )\), and is monotonically decreased when \(\tau \in (\pi , 2\pi )\).

By Lemma 1, we have

$$\begin{aligned} s= & {} \frac{\mathrm{e}^{\gamma _1 \tau _1 }\varphi (\tau _1 , -\gamma _1 )}{\sqrt{1+\gamma _1^2 }\sin \tau _1 },\quad \frac{\mathrm{d}s}{\mathrm{d}\tau _1 }=\frac{\varphi (\tau _1 , \gamma _1 )}{\sqrt{1+\gamma _1^2 }\sin ^{2}\tau _1 }, \nonumber \\ \end{aligned}$$
(22a)
$$\begin{aligned} {s}'= & {} \frac{\mathrm{e}^{-\gamma _1 \tau _1 }\varphi (\tau _1 , \gamma _1 )}{\sqrt{1+\gamma _1^2 }\sin \tau _1 },\quad \frac{\mathrm{d}{s}'}{\mathrm{d}\tau _1 }=\frac{\varphi (\tau _1 , -\gamma _1 )}{\sqrt{1+\gamma _1^2 }\sin ^{2}\tau _1 }.\nonumber \\ \end{aligned}$$
(22b)

By (22) and Lemma 1, it follows that, for \(s\in (0,+\infty )\), the parameter \(\tau _1 \in (0,\pi )\). Also, as \(\tau _1 \) varies from 0 to \(\pi , s\) and \({s}'\) increase monotonically from 0 to \(+\infty , s,{s}',\frac{\mathrm{d}s}{\mathrm{d}\tau _1 } \hbox { and } \frac{\mathrm{d}{s}'}{\mathrm{d}\tau _1 }\) remain positive and continuous.

To discuss the relation between the values of s and \({s}'\), it suffices to note the following:

  1. (i)

    for \(0<\tau <\pi ,\)

    $$\begin{aligned} \frac{\mathrm{d}s}{\mathrm{d}{s}'}=\frac{\varphi (\tau _1 ,\;\gamma _1 )}{\varphi (\tau _1 ,\;-\gamma _1 )}>0, \end{aligned}$$
    (23)

    and increases monotonically from 1 at \(\tau _1 \rightarrow +0\) to \(\frac{1+\mathrm{e}^{\gamma _1 \pi }}{1+\mathrm{e}^{-\gamma _1 \pi }} \hbox {at } \tau _1 \rightarrow \pi -0\), since

    $$\begin{aligned} \frac{\mathrm{d}^{2}s}{\mathrm{d}{s}'^{2}}&=\frac{\partial }{\partial \tau _1 }\left\{ {\frac{\varphi (\tau _1 ,\;\gamma _1 )}{\varphi (\tau _1 ,\;-\gamma _1 )}} \right\} \frac{1}{\frac{\mathrm{d}{s}'}{\mathrm{d}\tau _1 }}\nonumber \\&=\frac{2(1+\gamma _1^2 )^{\frac{3}{2}}\sin ^{3}\tau _1 }{[\varphi (\tau _1 ,\;-\gamma _1 )]^{3}}\left[ \sinh \gamma _1 \tau _1 -\gamma _1 \sin \tau _1 \right] >0 \end{aligned}$$
    (24)

    for \(0<\tau <\pi ,\) and hence, \(1<\frac{\mathrm{d}s}{\mathrm{d}{s}'}<\frac{1+\mathrm{e}^{\gamma _1 \pi }}{1+\mathrm{e}^{-\gamma _1 \pi }}\).

  2. (ii)

    for \(\tau _1 \rightarrow \pi -0\), the correspondence function (22) has a rectilinear asymptote

    $$\begin{aligned} s=\frac{1+\mathrm{e}^{\gamma _1 \pi }}{1+\mathrm{e}^{-\gamma _1 \pi }}{s}'+\bar{{a}}, \end{aligned}$$
    (25)

    where

    $$\begin{aligned} {\bar{a}}=\mathop {\lim }\limits _{\tau \rightarrow \pi -0} \left[ s-\frac{1+\mathrm{e}^{\gamma _1 \pi }}{1+\mathrm{e}^{-\gamma _1 \pi }}{s}'\right] =-\frac{2\gamma _1 (1+\mathrm{e}^{\gamma _1 \pi })}{\sqrt{1+\gamma _1^2 }}<0. \end{aligned}$$
  3. (iii)

    Because \(\frac{\mathrm{d}^{2}s}{\mathrm{d}{s}'^{2}}>0 \hbox { and } \bar{{a}}<0\), the curve of Eq. (22) is located above the asymptote (20).

In the following, we will discuss the properties of (21). From (21), we have

  1. (i)

    For \(\tau _2 \rightarrow +0, s_1 \hbox { and } {s}'\rightarrow +\infty .\)

  2. (ii)

    \({s}'=0\) for a certain \(\tau _2 ={\tau }'_2 (0<{\tau }'_2 <\pi )\) determined by the equation \({s}'({\tau }'_2 )=0\) or \(1+\mathrm{e}^{-\gamma _2 \tau _2 }(\cos \tau _2 +\gamma _2 \sin \tau _2 )=0, \hbox {where} {s}'(\tau _2 )>0\).

  3. (iii)

    Differentiating (21), we have

    $$\begin{aligned} \frac{\mathrm{d}s_1 }{\mathrm{d}\tau _2 }= & {} -\frac{1+\mathrm{e}^{-\gamma _2 \tau _2 }(\cos \tau _2 +\gamma _2 \sin \tau _2 )}{\sqrt{1+\gamma _2^2 }\sin ^{2}\tau _2 }, \end{aligned}$$
    (26)
    $$\begin{aligned} \frac{\mathrm{d}{s}'}{\mathrm{d}\tau _2 }= & {} -\frac{1+\mathrm{e}^{\gamma _2 \tau _2 }(\cos \tau _2 -\gamma _2 \sin \tau _2 )}{\sqrt{1+\gamma _2^2 }\sin ^{2}\tau _2 }, \end{aligned}$$
    (27)

and

$$\begin{aligned} \frac{\mathrm{d}s_1 }{\mathrm{d}{s}'}=\frac{1+\mathrm{e}^{-\gamma _2 \tau _2 }(\cos \tau _2 +\gamma _2 \sin \tau _2 )}{1+\mathrm{e}^{\gamma _2 \tau _2 }(\cos \tau _2 -\gamma _2 \sin \tau _2 )}. \end{aligned}$$
(28)

Let \(g(\tau _2 )=1+\mathrm{e}^{-\gamma _2 \tau _2 }(\cos \tau _2 +\gamma _2 \sin \tau _2 )\), then we have

$$\begin{aligned} \frac{\mathrm{d}g(\tau _2 )}{\mathrm{d}\tau _2 }=-(1+\gamma _2^2 )\mathrm{e}^{-\gamma _2 \tau _2 }\sin \tau _2 <0. \end{aligned}$$

Hence, \(1+\mathrm{e}^{-\gamma _2 \tau _2 }(\cos \tau _2 +\gamma _2 \sin \tau _2 )>0\) when \(0<\tau _2 <{\tau }'_1 \) and similarly

$$\begin{aligned} 1+\mathrm{e}^{\gamma _2 \tau _2 }(\cos \tau _2 -\gamma _2 \sin \tau _2 )>0 \end{aligned}$$

for \(0<\tau _2 <{\tau }'_2 \), then for these values of \(\tau _2 , \frac{\mathrm{d}{s}'}{\mathrm{d}\tau _2 }<0 \hbox { and } \frac{\mathrm{d}s_1 }{\mathrm{d}\tau _2 }<0\). Also, \(\frac{\mathrm{d}s_1 }{\mathrm{d}{s}'}>0\), so that as \(\tau _2 \) varies from 0 to \({\tau }'_2 , {s}'\) decreases monotonically from \(+\infty \) to 0, and \(s_{1}\) decreases from \(+\infty \) to \(s_1 ({\tau }'_2 )>0\). Hence, the interval of smallest positive values of \(\tau _2 \) needed to know all points of the half line \({S}'\) is \(0<\tau _2 <{\tau }'_2\).

  1. (i)

    Since

    $$\begin{aligned} \frac{\mathrm{d}^{2}s_1 }{\mathrm{d}{s}'^{2}}= & {} -\frac{2(1+\gamma _2^2 )^{\frac{3}{2}}\sin ^{3}\tau _2 }{[1+\mathrm{e}^{\gamma _2 \tau _2 }(\cos \tau _2 -\gamma _2 \sin \tau _2 )]^{3}}\nonumber \\&\left[ \sinh \gamma _2 \tau _2 +\gamma _2 \sin \tau _2 \right] >0 \end{aligned}$$
    (29)

    for all values of \(\tau _2 \) in the interval \(0<\tau _2 <{\tau }'_2 \), then as \({s}'\) increases from 0 to \(+\infty , \frac{\mathrm{d}s_1 }{\mathrm{d}{s}'}\) increases monotonically from 0 (at \({s}'=0\)) to + 1 (at \({s}'\rightarrow +\infty )\), i.e., \(0<\frac{\mathrm{d}s_1 }{\mathrm{d}{s}'}<1\). Equation (22) has the asymptote \(s_1 ={s}'-\frac{4\gamma _2 }{\sqrt{1+\gamma _2^2 }}\), and, due to the fact that \(\frac{\mathrm{d}^{2}s_1 }{\mathrm{d}{s}'^{2}}>0\), this curve is located above the asymptote. These properties are sufficient to construct a graph of the correspondence function (21).

Construct the curves (18) and (21) on one plane. The fixed points are determined analytically by the following equations

$$\begin{aligned} \left\{ {\begin{array}{l} \frac{\mathrm{e}^{-\gamma _1 \tau _1 }-\cos \tau _1 +\gamma _1 \sin \tau _1 }{\sqrt{1+\gamma _1^2 }\sin \tau _1 }=\frac{\mathrm{e}^{\gamma _2 \tau _2 }+\cos \tau _2 +\gamma _2 \sin \tau _2 }{\sqrt{1+\gamma _2^2 }\sin \tau _2 }, \\ \frac{\mathrm{e}^{\gamma _1 \tau _1 }-\cos \tau _1 -\gamma _1 \sin \tau _1 }{\sqrt{1+\gamma _1^2 }\sin \tau _1 }=\frac{\mathrm{e}^{-\gamma _2 \tau _2 }+\cos \tau _2 -\gamma _2 \sin \tau _2 }{\sqrt{1+\gamma _2^2 }\sin \tau _2 }, \\ \end{array}} \right. \end{aligned}$$
(30)

which is obtained from Eqs. (18) and (21) by eliminating \({s}'\) and putting \(s_1 =s\).

It is easy to show that there exists only one point of intersection of the curves (18) and (21). In fact, the existence of at least one point of intersection follows from the continuity of these curves and from the inequalities.

$$\begin{aligned} s_1 -s= & {} -\frac{2\gamma _2 }{\sqrt{1+\gamma _2^2 }}+\frac{2\gamma _1 }{\sqrt{1+\gamma _1^2 }}>0 \hbox { for } {s}'=0,\nonumber \\&s_1 -s<0 \hbox { for sufficiently large } {s}'. \end{aligned}$$
(31)

Remark 3

The slopes of the asymptotes of the curves (18) and (21) are equal, respectively, to \(\frac{1+\mathrm{e}^{\gamma _1 \pi }}{1+\mathrm{e}^{-\gamma _1 \pi }}\) and to 1, i.e., the asymptote of the curve (18) is steeper than the asymptote of the curve (21).

Further, if several points of intersection did exist, then for the first of them (the one with smallest \({s}')\), we should have \(\frac{\mathrm{d}s_1 }{\mathrm{d}{s}'}<\frac{\mathrm{d}s}{\mathrm{d}{s}'}\), and for the following one \(\frac{\mathrm{d}s_1 }{\mathrm{d}{s}'}>\frac{\mathrm{d}s}{\mathrm{d}{s}'}\). The latter is impossible since \(0<\frac{\mathrm{d}s_1 }{\mathrm{d}{s}'}<1 \hbox { and } \frac{\mathrm{d}s}{\mathrm{d}{s}'}>1\)(for any values of \({s}')\). Thus, there is one unique point of intersection and therefore one unique fixed point if \(0<h_1<1 \hbox { and } -1<h_2 <0\). The fixed point is stable since \(0<\frac{\mathrm{d}s_1 }{\mathrm{d}s}<1 \).

Therefore, for \(0<h_1<1 \hbox { and } -1<h_2 <0\) there is a unique stable limit cycle, to which all phase paths tend to: (for \(t\rightarrow +\infty )\). Thus, the memristor circuit has a mode of self-excitation.

The period of the self-oscillations is clearly equal to

$$\begin{aligned} T=\frac{2}{\sqrt{\alpha \xi }}\left[ {\frac{\bar{{\tau }}_1 }{\omega _1 }+\frac{\bar{{\tau }}_2 }{\omega _2 }} \right] . \end{aligned}$$
(32)

(in units of the dimensionless time), where \(\bar{{\tau }}_1 \hbox { and } \bar{{\tau }}_2 \) are values of \(\tau _1 \hbox { and } \tau _2 \) in a limit cycle.

4 Self-sustained oscillation with discontinuous function

If we replace Eq. (5) with the following function [34, 36]

$$\begin{aligned} q_m (x)=-ax+\frac{b}{2}x\left| x \right| , \end{aligned}$$
(33)

where \(a>0, b>0\), Eq. (4) becomes as

$$\begin{aligned} {\ddot{x}}(t)+\alpha (-a+b\left| x \right| )\dot{x}(t)+\alpha \xi x(t)=0. \end{aligned}$$
(34)

Similar to the previous approach, let \(t=\tau /{\sqrt{\alpha \xi }}\) we still replace \(\tau \) with t, then Eq. (3) becomes

$$\begin{aligned} {\ddot{x}}(t)+\varepsilon (-a+b\left| x \right| )\dot{x}(t)+x(t)=0, \end{aligned}$$
(35)

where

$$\begin{aligned} \varepsilon =d=\sqrt{\alpha /\xi }. \end{aligned}$$

Theorem 1

[33] The equation \(\ddot{x}(t)+\varepsilon f(x)\dot{x}(t)+g(x)=0\) has a unique periodic solution if f and g are continuous, and \(F(x)\equiv \int _0^x f(u)\mathrm{d}u \) is an odd function, and F(x) is zero only at \(x=0, x=C, x=-\,C\), for some \(C>0\) and \(F(x)\rightarrow 0 \hbox { as } x\rightarrow \infty \) monotonically for \(x>C\). In addition, g(x) must be an odd function, and \(g(x)>0\) for \(x>0\).

Fig. 3
figure 3

The representative point P on a segment of a phase path in the left and a closed path : P leaves A and returns to A an infinite number of times in the right

Full size image
Fig. 4
figure 4

The unique equilibrium (0, 0) of system (4) with (5) is a stable node, where \(\alpha =1.75,\;\xi =1, a=1.6, b=1\): a wave plot, b phase plane plot

Full size image
Fig. 5
figure 5

The unique equilibrium (0, 0) of system (4) with (5) is an unstable node and a stable periodic solution occurs, where \(\alpha =1.75,\;\xi =1\), \(a=-\,0.8\), \(b=1\): a wave plot, b phase plane plot

Full size image
Fig. 6
figure 6

The unique equilibrium (0, 0) of system (4) with (5) is a stable focus, where \(\alpha =1.75, \xi =1, a=1.2\), \(b=1\): a wave plot, b phase plane plot

Full size image

Here,

$$\begin{aligned} F(x)=\left\{ {\begin{array}{l} (-ax+\frac{b}{2}x^{2}),\quad x>0, \\ (-ax-\frac{b}{2}x^{2}),\quad x<0. \\ \end{array}} \right. \end{aligned}$$
(36)

In the following, we will find how the system evolves to a limit cycle, obviously the sgn(x) can expand into the following Fourier series

$$\begin{aligned} \hbox {sgn}(x)=\frac{4}{\pi }\sum _{n=0}^\infty {\frac{(-1)^{n}}{(2n+1)}\cos (2n+1)x} , \end{aligned}$$
(37)

Using the multiple-scale method and setting \(\tau =t\) which represents the fast time scale of oscillations and \(T=\varepsilon t\) which represents the slow amplitude drift, we have

$$\begin{aligned} {\dot{x}}=\frac{\partial x}{\partial \tau }+\varepsilon \frac{\partial x}{\partial T}, \end{aligned}$$
(38)

and

$$\begin{aligned} {\ddot{x}}=\frac{\partial ^{2}x}{\partial \tau ^{2}}+2\varepsilon \frac{\partial ^{2}x}{\partial \tau \partial T}+\varepsilon ^{2}\frac{\partial ^{2}x}{\partial T^{2}}. \end{aligned}$$
(39)

Denote

$$\begin{aligned}&x_\tau \triangleq \frac{\partial x}{\partial \tau },\;x_T \triangleq \frac{\partial x}{\partial T},x_{\tau \tau } \triangleq \;\frac{\partial ^{2}x}{\partial \tau ^{2}},\nonumber \\&x_{TT} \triangleq \frac{\partial ^{2}x}{\partial T^{2}},\;x_{\tau T} \triangleq \frac{\partial ^{2}x}{\partial \tau \partial T}. \end{aligned}$$
(40)

Let

$$\begin{aligned} x(t)=x_0 (\tau ,T)+\varepsilon x_1 (\tau ,T)+O(\varepsilon ^{2}). \end{aligned}$$
(41)

Substituting Eqs. (38)–(41) into Eq. (35), we can easily obtain the following leading order

$$\begin{aligned} x_{0\tau \tau } +x_0 =0, \end{aligned}$$
(42)

and the first order is

$$\begin{aligned} x_{1\tau \tau } +x_1 =x_{0\tau } (a-b\hbox {sgn}(x)x_0 )-2x_{0\tau T} . \end{aligned}$$
(43)

The solution to Eq. (42) is

$$\begin{aligned} x_0 =A(T)\mathrm{e}^{i\tau }+A^{*}(T)\mathrm{e}^{-i\tau }, \end{aligned}$$
(44)

and so, using Eqs. (37) and (44), Eq. (43) becomes

$$\begin{aligned}&x_{1\tau \tau } +x_1 =-2iA_T \mathrm{e}^{i\tau }+2iA_T^*\mathrm{e}^{-i\tau }+(iA\mathrm{e}^{i\tau } -iA^{*}\mathrm{e}^{-i\tau }) \nonumber \\&\quad \cdot \left\{ {(a-b(A\mathrm{e}^{i\tau }+A^{*}\mathrm{e}^{-i\tau }))\frac{2}{\pi }\left( {\sum \limits _{j=0}^\infty {\frac{(-1)^{j}}{(2j+1)}\left[ {\mathrm{e}^{i(2j+1)\tau }+\mathrm{e}^{-i(2j+1)\tau }} \right] } } \right) } \right\} \nonumber \\&=-2iA_T \mathrm{e}^{i\tau }+2iA_T^*\mathrm{e}^{-i\tau }+iaA\mathrm{e}^{i\tau }-iaA^{*}\mathrm{e}^{-i\tau } \nonumber \\&\quad -\,\frac{2b}{\pi }\left\{ {\left( {\sum \limits _{j=0}^\infty {\frac{(-1)^{j}}{(2j+1)}iA^{2}\left[ {\mathrm{e}^{i(2j+3)\tau }+\mathrm{e}^{i(1-2j)\tau }} \right] } } \right) } -\,{\left( {\sum \limits _{j=0}^\infty {\frac{(-1)^{j}}{(2j+1)^{2}}iA^{*2}\left[ {\mathrm{e}^{i(2j-1)\tau }+\mathrm{e}^{-i(2j+3)\tau }} \right] } } \right) } \right\} \nonumber \\ \end{aligned}$$
(45)
Fig. 7
figure 7

The unique equilibrium (0, 0) of system (4) with (5) is an unstable focus and a stable periodic solution occurs, where \(\alpha =1.75,\;\xi =1, a=-\,1.2,b=1\): a wave plot, b phase plane plot

Full size image
Fig. 8
figure 8

The equilibrium (0, 0) of system (4) with (33) is unstable and a periodic solution occurs, where \(\alpha =1,\;\xi =100, a=10,b=1\): a wave plot, b phase plane plot

Full size image
Fig. 9
figure 9

The equilibrium (0, 0) of system (51) with (36) is unstable and a periodic solution occurs, where \(\alpha =10,\;\xi =0.1, a=0.1,b=0.5\): a wave plot, b phase plane plot

Full size image

The secularity condition is

$$\begin{aligned} 2A_T =aA-\frac{2b}{\pi }\left( {A^{2}+\frac{A^{*2}}{3}} \right) . \end{aligned}$$
(46)

Note that the substitution \(\hbox {sgn}(x)=\frac{4}{\pi }\cos t\) has omitted the final term in Eq. (46). In fact, it is necessary to maintain terms up to and including \( j=1\) at this order.

Letting

$$\begin{aligned} A=\frac{1}{2}\beta (T)\mathrm{e}^{i\theta (T)}, \end{aligned}$$
(47)

and substituting (47) into Eq. (46), it is straightforward to show that \(\theta (T)\) is identically zero and that

$$\begin{aligned} 2\frac{\mathrm{d}\beta (T)}{\mathrm{d}T}=a\beta (T)-\frac{4b}{3\pi }\beta ^{2}(T). \end{aligned}$$
(48)

If \(\beta _0 \) is the initial values of \(\beta \) and by dependence of solutions of differential equations on initial values, then the solution for Eq. (48) is

$$\begin{aligned} \beta (T)=\frac{3\pi a\beta _0 }{4b\beta _0 -(4b\beta _0 -3\pi a)\mathrm{e}^{-\frac{aT}{2}}}. \end{aligned}$$
(49)

Hence, for \(a>0,b>0,\;\beta (T)\rightarrow \frac{3\pi a}{4b} \hbox { as } T\rightarrow \infty \). It has been shown that the limit cycle of a discontinuous version of the memristor-based circuit can be solved for small \(\varepsilon \). The Fourier series expansion of sgn(x) is needed, but only two terms are required to successfully analyze the system to first order.

For large \(\varepsilon \), derive \(t=\varepsilon {t}',\;\hbox {set}\;\delta =1/{\varepsilon ^{2}}\) and drop the primes. Then, Eq. (35) becomes

$$\begin{aligned} \delta {\ddot{x}}(t)+(-a+b\left| x \right| ){\dot{x}}(t)+x(t)=0. \end{aligned}$$
(50)

By using the Lienard transformation [26], we have

$$\begin{aligned} \left\{ {\begin{array}{l} {\dot{y}}=-x, \\ \delta {\dot{x}}=y-F(x), \\ \end{array}} \right. \end{aligned}$$
(51)

where F(x) is given by Eq. (36). Hence, for large \(\varepsilon \) (i.e., small \(\delta )\), one can see that \(y\rightarrow F(x)\). In the following, we will compute the transit time S of a closed phase path (limit cycle).

In the phase plane with axes x and y, the state at time \(t_{0}\) consists of the pair of values (\(x(t_{0})\), \(y(t_{0}))\). These values of x and y represented by a point P in the phase plane serve as initial conditions for the first-order differential equations (51), and therefore determine all the states through which the system passes in a particular motion (see Fig. 3). The succession of states given parametrically by

$$\begin{aligned} x=x(t),\;y=y(t), \end{aligned}$$

traces out a curve through the initial point P: (\(x(t_{0})\), \(y(t_{0}))\), called a phase path.

In the representation on the phase plane, the time t is not involved quantitatively, but can be featured by the following considerations. Figure 3 shows a segment \(\widehat{AB}\) of a phase path. Suppose that the system is in a state A at time \( t=t_{A}\). The moving point P represents the states at times \(t\ge t_A \); it moves steadily along \(\widehat{AB}\) (from left to right in \(y>0\)) as t increases, and is called a representative point on \(\widehat{AB}\).

The velocity of P along the curve \(\widehat{AB}\) is given in component form by

$$\begin{aligned} \left( {\dot{x}}(t),{\dot{y}}(t)\right) =\left( \frac{1}{\delta }(y-F(x)),-x\right) , \end{aligned}$$

[from (51)]: This depends only on its position P: (x, y), and not at all on t and \(t_{A}\) (this is true only for autonomous equations). If \(t_{B}\) is the time P reaches B, the time \(S_{AB}\) taken for P to move from A to B,

$$\begin{aligned} S_{AB} =t_B -t_A , \end{aligned}$$

is independent of the initial time \(t_{A}\). The quantity is called the transit time from A to B along the phase path.

The transit time \(S_{AB}\) of the representative point P from state A to state B along the phase path can be expressed as

$$\begin{aligned} S_{AB} =\int _{t_A }^{t_B } \mathrm{d}t =\int _{t_A }^{t_B } {\left( {\frac{\mathrm{d}y}{\mathrm{d}t}} \right) ^{-1}\left( {\frac{\mathrm{d}y}{\mathrm{d}t}} \right) dt} =\int _{t_A }^{t_B } {\frac{\mathrm{d}y}{\dot{y}}} . \end{aligned}$$

We consider the case when a phase path is a closed curve. Hence, the time which is derived to complete a limit cycle in this limit is given by

$$\begin{aligned} S=\oint {\mathrm{d}t} =\int {\frac{\mathrm{d}y}{\dot{y}}} . \end{aligned}$$
(52)

The response in this limit is made up of a fast phase (which is derived to be negligible) and a slow phase. The function F(x) has extreme values of \(\pm \frac{a^{2}}{2b}\;\hbox {at}\;x=\mp \frac{a}{b},\) respectively. The slow phase starts at \((x,F(x))=(\frac{a}{b}(1+\sqrt{2}),\;\frac{a^{2}}{b})\) and ends at the minimum of F(x) given by \((\frac{a}{b},\;-\frac{a^{2}}{2b})\). The slow phase starts again at \((x,F(x))=(-\frac{a}{b}(1+\sqrt{2}),\;-\frac{a^{2}}{b})\) and ends again at the maximum of F(x) given by \((x,F(x))=(-\frac{a}{b},\;\frac{a^{2}}{2b})\). Hence, Eq. (52) becomes

$$\begin{aligned} S= & {} 2\int {\frac{{F}'(x)}{-x}\mathrm{d}x} =2\int _{\frac{a}{b}(1+\sqrt{2})}^{\frac{a}{b}} {\left( -b+\frac{a}{x}\right) \mathrm{d}x}\nonumber \\= & {} 2\left. {\left[ {-bx+a\ln x} \right] } \right| _{\frac{a}{b}(1+\sqrt{2})}^{\frac{a}{b}} =2a[\sqrt{2}-\ln (1+\sqrt{2})]. \end{aligned}$$

The period of the limit cycle of Eq. (35) for large \(\varepsilon \) is therefore given by \((2a[\sqrt{2}-\ln (1+\sqrt{2})])\varepsilon \approx 1.0657a\varepsilon \).

5 Numerical examples

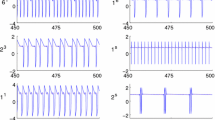
In this section, first we consider Eq. (4) with (5) and set \(\alpha =1.75,\;\xi =1\) and for different a, b, computer simulations may see Figs. 4, 5, 6 and 7. By the previous analysis, we know that the unique equilibrium (0, 0) is a node if \(a<-2/d\;\hbox {or}\;a>2/d\), and it is stable for \(a>0\) (see Fig. 4) and it is unstable for \(a<0\) (see Fig. 5). If we derive \(\alpha =1.75,\;\xi =1,a=-0.8,b=1\), based on the analytical results in the above section 3, we can calculate \(d=1.3229,h_1 =0.6614,h_2 =-0.5292,\omega _1 =0.75,\omega _2 =0.8485\) [see Eq. (14)], and furthermore, we can obtain \({\overline{\tau }}_1 =5.0291,{\overline{\tau }} _{2} =5.6896\) [see Eq. (32)]. Hence, the analytical value of the approximate period is \(T=10.137\), but its numerical value based on the computer simulation is 10.139 (see Fig. 5, where we use OED45 in MATLAB to calculate, which usually is the function of choice among the ODE solvers and compares method of orders four and five to estimate error and determine step size). From these numerical results, we have found there are some errors between the analytical method and the numerical method. This is because on the one hand, the proposed method in this paper is a kind of approximately analytical method, and on the other hand, our numerical simulation method is use of OED45 in MATLAB which is based on the Runge–Kutta(4,5) integration method. From Figs. 6 and 7, the unique equilibrium (0, 0) is a focus if \(-2/d<\;a<2/d\), it is a stable focus for \(a>0\) and it is an unstable focus for \(a<0\) (see Figs. 6, 7). If we derive \(\alpha =1.75,\;\xi =1,a=-\,1.2,b=1\), we can calculate the analytical value of the approximate period is 10.444, but its numerical value based on the on computer simulation is 10.447 (see Fig. 7). The results of theoretical analysis and computer simulations are basically coincident.

Next, we reconsider Eq. (4) with (33) and let \(\alpha =1,\;\xi =100,a=10,b=1\), we can calculate the analytical value of the approximate amplitude is 23.562, but its numerical value based on the computer simulation (see Fig. 8) is 23.567. If we derive \(\alpha =10,\;\xi =0.1,a=0.1,b=0.5\), we have \(\varepsilon =10\), the analytical value of the approximate period is 1.0667, and its numerical value is 1.0669 (see Fig. 9). These also illustrate the correctness of our theoretical analysis.

The above results show that the analytical results are relatively accurate; this is because system parameters have a wide range of parameter space, but the numerical solutions for corresponding circuit model must have specific and fixed values of system parameters. Furthermore, more detailed studies across specific parameters are carried out using numerical approach alone; however, the focus of our work is obtaining tractable analytics for a nonlinear system rather than investigating numerical solutions. These analytical results provide a direct connection between system parameters and a memristor-based circuit model. By showing how period and amplitude scale with system parameters, these results help explain results observed in numerical simulations.

6 Conclusions

It has been shown that a simple circuit with an inductor, a capacitor and a flux-controlled memristor can exhibit self-sustained oscillation; in particular, the flux–charge characteristic curves with continuous piecewise-linear or discontinuous function are applied.

For the analysis of continuous piecewise-linear systems, the point transformation method of Andronov has been a useful tool. The geometric intuition of the method is very clear and helps to the topological analysis of the dynamical system. The method does not require the use of more complex tools. At the same time, the multiple-scale method has also been a useful approach for the analysis of discontinuous systems. In our analysis, the Fourier series expansion of sign function is applied, but only two terms are needed to successfully analyze the system to first order.

Continuous piecewise-linear or discontinuous models can be considered as the combination of several different linear systems, and each one describes the dynamics in a part of the phase space. Within every section of the phase space, the dynamics are very simple but the global dynamics can be very complex and even chaotic [23].

In this paper, our main contribution is that the period and amplitude of a limit cycle are derived analytically. To the best of the authors’ knowledge, we do not find the existing literature on memristor to analytically study the approximate periodic solution. We have presented, to our knowledge, the first analytical expressions for the period and amplitude of a memristor-based circuit. These compact expressions are in good agreement with numerical solutions of corresponding circuit. The formulas are shown to be useful by permitting quick comparisons relative to a simple memristor-based oscillator. As presented in this paper, the second-order piecewise-linear systems can be combined as higher-order systems to construct chaotic oscillators, which will be our future works.