N-order rogue waves and their novel colliding dynamics for a transient stimulated Raman scattering system arising from nonlinear optics

Abstract

We report the novel colliding dynamics of the rogue waves (RWs) for a three-component transient stimulated Raman scattering system arising from nonlinear optics. The N-order RW solutions are constructed by utilizing the generalized Darboux transformation scheme. Then, the dynamics of the RWs are analyzed. As $N\ge 2$, the multiple RWs collide towards a central point. During the collisions and interactions, the peaks and troughs increase greatly. It is also interesting and magical that all the RWs possess exquisite symmetrical structures.

1 Introduction

Raman scattering effect was reported initially by Raman and Krishnan and by Landsberg and Mandelstam in 1928, respectively. It is an inelastic scattering phenomenon of photons by matter, meaning that there exist an exchange of energy and a change in the light’s propagation direction after being scattered. The observation of stimulated, as opposed to spontaneous Raman scattering, was however not possible until the development of the laser, a powerful coherent source of light based on luminescent semiconductor materials. Stimulated Raman scattering (SRS) is a typical nonlinear effect in optics. It can take place when some Stokes photons have previously been generated by spontaneous Raman scattering (and somehow forced to remain in the material), or when deliberately injecting Stokes photons (“signal light”) together with the original light (“pump light”). Since SRS was first observed by Woodybury and Ng [1], it has become one of two main tools to stimulate nonlinear optical pluses in modern optics (another one is the well-known stimulated Brillouin scattering) [2], and has extensively employed in a variety of optical systems, such as fiber optics [3, 4], ultra-fast photon [5], spectroscopy and microscope optics [6], fiber amplifier [7, 8], wavelength division multiplexing technique [9, 10].

Transient stimulated Raman scattering (TSRS) interactions in the molecular gas H$_2$ and other gases were first reported by Hagenlocker, Minck and Rado [11]. In transient interactions, the light pulse durations are short compared to T$_2$, the molecular de-excitation time, due to molecular collisions [12]. TSRS can be used to excite ultra-fast and ultra-short optical pulse [13, 14]. Very recently, it is even exploited to develop new optical fiber systems, e.g., gas-filled hollow-core photonic crystal fibers [15,16,17].

In this article, we deal with a three-component coupled TSRS system which reads [18, 19]

$$\begin{aligned} {q_t}= & {} - \frac{i}{2}p, \end{aligned}$$

(1)

$$\begin{aligned} {p_x}= & {} 2iqw, \end{aligned}$$

(2)

$$\begin{aligned} {w_x}= & {} i\left( {p{\overline{q}} - q{\overline{p}}} \right) , \end{aligned}$$

(3)

where $q=q(x,t)$ and $p=p(x,t)$ are complex functions, and $w=w(x,t)$ is a real function, x and t represents the normalized displacement ant time variables, respectively; the bar on the top of identifiers represents the conjugate of the indicated complex numbers. Equations (1)–(3) are traced back to the normalization and neglecting diffraction for a TSRS system, where q, p and w can be transformed back into the off-diagonal density-matrix element, pump electric fields, and Stokes electric fields in optical fields [18, 20].

Solitons and breathers are generally generated due to nonlinear factors and dispersion effects in nonlinear system [21, 22]. Rogue waves (RWs), also called extreme waves or monster waves, were often observed in ocean and coast [23, 24]. Because of the convenience of the desktop-based experiments, the research on optical RWs has made a great progress in the past two decades [25, 26]. Mathematically, RWs can be expressed as the rational function or semi-rational function solutions of nonlinear evolution equations [27]. Subsequently, Ohta et. al. [28, 29] and Guo et. al. [30] extended Darboux transformation (DT), afterwards called as generalized Darboux transformation (GDT), to seek for the RWs of nonlinear equations. Lately, GDT was further extended to obtain the hybrid breather and RW solutions [31].

In Ref. [18], by converting the system (1)–(3) to the Ablowitz–Kaup–Newell–Segur system, then combining DT and iterated Bäcklund transformation, the multi-soliton solutions were acquired for the system. The trivial initial solutions, explicit N-soliton solutions in determinant form were presented by DT method in Ref. [19]. The first-order RW solutions of the system (1)–(3) were constructed, and their extremum and asymptotic behaviors were also analyzed in Ref. [32].

Because the higher-order solutions can exhibit richer dynamical properties of nonlinear systems [33, 34], they are often utilized to explore new natures during the collisions and interactions [35], such as resonant behavior [36], nonlinear superposition effect [37].

In this work, our main effort will be focused on the higher-order RW solutions and their colliding dynamics for the TSRS system (1)–(3). In Sect. 2, the N-order RW solutions of the system are constructed by the GDT method. The novel colliding dynamical properties are discussed in Sect. 3. Some conclusions are given in the final section.

2 Higher-order RW solutions for the TSRS system (1)–(3)

The first step of applying the GDT scheme is to find the Lax pairs of the equation. The system (1)–(3) has the following Lax pairs [19]

$$\begin{aligned} {\varPsi _x} = U\varPsi ,{\varPsi _t} = V\varPsi ,\varPsi = \left( \begin{array}{l} {\psi _1} \\ {\psi _2} \\ \end{array} \right) , \end{aligned}$$

(4)

where

$$\begin{aligned} U= & {} - i\lambda {\sigma _1} + {Q^{[0]}},\\ {\sigma _1}= & {} \left( {\begin{array}{*{20}{c}} 1 &{} 0 \\ 0 &{} -1 \\ \end{array}} \right) ,\\ {Q^{[0]}}= & {} \left( {\begin{array}{*{20}{c}} 0 &{} {{q^{[0]}}} \\ { - {\overline{q^{[0]}}}} &{} 0 \\ \end{array}} \right) ,\\ V= & {} \frac{1}{{4\lambda }}\left( {\begin{array}{*{20}{c}} {i{w^{[0]}}} &{} { - {p^{[0]}}} \\ {\overline{p^{[0]}}} &{} {-i{w^{[0]}}} \\ \end{array}} \right) , \end{aligned}$$

and $\lambda$ is spectral eigenvalue parameter, ${q^{[0]}},{p^{[0]}}$ and ${w^{[0]}}$ are a set of initial solutions of the system (1)–(3).

Remark 1

The system (1)–(3) can be expressed as the compatible condition of the Lax pairs (4), namely, ${U_t} - {V_x} + UV -VU= 0$.

According to the GDT scheme, we derive the onefold DT as follows

$$\begin{aligned} {\varPsi ^{[1]}} = T[1]\varPsi ,\varPsi _x^{[1]} = {U^{[1]}}{\varPsi ^{[1]}},\varPsi _t^{[1]} = {V^{[1]}}{\varPsi ^{[1]}}, \end{aligned}$$

(5)

where T[1] has to satisfy

$$\begin{aligned} {T_x[1]} = {U^{[1]}}T[1] - T[1]U,{T_t[1]} = {V^{[1]}}T[1] - T[1]V, \end{aligned}$$

(6)

with

$$\begin{aligned} {U^{[1]}}= & {} - i\lambda {\sigma _1} + {Q^{[1]}},\\ {Q^{[1]}}= & {} \left( {\begin{array}{*{20}{c}} 0 &{} {{q^{[1]}}} \\ { - {\overline{q^{[1]}}}} &{} 0 \\ \end{array}} \right) ,\\ {V^{[1]}}= & {} \frac{1}{{4\lambda }}\left( {\begin{array}{*{20}{c}} {i{w^{[1]}}} &{} { - {p^{[1]}}} \\ {\overline{p^{[1]}}} &{} { - i{w^{[1]}}} \\ \end{array}} \right) . \end{aligned}$$

Supposing

$$\begin{aligned} T[1]= & {} \lambda I - {M^{[1]}}, \end{aligned}$$

(7)

$$\begin{aligned} {M^{[1]}}= & {} \left( {\begin{array}{*{20}{c}} {m_{11}^{[1]}} &{} {{m_{12}^{[1]}}} \\ {{m_{21}^{[1]}}} &{} {{m_{22}^{[1]}}} \\ \end{array}} \right) , \end{aligned}$$

(8)

then substituting $T_x[1]=-M_x^{[1]}$ and $T_t[1]=-M_t^{[1]}$ into (6), it yields the DT solutions

$$\begin{aligned} q^{[1]}= & {} {q^{[0]}} - 2i{m_{12}^{[1]} }, \end{aligned}$$

(9)

$$\begin{aligned} p^{[1]}= & {} {p^{[0]}} + 4m_{12t}^{[1]} , \end{aligned}$$

(10)

$$\begin{aligned} w^{[1]}= & {} {w^{[0]}} + 4i{m_{11t}^{[1]} }. \end{aligned}$$

(11)

Now, we take a set of initial solutions q, p and w for the system (1)–(3) as follows

$$\begin{aligned} {q^{[0]}} = {p^{[0]}} = {e^{ - \frac{i}{2}t}},{w^{[0]}} = 0. \end{aligned}$$

(12)

Therefore, $\varPhi _1$ and $\varPhi _2$ are the solutions of the Lax pair equations (4) with the initial solutions (12) corresponding to $\lambda =\lambda _1=ih$ and $\lambda =\lambda _2=-ih$, respectively, where

$$\begin{aligned}&{\varPhi _{{1}}} \buildrel \varDelta \over = \left( \begin{array}{l} {\phi _{{{11}}}} \\ {\phi _{{{21}}}} \\ \end{array} \right) \\&\quad =\left( \begin{array}{l} \left( {{c_1}{e^{\sqrt{{h^2} - 1} \left( {x - \frac{1}{{4ih}}t} \right) }} - {c_2}{e^{ - \sqrt{{h^2} - 1} \left( {x - \frac{1}{{4ih}}t} \right) }}} \right) {e^{ - \frac{i}{4}t}} \\ \left( {{c_1}{e^{ - \sqrt{{h^2} - 1} \left( {x - \frac{1}{{4ih}}t} \right) }} - {c_2}{e^{\sqrt{{h^2} - 1} \left( {x - \frac{1}{{4ih}}t} \right) }}} \right) {e^{\frac{i}{4}t}} \\ \end{array} \right) ,\\&{\varPhi _2} \buildrel \varDelta \over = \left( \begin{array}{l} {\phi _{12}} \\ {\phi _{22}} \\ \end{array} \right) \\&\quad =\left( \begin{array}{l} \left( { - {c_1}{e^{ - \sqrt{{h^2} - 1} \left( {x + \frac{1}{{4ih}}t} \right) }} + {c_2}{e^{\sqrt{{h^2} - 1} \left( {x + \frac{1}{{4ih}}t} \right) }}} \right) {e^{ - \frac{i}{4}t}} \\ \left( {{c_1}{e^{\sqrt{{h^2} - 1} \left( {x + \frac{1}{{4ih}}t} \right) }} - {c_2}{e^{ - \sqrt{{h^2} - 1} \left( {x + \frac{1}{{4ih}}t} \right) }}} \right) {e^{\frac{i}{4}t}} \\ \end{array} \right) , \end{aligned}$$

in which ${c_1} = \frac{{\sqrt{\left( {h - \sqrt{{h^2} - 1} } \right) } }}{{\sqrt{{h^2} - 1} }},{c_2} = \frac{{\sqrt{\left( {h + \sqrt{{h^2} - 1} } \right) } }}{{\sqrt{{h^2} - 1} }},h = 1 + {f^2}.$

By expanding $\varPhi _1$ and $\varPhi _2$ in the above expressions with respect to $h=1+f^2$ at $f=0$, it follows

$$\begin{aligned}&{\varPhi _1}\left( {i\left( {1 + {f^2}} \right) } \right) = \varPhi _1^{(0)} + \varPhi _1^{(1)}{f^2} + \varPhi _1^{(2)}{f^4}\nonumber \\&\quad + \cdots + \varPhi _1^{(n)}{f^{2n}} + \cdots , \end{aligned}$$

(13)

$$\begin{aligned}&{\varPhi _2}\left( { - i\left( {1 + {f^2}} \right) } \right) = \varPhi _2^{(0)} + \varPhi _2^{(1)}{f^2} + \varPhi _2^{(2)}{f^4}\nonumber \\&\quad + \cdots + \varPhi _2^{(n)}{f^{2n}} + \cdots , \end{aligned}$$

(14)

where

$$\begin{aligned}&\varPhi _1^{(0)} \buildrel \varDelta \over = \left( \begin{array}{l} {\phi _{110}} \\ {\phi _{210}} \\ \end{array} \right) = \left( \begin{array}{l} \left( {1 + 2\theta } \right) {e^{ - \frac{i}{4}t}} \\ \left( {1 - 2\theta } \right) {e^{\frac{i}{4}t}} \\ \end{array} \right) ,\\&\varPhi _2^{(0)} \buildrel \varDelta \over = \left( \begin{array}{l} {\phi _{120}} \\ {\phi _{220}} \\ \end{array} \right) = \left( \begin{array}{l} - \left( {1 - 2{{\overline{\theta }}}} \right) {e^{ - \frac{i}{4}t}} \\ \left( {1 + 2{\overline{\theta }}} \right) {e^{\frac{i}{4}t}} \\ \end{array} \right) ,\\&\varPhi _{{1}}^{(1)} \buildrel \varDelta \over = \left( \begin{array}{l} {\phi _{111}} \\ {\phi _{211}} \\ \end{array} \right) = \left( \begin{array}{l} \left( {\frac{2}{3}{\theta ^3} + {\theta ^2} + \frac{1}{2}\theta - \frac{i}{2}t - \frac{1}{4}} \right) {e^{ - \frac{i}{4}t}} \\ \left( { - \frac{2}{3}{\theta ^3} + {\theta ^2} - \frac{1}{2}\theta + \frac{i}{2}t - \frac{1}{4}} \right) {e^{\frac{i}{4}t}} \\ \end{array} \right) ,\\&\varPhi _2^{(1)} \buildrel \varDelta \over = \left( \begin{array}{l} {\phi _{121}} \\ {\phi _{221}} \\ \end{array} \right) =\left( {\begin{array}{*{20}{c}} {\left( {\frac{2}{3}{\overline{\theta }^3}-{{\overline{\theta }} ^{2}} + \frac{1}{2}{\overline{\theta }}+\frac{i}{2}t+\frac{1}{4}} \right) {e^{ - \frac{i}{4}t}}}\\ {\left( {\frac{2}{3}{\overline{\theta }^3} + {\overline{\theta }^2}+\frac{1}{2}{\overline{\theta }} + \frac{i}{2}t - \frac{1}{4}} \right) {e^{\frac{i}{4}t}}} \\ \end{array}} \right) ,\\&\varPhi _{{1}}^{(2)} \buildrel \varDelta \over = \left( \begin{array}{l} {\phi _{112}} \\ {\phi _{212}} \\ \end{array} \right) \\&\quad = \left( \begin{array}{l} \left( {\frac{1}{{15}}{\theta ^5} + \frac{1}{6}{\theta ^4} + \frac{1}{2}{\theta ^3} - \frac{i}{2}t{\theta ^2} + \frac{1}{4}{\theta ^2} - \frac{i}{2}t\theta - \frac{1}{{16}}\theta + \frac{3}{8}it + \frac{3}{{32}}} \right) {e^{ - \frac{i}{4}t}} \\ \left( { - \frac{1}{{15}}{\theta ^5} + \frac{1}{6}{\theta ^4} - \frac{1}{2}{\theta ^3} + \frac{i}{2}t{\theta ^2} + \frac{1}{4}{\theta ^2} - \frac{i}{2}t\theta + \frac{1}{{16}}\theta - \frac{3}{8}it + \frac{3}{{32}}} \right) {e^{\frac{i}{4}t}} \\ \end{array} \right) ,\\&\varPhi _2^{(2)} \buildrel \varDelta \over =\left( \begin{array}{l} {\phi _{112}} \\ {\phi _{212}} \\ \end{array} \right) = \left( \begin{array}{l} - \overline{\phi _{212}} \\ \overline{\phi _{112}} \\ \end{array} \right) , \end{aligned}$$

with $\theta = x + \frac{i}{4}t,{\overline{\theta }} = x - \frac{i}{4}t.$

2.1 First-order RW solutions

Proposition 1

$\varPhi _1^{(0)}$ and $\varPhi _2^{(0)}$ are the solutions of the Lax pairs equations (4) corresponding to $\lambda =\lambda _1=i$ and $\lambda =\lambda _2=\overline{\lambda _1}=-i$ with the initial solutions (12).

The proposition can be verified by substituting $\varPhi _1^{(0)}$ and $\varPhi _2^{(0)}$ into the Lax pairs equations (4).

Theorem 1

The system (1)–(3) has the following onefold DT

$$\begin{aligned} T[1] = {T_1}\left( {\lambda ,{\lambda _1},{\lambda _2}} \right) = \lambda I - M_r^{[1]}, \end{aligned}$$

(15)

where

$$\begin{aligned} M_r^{[1]}= & {} \left( {\begin{array}{*{20}{c}} {m_{11r}^{[1]}} &{} {m_{12r}^{[1]}} \\ {m_{21r}^{[1]}} &{} {m_{22r}^{[1]}} \\ \end{array}} \right) ,\\ m_{11r}^{[1]}= & {} \frac{1}{{{\varDelta _1}}}\left( {{\lambda _1}{\phi _{110}}{\phi _{220}} - {\lambda _2}{\phi _{120}}{\phi _{210}}} \right) ,\\ m_{12r}^{[1]}= & {} \frac{1}{{{\varDelta _1}}}\left( {{\lambda _2} - {\lambda _1}} \right) {\phi _{110}}{\phi _{120}},\\ m_{21r}^{[1]}= & {} \frac{1}{{{\varDelta _1}}}\left( {{\lambda _1} - {\lambda _2}} \right) {\phi _{210}}{\phi _{220}},\\ m_{22r}^{[1]}= & {} \frac{1}{{{\varDelta _1}}}\left( {\lambda _2} {\phi _{110}}{\phi _{220}} - {\lambda _1}{\phi _{120}}{\phi _{210}}\right) ,\\ {\varDelta _1}= & {} {\phi _{110}}{\phi _{220}} - {\phi _{120}}{\phi _{210}}, \end{aligned}$$

and T[1] satisfies Eq. (6). Then, the system (1)–(3) has the first-order RW solutions

$$\begin{aligned}&q_r^{[1]} = {q^{[0]}} - 4\frac{{{\phi _{110}}{\phi _{120}}}}{{{\varDelta _1}}}=\frac{{\left( {8it - {t^2} - 16{x^2} + 12} \right) }}{{{t^2} + 16{x^2} + 4}}{e^{ - \frac{{{1}}}{{{2}}}it}}, \end{aligned}$$

(16)

$$\begin{aligned}&p_r^{[1]} = {p^{[0]}} - 8i{\left( {\frac{{{\phi _{110}}{\phi _{120}}}}{{{\varDelta _1}}}} \right) _t}\nonumber \\&\quad =\frac{{\left( { - {t^4} + {{8}}i{t^3} + {{8}}\left( { - 4{x^2} + 3} \right) {t^2} + {{32}}\left( {{{4}}i{x^2} - i} \right) t - {{16}}{{\left( {{{4}}{x^2} + {{1}}} \right) }^2}} \right) }}{{{{\left( {{t^2} + 16{x^2} + 4} \right) }^2}}}\nonumber \\&{e^{ - \frac{{{1}}}{{{2}}}it}}, \end{aligned}$$

(17)

$$\begin{aligned}&w_r^{[1]} = - 4{\left( {\frac{{{\phi _{110}}{\phi _{220}} + {\phi _{210}}{\phi _{120}}}}{{{\varDelta _1}}}} \right) _t}=\frac{{128xt}}{{{{\left( {{t^2} + 16{x^2} + 4} \right) }^2}}}. \end{aligned}$$

(18)

Remark 2

${\left. {T[1]} \right| _{\lambda = {\lambda _j}}}\left( \begin{array}{l} {\phi _{1j0}} \\ {\phi _{2j0}} \\ \end{array} \right) = 0,j = 1,2.$

Owing to that the first-order RW solutions (16)–(18) have been obtained in Refs. [32], their detailed proofs and plots are no longer given. Readers can learn more from this literature.

2.2 Second-order RW solutions

Consideration of Remark 2, as carrying out the twofold DT, we are able to use the following $\varPsi _j[1]$ to replace $\varPsi ^{[1]}$

$$\begin{aligned} {\varPsi _j}[1]= & {} {\mathop {\lim }\limits _{f \rightarrow 0}} \frac{{\left( {{\lambda _j}{f^2} + {{\left. {T[1]} \right| }_{\lambda = {\lambda _j}}}} \right) \left( {\varPhi _j^{(0)} + \varPhi _j^{(1)}{f^2} + \cdots } \right) }}{{{f^2}}}\nonumber \\= & {} {\lambda _j}\varPhi _j^{(0)} + {\left. {T[1]} \right| _{\lambda = {\lambda _j}}}\varPhi _j^{(1)},j = 1,2. \end{aligned}$$

(19)

It is necessary to denote

$$\begin{aligned} {\varPsi _1}[1] \buildrel \varDelta \over = \left( \begin{array}{l} {\phi _{11}}[1] \\ {\phi _{21}}[1] \\ \end{array} \right) ,{\varPsi _2}[1] \buildrel \varDelta \over = \left( \begin{array}{l} {\phi _{12}}[1] \\ {\phi _{22}}[1] \\ \end{array} \right) , \end{aligned}$$

(20)

and redefine the twofold DT as

$$\begin{aligned} {\varPsi ^{[2]}} = T[2]\varPsi [1],\varPsi _x^{[2]} = {U^{[2]}}{\varPsi ^{[2]}},\varPsi _t^{[2]} = {V^{[2]}}{\varPsi ^{[2]}}. \end{aligned}$$

(21)

Theorem 2

The system (1)–(3) has the twofold DT as

$$\begin{aligned} T[2] = {T_2}\left( {\lambda ,{\lambda _1},{\lambda _2}} \right) = \lambda I -M_r^{[2]}, \end{aligned}$$

(22)

where

$$\begin{aligned} M_r^{[2]}= & {} \left( {\begin{array}{*{20}{c}} {m_{11r}^{[2]}} &{} {m_{12r}^{[2]}} \\ {m_{21r}^{[2]}} &{} {m_{22r}^{[2]}} \\ \end{array}} \right) ,\\ m_{11r}^{[2]}= & {} \frac{1}{{{\varDelta _2}}}\left( {{\lambda _1}{\phi _{11}}[1]{\phi _{22}}[1] - {\lambda _2}{\phi _{21}}[1]{\phi _{12}}[1]} \right) ,\\ m_{21r}^{[2]}= & {} \frac{1}{{{\varDelta _2}}}\left( {{\lambda _{{1}}}-{\lambda _{{2}}}} \right) {\phi _{{{2}}1}}[1]{\phi _{{{2}}2}}[1],\\ m_{2{{2}}r}^{[2]}= & {} \frac{1}{{{\varDelta _2}}}\left( {{\lambda _{{2}}}{\phi _{11}}[1]{\phi _{22}}[1] - {\lambda _{{1}}}{\phi _{21}}[1]{\phi _{12}}[1]} \right) ,\\ {\varDelta _2}= & {} {\phi _{11}}[1]{\phi _{22}}[1] - {\phi _{21}}[1]{\phi _{12}}[1]. \end{aligned}$$

T[2] satisfies

$$\begin{aligned} {T_x}[2] = {U^{[2]}}T[2] - T[2]{U^{[1]}},{T_t}[2] = {V^{[2]}}T[2] - T[2]{V^{[1]}}, \end{aligned}$$

(23)

with

$$\begin{aligned} {U^{[2]}} = - i\lambda {\sigma _1} + \left( {\begin{array}{*{20}{c}} 0 &{} {{q^{[2]}}} \\ { - {\overline{q^{[2]}}}} &{} 0 \\ \end{array}} \right) ,{V^{[2]}} = \frac{1}{{4\lambda }}\left( {\begin{array}{*{20}{c}} {i{w^{[2]}}} &{} { - {p^{[2]}}} \\ {\overline{p^{[2]}}} &{} {-i{w^{[2]}}} \\ \end{array}} \right) . \end{aligned}$$

(24)

Thus, we can calculate out the second-order RW solutions of the system (1)–(3) as

$$\begin{aligned} q_r^{[2]}= & {} q_r^{[1]} - 4\frac{{{\phi _{11}}[1]{\phi _{12}}[1]}}{{{\varDelta _2}}} , \end{aligned}$$

(25)

$$\begin{aligned} p_r^{[2]}= & {} p_r^{[1]} - 8i{\left( {\frac{{{\phi _{11}}[1]{\phi _{12}}[1]}}{{{\varDelta _2}}}} \right) _t}, \end{aligned}$$

(26)

$$\begin{aligned} w_r^{[2]}= & {} w_r^{[1]} - 4{\left( {\frac{{{\phi _{11}}[1]{\phi _{22}}[1] + {\phi _{21}}[1]{\phi _{12}}[1]}}{{{\varDelta _2}}}} \right) _t}.\nonumber \\ \end{aligned}$$

(27)

Remark 3

${\left. {T[2]} \right| _{\lambda = {\lambda _j}}}{\varPsi _j}[1] = 0,j = 1,2.$

Proof

It follows from (22)

$$\begin{aligned} {T_x}[2] = - (M_r^{[2]})_x,{T_t}[2]= - (M_r^{[2]})_t. \end{aligned}$$

(28)

Then, substituting (28) into (23) leads

$$\begin{aligned} q_r^{[2]}= & {} q_r^{[1]} - 2im_{12r}^{[2]}, \end{aligned}$$

(29)

$$\begin{aligned} p_r^{[2]}= & {} p_r^{[1]} + 4{\left( {m_{12r}^{[2]}} \right) _t}, \end{aligned}$$

(30)

$$\begin{aligned} w_r^{[2]}= & {} w_r^{[1]} + 4i{\left( {m_{11r}^{[2]}} \right) _t}. \end{aligned}$$

(31)

Noticing that $\lambda _1=i,\lambda _2=-i$, and the expressions of $m_{11r}^{[2]},m_{12r}^{[2]},m_{21r}^{[2]}$ and $m_{22r}^{[2]}$ defined by (22), the second-order RW solutions (25)–(27) can be derived.

The explicit expressions of the second-order RW solutions (25)–(27) are given in Appendix I. $\square$

2.3 Third-order RW solutions

Next, we will construct the third-order RW solutions which are based on the second-order RW solutions (25)–(27). It is requisite to redefine the threefold DT. Noticing Remark 3, we take the following $\varPsi _j[2]$ to replace $\varPsi ^{[2]}$ used in the twofold DT

$$\begin{aligned}&\varPsi _j^{}[2] \buildrel \varDelta \over = \left( \begin{array}{l} {\phi _{1j}}[2] \\ {\phi _{2j}}[2] \\ \end{array} \right) = {\mathop {\lim }\limits _{f \rightarrow 0}} \frac{{\left( {\lambda _j^{}{f^2} + {{\left. {T[2]} \right| }_{\lambda = {\lambda _j}}}} \right) \left( {{\lambda _j}{f^2} + {{\left. {T[1]} \right| }_{\lambda = {\lambda _j}}}} \right) \left( {\varPhi _j^{(0)} + \varPhi _j^{(1)}{f^2} + \varPhi _j^{(2)}{f^4} + \cdots } \right) }}{{{f^4}}}\nonumber \\&\quad = \lambda _j^2\varPhi _j^{(0)} + \lambda _j^{}{\left. {\left( {T[2] + T[1]} \right) } \right| _{\lambda = {\lambda _j}}}\varPhi _j^{(1)} + {\left. {\left( {T[2]T[1]} \right) } \right| _{\lambda = {\lambda _j}}}\varPhi _j^{(2)},j = 1,2, \end{aligned}$$

(32)

namely, define

$$\begin{aligned} {\varPsi ^{[3]}} = T[3]\varPsi [2],\varPsi _x^{[3]} = U^{[3]}{\varPsi ^{[3]}},\varPsi _t^{[3]} = {V^{[3]}}{\varPsi ^{[3]}}, \end{aligned}$$

(33)

where $U^{[3]}$ and $V^{[3]}$ are just replaced respectively by $U^{[2]}$ and $V^{[2]}$ in the expressions (24), while the superscript ‘[2]’ related the identifiers q, p and w in (24) is replaced by ‘[3]’, respectively. Here, the quotation mark ‘’ added in ‘[2]’ and ‘[3]’ is to distinguish the citation numbers [2] and [3] to the References.

Fig. 1

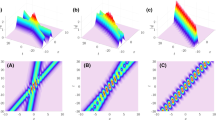
The spatiotemporal pattern of the second-order RW |q|. The plots are given by the solution (25). a, b and c are the 3-dimension, density and contour views, respectively

Through supposing

$$\begin{aligned} T[3] = \lambda I - M_r^{[3]} , \end{aligned}$$

(34)

we are able to attain the third-order RW solutions

$$\begin{aligned} q_r^{[3]}= & {} q_r^{[2]} - 2im_{12r}^{[3]}, \end{aligned}$$

(35)

$$\begin{aligned} p_r^{[3]}= & {} p_r^{[2]} + 4{\left( {m_{12r}^{[3]}} \right) _t}, \end{aligned}$$

(36)

$$\begin{aligned} w_r^{[3]}= & {} w_r^{[2]} + 4i{\left( {m_{11r}^{[3]}} \right) _t}, \end{aligned}$$

(37)

where

$$\begin{aligned} M_r^{[3]}= & {} \left( {\begin{array}{*{20}{c}} {m_{11r}^{[3]}} &{} {m_{12r}^{[3]}} \\ {m_{21r}^{[3]}} &{} {m_{22r}^{[3]}} \\ \end{array}} \right) ,\\ m_{11r}^{[3]}= & {} \frac{1}{{{\varDelta _3}}}\left( {{\lambda _1}{\phi _{11}}[2]{\phi _{22}}[2] - {\lambda _2}{\phi _{21}}[2]{\phi _{12}}[2]} \right) ,\\ m_{12r}^{[3]}= & {} \frac{1}{{{\varDelta _3}}}\left( {{\lambda _2}-{\lambda _{{1}}}} \right) {\phi _{{{1}}1}}[2]{\phi _{12}}[2],\\ m_{21r}^{[3]}= & {} \frac{1}{{{\varDelta _3}}}\left( {{\lambda _{{1}}}-{\lambda _{{2}}}} \right) {\phi _{{{2}}1}}[2]{\phi _{{{2}}2}}[2],\\ m_{22r}^{[3]}= & {} \frac{1}{{{\varDelta _3}}}\left( {{\lambda _{{2}}}{\phi _{11}}[2]{\phi _{22}}[2] - {\lambda _{{1}}}{\phi _{21}}[2]{\phi _{12}}[2]} \right) ,\\ {\varDelta _3}= & {} {\phi _{11}}[2]{\phi _{22}}[2] - {\phi _{21}}[2]{\phi _{12}}[2]. \end{aligned}$$

The detailed expressions to x and t of the third-order RW solutions (35)–(37) are given in Appendix II.

2.4 Nth-order RW solutions

By continuing the iterative process above, we can finally construct the Nth-order RW solutions of the system (1)–(3).

Theorem 3

The N-fold DT of the system (1)–(3) is

$$\begin{aligned} T[N] = {T_N}\left( {\lambda ,{\lambda _1},{\lambda _2}} \right) = \lambda I - M_r^{[N]}, \end{aligned}$$

(38)

where

$$\begin{aligned}&M_r^{[N]}= \left( {\begin{array}{*{20}{c}} {m_{11r}^{[N]}} &{} {m_{12r}^{[N]}} \\ {m_{21r}^{[N]}} &{} {m_{22r}^{[N]}} \\ \end{array}} \right) ,\\&m_{11r}^{[N]}= \frac{1}{{{\varDelta _N}}}({\lambda _1}{\phi _{11}}[N - 1]{\phi _{22}}[N - 1] - {\lambda _2}{\phi _{21}}[N - 1]{\phi _{12}}[N - 1]),\\&m_{12r}^{[N]} = \frac{1}{{{\varDelta _N}}} \left( {{\lambda _2}-{\lambda _{{1}}}} \right) {\phi _{{{1}}1}}[N - 1]{\phi _{12}}[N - 1],\\&m_{21r}^{[N]}= \frac{1}{{{\varDelta _N}}}\left( {{\lambda _{{1}}}-{\lambda _{{2}}}} \right) {\phi _{{{2}}1}}[N - 1]{\phi _{{{2}}2}}[N - 1],\\&m_{22r}^{[N]} = \frac{1}{{{\varDelta _N}}}({\lambda _{{2}}}{\phi _{11}}[N-1]{\phi _{22}}[N-1] - {\lambda _{1}}{\phi _{21}}[N - 1]{\phi _{12}}[N - 1]),\\&{\varDelta _N} = {\phi _{11}}[N - 1]{\phi _{22}}[N - 1] - {\phi _{21}}[N - 1]{\phi _{12}}[N - 1].\\&\left( \begin{array}{l} {\phi _{1j}}[N - 1] \\ {\phi _{2j}}[N - 1] \\ \end{array} \right) = \lambda _j^{N - 1}\varPhi _j^{(0)} + \lambda _j^{N - 2}{\left. {\left( {\sum \limits _{k = 1}^{N - 1} {T[k]} } \right) } \right| _{\lambda = {\lambda _j}}}\varPhi _j^{(1)}\\&\quad + \lambda _j^{N - 3}{\left. {\left( {\sum \limits _{1 \le l< k \le N - 1} {T[k]T[l]} } \right) } \right| _{\lambda = {\lambda _j}}}\varPhi _j^{(2)}\\&\quad + \lambda _j^{N - 4}{\left. {\left( {\sum \limits _{1 \le s< l< k \le N - 1} {T[k]T[l]T[s]} } \right) } \right| _{\lambda = {\lambda _j}}}\varPhi _j^{(3)} + \cdots \\&\quad + \lambda _j^{N - (n + 1)}{\left. {\left( {\sum \limits _{1 \le {s_1}< {s_2}< \cdots< {s_{n - 1}} < {s_n} \le N - 1} {T[{s_n}]T[{s_{n - 1}}] \cdots T[{s_1}]} } \right) } \right| _{\lambda = {\lambda _j}}}\varPhi _j^{(n)} \\&\quad + \cdots + {\left. {\left( {T[N - 1]T[N - 2] \cdots T[1]} \right) } \right| _{\lambda = {\lambda _j}}}\varPhi _j^{(N - 1)},j = 1,2, \end{aligned}$$

and T[N] satisfies the conditions as

$$\begin{aligned} {T_x}[N]= & {} {U^{[N]}}T[N] - T[N]{U^{[N - 1]}},{T_t}[N] \nonumber \\= & {} {V^{[N]}}T[N] - T[N]{V^{[N - 1]}}, \end{aligned}$$

(39)

where

$$\begin{aligned} {U^{[N]}}= & {} - i\lambda {\sigma _1} + \left( {\begin{array}{*{20}{c}} 0 &{} {{q^{[N]}}} \\ { - {\overline{q^{[N]}}}} &{} 0 \\ \end{array}} \right) ,\\ {V^{[N]}}= & {} \frac{1}{{4\lambda }}\left( {\begin{array}{*{20}{c}} {i{w^{[N]}}} &{} { - {p^{[N]}}} \\ {\overline{p^{[N]}}} &{} { - i{w^{[N]}}} \\ \end{array}} \right) . \end{aligned}$$

Finally, the Nth-order RW solutions of the system (1)–(3) can be obtained as

$$\begin{aligned} q_r^{[N]}= & {} q_r^{[N - 1]} - 4\frac{{{\phi _{11}}[N - 1]{\phi _{12}}[N - 1]}}{{{\varDelta _N}}}, \end{aligned}$$

(40)

$$\begin{aligned} p_r^{[N]}= & {} p_r^{[N - 1]} - 8i{\left( {\frac{{{\phi _{11}}[N - 1]{\phi _{12}}[N - 1]}}{{{\varDelta _N}}}} \right) _t}, \nonumber \\ \end{aligned}$$

(41)

$$\begin{aligned} w_r^{[N]}= & {} w_r^{[N - 1]} \nonumber \\&- 4\left( {\frac{{{\phi _{11}}[N - 1]{\phi _{22}}[N - 1] + {\phi _{21}}[N - 1]{\phi _{12}}[N - 1]}}{{{\varDelta _N}}}} \right) _t,\nonumber \\ \end{aligned}$$

(42)

where

$$\begin{aligned}&{\varPsi _j}[N - 1] = \left( \begin{array}{l} {\phi _{1j}}[N - 1] \\ {\phi _{{{2}}j}}[N - 1] \\ \end{array} \right) \\&={\mathop {\lim }\limits _{f \rightarrow 0}} \frac{{\left( {{\lambda _j}{f^2} + T[N - 1){|_{\lambda = {\lambda _j}}} \cdots \left( {{\lambda _j}{f^2} + T[1]{|_{\lambda = {\lambda _j}}}} \right) \left( {\varPhi _j^{(0)} + \cdots } \right) } \right) }}{{{f^{2(N - 1)}}}},\nonumber \\&\quad j = 1,2. \end{aligned}$$

The proof of the Theorem 3 could be come true by the similar iteration method performed in the Theorem 2. We here omit the derivation.

Fig. 2

The spatiotemporal pattern of the third-order RW |q|. The plots are given by the solution (35). a, b and c are the 3-dimension, density and contour views, respectively

Fig. 3

The extreme values of the first-, second-, and third-order RWs of |q|. The plots are given by the solutions (16), (25) and (35) with $t=0$. The maximum values of the first-, second-, and third-order RWs reach 3, 5 and 7, respectively

Fig. 4

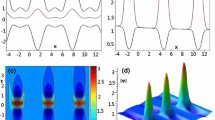
The spatiotemporal pattern of the second-order RW |p|. The plots are given by the solution (26). a, b and c are the 3-dimension, density and contour views, respectively

Remark 4

$$\begin{aligned} {\left. {T[N]} \right| _{\lambda = {\lambda _j}}}\left( \begin{array}{l} {\varPhi _{1j}}[N - 1] \\ {\varPhi _{2j}}[N - 1] \\ \end{array} \right) = 0,j = 1,2. \end{aligned}$$

Fig. 5

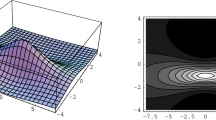
The spatiotemporal pattern of the third-order RW |p|. The plots are given by the solution (36). a, b and c are the 3-dimension, density and contour views, respectively

Fig. 6

The spatiotemporal pattern of the second-order RW w. The plots are given by the solution (27). a, b and c are the 3-dimension, density and contour views, respectively

Fig. 7

The spatiotemporal pattern of the third-order RW w. The plots are given by the solution (37). a, b and c are the 3-dimension, density and contour views, respectively.

3 Dynamics of the multiple RWs

In order to explore the dynamics of the multiple RWs of the TSRS system (1)–(3), we demonstrate the spatiotemporal evolution plots of the second- and third-order RW solutions in 3-dimension, density and contour views (see Figs. 1, 2, 3, 4, 5, 6, and 7). From these figures, we careful analyzed their geometrical structures, changes of peak and trough numbers.

(i) Symmetrical structure.

The symmetry is a class of fundamental features in physical systems, such as gravitation versus repulsion, particle versus antiparticle, incident versus reflected lights. In general, the symmetrical structures have excellent stability and robustness.

In photoelectric systems, the symmetry is even more omnipresent from crystal structures of luminescent material, to the various periodical and doubly periodical light waves. The symmetry in optics has gradually attracted attention. Recently, based on the symmetry theory, the concept of symmetry breaking has been introduced in order to deal with local nonequilibrium and/or instability states in more complex applications, e.g. spontaneous symmetry breaking in a parity-time optical coupled system that judiciously involves a complex index potential [38].

One of the difficulties for the symmetry research is how to describe these structures mathematically. The analytical solutions obtained in Sect. 2 provide a way to unearth the geometrical structures.

It is magical that all the RWs of the system (1)–(3) exhibit exquisite symmetry consisting of multiple peaks and troughs. Moreover, |q|, |p| and w show different symmetrical structures. Next, we make a careful analysis. Both |q| and |p| are symmetric with respect to the $x-$axis, $t-$axis, and coordinate central point (0, 0), respectively (see Figs. 1, 2, 4, and 5). w is symmetric with respect to the point (0, 0), and antisymmetric with respect to the $x-$axis and $t-$axis, and (see Figs. 6 and 7). We take the first-order RWs as examples to verify the symmetry observed from their figures. From the first-order RW solutions (16)–(17), we can acquire

$$\begin{aligned}&|q(x,t)| = \frac{{\sqrt{{t^4} + \left( {32{x^2} + 40} \right) {t^2} + 16{{\left( {4{x^2} - 3} \right) }^2}} }}{{\left( {{t^2} + 16{x^2} + 4} \right) }}, \end{aligned}$$

(43)

$$\begin{aligned}&|p(x,t)|\nonumber \\&= \frac{{8\sqrt{{{\left( {3{t^2} - 16{x^2} - 2 - \frac{1}{8}\left( {{t^2} + 16{x^2}} \right) } \right) }^2} + {t^2}{{\left( {{t^2} + 16x^2 - 4} \right) }^2}} }}{{{{\left( {{t^2} + 16{x^2} + 4} \right) }^2}}}.\nonumber \\ \end{aligned}$$

(44)

It is seen that

$$\begin{aligned} |q( - x,t)|= & {} |q(x, - t)|= |q(-x, - t)| = |q(x,t)|,\\ |p( - x,t)|= & {} |p(x, - t)| = |p(-x, - t)| = |p(x,t)|. \end{aligned}$$

For the first-order RW solution (18) of w, it is easy to attain that

$$\begin{aligned}&w(-x,-t)=w(x,t),w(-x,t)\\&\quad =w(x,-t)=-w(x,t). \end{aligned}$$

Table 1 The peak and trough numbers of the RWs

(ii) The peak and trough numbers.

The peak and trough are two types of wave propagation patterns in spatiotemporal fields, which are related to the amplitudes, frequencies and energies of waves. Table 1 gives the peak and trough number of q, p and w with the first-, second-, and third-order RWS. It is seen that the peak and trough numbers of the RWs rapidly increase as the order increases for the TSRS system (1)–(3). Why does this happen? It can be regarded as the result of the collision of multiple RWs. When these RWs hit toward the coordinate origin (0, 0) at the same time, the interaction between peaks and troughs becomes more complex than that in the lower-order case, and eventually generates more peaks and troughs. The changes of the peak and trough numbers are the same for |p| and w. Because all the RWs of |q| with different orders always possess a central peak which does not split, the changes of |q| is different from |p| and w. On the whole, as the order of the RWs is increased once, it will cause each peak and trough to split into two pieces except the central peak of |q|.

In addition, the collisions are often accompanied by nonlinear superposition of amplitudes. Just as in the case of collisions of multiple solitons or multiple breathers, there exist amplitude superpositions at the collision point [35, 39]. Among |q|, |p| and w, the amplitude superposition effect of |q| is the most significant. The maxima of the first-, second- and third-order RWs of |q| can reach 3, 5 and 7, respectively (see Fig. 3).

It is noticeable that not all multiple RWs will collide. Under some conditions, the multiple RWs may be arranged dispersedly without collision [29, 30].

4 Conclusions

In this article, the N-order RW solutions were obtained for the TSRS system (1)–(3) by the GDT scheme. Furthermore, the dynamical properties of the solutions are analyzed. As $N\ge 2$, the RWs will collide towards the coordinate origin. As the results, the peaks and troughs of higher-order RWs are almost twice as high as that of lower-order RWs. It is also interesting that all the RWs possess exquisite geometric symmetry. During the process, there exists the nonlinear superposition effect to amplitudes.

Within our best knowledge, a lot of higher-order RW solutions have reported ceaselessly for various nonlinear evolution systems (equations) in recent decade; however, the richness and novelty of dynamical properties, demonstrated by the higher-order RWs of the TSRS system (1)–(3), are highly rare. The richness of optical pulses will make it possible to transmit more information by modulation. In essence, these properties are determined by certain inherent mechanics arising from the refractive rate of optical frequency spectrum in photoconductive and reflective materials. Fortunately, the study here reconstruct the RW collision process in theory. Therefore, these results would contribute to more understanding to the TSRS systems, and help to develop a new generation of optical fiber systems with more excellent properties.

Appendices

Appendix I

The second-order RW solutions of Eqs. (1)–(3) are expressed in details as follows

$$\begin{aligned} q_r^{[2]}= & {} - 24\frac{{{H_{2q}}}}{{{G_{2q}}}}{{\mathrm{e}}^{ - \frac{1}{2}it}},\\ p_r^{[2]}= & {} - 24\frac{{{H_{2p}}}}{{{G_{2p}}}}{{\mathrm{e}}^{ - \frac{1}{2}it}},\\ w_r^{[2]}= & {} \frac{{{H_{2w}}}}{{{G_{2w}}}}, \end{aligned}$$

where

$$\begin{aligned}&{H_{2q}} = - \frac{1}{{24}}{t^6} + i{t^5} + \left( { - 2{x^2} + \frac{19}{2}} \right) {t^4} \\&\quad + \left( {32i{x^2} - 40i} \right) {t^3} + \left( { - 32{x^4} + 48{x^2} - 66} \right) {t^2}\\&\quad + \left( {256i{x^4} + 384i{x^2} - 48i} \right) t - \frac{{512{x^6}}}{3} \\&\quad + 384{x^4} + 480{x^2} - 120,\\&{G_{2q}} = {t^6} + \left( {48{x^2} + 12} \right) {t^4} \\&\quad + \left( {768{x^4} + 3456{x^2} + 432} \right) {t^2}\\&\quad + 4096{x^6} + 3072{x^4} + 6912{x^2} + 576,\\&{H_{2p}} =- \frac{1}{{24}}{t^{12}} + i{t^{11}} + \left( { - 4{x^2} + 11} \right) {t^{10}}\\&\quad + \left( {80i{x^2} - 68i} \right) {t^9}+ \left( { - 160{x^4} + 432{x^2} - 234} \right) {t^8}\\&\quad +\left( {2560i{x^4} + 768i{x^2} + 288i} \right) {t^7}\\&\quad + \left( {3584{x^4} + 9600{x^2} - 864 - \frac{{10240{x^6}}}{3}} \right) {t^6}\\&\quad + \left( - 40960{x^8} - 40960{x^6} + 82944{x^4} \right. \\&\quad \left. + 50688{x^2} + 864 \right) {t^4}+ \left( 327680i{x^8} + 1245184i{x^6}\right. \\&\quad \left. + 1400832i{x^4} + 258048i{x^2} + 11520i \right) {t^3}\\&\quad + \left( - 262144{x^{10}} - 589824{x^8} + 4030464{x^6} \right. \\&\quad \left. + 4055040{x^4} + 912384{x^2} + 6912 \right) {t^2}\\&\quad + (1048576i{x^{10}} + 3932160i{x^8} - 5111808i{x^6}\\&\quad - 3833856i{x^4} - 995328i{x^2} + 27648i)t\\&\quad - \frac{{2097152}}{3}{\left( {{x^6} + \frac{3}{4}{x^4} + \frac{{27{x^2}}}{{16}} + \frac{9}{{64}}} \right) ^2},\\&{G_{2p}}=\left( {t^6} + \left( {48{x^2} + 12} \right) {t^4} + \left( {768{x^4} + 3456{x^2} + 432} \right) {t^2} \right. \\&\quad \left. + 4096{x^6} \right. {\left. { + 3072{x^4} + 6912{x^2} + 576} \right) ^2},\\&{H_{2w}} = 384\left( {t^8} + \left( {64{x^2} + 144} \right) {t^6}\right. \\&\quad \left. + \left( {1536{x^4} + 768{x^2} + 864} \right) {t^4} \right. \\&\quad + \left( {16384{x^6} + 12288{x^4} + 3072{x^2} + 2304} \right) {t^2} + 65536{x^8}\\&\quad \left. { + 589824{x^6} + 221184{x^4} + 36864{x^2} + 20736} \right) xt,\\&{G_{2w}} = \left( {t^6} + \left( {48{x^2} + 12} \right) {t^4} \right. \left. + \left( {768{x^4} + 3456{x^2} + 432} \right) {t^2} \right. \\&\quad {\left. { + 4096{x^6} + 3072{x^4} + 6912{x^2} + 576} \right) ^2}. \end{aligned}$$

Appendix II

The third-order RW solutions of Eqs. (1)–(3) are expressed in details as follows

$$\begin{aligned} q_r^{[3]}= & {} 48\frac{{{H_{3q}}}}{{{G_{3q}}}}{{\mathrm{e}}^{ - \frac{1}{2}it}},\\ p_r^{[3]}= & {} - 24\frac{{{H_{3}}}}{{{G_{3p}}}}{{\mathrm{e}}^{ - \frac{1}{2}it}},\\ w_r^{[3]}= & {} 768 \frac{{{H_{3q}}}}{{{G_{3q}}}}, \end{aligned}$$

where

$$\begin{aligned}&{H_{3q}} = - \frac{1}{{48}}{t^{12}} + {t^{11}}i + \left( {\frac{{43}}{2} - 2{x^2}} \right) {t^{10}} \\&\quad + \left( {80i{x^2} - 260i} \right) {t^9} + \left( { - 80{x^4} + 1080{x^2} - 1845} \right) {t^8} \\&\quad + \left( {2560i{x^4} - 3840i{x^2} + 7200i} \right) {t^7}\\&\quad + \left( {19200{x^4} + 16320{x^2} + 9360 - \frac{{5120{x^6}}}{3}} \right) {t^6}\\&\quad + \left( {40960i{x^6} + 92160i{x^4} - 23040i{x^2} + 17280i} \right) {t^5}\\&\quad + \left( - 20480{x^8} + 143360{x^6} + 1958400{x^4} + 1324800{x^2} \right. \\&\quad \left. - 75600 \right) {t^4}+ (327680i{x^8} + 1638400i{x^6} - 9216000i{x^4}\\&\quad -6451200i{x^2} + 748800i ){t^3}+( - 131072{x^{10}} \\&\quad + 491520{x^8} + 4177920{x^6}-15667200{x^4}\\&\quad - 10713600{x^2} + 1468800){t^2}+ \left( 1048576i{x^{10}}\right. \\&\quad \left. + 3932160i{x^8} + 13762560i{x^6} - 7372800i{x^4}\right. \\&\quad \left. - 2764800i{x^2} + 691200i \right) t+ 1209600 - \frac{{1048576{x^{12}}}}{3}\\&\quad + 1572864{x^{10}} + 4915200{x^8}+ 14745600{x^6} \\&\quad - 19353600{x^4} - 9676800{x^2},\\&{G_{3q}} = {t^{12}} + 96{t^{10}}{x^2} + 3840{t^8}{x^4} + 81920{t^6}{x^6}\\&\quad + 983040{t^4}{x^8}+ 6291456{t^2}{x^{10}} + 16777216{x^{12}} \\&\quad + 24{t^{10}} + 17280{t^8}{x^2}+ 798720{t^6}{x^4} + 12779520{t^4}{x^6}\\&\quad + 70778880{t^2}{x^8}+ 25165824{x^{10}} + 2160{t^8} + 1797120{t^6}{x^2} \\&\quad + 149760{t^6} + 9216000{t^4}{x^4}+ 460062720{t^2}{x^6}\\&\quad + 141557760{x^8} + 13824000{t^4}{x^2}+ 221184000{t^2}{x^4}\\&\quad + 613416960{x^6} + 864000{t^4} + 248832000{t^2}{x^2}\\&\quad + 221184000{x^4}+ 12441600{t^2}+ 199065600{x^2} + 8294400, \end{aligned}$$

$$\begin{aligned}&{H_{3p}} = ( - 68797071360000 + 5863676313600{t^{10}}{x^2}\\&\quad +14631321600{t^{12}}+ 317708697600{t^{10}}\\&\quad - 3302259425280000{x^2} +934502400{t^{16}}{x^4}\\&\quad + 55349084160{t^{14}}{x^6} + 1545244508160{t^{12}}{x^8}\\&\quad +24653246496768{t^{10}}{x^{10}}+ 233232830300160{t^8}{x^{12}} \\&\quad + 1252412463513600{t^6}{x^{14}}+3209886758338560{t^4}{x^{16}}\\&\quad + 1385384650997760{t^2}{x^{18}} + 242749440{t^{16}}{x^2}\\&\quad +55738368000{t^{14}}{x^4} + 4413770956800{t^{12}}{x^6}\\&\quad + 132747205017600{t^{10}}{x^8} + 1731416744263680{t^8}{x^{10}}\\&\quad +9302641465098240{t^6}{x^{12}}+ 24306078921523200{t^4}{x^{14}} \\&\quad + 144723218006016000{t^2}{x^{16}}+ 597196800{t^{14}}{x^2}\\&\quad + 3116571033600{t^{12}}{x^4} + 171102563205120{t^{10}}{x^6}\\&\quad +1042250150707200{t^8}{x^8}+ 25878842258227200{t^6}{x^{10}} \\&\quad +101828091130675200{t^4}{x^{12}}+ 437509420587417600{t^2}{x^{14}}\\&\quad + 372385382400{t^{12}}{x^2} +81575490355200{t^{10}}{x^4}\\&\quad - 7063369836134400{t^8}{x^6} + 31944127964774400{t^6}{x^8}\\&\quad + 135834568438579200{t^4}{x^{10}}+1109637442673049600{t^2}{x^{12}}\\&\quad - 1424967069597696{t^2}{x^{20}} + 322560{t^{18}}{x^2} \\&\quad -192{t^{22}}{x^2} - 16896{t^{20}}{x^4}- 901120{t^{18}}{x^6} - 32440320{t^{16}}{x^8}\\&\quad -830472192{t^{14}}{x^{10}} - 15502147584{t^{12}}{x^{12}}\\&\quad - 212600881152{t^{10}}{x^{14}} - 2126008811520{t^8}{x^{16}} \\&\quad -15118284881920{t^6}{x^{18}}- 72567767433216{t^4}{x^{20}}\\&\quad - 211106232532992{t^2}{x^{22}}+145152{t^{20}}{x^2}\\&\quad + 8171520{t^{18}}{x^4} + 250675200{t^{16}}{x^6} \\&\quad +4246732800{t^{14}}{x^8}+ 27481079808{t^{12}}{x^{10}} \\&\quad - 372051542016{t^{10}}{x^{12}} -10436770529280{t^8}{x^{14}} \end{aligned}$$

$$\begin{aligned}&\quad - 108233175859200{t^6}{x^{16}} - 577243604582400{t^4}{x^{18}} \\&\quad -449198603580211200{x^{12}}- 328132065440563200{x^{10}}\\&\quad + 3135283200000{t^8} -295491065610240000{x^8}\\&\quad + 37933940736000{t^6} - 98236102606848000{x^6} \\&\quad +106062151680000{t^4}- 43296290242560000{x^4} \\&\quad + 343985356800000{t^2} -3649684635648000{t^8}{x^4}\\&\quad - 13086731796480000{t^6}{x^6} + 162585315901440000{t^4}{x^8}\\&\quad +1078953337316966400{t^2}{x^{10}}- 541776936960000{t^8}{x^2} \\&\quad - 3247221768192000{t^6}{x^4}+28668504047616000{t^4}{x^6}\\&\quad + 993319635124224000{t^2}{x^8} - 692174979072000{t^6}{x^2} \\&\quad +22427845263360000{t^4}{x^4}+ 98333947330560000{t^2}{x^6} \\&\quad + 1674062069760000{t^4}{x^2} +76685802209280000{t^2}{x^4}\\&\quad + 4127824281600000{t^2}{x^2} - 871679074605465600it{x^{12}} \\&\quad -127975292928000i{t^9}{x^2}- 1009444445591961600it{x^{10}} \\&\quad - 804675007807488000it{x^8} -1013760i{t^{19}}{x^2}\\&\quad - 24883200i{t^{17}}{x^2} - 1875640320i{t^{15}}{x^4} \\&\quad -2884239360i{t^{15}}{x^2} - 108291686400i{t^{13}}{x^4}\\&\quad - 14119537213440i{t^{11}}{x^6} - 307757894860800i{t^9}{x^8} \\&\quad -172777257188720640it{x^{16}}- 37955174400i{t^{13}}{x^2} \\&\quad - 14663968358400i{t^{11}}{x^4}- 1781521396531200i{t^9}{x^6}\\&\quad - 396318966231859200it{x^{14}} - 3000316723200i{t^{11}}{x^2} \\&\quad -961884979200000i{t^9}{x^4}- 1146617856000i{t^5} \\&\quad - 275188285440000it - 15552i{t^{21}} \\&\quad -26276659200i{t^{11}}- 414720i{t^{17}}- 2587852800i{t^{13}}\\&\quad - 812187648000i{t^9} -4299816960000i{t^7}\\&\quad + 58851789373440i{t^9}{x^{12}} + 538073502842880i{t^7}{x^{14}}\\&\quad +2931572877557760i{t^5}{x^{16}}+ 8312307905986560i{t^3}{x^{18}}\\&\quad + 8233143068786688it{x^{20}} + 94560583680i{t^{13}}{x^6}\\&\quad + 7379122913280i{t^{11}}{x^8} + 183585692712960i{t^9}{x^{10}} \\&\quad + 2261300281344000i{t^7}{x^{12}}+ 14360996248289280i{t^5}{x^{14}} \\&\quad +42006841739182080i{t^3}{x^{16}} + 38790770227937280it{x^{18}}\\&\quad + 810589177774080i{t^7}{x^{10}} + 47675167777751040i{t^5}{x^{12}}\\ \end{aligned}$$

$$\begin{aligned}&\quad + 143981047657267200i{t^3}{x^{14}}+ 1988422218547200i{t^7}{x^8}\\&\quad + 27939234706882560i{t^5}{x^{10}}+374332169650176000i{t^3}{x^{12}}\\&\quad + 169205760i{t^{15}} + 68797071360000i{t^3} + 8448i{t^{21}}{x^2} \\&\quad +675840i{t^{19}}{x^4} + 32440320i{t^{17}}{x^6}\\&\quad + 1038090240i{t^{15}}{x^8} + 23253221376i{t^{13}}{x^{10}}\\&\quad +372051542016i{t^{11}}{x^{12}}+ 580542139465728i{t^3}{x^{20}} \\&\quad + 844424930131968it{x^{22}} +15482880i{t^{17}}{x^4}\\&\quad + 3680501760i{t^{15}}{x^6} + 166471925760i{t^{13}}{x^8}\\&\quad + 4008009793536i{t^{11}}{x^{10}}+ 10616152522752000i{t^7}{x^6} \\&\quad + 38159442247680000i{t^5}{x^8}+ 290977162356326400i{t^3}{x^{10}} \\&\quad + 5705570451456000i{t^7}{x^4} +65458120163328000i{t^5}{x^6}\\&\quad + 283619239133184000i{t^3}{x^8} + 828622503936000i{t^7}{x^2} \\&\quad +31041238597632000i{t^5}{x^4}+ 143244675514368000i{t^3}{x^6}\\&\quad + 3756320096256000i{t^5}{x^2} +67145941647360000i{t^3}{x^4}\\&\quad + 245394567069696000it{x^6} + 6421059993600000i{t^3}{x^2} \\&\quad +63109846794240000it{x^4}+ 9906778275840000it{x^2} \\&\quad + 48i{t^{23}} + 840960i{t^{19}} -{t^{24}} - 281474976710656{x^{24}}\\&\quad + 1104{t^{22}} - 844424930131968{x^{22}} - 143136{t^{20}} \\&\quad -5383208929591296{x^{20}}+ 2638080{t^{18}} \\&\quad - 27707693019955200{x^{18}} + 12960000{t^{16}}\\&\quad -58334589411655680{x^{16}}+ 1542758400{t^{14}}\\&\quad - 191479949977190400{x^{14}},\\&{G_{3p}} = ({t^{12}} + 96{t^{10}}{x^2} + 3840{t^8}{x^4} +81920{t^6}{x^6} + 983040{t^4}{x^8}\\&\quad + 6291456{t^2}{x^{10}}+ 16777216{x^{12}} + 24{t^{10}} + 17280{t^8}{x^2} \\&\quad +798720{t^6}{x^4} + 12779520{t^4}{x^6}+ 70778880{t^2}{x^8} \\&\quad + 25165824{x^{10}} + 2160{t^8} +1797120{t^6}{x^2} + 9216000{t^4}{x^4}\\&\quad + 460062720{t^2}{x^6} + 141557760{x^8} + 149760{t^6} \\&\quad +13824000{t^4}{x^2}+ 221184000{t^2}{x^4} + 613416960{x^6} \\&\quad + 864000{t^4} +248832000{t^2}{x^2}+ 221184000{x^4} \\&\quad + 12441600{t^2} + 199065600{x^2} + 8294400)^{{2}}\\&{H_{3w}} = ({t^{20}} + 160{t^{18}}{x^2} + 11520{t^{16}}{x^4} \\&\quad +491520{t^{14}}{x^6} + 13762560{t^{12}}{x^8}+ 264241152{t^{10}}{x^{10}} \\&\quad + 3523215360{t^8}{x^{12}} +32212254720{t^6}{x^{14}}\\&\quad + 193273528320{t^4}{x^{16}} + 687194767360{t^2}{x^{18}} \\&\quad +1099511627776{x^{20}}+ 360{t^{18}} + 51840{t^{16}}{x^2} \\&\quad + 3317760{t^{14}}{x^4} +123863040{t^{12}}{x^6}\\&\quad + 2972712960{t^{10}}{x^8} + 47563407360{t^8}{x^{10}} \\&\quad +507343011840{t^6}{x^{12}}+ 3478923509760{t^4}{x^{14}}\\&\quad + 13915694039040{t^2}{x^{16}}+24739011624960{x^{18}}\\ \end{aligned}$$

$$\begin{aligned}&\quad + 58320{t^{16}} + 1566720{t^{14}}{x^2} + 205701120{t^{12}}{x^4} \\&\quad +13377208320{t^{10}}{x^6}+ 327942144000{t^8}{x^8} \\&\quad + 3424565329920{t^6}{x^{10}}+13480828600320{t^4}{x^{12}}\\&\quad + 26285199851520{t^2}{x^{14}} + 250482492702720{x^{16}}\\&\quad +1175040{t^{14}}+ 60825600{t^{12}}{x^2} \\&\quad + 6317015040{t^{10}}{x^4} +983826432000{t^8}{x^6}\\&\quad + 15741222912000{t^6}{x^8} + 25874493603840{t^4}{x^{10}}\\&\quad +63780264345600{t^2}{x^{12}}+ 315422398218240{x^{14}} \\&\quad + 34214400{t^{12}} +1161216000{t^{10}}{x^2} + 301252608000{t^8}{x^4}\\&\quad + 35417751552000{t^6}{x^6} + 77120667648000{t^4}{x^8} \\&\quad +76101451776000{t^2}{x^{10}}+ 574022379110400{x^{12}}\\&\quad + 522547200{t^{10}} +41803776000{t^8}{x^2}\\&\quad + 8676075110400{t^6}{x^4} + 138817201766400{t^4}{x^6}\\&\quad + 171228266496000{t^2}{x^8} + 547930452787200{x^{10}} \\&\quad +15676416000{t^8}+ 1003290624000{t^6}{x^2} \\&\quad + 31417329254400{t^4}{x^4}+256842399744000{t^2}{x^6}\\&\quad + 1027369598976000{x^8} + 322486272000{t^6} \\&\quad +3248750592000{t^4}{x^2}+ 51980009472000{t^2}{x^4} \\&\quad + 1320903770112000{x^6} +913711104000{t^4}\\&\quad + 4777574400000{t^2}{x^2} + 233910042624000{x^4} \\&\quad +1194393600000{t^2}+ 19110297600000{x^2} \\&\quad + 4299816960000)tx,\\&{G_{3w}} = ( {t^{12}} + 96{t^{10}}{x^2} + 3840{t^8}{x^4} +81920{t^6}{x^6}\\&\quad + 983040{t^4}{x^8} + 6291456{t^2}{x^{10}} + 16777216{x^{12}} + 24{t^{10}}\\&\quad +17280{t^8}{x^2} + 798720{t^6}{x^4}+ 12779520{t^4}{x^6}\\&\quad + 70778880{t^2}{x^8}+ 25165824{x^{10}} +2160{t^8}\\&\quad + 1797120{t^6}{x^2} + 9216000{t^4}{x^4} + 460062720{t^2}{x^6}\\&\quad +141557760{x^8}+ 149760{t^6} + 13824000{t^4}{x^2} \\&\quad + 221184000{t^2}{x^4} +613416960{x^6}+ 864000{t^4}\\&\quad + 248832000{t^2}{x^2} + 221184000{x^4} +12441600{t^2}\\&\quad + 199065600{x^2} + 8294400 )^{2}. \end{aligned}$$