Rogue wave solutions in nonlinear optics with coupled Schrödinger equations

Abstract

In this article, the first and second-order rogue wave solutions are obtained which are localized in both space and time that appear from nowhere and disappear without a trace. The coupled NLSEs with time-dependent coefficients are considered that describe the effects of ultrashort optical pulse propagation in nonlinear optics and quantum physics. The similarity transformation is used to investigate these rational-like (rogue wave) solutions. Moreover, the 3D graphical representations and contour plots have depicted with different parameters of gravity field and external magnetic field.

1 Introduction

The study of rogue waves has become a hot and interesting topic in the field of nonlinear science. The rogue wave is a giant single wave which was firstly found in the ocean (Muller et al. 2005; Akhmediev et al. 2009) and the amplitude of this wave is higher than its surrounding waves. The importance of these waves have also been observed in many fields like optical fibers (Solli et al. 2007; Zhang et al. 2014; Zheng-Yi and Song-Hua 2012), Bose–Einstein condensates (BECs) (Bludov et al. 2009), super fluids (Ganshin et al. 2008), and so on Younis et al. (2015), Cheemaa and Younis (2016), Geng and Lv (2012), Ali et al. (2015), Triki and Wazwaz (2011), Fan (2001), Ablowitz and Clarkson (1991), Bekir et al. (2012), Akhmediev et al. (2009), Kharif and Pelinovsky (2003), Janssen (2003), Onorato et al. (2001), Dai et al. (2012), Wang et al. (2011, 2012), Wang and Dai (2012), Yan (2010a, b), Peregrine (1983), Akhmediev et al. (2009), Song et al. (2010), Meng et al. (2015), Cheng et al. (2014). However, it is very difficult to explain the rogue waves using the linear theories based on the superposition principles. These theories (Kharif and Pelinovsky 2003; Janssen 2003; Onorato et al. 2001), can be used to demonstrate, why the rogue waves can appear from nowhere. In recent years, it becomes an important issue for ones to study the rogue waves theoretically in the fields of the nonlinear science (Dai et al. 2012; Wang et al. 2011, 2012; Wang and Dai 2012; Yan 2010a). The Darboux transformation (Peregrine 1983; Akhmediev et al. 2009), the similarity transformation and the numerical simulation (Yan 2010a, b; Akhmediev et al. 2009; Song et al. 2010) were used to analyze the occurrence of these waves and the larger amplitudes. One of the important known model for the rogue waves is considered and called the NLSE.

$$\begin{aligned} i q_{t}+\frac{1}{2}q_{xx}+|q|^2 q=0. \end{aligned}$$

(1)

The NLSE is a basic or fundamental model to describe the numerous nonlinear physical phenomena, particular in quantum mechanics and nonlinear optics. In this article, we investigate the 1st and 2nd order rogue wave solutions to the coupled NLSEs with time dependent coefficients in non-Kerr media. This coupled model is read as:

$$\begin{aligned}&i q_{t}+a_1(t) q_{xx}+b_1(t) |r|^2 q=0 \end{aligned}$$

(2)

and

$$\begin{aligned}&\nonumber \\&i r_{t}+a_2(t) r_{xx}+b_2(t) |q|^2 r=0. \end{aligned}$$

(3)

The q(x, t) and r(x, t) represent the electromagnetic wave fields that propagate along two components named as spatial x and temporal t. The coefficients $a_l(t)$ and $b_l(t)$ for $l=1,2,$ represent the GVD and XPM, respectively.

The aim of this paper is to construct rogue wave solutions to the Eqs. (2) and (3). The similarity transformation tool is used to investigate the waves. The following transformation is considered to construct the solutions.

$$\begin{aligned}&q(x,t) = P_1(x,t)e^{i \phi _1(x,t)}\end{aligned}$$

(4)

and

$$\begin{aligned}&\nonumber \\&r(x,t) = P_2(x,t)e^{i \phi _2(x,t)}, \end{aligned}$$

(5)

where $P_l(x, t)$ for $l = 1,2$ are the amplitude components of the wave solutions and while the phase component $\phi _l(x, t)$ is given by the following equation.

$$\begin{aligned} \phi _l(x,t)=-\,k_lx+\omega _l t +\theta _l. \end{aligned}$$

(6)

In the following section, the similarity transformation has been applied to investigate the explicit solutions.

2 Explicit solutions

Firstly, we consider the following transformation for the envelope fields q and r, see also (Younis et al. 2015).

$$\begin{aligned}&q=(q_R+i q_I)e^{i \phi _1}\end{aligned}$$

(7)

and

$$\begin{aligned}&{ and }\nonumber \\&r=(r_R+i r_I)e^{i \phi _2}, \end{aligned}$$

(8)

where $q_R\equiv q_R(x,t)$, $q_I\equiv q_I(x,t)$, $r_R\equiv r_R(x,t)$, $r_I\equiv r_I(x,t)$, $q\equiv q(x,t)$, $r\equiv r(x,t)$, $\phi _1\equiv \phi _1(x,t)$, and $\phi _2\equiv \phi _2(x,t)$. The intensity of above transformation can be given by the following equations.

$$\begin{aligned}&|q|^2 = |q_R|^2+|q_I|^2=P^2_l\end{aligned}$$

(9)

and

$$\begin{aligned}&\nonumber \\&|r|^2 =|r_R|^2+|r_I|^2=P^2_{\bar{l}}. \end{aligned}$$

(10)

For $l=1$ and phase $\bar{l}=3-l$, the real functions depend on the variables x (space) and t (time). Substitute the Eqs. (7)–(10) into Eqs. (2) and (3), which yield the following coupled equations.

$$\begin{aligned}&-\,q_R\phi _{1t}-i q_{I}\phi _{1t}+i q_{Rt}-q_{It}-a_1(t)q_R\phi ^2_{1x}-ia_1(t) q_I\phi ^2_{1x}\nonumber \\&\quad +\,i a_1(t)q_R\phi _{1xx}-a_1(t)q_I\phi _{1xx}+2i a_1(t) q_{Rx}\phi _{1x}-2a_1(t)q_{Ix}\phi _{1x}\nonumber \\&\quad +\,a_1(t)q_{Rxx}+i a_1(t)q_{Ixx}+b_1(t)P^2_{\bar{l}} q_R+i b_1(t)P^2_{\bar{l}} q_I=0, \end{aligned}$$

(11)

$$\begin{aligned}&-\,r_R\phi _{2t}-i r_{I}\phi _{2t}+i r_{Rt}-r_{It}-a_2(t)r_R\phi ^2_{2x}-ia_2(t) r_I\phi ^2_{2x}\nonumber \\&\quad +\,i a_2(t)r_R\phi _{2xx}-a_2(t)r_I\phi _{2xx}+2i a_2(t) r_{Rx}\phi _{2x}-2a_2(t)r_{Ix}\phi _{2x}\nonumber \\&\quad +\,a_2(t)r_{Rxx}+i a_2(t)r_{Ixx}+b_2(t)P^2_{l} r_R+i b_2(t)P^2_{l} r_I=0. \end{aligned}$$

(12)

The following set of equations can be obtained. The real parts take the form.

$$\begin{aligned}&-\,q_R\phi _{1t}-q_{It}-a_1(t)q_R\phi ^2_{1x}-a_1(t)q_I\phi _{1xx}\nonumber \\&\quad -\,2a_1(t)q_{Ix}\phi _{1x}+a_1(t)q_{Rxx}+b_1(t)P^2_{\bar{l}} q_R=0, \end{aligned}$$

(13)

$$\begin{aligned}&-\,r_R\phi _{2t}-r_{It}-a_2(t)r_R\phi ^2_{2x}-a_2(t)r_I\phi _{2xx}\nonumber \\&\quad -\,2a_2(t)r_{Ix}\phi _{2x}+a_2(t)r_{Rxx}+b_2(t)P^2_{l} r_R=0, \end{aligned}$$

(14)

and imaginary parts are

$$\begin{aligned}&-\, q_{I}\phi _{1t}+ q_{Rt}-a_1(t)q_I\phi ^2_{1x}+a_1(t)q_R\phi _{1xx}\nonumber \\&+\,2a_1(t) q_{Rx}\phi _{1x}+a_1(t)q_{Ixx}+b_1(t)P^2_{\bar{l}} q_I=0, \end{aligned}$$

(15)

$$\begin{aligned}&-\, r_{I}\phi _{2t}+ r_{Rt}-a_2(t)r_I\phi ^2_{2x}+a_2(t)r_R\phi _{2xx}\nonumber \\&+\,2a_2(t) r_{Rx}\phi _{2x}+a_2(t)r_{Ixx}+b_2(t)P^2_{l} r_I=0. \end{aligned}$$

(16)

For the real functions $q_R(x,t), q_I(x,t),r_R(x,t),r_I(x,t)$, $\phi _1 (x,t)$ and $\phi _2 (x,t)$, introducing the new variables $\eta (x,t)$ and $\tau (t)$ and further utilizing the similarity transformations, we have the following transformation

$$\begin{aligned} q_{R}&= {} A(t)+B(t)P(\eta (x,t),\tau (t)), \end{aligned}$$

(17)

$$\begin{aligned} q_{I}&= C(t)Q(\eta (x,t),\tau (t)),\end{aligned}$$

(18)

$$\begin{aligned} \phi _1&= \zeta _1(x,t)+\lambda _1~\tau (t),\end{aligned}$$

(19)

$$\begin{aligned} r_{R}&= G(t)+H(t)M(\eta (x,t),\tau (t)),\end{aligned}$$

(20)

$$\begin{aligned} r_{I}&= N(t)S(\eta (x,t),\tau (t)),\end{aligned}$$

(21)

$$\begin{aligned} \phi _2&= \zeta _2(x,t)+\lambda _2~\tau (t), \end{aligned}$$

(22)

The derivation of similarity transformation are:

$$\begin{aligned} q_{Rt}&= A_t+B_tP+BP_\eta \eta _t+BP_\tau \tau _t, \end{aligned}$$

(23)

$$\begin{aligned} q_{Rx}&= BP_\eta \eta _x,\end{aligned}$$

(24)

$$\begin{aligned} q_{Rxx}&= BP_{\eta \eta }\eta ^2_x+BP_\eta \eta _{xx},\end{aligned}$$

(25)

$$\begin{aligned} q_{It}&= C_tQ+CQ_\eta \eta _t+CQ_\tau \tau _t,\end{aligned}$$

(26)

$$\begin{aligned} q_{Ix}&= CQ_\eta \eta _x,\end{aligned}$$

(27)

$$\begin{aligned} q_{Ixx}&= CQ_{\eta \eta }\eta ^2_x+CQ_\eta \eta _{xx},\end{aligned}$$

(28)

$$\begin{aligned} \phi _{1t}&= \zeta _{1t}+\lambda _1~\tau _t,\end{aligned}$$

(29)

$$\begin{aligned} \phi _{1x}&= \zeta _{1x},\end{aligned}$$

(30)

$$\begin{aligned} \phi _{1xx}&= \zeta _{1xx},\end{aligned}$$

(31)

$$\begin{aligned} r_{Rt}&= G_t+H_tM+HM_\eta \eta _t+HM_\tau \tau _t,\end{aligned}$$

(32)

$$\begin{aligned} r_{Rx}&= HM_\eta \eta _x,\end{aligned}$$

(33)

$$\begin{aligned} r_{Rxx}&= HM_{\eta \eta }\eta ^2_x+HM_\eta \eta _{xx},\end{aligned}$$

(34)

$$\begin{aligned} r_{It}&= N_tS+NS_\eta \eta _t+NS_\tau \tau _t,\end{aligned}$$

(35)

$$\begin{aligned} r_{Ix}&= NS_\eta \eta _x,\end{aligned}$$

(36)

$$\begin{aligned} r_{Ixx}&= NS_{\eta \eta }\eta ^2_x+NS_\eta \eta _{xx},\end{aligned}$$

(37)

$$\begin{aligned} \phi _{2t}&= \zeta _{2t}+\lambda _2~\tau _t,\end{aligned}$$

(38)

$$\begin{aligned} \phi _{2x}&= \zeta _{2x},\end{aligned}$$

(39)

$$\begin{aligned} \phi _{2xx}&= \zeta _{2xx}. \end{aligned}$$

(40)

where $\lambda _1$ and $\lambda _2$ are constants. Substituting the Eqs. (17)–(40) into Eqs. (13)–(16), we obtain the following set of equations.

$$\begin{aligned}&-\,(A+BP)(\zeta _{1t}+\lambda _{1}\tau _t)-(C_tQ+CQ_\eta \eta _t+CQ_\tau \tau _t)\nonumber \\&\quad -\,a_1(t)(A+BP)\zeta ^2_{1x}-a_1(t)CQ\zeta _{1xx}-2a_1(t)(CQ_\eta \eta _x)\zeta _{1x}\nonumber \\&\quad +\,a_1(t)BP_{\eta \eta }\eta ^2_{x}+a_1(t)BP_\eta \eta _{xx}+b_1(t)P^2_{\bar{l}}(A+BP)=0, \end{aligned}$$

(41)

$$\begin{aligned}&-\,CQ(\zeta _{1t}+\lambda _{1}\tau _t)+A_t+B_tP+BP_\eta \eta _t+BP_\tau \tau _t\nonumber \\&\quad -\,a_1(t)CQ\zeta ^2_{1x}+a_1(t)(A+BP)\zeta _{1xx}+2a_1(t)BP_\eta \eta _x\zeta _{1x}\nonumber \\&\quad +\,a_1(t)CQ_{\eta \eta }\eta ^2_x+a_1(t)CQ_\eta \eta _{xx}+b_1(t)P^2_{\bar{l}}CQ=0, \end{aligned}$$

(42)

$$\begin{aligned}&-\,(G+HM)(\zeta _{2t}+\lambda _2\tau _t)-(N_tS+NS_\eta \eta _t+NS_\tau \tau _t)\nonumber \\&\quad -\,a_2(t)(G+HM)\zeta ^2_{2x}-a_2(t)NS\zeta _{2xx}-2a_2(t)(NS_\eta \eta _x)\zeta _{2x}\nonumber \\&\quad +\,a_2(t)HM_{\eta \eta }\eta ^2_x+a_2(t)HM_\eta \eta _{xx}+b_2(t)P^2_{l}(G+HM)=0, \end{aligned}$$

(43)

$$\begin{aligned}&-\,NS(\zeta _{2t}+\lambda _{2}\tau _t)+G_t+H_tM+HM_\eta \eta _t+HM_\tau \tau _t\nonumber \\&\quad -\,a_2(t)NS\zeta ^2_{2x}+a_2(t)(G+HM)\zeta _{2xx}+2a_2(t)HM_\eta \eta _x\zeta _{2x}\nonumber \\&\quad +\,a_2(t)NS_{\eta \eta }\eta ^2_x+a_2(t)NS_\eta \eta _{xx}+b_2(t)P^2_{l}NS=0. \end{aligned}$$

(44)

The following similarity reduction can be obtained, after the simplification of above equations.

$$\begin{aligned}&\eta _{xx}=0,\end{aligned}$$

(45)

$$\begin{aligned}&\eta _t+2a_1(t)\eta _x\zeta _{1x}=0,\end{aligned}$$

(46)

$$\begin{aligned}&\sigma _t+a_1(t)\sigma \zeta _{1xx}=0~~,~~(\sigma =A,B,C),\end{aligned}$$

(47)

$$\begin{aligned}&\zeta _{1t}+a_1(t)\zeta ^2_{1x}-b_1(t)P_{\bar{l}}^2=0,\end{aligned}$$

(48)

$$\begin{aligned}&-\,(A+BP)\lambda _1\tau _t-CQ_\tau \tau _t+a_1(t)BP_{\eta \eta }\eta ^2_x=0,\end{aligned}$$

(49)

$$\begin{aligned}&-\,CQ\lambda _1\tau _t+BP_\tau \tau _t+a_1(t)CQ_{\eta \eta }\eta ^2_x=0,\end{aligned}$$

(50)

$$\begin{aligned}&\eta _t+2a_2(t)\eta _x\zeta _{2x}=0,\end{aligned}$$

(51)

$$\begin{aligned}&\varrho _t+a_2(t)\varrho \zeta _{2xx}=0~~,~~(\varrho =G,H,N),\end{aligned}$$

(52)

$$\begin{aligned}&\zeta _{2t}+a_2(t)\zeta ^2_{2x}-b_2(t)P_{l}^2=0,\end{aligned}$$

(53)

$$\begin{aligned}&-\,(G+HM)\lambda _2\tau _t-NS_\tau \tau _t+a_2(t)HM_{\eta \eta }\eta ^2_x=0,\end{aligned}$$

(54)

$$\begin{aligned}&-\,NS\lambda _2\tau _t+HM_\tau \tau _t+a_2(t)NS_{\eta \eta }\eta ^2_x=0, \end{aligned}$$

(55)

where $\eta (x,t), \zeta _{1}(x,t),$ $\zeta _{2}(x,t),$ A(t), B(t),  C(t),  G(t),  H(t),  $P(\eta ,\tau ),$ N(t),  $M(\eta ,\tau ),$ $S(\eta ,\tau )$ and $Q(\eta ,\tau )$ are unknown functions which will be determined later. It may also be noted that $b_l(t)P^2_{\bar{l}}\ne 0$, because $b_l(t)$ is the coupling co-efficient. If it is zero, then there will be no coupling exist. So, it does not hold. After performing some algebra computation, it is followed from the above equations.

$$\begin{aligned}&\eta =\alpha (t)x+\beta (t),\end{aligned}$$

(56)

$$\begin{aligned}&\zeta _{1(x,t)}=-\,\frac{\alpha _tx^2}{4a_1(t)\alpha (t)}-\frac{\beta _tx}{2a_1(t)\alpha (t)}-\zeta _0(t),\end{aligned}$$

(57)

$$\begin{aligned}&\zeta _{2(x,t)}=-\,\frac{\alpha _tx^2}{4a_2(t)\alpha (t)}-\frac{\beta _tx}{2a_2(t)\alpha (t)}-\zeta _0(t),\end{aligned}$$

(58)

$$\begin{aligned}&A(t)=a_0\sqrt{|\alpha |},~B(t)=bA,~C(t)=dA,\end{aligned}$$

(59)

$$\begin{aligned}&G(t)=b_0\sqrt{|\alpha |},~H(t)=bG,~N(t)=dG, \end{aligned}$$

(60)

where $a_0,b_0,b$ and d are constants, $\alpha (t)$ is the inverse of the wave width, and $-\beta (t)/\alpha (t)$ is the position of its center of mass. The $\alpha (t),\beta (t)$ and $\zeta _l(t)$ for $l=1,2$ are all free functions with respect to time t. The Eqs. (49), (50), (54), (55) have further reduced to the following equations.

$$\begin{aligned}&\tau (t)=\frac{1}{2}\int ^t_0\alpha ^2(s)ds,\alpha ^2=2A^2 ~~or~~ \alpha ^2=2G^2, \end{aligned}$$

(61)

$$\begin{aligned}&(1+bP)\lambda _1+dq_\tau +bP_{\eta \eta }=0,\end{aligned}$$

(62)

$$\begin{aligned}&dQ\lambda _{1}-bP_\tau -2dQ_{\eta \eta }=0,\end{aligned}$$

(63)

$$\begin{aligned}&(1+bM)\lambda _{2}+dr_{\tau }+bM_{\eta \eta }=0,\end{aligned}$$

(64)

$$\begin{aligned}&dS\lambda _2-bP_\tau -2dM_{\eta \eta }=0. \end{aligned}$$

(65)

Using the method given in Akhmediev et al. (2009), Peregrine (1983), we obtain the rational solutions of first-order:

$$\begin{aligned}&P(\eta ,\tau )=-\,\frac{4}{R_1(\eta ,\tau )b}~,~Q(\eta ,\tau )=-\,\frac{8\tau }{R_1(\eta ,\tau )d},\end{aligned}$$

(66)

$$\begin{aligned}&M(\eta ,\tau )=-\,\frac{4}{R_1(\eta ,\tau )b}~,~S(\eta ,\tau )=-\,\frac{8\tau }{R_1(\eta ,\tau )d}. \end{aligned}$$

(67)

where $R_1=1+2\eta ^2+4\tau ^2$.

Now the solutions of second order take the forms:

$$\begin{aligned}&P(\eta ,\tau )=\frac{P_1(\eta ,\tau )}{R_2(\eta ,\tau )b}~,~Q(\eta ,\tau )=\frac{Q_1(\eta ,\tau )\tau }{R_2(\eta ,\tau )d},\end{aligned}$$

(68)

$$\begin{aligned}&P_1(\eta ,\tau )=\frac{3}{8}-9\tau ^2-\frac{3\eta ^2}{2}-6\eta ^2\tau ^2-10\tau ^4-\frac{\eta ^4}{2},\end{aligned}$$

(69)

$$\begin{aligned}&Q_1(\eta ,\tau )=-\,\frac{15}{4}+2\tau ^2-3\eta ^2+4\eta ^2\tau ^2+4\tau ^4+\eta ^4,\end{aligned}$$

(70)

$$\begin{aligned}&M(\eta ,\tau )=\frac{M_1(\eta ,\tau )}{R_2(\eta ,\tau )b}~,~S(\eta ,\tau )=\frac{S_1(\eta ,\tau )\tau }{R_2(\eta ,\tau )d},\end{aligned}$$

(71)

$$\begin{aligned}&M_1(\eta ,\tau )=\frac{3}{8}-9\tau ^2-\frac{3\eta ^2}{2}-6\eta ^2\tau ^2-10\tau ^4-\frac{\eta ^4}{2},\end{aligned}$$

(72)

$$\begin{aligned}&S_1(\eta ,\tau )=-\,\frac{15}{4}+2\tau ^2-3\eta ^2+4\eta ^2\tau ^2+4\tau ^4+\eta ^4,\end{aligned}$$

(73)

$$\begin{aligned}&R_2(\eta ,\tau )=\frac{3}{32}+\frac{33}{8}\tau ^2+9\frac{9\eta ^2}{16}-\frac{3\eta ^2\tau ^2}{2}+\frac{9\tau ^4}{2}+\frac{\eta ^4}{8}\nonumber \\&\quad \frac{2\eta ^6}{3}\eta ^2\tau ^6+\eta ^2\tau ^6+\frac{\eta ^4\tau ^2}{2}+\frac{\eta ^6}{12}. \end{aligned}$$

(74)

Thus, the following solutions can be obtained:

$$\begin{aligned}&q=A(1+bP+i dQ)e^{i(\zeta _1+\tau )}, \end{aligned}$$

(75)

and

$$\begin{aligned}&\nonumber \\&r=G(1+bM+i dS)e^{i(\zeta _2+\tau )}, \end{aligned}$$

(76)

where $\zeta _1(x,t),\zeta _2(x,t),A(t),G(t),\tau (t),P(\eta ,\tau ),Q(\eta ,\tau ),M(\eta ,\tau ),S(\eta ,\tau )$ are expressed by the Eqs. (57)–(61), (66)–(68) and (71), respectively. In the following section, the rogue wave solutions are constructed.

3 Rogue wave solutions

For the first-order solution, we focus to construct the rogue wave structures to NLSEs with time-dependent coefficients. After substituting the Eq. (66) into Eq. (75) and also Eq. (67) into Eq. (76), we have the following first-order rational-like solution to the Eqs. (2) and (3):

$$\begin{aligned}&q= a_0\sqrt{|\alpha |}\bigg (1-\frac{4+8i \tau }{1+2\eta ^2+4\tau ^2}\bigg )e^{i(\zeta _1,\tau )} \end{aligned}$$

(77)

and

$$\begin{aligned}&\nonumber \\&r= b_0\sqrt{|\alpha |}\bigg (1-\frac{4+8i \tau }{1+2\eta ^2+4\tau ^2}\bigg )e^{i(\zeta _2,\tau )}, \end{aligned}$$

(78)

whose amplitudes are given by

$$\begin{aligned}&|q|^2= a^2_0{|\alpha |}\frac{[2(\alpha (t)x+\beta (t))^2+4\tau ^2-3]^2+64\tau ^2(t)}{[1+2(\alpha (t)x+\beta (t))^2+4\tau ^2(t)]^2} \end{aligned}$$

(79)

and

$$\begin{aligned}&\nonumber \\&|r|^2= b^2_0{|\alpha |}\frac{[2(\alpha (t)x+\beta (t))^2+4\tau ^2-3]^2+64\tau ^2(t)}{[1+2(\alpha (t)x+\beta (t))^2+4\tau ^2(t)]^2}, \end{aligned}$$

(80)

respectively. Let us choose the function $\alpha (t)=b+l \cos (\omega t)$ to exhibit the nonlinear dynamical behavior of the rogue waves which change the gravity field $b=\delta mg$ (where $\delta$ is a constant) and the time-dependent external magnetic field $l\cos (\omega t)$.

Two cases are under consideration for the nonlinear dynamical behavior of the rogue waves in the presence of gravity field (when $l=0$ and $l\ne 0).$

The nonlinear dynamical behavior of the rogue waves is studied when there is only the gravity field; namely, $l=0.$ The value of $\alpha (t)=b$ only, then amplitudes corresponding to the above solutions are given by

$$\begin{aligned}&|q|^2= a^2_0{b^2}\frac{[4(bx+\beta (t))^2+4\tau ^2-3]^2+64\tau ^2(t)}{[1+4(bx+\beta (t))^2+4\tau ^2(t)]^2}\end{aligned}$$

(81)

and

$$\begin{aligned}&\nonumber \\&|r|^2= b^2_0{b^2}\frac{[4(bx+\beta (t))^2+4\tau ^2-3]^2+64\tau ^2(t)}{[1+4(bx+\beta (t))^2+4\tau ^2(t)]^2}. \end{aligned}$$

(82)

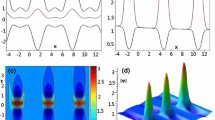
The Figs. 1, 2, and 3 have depicted for the amplitude given in Eqs. (63) and (64) at $a_0=b_0=1$ along with different values of b and $\beta .$ It can be noted that the amplitude is maximum at $b=0.61$ and $\beta =0.5$. Its graphical representation is given in Fig. 2.

The nonlinear dynamical behaviour of the rouge waves is also studied, when there exists the gravity field and the external magnetic field $l\ne 0.$ We suppose $\alpha (t)=0.86 + 1.2\cos (0.1t)$ and $\beta (t)=0.35t^2,$ then the nonlinear dynamic behaviour of the rational solution is shown in the Fig. 4.

Fig. 1

The 3D graph and contour plot of the first order rogue wave propagation for the intensity $|q|^2=|r|^2$ with $\beta =0.5$ and the gravity field $b=0.5$

Fig. 2

The 3D graph and contour plot of the first order rogue wave propagation for the intensity $|q|^2=|r|^2$ with $\beta =0.5$ and the gravity field $b=0.61$

Fig. 3

The 3D graph and contour plot of the first order rogue wave propagation for the intensity $|q|^2=|r|^2$ with $\beta =0.5$ and the gravity field $b=0.3$

Fig. 4

The 3D graph and contour plot of the first order rogue wave propagation for the intensity $|q|^2=|r|^2$ with $\alpha (t)=0.86 + 1.2\cos (0.1t)$ and $\beta (t)=0.35t^2$

For the second-order solution, we focus to construct the rogue wave structures to NLSEs with time-dependent coefficients. After substituting the Eq. (68) into Eq. (75) and Eq. (71) into Eq. (76), we obtain the rational-like solution to Eqs. (2) and (3).

$$\begin{aligned}&q= a_0\sqrt{|\alpha |}\bigg (1+\frac{P_1}{R_2}+i\frac{Q_1\tau }{R_2}\bigg )e^{i(\zeta _1+\tau )} \end{aligned}$$

(83)

and

$$\begin{aligned}&\nonumber \\&r= b_0\sqrt{|\alpha |}\bigg (1+\frac{M_1}{R_2}+i\frac{S_1\tau }{R_2}\bigg )e^{i(\zeta _2+\tau )}, \end{aligned}$$

(84)

whose intensities are given by

$$\begin{aligned}&|q|^2= a^2_0|\alpha |\bigg (\bigg (1+\frac{P_1}{R_2}\bigg )^2+\bigg (\frac{Q_1\tau }{R_2}\bigg )^2\bigg ) \end{aligned}$$

(85)

and

$$\begin{aligned}&\nonumber \\&|r|^2= b^2_0|\alpha |\bigg (\bigg (1+\frac{M_1}{R_2}\bigg )^2+\bigg (\frac{S_1\tau }{R_2}\bigg )^2\bigg ), \end{aligned}$$

(86)

respectively. Where $P_1(\eta ,\tau ), Q_1(\eta ,\tau ),$ $M_1(\eta ,\tau ),$ $S_1(\eta ,\tau )$ and $R_2(\eta ,\tau )$ are expressed by the Eqs. (69)–(70) and (72)–(74), respectively.

It is also noted that the effect of the gravity field on the second order rogue wave is similar to the first order rogue wave. We suppose that $b=0.5$ and $\beta =0.2,$ then nonlinear dynamical behaviour of the second order rogue wave depicted in the Fig. 5. We compare it with the first order rogue wave solution, it is found that there are six small peaks around the one high peak in the second order rogue waves and maximum energy of the wave is focus on the high peak and amplitude of the second order rational like solution is larger than the first order solution.

If $\alpha =0.5$ and $\beta (t)=0.5\exp (\frac{1}{\cosh (0.2t^3)}),$ then the second order rogue wave pattern shown in the Fig. 6. Suppose that $\alpha =0.5$ and $\beta (t)=0.5\exp (\frac{1}{\cosh (0.2t^2)}),$ then the second order rogue wave pattern has shown in the Fig. 7. Suppose that $\alpha =0.5$ and $\beta (t)=0.5\exp (\frac{1}{\cosh (0.2t)}),$ then the second order rogue wave pattern has shown in the Fig. 8.

We also study the behaviour of the second order rogue waves when the gravity field and magnetic field exist. Suppose that $\alpha = 0.5 + 1.2\cos (8t)$ and $\beta (t)=0.2t,$ then the wave pattern has shown in the Fig. 9.

Fig. 5

The 3D graph and contour plot of the second order rogue wave propagation for the intensity $|q|^2=|r|^2$ with $b=0.5$ and $\beta =0.2.$

Fig. 6

The 3D graph and contour plot of the second order rogue wave propagation for the intensity $|q|^2=|r|^2$ with $\alpha =0.5$ and $\beta (t)=0.5\exp (\frac{1}{\cosh (0.2t^3)})$

Fig. 7

The 3D graph and contour plot of the second order rogue wave propagation for the intensity $|q|^2=|r|^2$ with $\alpha =0.5$ and $\beta (t)=0.5\exp (\frac{1}{\cosh (0.2t)})$

Fig. 8

The 3D graph and contour plot of the second order rogue wave propagation for the intensity $|q|^2=|r|^2$ with $\alpha = 0.5$ and $\beta (t)=0.5\exp \frac{1}{\cosh (0.2t)}$

Fig. 9

The 3D graph and contour plot of the second order rogue wave propagation for the intensity $|q|^2=|r|^2$ with $\alpha (t)=0.5 + 1.2\cos (8t)$ and $\beta (t)=0.2t$

4 Conclusion

In this article, we constructed the two forms of rogue wave solutions in a selected case of coupled NLSEs with variable coefficients. This coupled system is considered with GVD and XPM that describes the dynamics of waves in nonlinear optics and quantum physics. The similarity transformation is used to construct the explicit rogue wave solutions (rational-like solutions) of first and second order. It is also noted that the 3D graphical representations and corresponding contour plots have depicted with different values of gravity field and external magnetic field.