Comment on “Exponential ultimate boundedness of fractional-order differential system via periodically intermittent control” [Nonlinear Dyn 2019;92(2), 247–265]

Abstract

In this note, some points to paper (Xu L.G., Liu W.,” Hu ”H.X.:“Exponential ultimate boundedness of fractional-order differential system via periodically intermittent control” [Nonlinear Dyn 2019;92(2), 247–265) are presented. Fractional calculus is of memory property which is different from integral calculus. But this important property is neglected in the proof processes of the main theoretical achievements. We analyze these errors in Laplace domain and time domain. Lastly, some counterexamples are presented against the intermittent stability conditions in Xu et al. (Nonlinear Dyn 92(2):247–265, 2019. https://doi.org/10.1007/s11071-019-04877-y).

1 Introduction

In [1], exponential ultimate boundedness of fractional-order differential system is investigated via periodically intermittent control. But fractional calculus possesses the property of non-locality, memory and history-dependent, and initial value is an important parameter of fractional calculus [2]. This important property is neglected in the proof processes of the theoretical achievements. It is very necessary to point out these problems to avoid misleading.

Firstly, let us review some Lemmas in [1].

Caputo fractional derivative is defined as:

$$\begin{aligned} \begin{aligned} ^{C}_{t_{0}}D_{t}^{q}y(t)&=\frac{1}{\varGamma (n-q)}\\&\quad \int _{t_{0}}^t\frac{y^{(n)}(\eta )}{(t-\eta )^{q+1-n}}d\eta , \qquad n-1<q<n \end{aligned} \end{aligned}$$

(1)

where symbol C denotes the Caputo fractional derivative, $t_{0}$ denotes the beginning time of fractional derivative.

Remark 1

Formula (1) reflects fractional derivative with $q-$ order from time $t_{0}$ to t about variable time t. Obviously, the calculating results of the fractional derivative is relevant with initial time $t_{0}$.

Lemma 4 in Section 3 of [1] is depicted as:

Let $0< q < 1$, h(t) is a continuous function on $[t_{0},+\infty )$, If there exist constants $k_{1} \in R$and $k_{2} >0$such that

$$\begin{aligned} \begin{aligned} _{t_{0}}^CD^q_t h(t)&\le k_{1} h(t)+k_{2}\\ h(t_{0})&=h_{t_{0}} \end{aligned} \end{aligned}$$

(2)

Then

$$\begin{aligned} \begin{aligned} h(t)&\le h_{t_{0}}E_{q}(k_{1}(t-t_{0})^{q})\\&\quad +k_{2}(t-t_{0})^{q}E_{q,q+1}(k_{1}(t-t_{0})^{q})\\ t&\ge {t_{0}} \end{aligned} \end{aligned}$$

(3)

Remark 2

It cannot be neglected that $t_{0}$ in (2) must be equal to $t_{0}$ in (3) according to the proof process of Lemma 4 in [1]. But the authors neglect this condition in the proof process of Theorem 1 in [1].

2 Theorem analysis

From function (20) and function (21) in [1], we can get

$$\begin{aligned} _{t_{0}}^CD^q_t V\le -\alpha _{1}V+\zeta _{2}^{-1}J^{T}J \end{aligned}$$

(4)

when $t\in [nT, nT+\tau )$, and

$$\begin{aligned} \begin{aligned} _{t_{0}}^CD^q_t V\le \beta _{1}V+\zeta _{2}^{-1}J^{T}J \end{aligned} \end{aligned}$$

(5)

when $t\in [nT+\tau , (n+1)T)$.

Then, the authors claim that step (1), (2), (3), (4), (5) and (6) of Theorem 1 can be drawn according to Lemma 4 in [1]. Let us analyze the proof process and the conclusion in Laplace domain and time domain, respectively.

2.1 Laplace domain analysis

From function (24) in [1], we can see $t_{0}=0$. Then, let us analyze the proof processes step by step according to Laplace transform and inverse Laplace transform.

(1) When $t\in [0, \tau )$,

$$\begin{aligned} \begin{aligned} _{0}^CD^q_t V\le -\alpha _{1}V+\zeta _{2}^{-1}J^{T}J. \end{aligned} \end{aligned}$$

(6)

There exists a nonnegative function $\xi _{1}(t)$ satisfying

$$\begin{aligned} \begin{aligned}&_{0}^CD^q_t V+\xi _{1}(t)= -\alpha _{1}V+\zeta _{2}^{-1}J^{T}J\\ \end{aligned} \end{aligned}$$

(7)

Making the Laplace transform,

$$\begin{aligned} \begin{aligned} s^{q} V(s)-s^{q-1} V(0)+\xi _{1}(s)=-\alpha _{1}V(s)+\frac{\zeta _{2}^{-1}J^{T}J}{s} \end{aligned} \end{aligned}$$

(8)

By the inverse Laplace transform, we can get

$$\begin{aligned} \begin{aligned} V(\tau )\le V(0)E_{q}(-\alpha _{1}t^{q})+\zeta _{2}^{-1}J^{T}Jt^{q}E_{q,q+1}(-\alpha _{1}t^{q}) \end{aligned} \end{aligned}$$

(9)

(2) When $t\in [\tau , T)$,

$$\begin{aligned} \begin{aligned} _{0}^CD^q_t V\le \beta _{1}V+\zeta _{2}^{-1}J^{T}J. \end{aligned} \end{aligned}$$

(10)

There also exists nonnegative functions $\xi _{2}(t)$ satisfying

$$\begin{aligned} \begin{aligned}&_{0}^CD^q_t V+\xi _{2}(t)= \beta _{1}V+\zeta _{2}^{-1}J^{T}J.\\ \end{aligned} \end{aligned}$$

(11)

According to function (7) and (11), we have

$$\begin{aligned} \left\{ \begin{array}{l} _{0}^CD^q_t V(t)=-\alpha _{1}V(t)-\xi _{1}(t)+\zeta _{2}^{-1}J^{T}J,\qquad t\in [0, \tau )\\ _{0}^CD^q_t V(t)=\beta _{1}V(t)-\xi _{2}(t)+\zeta _{2}^{-1}J^{T}J, \qquad t\in [\tau , T)\\ \end{array}\right. \end{aligned}$$

(12)

Define u(t) as

$$\begin{aligned} u(t)=\left\{ \begin{array}{l} 0,\qquad t<0\\ 1,\qquad t\ge 0\\ \end{array}\right. \end{aligned}$$

(13)

and function (12) can be expressed as

$$\begin{aligned} \begin{aligned} _{0}^CD^q_t V(t)&=(-\alpha _{1}V(t)-\xi _{1}(t)\\&\quad +\zeta _{2}^{-1}J^{T}J)(u(t)-u(t-\tau ))\\&\quad +(\beta _{1}V(t)-\xi _{2}(t)\\&\quad +\zeta _{2}^{-1}J^{T}J)u(t-\tau ) \end{aligned} \end{aligned}$$

(14)

Making the Laplace transform ,

$$\begin{aligned} \begin{aligned}&s^{q} V(s)-s^{q-1} V(0)=\pounds [(-\alpha _{1}V(t)-\xi _{1}(t)\\&\quad +\zeta _{2}^{-1}J^{T}J)(u(t)-u(t-\tau ))]\\&\quad +\pounds [(\beta _{1}V(t)-\xi _{2}(t)+\zeta _{2}^{-1}J^{T}J)u(t-\tau )]\\ \end{aligned} \end{aligned}$$

(15)

Obviously, the conclusion $V(t)\le V(\tau )E_{q}(\beta _{1}(t-\tau )^{q})+\zeta _{2}^{-1}J^{T}J(t-\tau )^{q}E_{q,q+1}(\beta _{1}(t-\tau )^{q})$ (formula (26) in [1]) cannot be drawn from formula (15) when $t\in [\tau , T)$.

Similarly, the conclusions in step (3), (4), (5) and (6) of Theorem 1 cannot also be directly drawn from Lemma 4 in [1].

We can also further analyze the incorrectness of the proof process of Theorem 1 in [1] in time domain.

2.2 Time-domain analysis

According to (20) and (21) in [1], we can get

$$\begin{aligned} \begin{aligned} _{t_{0}}^CD^q_t V(t)&\le \sum _{j=0}^{n}(-\alpha _{1}V(t)\\&\quad +\zeta _{2}^{-1}J^{T}J)(u(t-jT)\\&\quad -u(t-jT-\tau ))\\&\quad +\sum _{j=0}^{n}(\beta _{1}V(t)\\&\quad +\zeta _{2}^{-1}J^{T}J)(u(t-jT-\tau )\\&\quad -u(t-(j+1)T)). \end{aligned} \end{aligned}$$

(16)

There must exist nonnegative functions $\xi _{j1}(t)$ and $\xi _{j2}(t)$ ($j=0,1,2,\cdots ,n$) satisfying

$$\begin{aligned} \begin{aligned}&_{t_{0}}^CD^q_t V(t)=\sum _{j=0}^{n}(-\alpha _{1}V-\xi _{j1}(t)\\&\quad +\zeta _{2}^{-1}J^{T}J)(u(t-jT)-u(t-jT-\tau ))\\&\quad +\sum _{j=0}^{n}(\beta _{1}V(t)-\xi _{j2}(t)\\&\quad +\zeta _{2}^{-1}J^{T}J)(u(t-jT-\tau )-u(t-(j+1)T)). \end{aligned} \end{aligned}$$

(17)

(1) when $t\in [0, \tau )$, it gets:

$$\begin{aligned} \begin{aligned}&_{0}^CD^q_t V(t)=(-\alpha _{1}V(t)-\xi _{01}(t)+\zeta _{2}^{-1}J^{T}J) \end{aligned} \end{aligned}$$

(18)

According to Lemma 4 in [1], it yields

$$\begin{aligned} \begin{aligned} V(t)\le V(0)E_{q}(-\alpha _{1}t^{q})+\zeta _{2}^{-1}J^{T}Jt^{q}E_{q,q+1}(-\alpha _{1}t^{q}) \end{aligned} \end{aligned}$$

(19)

Especially,

$$\begin{aligned} \begin{aligned} V(\tau )\le V(0)E_{q}(-\alpha _{1}\tau ^{q})+\zeta _{2}^{-1}J^{T}J\tau ^{q}E_{q,q+1}(-\alpha _{1}\tau ^{q}) \end{aligned} \end{aligned}$$

(20)

(2) when $t\in [\tau , T)$, we can get

$$\begin{aligned} \begin{aligned}&_{0}^CD^q_t V(t)=(-\alpha _{1}V(t)-\xi _{01}(t)\\&\quad +\zeta _{2}^{-1}J^{T}J)(u(t)-u(t-\tau ))\\&\quad +(\beta _{1}V(t)-\xi _{02}(t)+\zeta _{2}^{-1}J^{T}J)u(t-\tau ) \end{aligned} \end{aligned}$$

(21)

According to fractional integral, we get

$$\begin{aligned} \begin{aligned} V(t)&=V(0)+\frac{1}{\varGamma (q)}\times \int _{0}^t(t-\eta )^{q-1}(_{0}^CD^q_\eta V(\eta ))d\eta \\&=V(0)+\frac{1}{\varGamma (q)}t^{q-1}*(_{0}^CD^q_t V(t))\\&=V(0)+\frac{1}{\varGamma (q)}t^{q-1}*(-\alpha _{1}V(t)-\xi _{01}(t)\\&\quad +\zeta _{2}^{-1}J^{T}J)(u(t)-u(t-\tau ))\\&\quad +\frac{1}{\varGamma (q)}t^{q-1}*(\beta _{1}V(t)-\xi _{02}(t)\\&\quad +\zeta _{2}^{-1}J^{T}J)u(t-\tau ) \end{aligned} \end{aligned}$$

(22)

where symbol $*$ represents convolution operation.

Define $V(\tau )$ as

$$\begin{aligned} \begin{aligned} V(\tau )&=V(0)+\frac{1}{\varGamma (q)}\\&\quad \times \int _{0}^\tau (\tau -\eta )^{q-1}(-\alpha _{1}V(\eta )-\xi _{01}(\eta )\\&\quad +\zeta _{2}^{-1}J^{T}J)d\eta \end{aligned} \end{aligned}$$

(23)

Although the length of the signal $(-\alpha _{1}V(t)-\xi _{01}(t)+\zeta _{2}^{-1}J^{T}J)(u(t)-u(t-\tau ))$ is $\tau$, the length of $t^{q-1}*(-\alpha _{1}V-\xi _{01}(t)+\zeta _{2}^{-1}J^{T}J)(u(t)-u(t-\tau ))$ is infinite according to the rule of convolution operation.

Obviously,

$$\begin{aligned}&\frac{1}{\varGamma (q)}\times \int _{0}^t(t-\eta )^{q-1}(-\alpha _{1}V(\eta )-\xi _{01}(\eta )\nonumber \\&\qquad +\zeta _{2}^{-1}J^{T}J)(u(\eta )-u(\eta -\tau ))d\eta \nonumber \\&\quad \ne \frac{1}{\varGamma (q)}\times \int _{0}^\tau (\tau -\eta )^{q-1}(-\alpha _{1}V(\eta )\nonumber \\&\qquad -\xi _{01}(\eta )+\zeta _{2}^{-1}J^{T}J)d\eta =V(\tau ) \end{aligned}$$

(24)

when $t>\tau$.

Then, we can get

$$\begin{aligned} \begin{aligned} V(t)&= V(0)+ \frac{1}{\varGamma (q)}\times \int _{0}^t(t-\eta )^{q-1}(-\alpha _{1}V(\eta )\\&\quad -\xi _{01}(\eta )\\&\quad +\zeta _{2}^{-1}J^{T}J)(u(\eta )-u(\eta -\tau )d\eta \\&\quad +\frac{1}{\varGamma (q)}\times \int _{0}^t(t-\eta )^{q-1}(\beta _{1}V(\eta )-\xi _{02}(\eta )\\&\quad +\zeta _{2}^{-1}J^{T}J)u(\eta -\tau )d\eta \\&\ne V(0)+\frac{1}{\varGamma (q)}\times \int _{0}^\tau (\tau -\eta )^{q-1}(-\alpha _{1}V(\eta )\\&\quad -\xi _{01}(\eta )+\zeta _{2}^{-1}J^{T}J)(u(\eta )-u(\eta -\tau ))d\eta \\&\quad +\frac{1}{\varGamma (q)}\times \int _{0}^t(t-\eta )^{q-1}(\beta _{1}V-\xi _{02}(\eta )\\&\quad +\zeta _{2}^{-1}J^{T}J)u(\eta -\tau )d\eta \\ \end{aligned} \end{aligned}$$

(25)

It shows that V(t) is affected by the history process of before time $\tau$ when $t>\tau$.

That is to say

$$\begin{aligned} \begin{aligned} V(t)&\ne V(\tau )+\frac{1}{\varGamma (q)}\times \int _{0}^t(t-\eta )^{q-1}(\beta _{1}V(\eta )\\&\quad -\xi _{01}(\eta )+\zeta _{2}^{-1}J^{T}J)(u(\eta )-u(\eta -\tau ))d\eta \\ \end{aligned} \end{aligned}$$

(26)

Obviously, we cannot directly get the following conclusion

$$\begin{aligned} \begin{aligned}&V(t)\le V(\tau )E_{q}( \beta _{1}(t-\tau )^{q})\\&\quad +\zeta _{2}^{-1}J^{T}J(t-\tau )^{q}E_{q,q+1}(\beta _{1}(t-\tau )^{q}) \end{aligned} \end{aligned}$$

(27)

even though $\xi _{02}(t)\ge 0$.

(3) when $t\in [T, T+\tau )$, we have

$$\begin{aligned}&_{0}^CD^q_t V(t)=(-\alpha _{1}V(t)-\xi _{01}(t)\nonumber \\&\quad +\zeta _{2}^{-1}J^{T}J)(u(t)-u(t-\tau ))\nonumber \\&\quad +(\beta _{1}V(t)-\xi _{02}(t)\nonumber \\&\quad +\zeta _{2}^{-1}J^{T}J)(u(t-\tau )-u(t-T))\nonumber \\&\quad +(-\alpha _{1}V-\xi _{11}(t)+\zeta _{2}^{-1}J^{T}J)u(t-T) \end{aligned}$$

(28)

Take fractional integral and get

$$\begin{aligned} \begin{aligned} V(t)&=V(0)+\frac{1}{\varGamma (q)}\\&\quad \times \int _{0}^t(t-\eta )^{q-1}(_{0}^CD^q_\eta V(\eta ))d\eta \\&=V(0)+\frac{1}{\varGamma (q)}t^{q-1}*(_{0}^CD^q_t V(t))\\&\quad =V(0)+\frac{1}{\varGamma (q)}t^{q-1}*(-\alpha _{1}V(t)-\xi _{01}(t)\\&\quad +\zeta _{2}^{-1}J^{T}J)(u(t)-u(t-\tau ))\\&\quad +\frac{1}{\varGamma (q)}t^{q-1}*(\beta _{1}V(t)-\xi _{02}(t)\\&\quad +\zeta _{2}^{-1}J^{T}J)(u(t-\tau )-u(t-T))\\&\quad +\frac{1}{\varGamma (q)}t^{q-1}*(-\alpha _{1}V(t)\\&\quad -\xi _{11}(t)+\zeta _{2}^{-1}J^{T}J)u(t-T) \end{aligned} \end{aligned}$$

(29)

Similar to step (2), we have

$$\begin{aligned} \begin{aligned}&\frac{1}{\varGamma (q)}\times \int _{0}^t(t-\eta )^{q-1}(-\alpha _{1}V(\eta )\\&\qquad -\xi _{01}(\eta )+\zeta _{2}^{-1}J^{T}J)(u(\eta )-u(\eta -\tau ))d\eta \\&\quad \ne \frac{1}{\varGamma (q)}\times \int _{0}^T(T-\eta )^{q-1}(-\alpha _{1}V(\eta )\\&\qquad -\xi _{01}(\eta )+\zeta _{2}^{-1}J^{T}J)(u(\eta )-u(\eta -\tau ))d\eta \end{aligned} \end{aligned}$$

(30)

and

$$\begin{aligned} \begin{aligned}&\frac{1}{\varGamma (q)}\times \int _{0}^t(t-\eta )^{q-1}(\beta _{1}V(\eta )\\&\qquad -\xi _{02}(\eta )+\zeta _{2}^{-1}J^{T}J)(u(\eta -\tau )-u(\eta -T))d\eta \\&\quad \ne \frac{1}{\varGamma (q)} \times \int _{0}^T(T-\eta )^{q-1}(\beta _{1}V(\eta )\\&\qquad -\xi _{02}(\eta )+\zeta _{2}^{-1}J^{T}J)(u(\eta -\tau )-u(\eta -T))d\eta \end{aligned} \end{aligned}$$

(31)

when $t>T$.

Then, we can draw

$$\begin{aligned} \begin{aligned}&V(t)\ne V(T)+\frac{1}{\varGamma (q)}\times \int _{T}^t(t-\eta )^{q-1}(-\alpha _{1}V(\eta )\\&\quad -\xi _{11}(\eta )+\zeta _{2}^{-1}J^{T}J)u(\eta -T)d\eta \ \end{aligned} \end{aligned}$$

(32)

The following conclusion cannot also be directly drawn

$$\begin{aligned} \begin{aligned}&V(t)\le V(T)E_{q}(-\alpha _{1}(t-T)^{q})\\&\quad +\zeta _{2}^{-1}J^{T}J(t-T)^{q}E_{q,q+1}\\&\quad (-\alpha _{1}(t-T)^{q}) \end{aligned} \end{aligned}$$

(33)

Similarly, the following conclusions cannot also hold

• (i) $V(t)\le V(T+\tau )E_{q}( \beta _{1}(t-T-\tau )^{q})+\zeta _{2}^{-1}J^{T}J(t-T-\tau )^{q}E_{q,q+1}(\beta _{1}(t-T-\tau ))^{q})$ when $t\in [T+\tau , 2T]$,

• (ii) $V(t)\le V(nT)E_{q}(-\alpha _{1}(t-nT)^{q})+\zeta _{2}^{-1}J^{T}J(t-nT)^{q}E_{q,q+1}(-\alpha _{1}(t-nT)^{q})$ when $t\in [nT, nT+\tau ]$,

• (iii) $V(t)\le V(nT+\tau )E_{q}( \beta _{1}(t-nT-\tau )^{q})+\zeta _{2}^{-1}J^{T}J(t-nT-\tau )^{q}E_{q,q+1}(\beta _{1}(t-nT-\tau ))^{q})$ when $t\in [nT+\tau , (n+1)T]$.

The analysis results in Laplace domain and time domain all show that the conclusions in [1] are incorrect.

3 Counterexamples

To illustrate these errors, we take some counterexamples to verify our analysis.

Example 1

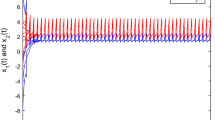
Suppose $x_{1}(t),x_{2}(t)\in R$ satisfying

$$\begin{aligned} \begin{aligned}&_{0}^CD^{0.4}_{t}x_{1}(t)=\left\{ \begin{array}{lr} -3x_{1}(t),\qquad 0< t\le 1\\ 0, \qquad t>1 \end{array} \right. \\&\frac{d}{dt}x_{2}(t)=\left\{ \begin{array}{lr} -3x_{2}(t),\qquad 0< t\le 1\\ 0, \qquad t>1 \end{array} \right. \end{aligned} \end{aligned}$$

(34)

Set the initial values as $x_{1}(0)=1$, $x_{2}(0)=1$ and take numerical simulation. The simulation result is shown in Fig. 1. Numerical result shows that $x_{1}(t)\ne x_{1}(1)$ and $x_{2}(t)=x_{2}(1)$ when $t>1$. From Fig. 1, we can see that the length of $_{0}^CD^{0.4}_{t}x_{1}(t)$ is 1 but the length of $x_{1}(t)$ is infinite, which is different from integer calculus.

Fig. 1

$x_{1}(t)$ and $V_{2}(t)$ in example (1) with time t

Example 2

Suppose $x_{1}(t),x_{2}(t),x_{3}(t)\in R$ satisfying

$$\begin{aligned} \begin{aligned} _{0}^CD^{0.15}_{t}x_{1}(t)&=\left\{ \begin{array}{lr} -0.8x_{1}(t),\qquad \qquad 0< t\le 1\\ 0.4x_{1}(t), \qquad \quad \qquad t>1 \end{array} \right. \\ _{0}^CD^{0.15}_{t}x_{2}(t)&=\left\{ \begin{array}{lr} 0.8x_{2}(t),\qquad \quad \qquad 0< t\le 1\\ 0.4x_{2}(t), \qquad \quad \qquad t>1 \end{array} \right. \\ x^{2}_{3}(t)&=4E_{0.15}(0.8*(t-1)^{0.15}),\qquad t>1\\ \end{aligned} \end{aligned}$$

(35)

Constructing positive functions as: $V_{1}(t)=x_{1}^{2}(t)$ , $V_{2}(t)=x_{2}^{2}(t)$ and $V_{3}(t)=x_{3}^{2}(t)$, according to $_{0}^CD^{0.15}_{t}V_{1}(t)\le 2x_{1}(t){_{0}^CD^{0.15}_{t}}x_{1}(t)$ and $_{0}^CD^{0.15}_{t}V_{2}(t)\le 2x_{2}(t){_{0}^CD^{0.15}_{t}}x_{2}(t)$, we have

$$\begin{aligned} \begin{aligned}&_{0}^CD^{0.15}_{t}V_{1}(t)\le \left\{ \begin{array}{lr} -1.6V_{1}(t),\qquad 0< t\le 1\\ 0.8V_{1}(t), \qquad t>1 \end{array} \right. \\&_{0}^CD^{0.15}_{t}V_{2}(t)\le \left\{ \begin{array}{lr} 1.6V_{2}(t),\qquad 0< t\le 1\\ 0.8V_{2}(t), \qquad t>1 \end{array} \right. \end{aligned} \end{aligned}$$

(36)

Set the initial values as $x_{1}(0)=\frac{2}{E_{0.15}((-0.8)*1^{0.15})}$, $x_{2}(0)=\frac{2}{E_{0.15}((0.8)*1^{0.15})}$ and we can get $V_{1}(1)=4$, $V_{2}(1)=4$, and $V_{3}(1)=4$. According to the proof process of Theorem 1 in [1], we can get $V_{1}(t)<V_{3}(t)$ and $V_{2}(t)<V_{3}(t)$ when $t>1$. But the numerical simulation (shown in Fig. 2) shows that $V_{1}(t)>V_{3}(t)$ and $V_{2}(t)<V_{3}(t)$ when $t>1$. Obviously, the proof process of Theorem 1 in [1] is incorrect.

Fig. 2

$V_{1}(t)$, $V_{2}(t)$ and $V_{3}(t)$ in example (2) with time t

Fig. 3

V(t) in example (3) with time t

Example 3

According to function (4) in [1], we suppose $x(t)\in R$, $q=0.3$,$t_{0}=0$, $A=2$, $f(x(t))=2.1x(t)u(t-2)$, $J=0$ and get

$$\begin{aligned} \begin{aligned}&_{0}^CD^{0.3}_{t}x(t)= -2x(t)+2.1x(t)u(t-2)+\mu (x(t)) \end{aligned} \end{aligned}$$

(37)

where $\mu (x(t))$ is an intermittent controller.

Generally, the beginning time of control input is uncertain. We suppose that system (37) is controlled via intermittent control when $t>2$ and define the intermittent control as

$$\begin{aligned} \begin{aligned}&\mu (x(t))= \left\{ \begin{array}{lr} 0, \qquad 0<t<2\\ -2x(t),\qquad 2+0.4n\le t<2+0.4n+0.2\\ 0, \qquad 2+0.4n+0.2\le t<2+0.4n+0.4 \end{array} \qquad n=0,1,2,3,\ldots \right. \\ \end{aligned} \end{aligned}$$

(38)

then, we can get the controlled system as

$$\begin{aligned} \begin{aligned}&_{0}^CD^{0.3}_{t}x(t)= \left\{ \begin{array}{lr} -2x(t), \qquad 0<t<2\\ -1.9x(t),\qquad 2+0.4n\le t<2+0.4n+0.2\\ 0.1x(t), \qquad 2+0.4n+0.2\le t<2+0.4n+0.2 \end{array} \qquad n=0,1,2,3,\cdots \right. \\ \end{aligned} \end{aligned}$$

(39)

According to Theorem 1 in [1], we can get $A=-2,K=-2$. Suppose $P=1$, $\zeta _{1}=2.1$, $\zeta _{2}=0$, $\alpha _{1}=3.8$, $\beta _{1}=0.2$ and get

• (1) $\Vert f(x_{1}(t))-f(x_{2}(t))\Vert \le 2.1\Vert x_{1}(t)-x_{2}(t)\Vert$, we can set $l_{f}=2.1$.

• (2) When $2+0.4n\le t<2+0.4n+0.2$, $A^{T}P+K^{T}P+PA+PK+\zeta _{1}P^{2}+\zeta _{1}^{-1}l_{f}^{2}+\zeta _{2}P^{2}+\alpha _{1}P\le 0$,

• (3) When $2+0.4n+0.2\le t<2+0.4n+0.4$ , $A^{T}P+PA+\zeta _{1}P^{2}+\zeta _{1}^{-1}l_{f}^{2}+\zeta _{2}P^{2}-\beta _{1}P\le 0$,

• (4) $E_{0.3}(-3.8*0.2^{0.3})E_{0.3}(0.2*0.2^{0.3})=0.9929 \le 1$.

Obviously, example 3 satisfies the conditions of Theorem in [1]. Construct a positive function as: $V(t)=x^{2}(t)$ and set the initial value as $x(0)=6$. We can get $V(2+0.4)\le V(2){E_{0.3}((-3.8)*0.2^{0.3}})E_{0.3}((0.2)*0.2^{0.3})\le V(2)$ according to the proof process of Theorem 1 in [1]. Similarly, we can get $V(2)\ge V(2+0.4)\ge V(2+0.8)\ge \cdots$.

We take numerical simulation at the same condition and the simulation result is shown in Fig. 3. Figure 3 shows that $V(2)\le V(2+0.4)\le V(2+0.8)\le \cdots$ , which contradicts with the theoretical analysis according to Theorem 1 [1].

Figures 1, 2 and 3 show that fractional order system is related to historical process as the memory property of fractional calculus. The numerical results show that the conclusion of Theorem 1 in [1] is incorrect. Obviously, the conclusion in Theorem 2 in [1] is also incorrect.

4 Conclusion

As mentioned above, we have analyzed the prove process and the conclusion of Theorem 1 in [1] are incorrect. It is necessary to point out these errors to avoid misleading.