1 Introduction

Differential systems arise from a lot of applications such as commerce, finance, medicine, neural networks [1,2,3,4]. Among these applications, boundedness is an essential and useful characteristic to analyze their dynamic behavior. Notably, it provides an effective tool to estimate the asymptotical controllability and thus plays an indispensable role in nonlinear control systems. Thus, the boundedness research of differential systems becomes a hot topic and develops rapidly (see, e.g., [5,6,7,8,9,10,11]).

Meanwhile, there are also developed many useful control methods to measure the boundedness of nonlinear control systems, such as impulsive control [12,13,14], fuzzy control [15, 16], dissipative control [17, 18] and intermittent control [19,20,21] and so on. Intermittent control, which was first proposed by Deissenberg [17] to achieve optimal control of linear economic models, has been used for a wide variety of applications such as mechanics, neural networks, chaotic control and secure communication. For example, the intermittent control offers an impressive way to tackle the signal-loss problems which may occur during the transmission and even the chaotic phenomena due to sensitive dependence on initial conditions. As is well known, the intermittent control and the impulsive control are regarded as the discontinuous control methods. Compared with the continuous control methods, the discontinuous control methods have main advantages in saving working time and reducing the control cost. Furthermore, compared with the impulsive control, the periodically intermittent control has the advantage of easier operation due to it has a nonzero control time. Therefore, a large number of important results in terms of intermittent control (for example [17,18,19,20,21,22]) have been reported in the last decade.

On the other hand, as an extension of the classical integer-order calculus, fractional calculus [23, 24] has gained considerable popularity and importance in many different fields, such as physics, chemistry, control systems, aerodynamics, biological networks, coelastic materials and thermo-elasticity. Because the fractional-order differential operator has the memory and hereditary properties, the fractional-order differential systems can more exactly describe the actual phenomena than the integer-order ones. On the other side, as we know, the standard Lyapunov function method plays a key role in the stability analysis of integer-order differential systems. However, for arbitrary \(0<q<1\), the Leibniz chain rule with Caputo fractional-order derivatives \(_{t_0}^CD_t^{q}(fg)=(_{t_0}^CD_t^{q}g)f+(_{t_0}^CD_t^{q}f)g\) cannot be derived [25], in which a counterexample has been given. In addition, the most difficulty that we have to overcome is to construct a suitable Lyapunov function(al) and calculate its fractional-order derivative, which is also the main reason that there is not many practical studies on this subject. Although some effective control methods have been developed to investigate the stability, stabilization, synchronization and quasi-synchronization of the fractional-order differential systems (see for example [26,27,28,29,30,31]), the problem of the intermittent control for the boundedness of the fractional-order differential systems is more complicated and still open.

Motivated by the above discussion, our main purpose is to fill this gap in this paper. Firstly, we propose a class of fractional-order differential systems and present two new lemmas about the monotonicity of the Mittag-Leffler function. Based on these lemmas, and utilizing the Lyapunov function and the periodically intermittent controller, several related sufficient conditions ensuring the exponential ultimate boundedness of the addressed fractional-order differential systems are derived. From our results, we shall see that the intermittent controller can make the unstable system into the stable one. Moreover, the obtained results on the boundedness of the addressed systems still hold even \(q=1\).

The main contributions of this paper can be summarized as follows: (i) the periodically intermittent control is introduced for the first time to the boundedness analysis of the fractional-order differential systems; (ii) the monotonicity of the function \(H(t)=t^qE_{q,q+1}(at^q)\) is discussed; (iii) some sufficient conditions are derived to ensure the exponential ultimate boundedness of the considered systems.

This paper is organized as follows. We formulate a class of fractional-order differential systems with periodically intermittent controller and indicate some elementary notations and definitions in Sect. 2. Four useful lemmas and several criteria ensuring exponential ultimate boundedness are addressed in Sect. 3. A numerical simulation illustrated the effectiveness of the derived bounded results in Sect. 4. Finally, the conclusion of this paper is drawn in Sect. 5.

2 Preliminaries

Let \({\mathbb {N}}\) be the natural numbers, \(I_n\) be the nth identity matrix and \({\mathbb {R}}^n\) (\({\mathbb {R}}^{n\times n}\)) be the set of n(\(n\times n\))-dimensional real vectors (matrices). \(\Vert \cdot \Vert \) denotes the Euclidean norm in \({\mathbb {R}}^n\), \({\mathbb {R}}_+=[0,\infty )\). \(\lambda _{\max }(\cdot )\) and \(\lambda _{\min }(\cdot )\) denote the maximum and the minimum eigenvalue of the corresponding matrix, respectively. For convenience, some useful definitions and facts in [32] are listed here.

Gamma function\(\varGamma (z)\):

$$\begin{aligned} \varGamma (z)=\int _0^\infty e^{-t}t^{z-1}\mathrm{d}t, \end{aligned}$$

where the real part Re(z) of complex number z satisfies \(Re(z)>0\).

Caputo fractional derivative:

$$\begin{aligned}&_{t_0}^CD_t^{q}y(t)=\frac{1}{\varGamma (n-q)}\int _{t_0}^t\frac{y^{(n)}(s)}{(t-s)^{q+1-n}}\mathrm{d}s,\nonumber \\&\quad n-1< q < n. \end{aligned}$$
(1)

One-parameter Mittag-Leffler function:

$$\begin{aligned} E_\alpha (z)=\sum _{k=0}^{\infty }\frac{z^k}{\varGamma (k\alpha +1)},\quad (\alpha >0). \end{aligned}$$
(2)

Two-parameter Mittag-Leffler function

$$\begin{aligned} E_{\alpha ,\beta }(z)=\sum _{k=0}^{\infty }\frac{z^k}{\varGamma (k\alpha +\beta )},\quad (\alpha>0,\beta >0). \end{aligned}$$
(3)

Obviously, \(E_\alpha (z)=E_{\alpha ,1}(z)\).

In this paper, we consider the following fractional-order differential systems:

$$\begin{aligned} _{t_0}^CD_t^{q}x(t)&=Ax(t)+f(x(t))+\mu (t)+J, t\ge 0,\nonumber \\ x(0)&=x_0, \end{aligned}$$
(4)

where \(x(t)=(x_1(t), \ldots , x_n(t))^T\in {\mathbb {R}}^n\) denotes the system state. \(A\in {\mathbb {R}}^{n\times n}\), \(f(x(t))=(f_1(x_1(t)), \ldots , f_n(x_n(t)))^T:{\mathbb {R}}^n\rightarrow {\mathbb {R}}^n\) with \(f_i(0)=0\) denotes the activation function of the system state, \(i=1,2,\ldots ,n, n\) is the number of units in a differential system. \(0<q<1\), and \(J\in {\mathbb {R}}^n\) is are an external bias vector. Let \(\mu (t)\) be an intermittent controller, which is described by

$$\begin{aligned} \mu (t)=\left\{ \begin{array}{ll} Kx(t),&{}\quad nT\le t< nT+\tau ,\\ 0,&{}\quad nT+\tau \le t<(n+1)T,\\ \end{array}\right. \end{aligned}$$
(5)

where \(K\in {\mathbb {R}}^{n\times n}\) is the control gain matrix, \(T>0\) denotes the control period and \(\tau >0\) is called the control width. Under control law (5), system (4) can be rewritten as

$$\begin{aligned}&_{t_0}^CD_t^{q}x(t)=Ax(t)+f(x(t))+J+Kx(t),\nonumber \\&\quad nT\le t< nT+\tau ,\nonumber \\&_{t_0}^CD_t^{q}x(t)=Ax(t)+f(x(t))+J,\nonumber \\&\quad nT+\tau \le t<(n+1)T. \end{aligned}$$
(6)

This is a classical switched system where the switching rule only depends on the time.

Definition 1

System (6) is said to be globally exponentially ultimately bounded if there exist constants \(r> 0\), \(K > 0\) and \(M\ge 0\) such that for any solution with the initial condition \(x_0\in {\mathbb {R}}^n\), \(\Vert x(t)\Vert \le K\Vert x_0\Vert e^{-r t}+M\), \(t\ge 0\).

3 Main results

In this section, some useful lemmas would be presented at first, then, the global exponential ultimate boundedness of the fractional-order differential systems (4) would be investigated using these lemmas.

Lemma 1

[33] Let \(y(t)\in {\mathbb {R}}^n\) be a vector of differentiable function. Then for any time constant \(t\ge t_0\), the following relationship holds

$$\begin{aligned} _{t_0}^CD_t^{q}(y^T(t){\mathscr {P}}y(t))\le 2y^T(t){\mathscr {P}}_{t_0}^CD_t^qy(t), \end{aligned}$$
(7)

where \(q\in (0,1)\), \({\mathscr {P}}\in {\mathbb {R}}^{n\times n}\) is a constant, symmetric and positive definite matrix.

Lemma 2

[34] Let \(X\in {\mathbb {R}}^n , Y\in {\mathbb {R}}^n\), and a scalar \(\xi >0\). Then, it holds that

$$\begin{aligned} X^TY+Y^TX\le \xi X^TX+\xi ^{-1}Y^TY. \end{aligned}$$
(8)

Lemma 3

For any \(q\in (0, 1)\), \(a\in {\mathbb {R}}\) and \(t\in {\mathbb {R}}_+\), the function \(H(t)=t^qE_{q,q+1}(at^q)\) is a monotonically increasing function.

Proof

From the assumptions, we easily get

$$\begin{aligned}&\frac{\mathrm{d}}{\mathrm{d}t}\left[ t^q E_{q,q+1}(a t^q)\right] \nonumber \\&\quad =\frac{\mathrm{d}}{\mathrm{d}t}\left[ t^q\sum _{k=0}^{\infty }\frac{(a t^q)^k}{\varGamma (kq+q+1)}\right] \nonumber \\&\quad =q t^{q-1}\sum _{k=0}^{\infty }\frac{(a t^q)^k}{\varGamma (kq+q+1)}+t^q\sum _{k=0}^{\infty }\frac{a^k \cdot q k\cdot t^{q k-1}}{\varGamma (kq+q+1)}\nonumber \\&\quad =t^{q-1}\left[ q\sum _{k=0}^{\infty }\frac{(a t^q)^k}{\varGamma (kq+q+1)}+\,t\sum _{k=0}^{\infty }\frac{a^k \cdot q k\cdot t^{q k-1}}{\varGamma (kq+q+1)}\right] \nonumber \\&\quad =t^{q-1}\sum _{k=0}^{\infty }\frac{(a t^q)^k}{\varGamma (kq+q+1)}(q+q k)\nonumber \\&\quad =t^{q-1}\sum _{k=0}^{\infty }\frac{(a t^q)^k}{\varGamma (kq+q)}=t^{q-1}E_{q,q}(a t^q)>0. \end{aligned}$$
(9)

Therefore, H(t) is a monotonically increasing function. \(\square \)

Lemma 4

Let \(0<q<1\), \(\hbar (t)\) is a continuous function on \([t_0,+\infty )\), if there exist constants \(\kappa _1\in {\mathbb {R}}\) and \(\kappa _2\ge 0\) such that

$$\begin{aligned}&_{t_0}^CD_t^{q}\hbar (t)\le \kappa _1\hbar (t)+\kappa _2,\nonumber \\&\hbar (t_0)=\hbar _{t_0}, \end{aligned}$$
(10)

then

$$\begin{aligned}&\hbar (t)\le \hbar _{t_0}E_q(\kappa _1(t-t_0)^q)\nonumber \\&\quad +\kappa _2(t-t_0)^qE_{q,q+1} (\kappa _1(t-t_0)^q),\nonumber \\&\quad t\ge t_0. \end{aligned}$$
(11)

Proof

The proof of Lemma 4 is similar to that of Lemma 3 in [35], so be omitted here. And by the way, if \(\kappa _1<0\), Lemma 4 is exactly Lemma 3 in [35]. \(\square \)

Theorem 1

Assume that there exist several positive constants \( l_f\), \(\xi _1\), \(\xi _2\), \(\gamma \), \(\alpha _1\), \(\beta _1\) and a symmetric positive definite matrix \(P\in {\mathbb {R}}^{n\times n}\) such that

  1. (i)

    for \(\forall x_1,x_2\in {\mathbb {R}}^n\),

    $$\begin{aligned} {\Vert f(x_1)-f(x_2)\Vert \le l_f\Vert x_1-x_2\Vert ,} \end{aligned}$$
    (12)
  2. (ii)
    $$\begin{aligned}&A^TP+K^TP+PA+PK+\xi _1P^2\nonumber \\&\quad +\xi _1^{-1}l_f^2I_n+\xi _2P^2+\alpha _1 P\le 0, \end{aligned}$$
    (13)
  3. (iii)
    $$\begin{aligned}&A^TP+PA+\xi _1P^2+\xi _1^{-1}l_f^2I_n\nonumber \\&\quad +\xi _2P^2-\beta _1 P\le 0, \end{aligned}$$
    (14)
  4. (iv)
    $$\begin{aligned} \gamma =E_q(-\alpha _1\tau ^q) E_q(\beta _1(T-\tau )^q)<1. \end{aligned}$$
    (15)

Then, System (6) is globally exponentially ultimately bounded and the solution x(t) will exponentially converge to the compact set defined by

$$\begin{aligned}&S=\left\{ x(t)\in {\mathbb {R}}^n\left| \Vert x(t)\Vert \right. \right. \nonumber \\&\left. \left. \quad \le \sqrt{\frac{\lambda \xi _2^{-1}J^TJ}{\lambda _{\mathrm{min}}(P)} \left( \frac{2+\lambda _3-\gamma }{1-\gamma }\right) }\right. \right\} , \end{aligned}$$
(16)

where \(\lambda =\max \{\tau ^qE_{q,q+1}(\beta _1\tau ^q),(T-\tau )^qE_{q,q+1}(\beta _1(T-\tau )^q)\}\) and \(\lambda _3=E_q(\beta _1(T-\tau )^q)\).

Proof

Consider the candidate Lyapunov function

$$\begin{aligned} V=x^T(t)Px(t). \end{aligned}$$
(17)

Obviously, we have

$$\begin{aligned} \lambda _{\mathrm{min}}(P)\Vert x(t)\Vert ^2\le V(x(t))\le \lambda _{\mathrm{max}}(P)\Vert x(t)\Vert ^2. \end{aligned}$$
(18)

By Lemma 1, we obtain the q-order Caputo derivatives of V(x(t)) along the trajectories of the first subsystem of system (6) for \(t\in [nT,nT+\tau )\), \(n\in {\mathbb {N}}\), as follows

$$\begin{aligned} _{t_0}^CD_t^{q}V&\le [x^T(t)A^T+f^T(x(t))\nonumber \\&\quad +x^T(t)K^T+J^T]Px(t)\nonumber \\&\quad +x^T(t)P[Ax(t)+f(x(t))+Kx(t)+J]\nonumber \\&= x^T(t)A^TPx(t)+f^T(x(t))Px(t)\nonumber \\&\quad +x^T(t)K^TPx(t)+J^TPx(t)\nonumber \\&\quad +x^T(t)PAx(t)\nonumber \\&\quad +x^T(t)Pf(x(t))+x^T(t)PKx(t)\nonumber \\&\quad +x^T(t)PJ\nonumber \\&= x^T(t)[A^TP+K^TP+PA+PK]x(t)\nonumber \\&\quad +f^T(x(t))Px(t)+x^T(t)Pf(x(t))\nonumber \\&\quad +J^TPx(t)+x^T(t)PJ. \end{aligned}$$
(19)

Taking into account Lemma 2 and (12)–(14), we obtain

$$\begin{aligned} _{t_0}^CD_t^{q}V&\le x^T(t)[A^TP+K^TP+PA+PK]x(t)\nonumber \\&\quad +\xi _1x^T(t)P^2x(t)+\xi _1^{-1}f^T(x(t))f(x(t))\nonumber \\&\quad +\xi _2x^T(t)P^2x(t)+\xi _2^{-1}J^TJ\nonumber \\&\le x^T(t)[A^TP+K^TP+PA+PK]x(t)\nonumber \\&\quad +\xi _1x^T(t)P^2x(t)+\xi _1^{-1}l_f^2x^T(t)x(t)\nonumber \\&\quad +\xi _2x^T(t)P^2x(t)+\xi _2^{-1}J^TJ\nonumber \\&= x^T(t)[A^TP+K^TP+PA+PK+\xi _1P^2\nonumber \\&\quad +\xi _1^{-1}l_f^2I_n\nonumber \\&\quad +\xi _2P^2]x(t)+\xi _2^{-1}J^TJ\nonumber \\&= -\alpha _1 V+x^T(t)[A^TP+K^TP+PA+PK\nonumber \\&\quad +\xi _1P^2+\xi _1^{-1}l_f^2I_n+\xi _2P^2\nonumber \\&\quad +\alpha _1 P]x(t)+\xi _2^{-1}J^TJ \nonumber \\&\le -\alpha _1 V+\xi _2^{-1}J^TJ. \end{aligned}$$
(20)

Similarly, when \(t\in [nT+\tau ,(n+1)T)\), we have

$$\begin{aligned} _{t_0}^CD_t^{q}V&\le [x^T(t)A^T+f^T(x(t))+J^T]Px(t)\nonumber \\&\quad +x^T(t)P[Ax(t)+f(x(t))+J]\nonumber \\&=x^T(t)[A^TP+PA]x(t)\nonumber \\&\quad +f^T(x(t))Px(t)+x^T(t)Pf(x(t))\nonumber \\&\quad +x^T(t)PJ+J^TPx(t)\nonumber \\&\le \beta _1 V+x^T(t)[A^TP+PA+\xi _1P^2\nonumber \\&\quad +\xi _1^{-1}l_f^2I_n+\xi _2P^2-\beta _1 P]x(t)+\xi _2^{-1}J^TJ\nonumber \\&\le \beta _1 V+\xi _2^{-1}J^TJ. \end{aligned}$$
(21)

Next, taking into account (20) and (21), we will estimate V(t). For \(t\in [nT,nT+\tau )\), by (20) and Lemma 4, we have

$$\begin{aligned}&V(t)\le V(nT)E_q(-\alpha _1(t-nT)^q)\nonumber \\&\quad +\xi _2^{-1}J^TJ(t-nT)^qE_{q,q+1}(-\alpha _1(t-nT)^q). \end{aligned}$$
(22)

On the other hand, when \(t\in [nT+\tau ,(n+1)T)\), by (21) and Lemma 4, we have

$$\begin{aligned} V(t)&\le V(nT+\tau )E_q(\beta _1(t-(nT+\tau ))^q)\nonumber \\&\quad +\xi _2^{-1}J^TJ(t-(nT+\tau ))^qE_{q,q+1}\nonumber \\&(\beta _1(t-(nT+\tau ))^q). \end{aligned}$$
(23)

From (22), (23), it follows that:

(1) when \(t\in [0,\tau )\), we obtain

$$\begin{aligned} V(t)&\le V(0)E_q(-\alpha _1 t^q)\nonumber \\&\quad +\xi _2^{-1}J^TJt^qE_{q,q+1}(-\alpha _1 t^q), \end{aligned}$$
(24)

and

$$\begin{aligned} V(\tau )&\le V(0)E_q(-\alpha _1 \tau ^q)\nonumber \\&\quad +\xi _2^{-1}J^TJ\tau ^qE_{q,q+1}(-\alpha _1 \tau ^q); \end{aligned}$$
(25)

(2) when \(t\in [\tau ,T)\), we have

$$\begin{aligned} V(t)&\le V(\tau )E_q(\beta _1(t-\tau )^q)\nonumber \\&\quad +\xi _2^{-1}J^TJ(t-\tau )^qE_{q,q+1}(\beta _1(t-\tau )^q)\nonumber \\&\le [V(0)E_q(-\alpha _1 \tau ^q)\nonumber \\&\quad +\xi _2^{-1}J^TJ\tau ^qE_{q,q+1}(-\alpha _1 \tau ^q)]E_q(\beta _1(t-\tau )^q)\nonumber \\&\quad +\xi _2^{-1}J^TJ(t-\tau )^qE_{q,q+1}(\beta _1(t-\tau )^q)\nonumber \\&= V(0)E_q(-\alpha _1\tau ^q)E_q(\beta _1(t-\tau )^q)\nonumber \\&\quad +\xi _2^{-1}J^TJ\tau ^qE_{q,q+1}(-\alpha _1 \tau ^q)E_q(\beta _1(t-\tau )^q)\nonumber \\&\quad +\xi _2^{-1}J^TJ(t-\tau )^qE_{q,q+1}(\beta _1(t-\tau )^q),\end{aligned}$$
(26)
$$\begin{aligned} V(T)&\le V(0)E_q(-\alpha _1\tau ^q)E_q(\beta _1(T-\tau )^q)\nonumber \\&\quad +\xi _2^{-1}J^TJ\tau ^qE_{q,q+1}(-\alpha _1 \tau ^q)E_q(\beta _1(T-\tau )^q)\nonumber \\&\quad +\xi _2^{-1}J^TJ(T-\tau )^qE_{q,q+1}(\beta _1(T-\tau )^q); \end{aligned}$$
(27)

(3) when \(t\in [T,T+\tau )\), we have

$$\begin{aligned} V(t)&\le V(T)E_q(-\alpha _1 (t-T)^q)\nonumber \\&\quad +\xi _2^{-1}J^TJ(t-T)^qE_{q,q+1}(-\alpha _1(t-T)^q)\nonumber \\&\le [V(0)E_q(-\alpha _1 \tau ^q)E_q(\beta _1(T-\tau )^q)\nonumber \\&\quad +\xi _2^{-1}J^TJ\tau ^qE_{q,q+1}(-\alpha _1 \tau ^q)E_q(\beta _1(T-\tau )^q)\nonumber \\&\quad +\xi _2^{-1}J^TJ(T-\tau )^qE_{q,q+1}\nonumber \\&\quad (\beta _1(T-\tau )^q)]E_q(-\alpha _1 (t-T)^q) \nonumber \\&\quad +\xi _2^{-1}J^TJ(t-T)^qE_{q,q+1}(-\alpha _1(t-T)^q)\nonumber \\&=V(0)E_q(-\alpha _1 \tau ^q)E_q\nonumber \\&\quad (\beta _1(T-\tau )^q)E_q(-\alpha _1 (t-T)^q)\nonumber \\&\quad +\xi _2^{-1}J^TJ[\tau ^qE_{q,q+1}(-\alpha _1 \tau ^q)E_q(\beta _1(T-\tau )^q)\nonumber \\&\quad +(T-\tau )^qE_{q,q+1}\nonumber \\&\quad (\beta _1(T-\tau )^q)]E_q(-\alpha _1 (t-T)^q) \nonumber \\&\quad +\xi _2^{-1}J^TJ(t-T)^qE_{q,q+1}(-\alpha _1(t-T)^q), \end{aligned}$$
(28)
$$\begin{aligned} V(T+\tau )&\le V(0)E_q(-\alpha _1 \tau ^q)E_q\nonumber \\&\quad (\beta _1(T-\tau )^q)E_q(-\alpha _1 \tau ^q)\nonumber \\&\quad +\xi _2^{-1}J^TJ[\tau ^qE_{q,q+1}(-\alpha _1 \tau ^q)E_q(\beta _1(T-\tau )^q)\nonumber \\&\quad +(T-\tau )^qE_{q,q+1}(\beta _1(T-\tau )^q)]E_q(-\alpha _1 \tau ^q) \nonumber \\&\quad +\xi _2^{-1}J^TJ\tau ^qE_{q,q+1}(-\alpha _1\tau ^q); \end{aligned}$$
(29)

(4) when \(t\in [T+\tau ,2T)\), we have

$$\begin{aligned} V(t)&\le V(T+\tau )E_q(\beta _1(t-(T+\tau ))^q)\nonumber \\&\quad +\xi _2^{-1}J^TJ(t-(T+\tau ))^qE_{q,q+1}(\beta _1(t-(T+\tau ))^q)\nonumber \\&\quad \le [V(0)E_q(-\alpha _1 \tau ^q)E_q(\beta _1(T-\tau )^q)E_q(-\alpha _1\tau ^q)\nonumber \\&\quad +\xi _2^{-1}J^TJ\tau ^qE_{q,q+1}(-\alpha _1 \tau ^q)E_q\nonumber \\&\quad (\beta _1(T-\tau )^q)E_q(-\alpha _1 \tau ^q)\nonumber \\&\quad +\xi _2^{-1}J^TJ(T-\tau )^qE_{q,q+1}(\beta _1(T-\tau )^q)E_q(-\alpha _1 \tau ^q)\nonumber \\&\quad +\xi _2^{-1}J^TJ\tau ^qE_{q,q+1}(-\alpha _1\tau ^q)]E_q(\beta _1(t-(T+\tau ))^q)\nonumber \\&\quad +\xi _2^{-1}J^TJ(t-(T+\tau ))^qE_{q,q+1}(\beta _1(t-(T+\tau ))^q)\nonumber \\&=V(0)E_q(-\alpha _1 \tau ^q)E_q\nonumber \\&\quad (\beta _1(T-\tau )^q)E_q(-\alpha _1 \tau ^q)E_q(\beta _1(t-(T+\tau ))^q)\nonumber \\&\quad +\xi _2^{-1}J^TJ\tau ^qE_{q,q+1}\nonumber \\&\quad (-\alpha _1 \tau ^q)E_q(\beta _1(T-\tau )^q) E_q(-\alpha _1 \tau ^q)E_q\nonumber \\&\quad (\beta _1(t-(T+\tau ))^q)\nonumber \\&\quad +\xi _2^{-1}J^TJ(T-\tau )^qE_{q,q+1}\nonumber \\&\quad (\beta _1(T-\tau )^q)E_q(-\alpha _1 \tau ^q)E_q(\beta _1(t-(T+\tau ))^q)\nonumber \\&\quad +\xi _2^{-1}J^TJ\tau ^qE_{q,q+1}(-\alpha _1\tau ^q)E_q(\beta _1(t-(T+\tau ))^q)\nonumber \\&\quad +\xi _2^{-1}J^TJ(t-(T+\tau ))^qE_{q,q+1}(\beta _1(t-(T+\tau ))^q), \end{aligned}$$
(30)
$$\begin{aligned} V(2T)&\le V(0)E_q(-\alpha _1 \tau ^q)E_q\nonumber \\&\quad (\beta _1(T-\tau )^q)E_q(-\alpha _1 \tau ^q)E_q(\beta _1(T-\tau )^q)\nonumber \\&\quad +\xi _2^{-1}J^TJ\tau ^qE_{q,q+1}(-\alpha _1 \tau ^q)E_q(\beta _1(T-\tau )^q) E_q\nonumber \\&\quad (-\alpha _1 \tau ^q)E_q(\beta _1(T-\tau )^q)\nonumber \\&\quad +\xi _2^{-1}J^TJ(T-\tau )^qE_{q,q+1}\nonumber \\&\quad (\beta _1(T-\tau )^q)E_q(-\alpha _1 \tau ^q)E_q(\beta _1(T-\tau )^q)\nonumber \\&\quad +\xi _2^{-1}J^TJ\tau ^qE_{q,q+1}(-\alpha _1\tau ^q)E_q(\beta _1(T-\tau )^q)\nonumber \\&\quad +\xi _2^{-1}J^TJ(T-\tau )^qE_{q,q+1}(\beta _1(T-\tau )^q). \end{aligned}$$
(31)

By induction, we have:

(5) when \(t\in [nT,nT+\tau )\),

$$\begin{aligned} V(t)&\le V(nT)E_q(-\alpha _1(t-nT)^q)\nonumber \\&\quad +\xi _2^{-1}J^TJt^qE_{q,q+1}(-\alpha _1(t-nT)^q)\nonumber \\&\le V(0)(E_q(-\alpha _1\tau ^q)\nonumber \\&\quad E_q(\beta _1(T-\tau )^q))^nE_q(-\alpha _1 (t-nT)^q)\nonumber \\&\quad +\left[ \sum _{i=1}^{n}(\tau ^qE_{q,q+1}(-\alpha _1 \tau ^q)E_q(\beta _1(T-\tau )^q)\right. \nonumber \\&\left. \quad +\,(T-\tau )^qE_{q,q+1}\right. \nonumber \\&\left. \quad (\beta _1(T-\tau )^q))(E_q(-\alpha _1\tau ^q)E_q(\beta _1(T-\tau )^q))^{i-1}\right] \nonumber \\&\quad E_q(-\alpha _1 (t-nT)^q)\xi _2^{-1}J^TJ\nonumber \\&\quad +\xi _2^{-1}J^TJ(t-nT)^qE_{q,q+1}(-\alpha _1(t-nT)^q); \end{aligned}$$
(32)

(6) when \(t\in [nT+\tau ,(n+1)T)\), we have

$$\begin{aligned} V(t)&\le V(nT+\tau )E_q(\beta _1(t-(nT+\tau ))^q)\nonumber \\&\quad +\xi _2^{-1}J^TJ(t-(nT+\tau ))^qE_{q,q+1}\nonumber \\&\quad (\beta _1(t-(nT+\tau ))^q)\nonumber \\&\le V(0)[E_q(-\alpha _1 \tau ^q)\nonumber \\&\quad E_q(\beta _1(T-\tau )^q)]^nE_q(-\alpha _1 \tau ^q)E_q(\beta _1(t-(nT+\tau ))^q)\nonumber \\&\quad +[\blacktriangle +\blacksquare ]\xi _2^{-1}J^TJE_q\nonumber \\&\quad (\beta _1( t-(nT+\tau ))^q)\nonumber \\&\quad +\xi _2^{-1}J^TJ(t-(nT+\tau ))^qE_{q,q+1}\nonumber \\&\quad (\beta _1(t-(nT+\tau ))^q), \end{aligned}$$
(33)

where \(\blacktriangle =\sum _{i=0}^{n}\tau ^qE_{q,q+1}(-\alpha _1 \tau ^q)[E_q(-\alpha _1 \tau ^q)E_q(\beta _1(T-\tau )^q)]^i\) and \(\blacksquare =\sum _{i=1}^{n}(T-\tau )^qE_{q,q+1}(\beta _1(T-\tau )^q)E_q(-\alpha _1 \tau ^q)[E_q(-\alpha _1 \tau ^q)E_q(\beta _1(T-\tau )^q)]^{i-1}\).

By Lemma 3, we have

$$\begin{aligned}&(t-nT)^qE_{q,q+1}(-\alpha _1(t-nT)^q)<\tau ^qE_{q,q+1} (-\alpha _1\tau ^q),\nonumber \\&\quad t\in [nT,nT+\tau ) \end{aligned}$$
(34)

and

$$\begin{aligned}&(t-(nT+\tau ))^q E_{q,q+1}(\beta _1(t-(nT+\tau ))^q)\nonumber \\&\quad <(T-\tau )^qE_{q,q+1}(\beta _1(T-\tau )^q),\nonumber \\&\quad t\in [nT+\tau ,(n+1)T). \end{aligned}$$
(35)

From (32)–(35) and the fact that \(0<E_q(x)\le 1\) for \(0<q<1\) and \(x\le 0\), we have

$$\begin{aligned}&V(t)\le V(0)(E_q(-\alpha _1\tau ^q)E_q(\beta _1(T-\tau )^q))^n\nonumber \\&\quad +\lambda \xi _2^{-1}J^TJ\nonumber \\&\quad \left( \frac{1-\gamma ^n}{1-\gamma } (1+E_q(\beta _1(T-\tau )^q))+1\right) ,\nonumber \\&\quad t\in [nT,nT+\tau ), \end{aligned}$$
(36)

and

$$\begin{aligned}&V(t)\le V(0)[E_q(-\alpha _1 \tau ^q)E_q(\beta _1(T-\tau )^q)]^n\nonumber \\&\quad E_q(\beta _1(t-(nT+\tau ))^q)\nonumber \\&\quad +\lambda \xi _2^{-1}J^T J\nonumber \\&\quad \left( \frac{1-\gamma ^{n+1}}{1-\gamma } +\frac{1-\gamma ^{n+1}}{1-\gamma }E_q(\beta _1(T-\tau )^q))\right) ,\nonumber \\&\quad t\in [nT+\tau ,(n+1)T). \end{aligned}$$
(37)

Combining (36) and (37), we obtain

$$\begin{aligned} V(t)&\le V(0)[E_q(-\alpha _1 \tau ^q)E_q(\beta _1(T-\tau )^q)]^n\lambda _1\nonumber \\&\quad +\lambda \xi _2^{-1}J^TJ\left( \frac{1-\gamma ^n}{1-\gamma } +1+\frac{1-\gamma ^{n+1}}{1-\gamma }\lambda _3\right) ,\nonumber \\&\qquad t\in [nT,(n+1)T), \end{aligned}$$
(38)

where \(\lambda _1=\max \{\lambda _2,1\}\), \(\lambda _2=\max _{\theta \in [0,T-\tau ]}E_q(\beta _1\theta ^q)\) and \(\lambda _3=E_q(\beta _1(T-\tau )^q)\). Therefore, for any \(t\ge t_0\),

$$\begin{aligned} V(t)&\le V(0)[E_q(-\alpha _1 \tau ^q)E_q(\beta _1(T-\tau )^q)]^{\frac{t}{T}-1}\lambda _1\nonumber \\&\quad +\lambda \xi _2^{-1}J^TJ\nonumber \\&\left( \frac{1-\gamma ^{\frac{t}{T}}}{1-\gamma } +1+\frac{1-\gamma ^{\frac{t}{T}+1}}{1-\gamma }\lambda _3\right) . \end{aligned}$$
(39)

By (18) and (39), we have

$$\begin{aligned} \Vert x(t)\Vert&\le \sqrt{\frac{\lambda _{\mathrm{max}}(P)}{\lambda _{\mathrm{min}}(P)}\Vert x(0)\Vert ^2\gamma ^{\frac{t}{T}-1} \lambda _1+\frac{\lambda \xi _2^{-1}J^TJ}{\lambda _{\mathrm{min}}(P)} \left( \frac{1-\gamma ^{\frac{t}{T}}}{1-\gamma }+1+ \frac{1-\gamma ^{\frac{t}{T}+1}}{1-\gamma }\lambda _3\right) }\nonumber \\&\le \sqrt{\frac{\lambda _1\lambda _{\mathrm{max}}(P)}{\gamma \lambda _{\mathrm{min}} (P)}}\Vert x(0)\Vert e^{\frac{\ln \gamma }{2T}t} +\sqrt{\frac{\lambda \xi _2^{-1}J^TJ}{\lambda _{\mathrm{min}}(P)} \left( \frac{2+\lambda _3-\gamma }{1-\gamma }\right) }, \end{aligned}$$
(40)

which concludes the proof. \(\square \)

Corollary 1

Suppose that all conditions in Theorem 1 hold. Then, System (6) with \(J=0\) is globally exponentially stable with the exponential convergence rate \(r=-\frac{\ln \gamma }{2T}\).

Remark 1

As Li et al. point out in [19], the periodic feedback will reduce to the general continuous feedback when \(\tau \rightarrow T\). In this case, Conditions (i) and (ii) in the theorem are enough for ensuring the globally exponential ultimate boundedness of the system (4) with the continuous feedback control \(\mu (t)=Kx(t)\) for any \(\tau \ge 0\). In fact, \(\tau \rightarrow T\), Condition (iii) is otiose, and Condition (iv) holds obviously since \(E_q(-\alpha _1T^q)<1\) and \(E_q(0)=1\).

Replacing \(K\in {\mathbb {R}}^{n\times n}\) by \(k\in {\mathbb {R}}\) in (5), we obtain the following special intermittent controller

$$\begin{aligned} \mu (t)=\left\{ \begin{array}{l} kx(t),\; nT\le t< nT+\tau \\ 0,\;nT+\tau \le t<(n+1)T\\ \end{array}\right. \end{aligned}$$
(41)

where \(k\in {\mathbb {R}}\).

Corollary 2

If all the conditions in Theorem 1 hold, except that Condition (ii) is replaced by

(ii)\('\):
$$\begin{aligned} \alpha _1+\beta _1+2k\le 0. \end{aligned}$$
(42)

Then, System (4) under the controller (41) is globally exponentially ultimately bounded and the solution x(t) will exponentially converge to the compact set defined by

$$\begin{aligned} S&=\left\{ x(t)\in {\mathbb {R}}^n\left| \Vert x(t)\Vert \right. \right. \nonumber \\&\left. \left. \le \sqrt{\frac{\lambda \xi _2^{-1}J^TJ}{\lambda _{\mathrm{min}}(P)} \left( \frac{2+\lambda _3-\gamma }{1-\gamma }\right) }\right. \right\} , \end{aligned}$$
(43)

where \(\lambda =\max \{\tau ^qE_{q,q+1}(\beta _1\tau ^q),(T-\tau )^qE_{q,q+1}(\beta _1(T-\tau )^q)\}\) and \(\lambda _3=E_q(\beta _1(T-\tau )^q)\).

Proof

The proof is similar to that of Theorem 1 and then omitted.

If fractional-order \(q=1\), the fractional-order differential system (6) turns to the following integer-order differential systems

$$\begin{aligned}&{\dot{x}}(t)=Ax(t)+f(x(t))+J+Kx(t),\nonumber \\&\quad nT\le t< nT+\tau ,\nonumber \\&{\dot{x}}(t)=Ax(t)+f(x(t))+J,\nonumber \\&\quad nT+\tau \le t<(n+1)T, \end{aligned}$$
(44)

where \(K\in {\mathbb {R}}^{n\times n}\). \(\square \)

Remark 2

When \(q=1\), Lemma 3 still holds. In fact, when \(q=1\), \(H(t)=t^qE_{q,q+1}(at^q)=\frac{e^{at}-1}{a}\). So, \({\dot{H}}(t)=e^{at}>0,\) and Lemma 3 still holds for \(q=1\).

With the help of Remark 2, we can know that the above results and their proofs still hold for \(q=1\). Therefore, the following results are valid.

Theorem 2

If all the conditions in Theorem 1 hold, except that Condition (iv) is replaced by

(iv)\('\):
$$\begin{aligned} \beta _1T-(\alpha _1+\beta _1)\tau <0. \end{aligned}$$
(45)

Then, System (44) is globally exponentially ultimately bounded and the solution x(t) will exponentially converge to the compact set defined by

$$\begin{aligned} S&=\left\{ x(t)\in {\mathbb {R}}^n\left| \Vert x(t)\Vert \right. \right. \nonumber \\&\left. \left. \le \sqrt{\frac{\lambda \xi _2^{-1}J^TJ}{\lambda _{\mathrm{min}}(P)} \left( \frac{2+\lambda _3-\gamma }{1-\gamma }\right) }\right. \right\} , \end{aligned}$$
(46)

where \(\lambda =\max \{\frac{e^{\beta _1\tau }-1}{\beta _1},\frac{e^{\beta _1(T-\tau )}-1}{\beta _1}\}\) and \(\lambda _3=e^{\beta _1(T-\tau )}\).

Corollary 3

Suppose that all conditions in Theorem 2 hold. Then, System (44) with \(J=0\) is globally exponentially stable.

Remark 3

The linear matrix inequalities may help us to verify the negative definiteness of the left of (13) and (14). In fact, according to the theory of the Schur complement, one can know that the following inequalities (47) and (48) imply (13) and (14), respectively.

$$\begin{aligned}&\left( \begin{array}{c@{\quad }c}{\mathscr {G}}\quad &{}\left( \sqrt{\xi _1+\xi _2}P+\frac{1}{\sqrt{\xi _1+\xi _2}}K\right) ^T\\ \left( \sqrt{\xi _1+\xi _2}P+\frac{1}{\sqrt{\xi _1+\xi _2}}K\right) \quad &{}-I_n\end{array}\right) <0, \end{aligned}$$
(47)
$$\begin{aligned}&\left( \begin{array}{c@{\quad }c}A^TP+PA+\xi _1^{-1}l_f^{2}I_n-\beta _1P \quad &{}\sqrt{\xi _1+\xi _2}P\\ \sqrt{\xi _1+\xi _2}P \quad &{}-I_n\end{array}\right) <0, \end{aligned}$$
(48)

where \({\mathscr {G}}=A^TP+PA+\xi _1^{-1}l_f^{2}I_n+\alpha _1P+\frac{1}{\xi _1+\xi _2}(I_n-K^T-K)\).

Remark 4

Though some interesting results concerning the intermittent control problem of the fractional-order differential systems have been reported [36,37,38], these results are limited to the stability. Obviously, these results are not appropriate for the exponential ultimate boundedness of fractional-order differential systems. Therefore, techniques and methods for the boundedness of fractional-order differential systems with intermittent control should be developed and explored. In order to prove our theory, a new fractional-order differential inequality needs to be introduced, the monotonicity of the function \(H(t)=t^qE_{q,q+1}(at^q)\) needs to be discussed, and the upper bound of \(\Vert x(t)\Vert \) should be estimated, which lead to a more difficult and complex proof process than the one in [36,37,38].

4 Illustrative example

The following illustrative example will demonstrate the effectiveness of our results.

Fig. 1
figure 1

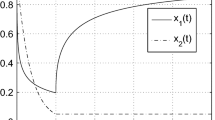
State trajectories of Sys. (6) with the initial values \((\hbox {x}_1(0)\),\(\hbox {x}_2(0))^T=(1.5,-1.5)^T\), \((9.5,-2.5)^T\), \((-1.5,3.5)^T\), \((-9,4)^T,(-5,2)^T\)

Full size image

Example 1

Consider system (6) with the following parameters

$$\begin{aligned}&A={\left( \begin{array}{cc}0.3&{}\quad -0.1\\ 0.1&{}\quad 0.2\end{array}\right) }, J=\left( \begin{array}{cc}1\\ 2\end{array}\right) , K={\left( \begin{array}{cc}-1&{}\quad 0.1\\ -0.2&{}\quad -1\end{array}\right) },\\&f(t,x(t))=0.1*(\tanh (x_1),\tanh (x_2))^T,\\&\quad T=2, \tau =1.5, q=0.7\\ \end{aligned}$$

Taking

$$\begin{aligned}&P=\left( \begin{array}{cc}1&{}\quad 0\\ 0&{}\quad 1\end{array}\right) ,\\&\xi _1=\xi _2=0.1, \xi _1^{-1}=\xi _2^{-1}=10, \alpha _1=\beta _1=1. \end{aligned}$$

By simple computation, we have \(l_f=0.1\),

$$\begin{aligned}&A^TP+K^TP+PA+PK+\xi _1P^2+\xi _1^{-1}l_f^2I_2+\xi _2P^2\\&\qquad +\alpha _1 P={\left( \begin{array}{c@{\quad }c}-0.1&{}-0.1\\ -0.1&{}-0.3\end{array}\right) }\le 0,\\&A^TP+PA+\xi _1P^2+\xi _1^{-1}l_f^2I_2+\xi _2P^2\\&\qquad -\,\beta _1 P={\left( \begin{array}{c@{\quad }c}-0.05&{}0.05\\ 0.05&{}-0.3\end{array}\right) }\le 0.\\&\gamma =E_q(-\alpha _1\tau ^q) E_q(\beta _1(T-\tau )^q)\\&\quad =E_{0.7}(-1.5^{0.7}) E_{0.7}(0.5^{0.7})=0.6536<1,\\&\lambda =\max \{\tau ^qE_{q,q+1}(\beta _1\tau ^q),\\&\quad (T-\tau )^q E_{q,q+1}(\beta _1(T-\tau )^q)\}\\&\quad =\max \{1.5^{0.7} E_{0.7,1.7}(1.5^{0.7}), 0.5^{0.7} E_{0.7,1.7}(0.5^{0.7})\}\\&\quad =\max \{5.2789,1.1289\}=5.2789,\\&\lambda _3=E_q(\beta _1(T-\tau )^q)=E_{0.7}(0.5^{0.7})=2.1289. \end{aligned}$$

It follows from Theorem 1 that System (6) is globally exponentially ultimately bounded and the solution x(t) will exponentially converge to the compact set defined by

$$\begin{aligned} S&=\left\{ x(t)\in {\mathbb {R}}^n\left| \Vert x(t)\Vert \right. \right. \nonumber \\&\left. \left. \le \sqrt{\frac{\lambda \xi _2^{-1}J^TJ}{\lambda _{\mathrm{min}}(P)} \left( \frac{2+\lambda _3-\gamma }{1-\gamma }\right) }=51.4593\right. \right\} . \end{aligned}$$
(49)
Fig. 2
figure 2

State trajectories of the Sys. (6) without intermittent controller, with the initial values \((\hbox {y}_1(0),\hbox {y}_2(0))^T=(1.5,-1.5)^T\), \((9.5,-2.5)^T\), \((-1.5,3.5)^T\), \((-9,4)^T,(-5,2)^T\)

Full size image
Fig. 3
figure 3

State trajectories of Sys. (6) with \(J=(0,0)^T\) and the initial values \((\hbox {x}_1(0),\hbox {x}_2(0))^T=(1.5,-1.5)^T\), \((9.5,-2.5)^T\), \((-1.5,3.5)^T, (-9,4)^T,(-5,2)^T\)

Full size image

The numerical simulation of the periodically intermittent control system (6) is shown in Fig. 1, and the corresponding original system is shown in Fig. 2. From Figs. 1 and 2, we see that intermittent controller can make the unbounded system into the bounded one.

Remark 5

If \(J=(0,0)^T\) and all other parameters are the same as that of Example 1. It follows from Corollary 1 that system (6) is globally exponentially stable. The numerical simulation of the periodically intermittent control system (6) with \(J=(0,0)^T\) is shown in Fig. 3 and the corresponding original system with \(J=(0,0)^T\) is shown in Fig. 4. From Figs. 3 and 4, we see that intermittent controller can make the unstable system into the stable one.

5 Conclusion

Fig. 4
figure 4

State trajectories of the Sys. (6) without intermittent controller, with \(J=(0,0)^T\) and the initial values \((\hbox {x}_1(0),\hbox {x}_2(0))^T=(1.5,-1.5)^T\), \((9.5,-2.5)^T\), \((-1.5,3.5)^T\), \((-9,4)^T,(-5,2)^T\)

Full size image

In this paper, we have investigated the exponential ultimate boundedness for a class of fractional-order differential systems by means of periodically intermittent control. By utilizing the Lyapunov function method and the monotonicity of the Mittag-Leffler function along with the periodically intermittent controller, sufficient conditions ensuring the exponential ultimate boundedness of the addressed systems have been derived. Both theoretical and numerical analysis have shown the effectiveness of the contributed results.

Although the problem of the intermittent control for the boundedness of the fractional-order differential systems has been discussed in this paper, the time delays were ignored in the addressed systems. As is well known, time delays are usually inevitable in many practical systems. They can deteriorate the control performance and can even destroy the stability and the boundedness of the systems. Therefore, it is significant to investigate the boundedness of fractional-order delay differential systems. How to extend the current results to the delay case is still a challenge, which is our future research topic.