A predictor–corrector time integration algorithm for dynamic analysis of nonlinear systems

Abstract

This paper presents a step-by-step time integration algorithm for efficiently solving second-order nonlinear dynamic problems. The method employs the rewriting of motion as two sets of first-order differential equations. The interpolation of the relevant quantities is achieved by a particular quadratic polinomial expression for the velocities and forces and is defined by values at the boundaries of the time step. Then the time definite integrals of both first-order ordinary differential equations define the numerical relations in the step. An accurate extrapolation predictor and an adaptive time stepping procedure are used as the time predictor–corrector method.

1 Introduction

The numerical simulation of the behaviour of nonlinear systems by direct integration of the motion equation is a current problem in computational dynamics. In the worst cases, N-body problems or finite element models resulting from the spatial discretization often lead to the time integration of stiff ordinary differential equations. This requirement is almost always carried out by explicit or implicit step-by-step approaches [1,2,3,4,5,6]. The computational approach by explicit schemes is very simple but numerical instability is an issue. As regards this a very small time step should be utilized for analysing the considered stiff problems. In this respect, fewer problems are encountered in the implicit approaches. In these the extrapolation (predictor phase) is followed by an iterative scheme (corrector phase) such as the Newton–Raphson iteration for the solution of the balance equation. Some of the first implicit time integration procedures used were the Houbolt, Newmark, and Wilson methods [4, 7]. Of these, the Newmark method was soon recognized to be most effective and is now widely used. In fact, in the trapezoidal rule version this method is second-order accurate and unconditionally stable in the linear analysis. However, in nonlinear analyses the stability of such a method is not assured. So research has focused on establishing more effective time integration schemes for nonlinear cases.

Schemes that obtain stable solutions can be carried out by requiring the conservation or decrease in the total energy of the Hamiltonian system within each time step. Such energy conserving algorithms have initially appeared in elastodynamics in the works [8] and [9]. Subsequently, schemes that preserve energy as well as linear and angular momentum in the time interval have been introduced in [10] (the energy-momentum method). In [11] a modification of the energy-momentum method which allows us to include numerical dissipation is introduced. These conservation properties are enforced into the equation of motion via Lagrange multipliers. Better computational characteristics are achieved by the use of adaptive time stepping procedures [12] and controllable numerical dissipation [13, 14]. More recently, schemes based on time finite element discretizations have been carried out (see [15, 16] and related bibliography). In these the Newmark family formulas can be recovered by the choice of representative constants and the algorithmic energy conservation is implicitly preserved. Finally, it seems that an appropriate representation and discretization of the motion equation lead to an appreciable difference in the time integration schemes with regard to stability [17,18,19,20].

An essential feature for a time integration scheme, as existing literature suggests (see for example [21]), is (at least) second-order accuracy. It is also desirable that the algorithm is based on a single-step scheme. Such an attribute is achieved if the solution of the motion equation at the current time depends only on the solution at the previous time step. One-step algorithms, however, may be cast into a spectrally equivalent linear multistep form. Finally, efficiency and robustness is obtained if additional variables, like Lagrange multipliers, are not involved in the algorithm and the method has no parameters which need to be chosen or adjusted by the analyst depending on the specific case. In this respect in [22,23,24] an effective implicit time integration method, referred to as the Bathe method, was introduced for linear and nonlinear analyses. The procedure uses a single-step, but two sub-steps where the trapezoidal rule is used in the first sub-steps and the three-points backward differential formula is employed in the second sub-steps.

An alternative approach to the time integration formulation is based on the rewriting of motion as two sets of first-order differential equations. One set specifies the motion in terms of the time derivative of the momenta and another defines the momenta in terms of the time derivative of the displacements. In this way energy and momentum conservation laws can be imposed in a simple manner while temporal compatibility between velocity and displacements can be properly relaxed [25,26,27,28].

In this paper the time definite integrals of both first-order ordinary differential equations define the numerical relations in the step. A quadratic polinomial expression for the velocity and internal and external forces is defined by values at the boundaries of the time step. In particular, related values are taken at the beginning of each step while values and time derivative are taken at the end of the step. Such a choice, used together with a accurate extrapolation predictor and an adaptive time stepping procedures, gives an effective time step-by-step procedure. The performed tests shown that stable and accurate solutions are obtained even for stiff nonlinear problems with reduced period elongation and high-frequency algorithmic damping in the analysis. Finally, the increase in computational effort due to the evaluation of the first derivative of the internal force vector, and consequent evaluation of the second derivative in the iteration matrix definition, is balanced by the increase in the range of stability of the time integration process and by the reduction in the number of Newton–Raphson iterations in the steps.

The paper is set out in the following way. In Sect. 2 we describe the temporal discretization that defines the current widely used (Newmark, Bathe) and the presented direct, implicit, single-step itegration schemes. The definition of related nonlinear problems is also given. In Sect. 3 we discuss on the stability and accuracy of the presented scheme. Section 4 contains the description of the adaptive time predictor–corrector solution algorithm. N-body and finite element structural models are formulated and analysed to compare the described solution methods in Sect. 5. Final conclusions are drawn in Sect. 6.

2 Approximation in the time domain

The semidiscrete formulation of the equation of motion can be written, after spatial discretization with $\mathbf{u}\in \mathbb {R}^{N}$ unknown parameters vector and inclusion of boundary conditions, in the form

$$\begin{aligned}&\mathbf{M}{} \mathbf{u}_{,tt}(t) + \mathbf{C}{} \mathbf{u}_{,t}(t) + \mathbf{f}(\mathbf{u}(t)) - \mathbf{p}(t) = \mathbf{0} , \nonumber \\&\mathbf{u}(0) = \mathbf{u}^* , \quad \mathbf{u}_{,t}(0) = \mathbf{u}_{,t}^* , \end{aligned}$$

(1)

where $\mathbf{u}_{,tt}$ denotes the acceleration, while $\mathbf{u}^*$ and $\mathbf{u}_{,t}^*$ represent the initial displacements and initial velocities, respectively. In (1) t is the time coordinate, $\mathbf{M}{} \mathbf{u}_{,tt}$ is the inertia force, $\mathbf{C}{} \mathbf{u}_{,t}$ the damping force, $\mathbf{f}(\mathbf{u})$ the internal force and $\mathbf{p}$ the external force. We refer to dynamic systems with $V(\mathbf{u}(\mathbf{x},t))$ internal energy, $T(\mathbf{u}_{,t}(\mathbf{x},t))$ kinetic energy and $L(\mathbf{u}(\mathbf{x},t),t)$ external work where $\mathbf{x}$ is the spatial coordinate. Then forces are defined as

$$\begin{aligned}&\mathbf{M}{} \mathbf{u}_{,tt}(t) = \frac{d}{\mathrm{d}t}\frac{\partial T(\mathbf{u}_{,t}(t))}{\partial \mathbf{u}_{,t}} , \quad \mathbf{f}(\mathbf{u}(t)) = \frac{\partial V(\mathbf{u}(t))}{\partial \mathbf{u}} , \nonumber \\&\mathbf{p}(t) = \frac{\partial L(\mathbf{u}(t),t)}{\partial \mathbf{u}} . \end{aligned}$$

(2)

For the time integration of the semidiscrete initial value problem (1) we refer to the current time step $\varDelta t = \tilde{t} - \bar{t}$. In the following we refer with the accent mark $\bar{\circ }$ and $\tilde{\circ }$ quantities defined in the initial and the final time of the step, respectively. By assuming the state variables $\bar{\mathbf{u}}$, $\bar{\mathbf{u}}_{,t}$, $\bar{\mathbf{u}}_{,tt}$, as known and making the external forces $\mathbf{p}(t)$ for all t, the time integration is restricted to the successive solution of the state variables at the end of each step $\tilde{\mathbf{u}}$, $\tilde{\mathbf{u}}_{,t}$, $\tilde{\mathbf{u}}_{,tt}$.

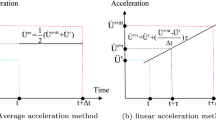
2.1 Newmark average acceleration scheme

In order to realize the step-by-step integration, the set of variables is reduced to the $\tilde{\mathbf{u}}$ displacement parameters vector alone by the Newmark approximations

$$\begin{aligned}&\tilde{\mathbf{u}}_{,t} = \frac{\gamma }{\beta \varDelta t}(\tilde{\mathbf{u}}-\bar{\mathbf{u}}) + \Bigl (1-\frac{\gamma }{\beta }\Bigr )\bar{\mathbf{u}}_{,t} + \Bigl (1-\frac{\gamma }{2 \beta }\Bigr )\varDelta t\bar{\mathbf{u}}_{,tt} , \end{aligned}$$

(3)

$$\begin{aligned}&\tilde{\mathbf{u}}_{,tt} = \frac{1}{\beta \varDelta t^2}(\tilde{\mathbf{u}}-\bar{\mathbf{u}}) - \frac{1}{\beta \varDelta t}\bar{\mathbf{u}}_{,t} + \Bigl (1-\frac{1}{2 \beta }\Bigr )\bar{\mathbf{u}}_{,tt} . \end{aligned}$$

(4)

Here we use the average acceleration scheme by adopting $\gamma =1/2$ and $\beta =1/4$. Such a choice makes expressions (3) and (4) second order accurate and the related method unconditionally stable in linear problems. By inserting relations (3) and (4) in Eq. (1) written at the $\tilde{t}$ time, we arrive at the nonlinear equation

$$\begin{aligned}&\frac{2}{\varDelta t}\Bigl (\frac{2}{\varDelta t}{} \mathbf{M}+\mathbf{C}\Bigr )\tilde{\mathbf{u}} + \mathbf{f}(\tilde{\mathbf{u}}) - \mathbf{M}\Bigl (\frac{4}{\varDelta t^2}\bar{\mathbf{u}}+\frac{4}{\varDelta t}\bar{\mathbf{u}}_{,t}+\bar{\mathbf{u}}_{,tt}\Bigr )\nonumber \\&- \mathbf{C}\Bigl (\frac{2}{\varDelta t}\bar{\mathbf{u}}+\bar{\mathbf{u}}_{,t}\Bigr ) - \tilde{\mathbf{p}} = \mathbf{0} \end{aligned}$$

(5)

in the unknown $\tilde{\mathbf{u}}$ vector.

2.2 Bathe two equal spaced sub-steps scheme

In the Bathe integration scheme we calculate the unknown displacements, velocities, and accelerations at time $\tilde{t}=\bar{t}+\varDelta t$ by considering the time step $\varDelta t$ to consist of two sub-steps. Generally, the sub-step sizes are $\gamma \varDelta t$ and $(1-\gamma ) \varDelta t$ for the first and second sub-steps, respectively. By using the trapezoidal rule over the first time interval $\gamma \varDelta t$, we have the following assumptions on velocity and acceleration at the intermediate $\hat{t}=\bar{t}+\gamma \varDelta t$ time

$$\begin{aligned}&\hat{\mathbf{u}}_{,t} = \frac{2}{\gamma \varDelta t}(\hat{\mathbf{u}}-\bar{\mathbf{u}}) - \bar{\mathbf{u}}_{,t} , \quad \hat{\mathbf{u}}_{,tt} = \frac{4}{\gamma ^2\varDelta t^2}(\hat{\mathbf{u}}-\bar{\mathbf{u}}) \nonumber \\&- \frac{4}{\gamma \varDelta t}\bar{\mathbf{u}}_{,t} - \bar{\mathbf{u}}_{,tt} . \end{aligned}$$

(6)

With the (6) assuptions the motion Eq. (1) becomes an algebraic nonlinear equation in the $\hat{\mathbf{u}}$ unknown vector. Once the displacements $\hat{\mathbf{u}}$ have been computed, the velocities $\hat{\mathbf{u}}_{,t}$ and accelerations $\hat{\mathbf{u}}_{,tt}$ are obtained from the relations given above in (6). Then, in the second sub-step the following Euler 3-point backward rule is utilized

$$\begin{aligned} \tilde{\mathbf{u}}_{,t} = c_{1}\bar{\mathbf{u}} + c_{2}\hat{\mathbf{u}} + c_{3}\tilde{\mathbf{u}} , \quad \tilde{\mathbf{u}}_{,tt} = c_{1}\bar{\mathbf{u}}_{,t} + c_{2}\hat{\mathbf{u}}_{,t} + c_{3}\tilde{\mathbf{u}}_{,t} , \end{aligned}$$

(7)

where

$$\begin{aligned} c_{1} = \frac{1-\gamma }{\gamma \varDelta t} , \quad c_{2} = \frac{-1}{(1-\gamma )\gamma \varDelta t} , \quad c_{3} = \frac{2-\gamma }{(1-\gamma )\varDelta t} . \end{aligned}$$

(8)

The equally spaced $\gamma =1/2$ sub-step choice seems to provide good computational characteristics for a large class of nonlinear problems [29, 30] and is adopted here. Then, by inserting relations (6) in the motion equation at the $\hat{t}$ time, we have

$$\begin{aligned}&\frac{4}{\varDelta t}\Bigl (\frac{4}{\varDelta t}{} \mathbf{M}+\mathbf{C}\Bigr )\hat{\mathbf{u}} + \mathbf{f}(\hat{\mathbf{u}}) - \mathbf{M}\Bigl (\frac{16}{\varDelta t^2}\bar{\mathbf{u}}+\frac{8}{\varDelta t}\bar{\mathbf{u}}_{,t}+\bar{\mathbf{u}}_{,tt}\Bigr )\nonumber \\&- \mathbf{C}\Bigl (\frac{4}{\varDelta t}\bar{\mathbf{u}}+\bar{\mathbf{u}}_{,t}\Bigr ) - \hat{\mathbf{p}} = \mathbf{0} . \end{aligned}$$

(9)

After that, the time step is completed by computing the solution of the motion equation at the $\tilde{t}$ final step time:

$$\begin{aligned}&\frac{3}{\varDelta t}\Bigl (\frac{3}{\varDelta t}{} \mathbf{M}+\mathbf{C}\Bigr )\tilde{\mathbf{u}} + \mathbf{f}(\tilde{\mathbf{u}}) + - \frac{1}{\varDelta t}{} \mathbf{M}\Bigl (\frac{12}{\varDelta t}\hat{\mathbf{u}}+4\hat{\mathbf{u}}_{,t}-\frac{3}{\varDelta t}\bar{\mathbf{u}}-\bar{\mathbf{u}}_{,t}\Bigr )\nonumber \\&- \frac{1}{\varDelta t}{} \mathbf{C}(4\hat{\mathbf{u}}-\bar{\mathbf{u}}) - \tilde{\mathbf{p}} = \mathbf{0} . \end{aligned}$$

(10)

Equation (10) is as usual obtained by inserting (7) in (1).

2.3 An integration of first order momenta and equilibrium equations

An equivalent statement of motion Eq. (1) in terms of 2N first order equations may be written in the form

$$\begin{aligned}&\mathbf{u}_{,t}(t) = \mathbf{v}(t) , \end{aligned}$$

(11)

$$\begin{aligned}&\mathbf{M}{} \mathbf{v}_{,t}(t) + \mathbf{C}{} \mathbf{u}_{,t}(t) = \mathbf{g}(t) = \mathbf{p}(t) - \mathbf{f}(\mathbf{u}(t)) . \end{aligned}$$

(12)

The equations of motion in the first-order form (11) and (12) are in agreement with Hamilton’s canonical equations where the system motion is described by means of the 2N paired quantities $(\mathbf{u},\mathbf{M}{} \mathbf{v})$ which constitute the phase space. In the current time step from $\bar{t}$ to $\tilde{t}=\bar{t}+\varDelta t$ we assume the quadratic approximation $\mathbf{v}(t)=\mathbf{v}_{0}+\mathbf{v}_{1}t+\mathbf{v}_{2}t^{2}$ of the velocity vector with

$$\begin{aligned} \mathbf{v}(\bar{t})=\bar{\mathbf{v}} , \quad \mathbf{v}(\tilde{t})=\tilde{\mathbf{v}} , \quad \mathbf{v}_{,t}(\tilde{t})=\tilde{\mathbf{a}} , \end{aligned}$$

(13)

where definition

$$\begin{aligned} \tilde{\mathbf{a}} = \mathbf{M}^{-1}(\tilde{\mathbf{p}} - \mathbf{f}(\tilde{\mathbf{u}}) - \mathbf{C}\tilde{\mathbf{v}}) \end{aligned}$$

(14)

is used. Then integration of Eq. (11) in the step leads to the following relation between the displacements $\tilde{\mathbf{u}}$ and the velocities $\tilde{\mathbf{v}}$ at the current $\tilde{t}$ time:

$$\begin{aligned}&\tilde{\mathbf{u}}-\bar{\mathbf{u}} = \int _{\bar{t}}^{\bar{t}+\varDelta t}{} \mathbf{u}_{,t}(t)\mathrm{d}t = \int _{\bar{t}}^{\bar{t}+\varDelta t}{} \mathbf{v}(t)\mathrm{d}t\nonumber \\&\quad = \frac{1}{3}\varDelta t\bar{\mathbf{v}}+\frac{2}{3}\varDelta t\tilde{\mathbf{v}}-\frac{1}{6}\varDelta t^{2}\tilde{\mathbf{a}} . \end{aligned}$$

(15)

Likewise the quadratic approximation $\mathbf{g}(t)=\mathbf{g}_{0}+\mathbf{g}_{1}t+\mathbf{g}_{2}t^{2}$ of the force vector with

$$\begin{aligned}&\mathbf{g}(\bar{t})=\bar{\mathbf{p}}-\mathbf{f}(\bar{\mathbf{u}})=\bar{\mathbf{g}} , \quad \mathbf{g}(\tilde{t})=\tilde{\mathbf{p}}-\mathbf{f}(\tilde{\mathbf{u}})=\tilde{\mathbf{g}}(\tilde{\mathbf{u}}) ,\nonumber \\&\quad \mathbf{g}_{,t}(\tilde{t})=\tilde{\mathbf{p}}_{,t}-\mathbf{f}_{,\mathbf{u}}(\tilde{\mathbf{u}})\tilde{\mathbf{v}}=\tilde{\mathbf{g}}_{,t}(\tilde{\mathbf{u}},\tilde{\mathbf{v}}) \end{aligned}$$

(16)

is assumed. By integrating in the step and by using expressions (16) it follows that

$$\begin{aligned} \int _{\bar{t}}^{\bar{t}+\varDelta t}{} \mathbf{g}(t)\mathrm{d}t = \frac{1}{3}\varDelta t\bar{\mathbf{g}}+\frac{2}{3}\varDelta t\tilde{\mathbf{g}}(\tilde{\mathbf{u}}) -\frac{1}{6}\varDelta t^{2}\tilde{\mathbf{g}}_{,t}(\tilde{\mathbf{u}},\tilde{\mathbf{v}}) , \end{aligned}$$

(17)

while

$$\begin{aligned}&\int _{\bar{t}}^{\bar{t}+\varDelta t}{} \mathbf{M}{} \mathbf{v}_{,t}(t)\mathrm{d}t = \mathbf{M}(\tilde{\mathbf{v}}-\bar{\mathbf{v}}) , \nonumber \\&\int _{\bar{t}}^{\bar{t}+\varDelta t}{} \mathbf{C}{} \mathbf{u}_{,t}(t)\mathrm{d}t = \mathbf{C}(\tilde{\mathbf{u}}-\bar{\mathbf{u}}) . \end{aligned}$$

(18)

Therefore Eq. (12) becomes a nonlinear equation in the $\tilde{\mathbf{u}}$ and $\tilde{\mathbf{v}}$ unknown vectors. Besides, by (15) the following relation of the $\tilde{\mathbf{v}}$ vector in function of the $\tilde{\mathbf{u}}$ vector resuts:

$$\begin{aligned} \mathbf{D}\tilde{\mathbf{v}} = \tilde{\mathbf{u}}-\bar{\mathbf{u}} - \frac{1}{3}\varDelta t\bar{\mathbf{v}} + \frac{1}{6}\varDelta t^2\mathbf{M}^{-1}(\tilde{\mathbf{p}} - \mathbf{f}(\tilde{\mathbf{u}})) = \tilde{\mathbf{q}}(\tilde{\mathbf{u}}) , \end{aligned}$$

(19)

where

$$\begin{aligned} \mathbf{D} = \frac{1}{3}\varDelta t\Bigl (2\mathbf{I}+\frac{1}{2}\varDelta t\mathbf{M}^{-1}{} \mathbf{C}\Bigr ) . \end{aligned}$$

(20)

Then, by defining $\tilde{\mathbf{v}}_{D}(\tilde{\mathbf{u}}) = \mathbf{D}^{-1}\tilde{\mathbf{q}}(\tilde{\mathbf{u}})$, the nonlinear motion equation is written as

$$\begin{aligned}&\mathbf{M}\tilde{\mathbf{v}}_{D}(\tilde{\mathbf{u}}) + \mathbf{C}\tilde{\mathbf{u}} - \frac{2}{3}\varDelta t\tilde{\mathbf{g}}(\tilde{\mathbf{u}}) + \frac{1}{6}\varDelta t^{2}\tilde{\mathbf{g}}_{,t}(\tilde{\mathbf{u}},\tilde{\mathbf{v}}_{D}(\tilde{\mathbf{u}}))\nonumber \\&\quad - \mathbf{M}\bar{\mathbf{v}} - \mathbf{C}\bar{\mathbf{u}} - \frac{1}{3}\varDelta t\bar{\mathbf{g}} = \mathbf{0} . \end{aligned}$$

(21)

for $\tilde{\mathbf{u}}\in \mathbb {R}^{N}$ alone.

3 Stability and accuracy of the presented scheme

To investigate and compare the properties of stability and accuracy of the described time integration schemes we refer mainly to [4, 31]. We consider the homogeneous undamped single-degree-of-freedom model equation

$$\begin{aligned} u_{,tt} - \omega u = 0 , \end{aligned}$$

(22)

in which $\omega$ is the free vibration frequency and $T=2\pi /\omega$ the related period. Equation (22) has an analytical solution of the form

$$\begin{aligned} u_{a} = c_{1} sin (\omega t) + c_{2} cos (\omega t) , \end{aligned}$$

(23)

where the constants of integration $c_{1}$ and $c_{2}$ are determined by the given initial conditions. In the described numerical integration techniques, displacement, velocity and acceleration at the $\tilde{t}$ time can be expressed in terms of their values at the $\bar{t}$ time as

$$\begin{aligned} \tilde{\mathbf{r}} = \mathbf{A} \bar{\mathbf{r}} \end{aligned}$$

(24)

in which $\mathbf{r}^{T}=\{u \,\,\, \varDelta t v \,\,\, \varDelta t^{2} a\}$ and $\mathbf{A}$ is the amplification matrix. The explicit definition of the $\mathbf{A}$ matrix for the Newmark and the Bathe schemes can be found in the cited literature while for the presented scheme it can be computed by referring to the application of the expressions in Sect. 2.3 to the linear Eq. (22):

$$\begin{aligned}&\tilde{u}-\bar{u}-\frac{1}{3}\frac{\tau }{\omega }\bar{v}-\frac{2}{3}\frac{\tau }{\omega }\tilde{v}+\frac{1}{6}\frac{\tau ^2}{\omega ^2}\tilde{a} = 0 , \end{aligned}$$

(25)

$$\begin{aligned}&\tilde{v}-\bar{v}+\frac{1}{3}\tau \omega \bar{u}+\frac{2}{3}\tau \omega \tilde{u}-\frac{1}{6}\tau ^2\tilde{v} = 0 , \end{aligned}$$

(26)

$$\begin{aligned}&\omega ^2\tilde{u}+\tilde{a} = 0 , \end{aligned}$$

(27)

where $\tau =\omega \varDelta t$. Then (24) gives:

$$\begin{aligned}&\mathbf{A} = \frac{1}{\omega \tau (\tau ^4+4\tau ^2+36)}\nonumber \\&\qquad \left[ \begin{array}{ccc} -2\tau (7\omega \tau ^2-18\omega ) &{} -2\omega (\tau ^3-18\tau ) &{} 0 \\ 2\tau ^2(\omega \tau ^3-18\omega \tau ) &{} 2\omega \tau (-7\tau ^2+18) &{} 0 \\ 2\tau ^3(7\omega \tau ^2-18\omega ) &{} 2\omega \tau ^2(\tau ^3-18\tau ) &{} 0 \\ \end{array}\right] . \end{aligned}$$

(28)

The stability and accuracy of the integration schemes are determined from the spectral properties of the $\mathbf{A}$ matrix. In the following we refer to the invariants of $\mathbf{A}$: $\alpha _1$$=$ 1/2 trace $\mathbf{A}$, $\alpha _2$$=$ sum of principal minors of $\mathbf{A}$, $\alpha _3$$=$ determinant $\mathbf{A}$. By the definition (28) it follows that $\alpha _3=0$ and $\alpha _1^2<\alpha _2$. Therefore

$$\begin{aligned}&\lambda _{1,2} = \alpha _1\pm \sqrt{\alpha _1^2-\alpha _2} = \alpha _2^{\frac{1}{2}}[cos(\phi )\pm i\,sin(\phi )] ,\nonumber \\&tan(\phi )=\pm \frac{\gamma _2}{\gamma _1} , \end{aligned}$$

(29)

is the couple of complex conjugates ($\lambda _3=0$) eigenvalues of the $\mathbf{A}$ matrix. In (29) we define $\gamma _2=\sqrt{\alpha _2-\alpha _1^2}$ and $\gamma _1=\alpha _1$. We can show that the general solution of the difference Eq. (24) is

$$\begin{aligned} u_n = \rho _p^n (\hat{c}_{1} cos(\hat{\omega } t_n) + \hat{c}_{2} sin(\hat{\omega } t_n) ) , \end{aligned}$$

(30)

where $\rho _p = \sqrt{\gamma _1^2+\gamma _2^2}$, $t_n = n \varDelta t$, $\hat{\omega } = \phi /\varDelta t$ and $\hat{c}_{1}$, $\hat{c}_{2}$ are constants determined by the initial conditions. Measures of the relative accuracy can then be obtained by comparison between the (23) analytical solution and the (30) numerical solution. In particular, we define the period elongation (PE) and the amplitude decay (AD) by

$$\begin{aligned}&PE = \frac{\hat{T}-T}{T} = \frac{\omega \varDelta t-\phi }{\phi } ,\nonumber \\&AD = \frac{\rho _p^n-\rho _p^{n+\hat{T}/\varDelta t}}{\rho _p^n} = 1-\rho _p^{2\pi /\phi } , \end{aligned}$$

(31)

where $\hat{T}=2\pi /\hat{\omega }$. Likewise we can observe that stability of the numerical solution is achieved if the spectral radius $\rho (\mathbf{A})=\max \{|\lambda _1|,|\lambda _2|,|\lambda _3|\}$ of matrix $\mathbf{A}$ is less than or equal to 1.

To represent the behaviour of the above defined stability and accuracy measures we choose a sufficiently small $d\tau$ increment of $\tau$. Then, for each $\tau _n=n\,d\tau$ point the $\mathbf{A}_n=\mathbf{A}(\tau =2\pi \tau _n)$ matrix and related $\lambda _n=\lambda _{nRe}\pm i\,\lambda _{nIm}$ complex conjugates eigenvalues are computed. By referring to the discrete values

$$\begin{aligned} \phi _n = \arctan \Bigl (\frac{\lambda _{nIm}}{\lambda _{nRe}}\Bigr ) , \quad \rho _{pn} = \sqrt{\lambda _{nRe}^2+\lambda _{nIm}^2} , \end{aligned}$$

(32)

we can evaluate

$$\begin{aligned} PE_n = 100\frac{2\pi \tau _n-\phi _n}{\phi _n} , \quad AD_n = 100[1-\rho _{pn}^{2\pi /\phi _n}] .\nonumber \\ \end{aligned}$$

(33)

In (33) $PE_n$ and $AD_n$ are the percentage period elongation and percentage amplitude decay, respectively. Finally, by the spectral radius $\rho _{pn}$ computed in (32) the stability of the scheme is checked. The curves obtained for increasing values of the relative $\omega \varDelta t$ time step are given in Figs. 1 and 2. The (HFDI) fourth degree integration of Hamilton’s canonical equations scheme can be seen to perform well when compared to the Newmark and Bathe schemes. In particular, the HFDI scheme provides a very small period elongation with an unconditional stable condition and a good annihilation attribute of the high-frequency mode responses. On the other hand, compared with the other methods, the presented method shows a larger amplitude decay effect.

Fig. 1

Spectral radii of approximation operators

Fig. 2

Percentage period elongations and amplitude decays

4 Adaptive time predictor–corrector solution algorithm

Equation (5) for the Newmark scheme, Eq. (9) (or (10)) for the standard Bathe scheme and (21) for the presented scheme represent a nonlinear system of algebraic equations of the type

$$\begin{aligned} \mathbf{F}(\mathbf{u}_{n+1}) = \mathbf{0} , \quad n=0,1,\dots \end{aligned}$$

(34)

defined at the $t_{n+1}=t_{n}+\varDelta t_{n+1}=\tilde{t}$ time with the $\mathbf{u}_{n+1}=\tilde{\mathbf{u}}$ (or $\hat{\mathbf{u}}$ at $\hat{t}$) unknown vector. The velocities and accelerations at the end of the time step can then be obtained, for the above mentioned schemes, by relations (3) and (4), (7), (19) and (14) respectively. The Newton–Rapson iterative method can be used as corrector to solve system (34) by linearization

$$\begin{aligned}&\mathbf{F}\Bigl (\mathbf{u}_{n+1}^{(k+1)}\Bigr ) = \mathbf{F}\Bigl (\mathbf{u}_{n+1}^{(k)}\Bigr ) + \frac{\partial \mathbf{F}\Bigl (\mathbf{u}_{n+1}^{(k)}\Bigr )}{\partial \mathbf{u}_{n+1}} \Bigl (\mathbf{u}_{n+1}^{(k+1)}-\mathbf{u}_{n+1}^{(k)}\Bigr ) \nonumber \\&\qquad \qquad + \mathbf{O}\Bigl (\varDelta t_{n}^{2}\Bigr ) = \mathbf{0} , \end{aligned}$$

(35)

$k=0,1,\ldots$.

The same initialization formula is used as predictor for all adopted integration schemes. When $n=0$ the iterative process is initialized by the formula $\mathbf{u}_{1}^{(0)}=\mathbf{u}^{*}+\varDelta t_{0}\mathbf{u}_{,t}^{*}$. When $n>0$ the initialization is performed by the fourth order extrapolation $\mathbf{u}_{n+1}^{(0)}(t)=\sum _{i=0}^{4}{} \mathbf{c}_{n+1,i}t^{i}$ with coefficient vectors $\mathbf{c}_{i}$ determined by impositions:

$$\begin{aligned}&\mathbf{u}_{n+1}^{(0)}(-\varDelta t_{n}) = \mathbf{u}_{n-1} , \quad \mathbf{u}_{n+1}^{(0)}(0) = \mathbf{u}_{n} ,\nonumber \\&\frac{d}{\mathrm{d}t}{} \mathbf{u}_{n+1}^{(0)}(-\varDelta t_{n}) = \mathbf{v}_{n-1} , \quad \frac{d}{\mathrm{d}t}{} \mathbf{u}_{n+1}^{(0)}(0) = \mathbf{v}_{n} ,\nonumber \\&\frac{d^2}{\mathrm{d}t^2}{} \mathbf{u}_{n+1}^{(0)}(0) = \mathbf{a}_{n} . \end{aligned}$$

(36)

Note that the $\mathbf{u}_{n+1}^{(0)}(t)$ extrapolation defined by (36) has the same approximation of that defined in the proposed 2.3 scheme for displacements. Finally,

$$\begin{aligned} \mathbf{u}_{n+1}^{(0)} = \mathbf{u}_{n+1}^{(0)}(\varDelta t_{n+1}) \end{aligned}$$

(37)

represents the predictor point for the $n+1$ step of the solution algorithm. Such an accurate extrapolation is effective for the proposed algorithm because the scheme described in Sect. 2.3 has been shown to provide very accurate velocities and accelerations at the solution points. Furthermore, tests show that the presented method takes advantage in computational performance of the choice of an accurate extrapolation formula, whereas the Newmark and Bathe methods seem to be insensitive to such a choice.

Table 1 HFDI scheme: summary of computations for the current $t_{n} \rightarrow t_{n+1} = t_{n}+\varDelta t_{n+1}$ time step

By choosing the fixed tolerance $\eta =10^{-8}$, the formula

$$\begin{aligned} \frac{ \parallel \mathbf{u}_{n+1}^{(k+1)} - \mathbf{u}_{n+1}^{(k)} \parallel }{ \parallel \mathbf{u}_{n+1}^{(k+1)} \parallel } \le \eta \end{aligned}$$

(38)

is adopted as convergence criterion for the k-th Newton–Raphson iteration. The length $\varDelta t_{n+1}=\mu _{n+1}\varDelta t_{n}$ of the extrapolation parameter in the $n+1$-th predictor–corrector step is chosen as a function of the iterations $N^{(it)}_{n}$ performed in the previous corrector step and a $\bar{N}^{(it)}$ target iteration count. Estimate

$$\begin{aligned} \mu _{n+1} = \mu _{n} \biggl [ \frac{ \bar{N}^{(it)} }{ N^{(it)}_{n} } \biggl ]^{1/2} \end{aligned}$$

(39)

is adopted to save computational costs in the analysis because high $\mu _{(n)}$ values can be reached. Evaluation (39) also takes into account the smoothness of the solution and then leads to an adaptive time stepping procedure that improves the accuracy of the approximation. Finally, if divergence in corrector iterations occurs a new predictor–corrector step is performed with the length $\mu _{(k)}$ halved.

In the $\varDelta t_{n+1}$ time step, stable behavior of the time integration method, in the absence of numerical dissipation, is verified by referring to the condition

$$\begin{aligned} \varDelta E_{n+1} = V_{n+1} - V_{n} + T_{n+1} - T_{n} - \varDelta L_{n+1} = 0 , \end{aligned}$$

(40)

as a sufficient stability condition in the nonlinear dynamical schemes (see, e.g., [8] and [10]). In the following we refer to $W_{n}=V_{n}+T_{n}$ for the sum of the internal and the kinetic energies and we assume that physical dissipation is not present. Equation (40) expresses the conservation of the $\varDelta E$ total energy in the step where $\varDelta L$ symbolizes the work done by external forces within the time step. Here we use the trapezoidal rule to calculate the work of the external forces:

$$\begin{aligned}&\varDelta L_{n+1} = \int _{t_{n}}^{t_{n+1}} \mathbf{u}_{t}^{T}(t)\mathbf{p}(t)\mathrm{d}t \nonumber \\&\qquad = \frac{1}{2}(\mathbf{u}_{n+1}-\mathbf{u}_{n})(\mathbf{p}_{n}+\mathbf{p}_{n+1}) . \end{aligned}$$

(41)

As regards consistency, in the numerical tests, accuracy in the $\mathbf{z}$ quantity of interest is calculated by the mean-square norm of the error $\varepsilon _\mathbf{z}$ according to

$$\begin{aligned} \varepsilon _\mathbf{z} = \frac{ \biggl ( \int _{0}^{T} \bigl [ \mathbf{z}(t) - \mathbf{z}^{*}(t) \bigl ]^{T} \bigl [ \mathbf{z}(t) - \mathbf{z}^{*}(t) \bigl ] \biggl )^{1/2} }{ \biggl ( \int _{0}^{T} \mathbf{z}^{*}(t)^{T}\mathbf{z}^{*}(t) \biggl )^{1/2} } , \end{aligned}$$

(42)

where $T_{o}$ is the chosen time of observation. In (42) $\mathbf{z}^{*}(t)$ denotes the reference solution which has been calculated with the Newmark algorithm and by using a $\varDelta t=10^{-4}T_{o}$ constant time step. Integrals of expression (42) are computed by a sum on the steps carried out in the analysis and by using the trapezoidal rule as in (41) formula in the $\varDelta t_{n+1}$ step. Values of $\mathbf{z}^{*}(t)$ at the $t_{n}$ and $t_{n+1}$ time are detected as a linear interpolation of the neighbouring reference solution points.

We note that in the (21) nonlinear equilibrium equation the time derivative $\tilde{\mathbf{p}}_{,t}$ of the external force must be computed. Of course, simple numerical approximations of such a derivative can be defined also for discontinuity behaviour of $\mathbf{p}(t)$ in the $\tilde{t}$ time. Here, to keep the integration scheme defined in the single step, the $\tilde{\mathbf{p}}_{,t}=(\mathbf{p}(t_{n+1})-\mathbf{p}(t_{n}))/\varDelta t_{n+1}$ approximation was used. Finally, the computations carried out by the algotithm to accomplish the $n+1$ step by means of the HFDI scheme are summarized in Table 1.

5 Numerical tests

Some numerical tests have been carried out with the suggested algorithms. The described integration algorithms resulting from Newmark, Bathe and presented HFDI equations have been compared. As stated, predictor–corrector steps are characterized by the use of Newton–Raphson method as corrector with assigned $\bar{N}^{(it)}$ target iteration counts. Tables report the number steps of predictor–corrector steps and the $N^{(it)}_{\small mv }$ mean value of the number of Newton–Raphson iterations in the steps

$$\begin{aligned} N^{(\mathrm{it})}_{\small mv } = \sum _{i=1}^{\mathrm{steps}} N^{(\mathrm{it})}_{\small tot } / \mathrm{steps} . \end{aligned}$$

(43)

$N^{(it)}_{\small tot }$ is the total number of iterations and ${t}_{T}$ the CPU time (s) spent in the whole analysis. For the Bathe like algorithm the $N^{(it)}_{\small tot }$ value in (43) is the sum of the iterations needed for convergence for the first and second sub-step. In the case of divergence of the corrector phase we mark one step in the steps count while the number of Newton–Raphson iterations performed are sum in the $N^{(it)}_{\small tot }$ value. The $\varDelta t_{\small mv }$ mean value of the $\varDelta t_{n}$ time integration steps used in the analysis is also reported as a computational characteristic of the adopted scheme.

Traversing the assigned $T_{o}$ observation time is adopted as the stopping criteria of the step-by-step analysis. Also, in the analysis there is a maximum number of iterations $N^{(it)}_{\small max }$ permitted in the corrector step. This is done because the convergence of the iterations may not occur or becomes very slow. We make $N^{(it)}_{\small max }=2\bar{N}^{(it)}$. If the number of corrector iterations exceeds $N^{(it)}_{\small max }$ we treat this circumstance as divergence and initialize a new corrector step as described in Sect. 4. Finally, the initial $\varDelta t_{0}$ value in the extrapolation is chosen in such a way that convergence of the first step is attained at $\bar{N}^{(it)}$ corrector iteration.

5.1 Motion of a dumbbell

The motion of a dumbbell in the two-dimensional ambient space (x, y) is examined here. The dumbbell is modelled as a two-body problem where additional background material on the motion of a several particles system in a potential field can be found in standard books on classical mechanics, see e.g. [32]. By referring to Fig. 3, we assume $m_{1}=m_{2}=1$ with $\mathbf{u}^{T}=\{ u_{1} \,\, v_{1} \,\, u_{2} \,\, v_{2} \}$. The initial conditions are given by $\mathbf{u}^{*T}=\{ 0 \,\, 0 \,\, 1 \,\, 0 \}$ and $\mathbf{u}_{,t}^{*T}=\{ 0 \,\, 10 \,\, 0 \,\, 5 \}$. The following Leonard-Jones-type potential, which is often employed in molecular dynamic simulations, is assumed to define the interaction of the two bodies:

$$\begin{aligned}&V(r) = A \biggl [ \biggl (\frac{\sigma }{r}\biggl )^{5} - \biggl (\frac{\sigma }{r}\biggl )^{3} \biggl ] , \nonumber \\&r = [(u_{2}-u_{1})^{2}+(v_{2}-v_{1})^{2}]^{\frac{1}{2}} . \end{aligned}$$

(44)

In (44) r is the distance between the position of the centers of the two bodies. We make $\sigma = (3/5)^{1/2}$, such that $r=r_{0}=1$ characterizes the internal force free configuration. Accordingly, if $r<1$, the resulting force is repulsive, whereas $r>1$ implies attraction of the two bodies. We can refer to [15] and [20] for the numerical instabilities which are introduced in the time integration of such dynamic systems.

Fig. 3

Dumbell: initial configuration and problem definition

Table 2 Dumbell: computational characteristics of time integration algorithms for $T_{o}=$2

We investigate the quasi-rigid case related to $A=10^{6}$. The integration process analyzes the behaviour of the system for $T_{o}=2$. Computational performances are reported in Table 2 for each of described integration schemes, unless it becomes unstable (div), and increasing values of the $\bar{N}^{(it)}$ target iteration counts. We note that, due to a fast convergence of the Newton iterations, in the HFDI procedure large increments of $\varDelta t_{\small mv }$ values are achieved when small increments of $\bar{N}^{it}$ are fixed.

To illustrate the motion, Fig. 4 contains a sequence of configurations calculated by the considered algorithms. An unstable behaviour of the Newmark scheme is observed for the required $\bar{N}^{(it)}$=4.5 where $\varDelta t_{\small mv }$=0.26 results. This value is computed by referring to t from 0 to the beginning of the unphysical motion. Accurate representations are obtained by the Bathe $\bar{N}^{(it)}$=2$\cdot$4.5 ($\varDelta t_{\small mv }$=0.40) and the presented $\bar{N}^{(it)}$=3.3 ($\varDelta t_{\small mv }$=0.45) algorithms, although a period elongation increase is observed in the Bathe experimentations. Likewise, the longitudinal stretch $\lambda =(r-r_{0})/r_{0}$ is plotted versus time in the Fig. 5. Of course high frequency are not represented while the mean value is provided by the algorithms. Finally, the increment of the total energy (40) is shown in Fig. 6 where stable behaviour is represented by oscillations contained in the neighbourhood of zero. A pronounced overshooting in the response is also encountered in the Bathe integration. The observed increase of the increment of total energy in the presented method, however, is limited also for long periods of analysis. To showing this Fig. 7 reports the evolution of the normalized increment of the total energy $\varDelta E / W$ with $T_{o}=10$ for several $\bar{N}^{(it)}$ values.

5.2 Motion of a tetrahedra

In this example we consider the motion of a tetrahedra-type structure in three-dimensional space analyzed in [15]. The structure (see Fig. 8) is treated as 4-body $m_{i}=1$, $i=1,\ldots ,4$ problem where the particles are connected by means of nonlinear elastic springs. By denoting with $r^{ij}$ the distance between the ith and the jth particle, for defining the potential energy of the elastic springs we make use of the Neo-Hooke-type potential given by [33]:

$$\begin{aligned}&V^{ij}(r^{ij})\!=\!\frac{k^{ij}}{6} \biggl [ r^{ij^{2}}\!+\!\biggl ( 2 \frac{r_{0}^{ij}}{r^{ij}}-3 \biggl ) r_{0}^{ij^{2}} \biggl ] ,\nonumber \\&r^{ij}\!=\![(u_{i}-u_{j})^{2}+(v_{i}-v_{j})^{2}+(w_{i}-w_{j})^{2}]^{\frac{1}{2}}, \end{aligned}$$

(45)

Fig. 4

Dumbell: sequence of configurations $t=$0..2; reference solution by solid line

Fig. 5

Dumbell: plot of stretch; reference solution by solid line

Fig. 6

Dumbell: increment of the total energy $t=$0..2

Fig. 7

Dumbell: normalized increments of the total energy $t=$0..10 in HFDI

$i,j=1,\ldots ,4$. The spring constants are assumed to be given by $k^{ij}=1$ for $(i,j)\ne (1,2)$ while $k^{ij}=10^{3}$ for $(i,j)=(1,2)$. In (45) $r_{0}^{ij}$ is the distance between particles in the force-free configuration where the relation $V^{ij}(r_{0}^{ij})=0$ holds. In view of (45), the forces of interaction are given by

$$\begin{aligned}&\mathbf{f}^{ij}(r^{ij}) = f^{ij}(r^{ij})\mathbf{e}^{ij} = \frac{dV^{ij}(r^{ij})}{dr^{ij}}{} \mathbf{e}^{ij} \nonumber \\&= \frac{k^{ij}}{3} \biggl [ r^{ij} - \biggl ( \frac{r_{0}^{ij}}{r^{ij}} \biggl )^{2} r_{0}^{ij} \biggl ] \mathbf{e}^{ij} . \end{aligned}$$

(46)

In (46) $\mathbf{e}^{ij}$ is the director individualized by the related i and j particles and $\mathbf{f}^{ij}(r_{0}^{ij})=\mathbf{0}$. The displacement vector of the i body of tetrahedra is represented by $\mathbf{u}_{i}^{T}=\{ u_{i} \,\, v_{i} \,\, w_{i} \}$. Then the initial position is described by the definitions $\mathbf{u}_{1}^{T}=\{ 0 \,\, 0 \,\, 0 \}$, $\mathbf{u}_{2}^{T}=\{ 1 \,\, 0 \,\, 0 \}$, $\mathbf{u}_{3}^{T}=\{ 0 \,\, 1 \,\, 0 \}$, $\mathbf{u}_{4}^{T}=\{ 0 \,\, 0 \,\, 1 \}$.

Fig. 8

Tetrahedra: initial configuration and problem definition

Starting at rest ($\mathbf{u}_{i,t}^{*}=\mathbf{0}$ for all i), the tetrahedra is subjected to a spatially fixed external load P(t) acting in the x direction on the first particle with time history as described in Fig. 8. For the considered integration methods Table 3 reports the related computational performances for increasing values of the $\bar{N}^{(it)}$ required iterations and for a $T_{o}=50$ observation time. In the Newmark scheme the reported steps values denotes that several divergences in corrector iterations occurs for high values of $\bar{N}^{(it)}$. A stable and efficient behaviour of Bathe and HFDI algorithms is also observed.

Table 3 Tetrahedra: computational characteristics of time integration algorithms for $T_{o}=$50

Accurancy in the analysis is evaluated by computing the error $\varepsilon _\mathbf{u}$ and $\varepsilon _\mathbf{f}$ in (42) for the $\mathbf{u}^{T}=\{ \mathbf{u}_{1}^{T} \,\, \mathbf{u}_{2}^{T} \,\, \mathbf{u}_{3}^{T} \,\, \mathbf{u}_{4}^{T} \}$ and $\mathbf{f}^{T}=\{ \mathbf{f}^{12^{T}} \,\, \mathbf{f}^{13^{T}} \,\, \mathbf{f}^{14^{T}} \,\, \mathbf{f}^{23^{T}} \,\, \mathbf{f}^{24^{T}} \,\, \mathbf{f}^{34^{T}} \}$ vectors, respectively. Figures 9 and 10, by varying the $\varDelta t_{\small mv }$ time step mean value, show that a better approximation of the quantities of interest is obtained by the HFDI algorithm in respect to the Newmark and Bathe algorithm. In effect the time step reported in the Bathe pattern takes in account both the sub-steps. We note how a non constant coefficient in the order of the approximations is obtained due to the adaptive time step size (see Fig. 11). In Fig. 12 and 13 we also report the sequence of configurations in the $x-y$ plane of the body 1 and the evolution of $f^{12}$ interaction force for $\varDelta t_{\small mv }$ about the value 0.30, respectively. As we can see, this test shows the overall effective behaviour of the HFDI integation procedure.

5.3 Articulated system

Here, we study the behaviour of an articulated system. The dynamics of three masses $m_{1}=m_{2}=m_{3}=$1 is stimulated by a force P(t) acting on mass $m_{1}$ and in the y-coordinate direction (see Fig. 14). Internal forces are due to the potential

$$\begin{aligned}&V(r,\alpha ) = \frac{1}{2}k_{e}\Big [\big (r^{12}-h\big )^{2}+\big (r^{23}-h\big )^{2}\Big ]\nonumber \\&+ \frac{1}{2}k_{f}\big (\alpha ^{12}-\alpha ^{23}\big )^{2} . \end{aligned}$$

(47)

The first term of the potential (47) expresses internal forces proportional to the distance $r^{ij}$ between $m_{i}$ and $m_{j}$ masses and with spring stiffness $k_{e}$ in the $r^{ij}=h$ force-free configuration. The second term of the potential (47) expresses an internal force proportional to the angle $\alpha ^{12}-\alpha ^{23}$ between $(m_{1},m_{2})$ body and $(m_{2},m_{3})$ body with spring stiffness $k_{f}$ in the $\alpha ^{12}=\alpha ^{23}$ force-free configuration. We assume $h=$0.5 and $k_{e}= 10^{7}$, $k_{f}= 10^{3}$. Time-stepping schemes applied to such three body problems can be found in [18].

The system is characterized by Cartesian state variables $\mathbf{u}^{T}=\{u_{1}\,v_{1}\,u_{2}\,v_{2}\,u_{3}\,v_{3}\}$. The definition of dynamical motion equations is here similar to that of the previous example. For completeness, we give the explicit formulae used for the definitions of the geometrical parameters $r^{ij}$ and $\alpha ^{ij}$:

$$\begin{aligned} r^{ij}= & {} \Big [\big (u_{j}-u_{i}\big )^{2}+\big (v_{j}-v_{i}\big )^{2}\Big ]^{\frac{1}{2}} , \end{aligned}$$

(48)

$$\begin{aligned} \alpha ^{ij}= & {} \arctan \bigg ( \frac{v_{j}-v_{i}}{u_{j}-u_{i}} \bigg ) . \end{aligned}$$

(49)

Applications of described integration schemes for increasing values of the target iteration count are investigated. Table 4 reports the computational characteristics performed in the time integration processes for the observing time $T_{o}=$0.5.

The motion of the articulated system, computed by Newmark, Bathe and HFDI methods with $\bar{N}^{it}=$5.0 is shown in Fig. 15. The evolution of the $\varDelta \alpha =\alpha ^{12}-\alpha ^{23}$ relative angle at the central body versus the time is also shown in Fig. 16 for the $\varDelta t_{\small mv }$ quantity about the value 0.0065. For the same $\varDelta t_{\small mv }$ value the increment of the total energy $\varDelta E_{n}$ in the step is shown in Fig. 17. The unstable behaviour in the Newmark formulation is observed. As can be seen, an unphysical chaotic motion of the system occurs at about $t=$0.2. Accurate representations are obtained by the presented HFDI algorithms, while a pronounced period elongation is observed in the Bathe experimentations. High frequency are not reproduced exactly although the mean value is provided by the algorithms. Finally, for several assigned values of $\bar{N}^{it}$ and for the long observation time $T_{o}=$3, the behaviour of the normalized increment of the total energy in the HFDI approach is showed in Fig. 18. We note that appreciable values of the energy increment are encountered only for high time steps and after many evolutions of the articulated system.

Fig. 9

Tetrahedra: truncation error of displacements

Fig. 10

Tetrahedra: truncation error of interaction forces

Fig. 11

Tetrahedra: adaptive time step size for several $\bar{N}^{(it)}$ values in HFDI based algorithm

Fig. 12

Tetrahedra: sequence of configurations of body 1 in the $x-y$ plane, Bathe $\bar{N}^{it}=$2$\cdot$4.0 and HFDI $\bar{N}^{it}=$4.0, $t=$0..50

Fig. 13

Tetrahedra: evolution of $f^{12}$ interaction force, Bathe $\bar{N}^{it}=$2$\cdot$4.0 and HFDI $\bar{N}^{it}=$4.0

5.4 Finite element Timoshenko beam

The plane movement of a toss rule is now investigated (examples of solutions of such a dynamical problem can be found in [19, 20, 34]). The characteristics of the examined time integration schemes will be shown here in connection with one-dimensional finite element discretizations. Standard linear two node shape functions for horizontal u and vertical v displacements and the rotation $\alpha$ of the cross section are used. Since the Timoshenko beam model is considered in the examined beam, only $C^{0}$ continuity for the displacements and rotations is needed at the element boundaries. A total Lagrangian co-rotational formulation is used to describe the motion of the element from the initial to the final deformed configuration. For a detailed account of the main co-rotational framework we can refer to the textbook [35] and to the articles [36,37,38].

In summary, the kinematic is split into two stages. First, a rigid translation and rotation of the local element frame is considered. This rigid motion is accompanied by deformation displacements with respect to the local element frame. We refer to the referential coordinate $\xi$ along the beam element centerline $-h/2\le \xi \le +h/2$. Then, by referring to the deformational displacements expressed in the local system, the total deformation energy V is obtained from:

$$\begin{aligned} V = \frac{1}{2} \int _{-h/2}^{+h/2} \big ( \mathrm{EA} \varepsilon ^{2} + \mathrm{GA} \gamma ^{2} + \mathrm{EJ} \chi ^{2} \big ) d\xi \end{aligned}$$

(50)

where EA, GA and EJ represent the axial, shear and flexural rigidities, respectively. In the $\mathbf{u}^{T}(\xi )=\{ u(\xi ) \,\, v(\xi ) \,\, \alpha (\xi ) \}$ state variable representation, measurements of the axial $\varepsilon$ and transversal $\gamma$ strain, together with the usual definition of the curvature $\chi$, are formulated by the following expressions:

$$\begin{aligned}&\varepsilon = \cos (\alpha _{o})\!\!-\!\!1\!\!+\!\!\big (C_{e}\cos (\alpha _{o})\!\!-\!\!S_{e}\sin (\alpha _{o})\big )u_{,\xi }\!\! \nonumber \\&\quad + \big (C_{e}\sin (\alpha _{o})\!\!+\!\!S_{e}\cos (\alpha _{o})\big )v_{,\xi }, \end{aligned}$$

(51)

$$\begin{aligned}&\gamma = -\!\sin (\alpha _{o})\!\!-\!\!\big (E_{e}\cos (\alpha _{o})\!\!+\!\!C_{e}\sin (\alpha _{o})\big )u_{,\xi }\!\!\nonumber \\&\quad +\big (C_{e}\cos (\alpha _{o})\!\!-\!\!S_{e}\sin (\alpha _{o})\big )v_{,\xi } , \end{aligned}$$

(52)

$$\begin{aligned}&\chi =\alpha _{,\xi } , \end{aligned}$$

(53)

where $S_{e}=\sin (\hat{\alpha })$ and $C_{e}=\cos (\hat{\alpha })$ specify the orientation ($\hat{\alpha }$) of the element in the initial configuration. We refer to an element with nodes i and j at the boundaries. Definitions like $\alpha _{o}=(\alpha _{i}+\alpha _{j})/2$ are used at the centre of the element.

Fig. 14

Articulated system: initial configuration and problem definition

Table 4 Articulated system: computational characteristics of time integration algorithms for $T_{o}=$0.5

The elemental internal force vector is then derived from the differentation of potential (50) with respect to the nodal parameters of the vector $\mathbf{u}^{T}=\{ u_{i} \,\, u_{j} \,\, v_{i} \,\, v_{j} \alpha _{i} \,\, \alpha _{j} \}$ in the $\mathbf{u}(\xi )$ interpolation. The elemental inertia force vector is derived from the differentation of kinetic energy here defined by

$$\begin{aligned} T= & {} \frac{1}{2}\Big [\rho hA\frac{1}{2}\big (u_{i,t}^{2}+u_{j,t}^{2}+v_{i,t}^{2}+v_{j,t}^{2}\big )\nonumber \\&\quad +\frac{1}{12}\rho h^{3}A\frac{1}{2}\big (\alpha _{i,t}^{2}+\alpha _{j,t}^{2}\big )\Big ] \end{aligned}$$

(54)

with respect to the first derivative of nodal parameters. By the definition (54) of the elemental kinetic energy, matrix $\mathbf{M}$ can be represented as a diagonal matrix. This simplifies the computation of the nonlinear motion Eq. (21) wherever an accurate representation of the inertia forces is achieved.

The geometry, material, position of loads and load function of the rule are described in Fig. 19. For discretization $N_{el}=$6 beam elements as described above are used. Table 5 shows the behaviour of the three different integration processes for $T_{o}=$0.1. The divergent behaviour of the corrector phase in the Newmark approach for high $\bar{N}^{it}$ values can be seen while a stable and efficient behaviour of Bathe and HFDI algorithms is verified. Accuracy in the analysis is now evaluated by compute the error $\varepsilon _{\alpha _{\small mv }}$ and $\varepsilon _{m_{\small c }}$ related to the definitions:

$$\begin{aligned} \alpha _{\small mv } = \frac{1}{N_{el}} \sum _{e=1}^{N_{el}} \alpha _{o}^{(e)} , \quad m_{\small c } = \mathrm{EJ} \chi \big |_{x=x_{\small c }} , \end{aligned}$$

(55)

where $\alpha _{o}^{(e)}$ refers to the elemental e value and $x_{\small c }$ is the x coordinate at the centre of the bar.

Fig. 15

Articulated system: sequence of configurations $t=0..0.5$; reference solution by solid line

Fig. 16

Articulated system: evolution of $\varDelta \alpha =\alpha ^{12}-\alpha ^{23}$ angle, Bathe $\bar{N}^{it}= 2\cdot 4.5$ and HFDI $\bar{N}^{it}=4.0$

Fig. 17

Articulated system: evolution of $\varDelta E_{n}$ total energy increment, Bathe $\bar{N}^{it}=2\cdot 4.5$ and HFDI $\bar{N}^{it}=4.0$

Fig. 18

Articulated system: normalized increments of the total energy $t=$0..3 in HFDI

Figures 20 and 21, for increasing $\varDelta t_{\small mv }$ time step mean values, show that the best approximation of the quantities of interest is obtained by the HFDI algorithm compared to the Newmark and Bathe algorithm. Moreover, we note that the time step reported in the Bathe patterns takes into account both the sub-steps. As usual, a non constant coefficient in the order of the approximations is obtained due to the adaptive time step size (as reported in Fig. 22). In Fig. 23 we report the evolution of mean value $\alpha _{,t\small mv }$ of the angular velocity $\alpha _{,t}$ defined as in expression (55). Likewise, Fig. 24 shows the evolution of central value $N{\small c }$ of the axial stress $EA\varepsilon$. A highly effective behaviour of the HFDI integation procedure is verified. Furthermore, no significant differences were detected in computational performances for refined meshes of the beam.

6 Conclusions

The presented work is concerned with the development of an effective time integration algorithm in nonlinear dynamic problems. The algorithm is based on a predictor–corrector procedure and employs the rewriting of motion as two sets of first-order differential equations. The features of the presented procedure are: a particular quadratic polinomial expression for the relevant quantities such as velocities and forces in the interpolation, a suitable extrapolation in the predictor phase and an optimization of the number of iterations in the corrector phase which generates an efficient adaptive time stepping selection. Furthermore, the following attributes characterize the type of integrators taken into account: (i) the approximation scheme is at least second-order accuracy; (ii) it is applicable to general nonlinear analyses; (iii) it does not involve additional variables or artificial parameters chosen by the user; (iv) it is a single-step scheme with self-starting attribute. For comparison, the widely used integration methods with the above characteristics such as Newmark and Bathe schemes are implemented with the same algorithm approach.

Fig. 19

Toss rule: geometry, material, loads and deformation

Table 5 Toss rule: computational characteristics of time integration algorithms for $T_{o}=0.1$

In the tests performed, N-body and finite element structural models are formulated and analized to compare the considered solution methods. For the presented algorithm, the tests show that stable and accurate solutions are obtained even for stiff nonlinear problems while there is reduced period elongation and high-frequency algorithmic damping in the analysis. The increase in computational effort due to the evaluation of the first derivative of the internal force vector, and consequent evaluation of the second derivative in the iteration matrix definition, is balanced by the increase in the range of stability of the time integration process and by the reduction in the number of Newton–Raphson iterations in the steps.

Fig. 20

Toss rule: truncation error of angular mean value $\alpha _{\small mv }$

Fig. 21

Toss rule: truncation error of bending moment central value $m_{\small c }$

Fig. 22

Toss rule: adaptive time step size for several $\bar{N}^{(it)}$ values in HFDI based algorithm

Fig. 23

Toss rule: evolution of mean value $\alpha _{,t\small mv }$ of the angular velocity $\alpha _{,t}$

Fig. 24

Toss rule: evolution of central value $N{\small c }$ of the axial stress $EA\varepsilon$

Therefore, if compared with widely used integration schemes with the above characteristics, such as the Newmark and Bathe schemes, the proposed method requires less computational effort combined with valuable accuracy and stability in the time analysis.