Abstract
We present a conservative/dissipative time integration scheme for nonlinear mechanical systems. Starting from a weak form, we derive algorithmic forces and velocities that guarantee the desired conservation/dissipation properties. Our approach relies on a collection of linearly constrained quadratic programs defining high order correction terms that modify, in the minimum possible way, the classical midpoint rule so as to guarantee the strict energy conservation/dissipation properties. The solution of these programs provides explicit formulas for the algorithmic forces and velocities which can be easily incorporated into existing implementations. Similarities and differences between our approach and well-established methods are discussed as well. The approach, suitable for reduced-order models, finite element models, or multibody systems, is tested and its capabilities are illustrated by means of several examples.
Similar content being viewed by others
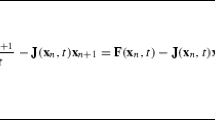
Avoid common mistakes on your manuscript.
1 Introduction
A key feature in the numerical approximations of conservative mechanical systems is their ability to exactly preserve the first integrals of their motion (energy, momenta, symplecticity, ...), replicating the properties of the continuous counterparts (see, e.g., [1, 2]). This interest in structure preserving integrators is hence justified by the qualitative similarity between the dynamical behaviour of a mechanical system and the discrete dynamics generated by the time integration scheme [3]. In addition, a wealth of evidence supports the fact that this kind of time-stepping methods behaves extremely well for long-term simulations [4,5,6,7,8,9].
It is not easy to formulate numerical schemes that unconditionally preserve one or more invariants of the discrete motion. Generally speaking, this goal is accomplished by ensuring that some of the (abstract) geometric structures that appear in the continuous picture are replicated in the discrete dynamics. Since it is well-known that, in general, all invariants cannot be preserved for a fixed time step size scheme, different families of methods strive for the preservation of specific subsets of the various symmetries of the continuous system. For example, some numerical methods resemble discrete Hamiltonian systems [6], based on discrete gradient operators, and unconditionally preserve the energy and the (at most quadratic) momenta. Other methods emanate from discrete variational principles [10] and obtain the update formula from the stationarity conditions of these principles. In fact, it is possible to formulate methods that preserve energy, momenta, and the symplectic form of the system, if the time step size is added as an unknown to the method’s equations [7].
In the context of nonlinear elastodynamics, the first energy and momentum conserving algorithms were developed by Simo and co-workers [4]. This pioneering work showed that for Saint Venant–Kirchhoff materials, such structure preserving methods can be easily obtained by a simple modification of the midpoint rule in which the stress, instead of being evaluated at the midpoint instant, should be taken as the average of the stresses at the endpoints of the time interval. Since the constitutive law is linear in the strain, this turns to be equivalent to compute the algorithmic stress with the average of the strains at the endpoints of the time interval. This simple idea was later applied to the conserving integration of shells [5], rods [11, 12], contact mechanics [13], multibody systems [14, 15], etc., and generalized to elastic materials of arbitrary type [16, 17]. The key idea for such generalization is the definition of a discrete gradient operator, a consistent approximation of the gradient that guarantees the strict conservation of energy in Hamiltonian systems [16, 18,19,20]. Alternatively, one might derive conserving methods by defining an average vector field [8, 21]. In the context of the continuous Galerkin method, an optimization approach was employed to systematically develop high-order energy conserving schemes [22, 23]. Very recently, a new mixed variational framework that takes advantage of the structure of polyconvex stored energy functions was proposed [24], and the properties of several formulas for the discrete gradient that are available in the literature were carefully analyzed in the context of multibody systems [25].
Many Hamiltonian problems are modeled with stiff differential equations for which conserving integration schemes might not be the most robust. For these problems, numerical methods with controllable numerical dissipation in the high-frequency range provide often a practical solution [26,27,28,29,30]. Based on a modification of the discrete gradient operator, Armero and Romero [9, 31] developed a family of schemes for nonlinear three-dimensional elastodynamics that exhibits this kind of algorithmic dissipation, while preserving the momenta and providing a strict control of the energy, applicable to elastodynamics, as well as to rods and shells [32, 33]. Following an alternative path based on the average vector field, Gebhardt and co-workers have proposed similar conserving/dissipative methods for general solid and structural problems [34, 35].
This work considers the conservative/dissipative time integration of the equations of motion that typically arise during the analysis of nonlinear mechanical systems. More specifically, we present a novel approach that renders, by construction, methods with the desired conservation or dissipation properties. These methods discretize the equations of motion and add some perturbations related to the main field variables through a collection of ancillary linearly constrained quadratic programs that guarantee the conservation/dissipation properties. This kind of programs are analytically solvable and therefore, very attractive from the computational point of view. One possible interpretation of the contributions in this article is that it results in conservative/dissipative methods where the geometric arguments typically employed for their design have been replaced by optimality conditions.
The perturbations proposed in the new methods are designed to correct some of the unwanted effects coming from the discretization of the governing equations. From a geometric point of view, the idea is to redesign the problem in such a way that the behavior of the system on the discrete constrained sub-manifold remains unaltered, but acts as an attractor for trajectories outside of it. Since the constrained programs can be solved in closed form, corrected formulas for the algorithmic internal forces and generalized velocities can be provided, and thus easily incorporated in existing simulation codes. The similarities and differences of the newly proposed method with respect to existing ones are pointed out and discussed critically.
The remaining of the article is organized as follows: In Sect. 2, we present the basic framework for nonlinear mechanical systems. In Sect. 3, we address in a comprehensive manner the new time discretization. In Sect. 4, we present several examples of increasing complexity for the verification of the method. Finally, conclusions, limitations and future work are presented in Sect. 5. Additionally, the “Appendix” introduces the precision quotient, with which the correctness of an implementation can be tested.
2 Mechanical framework
2.1 Statement
In this work we consider mechanical systems whose configuration is completely defined by a vector \(\varvec{q}\in Q\), where \(Q\subseteq \mathbb {R}^n\). Denoting by t the time, the state of the system at any instant is given by the pair \((\varvec{q}, \varvec{s})\in W\equiv TQ\), where \(\varvec{s}=\dot{\varvec{q}}\) is the velocity, and in which we have employed the notation \(\dot{(\cdot )} = \frac{\mathrm {d}(\cdot )}{\mathrm {d}t}\). The dynamical behavior of this system, for \(t\in [t_a,t_b]\) is governed by the variational equation:
where \((\delta \varvec{q},\delta \varvec{s})\in TW\) are admissible variations of the generalized coordinates and velocities, \(\varvec{p}(\dot{\varvec{q}})\in T_{\varvec{s}}^*S\) and \(\varvec{\pi }(\varvec{s})\in T_{\varvec{s}}^*S\) stand for the generalized-coordinate-based and generalized-velocity-based momenta, respectively, \(\varvec{f}^{\text {int}}\in T_{\varvec{q}}^*Q\) is the vector of internal forces, \(\varvec{f}^{\text {ext}}\in T_{\varvec{q}}^*Q\) is the vector of external loads that can be of conservative or non-conservative nature, and finally, \(\bigl \langle \cdot ,\cdot \bigr \rangle \) represents a suitable pairing. Additionally, we assume the following two conditions: (i) the system possesses a positive-definite symmetric mass matrix \(\varvec{M}\) such that
and, (ii) both the internal and the external forces derive from potential functions depending only on the configuration \(\varvec{q}\), i.e.,
and we define the total potential energy of the system as \(V=V^{\text {int}}+V^{\text {ext}}\).
We would like to analyze next the implications that symmetry has on the form of the internal forces and the appropriate notions of linear and angular momentum in the abstract space Q. For that, the relation between the configuration space Q and the ambient space \(\mathbb {R}^3\) has to be carefully considered. We start by defining \(\varPhi :\mathbb {R}^3 \times Q\rightarrow Q\) to be a smooth action of \(\mathbb {R}^3\) on the configuration space such that \(\varPhi (\varvec{a},\varvec{q})\) is the configuration of the system after all its points have been translated in space by constant vector \(\varvec{a}\). The infinitesimal generator of this translation at \(\varvec{q}\) is the vector \(\varvec{\tau }_{\varvec{a}}(\varvec{q})\in T_{\varvec{q}}Q\) defined as
with \(\epsilon \in \mathbb {R}\). Let us now assume internal potential energy is invariant under translations, i.e.,
Then, choosing a one parameter curve of translations \(\varPhi (\epsilon \,\varvec{a},\cdot )\) in Eq. (5) and differentiating with respect to \(\epsilon \), it follows that a translation invariant potential implies that the internal forces satisfy
To study the conservation of angular momentum, we must repeat the same argument but considering now a second smooth action \(\varPsi :\mathbb {R}^3\times Q \rightarrow Q\) such that \(\varPsi (\varvec{\theta },\varvec{q})\) is the configuration of the system after all its points have rotated in ambient space by the application of a rotation \(\exp [\hat{\varvec{\theta }}]\). Defining, as before, the infinitesimal generator of this action to be the vector \(\varvec{\rho }_{\varvec{\theta }}(\varvec{q})\in T_{\varvec{q}}Q\) calculated as
again with \(\epsilon \in \mathbb {R}\). If the potential energy is now rotation invariant, i.e.,
Then the internal force must satisfy
The precise notion of linear and angular momentum for the system defined in this section is provided by the following result:
Theorem 1
Consider a mechanical system with configuration space \(Q\subseteq \mathbb {R}^n\) and vanishing external forces. Let \(\varPhi (\varvec{a},\cdot ),\varPsi (\varvec{\theta },\cdot )\) be the translation and rotation actions on the configuration space with infinitesimal generators \(\varvec{\tau }_{\varvec{a}}\) and \(\varvec{\rho }_{\varvec{\theta }}\), respectively, and define the linear momentum \(\varvec{l}\in \mathbb {R}^3\) and the angular momentum \(\varvec{j}\in \mathbb {R}^3\) as the two quantities that verify
Then, the linear momentum is conserved if the potential energy is invariant with respect to translations. Similarly, if the potential energy is invariant under rotations, the angular momentum is a constant of the motion. Moreover, the total energy
is preserved by the motion, due to its time invariance.
Proof
The proof of momenta conservation follows from taking the derivative of these quantities and using (1) with admissible variations \((\delta \varvec{q}, \delta \varvec{s}) = (\varvec{\tau }_{\varvec{a}}(\varvec{q}), \varvec{0})\) and \((\varvec{\rho }_{\varvec{\theta }}(\varvec{q}), \varvec{0})\), respectively. The conservation of energy property follows similarly by choosing \((\delta \varvec{q}, \delta \varvec{s}) = ( \varvec{s}, \varvec{0})\). \(\square \)
3 Time discretization
The interest in the current work is in algorithms to approximate the solution of Eq. (1). To define them, let us start by considering a partition of the interval \([t_a,t_b]\) into disjoint subintervals \((t_n,t_{n+1}]\) with \(t_a=t_0<t_1<\ldots <t_N=t_b\), and \(\varDelta t_n = t_{n+1}-t_n\). Then, the integration algorithms that we consider are based on the midpoint approximation of Eq. (1) and of the form:
where the configuration and rate, respectively, at time \(t_n\) are approximated by \(\varvec{q}_n,\varvec{s}_n\), we have defined \(\varvec{\pi }_n = \varvec{M}\varvec{s}_n\), and we have used the notation \((\cdot )_{n+1/2} = \frac{1}{2} (\cdot )_n + \frac{1}{2} (\cdot )_{n+1}\). The update depends on the definition of an approximation to the internal force at the midpoint \(t_{n+1/2}\) that we have denoted as \(\varvec{\mathsf {f}}^{\mathrm {int}}\).
Equation (12) provides an implicit or explicit update \((\varvec{q}_n,\varvec{s}_n)\mapsto (\varvec{q}_{n+1},\varvec{s}_{n+1})\) that, together with the initial conditions of the configuration and velocity, suffices to generate discrete trajectories. We note that the approximation to the internal force in Eq. (12) is a function of two arguments that, by consistency, must satisfy
for all configurations \(\varvec{q}\in Q\).
We are interested, in particular, in formulating time integration schemes of the form (12) that preserve (some of) the invariants in the motion of the system (1), while controlling the value of the energy at all times. Let us first consider the update Eq. (12) with variations of the form \((\delta \varvec{q}, \delta \varvec{s})=(\varvec{0},\varvec{c})\), where \(\varvec{c}\) is an arbitrary but constant vector in TQ. Then, trivially, it follows that
Next, we would like to explore whether the proposed class of integration schemes preserves momenta for mechanical systems defined in the configuration space Q. The result, for every configuration space, is given next.
Theorem 2
Consider the time discretization (12) of a mechanical system with configuration space \(Q\subseteq \mathbb {R}^n\). Let \(\varPhi \) and \(\varPsi \) denote, as above, the actions of \(\mathbb {R}^3\) on Q representing, respectively, translations and rotations. The integration scheme preserves linear momentum if
for every \(\varvec{a}\in \mathbb {R}^3\). Likewise, the integration algorithm preserves angular momentum if for every \(\varvec{\theta }\in \mathbb {R}^3\)
The verification of conditions (2)–(2) depends, first, on the structure of Q. For example, if we consider \(Q\equiv \mathbb {R}^{3n}\), the configuration space of n particles in three-dimensional Euclidean space, conditions (15b)–(16b) are easily verified. Conditions (15a)–(16a) depend not only on Q but also on the form of \(\varvec{\mathsf {f}}^{\mathrm {int}}\) which has been, up to this point, left unspecified. For example, the canonical midpoint rule employs \(\varvec{\mathsf {f}}^{\mathrm {int}}(\varvec{x},\varvec{y}) = \varvec{f}^{\text {int}}((\varvec{x}+\varvec{y})/2)\), and preserves both linear and angular momenta, but not energy. In turn, the Energy-Momentum method [4, 5] provides an expression for this force that guarantees strict energy conservation in the discrete update map, without upsetting the preservation of momenta. Expanding on this idea, the Energy-Dissipative-Momentum-Conserving method [9, 31] adds controllable energy dissipation to the solution, so small that does not upset the accuracy of the solution, yet large enough that can damp out some of the spurious oscillations in the high-frequency part of the solution.
3.1 Discrete derivative
As already mentioned, the direct evaluation of the internal forces at the midpoint configuration does not guarantee, in general, the preservation of energy. There exist however, consistent approximations of these forces that strictly enforce this property of conservative equations.
To introduce the form of this “conservative” approximation of the internal energy let us assume as in Sect. 2 that the internal forces derive from a smooth potential \(V:Q\rightarrow \mathbb {R}\). Be aware that from now on, we remove the superindex \({\text {int}}\), since no external force is longer considered along the derivation presented next. The type of approximations we search for are referred in the literature as “discrete derivatives” [6] and are functions \(\varvec{\mathsf {f}}:Q\times Q\rightarrow \mathbb {R}\) that satisfy, for every \(\varvec{x},\varvec{y}\in Q\), two properties, namely:
- i.
Directionality:
$$\begin{aligned} \langle \varvec{\mathsf {f}}(\varvec{x},\varvec{y}),\varvec{y}-\varvec{x}\rangle =V(\varvec{y})-V(\varvec{x})\,. \end{aligned}$$(17) - ii.
Consistency:
$$\begin{aligned} \varvec{\mathsf {f}}(\varvec{x},\varvec{x}) = - DV(\varvec{x}) =\varvec{f}(\varvec{x}) , \end{aligned}$$(18)where D denotes the standard derivative operator.
When \(Q\subset \mathbb {R}\), there only exists one discrete derivative [8] and its closed form expression is given by
with the well-defined limit
In higher dimensions, there are actually an infinite number of discrete derivatives [8, 20] since only the component of \(\varvec{\mathsf {f}}\) along the direction of \(\varvec{y}-\varvec{x}\) needs to have a precise value in order to guarantee energy conservation, and its orthogonal complement is free to vary, as long as consistency of the approximation is preserved. This statement is formalized next:
Theorem 3
Any discrete derivative can be rewritten as
with \(\varvec{\mathsf {g}}(\varvec{x}, \varvec{y})\) a vector-valued function such that
and
where \(\varvec{\mathfrak {P}}_{(\varvec{y}-\varvec{x})}^\perp \) is the projection on the component perpendicular to \(\varvec{y}-\varvec{x}\).
Proof
Let \(\varvec{\mathsf {g}}(\varvec{x}, \varvec{y})\) be defined as
it is apparent that \(\varvec{\mathsf {g}}(\varvec{x}, \varvec{y})\) is perpendicular to \(\varvec{y}-\varvec{x}\) because \(\left\langle \varvec{\mathsf {f}}(\varvec{x}, \varvec{y}),\varvec{y}-\varvec{x}\right\rangle = V(\varvec{y})-V(\varvec{x})\), and
which tends to zero as \(\varvec{y} \rightarrow \varvec{x}\). \(\square \)
3.2 Conservative algorithmic force
We explore next a type of discrete derivative that is different to the one usually employed in nonlinear mechanics [4, 16]. For that, we construct first a convex combination of the (exact) derivative at two configurations, i.e.,
or in a more compact form
In this expression, the scalar \(\alpha ^{\mathrm {cons}}\) has to be determined in order to guarantee directionality, \(\varvec{f}_{a}\) is the averaged force
and \(\tilde{\varDelta }\varvec{f}\) is one half of the force jump between the configurations at times \(t_{n}\) and \(t_{n+1}\), i.e.,
Notice that this conservative approximation satisfies, by construction, the consistency condition (18). The satisfaction of directionality depends, as advanced, on the choice of the parameter \(\alpha ^{\mathrm {cons}}\). To enforce it, we select \(\alpha ^{\mathrm {cons}}\) by means of an optimality condition [20], namely, as the scalar that minimizes
Assuming \(\varvec{f}(\varvec{x}) \ne \varvec{f}(\varvec{y})\), this optimization problem is a linearly constrained quadratic program that can be solved in closed form. Moreover, the only requirement for the optimization problem to be convex is that \(\Vert \varvec{f}(\varvec{y})-\varvec{f}(\varvec{x})\Vert ^2_{\varvec{\mathfrak {G}}} > 0\). Its solution can be interpreted as the discrete derivative that is closest to \(\varvec{f}_m\), the continuous force at the midpoint \(\varvec{f}_{m}\), namely,
Here, \(\varvec{\mathfrak {G}}\) is a metric tensor. The Lagrangian of the optimization problem is
where \(\lambda ^{\mathrm {cons}}\) is a Lagrange multiplier that enforces directionality. To find the stationarity condition, the variation of \(\mathcal {L}\) is calculated as:
Now for the sake of brevity, let us introduce a discrete function defined as
From now on, we refer to this function as a conservation function, which allows the preservation energy in the discrete setting for a given fixed time step \(\varDelta t\). This conservation function is not unique and depends, in principle, on the shape of the approximated discrete form.
The stationarity condition for the associated Lagrangian function can be reformulated as the linear system that is explicitly given by
with
and
The solution of this program is
and
Notice that \(\alpha ^{\mathrm {cons}}\) does not depend on the chosen metric. Then, we can claim that the adopted construction affords a unique definition. This feature represents a main innovation of the current work. However and up to this point, it is not clear to which extent the current formula approaches the commonly used formulas like the one due to Gonzalez [6] or the one due to Harten et al. [21]; a comparison of that second method with the current one is beyond the scope of this work.
In contrast, the Lagrange multiplier \(\lambda ^{\mathrm {cons}}\) depends on the chosen metric. Finally, the conservative part of the discrete force takes the following explicit form:
In the context of nonlinear elastodynamics, the first term of the formula is equivalent to the definition proposed by Simo and Tarnow [4] that was derived in the context of Saint Venant–Kirchhoff materials. The second term can be interpreted as a correction for the most general hyperelastic case. The formula proposed by Gonzalez [6] cannot be algebraically reduced to the proposed expression, because the former is basically a correction for \(\varvec{f}_{m}\) and the latter, for \(\varvec{f}_{a}\).
The conserving force given by Eq. (42) can be rewritten in the form of Eq. (21) and therefore, is a discrete derivative with
where \(\varvec{\mathfrak {P}}_{({\varvec{y}-\varvec{x}})}^\parallel \) is the projection parallel to \(\varvec{y}-\varvec{x}\), and
3.3 Dissipative algorithmic force
To account for dissipation, let us assume the existence of a dissipative part of the algorithmic internal force that is proportional to \(\tilde{\varDelta }\varvec{f}\), this is
where \(\alpha ^{\mathrm {diss}}\) is a scalar whose precise definition is still open. This construction is supported by the analysis done by Romero [20], which showed that other choices may destroy the accuracy of the approximation. We will see later that this expression is very attractive since it provides an unifying treatment of both conservative and dissipative parts of the algorithmic internal force.
To find the value of \(\alpha ^{\mathrm {diss}}\), we define a discrete dissipation function \(\tilde{\mathcal {D}}_{f}(\varvec{x},\varvec{y})\), which must be positive semi-definite, at least second order in \(\Vert \varvec{y}-\varvec{x}\Vert \) to avoid spoiling the accuracy of the algorithm, and tend to 0 as \(\varvec{x}\) tends to \(\varvec{y}\). Then \(\alpha ^{\mathrm {diss}}\) can be obtained as the scalar that minimizes
This is also a linearly constrained quadratic program. The solution of this optimization problem can be interpreted as the smallest perturbation force that satisfies the dissipation relation \(\langle \varvec{y}- \varvec{x},\varvec{\mathsf {f}}^{\mathrm {diss}}\rangle =\mathcal {\tilde{D}}_{f}(\varvec{x},\varvec{y})\). Once again, \(\varvec{\mathfrak {G}}\) is a given metric tensor and the associated Lagrangian is simply
where \(\lambda ^{\mathrm {diss}}\) is a Lagrange multiplier that enforces the dissipation constraint. To formulate the stationarity condition, the variation of the associated Lagrangian has to be computed. This procedure yields
Noting that \(\delta \varvec{\mathsf {f}}^{\mathrm {diss}} = \delta \alpha ^{\mathrm {diss}} \tilde{\varDelta }\varvec{f}\), the stationarity condition of the Lagrangian can be written explicitly as
with
The solution of this linearly constrained quadratic program is
and
As in the case of the conservative part of the algorithmic force, the parameter \(\alpha ^{\mathrm {diss}}\) does not depend on the chosen metric and therefore, it is unique. However and up to this point, it is not clear to which extent the current formula approaches already established formulas, especially the one due to Armero and Romero [9, 31]. As in the case of the conservative part of the approximation, the multiplier \(\lambda ^{\mathrm {diss}}\) depends on the chosen metric. Finally, the formula for the dissipative part of the algorithmic internal force takes the following explicit form:
Notice that this formula has the same structure as the second term of the conservative part of the algorithmic force. However, instead of the conservation function, the dissipation function appears in the numerator. This fact suggests that a unifying formula containing both conservative and dissipative parts is possible, which makes the approach very attractive.
3.4 Generalization and preservation of momenta
Assuming an additive composition of the algorithmic approximation of the force, that is,
we can write, using Eqs. (42) and (53),
This formula is very compact and a simple inspection confirms that when the dissipation is zero, the directionality condition is exactly verified.
To accommodate the preservation of linear and angular momenta as discussed in Eqs. (2) and (2), Eq. (55) must be modified as indicated next: Let G be a Lie group with algebra \(\mathfrak {g}\) and coalgebra \(\mathfrak {g}^{*}\), which acts on the configuration space \(Q\subseteq \mathbb {R}^{3n}\) by means of the action \(\varvec{\chi }:G\times Q\rightarrow Q\). For every \(\varvec{\xi }\in \mathfrak {g}\), let \(\varvec{\xi }_Q: Q\rightarrow TQ\) denote the infinitesimal generator of the action. Following again Gonzalez [6], we can define G-equivariant derivatives. If \(V:Q\rightarrow \mathbb {R}\) is a G-invariant function, its G-invariant discrete derivative is a smooth map \(\varvec{\mathsf {f}}^G:Q\times Q\rightarrow \mathbb {R}\) that satisfies the requirements of discrete derivatives and, moreover, the equivariance and orthogonality condition, namely,
for all \(\varvec{x}, \varvec{y} \in Q\), \({\varvec{g}}\in G\), and
To construct a G-equivariant discrete derivative, consider invariant functions under the symmetry action denoted by \(\pi _i\), \(i=1,2,....,q\) where q is the dimension of the quotient space Q / G. Let \(\varvec{\varPi }=(\pi _1, \pi _2,...,\pi _q)\). If \(V:Q\rightarrow \mathbb {R}\) is G-invariant, a reduced function \(\tilde{V}\) can be defined by the relation \(V=\tilde{V}\circ \varvec{\varPi }\). If each of the invariants is at most of degree two, then a G-equivariant discrete derivative for V can be constructed as
where, as before \(\varvec{x}, \varvec{y} \in Q\). In particular, the formulation of a G-equivariant discrete derivative that preserves linear and angular momenta (cf. Eqs. 2 and 2) is straightforward.
The expression of the G-equivariant force in the current context is given by
with \(\varvec{z}=(\varvec{x}+\varvec{y})/2\) and
3.5 Interpretation of the conservative algorithmic force
There exist infinite second order accurate approximations of the midpoint force that that lead to energy and momentum conserving discretizations [20]. A general expression for the algorithmic force that is in agreement with the definition of the discrete derivative is given by
where \(\varvec{\mathfrak {G}}\) is the matrix representation of a suitable metric tensor and its associated conservation function is
As shown in [20], the choice of the metric tensor in Eq. (61) is crucial, since a wrong choice can destroy the accuracy of the solution even when the directionality and consistency properties are verified. The general expression can be reduced to the original formula proposed in [6] just by adopting the standard Euclidean metric tensor, i.e.,
Until now, this original formula has been regarded as the optimal one from the implementation point of view. By visual inspection of Eq. (42), it is also possible to claim that the formula derived in this work is as easy to implement as the original one given in Eq. (63). Moreover, the new formula requires only evaluations at the endpoints of the time interval and not at the midpoint.
Next, we would like to analyze the formula (42) in terms of the general expression provided by Eq. (61). First, defining \(\varvec{z}\) to be the average \(\varvec{z}=(\varvec{x}+\varvec{y})/2\), we make use of Taylor’s theorem to compute
and
The averaged force can be expressed as
and
The force jump can be written as
and
Now putting everything together, we can rewrite Eq.(42) as
Taking a look at this expression, it is apparent that the discrete force (42) is a second order perturbation of the midpoint approximation and that the metric employed for the definition of the conserving correction is just
We conclude that the an integration scheme based on Eq. (27) would behave locally in a very similar manner to a method based on Eq. (61) with metric (71). Their global behavior can, in general, differ.
3.6 Dissipative algorithmic velocity
As proposed in [9, 31], the generalized velocity can also be expressed as the linear combination of a conservative and a dissipative component. If the mass matrix is configuration-independent, the midpoint rule provides precisely the conservative part of the velocity. Following the ideas adopted for the formulation of the dissipative part of the algorithmic force, we find next the smallest perturbation of the midpoint velocity that guarantees dissipation according to a given dissipation function \(\tilde{\mathcal {D}}_{s}(\varvec{u},\varvec{v})\), which must be non-negative, at least second order accurate in \(\Vert \varvec{v}-\varvec{u}\Vert \), and tend to 0 as \(\varvec{u}\) tends to \(\varvec{v}\).
According to the midpoint rule, the conservative part of the algorithmic velocity can be expressed as
where the velocity \(\varvec{u}\) corresponds to time instant \(t_{n}\), the velocity \(\varvec{v}\) corresponds to time instant \(t_{n+1}\) and \(\varvec{w}\) is the averaged velocity. This particular choice preserves linear and angular momenta. The preservation of energy is guaranteed when the relation
is satisfied, with T being the kinetic energy. Equivalently, this expression can be obtained from \(\langle \delta \varvec{s}_{n+1/2}, \varvec{\pi }(\varvec{\mathsf {s}}^{\mathrm {cons}})\rangle =T(\varvec{v})-T(\varvec{u})\) when the variation is of the form \(\delta \varvec{s}_{n+1/2}=\varvec{v}-\varvec{u}\). It is apparent that the conservative part of the algorithmic velocity adopted fulfills this condition without need for further corrections.
Now we follow an idea that is slightly different to the one previously used to derive the dissipative part of the algorithmic force. Henceforth, let us assume the existence of a dissipative part of the algorithmic velocity proportional to \(\varvec{\mathsf {s}}^{\mathrm {cons}}\), this is
where \(\beta ^{\text {diss}}\) is a scalar to be found that must guaranteed the dissipation of energy according to a given dissipation function \(\tilde{\mathcal {D}}_{s}(\varvec{u},\varvec{v})\). This scalar can be obtained as the minimizer of
where \(\varvec{M}\) is the mass matrix. Equation (75) defines a quadratic program with linear constraints. Its solution can be interpreted as the smallest non-conservative velocity perturbation that satisfies for a discrete variation of the form \(\delta \varvec{s}_{n+1/2}=\varvec{v}-\varvec{u}\), an energy dissipation according to the adopted rule. The associated Lagrangian function of the optimization problem is
where \(\mu ^{\text {diss}}\) is a Lagrange multiplier that enforces the dissipation constraint. To formulate the stationarity condition, the variation of the associated Lagrangian function has to be computed. This procedure yields
Noting that \(\delta \varvec{\mathsf {s}}^{\mathrm {diss}}=\delta \beta ^{\mathrm {diss}}\varvec{\mathsf {s}}^{\mathrm {cons}}\), the stationarity condition of the Lagrangian can be written explicitly as
with
and
The solution of this linearly constrained quadratic program is
and
Finally, the formula for the dissipative part of the algorithmic velocity takes the following explicit form:
Assuming an additive composition of the algorithmic approximation of the velocity, that is,
we can write
This formula is identical to the formula proposed in [9, 31] that was derived by employing only geometric arguments. This time, it can be clearly interpreted as an optimal approximation.
3.7 Final equations
The combination of all ingredients discussed here yields the full discrete formulation of the dynamic equilibrium for nonlinear mechanical systems. These consist of two residuals, one for the generalized velocities and another for the generalized coordinates, namely,
where both residuals have to be minimized at every time step. This task is accomplished by means of a Newton-Raphson algorithm.
The generalized-velocity-based momentum term in its algorithmic form is
The generalized-coordinate-based momentum term in its discrete version becomes
The generalized-coordinate-based momentum rate term in its algorithmic form is
Finally, the generalized internal force becomes
In the case of accommodating the preservation of linear and angular momenta, we require the G-equivariant version given by
where
and \(\varvec{\varPi }_{n}=\varvec{\varPi }(\varvec{q}_{n})\). The discrete conservation function is given by
and its G-equivariant version given by
The most basic discrete dissipation function at the level of the generalized internal force that can be chosen is
or its G-equivariant counterpart expressed as
where \(\tilde{\varvec{q}}_{n}\) could correspond to an intermediate configuration, and \(\varvec{D}\) is constant, symmetric and positive semi-definite. The dissipation function for the velocity is of the form
or its G-equivariant version given by
where \(\tilde{\varvec{s}}_{n}\) could correspond to an intermediate configuration. With this setting, unconditional stability in the nonlinear sense can be achieved. The chosen dissipation functions correspond to those proposed in [9, 31] for the EDMC-1/2.
4 Numerical results
In this section, we present four numerical examples which were chosen to show the potentialities of the proposed approach. With these, we do not pretend to test the new approach exhaustively, but at rather provide some insight on its properties. For this purpose, we study first two examples involving two-mass systems with potential functions that can arise in the context of reduced-order models, and then two examples of nonlinear elastic shell structures employing a neo-Hookean material. Additionally, we briefly discuss the dissipation properties of the proposed scheme in the high-frequency range.
4.1 Reduced-order models
The first example is a mechanical system with two degrees of freedom whose potential function possesses polynomial complexity. The second one considers another mechanical system with also two degrees of freedom, but whose potential function shows non-polynomial complexity. Here, we adopt the most basic discrete dissipation functions at the level of the generalized internal force and at the level of the generalized velocity that are given by
in which \(\varvec{D}\) is a constant symmetric semi-positive definite matrix, and
where \(\chi _{f}\) and \(\chi _{s}\) in \(\mathbb {R}_{\ge 0}\) are merely dissipation parameters. For both examples, four cases are considered: i) fully conservative, i.e., \(\chi _{f}=\chi _{s}=0\); ii) dissipative at the level of the generalized internal force, i.e., \(\chi _{f}\ne 0\) and \(\chi _{s}=0\); iii) dissipative at the level of the generalized velocities, i.e., \(\chi _{f}=0\) and \(\chi _{s}\ne 0\); and, iv) fully dissipative, i.e., \(\chi _{f}\ne 0\) and \(\chi _{s}\ne 0\). Additionally, to numerically gain some insight about the accuracy of the method, we provide for these two examples and all cases the second quotient of precision \(Q_{\mathrm {II}}(t)\) computed on the basis of the corresponding states \(\varvec{\xi }\in W\), namely \(\varvec{\xi }=(\varvec{q},\varvec{s})\). The definition of \(Q_{\mathrm {II}}(t)\) is presented in the “Appendix”.
4.1.1 Two-mass system with a polynomial potential
Here, we consider a nonlinear oscillatory mechanical system with potential function
This kind of systems naturally arises in the context of reduced-order models, see for instance [36, 37]. To perform our computations, we adopt a model with two degrees of freedom used as a demonstrator in [36]. The non-zero mechanical properties are \(M_{11}=M_{22}=1\,\mathrm {Kg}\), \(V_{11}^{\mathrm {II}}=V_{22}^{\mathrm {II}}=16\,\mathrm {N/m}\), \(V_{12}^{\mathrm {II}}=V_{21}^{\mathrm {II}}=-15\,\mathrm {N/m}\) and \(V_{1111}^{\mathrm {IV}}=15\,\mathrm {N/m^3}\). The simulation parameters are initial time \(t_{i}=0\,\mathrm {s}\), final time \(t_{f}=T\,\mathrm {s}\), simulation time \(T=50~\mathrm {s}\), time step \(\varDelta t=0.001\,\mathrm {s}\) and relative iteration tolerance \(\varepsilon =10^{-10}\). Additionally, for the dissipative cases, we set \(\chi _{f}=0.0025\) and \(\chi _{s}=0.008\) as well as \(\varvec{D}=\varvec{V}^{\mathrm {II}}\). The initial conditions employed are
Figure 1 shows the idealized mechanical system under consideration and Fig. 2 presents a plot of the potential function, which is clearly convex within the region where the dynamics of the system takes place. Figure 3 shows different plots for the solution of the fully conservative case. We can observe the very complex and nonlinear oscillatory behavior, which is also in excellent agreement with those results presented in [36].
Two masses connected by linear springs between two walls. The first mass is also connected to the left wall through a nonlinear spring
Potential function with polynomial complexity
Fully conservative case; extended configuration and velocity diagrams
Fully conservative case; energy and \(Q_{\mathrm {II}}\)
Dissipative case at the level of internal forces; energy and \(Q_{\mathrm {II}}\)
Dissipative case at the level of generalized velocities; energy and \(Q_{\mathrm {II}}\)
Fully dissipative case; energy and \(Q_{\mathrm {II}}\)
On the left of Figs. 4, 5, 6 and 7, the evolution of the kinetic, potential, and total energies is shown. On the right of these figures, we show the second precision quotient also as a function of time. Figure 4 evidently corresponds to the fully conservative case. Figure 5 shows the dissipative case at the level of the generalized internal forces. Figure 6 corresponds to the dissipative case at the level of the generalized velocities. Finally, Fig. 7 corresponds to the fully dissipative case. In the latter, the energy decay is larger than the two previous cases.
For all cases the second quotient of precision is almost constant and its value is approximately 4. Therefore, as expected, the numerical method is second-order accurate. According to Eq. (115), a method of a given order is unable to produce solutions with higher quotients of precision. In [38], it is stated that even if the method is correctly implemented, it is not trivial to find the right set of parameters in order to numerically obtain precision quotients of a high quality like the one presented herein.
4.1.2 Two-mass system with a non-polynomial potential
Next, we consider a nonlinear oscillatory mechanical system whose potential function is
in which the conditions \(V_{ab}^{\mathrm {II}}=V_{ba}^{\mathrm {II}}\), \(V_{ab}^{\mathrm {N}}=V_{ba}^{\mathrm {N}}\) and \(V_{ab}^{\mathrm {D}}=V_{ba}^{\mathrm {D}}\) are used for the sake of simplicity. This kind of systems could arise in the context of Euler-Bernoulli beams [39, 40] or for structures with softening behavior [41].
To perform our computations, we adopt a model with two degrees of freedom. The non-zero constants of the model are are \(M_{11}=M_{22}=1\,\mathrm {Kg}\), \(V_{11}^{\mathrm {II}}=V_{22}^{\mathrm {II}}=10\,\mathrm {N/m}\), \(V_{11}^{\mathrm {N}}=V_{22}^{\mathrm {N}}=-V_{12}^{\mathrm {N}}=-V_{21}^{\mathrm {N}}=300\,\mathrm {N/m}\), \(V_{11}^{\mathrm {D}}=V_{22}^{\mathrm {D}}=-V_{12}^{\mathrm {D}}=-V_{21}^{\mathrm {D}}=5\,\mathrm {N/m^2}\) and \(n=3\).
The simulation parameters are initial time \(t_{i}=0\,\mathrm {s}\), final time \(t_{f}=T\,\mathrm {s}\), simulation time \(T=50\,\mathrm {s}\), time step \(\varDelta t=0.0001\,\mathrm {s}\), and relative iteration tolerance \(\varepsilon =10^{-10}\). Additionally, for the dissipative cases, we set \(\chi _{f}=0.001\) and \(\chi _{s}=0.001\) as well as \(\varvec{D}=\varvec{V}^{\mathrm {II}}\). The initial conditions employed are
Figure 8 shows the idealized mechanical system under consideration and Fig. 9 depicts the potential function, which is clearly non-convex within the region where the dynamics of the system takes place, see Fig. 10. This feature pushes the numerical method to its limits. On the left of Figs. 11, 12, 13 and 14 the kinetic, potential and total energies are plotted. On their right, these show the second precision quotient also as a function of time. Figure 11 depicts the energies in the conserving solution. Figures 12 and 13 plot the energies when dissipation is introduced in the internal forces and generalized velocities, respectively. Last, Fig. 14, provides the results obtained when both dissipation functions are employed, resulting in a larger dissipation of energy. In all cases, the second quotient of precision is very close to 4 for all time, confirming the second order accuracy of the method in all the simulations.
Nonlinear system with two masses connected by linear springs to two walls. Both masses are connected to each other by a nonlinear spring
Potential function with non-polynomial complexity
Fully conservative case; extended configuration and velocity diagrams
Fully conservative case; energy and \(Q_{\mathrm {II}}\)
Dissipative case at the level of internal forces; energy and \(Q_{\mathrm {II}}\)
Dissipative case at the level of generalized velocities; energy and \(Q_{\mathrm {II}}\)
Fully dissipative case; energy and \(Q_{\mathrm {II}}\)
4.2 Finite elasticity models
Here we analyze two finite elasticity models. The first one is a tumbling cylinder and the second one is a free-flying, single-layer, shell. In both cases, the spatial discretizations are based on a four-node shell element [34, 42], i.e., an extensible-director-based solid-degenerate shell model, in which the shear locking and the artificial thickness strains are controlled by means of the assumed natural strain method. Also, the enhancement of the strain field in the thickness direction and the cure of the membrane locking are achieved by means of the enhanced assumed strain method. Such element allows to consider unmodified three-dimensional constitutives laws. For the current study, we adopt the neo-Hookean hyperelastic material model, whose strain energy density is given by
with \(\varvec{C}\), the right Cauchy–Green deformation tensor, \(J = \sqrt{\det (\varvec{C})}\), \(I_1 = \mathrm {trace}(\varvec{C})\), and \(\lambda \) and \(\mu \) are the first and second Lamé parameters, respectively.
Tumbling cylinder—finite element representation
Tumbling cylinder (conservative)—sequence of motion
Tumbling cylinder (conservative)—momenta and energy
Tumbling cylinder (dissipative)—momenta and energy
4.2.1 Tumbling cylinder
This structure is a cylindrical shell subject to body loads with a prescribed time variation and was already investigated, for instance, in [5, 42, 43] and in many other works. The geometrical and material properties are the following: mean radius \(7.5\,\mathrm {m}\), height \(3.0\,\mathrm {m}\), thickness \(0.02\,\text {m}\), first Lamé parameter \(80\,\mathrm {MPa}\), second Lamé parameter \(80\,\mathrm {MPa}\) and mass density per volume unit \(1.0\,\mathrm {Kg/}\mathrm {m}^{3}\). The cylinder is discretized with 48 elements, in which 16 elements are located along the circumference and 3 elements along the height. The total number of nodes is 60. Moreover, no kinematic boundary conditions are enforced. For the dissipative case we set \(\chi = 0.25\). Figure 15 shows the finite element model of the tumbling cylinder. Additionally, the line segments A, B, C and D, to which the spatial loads are applied, are indicated in magenta. Table 1 presents the values for the loads that are applied to the structure. The loads are then multiplied with a function that describes the variation of the applied force over the time, which is defined in Eq. (105). Then \(\varvec{f}_{0}^{\mathrm {ext}}=f_{1}\hat{\varvec{i}}^{1}+f_{2}\hat{\varvec{i}}^{2}+f_{3}\hat{\varvec{i}}^{3}\) and \(\varvec{f}^{\mathrm {ext}}(t)=f(t)\varvec{f}_{0}^{\mathrm {ext}}\), in which the last expression is the applied load.
Free-flying single-layer plate—finite element representation
Figure 16 shows a motion sequence for the conservative case, where the original configuration is located at the upper-left corner of the plot, and some deformed configurations are sequentially shown from left to right and from the top to the bottom. Table 2 provides the stationary values for momenta and energy computed with the current method for both the conservative and the dissipative cases. Figure 17 shows the time history of momenta and energy for the conservative case. It can be observed that the linear momentum, angular momentum and total energy vary during the time in which the external load is active, i.e., the first \(1\,\mathrm {s}\). After the external loads vanish, these three quantities are identically preserved through the time. These results confirm that the newly proposed integration scheme preserves momenta and energy. Although the total energy remains constant, the potential and kinematic energies vary in time, complementing each other in such a way that the total energy is perfectly constant. Figure 18 shows the time history of momenta and energy for the dissipative case. Clearly, the momenta is identically preserved and energy is dissipated.
4.2.2 Free-flying single-layer plate
Free-flying single-layer plate (conservative)—sequence of motion
The structure considered in this last example is a rectangular flat plate, which consisting of a single material layer, subject to spatial loads with a prescribed time variation and was considered, for example, in [26, 42, 44] and in many other works. The geometrical and material properties are the following: length \(0.3\,\mathrm {m}\), width \(0.06\,\mathrm {m}\), thickness \(0.002\,\mathrm {m}\), first Lamé parameter \(0.0\,\mathrm {Pa}\), second Lamé parameter \(103.0\,\mathrm {GPa}\) and mass density per volume unit \(7.3\times 10^{3}\,\mathrm {Kg}/\mathrm {m}^{3}\). The plate is then discretized with 120 elements, 30 elements being located along the largest dimension and 4 elements along the smallest dimension. The total amount of nodes is 155 and for the dissipative case we set \(\chi = 0.5\). Figure 19 depicts the finite element discretization of this structure. The loads are applied over the line segments A, B and C, indicated in magenta on the figure. The reference point for the angular momentum is indicated with the symbol \(\square \). Table 3 gathers the values for the loads that are applied to the structure and Eq. (106) defines their scaling factor.
Figure 20 shows a motion sequence for the conservative case. The linear momentum, angular momentum and energy during the simulation are constant once reached the stationary state, and their values are provided in Table 4 for both the conservative and the dissipative cases. Momenta and energy values in time are plotted in Fig. 21 for the conservative case, proving that after the removal of the force, they all remain constant. Figure 22 shows the values in time of momenta and energy for the dissipative case. Once again, momenta is perfectly preserved and energy is artificially dissipated.
Free-flying single-layer plate (conservative)—momenta and energy
Free-flying single-layer plate (dissipative)—momenta and energy
4.2.3 On the dissipation properties
Dissipative schemes would be of little interest if the energy dissipation did not take place mostly in the high-frequency range. It is well-known that the dissipation of the high frequencies results in enhanced stability for the integration of stiff differential equations. Therefore, we could conclude that the only useful dissipative schemes are those that can annihilate the high-frequency content of the response without radically affecting the low frequency content of the response. In a nonlinear mechanical context, and to the best of our knowledge, there exists no dissipation function that only eliminates the high-frequency content and leaves untouched the low-frequency content. Dissipation always takes place along the whole frequency range. Moreover, there is no formal proof that the dissipation can be split in that sense for nonlinear problems and thus, we can only claim that some dissipation functions seem to be effective to address the high-frequency problem, fact that is mainly justified by experience. Further detailed analysis regarding intrinsic features of dissipation functions would fall outside the scope of the current work that addresses the derivation of a new structure preserving schema that is enriched with the inclusion of numerical dissipation. The choice of a particular dissipation function is left to the structural analyst based on the special demands of the problem to be solved.
Keeping these limitations in mind, the free-flying single-layer plate turns to be a suitable example to show the good dissipation properties of the new proposed scheme. Figure 23, to the left, presents the amplitude spectrum based on the fast Fourier transform of the potential energy for both, the conservative and dissipative cases within the time range 0.06–0.1 s such that the direct influence of the initial transient is avoided. The subsequent analysis corresponds to the frequency range 100–2000 Hz and to the energy amplitude range 0–20 J. Figure 23, to the right, presents the same information, but for the energy amplitude range 0–2 J. Clearly, the dissipative algorithm works very effectively beyond \(600\text { Hz}\). For the kinetic energy, Fig. 24, to the left and to the right, shows almost identical dissipative properties. Up to \(600\text { Hz}\), even if slightly different due to some dissipation within 200–210 Hz, the behavior for the conservative and dissipative cases looks similar. Thus, we can claim that the proposed scheme seems to have very interesting dissipation properties.
Effectiveness of the dissipative scheme at the potential energy level
Effectiveness of the dissipative scheme at the kinetic energy level
5 Concluding remarks
We considered the conservative/dissipative time integration in the context of nonlinear mechanical systems. A systematic approach to derive algorithmic internal forces and generalized velocities that ensure the preservation or the controlled dissipation of energy was presented. As a main concrete result, we proposed a new second-order formula for the algorithmic internal forces. Moreover, this formula was investigated from a geometric point of view and also interpreted for the fully conservative case in terms of a general approach available in the literature.
In contrast with conservative/dissipative methods available in the literature and based on the midpoint rule, the proposed formulas are perturbations of averaged evaluations, and thus not equivalent to existing ones.
The proposed methods are able to preserve the total energy of conservative equations, or add artificial dissipation in a controllable fashion, while preserving, in both cases, the linear and angular momenta of the system. Numerical tests verify all the previous assertions.
The proposed methods could be extended to integrate differential-algebraic equations or to include consistently dissipation functions involving derivatives with fractional orders, among others. The reformulation in the context of polyconvex large strain elasticity as well as of Lie Groups may yield interesting results. Beyond that, rigorous mathematical proofs on the robustness are still necessary.
References
Arnold VI (1989) Mathematical methods of classical mechanics. Springer, Berlin
Hairer E, Lubich C, Wanner G (2006) Geometric numerical integration, 2nd edn. Springer, Berlin
Stuart AM, Humphries AR (1996) Dynamical systems and numerical analysis. Cambridge University Press, Cambridge
Simo JC, Tarnow N (1992) The discrete energy-momentum method. Conserving algorithms for nonlinear elastodynamics. Z Angew Math Phys 43:757–792
Simo JC, Tarnow N (1994) A new energy and momentum conserving algorithm for the non-linear dynamics of shells. Int J Numer Methods Eng 37:2527–2549
Gonzalez O (1996) Time integration and discrete Hamiltonian systems. J Nonlinear Sci 6:449–467
Kane C, Marsden JE, Ortiz M (1999) Symplectic-energy-momentum preserving variational integrators. J Math Phys 40:3353–3371
McLachlan RI, Quispel GRW, Robideux N (1999) Geometric integration using discrete gradients. Philos Trans Math Phys Eng Sci 357:1021–1045
Armero F, Romero I (2001) On the formulation of high-frequency dissipative time-stepping algorithms for nonlinear dynamics. Part I: low-order methods for two model problems and nonlinear elastodynamics. Comput Methods Appl Mech Eng 190:2603–2649
Marsden JE, West M (2001) Discrete mechanics and variational integrators. Acta Numer 10:357–514
Simo JC, Tarnow N, Doblaré M (1995) Non-linear dynamics of three-dimensional rods: exact energy and momentum conserving algorithms. Int J Numer Methods Eng 38:1431–1473
Romero I, Armero F (2002) An objective finite element approximation of the kinematics of geometrically exact rods and its use in the formulation of an energy-momentum conserving scheme in dynamics. Int J Numer Methods Eng 54:1683–1716
Armero F, Petocz E (1998) Formulation and analysis of conserving algorithms for frictionless dynamic contact/impact problems. Comput Methods Appl Mech Eng 158:269–300
Goicolea JM, García Orden JC (2000) Dynamic analysis of rigid and deformable multibody systems with penalty methods and energy-momentum schemes. Comput Methods Appl Mech Eng 188:789–804
Betsch P, Hesch C, Sänger N, Uhlar S (2010) Variational integrators and energy-momentum schemes for flexible multibody dynamics. J Comput Nonlinear Dyn 5:031001-1–031001-11
Gonzalez O (2000) Exact energy-momentum conserving algorithms for general models in nonlinear elasticity. Comput Methods Appl Mech Eng 190:1763–1783
Laursen TA, Meng XN (2001) A new solution procedure for application of energy-conserving algorithms to general constitutive models in nonlinear elastodynamics. Comput Methods Appl Mech Eng 190:6300–6309
Gotusso L (1985) On the energy theorem for the Lagrange equations in the discrete case. Appl Math Comput 17:129–136
Itoh T, Abe K (1988) Hamiltonian-conserving discrete canonical equations based on variational difference quotients. J Comput Phys 76:85–102
Romero I (2012) An analysis of the stress formula for energy-momentum methods in nonlinear elastodynamics. Comput Mech 50:603–610
Harten A, Lax B, Leer P (1983) On upstream differencing and Godunov-type schemes for hyperbolic conservation laws. SIAM Rev 25:35–61
French DA, Schaeffer JW (1990) Continuous finite element methods which preserve energy properties for nonlinear problems. Appl Math Comput 39:271–295
Groß M, Betsch P, Steinmann P (2005) Conservation properties of a time fe method. Part IV: higher order energy and momentum conserving schemes. Int J Numer Methods Eng 63:1849–1897
Betsch P, Janz A, Hesch C (2018) A mixed variational framework for the design of energy-momentum schemes inspired by the structure of polyconvex stored energy functions. Comput Methods Appl Mech Eng 335:660–696
García Orden JC (2018) Energy and symmetry-preserving formulation of nonlinear constraints and potential forces in multibody dynamics. Nonlinear Dyn 95:823–837
Kuhl D, Ramm E (1996) Constraint energy momentum algorithm and its application to nonlinear dynamics of shells. Comput Methods Appl Mech Eng 136:293–315
Kuhl D, Crisfield MA (1999) Energy-conserving and decaying algorithms in non-linear structural dynamics. Int J Numer Methods Eng 45:569–599
Bottasso CL, Borri M (1997) Energy preserving/decaying schemes for non-linear beam dynamics using the helicoidal approximation. Comput Methods Appl Mech Eng 143:393–415
Bottasso CL, Borri M, Trainelli L (2001) Integration of elastic multibody systems by invariant conserving/dissipating algorithms. II. Numerical schemes and applications. Comput Methods Appl Mech Eng 190:3701–3733
Romero I (2016) High frequency dissipative integration schemes for linear and nonlinear elastodynamics. In: Betsch P (ed) Structure-preserving integrators in nonlinear structural dynamics and flexible multibody dynamics. Springer, Berlin, pp 1–30
Armero F, Romero I (2001) On the formulation of high-frequency dissipative time-stepping algorithms for nonlinear dynamics. Part II: second-order methods. Comput Methods Appl Mech Eng 190:6783–6824
Romero I, Armero F (2002) Numerical integration of the stiff dynamics of geometrically exact shells: an energy-dissipative momentum-conserving scheme. Int J Numer Methods Eng 54:1043–1086
Armero F, Romero I (2003) Energy-dissipative momentum-conserving time-stepping algorithms for the dynamics of nonlinear cosserat rods. Comput Mech 31:3–26
Gebhardt CG, Hofmeister B, Hente C, Rolfes R (2019) Nonlinear dynamics of slender structures: a new object-oriented framework. Comput Mech 63:219–252
Gebhardt CG, Steinbach MC, Rolfes R (2019) Understanding the nonlinear dynamics of beam structures: a principal geodesic analysis approach. Thin-Walled Struct 140:357–372
Kerschen G, Golinval J-C, Vakakis AF, Bergman LA (2005) The method of proper orthogonal decomposition for dynamical characterization and order reduction of mechanical systems: an overview. Nonlinear Dyn 41:147–169
Jansen EL (2005) Dynamic stability problems of anisotropic cylindrical shells via simplified analysis. Nonlinear Dyn 39:349–367
Kreiss H-O, Ortiz OE (2014) Introduction to numerical methods for time dependent differential equations. Wiley, London
Kopmaz O, Gündoğdu O (2003) On the curvature of an Euler–Bernoulli beam. Int J Mech Eng Educ 31:132–142
Nayfeh AH, Pai PF (2008) Linear and nonlinear structural mechanics. Wiley, London
Ye F, Zi-Xiong G, Yi-Chao G (2018) An unconditionally stable explicit algorithm for nonlinear structural dynamics. J Eng Mech 144:04018034-1–04018034-8
Gebhardt CG, Rolfes R (2017) On the nonlinear dynamics of shell structures: combining a mixed finite element formulation and a robust integration scheme. Thin-Walled Struct 118:56–72
Betsch P, Sänger N (2009) On the use of geometrically exact shells in a conserving framework for flexible multibody dynamic. Comput Methods Appl Mech Eng 198:1609–1630
Vu-Quoc L, Tan XG (2003) Optimal solid shells for non-linear analyses of multilayer composites. II. Dynamics. Comput Methods Appl Mech Eng 192:1017–1059
Acknowledgements
Cristian Guillermo Gebhardt and Raimund Rolfes acknowledge the financial support of the Lower Saxony Ministry of Science and Culture (research project ventus efficiens, FKZ ZN3024) and the German Federal Ministry for Economic Affairs and Energy (research project Deutsche Forschungsplattform für Windenergie, FKZ 0325936E) that enabled this work.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Precision quotient
Precision quotient
It is very useful to have means for checking the correctness of integration algorithms during their development and implementation. Therefore, we introduce here two tests that can be applied once an integration scheme has been numerically implemented. According to Kreiss and Ortiz [38], the numerical solution of an initial value problem can be expanded as
where \(\varvec{\xi }(t)\) is the exact solution of the given initial value problem and \(\varvec{\psi }_{i}\) for \(i=1,\ldots ,n\) are smooth functions of the time t that do not depend on the reference time step h. A positive integer number k allows to define finer solutions based on the original resolution given by the time step h that are necessary to compute precision coefficients, a tool that may be very effective to check the correctness of a running program.
A first precision quotient can be defined as
where the numerator is computed as
and the denominator is given by
It is possible to show that for sufficiently small time steps, the first precision quotient can be directly approximated by \(2^{n}\), where n denotes the order of accuracy of the integration method, namely
The main issue with this definition is that the exact solution of the initial value problem is required and, in general, is not available, especially in the context of mechanical systems involving nonlinear constitutive relations. To circumvent this drawback, it is possible to define a second precision quotient as
where the numerator is computed as
and the denominator is given by
Notice that this concept removes intrinsically the need for the exact solution of the considered initial value problem. Once again, it is possible to show that for sufficiently small time steps, the second precision quotient can be approximated by \(2^{n}\) as well as in the case of the first precision quotient, namely
For the integration scheme considered in this work (an energy-conservative/dissipative method), accuracy of second order can be guaranteed, meaning that \(\log _{2}[Q_{\text {I}}(t)]\approx 2\) and \(\log _{2}[Q_{\text {II}}(t)]\approx 2\). Let us note that for the calculation of precision quotients, h has to be chosen small enough, and the choice may vary from case to case. In addition, if \(\Vert \varvec{\psi }_{n}(t)\Vert \) is very small, both tests may fail even if the implementation is right. For this reason it is sometime necessary to experiment with several initial conditions and time step sizes in order to achieve correct pictures. As a general rule, the quotients of accuracy show better performance when the trajectories are periodic or quasi-periodic.
Rights and permissions
About this article
Cite this article
Gebhardt, C.G., Romero, I. & Rolfes, R. A new conservative/dissipative time integration scheme for nonlinear mechanical systems. Comput Mech 65, 405–427 (2020). https://doi.org/10.1007/s00466-019-01775-3
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00466-019-01775-3