A bistable nonlinear electromagnetic actuator with elastic boundary for actuation performance improvement

Abstract

This study proposes a novel bistable nonlinear electromagnetic actuator with elastic boundary (BEMA-EB) to enhance the actuation performance when controlled by a harmonic input signal. The structure of the BEMA-EB has an inclined spring, one end of which is supported by an elastic boundary. The inclined spring produces bistable nonlinearity to realize the large-amplitude inter-well actuation responses, and the elastic boundary brings additional dynamic coupling to enhance the inter-well actuation performance. The governing equations of the BEMA-EB controlled by a harmonic input signal are formulated. To show the advantages of the BEMA-EB, the study performs comparison between the BEMA-EB, a bistable electromagnetic actuator which does not have elastic boundary, and an equivalent linear electromagnetic actuator. The results show that the BEMA-EB has a much broader inter-well actuation bandwidth and smaller input-signal-amplitude threshold of activating the favorable inter-well actuation, which verify the merits of both the bistable nonlinearity and elastic boundary. To develop insights into the nonlinear dynamic behaviors of the BEMA-EB, the bifurcation features are investigated in terms of the inclined spring stiffness, the input signal frequency and amplitude. Phase portraits and Poincare maps are presented to illustrate how the actuation responses of the BEMA-EB evolve corresponding to the changes of the above parameters. Finally, basin-of-attraction maps are given to uncover the occurring probabilities of the different types of the actuation responses with respect to the different distributions of the initial conditions. The results quantitatively corroborate that the likelihood of the favorable inter-well actuation is significantly increased by using the BEMA-EB.

1 Introduction

Electromagnetic actuators (EMAs) can transduce an electrical input signal into a mechanical motion and thus have served motion control applications in many industrial fields, e.g., robot control [1, 2], vibration control and structural test [3,4,5,6,7], and motion control of biomedical devices [8, 9]. The ubiquitous EMA structure is modeled based on a linear oscillator model that consists of a mover, a stator and a linear spring [3]. The function of the linear spring is to reset the mover’s position, i.e., using the linear spring restoring force to keep the mover at the equilibrium position when the EMA is in standby mode. Since the linear spring restoring force is always opposite to the moving direction of the mover, a significant portion of the input electrical energy will be consumed to conquer the resistance of the linear spring restoring force when exhibiting actuation, thereby reducing the transform efficiency. For the applications that require large actuation force (e.g., contactless power transmission systems [10]), the significantly high voltage (or high-current) electrical signal is needed to realize the desired actuation energy, which may cause current leakage and electrical breakdown [11]. Therefore, the EMA with high-efficiency actuation capability is highly demanded for the modern industry [11, 12].

To improve the actuation efficiency, using the nonlinear-oscillator-based EMA is an effective solution. In this manner, the linear spring is replaced by a nonlinear spring to enhance the efficiency of converting the input electric energy into the actuation energy. Researchers have performed various studies on the dynamic behaviors and applications of nonlinear oscillators. It was found that nonlinear oscillators are highly efficient in transducing the external input energy into kinetic energy compared to linear oscillators [13, 14]. A nonlinear oscillator with double potential wells (i.e., a bistable oscillator) draws much attention [15]. When the bistable oscillator is subjected to external excitation with a certain level, it will exhibit a special dynamic behavior “inter-well response” (i.e., the snap-through response). That is, the oscillator vibrates from one of the stable equilibria to the other, which leads to large-amplitude response [15,16,17,18,19,20].

Based on the advantages of the bistable oscillator’s large-amplitude inter-well response, a few researchers were inspired to use the bistable oscillator to design the actuators [21,22,23,24,25]. For example, Fang et al. [21] proposed a bistable piezoelectric vibration-driven locomotion system to magnify stroke output in the field of crawling robot motion. The results showed that the system is able to output high average locomotion speed in a wider frequency band due to the inter-well response of the bistable nonlinearity. Gude and Hufenbach [22] fabricated a bistable morphing structure with piezoelectric actuator to realize the large out-of-plane deformations of multilayered fiber-reinforced composites. Gray et al. [23] modified a bistable cantilever magnetic actuation mechanism to realize large actuation displacement and low switching energy. Li et al. [11] proposed a new actuation method using DE membranes with a properly designed beam-like bistable oscillator, which overcomes the high voltage consumption drawback. Gerson et al. [24] reported a novel approach to tune the bistable nonlinearity for enhancing the displacement response of micro actuators. The bistable structure has also been applied to the magneto active elastomer actuator [25].

Furthermore, it has been found that the bistable oscillator coupling with elastic boundary can dynamically change its bistable nonlinearity by reducing the depth of the potential energy well, which is more conducive to inter-well oscillation [26]. Such improvement measure was used in the piezoelectric bistable energy harvester, which has significantly improved the conversion efficiency of external excitation into kinetic energy of the oscillator mass, thereby improving energy harvesting efficiency [27,28,29]. However, the effect of such improvement measure on the EMA design remains uninvestigated. Different from the energy harvester, the EMA’s excitation position is on the mover of the actuator, not on the foundation of the structure. In nonlinear dynamics, different excitation positions may introduce significantly different dynamic behaviors.

Inspired by the demand of the high-efficiency actuation and benefit of the modified bistable nonlinearity, this paper proposes a new type of nonlinear EMA: bistable nonlinear electromagnetic actuator with elastic boundary (BEMA-EB), so as to significantly improve the actuation performance of the EMA. The proposed BEMA-EB’s structure has an inclined spring bistable structure and an elastic boundary, which realizes the dynamically changed bistable nonlinearity. Owing to the dynamically varied bistable nonlinearity, the BEMA-EB will exhibit significantly different dynamic behaviors from the previously reported bistable actuators in Refs. [21,22,23,24,25]. This study will show the actuation performance enhancement of the proposed BEMA-EB through comparisons between the proposed actuator, the bistable actuator without the elastic boundary and the equivalent linear actuator. To deeply understand the dynamic behaviors of the BEMA-EB, comprehensive numerical studies will be conducted in terms of the time historic response, phase portraits, Poincare maps, bifurcation and basin-of-attraction. The design guidelines of the BEMA-EB will be developed through this study, which can provide a new actuation mean for application of vibration control and locomotion system control.

The rest of this paper is organized as follows: Sect. 2 presents the schematic diagram of the BEMA-EB and its governing equations controlled by a harmonic input current signal. This section also presents the schematics and governing equations of a bistable electromagnetic actuator (BEMA) (which does not have elastic boundary) and an equivalent linear electromagnetic actuator (LEMA), both of which are used as the comparative counterparts. In Sect. 3, a series of numerical simulations are conducted to reveal the benefits of both the bistable nonlinearity and elastic boundary of the BEMA-EB for actuation performance enhancement. Section 4 performs bifurcation analyses to uncover the nonlinear dynamic behaviors of the BEMA-EB in terms of the inclined spring stiffness, the input signal frequency and amplitude. In Sect. 5, the influence of initial conditions on the responses of the BEMA-EB is discussed, which finally presents the occurring probabilities of the certain types of the responses. Section 6 concludes the main findings of this study.

2 Dynamic modeling

2.1 Description of the BEMA-EB

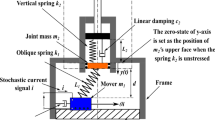
Figure 1 presents the schematic diagram of the BEMA-EB. The BEMA-EB has an inclined spring whose stiffness and undeformed length are k₁ and L₁. One end of the inclined spring is connected to the coil mover m₁, while the opposite end is supported by the elastic boundary. The elastic boundary comprises a linear spring with stiffness k₂ and undeformed length L₂, a linear damper with damping constant c₂, and a joint mass m₂. The adjustable bolt is used to adjust the positions of the joint mass m₂ in the elastic boundary. One end of the linear spring is connected to the bottom of the adjustable bolt to make sure the other end is flush with the middle frame. The width of the m₂ is too small, and thus is neglected. The vertical distance from the middle frame to the coil mover is d and satisfies d < L₁. Hence, the inclined spring is compressed in the upright position to induce two stable equilibria of m₁ which are symmetric about the center line, i.e., bistable nonlinearity. The coil mover m₁ slides on the linear track embedded with the permanent magnets. As a result, when the coil mover has an input current harmonic signal i, the coil mover will be subjected to an electromagnetic force $F = \varTheta i$, where $\varTheta$ is a constant that is related with the magnetic flux density and the coil length [3]. This study assumes that c₁ is the equivalent linear damping coming from the linear track.

Fig. 1

Schematic diagram of the BEMA-EB

2.2 Governing equations of the BEMA-EB

Define that the horizontal displacement from the coil mover to the center line is x, and the vertical displacement from m₂ to the middle frame is y. The total kinetic energy of the BEMA-EB is

$$ T_{1} = \frac{1}{2}m_{1} \dot{x}^{2} + \frac{1}{2}m_{2} \dot{y}^{2} $$

(1)

where the operator $(\mathop {}\limits^{.} )$ indicates the derivative with respect to time t. The total potential energy and virtual work done by non-conservative forces are

$$ V_{1} = \frac{1}{2}k_{1} \left( {\sqrt {(x^{2} + \left( {d - y} \right)^{2} )} - L_{1} } \right)^{2} + \frac{1}{2}k_{2} y^{2} - m_{2} gy $$

(2)

$$ \delta W = \left( {F - c_{1} \dot{x}} \right)\delta x - c_{2} \dot{y}\delta y $$

(3)

where g is the gravitational acceleration. F is the electromagnetic force, which is

$$ F = \varTheta i $$

(4)

where $i = I\sin \left( {2\pi \varOmega t} \right)$ (I and $\varOmega$ are the input signal amplitude (A) and frequency (Hz), respectively). Therefore, by applying the Euler–Lagrange equation, the governing equations of the BEMA-EB are

$$ m_{1} \ddot{x} + c_{1} \dot{x} + k_{1} x\left[ {1 - \frac{{L_{1} }}{{\sqrt {\left( {x^{2} + \left( {d - y} \right)^{2} } \right)} }}} \right] = \varTheta i $$

(5a)

$$ m_{2} \ddot{y} + c_{2} \dot{y} + k_{2} y + k_{1} \left( {y - d} \right)\left( {1 - \frac{{L_{1} }}{{\sqrt {\left( {x^{2} + \left( {d - y} \right)^{2} } \right)} }}} \right) - m_{2} g = 0. $$

(5b)

2.3 Linear frequencies of the BEMA-EB

To conveniently interpret the insights of the following results, the linear frequencies of the BEMA-EB (which is a two-degree-of-freedom system) are presented. The linear frequencies are equal to the natural frequencies of the linearization system of the BEMA-EB controlled by a very small input signal. Introducing the relative displacements from the equilibrium position $\left( {x_{s} = \sqrt {L_{1}^{2} - \left( {d - \frac{{m_{2} g}}{{k_{2} }}} \right)^{2} } ,y_{s} = \frac{{m_{2} g}}{{k_{2} }}} \right)$

$$ X = x - x_{s} ,\quad Y = y - y_{s} $$

(6)

Substituting Eq. (6) into (5), the governing equations of the BEMA-EB become

$$ m_{1} \ddot{X} + c_{1} \dot{X} + k_{1} \left( {X + x_{s} } \right)\left( {1 - \frac{{L_{1} }}{{\sqrt {\left( {\left( {X + x_{s} } \right)^{2} + \left( {D - Y} \right)^{2} } \right)} }}} \right) = \theta i $$

(7a)

$$ m_{2} \ddot{Y} + c_{2} \dot{Y} + k_{2} Y - k_{1} \left( {D - Y} \right)\left[ {1 - \frac{{L_{1} }}{{\sqrt {\left( {\left( {X + x_{s} } \right)^{2} + \left( {D - Y} \right)^{2} } \right)} }}} \right] = 0 $$

(7b)

where $D = d - y_{s}$. By multivariate Taylor series expansion at $(X = 0, Y = 0)$ and omitting high order terms, the reduced system of the BEMA-EB is obtained

$$ m_{1} \ddot{X} + c_{1} \dot{X} + K_{1} X - K_{2} Y + Q_{1} X^{2} + Q_{2} XY + Q_{3} Y^{2} = \theta i $$

(8a)

$$ m_{2} \ddot{Y} + c_{2} \dot{Y} - K_{3} X + K_{4} Y + Q_{4} X^{2} + Q_{5} XY + Q_{6} Y^{2} = 0 $$

(8b)

where

$$ \begin{aligned} K_{1} & = \frac{{k_{1} x_{s}^{2} }}{{L_{1}^{2} }},K_{2} = \frac{{k_{1} x_{s} D}}{{L_{1}^{2} }},K_{3} = \frac{{k_{1} x_{s} D}}{{L_{1}^{2} }},K_{4} = k_{2} + \frac{{k_{1} D^{2} }}{{L_{1}^{2} }},Q_{1} = \frac{{3k_{1} x_{s} D^{2} }}{{2L_{1}^{4} }},Q_{2} = - \frac{{k_{1} D\left( {D^{2} - 2x_{s}^{2} } \right)}}{{L_{1}^{4} }}, \\ Q_{3} & = - \frac{{k_{1} x_{s} \left( {2D^{2} - x_{s}^{2} } \right)}}{{2L_{1}^{4} }}, Q_{4} = - \frac{{k_{1} D\left( {D^{2} - 2x_{s}^{2} } \right)}}{{2L_{1}^{4} }},Q_{5} = - \frac{{k_{1} x_{s} \left( {2D^{2} - x_{s}^{2} } \right)}}{{L_{1}^{4} }},Q_{6} = - \frac{{3k_{1} Dx_{s}^{2} }}{{2L_{1}^{4} }}. \\ \end{aligned} $$

The two linear frequencies of the BEMA-EB are obtained by assume X and Y are small quantities

$$ \omega_{\text{BMEA - EB1}} = \left( {\frac{{K_{1} /m_{1} + K_{4} /m_{2} }}{2} - \sqrt {\left( {\frac{{K_{1} /m_{1} - K_{4} /m_{2} }}{2}} \right)^{2} + \frac{{K_{2} K_{3} }}{{m_{1} m_{2} }}} } \right)^{{\frac{1}{2}}} $$

(9a)

$$ \omega_{\text{BMEA - EB2}} = \left( {\frac{{K_{1} /m_{1} + K_{4} /m_{2} }}{2} + \sqrt {\left( {\frac{{K_{1} /m_{1} - K_{4} /m_{2} }}{2}} \right)^{2} + \frac{{K_{2} K_{3} }}{{m_{1} m_{2} }}} } \right)^{{\frac{1}{2}}} $$

(9b)

It is known that the even the input signal with small strength could still excite the large-amplitude actuation when the input signal frequency is close to the natural frequencies. As a result, it could be predicted that the input signal frequency to activate the large-amplitude actuation of the BEMA-EB is strongly related to the linear natural frequencies. This will be revealed in the following results.

2.4 Description of the comparative counterparts

Two comparative counterparts are presented to prove the advantage of the BEMA-EB. They are a bistable electromagnetic actuator without the elastic boundary (BEMA) and a linear electromagnetic actuator (LEMA), respectively, schematics of which are shown in Fig. 2a, b. The governing equation of the BEMA is

Fig. 2

Schematics of the two comparative counterparts. a BEMA; b LEMA

$$ m_{1} \ddot{x} + c_{1} \dot{x} + k_{1} x\left( {1 - \frac{{L_{1} }}{{\sqrt {\left( {x^{2} + d^{2} } \right)} }}} \right) = \varTheta i $$

(10)

When the BEMA is subjected to a tiny-amplitude input signal i, the BEMA will exhibit small oscillations. Consequently, the nonlinearity can be neglected so that its response is nearly identical that of a linearized actuator [30]. For meaningful comparison, the LEMA is defined as the linearization of the BEMA subjected to very small i. Assuming bistable actuator exhibits small oscillations, the coil mover m₁ vibrates around either stable equilibrium positions: the intra-well oscillation. That is, the response motion is expressed by $x = \delta x \pm \sqrt {L_{1}^{2} - d^{2} }$, where $\pm \sqrt {L_{1}^{2} - d^{2} }$ are the bistable equilibria and $\delta x \ll L_{1}$. As a result, the potential force of the inclined spring becomes

$$ F_{p} = k_{1} \left( {\delta x \pm \sqrt {L_{1}^{2} - d^{2} } } \right)\left( {1 - \frac{{L_{1} }}{{\sqrt {\left( {\left( {\delta x \pm \sqrt {L_{1}^{2} - d^{2} } } \right)^{2} + d^{2} } \right)} }}} \right) $$

(11)

After Taylor expansion with respect to the small quantity $\delta x/L_{1}$, and neglecting the higher order, a linear expression of potential force is obtained to be

$$ F_{p} \approx k_{1} \left( {1 - \frac{{d^{2} }}{{L_{1}^{2} }}} \right)\delta x = k_{l} \delta x $$

(12)

where k_l is the equivalent stiffness and the LEMA is realized with an equivalent damping constant c_l and k_l. Therefore, the governing equation of the LEMA is

$$ m_{1} \ddot{x} + c_{l} \dot{x} + k_{1} \left( {1 - \frac{{d^{2} }}{{L_{1}^{2} }}} \right)x = \varTheta i. $$

(13)

3 Numerical investigation and performance comparison

Numerical investigations are performed based on the governing equations of the BEMA-EB, BEMA and LEMA. In the following simulations, the parameters are set as follows: $L_{1} = 0.08\,{\text{m}}$, $d/L_{1} = 0.9$, $m_{1} = m_{2} = 0.1$ kg, $\varTheta = 1\,{\text{N/A}}$, and the stiffness of all springs is set in the range of 500–2000 N/m. The loss factor $\gamma_{n} = c_{n} /\sqrt {k_{n} m_{n} }$ is set to 0.1, where n represents different actuators and the initial coil mover position is set at one of the equilibria. All the calculations in this paper are based on the fourth-order Runge–Kutta method.

3.1 Comparison with the LEMA

To reveal the merits of bistable nonlinearity in EMAs, this section investigates the displacement amplitude and acceleration responses of the BEMA, BEMA-EB and LEMA versus the inclined spring stiffness (k₁), input signal frequency ($\varOmega$) and amplitude (I). The responses of the BEMA are shown as the blue square, whereas responses corresponding to the BEMA-EB are red circle. Besides, responses of the LEMA are shown as the claret star. In each circumstance, two figures are presented to show the coil mover’s displacement amplitude and the peak of acceleration responses. Note that, when the bistable nonlinear system exhibits intra-well oscillation, the displacement x has a nonzero bias apart from the vibration. Since this study is focus on the actuation’s dynamic feature instead of the absolute position, the following figures only present the vibration amplitudes. For actuation application, larger displacement amplitude and greater acceleration indicate better performance.

Figure 3 presents the displacement amplitude and acceleration amplitude responses of the BEMA, BEMA-EB and LEMA for different k₁. The stiffness of the linear spring of the elastic boundary is $k_{2} = 2000\,{\text{N/m}}$, the input signal frequency is $\varOmega = 6 \,{\text{Hz}}$, and the input signal amplitude is $I = 2\,{\text{A}}$, respectively. It is seen in Fig. 3a that the LEMA exhibits the considerably large displacement amplitude response for a small range of the stiffness k₁ near $k_{1} = 750\,{\text{N/m}}$. However, the BEMA could realize large inter-well oscillation for a wider range $100 < k_{1} < 1600\,{\text{N/m}}$, which indicates that the BEMA improves the robustness of the large-amplitude actuation against the variation of k₁ because of the bistable nonlinearity. Compared to the BEMA, a broader inclined spring stiffness range k₁ for large inter-well oscillation is obtained for the BEMA-EB. It is shown that with the elastic boundary, the BEMA-EB could realize inter-well motion within all parameters of the inclined stiffness k₁. To explore the exact range of k₁ for large inter-well oscillation, more simulations are conducted. The results show that the BEMA-EB could realize large inter-well oscillation in the range of $100 < k_{1} < 7050\,{\text{N/m}}$, which indicates that the BEMA-EB could further improve the robustness of the large-amplitude actuation against the variation of k₁.

Fig. 3

Displacement and acceleration amplitude responses for the BEMA, BEMA-EB and LEMA under different inclined spring stiffness (k₁) when $\varOmega = 6 {\text{Hz}}$, $I = 2 {\text{A}}$ and $k_{2} = 2000 {\text{N}}/{\text{m}}$. a Displacement amplitude; b acceleration responses

Figures 4 and 5 show the displacement amplitude and the envelope of the acceleration responses of the BEMA, BEMA-EB and LEMA when a forward swept harmonic input signal i with sweeping rate 0.025 Hz is employed. According to Fig. 3, LEMA exhibits large actuation when $k_{1} = 750\,{\text{N/m}}$. As a result, $k_{1} = 750 \,{\text{N/m}}$ is set, so as to use the optimally designed LEMA as the counterpart. Other parameters are: the spring stiffness of the elastic boundary $k_{2} = 2000\,{\text{N/m}}$ and input signal amplitude $I = 1\,{\text{A}}$. It is seen in Fig. 4 that LEMA only exhibits high efficiency (i.e., large-amplitude actuation displacement amplitude) in a narrow input signal frequency band near 6 Hz, while the BEMA and BEMA-EB have a wider inter-well actuation bandwidth. This indicates that both the BEMA and BEMA-EB outperform the LEMA in terms of the actuation bandwidth. It is seen that for the low frequency band ($\varOmega \le 2$ Hz), the BEMA exhibits intra-well response, where the acceleration actuation is small. Differently, with elastic boundary, the BEMA-EB still realizes large-amplitude inter-well response for $\varOmega \le 2$ Hz. Thus, the BEMA-EB could enhance the actuation performance for low-frequency input signal.

Fig. 4

Displacement amplitude and the envelope of the acceleration responses for the BEMA, BEMA-EB and LEMA with a slowly increasing sweeping input frequency ($\varOmega$) when $k_{1} = 750 {\text{N}}/{\text{m}}$, $I = 1 {\text{A}}$ and $k_{2} = 2000 {\text{N}}/{\text{m}}$. a Displacement amplitude; b acceleration responses

Fig. 5

Displacement amplitude and the envelope of the acceleration responses for the BEMA, BEMA-EB and LEMA with a slowly increasing sweeping input frequency ($\varOmega$) when $k_{1} = 1250 {\text{N}}/{\text{m}}$, $I = 1.5 {\text{A}}$ and $k_{2} = 2000 {\text{N}}/{\text{m}}$. a Displacement amplitude; b acceleration responses

Moreover, inclined spring stiffness $k_{1} = 1250\,{\text{N/m}}$ is set to further explore the displacement amplitude and acceleration responses. The stiffness of the elastic boundary is $k_{2} = 2000 \,{\text{N/m}}$, the input signal amplitude is $I = 1.5 {\text{A}}$, and the results are shown in Fig. 5. With the increase in k₁, the optimal input frequency of the LEMA is increased to be 7.75 Hz. However, the large-amplitude actuation bandwidth of the LEMA is still narrow. The BEMA has a wider inter-well actuation bandwidth than the LEMA, whereas the BEMA-EB further broadens the bandwidth. It can be concluded that the bistable nonlinearity can realize the broadband large-amplitude inter-well oscillation, leading to actuation performance enhancement; the elastic boundary brings the additional dynamic coupling to activate the inter-well actuation in low input signal frequency band.

Figures 6 and 7 present the displacement amplitude and acceleration amplitude responses of the BEMA, BEMA-EB and LEMA with the increase in input signal amplitude I. Two input signal frequencies $\varOmega = 6$ Hz and 4 Hz are employed in Figs. 6 and 7, respectively. It is seen in Fig. 6 that the displacement amplitude and acceleration responses of the BEMA, BEMA-EB and LEMA increase with the increase in input signal amplitude. The acceleration amplitude of the BEMA, BEMA-EB is close to the LEMA when only the intra-well responses are exhibited due to the small input signal amplitude. Once inter-well oscillation occurs by increasing the input signal amplitude, the actuation performances of both the BEMA and BEMA-EB are significantly improved. Furthermore, it can be clearly seen in Fig. 6a that the minimum input signal amplitude to activate the inter-well response of the BEMA-EB is smaller than that of the BEMA. In other words, smaller input signal amplitude is needed for the BEMA-EB to realize large-amplitude inter-well actuation responses.

Fig. 6

Displacement and acceleration amplitude responses for the BEMA, BEMA-EB and LEMA under different input amplitude (I) when $k_{1} = 2000 {\text{N}}/{\text{m}}$, $\varOmega = 6 {\text{Hz}}$ and $k_{2} = 2000 {\text{N}}/{\text{m}}$. a Displacement amplitude; b acceleration responses

Fig. 7

Displacement and acceleration amplitude responses for the BEMA, BEMA-EB and LEMA under different input amplitude (I) when $k_{1} = 2000 {\text{N}}/{\text{m}}$, $\varOmega = 4 {\text{Hz}}$ and $k_{2} = 2000 {\text{N}}/{\text{m}}$. a Displacement amplitude; b acceleration responses

Figure 7 shows the influence of input signal amplitude on the actuation performance for a relatively low input signal frequency $\varOmega = 4 {\text{Hz}}$. Similar tendency in Fig. 6 is obtained in Fig. 7. By comparing both Figs. 6 and 7, it is seen that larger input signal amplitude is required to activate the inter-well response for the BEMA-EB. By substituting the parameters into Eq. (9), the linear frequencies are $\omega_{\text{BEMA - EB1}} = 7.33$ Hz and $\omega_{\text{BEMA - EB2}} = 30.975$ Hz. However, the input signal frequency $\varOmega = 4$ Hz, which is further away from the linear frequencies. This indicates that it is more difficult for the input signal to activate the large-amplitude oscillation of the BEMA-EB to cross the potential barrier. As a result, stronger input signal is required to activate the large-amplitude inter-well actuation response. Nevertheless, the BEMA-EB still requires smaller input signal amplitude to activate the inter-well response compared to the BEMA. Overall, the BEMA-EB has a much broader inter-well actuation frequency band and requires smaller input signal amplitude to achieve the large-amplitude inter-well actuation.

3.2 Discussion of the elastic boundary benefits

To thoroughly explore the effects of the elastic boundary on the BEMA-EB, multiple linear spring stiffness $k_{2} = \left[ {500,1000,1500,2000} \right] \,{\text{N/m}}$ is set in the following simulations. $k_{1} = 2000\,{\text{N/m}}$ and $I = 2 {\text{A}}$ are employed, and the input signal frequency $\varOmega$ increases from 1 to 10 Hz, slowly sweeping at a rate of 0.025 Hz/s. In this section, the shading areas indicate the inter-well responses.

Figure 8 shows the acceleration responses of the BEMA and BEMA-EB for different k₂ in $1 \le \varOmega \le 10$ Hz. It is seen in Fig. 8a that the BEMA has a very narrow inter-well actuation bandwidth under $I = 2 {\text{A}}$. The optimal input signal frequency is near 9 Hz with a 350 m/s² acceleration. The input signal amplitude is magnified about 17.5 times due to the bistable nonlinearity. However, the BEMA only exhibits inefficient intra-well oscillation for the frequency band out of the shading area. In contrast, the BEMA-EB with each different linear stiffness k₂ has a broader inter-well actuation bandwidth, which outperforms the BEMA. A new variable $f_{e}$ is defined to represent the inter-well actuation bandwidth. $f_{e} = 2.6 {\text{Hz}}$ for the BEMA when $k_{1} = 2000\,{\text{N/m}}$ and $I = 2 {\text{A}}$. For the BEMA-EB, when $k_{2} = \left[ {500,1000,1500,2000} \right]$ N/m, $f_{e} = \left[ {7.5, 7.11, 7.1, 6.97} \right]$ Hz, respectively. Correspondingly, the inter-well actuation bandwidths of the BEMA-EB are 188%, 173%, 173%, 168% broadened compared to that of the BEMA under the same input signal, respectively. It is also seen in Fig. 8 that with the increase in k₂, the acceleration obtained in the BEMA-EB is larger and the actuation performance characteristic of the BEMA-EB seems closer to the BEMA. The BEMA can be regarded as a BEMA-EB with infinite linear stiffness k₂. As shown in Fig. 8f, for a very large elastic boundary spring stiffness $k_{2} = 10000$ N/m, it is seen that the BEMA-EB is unable to exhibit the inter-well response in the low frequency band. However, the peak actuation acceleration for the BEMA-EB is enhanced (the amplitude is greater than 300 m/s² when $\varOmega = 8.8$ Hz) compared to the cases in Fig. 8b–e. In general, the BEMA-EB has a wider inter-well frequency band than the BEMA. For the large linear stiffness k₂, the inter-well bandwidth of the BEMA-EB becomes narrower, but the peak acceleration performance is enhanced.

Fig. 8

Acceleration responses of the BEMA and BEMA-EB for different linear stiffness (k₂) under forward swept harmonic input signal when $k_{1} = 2000 {\text{N}}/{\text{m}}$, $I = 2 {\text{A}}$. a BEMA; b BEMA-EB with $k_{2} = 500 {\text{N}}/{\text{m}}$; c BEMA-EB with $k_{2} = 1000 {\text{N}}/{\text{m}}$; d BEMA-EB with $k_{2} = 1500 {\text{N}}/{\text{m}}$; e BEMA-EB with $k_{2} = 2000 {\text{N}}/{\text{m}}$; f BEMA-EB with $k_{2} = 10000 {\text{N}}/{\text{m}}$

Figure 9 presents the acceleration responses of the BEMA and BEMA-EB for different k₂ under backward swept harmonic input signal when $k_{1} = 2000\,{\text{N/m}}$, $I = 2 {\text{A}}$. $f_{e} = 5.73 {\text{Hz}}$ for the BEMA when subjected to the backward swept input signal, which is 120% wider than that under the forward swept input signal shown in Fig. 8. The BEMA-EB with different $k_{2} = \left[ {500,1000,1500,2000} \right]$ N/m under backward swept harmonic input signal exhibits $f_{e} = \left[ {7.34,6.69,6.97, 6.84} \right]$ Hz, respectively. Correspondingly, the inter-well bandwidth of the BEMA-EB is broadened by only 28.1%, 16.8%, 21.6%, 19.4% compared to that of the BEMA, respectively. Similarly, the results show that increasing the elastic boundary spring stiffness may decrease the inter-well bandwidth. Compared with the results in Fig. 9, it is seen that the forward swept input signal is beneficial to activating the favorable inter-well response.

Fig. 9

Acceleration responses of the BEMA and BEMA-EB for different linear stiffness (k₂) under backward swept harmonic input signal when $k_{1} = 2000 {\text{N}}/{\text{m}}$, $I = 2 {\text{A}}$. a BEMA; b BEMA-EB with $k_{2} = 500 {\text{N}}/{\text{m}}$; c BEMA-EB with $k_{2} = 1000 {\text{N}}/{\text{m}}$; d BEMA-EB with $k_{2} = 1500 {\text{N}}/{\text{m}}$; e BEMA-EB with $k_{2} = 2000 {\text{N}}/{\text{m}}$; f BEMA-EB with $k_{2} = 10000 {\text{N}}/{\text{m}}$

Figure 10 shows the displacement amplitude responses and corresponding acceleration amplitude responses for different linear stiffness k₂ with the increase in the input signal amplitude (I). In accordance with the above simulations, the parameters are set to $k_{1} = 2000\,{\text{N/m}}$, $\varOmega = 6 {\text{Hz}}$ and the linear stiffness $k_{2} = \left[ {500,1000,1500,2000,10000} \right]$ N/m. It is seen in Fig. 10 that both actuators exhibit intra-well responses when the input signal amplitude is not large enough. Afterward, with the increase in I, inter-well responses emerge. As I keeps increasing, all actuators could realize large-amplitude inter-well responses and obtain a considerable acceleration. The input signal amplitude threshold is defined to represent the minimum input signal amplitude to activate the inter-well response. It is seen in Fig. 10 that the input signal amplitude threshold for the BEMA-EB is smaller than that for the BEMA. The BEMA-EB has a better performance in displacement responses, while the BEMA has a larger peak acceleration amplitude. The acceleration amplitude obtained in the BEMA-EB increases with the increase in k₂, while the input amplitude threshold decreases with the increase in k₂. In conclusion, the BEMA-EB has a much broader inter-well actuation bandwidth and smaller input signal amplitude threshold of activating the favorable inter-well actuation.

Fig. 10

Actuation performance of the BEMA and BEMA-EB under different input signal amplitude (I) when $k_{1} = 2000 {\text{N}}/{\text{m}}$, $\varOmega = 6 {\text{Hz}}$. Filled (unfilled) geometry represents the inter (intra)-well responses. a Displacement responses; b acceleration responses

3.3 Mathematical interpretation

The actuation characteristics of the BEMA-EB mentioned above can be mathematically interpreted. According to Eq. (6), the expression of the bistable restoring force in the x direction for the BEMA is

$$ F\left( x \right)_{\text{BEMA}} = k_{1} x\left( {1 - \frac{{L_{1} }}{{\sqrt {\left( {x^{2} + d^{2} } \right)} }}} \right) $$

(14)

Thus, the corresponding potential energy of the BEMA is

$$ P\left( x \right)_{\text{BEMA}} = k_{1} \left( { - L_{1} \sqrt {\left( {x^{2} + d^{2} } \right)} + \frac{{x^{2} }}{2}} \right) $$

(15)

When the coil mover is at one of the equilibrium positions ($\pm \sqrt {L_{1}^{2} - d^{2} }$), $P\left( x \right)_{\text{BEMA}}$ has the minimum value, and its value is $- k_{1} \left( {\frac{{L_{1}^{2} + d^{2} }}{2}} \right)$. When the coil mover oscillates between the two equilibrium positions, the local maximum $P\left( x \right)_{\text{BEMA}}$ is $- k_{1} L_{1} d$. As a result, the kinetic energy of the coil mover must be able to complete the following energy conversion to realize inter-well oscillation in the BEMA.

$$ \Delta P\left( x \right)_{\text{BEMA}} = - k_{1} L_{1} d + k_{1} \left( {\frac{{L_{1}^{2} + d^{2} }}{2}} \right) = k_{1} \left( {\frac{{L_{1} - d}}{2}} \right)^{2} $$

(16)

For the BEMA-EB, the bistable restoring force in the x direction is

$$ F\left( x \right)_{\text{BEMA - EB}} = k_{1} x\left( {1 - \frac{{L_{1} }}{{\sqrt {\left( {x^{2} + \left( {d - y} \right)^{2} } \right)} }}} \right) $$

(17)

the corresponding potential energy of the BEMA-EB is

$$ P\left( x \right)_{E} = k_{1} \left( { - L_{1} \sqrt {\left( {x^{2} + \left( {d - y} \right)^{2} } \right)} + \frac{{x^{2} }}{2}} \right) $$

(18)

The local maximum $P\left( x \right)_{\text{BEMA - EB}}$ is $- k_{1} L_{1} \left( {d - y} \right)$ when $x = 0$, and the minimum $P\left( x \right)_{\text{BEMA - EB}}$ is $- k_{1} \left( {\frac{{L_{1}^{2} + \left( {d - \frac{{m_{2} g}}{{k_{2} }}} \right)^{2} }}{2}} \right)$ when the coil mover is at one of the equilibrium positions $\left( { \pm \sqrt {L_{1}^{2} - \left( {d - \frac{{m_{2} g}}{{k_{2} }}} \right)^{2} } } \right)$. Thus, the kinetic energy of the coil mover must be greater than $\Delta P\left( x \right)_{\text{BEMA - EB}}$ in the BEMA-EB to realize inter-well oscillation.

$$ \Delta P\left( x \right)_{\text{BEMA - EB}} = - k_{1} L_{1} \left( {d - y} \right) + k_{1} \left( {\frac{{L_{1}^{2} + \left( {d - \frac{{m_{2} g}}{{k_{2} }}} \right)^{2} }}{2}} \right) $$

(19)

The difference between $\Delta P\left( x \right)_{\text{BEMA}}$ and $\Delta P\left( x \right)_{\text{BEMA - EB}}$ is

$$ \Delta P = \Delta P\left( x \right)_{\text{BEMA}} - \Delta P\left( x \right)_{\text{BEMA - EB}} = \frac{{k_{2} \left( {m_{2} g\left( {dk_{2} - 0.5m_{2} g} \right) - L_{2} k_{1}^{2} y} \right)}}{{k_{1}^{2} }} $$

(20)

It is seen that $\Delta P$ is always greater than 0 when $k_{2} \ge 0.5m_{2} g/d$ and $y \le 0$. In this paper, $\frac{{0.5m_{2} g}}{d} = 6.81\,{\text{N/m}}$, and thus it is easy to satisfy $k_{2} \ge 0.5m_{2} g/d$. Besides, $y \le 0$ means $m_{2}$ is pushed up by the inclined spring, and thus $k_{1} \ge m_{2} g/\left( {L_{1} - d} \right) = 122.5\,{\text{N/m}}$ is required. In conclusion, it is easier for the BEMA-EB to induce inter-well oscillation than the BEMA because the additional coupling elastic boundary in the BEMA-EB reduces the depth of the potential energy well. In other words, the BEMA-EB has a smaller input signal amplitude threshold of activating the favorable inter-well actuation than the BEMA. Figure 11 shows the potential energy of the BEMA and BEMA-EB when $k_{1} = k_{2} = 2000 \,{\text{N/m}}$. It is seen that $\Delta P\left( x \right)_{\text{BEMA - EB}} < \Delta P\left( x \right)_{\text{BEMA}}$, and consequently the BEMA-EB has a smaller input signal amplitude threshold. Since the variation of potential energy is greater in the BEMA, the corresponding variation of kinetic energy is greater as well. $v_{i}$ and $v_{o}$ are defined as the velocity of the coil mover at the initial equilibrium position and $x = 0$, respectively. Thus,

Fig. 11

Potential energy of the coil movers for the BEMA and BEMA-EB when $k_{1} = k_{2} = 2000 {\text{N}}/{\text{m}}$

$$ \Delta P\left( x \right)_{\text{BEMA}} = \frac{{m_{1} v_{i}^{2} }}{2} - \frac{{m_{1} v_{0}^{2} }}{2} :{\text{BEMA}} $$

(21a)

$$ \Delta P\left( x \right)_{\text{BEMA - EB}} = \frac{{m_{1} v_{i}^{2} }}{2} - \frac{{m_{1} v_{0}^{2} }}{2} :{\text{BEMA - EB}} $$

(21b)

Because $\Delta P\left( x \right)_{\text{BEMA - EB}} < \Delta P\left( x \right)_{\text{BEMA}}$, $\left| {v_{i} - v_{o} } \right|_{\text{BEMA}}$ is greater than $\left| {v_{i} - v_{o} } \right|_{\text{BEMA - EB}}$. In other words, the coil mover’s acceleration of the BEMA is larger than that obtained in the BEMA-EB, which can also be seen in Figs. 3, 4, 5, 6, 7, 8, 9 and 10. It should be noted that this section qualitatively explains why the input signal amplitude threshold of the BEMA-EB is smaller from the governing equation through mathematical interpretation, and why the acceleration obtained in the BEMA is relatively larger.

4 Bifurcation analyses

To develop the insights into the nonlinear dynamic behaviors of the BEMA-EB, this section investigates the bifurcation features of the BEMA-EB in terms of the inclined spring stiffness (k₁), the input signal frequency ($\varOmega$) and amplitude (I). The bifurcation features of the counterpart BEMA are also presented in this section for comparative study. The linear stiffness $k_{2} = 2000 {\text{N}}/{\text{m}}$ is employed. Phase portraits and Poincare maps are presented to illustrate how the actuation responses of the BEMA and the BEMA-EB evolve corresponding to the change of the above parameters. The red points in this section represent the Poincare maps under the corresponding situation. Additionally, the stroboscopic time $T = 1/\varOmega$ is adopted in both the bifurcation diagrams and Poincare maps.

4.1 Bifurcation diagram for $\left( {k_{1} ,x} \right)$

Figures 12a and 13a depict bifurcation diagrams of the BEMA and BEMA-EB with respect to the inclined spring stiffness k₁ and coil mover’s displacement x when $I = 1.5 {\text{A}}$, $\varOmega = 6 {\text{Hz}}$. k₁ is ranged from 100 to 2000 N/m with a step of 0.1 N/m. It can be observed that k₁ has a significant impact on the displacement responses in both actuators. For the BEMA, when k₁ is less than 222 N/m, the displacement response is in a state of period-3 inter-well oscillation. It can be proved from Fig. 12b that there are three independent points in the Poincare map. Once k₁ grows up to 222 N/m, the steady-state response of the BEMA bifurcates to chaos as plenty of irregular dispersed points in Fig. 12c. Afterward, the steady-state response of the BEMA switches between period-3 inter-well oscillation and chaos in $633 < k_{1} < 1000 {\text{N}}/{\text{m}}$. As k₁ exceeds 1000 N/m, a large-amplitude period-1 inter-well motion is obtained, as shown in Fig. 12f. Finally, when k₁ is greater than 1600 N/m, the steady-state response of the BEMA will jump into another period-1 motion, the low-amplitude intra-well oscillation.

Fig. 12

a Bifurcation diagram of displacement response versus the inclined spring stiffness k₁ when $I = 1.5 {\text{A}}$, $\varOmega = 6 {\text{Hz}}$ for the BEMA. b–g Phase portraits and Poincare maps of the BEMA under different k₁

Fig. 13

a Bifurcation diagram of displacement response versus the inclined spring stiffness k₁ when $I = 1.5 {\text{A}}$, $\varOmega = 6 {\text{Hz}}$ and $k_{2} = 2000 {\text{N}}/{\text{m}}$ for the BEMA-EB. b–g Phase portraits and Poincare maps of the BEMA-EB under different k₁

Furthermore, more nonlinear phenomena of the BEMA-EB can be seen in Fig. 13a. A stable period-3 inter-well oscillation response of the BEMA-EB occurs in $100 \le k_{1} \le 230 {\text{N}}/{\text{m}}$, where Fig. 13b presents the phase portrait of one example $k_{1} = 100$ N/m. When k₁ is increased further to be 231 N/m, the period-3 response bifurcates to chaos, where the phase portrait exhibits an irregular motion. When $848 < k_{1} < 920 {\text{N}}/{\text{m}}$, period-3, period-6 and period-9 inter-well responses appear successively, which are shown in Fig. 13c–e, respectively. At $k_{1} = 921 {\text{N}}/{\text{m}}$, the period-9 response of the BEMA-EB suddenly becomes chaos, and this behavior persists until $k_{1} = 1870 {\text{N}}/{\text{m}}$. When k₁ is greater than 1870 N/m, period-3 inter-well oscillation response arises, where the phase portrait of the period-3 inter-well oscillation is shown in Fig. 13g. It is seen that the BEMA-EB can realize the favorable inter-well actuation for the entire range of the inclined spring stiffness k₁ when $I = 1.5 {\text{A}}$ and $\varOmega = 6 {\text{Hz}}$, whereas the BEMA only exhibits inter-well response for $k_{1} < 1600$ N/m. This indicates that the BEMA-EB improves the robustness of the large-amplitude actuation against the variation of k₁.

4.2 Bifurcation diagram for $\left( {\varOmega ,x} \right)$

The bifurcation diagram of coil mover’s displacement response ($x$) of the BEMA versus the input signal frequency ($\varOmega$) is shown in Fig. 14a. $k_{1} = 2000 {\text{N}}/{\text{m}}$, $I = 1.5 {\text{A}}$, and $\varOmega = 0.1{-}10$ Hz with an interval 0.01 Hz. It is observed from Fig. 14a that as $\varOmega$ increases, the BEMA displacement response x undergoes period-1, chaotic zone, periodic, chaotic zone and finally enters into period-1 response. When the BEMA is subjected to the low frequency input signal, only intra-well oscillation is obtained. Figure 14b depicts the phase portrait and Poincare map of the BEMA when $\varOmega = 6 {\text{Hz}}$. Afterward, a chaotic zone is obtained in $7.3 < \varOmega < 8.58 {\text{Hz}}$. There is a strange attractor representing chaos in the Poincare map shown in Fig. 14c, and the phase portrait shows disordered and irregular coil mover movements. In the middle of the chaotic zone, a period-5 inter-well motion is also discovered when $7.97 < \varOmega < 8.07 {\text{Hz}}$. Once $\varOmega$ exceeds 8.58 Hz, the response of the BEMA will be transformed into period-1 intra-well oscillation, which shows low-efficient actuation performance.

Fig. 14

a Bifurcation diagram of displacement response versus the input signal frequency $\varOmega$ when $k_{1} = 2000 {\text{N}}/{\text{m}}$, $I = 1.5 {\text{A}}$ for the BEMA. b–g Phase portraits and Poincare maps of the BEMA under different $\varOmega$

The nonlinear dynamic responses of the BEMA-EB are quite different from the BEMA, which are shown in Fig. 15a. When $\varOmega \le 1.5 {\text{Hz}}$, the BEMA-EB exhibits a period-1 disorder intra-well movement. Afterward, a period-1 inter-well oscillation is obtained in $1.51 < \varOmega < 1.93 {\text{Hz}}$, one example of which is shown in Fig. 15b. After that, chaotic and periodic responses occur repeatedly. Figure 15c shows a strange attractor of the BEMA-EB when $\varOmega = 1.94 {\text{Hz}}$, a period-3 inter-well oscillation is also observed in Fig. 15d when $\varOmega = 2.82 {\text{Hz}}$. Once $\varOmega$ exceeds 3.04 Hz, the BEMA-EB will realize a large-amplitude period-1 inter-well oscillation until 6.31 Hz, except in the range of 3.47–4.24 Hz, which are shown in Fig. 15d, e, respectively. Figure 15f shows the phase portrait and Poincare map of the BEMA-EB when $\varOmega = 5 {\text{Hz}}$. Large-amplitude inter-well response is obtained, where only one isolated point in the Poincare map is discovered in Fig. 15f. Figure 15g shows a period-5 inter-well oscillation when $\varOmega = 7.15 {\text{Hz}}$. Besides, extremely complex periodic nonlinear responses are obtained shown in the Periodic-zone in Fig. 15a. To show them more clearly, a locally enlarged graph of the Periodic-zone is presented in Fig. 16, which shows a series of periodic responses of the BEMA-EB. A multi-periodic inter-well response is illustrated in Fig. 16b when $\varOmega = 7.22 {\text{Hz}}$. Afterward, period-10 inter-well oscillation is also obtained. Once $\varOmega$ is up to 7.37 Hz, the BEMA-EB will suddenly become the low-amplitude intra-well oscillation. Figure 16d–g shows four types of the periodic intra-well oscillations, and they are period-8, period-4, period-2, and period-1 intra-well oscillation, respectively. Overall, the BEMA-EB has more abundant nonlinear characteristics, and a much broader inter-well actuation bandwidth, compared to the BEMA.

Fig. 15

a Bifurcation diagram of displacement response versus the input signal frequency $\varOmega$ when $k_{1} = k_{2} = 2000 {\text{N}}/{\text{m}}$, $I = 1.5 {\text{A}}$ for the BEMA-EB. b–g Phase portraits and Poincare maps of the BEMA-EB under different $\varOmega$

Fig. 16

a Bifurcation diagram of displacement response versus the input signal frequency $\varOmega$ when $k_{1} = k_{2} = 2000 {\text{N}}/{\text{m}}$, $I = 1.5 {\text{A}}$ for the BEMA-EB in the Periodic-zone. b–g Phase portraits and Poincare maps of the BEMA-EB under different $\varOmega$

4.3 Bifurcation diagram for $\left( {I,x} \right)$

Figures 17a and 18a show the bifurcation diagrams of the coil mover’s displacement response (x) of the BEMA and BEMA-EB versus the input signal amplitude (I), respectively. I = 0–3 A are used to explore the bifurcation features of the BEMA and BEMA-EB when $k_{1} = k_{2} = 2000 {\text{N}}/{\text{m}}$ and $\varOmega = 6 {\text{Hz}}$. It is seen in Figs. 17a and 18a that both the actuators undergo significantly different nonlinear dynamic responses with the increase in the input signal amplitude. The BEMA exhibits three types of the responses, which present the period-1 intra-well response, period-1 inter-well response and periodic inter-well response, respectively. Figure 17b–d shows the phase portraits and Poincare maps of the BEMA when $I = 2.24$, 2.25 and 2.91 A, which are the examples of the three responses, respectively. However, the BEMA-EB shows more types of the responses compared to the BEMA. After the period-1 intra-well response in $0 < I < 0.703 {\text{A}}$ and period-2 intra-well response in $0.704 < I < 0.77 {\text{A}}$, the steady-state response of the BEMA-EB bifurcates into chaos when I is up to 0.78 A. In a wide range of $0.78 < I < 1.815 {\text{A}}$, the BEMA-EB exhibits a large-amplitude chaotic inter-well response, except a period-7 response near $I = 0.82 {\text{A}}$, a period-5 response in $0.986 < I < 1.025 {\text{A}}$ and a period-3 response in $1.49 < I < 1.58 {\text{A}}$. Figure 18c–f shows the corresponding nonlinear characteristics following the sequence: period-7 inter-well, chaos, period-5 inter-well, and period-3 inter-well response. Finally, the BEMA-EB exhibits large-amplitude period-1 inter-well oscillation, the example of which is shown in Fig. 18g when $I = 2.24 {\text{A}}$. In conclusion, it is seen that the BEMA-EB exhibits more types of the nonlinear dynamic responses. The results also show that the BEMA-EB has a smaller input signal amplitude threshold than the BEMA, which verifies the advantages of the elastic boundary.

Fig. 17

a Bifurcation diagram of displacement response versus the input signal amplitude I when $k_{2} = 2000 {\text{N}}/{\text{m}}$, $\varOmega = 6 {\text{Hz}}$ for the BEMA. b–d Phase portraits and Poincare maps of the BEMA under different I

Fig. 18

a Bifurcation diagram of displacement response versus the input signal amplitude I when $k_{1} = k_{2} = 2000 {\text{N}}/{\text{m}}$, $\varOmega = 6 {\text{Hz}}$ for the BEMA-EB. b–g Phase portraits and Poincare maps of the BEMA-EB under different I

5 Influence of initial conditions

According to the above investigations, various distinct nonlinear responses could exist for both the BEMA and BEMA-EB, e.g., periodic inter-well response, periodic intra-well response and chaotic inter-well response. It is seen that the periodic inter-well response and chaotic inter-well response have large-amplitude displacement, which could realize actuation amplification. However, the initial conditions play a crucial role on deciding the response types of each actuator when the physical parameters are identical. To present the guideline of the initial condition selection, the basin-of-attraction maps are thoroughly investigated for the BEMA and BEMA-EB in this section. The physical parameters are set as follows: $k_{1} = k_{2} = 2000 {\text{N}}/{\text{m}}$, $I = 1.5 {\text{A}}$, $\varOmega = \left[ {4,5,6,7,8,9} \right] {\text{Hz}}$, and 401 × 401 initial conditions are taken from [− 0.05,0.05] m × [− 1,1] m/s. In each of the following basin-of-attraction maps, the red, blue and yellow scatter points represent different initial conditions, leading to the periodic inter-well oscillations, periodic intra-well oscillations and chaotic inter-well responses, respectively. When there are very few scatter points in a basin-of-attraction map under certain situation, the star patterns are used to replace the scatter points to make it more distinct.

5.1 Basin-of-attraction

Figure 19a–f shows the basin-of-attraction maps of the BEMA for $\varOmega = \left[ {4,5,6,7,8,9} \right] {\text{Hz}}$, respectively. All the figures in Fig. 19 exhibit a fractal structure except Fig. 19e. With the increase in $\varOmega$ from 4 to 6 Hz, the number of the periodic inter-well response’s initial conditions increases gradually, which indicates that the likelihood of the favorable periodic inter-well responses is enhanced. The largest occurring probability of the periodic inter-well responses of the BEMA is 43.77% when $\varOmega = 6 {\text{Hz}}$. When $\varOmega$ is greater than 6 Hz, chaotic response occurs in the BEMA. Figure 19d is a basin-of-attraction map with fractal structure which contains three distinct nonlinear dynamic responses. When $\varOmega = 8 {\text{Hz}}$, chaotic response becomes dominating among the BEMA’s steady-state responses, and the intra-well response disappears. Keeping increasing the $\varOmega$ to 9 Hz, the intra-well response emerges again and the inter-well oscillation is almost extinct. In general, the input signal frequency of the BEMA should be near 7 Hz if the aim is to obtain a desirable actuation output performance.

Fig. 19

Basin-of-attraction maps of the BEMA at different input signal frequency $\varOmega$ when $k_{1} = 2000 {\text{N}}/{\text{m}}$, $I = 1.5 {\text{A}}$. Red, blue and yellow scatter points represent periodic inter-well oscillations, periodic intra-well oscillations and chaotic inter-well responses, respectively. a$\varOmega = 4 {\text{Hz}}$; b$\varOmega = 5 {\text{Hz}}$; c Ω = 6 Hz; d$\varOmega = 7 {\text{Hz}}$; e$\varOmega = 8 {\text{Hz}}$; f$\varOmega = 9 {\text{Hz}}$

Figure 20 shows the basin-of-attraction maps of the BEMA-EB for $\varOmega = \left[ {4,5,6,7,8,9} \right] {\text{Hz}}$, respectively. There are some fractal structures and some banded regions in Fig. 20. The banded regions of initial conditions which lead to one of the distinct steady-state oscillation responses make it possible for this parameter set [15]. It seems that chaotic response is more pervasive in the BEMA-EB, and correspondingly, intra-well motion is seldom encountered. In Fig. 20a, only chaotic response and intra-well oscillation occur, and the occurring probability of chaos for the BEMA-EB is 68.31% when $\varOmega = 4 {\text{Hz}}$. Afterward, the periodic inter-well response becomes dominating, which shows a 100% occurring probability when $\varOmega = 5 {\text{Hz}}$. This means the BEMA-EB would obtain a desirable actuation output if the input signal frequency is 5 Hz. With the persistent growth of $\varOmega$, chaotic inter-well response appears again. Once $\varOmega$ exceeds 8 Hz, the intra-well oscillation gradually becomes the main response. It can be concluded that the BEMA-EB has a wider inter-well actuation bandwidth and the BEMA-EB could enhance the actuation performance for low-frequency input signal.

Fig. 20

Basin-of-attraction maps of the BEMA-EB at different input signal frequency $\varOmega$ when $k_{1} = k_{2} = 2000 {\text{N}}/{\text{m}}$, $I = 1.5 {\text{A}}$. Red, blue and yellow scatter points represent periodic inter-well oscillations, periodic intra-well oscillations and chaotic inter-well responses, respectively. a$\varOmega = 4 {\text{Hz}}$; b$\varOmega = 5 {\text{Hz}}$; c Ω = 6 Hz; d$\varOmega = 7 {\text{Hz}}$; e$\varOmega = 8 {\text{Hz}}$; f$\varOmega = 9 {\text{Hz}}$

5.2 Occurring probabilities of the different responses

Though basin-of-attraction maps could provide a reliable basis for selecting the ideal initial conditions, they might vary with respect to different excitation frequencies. Hence, the occurring probability of each type of the steady-state response is worth studying to quantitatively understand how the initial conditions influence the responses of the BEMA and BEMA-EB for a wide frequency band. A broader input signal frequency band $\varOmega = \left[ {1,2,3,4,5,6,7,8,9,10} \right]$ Hz is employed to show the occurring probabilities in this section. Figure 21 shows the occurring probabilities of each nonlinear dynamic responses in the BEMA and BEMA-EB, respectively. It is seen in Fig. 21 that the BEMA has a much greater occurring probabilities to exhibit periodic intra-well oscillation than the BEMA-EB. Furthermore, the periodic intra-well response occurring probability for the BEMA is equal to 1 when $\varOmega < 4 {\text{Hz}}$ (away from the natural frequency 7.5 Hz), which infers that the BEMA should not be employed in the low input signal frequency band. The intra-well responses become dominating for the BEMA again when $\varOmega > 9 {\text{Hz}}$. Differently, the low-amplitude intra-well responses seldom appear in the BEMA-EB when $\varOmega < 8 {\text{Hz}}$, which indicates that the BEMA-EB could obtain a considerable actuation performance (i.e., large-amplitude inter-well response) in a wide input signal frequency band. However, when $\varOmega > 8 {\text{Hz}}$, the intra-well responses quickly dominate the BEMA-EB’s steady-state response while this does not happen until $\varOmega > 9 {\text{Hz}}$ in the BEMA. Even so, the BEMA-EB could still be employed in high input signal frequency band by fixing the joint mass or using a huge linear stiffness k₂ to be transformed to the BEMA. Overall, it is worth pointing out that not only the BEMA-EB has a broad inter-well actuation bandwidth, but also has an optimal input signal frequency (i.e., 5 Hz) which leads to 100% occurring probability of exhibiting the favorable periodic inter-well response.

Fig. 21

Occurring probabilities of each nonlinear dynamic responses in the BEMA and BEMA-EB at different $\varOmega$ when $k_{1} = k_{2} = 2000 {\text{N}}/{\text{m}}$, $I = 1.5 {\text{A}}$. a BEMA; b BEMA-EB

6 Conclusion

This paper investigates the merits of a bistable electromagnetic actuator with elastic boundary (BEMA-EB) and its nonlinear dynamic responses. The BEMA-EB utilizes both the bistable nonlinearity introduced by the inclined spring and the elastic boundary to enhance the actuation performance when controlled by a harmonic input signal. Two counterparts are also modeled to present the benefits of both the bistable nonlinearity and elastic boundary. The first one is a bistable electromagnetic actuator without the elastic boundary (BEMA), and the second one is a linear electromagnetic actuator (LEMA). The results show that the bistable nonlinearity does have a tremendous effect on the actuation improvement of both the BEMA and BEMA-EB. However, the BEMA-EB employs the elastic boundary to bring the additional dynamic coupling to reduce the depth of the potential energy well. As a result, the BEMA-EB has a much broader inter-well actuation bandwidth and smaller input-signal-amplitude threshold of activating the favorable inter-well actuation. Furthermore, the bifurcation analyses indicate that both the BEMA and BEMA-EB have abundant nonlinear dynamic characteristics, including periodic inter-well, periodic intra-well and chaotic inter-well dynamic responses. The bifurcation analyses also testify that the BEMA-EB outperforms the BEMA by broadening the inter-well actuation bandwidth and reducing the input signal amplitude threshold of the inter-well actuation. In addition, the basin-of-attraction maps are investigated for both the BEMA and BEMA-EB, which leads to the occurring probabilities of each type of the response. The occurring probability results quantitatively illustrate that it is more likely for the BEMA-EB to achieve favorable large-amplitude inter-well actuation performance. Thus, the results validate that both the appropriately designed bistable nonlinearity and elastic boundary are beneficial to actuation performance enhancement of the electromagnetic actuators.

Appendix: Model validation using the MSC Adams software

The MSC Adams software is used to validate the mathematical model of the BEMA-EB. In the software, the 3D virtual prototype of the BEMA-EB is established, as shown in Fig. 22. The simulation parameters are listed in Table 1 (as same as Fig. 9e).

Fig. 22

The 3D virtual prototype of the BEMA-EB in Adams software. a Isometric graph; b planar graph

Table 1 The simulation parameters

The comparative results between the numerical results of the governing equations and Adams software are presented in Fig. 23. Figure 23 shows the acceleration responses obtained by the Adams for the BEMA-EB under forward swept harmonic input signal from 1 Hz to 10 Hz with the amplitude $I = 2 {\text{A}}$. The sweeping rate is 0.025 Hz/s. It is seen that the two results (Figs. 9e and 23) are in good agreement.

Fig. 23

a Acceleration responses obtained by the Adams for the BEMA-EB under forward swept harmonic input signal when $k_{1} = 2000 {\text{N}}/{\text{m}}$, $k_{2} = 2000 {\text{N}}/{\text{m}}$, $I = 2 {\text{A}}$. b Result of Fig. 9e

In addition, another forward swept response results of both Adams software and the governing equations are presented. $I = 1.5 {\text{A}}$, $k_{1} = 2000 {\text{N}}/{\text{m}}$, $k_{2} = 2000 {\text{N}}/{\text{m}}$ are employed in this calculation. Figure 24 shows the displacement, velocity and the acceleration responses of both the methods. It is seen that the numerical results are in good agreement with the Adams software results.

Fig. 24

Comparison between the numerical method and the Adams. The blue curves indicate the responses obtained by numerical method, while the red curves represent the Adams. a, b Displacement response; c, d velocity response; e, f acceleration response