Nonlinear dynamics of an asymmetric bistable energy harvester with an adjustable unilateral stopper

Abstract

Due to the broadband response and high sensitivity to low excitation levels, bistable energy harvesters (BEHs) have been viewed as an efficient method to overcome the shortcomings of linear energy harvesters only performing well near the resonant frequency. Previously, most strategies for performance enhancement of BEHs have been extensively discussed for systems with perfectly symmetric potentials. However, it is difficult to achieve a BEH with a perfectly symmetric potential due to practical constraints and previous investigations indicated that asymmetric potentials have a negative effect on the performance of BEH. Therefore, an adjustable unilateral stopper is introduced and positioned at the side with deeper potential well to broaden the response frequency band. Numerical simulations of bifurcation diagrams and maps of 0–1 test and output power indicate that the introduction of the stopper could enable the asymmetric BEH to realize interwell oscillation in a wider frequency range, and the performance are closely related to the collision gap, collision position, excitation frequency, as well as excitation levels. Regarding the basins of attraction, it is demonstrated that the stopper leads the system to achieve interwell oscillation with a high probability under certain excited conditions. Overall, this study provides a possible strategy for improving the performance of the asymmetric BEHs.

1 Introduction

With the rapid development of the technologies of communication and microelectronic sensors, the wireless sensor networks, portable devices, automatic detection systems and other related products have emerged one after another [1], and there are many low-power components in them. Nowadays, these devices are enabled by traditional batteries which need to be replaced and recharged frequently [2, 3]. To overcome this issue, the energy from environment can be considered to be harvested to power them [4, 5], and reduce the inconvenience of battery power to some extent. By applying the technology of energy harvesting, the ambient vibrational energy can be converted to into electricity to power electronics, thereby mitigating, to a certain extent, the inconvenience associated with battery-dependent power sources. At present, the energy conversion methods are mainly based on the electromagnetic [6,7,8], triboelectric [9, 10], electrostatic and piezoelectric [11, 12] effects. Piezoelectric energy harvesters received a lot of attention due to their high energy density [13,14,15]. Relevant studies have shown that piezoelectric energy harvesters have considerable research prospects in transportation [16, 17], ocean [18,19,20], fluids [21, 22] and other fields.

Traditional piezoelectric energy harvesters were based on linear systems, which has a limited bandwidth near their resonant frequencies. However, in reality, environmental vibration frequencies exhibit a wide frequency spectrum distribution. In this condition, the performance of the linear energy harvesters will be greatly degraded. To overcome this issue, there are some improved systems. For example, Ge et al. [23] proposed a zigzag piezoelectric energy harvester driven by a ball. This harvester collects low-frequency vibrational energy by adjusting the number of piezoelectric plates on the piezoelectric spring, which in turn alters the natural frequency. Wang et al. [24] designed a multi-beam piezoelectric energy harvester that utilizes L-shaped beams to reduce the natural frequency and adjust the formants of multiple beams to be similar, so that the energy harvester has multiple resonant frequencies in the 9–20 Hz frequency band. In addition, the nonlinearity due to mechanical structures [25, 26] and magnetic coupling [27,28,29] has been widely utilized in the design of energy harvesters in recent years due to its excellent ability to broaden the frequency band and increase the voltage [30]. Specifically, designs with multiple stable equilibrium positions [31, 32] are extensively studied. For instance, Zhou et al. [33, 34] introduced magnetic coupling nonlinearity to the piezoelectric beam, effectively transforming the linear energy harvester into a multi-stable system. This greatly expands the bandwidth of the energy harvester in the high energy output frequency band. Bistable energy harvester (BEH) has been studied intensively due to its transient and broadband responses. Hou et al. [35] designed a geometrically nonlinear piezoelectric energy harvester based on the origami structure, which exhibits bistable properties and can effectively harvest energy from low-frequency vibrations. Zhou et al. [36] proposed a flexible bistable energy harvester, which can automatically adjust the potential energy function of the beam during the vibration process, thereby facilitating the transition between potential wells and achieve a better energy harvesting efficiency. Additionally, there are other bistable energy harvesters reported in [37,38,39]. Subsequently, various tri-stable [40,41,42], quad-stable [43, 44], and quin-stable [45] energy harvesters were gradually designed to study their output power, bandwidth response, and nonlinear characteristics.

For the BEH, most studies concentrate on the systems with perfectly symmetric potential energy functions. However, achieving such symmetric potential wells in practical conditions is challenging due to materials instability, nonlinear forces, and external interference. Previous studies have shown that the asymmetric potential well has a negative effect on the output performance of BEH at moderate and low excitation levels [46,47,48]. Recently, Li et al. [49] further confirmed through experiments and simulations that asymmetry reduces the response bandwidth of BEH, referencing existing studies. To mitigate the adverse effects of asymmetry while harnessing its potential benefits, Wang et al. [50] inspired by the asymmetry of the swing of human lower limbs, proposed introducing an appropriate deflection angle. They verified the effectiveness of this approach through numerical simulation and experiments. Norenberg et al. [51] conducted a comprehensive analysis of the nonlinear dynamics of asymmetric BEH and concluded that there is an optimal deflection angle to eliminate the negative effects of asymmetry. Wang et al. [52] proposed an asymmetric tri-stable energy harvester with a compressible and rotatable magnet-spring oscillation system, which can obtain higher energy output performance than symmetrical systems by adjusting the appropriate spring stiffness. Since asymmetry is difficult to ignore, other asymmetric multi-stable systems have been studied, focusing on their nonlinear dynamics [53, 54].

In this paper, an asymmetric bistable energy harvester with an adjustable unilateral stopper is proposed to broaden the response bandwidth. In this design, the adjustable unilateral stopper is introduced and positioned on the side with deeper potential well. As explored in previous studies, there are various ways to introduce stoppers. As an example, Halim et al. [55] established a theoretical model of a one-way collision system, which utilized collision to achieve frequency conversion and enhance the performance of the system. Liu et al. [56] designed a MEMS piezoelectric energy harvester, incorporating a blocker to broaden the system’s response frequency band. They studied the bandwidth response of both single-sided stopper and double-sided system with varying collision stiffnesses through theoretical analysis and experiment, demonstrating that blocking can indeed widen the response frequency band of the system. Li et al. [57] proposed a unilateral stopper energy harvester and compared the results of theory, simulation and experiment. Zhou et al. [58, 59] further investigated the effects of different stopper types and materials on system performance and nonlinear dynamics through theory and experiments. Additionally, studies have been conducted to introduce blockers into magnetically coupled BEHs to improve the system’s performance [60, 61]. However, few studies have considered the combination of asymmetry and stopper to date.

Therefore, this paper considers the combination of asymmetric BEH and stopper to realize unilateral piecewise nonlinearity, which could overcome the negative effects of asymmetry to a certain extent by positioning the stopper at the side with deeper potential well. Herein, the nonlinear dynamic behaviors and output performance of the asymmetric piezoelectric BEH with an adjustable unilateral stopper are emphasized. The bifurcation diagram, maps of output power and 0–1 test are employed to investigate the effects of excitation frequency and amplitude on the system’s dynamic behaviors and output performance. Additionally, the multiple solutions of the system are emphasized by the means of basins of attraction.

The rest of this paper is as follows: Sect. 2 describes the dynamic modeling and outlines some parameter calculation methods, Sect. 3 delves into the analysis of potential energy function and restoring force, while the Sect. 4 explore the system’s output performance and nonlinear dynamics under harmonic excitation. Finally, conclusions are reached in Sect. 5.

2 Description and electromechanical modeling

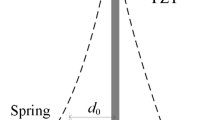
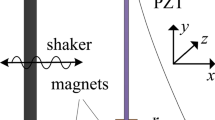
The schematic diagram of the piezoelectric bistable energy harvester is shown in Fig. 1a. It consists of a stainless steel beam with a length of l, two piezoelectric layers at the root, two end magnets, and two external magnet. By adjusting the system parameters, bistable configurations with double potential wells can be obtained. In practical conditions, perfectly symmetric potentials are difficult or even impossible to achieve, and previous literatures indicated that asymmetric potentials have a negative effect on the performance of the BEH. In this paper, an adjustable unilateral stopper is introduced and positioned at the side with deeper potential well to broaden the response bandwidth, as shown in Fig. 1b. To be noted, the distance in the vertical direction from the stopper to the root of the beam is l₀, and the collision gap in the horizontal direction from the stopper to the unstable equilibrium position of the beam is h₀.

Fig. 1

Schematic diagram of the asymmetric potential BEH without a and with b a unilateral stopper

For the system without external magnets and stopper, a linear energy harvester is obtained. According to Hamiltonian principle, the variational indicator of Lagrange function is zero [34], and satisfies Eq. (1).

$$\int_{{t_{1} }}^{{t_{2} }} {\delta \left[ {T\left( t \right) - V\left( t \right)} \right]} {\text{d}}t + \int_{{t_{1} }}^{{t_{2} }} {\delta W_{nc} \left( t \right)} {\text{d}}t = 0$$

(1)

where $T$ is the kinetic energy, $V$ is the potential energy, and $W_{nc}$ is the external excitation energy, which are all functions of time $t$, and δ is the variational sign.

This system follows the configuration of the second type of piezoelectric equation, and the dynamic model of the piezoelectric cantilever beam can be derived from relevant theory, considering the first-order mode shapes [33], as shown in Eq. (2).

$$\left\{ \begin{gathered} m\ddot{x} + c\dot{x} + F_{r} + \theta \overline{V} = F\cos (\omega t) \hfill \\ C_{p} \dot{\overline{V}} + \frac{{\overline{V}}}{R} - \theta \dot{x} = 0 \hfill \\ \end{gathered} \right.$$

(2)

where $m$, $c$ and $\theta$ represent the equivalent mass, damping and electromechanical coupling coefficients of the piezoelectric beam, $F_{r}$ denotes the nonlinear restoring force, $x$ and $R$ represent the tip displacement of the cantilever beam and external load resistance, $F$ and $\upomega$ represent the amplitude and frequency of the external excitation force, respectively. Additionally, $C_{p}$ and $\overline{V}$ correspond to the capacitance and output voltage of the piezoelectric layers, respectively. The superscript dot represents the derivative with respect to time t.

When the cantilever beam collides with the stopper, the nonlinear restoring force F_r changes [45] and it can be expressed as in Eq. (3).

$$\left\{ \begin{gathered} \begin{array}{*{20}l} {F_{r} = k_{1} x + k_{2} x^{2} + k_{3} x^{3} ,} \hfill & {\begin{array}{*{20}c} {\begin{array}{*{20}c} {} & {} \\ \end{array} } & {} \\ \end{array} \begin{array}{*{20}c} {} & {x \le x_{c} } \\ \end{array} } \hfill \\ \end{array} \hfill \\ \begin{array}{*{20}c} {F_{r} = k_{1} x + k_{2} x^{2} + k_{3} x^{3} + k_{0} \left( {x - x_{c} } \right),} & {x > x_{c} } \\ \end{array} \hfill \\ \end{gathered} \right.$$

(3)

where $k_{1}$, $k_{2}$, and $k_{3}$ represent the coefficients of nonlinear restoring force. $k_{0}$ and $x_{c}$ represent the additional stiffness during collision and the critical tip displacement of the cantilever, respectively. Additionally, the collision causes the variation of the damping coefficient and the electromechanical coupling coefficients [61], which can be shown in Eq. (4).

$$c = \left\{ \begin{gathered} c_{1} \hfill \\ c_{2} \hfill \\ \end{gathered} \right.\begin{array}{*{20}c} {} & , \\ \end{array} \theta = \left\{ \begin{gathered} \theta_{1} \begin{array}{*{20}c} {} & {} & {x \le x_{c} } \\ \end{array} \hfill \\ \theta_{2} \begin{array}{*{20}c} {} & {} & {x > x_{c} } \\ \end{array} \hfill \\ \end{gathered} \right.$$

(4)

where the subscripts 1 and 2 represent the equivalent damping and equivalent electromechanical coupling coefficients at the time of non-collision and collision. To be noted, the strain at the root of the cantilever beam will decrease greatly when the collision occurs, thus resulting in a sharp reduction in the electromechanical coupling coefficient.

In addition, the additional stiffness ($k_{0}$) can be expressed by Eq. (5) derived from the deflection curve formula and the principle of deflection superposition.

$$k_{0} = \frac{4kb}{{3b^{2} - 6b + 3 - \left( {3 - b} \right)\left( {1 - b} \right)^{3} }} - k$$

(5)

where $b$ is the ratio of l₀ to l. k is the approximate linear stiffness [62] of the cantilever beam expressed by Eq. (6).

$$k = \frac{3EI}{{l^{3} }}$$

(6)

where $EI$ stands for flexural stiffness. And the critical tip displacement $\left( {x_{c} } \right)$ is calculated as a function of the collision gap distance and the mode shape in the first-order mode. For the system investigated, the average output power in a certain time can be calculated as Eq. (7).

$$P = \frac{{E\left[ {\overline{V}^{2} } \right]}}{R}$$

(7)

In this paper, 0–1 test is applied to identify the characteristics of the response. For the time-series of the tip displacement x, it is discretized using a delay time which equals one-quarter of the period to $x = [X_{1} ,X_{1} , \ldots X_{i} , \ldots X_{N} ]$. New coordinates can be represented as in Eq. (8) [51].

$$\left\{ \begin{gathered} p_{n} \left( y \right) = \sum\limits_{j = 1}^{n} {x\left( {t_{j} } \right)\cos \left( {jy} \right)} \hfill \\ q_{n} \left( y \right) = \sum\limits_{j = 1}^{n} {x\left( {t_{j} } \right)\sin \left( {jy} \right)} \hfill \\ \end{gathered} \right.$$

(8)

where $y$ represents a random constant in the range of 0 to $2\pi$, and n represents a number in the range of 0 to ∞. When the system undergoes regular periodic motion, the mapped image in Eq. (8) on the coordinate system behaves as a bounded motion, while when the system undergoes irregular chaotic motion, the mapped image behaves as a chaotic Brownian motion. To analyze these two motions, the method of calculating the mean square deviation $M_{n}$ is employed to identify the diffusion motion and the non-diffuse motion, as shown in Eq. (9).

$$M_{n} \left( y \right) = \mathop {\lim }\limits_{N \to \infty } \frac{1}{N}\sum\limits_{j = 1}^{N} {\left( {\left[ {p_{j + n} \left( y \right) - p_{j} \left( y \right)} \right]^{2} + \left[ {q_{j + n} \left( y \right) - q_{j} \left( y \right)} \right]^{2} } \right)}$$

(9)

In order to intuitively represent periodic motion and chaotic motion with calculated numerical values, the Eq. (10) is established.

$$K_{c} = \mathop {\lim }\limits_{N \to \infty } \frac{{{\text{Cov}}\left( {t_{n} ,M_{n} } \right)}}{{\sqrt {{\text{Var}}\left( {t_{n} } \right){\text{Var}}\left( {M_{n} } \right)} }}$$

(10)

where ${\text{Cov}}$ and ${\text{Var}}$ are covariance and variance algorithms. Based on Eq. (10), multiple $y$ values are selected to calculate the result and take the median value. The closer the value of $K_{c}$ is to 0, the more regular the motion of the system is, and conversely, the closer the value of $K_{c}$ is to 1, the more chaotic the motion of the system.

3 Analysis of potential energy functions

In this section, the effects of various parameters of the stopper on the nonlinear restoring force and potential energy functions are investigated, where the potential energy functions can be obtained by integrating Eq. (3) with respect to tip displacement x. By studying the static characteristics of the unilateral stopper system, the theoretical basis that the system performance can be improved by stopper is proposed. Firstly, the nonlinear restoring force and potential energy functions of the asymmetric and symmetric bistable system are shown in Fig. 2. When the asymmetric coefficient is introduced, it is seen that the potential well on the left becomes shallower, and the right one becomes deeper, which means that it is more difficult for the asymmetric BEH to cross the right barrier and cause the response bandwidth to be narrow.

Fig. 2

Nonlinear restoring force a and potential energy functions b of the symmetric and asymmetric systems

When a stopper is introduced and positioned at the side with deeper potential wells, the restoring force and potential energy function of the system change significantly. Figure 3 shows nonlinear restoring force and potential energy functions of the asymmetric BEH with a stopper for h₀ = 0.5, 1.0, 1.5, 2.0 mm and l₀ = 60 mm. The change in the collision gap distance means the change in the critical displacement of the tip of the cantilever, as can be seen from the Fig. 3. Due to the introduction of the stopper, the nonlinear restoring force will become larger and the change trend will be steeper. By properly adjusting the collision gap (h₀) between the stopper and the beam, the potential well on the right side could become shallower. It is seen that the smaller the collision gap, the shallower the potential well, and the closer from the potential well to the origin. Due to the variation in the potential energy function, it can be inferred that the response bandwidth of system could be broadened through the introduction of the stopper.

Fig. 3

Nonlinear restoring force a and potential energy functions b for different collision gap

In addition, Fig. 4 illustrates the nonlinear restoring force and potential energy functions of the asymmetric BEH with different collision position $\left( {l_{0} = 50,60,70,80\;{\text{mm}}} \right)$ when the collision gap $\left( {h_{0} = 1.0\;{\text{mm}}} \right)$ is fixed. The change in the collision position is essentially a coupling effect of the change in collision stiffness and the change in the critical displacement of the tip of the cantilever. When the distance from the stopper to the root of the beam increases, the critical displacement of the tip of the cantilever becomes smaller and the collision stiffness becomes larger. In this condition, the potential well on the right side becomes shallower and it has a closer distance to the origin.

Fig. 4

Nonlinear restoring force a and potential energy function b for different collision positions

4 Dynamic analysis and performance assessment

4.1 Influence of asymmetric potential

In this section, the influence of the asymmetric potential on the performance of the BEH is firstly investigated. Under harmonic excitation with various excitation levels and frequencies, the output power of the system is calculated and the 0–1 test is undertaken by applying the stable state of the displacement response. Figure 5 illustrates the maps of 0–1 test and output power for the symmetric and asymmetric BEH, and the yellow areas in the maps of 0–1 test represent the excitation levels and frequencies resulting in chaotic oscillation. By comparing the maps of 0–1 tests in Fig. 5a, b, it is concluded that more excitation conditions lead to chaotic oscillation for the symmetric system. From the maps of output power, it is observed that the asymmetric potential has almost no influence on the solutions with an output power near 10 μW. However, the number of excitation conditions resulting in an output power near 6 μW are significantly reduced. Therefore, it can be concluded that the asymmetric potential has a negative influence on the performance of the BEH.

Fig. 5

Maps of 0–1 test and output power. a and c: Symmetric BEH; b and d: asymmetric BEH

Particularly, the bifurcation diagrams of tip displacement and output power versus excitation level at a frequency of 5.9 Hz are illustrated in Fig. 6a, b for the symmetric and asymmetric BEH for comparison. When the excitation level is relatively small, the oscillations of the symmetric and asymmetric BEH are all limited in a single potential well and low power is generated. For excitation levels larger than 0.18 g, large-amplitude interwell oscillation is obtained for the symmetric BEH, resulting in a larger output power. For the asymmetric BEH, the critical excitation level for achieving large-amplitude interwell motion is 0.21 g, and after that there are still many excitation levels leading to intrawell motion due to the sensitivity of the bistable system.

Fig. 6

Bifurcation diagrams of tip displacement and output power versus excitation level and frequency. a and c: Symmetric BEH; b and d: asymmetric BEH

In addition, bifurcation diagrams of tip displacement and output power versus excitation frequency are illustrated in Fig. 6c, d for the symmetric and asymmetric BEH under excitation with a level of 0.35 g. For the frequency below 1.7 Hz, the oscillation of the symmetric BEH is confined in a single potential well with small power output. From 1.7 to 4.3 Hz, there are chaotic, periodic-1, and periodic-3 interwell oscillations induced by different frequencies and the generated power shows an obvious trend of increasing. Except for the frequencies of 4.7 Hz, large-amplitude interwell oscillation is achieved from 4.3 to 7.4 Hz, and the largest output power reaches 8.5 μW. After experiencing the chaotic, periodic-1, and periodic-3 interwell oscillations in the frequency range from 7.4–9.1 Hz, the oscillation of the system is again confined into a single potential well. For the asymmetric BEH, the large-amplitude interwell oscillation generating large output power begins at a higher frequency of 7.4 Hz and end at a lower frequency of 5.1 Hz. Additionally, the frequency range for chaotic response becomes narrower from 8.4 to 9.2 Hz, among which there is periodic-3 oscillation induced at 8.7 Hz. By comprehensively comparing the maps of 0–1 test and output power as well as the bifurcation diagrams, conclusion can be drawn that the asymmetric potential has a negative influence on the output performance of the BEH, especially on the frequency range resulting periodic and chaotic interwell oscillation.

4.2 Analysis of the asymmetric system with a stopper

To broaden the response frequency range of the asymmetric BEH, an adjustable unilateral stopper is introduced and positioned at the side of with deeper potential well. In this section, the influence of the collision gap and the distance from the stopper to the root of the beam on the nonlinear dynamics and output performance are investigated.

When the distance from the stopper to the root of the beam is 60 mm, the maps of 0–1 test and output power for different collision gaps are depicted in Figs. 7, 8 for various excitation levels and frequencies. When the collision gap is very small with h₀ = 0.5 mm, the chaotic oscillation could be achieved at very low frequencies and relatively small excitation level, as seen in the map of 0–1 test in Fig. 7a. For excitation levels above 0.3 g, another chaotic region is observed near the frequency of 12 Hz. From the map of output power in Fig. 7c, it is seen that interwell periodic and chaotic motions are achieved in a relatively wider frequency range, and the generated output power in the investigated region is below 3 μW. With the collision gap increases to 1.0 mm (Fig. 7b), the chaotic oscillations at low frequencies are obtained at a larger excitation level, when compared with the results in Fig. 7a. Regarding the output power, the map in Fig. 7d shows that it is influenced greatly at lower excitation levels, while the influence is little for relatively larger excitation levels. In addition, the increase in the collision gap increases the effective vibration range of the system, thus leading to a higher output in the considered region.

Fig. 7

Maps of 0–1 test and output power for different collision gap. a and c: h₀ = 0.5 mm; b and d: h₀ = 1.0 mm

Fig. 8

Maps of 0–1 test and output power for different collision gap. a and c: h₀ = 1.5 mm; b and d: h₀ = 2.0 mm

With the collision gap further increasing to 1.5 and 2.0 mm (Fig. 8a, b), the excitation condition region leading to chaotic response becomes much smaller or even disappear. From the maps of output power in Fig. 8c, d, it is discovered that the relatively large output power is induced in a narrow frequency range for all excitation levels, and the largest power increases with an increase in the collision gap. By comparing the results in Figs. 7, 8 with that in Fig. 5, it is demonstrated that the introduction of the stopper with proper gaps could broaden the frequency range for interwell chaotic and periodic oscillation, while the output power is limited due to the reduction of vibration range.

Specially, the bifurcation diagrams of tip displacement and output power versus excitation frequency are provided in Fig. 9 for comparison when the excitation level is 0.35 g. For the collision gap of 0.5 mm, interwell chaotic motion is obtained at very low frequencies below 2.8 Hz, and the output power is larger than that induced by intrawell motion. In the frequency range from 2.8–to 3.9 Hz, single-periodic interwell oscillation is achieved and the output power shows an increasing trend. With the frequency further increasing, chaotic response is again obtained from 4 to 5.9 Hz, among which several frequencies lead to the periodic-1 and periodic-2 oscillation. From 5.9 to 9.9 Hz, the desirable large-amplitude interwell oscillation is again acquired, and the power increases with an increase in the frequency, with a maximum power of 1.86 μW generated at a frequency of 9.9 Hz. As the frequency increases, the frequency range of 10–12.8 Hz again witnesses the chaotic oscillation, and there are several isolated frequencies resulting in periodic-1 intrawell oscillation in the left potential well. Additionally, the periodic-2 intrawell oscillation is observed from 12.8 to 14.6 Hz, and after that the oscillation is always confined in the left potential well.

Fig. 9

Bifurcation diagrams of tip displacement and output power versus excitation frequency: a 0.5 mm; b 1.0 mm; c 1.5 mm; d 2.0 mm

As the collision gap increases to 1.0 mm, the bifurcation diagram of tip displacement and output power versus excitation frequency in Fig. 9b shows a similar variation trend as that in Fig. 9a. In more detail, the oscillation is limited in a single potential well when the frequency is below 1.7 and 1.8 Hz is a critical frequency for achieving interwell oscillation. Due to the high sensitivity of bistable system, the intrawell oscillation is achieved until the frequency increases to 5.7 Hz. With an increase in the frequency, the power shows an increasing trend and a maximum power of 2.3 μW is obtained at a frequency of 9.5 Hz. When the collision gap increases to 1.5 and 2.0 mm, the frequency range resulting in chaotic oscillation becomes narrower or even disappears, as illustrated in Fig. 9c, d. Regarding the periodic interwell motion, it is also achieved in a narrower frequency range and the maximum output power are respectively 2.74 and 3.13 μW at the frequencies of 9.1 and 8.6 Hz.

To investigate the influence of excitation level on the dynamic behaviors, Fig. 10 illustrates the bifurcation diagram of tip displacement and output power versus excitation frequency for the system with a collision gap of 1.0 mm under excitation with levels of 0.2 and 0.5 g. For excitation level of 0.2 g, the interwell oscillation is obtained from the frequency of 5.0 Hz and ends at 7.4 Hz with a maximum power of 1.6 μW generated, among which there are several frequencies leading to chaotic response and many isolated frequencies corresponding to intrawell oscillation. Additionally, a narrow frequency range from 3.8–4.2 Hz results in the chaotic response. As the excitation level increases to 0.5 g, chaotic oscillation is witnessed at very low frequencies. After alternatively realizing chaotic and periodic interwell motion, a maximum power of 2.8 μW is acquired at a frequency of 10.6 Hz. In the frequency range from 10.7–13.3 Hz, the chaotic oscillation is again observed. After the frequency of 13.3 Hz, the system is always confined in the left potential well, and the induced oscillation includes the periodic-2 and periodic-1 response.

Fig. 10

Bifurcation diagrams of tip displacement and output power versus excitation frequency for h₀ = 1.0 mm at excitations of a 0.2 g and b 0.5 g

To further evaluate the influence of the stopper on the dynamical behaviors and output performance of the system, the response under excitation of 0.35 g with several specific frequencies is considered for the system with l₀ = 60 mm and h₀ = 1 mm. When the frequency is 2.9 Hz, the displacement response, output voltage, phase orbit, Poincare map, and frequency spectrum of the voltage are illustrated in Fig. 11a for the asymmetric BEH with and without stopper. For the asymmetric BEH without stopper, the oscillation is confined in the deeper potential well and the generated power is only 0.02 μW. By introducing the stopper, the system could travel across the potential barrier chaotically and the corresponding output power is enhanced to 0.69 μW. From the frequency spectrum, it is seen that the energy mainly concentrates at 2.9 Hz which equals to the excitation frequency for the system without the stopper. For the chaotic response of the system with a stopper, the energy in the frequency spectrum is observed not only at 2.9 Hz, but also near the frequency of 8 Hz. As the excitation frequency increases to 5.1 Hz, the intrawell oscillation of the asymmetric BEH is enabled to the periodic-2 interwell oscillation by introducing the stopper, as can be seen from the phase orbit and Poincare map in Fig. 11b. For the initial interwell oscillation, the frequency spectrum of the voltage indicates that the energy is mainly distributed at 10.2 Hz, and there are also frequency components at 5.1 and 15.3 Hz. For the voltage response of the system with the stopper, its frequency components is at 2.55, 5.1 and 7.65 Hz, and dominant component is at 7.65 Hz. Regarding the output power, it is increased from 0.3 to 1.1 μW through the application of the stopper.

Fig. 11

Displacement, voltage, phase orbit, Poincare map, and frequency spectrum at different excitation frequencies: a 2.9 Hz; b 5.1 Hz; c 6.5 Hz; d7.8 Hz; e 9.0 Hz; f 11.4 Hz. Note that the blue and red color respectively represent the response of the asymmetric BEH without and with the stopper

For excitation frequency of 6.5 Hz, the asymmetric BEH could achieve large-amplitude interwell oscillation as in Fig. 11c, and the output power is 7.8 μW. By introducing the stopper, although the oscillation is interwell, the oscillating region is limited and the output power is reduced to 1.43 μW. With the frequency increasing to 7.8 Hz, the initial single periodic intrawell oscillation is changed to single periodic interwell oscillation as in Fig. 11d, and the output power is increased from 0.16 to 1.8 μW. Further increasing the frequency to 9.0 Hz, it is seen from the phase orbit and Poincare map in Fig. 11e that the initial chaotic response is transformed to single periodic interwell oscillation by introducing the stopper. On this occasion, the output power does not change much at about 2.1 μW. Again at the frequency of 11.4 Hz, the intrawell oscillation is enabled to chaotic oscillation, and the output power varies from 0.3 to 0.6 μW. From the comparison, it can be concluded that the stopper can be applied to enhance the performance of the asymmetric BEH for some initial intrawell and chaotic interwell oscillations. However, when the system is originally in periodic interwell vibration, the stopper will degrade the output performance.

To further study the influence of excitation level on the nonlinear dynamics and output performance, the bifurcation diagrams of tip displacement and output power versus excitation level are provided for the asymmetric system with l₀ = 60 mm and h₀ = 1 mm. For a low excitation frequency of 2.9 Hz, the bifurcation diagrams of tip displacement and output power versus excitation level in Fig. 12a indicates that the system’s oscillation is firstly limited in a single potential well, and then travels across the potential barrier for excitation level above 0.175 g. Near the excitation level of 0.32 g, several isolated levels lead to chaotic oscillation and the power relatively small. While, the chaotic oscillation induced by excitations above 0.45 g results in a larger output power due to the increase of the excitation level. For excitation frequency of 5.1 Hz, interwell oscillation could be achieved for very small levels although several isolated levels induce intrawell motion, as in Fig. 12b. From about 0.2 to 0.34 g, there are excitation levels corresponding to intrawell and chaotic oscillations with relatively low output power. With an increase in the levels, the generated power shows an increasing tend although there is still chaotic oscillation.

Fig. 12

Bifurcation diagrams of tip displacement and output power versus excitation level. a 2.9 Hz; b 5.1 Hz; c 6.5 Hz; d 7.8 Hz; e 9.0 Hz; f 11.4 Hz

Further increasing the excitation frequency to 6.5 Hz, the bifurcation diagrams in Fig. 12c illustrates that the large-amplitude interwell oscillation could be achieved for excitation above 0.14 g to generate considerable output power. Additionally, the level of 0.19 g is a critical acceleration for the system to realize interwell when the excitation frequency is 7.8 Hz. By comparing the results in Fig. 12c, d, it can be observed that more excitation levels above the critical acceleration lead to intrawell motion for the excitation frequency of 7.8 Hz. As the frequency increases to 9.0 Hz, the excitation levels below 0.31 g contribute to not only periodic-1 intrawell oscillation in two potential wells, but also periodic-2 oscillation in the left potential well. Regarding the levels above 0.31 g, periodic-1 interwell motion is acquired and large output power is induced. By comprehensively comparing Fig. 12a, e, it is demonstrated that the generated power by large-amplitude interwell motion increases with an increase in the frequency. For frequency of 11.4 Hz, the excitation level of 0.34 g to a critical value, below which the intrawell oscillation is obtained, while above it the induced oscillation is chaotic across the potential barrier.

In addition to the collision gap, the distance in the vertical direction from the stopper to the root of the beam is another important parameter influencing the performance significantly. For collision gap of h₀ = 1.0 mm, the maps of 0–1 test and output power for different collision positions (l₀ = 50, 70 and 80 mm) are illustrated in Fig. 13. When l₀ = 50 mm, the map of 0–1 test in Fig. 13a indicates that the chaotic oscillation at low frequencies is obtained for excitation level above about 0.45 g. Additionally, another chaotic region is observed from about 10 to 15 Hz when the excitation level is above 0.3 g. From the map of power output in Fig. 13b, it is seen that the considerable output power is generated within a limited area, and the maximum power in the investigated area is 3.7 μW. When l₀ increases to 70 and 80 mm (Fig. 13c–f), the chaotic response at low frequencies could be achieved at much lower excitation levels and the chaotic region becomes larger. For another chaotic response region, it shifts to higher frequencies with a narrower frequency range and obtained at lower excitation levels, with the increase of l₀. In addition, the maps of power output indicate that interwell oscillation is obtained in a broader frequency range and the maximum power at each excitation level is received at a higher frequency. In the considered region, the obtained maximum output powers are respectively 2.56 and 2.23 μW for l₀ equaling to 70 and 80 mm, which shows a decreasing trend with an increase in l₀. Overall, it is demonstrated that the increase of l₀ leads to interwell oscillation in a wider frequency range and the power output is limited much obviously.

Fig. 13

Maps of 0–1 test and output power for different collision position. a and b: l₀ = 50 mm; c and d: l₀ = 70 mm; e and f: l₀ = 80 mm

For l₀ equaling to 70 mm, the bifurcation diagrams of tip displacement and output power versus frequency under excitations with levels of 0.35 and 0.5 g are illustrated in Fig. 14a, c for comparison. It is seen that chaotic interwell oscillation can all be obtained at very lower frequencies. For excitation level of 0.35 g, another chaotic region is achieved from 10.3 to 13.0 Hz. While, the excitation level of 0.5 g witnesses a narrower frequency range for chaotic response from 11.4 to 13.4 Hz. The maximum output power are respectively 1.95 and 2.37 μW at the frequencies of 10 and 11.2 Hz for excitation levels of 0.35 and 0.5 g.

Fig. 14

Bifurcation diagrams of tip displacement and output power versus excitation frequency for l₀ = 70 mm: a 0.35 g; c 0.5 g. Bifurcation diagrams of tip displacement and output power versus excitation level for l₀ = 70 mm: b 5.9 Hz; d 7.8 Hz

Additionally, Fig. 14b, d show the bifurcation diagrams of tip displacement and output power versus excitation level at frequencies of 5.9 and 7.8 Hz. For frequency of 5.9 Hz, large-amplitude interwell oscillation could be achieved from very low excitation level, except for several isolated levels resulting in intrawell oscillation. In the range from 0.32–0.45 g, chaotic oscillation is achieved. On either side of the chaotic region, interwell periodic-2 oscillation is observed. As the frequency increases to 7.8 Hz, intrawell oscillation is obtained for excitation levels below 0.17 g, and the interwell oscillation under excitation with levels above 0.17 g is all on the high-energy branch.

For the bistable system, the oscillation is very sensitivity to the initial conditions. To investigate the multiple solutions of the system, basin of attraction is applied to consider the influence of initial conditions on the state of stable oscillation. Under excitation of 0.35 g and 5.9 Hz, the basins of attraction for the symmetric and asymmetric BEH without stopper are respectively illustrated in Fig. 15a, b, in which the initial displacement and velocity are meshed to 201 × 201 in the area of [−0.02, 0.02, –0.7,0.7] to repeat the calculation and estimate the stable state. For the symmetric BEH, basin of attraction in Fig. 15a indicates that all initial conditions could result in the interwell oscillation across the potential barrier, with a larger power output. When there is an asymmetry in the potential function, not only the interwell oscillation is observed in Fig. 15b, but also there are many initial conditions leading the system to have a stable state in the right potential well. From Fig. 20, it is seen that the probabilities to achieve the interwell and intrawell are respectively 66.8 and 33.2%. By comparing Fig. 15a, b, the negative effect of asymmetry in potential energy function on the performance of the system can be seen.

Fig. 15

Basins of attraction for the symmetric a and asymmetric b BEH without stopper under excitation of 0.35 g and 5.9 Hz. Note that the blue and red color respectively represent the final states of intrawell oscillation in the right potential well and interwell oscillation

To investigate the influence of excitation level on the multiple solutions, the basins of attraction of the asymmetric BEH without a stopper under excitation with a frequency of 5.9 Hz and an amplitude 0.2 and 0.5 g are depicted in Fig. 16. When the excitation level is relatively small, the system has a larger probability of 43.2% to have a final state confined in the right potential well, compared to the results in Fig. 15b. While, the probability to achieve interwell motion for generating larger output power decreases to 56.8%. By increasing the excitation level, the system are much easily to oscillate across the potential barrier with a higher probability of 66.8%, and a probability of 33.2% leads to the intrawell motion in the right potential well.

Fig. 16

Basin of attraction for the asymmetric BEH without a stopper at excitation with an amplitude 0.2 g (a) and 0.5 g (b)

By introducing the stopper to the system and positioning it on the side with deeper potential well, the influence of collision gap on the multiple solution characteristics are investigated for the l₀ equaling to 60 mm. For collision gaps of 0.5, 1.0 1.5, and 2.0 mm, the basins of attraction under excitation of 0.35 g and 5.9 Hz are illustrated in Fig. 17. When the collision gap is very small, there is no oscillation limited in a single potential, and initial conditions result in interwell oscillation. With the collision gap increasing to 1.0, 1.5 and 2.0 mm, the system has an increasing probability to be confined in the right potential well with the values of 2.1, 22.1 and 24.1%. On this occasion, the probabilities for interwell oscillation are respectively 97.9, 77.9, and 75.9% for the collision gaps of 1.0, 1.5 and 2.0 mm. By comparing the results with that in Fig. 15b, it is seen that the introduction of the stopper could enable the system to achieve interwell more frequently, and the probability for interwell oscillation decreases with an increase in the collision gap.

Fig. 17

Basin of attraction for the asymmetric BEH with a stopper with different collision gaps: a 0.5 mm; b 1.0 mm; c 1.5 mm; d 2.0 mm

For the collision gap of 1.0 mm, the influence of the distance in the vertical direction from the stopper to the root of the beam (l₀) on the basin of attraction is also investigated. For l₀ equaling 50 and 70 mm, the basins of attraction for the asymmetric BEH with a stopper under excitation of 0.35 g and 5.9 Hz are figured in Fig. 18. In Fig. 18a, the blue areas indicate that the asymmetric BEH to have a stable oscillation in the right potential well is with a probability of 8.6%, which is larger than the probability illustrated in Fig. 17b. With the distance from the stopper to the root of the beam increasing to 70 mm, the basin of attraction indicates that all initial conditions in the investigated areas lead to the interwell oscillation.

Fig. 18

Basin of attraction for the asymmetric BEH with a stopper at different collision positions: a l₀ = 50 mm; b l₀ = 70 mm

Additionally, to consider the influence of frequency on multiple solution characteristics, the basins of attraction for the asymmetric BEH with l₀ equaling 60 mm and h₀ equaling 1.0 mm under excitation of 0.35 g and various frequencies are illustrated in Fig. 19. When the excitation frequency is 2.9 Hz, as shown in Fig. 19a, there are two attractors corresponding to the interwell oscillation and intrawell vibration in the right potential well, and the probabilities for these two states are respectively 60.7 and 39.3% as seen in Fig. 20. As the excitation frequency increases to 5.1 Hz, the probability to oscillate in the right potential well decreases to 21.7%, and the system has a larger probability of 78.3% to achieve interwell oscillation (Fig. 19b and Fig. 20). Further increasing the excitation frequency to 6.5, 7.8z, and 9.0 Hz, the basins of attraction in Fig. 19c–e demonstrate that the system respectively has the probabilities of 98.5, 98.8 and 99.5% to cross the potential well, while the corresponding oscillations in the right potential well are with the probabilities of 1.5, 1.2 and 0.5%. With the frequency further increasing to 11.4 Hz, not only interwell oscillation and intrawell oscillation are noticed with the probabilities of 73.6 and 25.1%, but also there is 1.3% of the initial conditions leading to oscillation in the left potential well.

Fig. 19

Basin of attraction for the asymmetric BEH with a stopper at different excitation frequencies: a 2.9 Hz; b 5.1 Hz; c 6.5 Hz; d 7.8 Hz; e 9.0 Hz; f 11.4 Hz. Note that the green color represents the final state of intrawell oscillation in the left potential well

Fig. 20

Percentage graph for all basins of attraction

5 Conclusion

There is an asymmetry that is difficult to eliminate when bistable energy harvester (BEH) is actually manufactured, which makes the response frequency band for interwell vibration significantly narrow. In order to broaden the response frequency band of the asymmetric BEH, a unilateral stopper on the side with deeper potential well is applied to adjust the potential energy function, and the nonlinear dynamics of the corresponding system are investigated. Firstly, the electromechanical coupling model of the system is established based Hamilton's principle and Kirchhoff's law. Secondly, the dynamic behavior and performance of the system are studied by using the bifurcation diagram, maps of 0–1 test and power output, and the influence of system parameters and external excitations is emphasized. Finally, the multiple solution characteristics of the system are studied by the basin of attraction. The main conclusions are as follows:

• 1) Proper collision gap could enable the system to achieve periodic interwell oscillation from single potential well oscillation and chaotic oscillation, thus broadening the response frequency range. The smaller the collision gap is, the easier the asymmetric BEH can realize the oscillation across the potential barrier.

• 2) With a proper collision gap, the increasing of the distance in the vertical direction from the stopper to the root of the beam leads the system to achieve large-amplitude interwell motion more frequently.

• 3) The introduction of the stopper can enhance the performance of the asymmetric BEH for some initial intrawell and chaotic interwell oscillations. However, when the system is originally in periodic interwell vibration, the stopper will degrade the output performance.

To be noted, nonlinear dynamics of the BEH with an adjustable unilateral stopper are investigated by only numerical simulations and results indicate that the response frequency range could be broadened at certain conditions. In future work, theoretical analysis will be provided and experiments will be undertaken to verify the efficiency of the method.