1 Introduction

During the past ten years, the control of marine surface vessels (MSVs) has attracted extensive attention [1,2,3,4,5,6,7,8] due to its civil and military applications, such as marine environment monitoring, mining countermeasures, reconnaissance, surveillance and anti-submarine warfare. However, traditional control algorithms gradually lag behind the increasing demand for high-precision navigation trajectories and modern navigational safety, which are in urgent need of innovation and development.

The trajectory tracking control strategies for MSV are important research subjects, which have many control methods, such as fuzzy technique [9, 10], sliding mode control [11], adaptive control [12, 13], robust \(H_{\infty }\) control [14], backstepping control [15, 16], finite-time control [17, 18] and cascade control [19]. To deal with more stringent actual conditions, a MSV must be highly dependent on the prescribed trajectory to reach its destination in the specified time period, which means that the controller design must be very complex. For instance, [20] proposes a trajectory tracking control law that utilizes nonlinear model predictive control techniques to improve control accuracy in autonomous surface craft, and [21] investigates the tracking control problem of underwater robots with extended state feedback. In [22], the fuzzy technique is used to approximate a nonlinear descriptor system, and an appropriate fuzzy filter solution scheme is proposed to address the uncertain Markov packet dropouts problem. In [23], a dynamics-level finite-time fuzzy monocular visual servo scheme is proposed to regulate the desired pose of an unmanned surface vehicle.

In trajectory tracking control schemes, the uncertainty problem caused by external environmental interference is an important factor that cannot be ignored. Because unknown environmental disturbances are constantly changing, precise measurements cannot be made. Therefore, adaptive control strategies are proposed to estimate and compensate for these disturbances. To address the influence of ocean currents on MSVs, [24, 25] utilize ocean current observers to estimate unknown ocean currents to achieve more accurate control. In [26], a fuzzy control method is proposed to approximate unmodeled dynamics and time-varying disturbances using fuzzy logic. In [27, 28], a combination of neural network approximation methods and adaptive techniques is proposed to address the unknown disturbances and uncertain vessel dynamics.

In addition, complex environmental disturbances, such as low-frequency disturbances due to wind, waves and time-varying ocean currents, seriously affect the stability of MSV control. Therefore, robust control of MSVs is an important research topic. In [29], an observer is constructed to estimate unknown disturbances and a backstepping technique is used to design a novel trajectory tracking robust controller. In [30], complicated disturbances are estimated by a composite-error-based extended state observer, a feedforward-feedback form and an approximation compensation in the control law, and a composite-error-based active disturbance rejection control approach is developed. In [31, 32], a finite-time observer is developed to estimate unknown disturbances and sideslips. In [33], a neural network is used to deal with an uncertain model and utilized a dynamic surface control method to develop a robust path-following scheme for underactuated vessels. It is worth noting that some research methods introduce the barrier Lyapunov function (BLF) to improve the robustness of control. In [34], a control design for MSVs with unknown parameters and full-state constraints adopts the BLF and neural networks. In [35], a tan-type BLF is employed to deal with off-track error constraints, thus ensuring the robustness of the path-following controller for an underactuated MSV. The BLF can limit the error variables within a specified range, which prevents the tracking errors from becoming too large and improves the control precision.

In practical systems, inputs are bounded by the physical restrictions of actuators, as important nonsmooth nonlinear problems usually appear in many control systems. To address these input saturation problems, various methods are proposed; for example, an auxiliary dynamic system is used to compensate for the influence of input saturation. In [36], a simple and straightforward strategy is proposed to compensate for the effect of input saturation by adjusting only a single parameter. [37] develops a smooth auxiliary system to greatly improve the real-time compensation capability of a control system without any downtime. In [38, 39], an auxiliary dynamic system is used to address the input saturation effect for MSVs. In [18], a hyperbolic tangent function is employed to solve the nonsmooth problem by approximating the saturation term, and a finite-time trajectory tracking controller is proposed for MSVs.

Motivated by the observations described above, to improve the robustness of control in more complex practical conditions, this paper develops a robust trajectory tracking control method for an MSV that can simultaneously guarantee the specified performance and solve the problem of uncertain disturbances and input saturation. The contributions of this paper are summarized as follows:

  1. (1)

    The uncertainties are considered including the kinematic disturbances of ocean currents and the kinetic disturbances of wind and waves, and an adaptive estimate law and a finite-time disturbance observer are developed to estimate the uncertain terms of the system. Different from the approaches in [29, 30], the environmental disturbances are separated from the kinematic and kinetic processes, so the more complex disturbances can be more accurately estimated.

  2. (2)

    The asymmetric saturation nonlinearity is expressed as a continuous differentiable formulation by exploring a Gaussian error function, and an auxiliary dynamic system is employed to address the input saturation, thus avoiding the physical limitations of the actuator. Different from methods that address input saturations in [18, 39], the proposed treatment method can cope with more realistic asymmetric smooth inputs, with the use of a smooth switching function, which effectively avoids the singularity problem of an auxiliary dynamic system.

  3. (3)

    Based on the tan-type BLF technique and a backstepping method, a robust trajectory tracking controller is designed that demonstrates excellent robust performance in complicated environments with low-frequency disturbances. This approach is different from the traditional backstepping method and dynamic surface design in [29, 33]; the introduction of the BLF constrains the dynamic error and prevents the tracking error from becoming too large, which makes the control more robust.

  4. (4)

    It is proven that all the closed-loop signals are semi-globally uniformly ultimately bounded, despite the presence of uncertain disturbances and input saturations. The simulation results show that the proposed control method exhibits better performance.

This paper is organized as follows. Section 2 presents the preliminaries and dynamics of MSVs. A robust trajectory tracking control method for an MSV is proposed in Section 3. Section 4 shows numerical simulations that demonstrate the effectiveness of the proposed approach. Section 5 provides conclusions and some future research plans.

2 Preliminaries and problem formulation

2.1 Preliminaries

Notations

Throughout this paper, for a vector \(\left\{ \cdot \right\}\), let \(\left\| \cdot \right\|\) represent the Euclidean 2-norm. \(\lambda_{\min }\) and \(\lambda_{\max }\) represent the minimum and maximum eigenvalues of a matrix \(\left\{ \cdot \right\}\), respectively.\(diag\left\{ \cdot \right\}\) represents a block diagonal matrix.\(R^{n \times n}\) represents the \(n \times n\)-dimensional Euclidean space. Given vectors \(c = \left[ {c_{1} ,c_{2} , \cdots ,c_{n} } \right]^{T} \in {\mathbb{R}}^{n}\) and \(\theta \in {\mathbb{R}}\), define \(c^{\theta } = \left[ {c_{1}^{\theta } ,} \right.\left. {c_{2}^{\theta } , \cdots ,c_{n}^{\theta } } \right]\), \(sig^{\theta } \left( c \right) = \left[ {\left| {c_{1} } \right|^{\theta } sign\left( {c_{1} } \right), \cdots ,\left| {c_{n} } \right|^{\theta } sign\left( {c_{n} } \right)} \right]^{T}\), where \(sign\left( \cdot \right)\) is the signum function.

Lemma 1

[40] Consider a nonlinear dynamical system

$$ \dot{x}\left( t \right) = f\left( {x\left( t \right)} \right),x\left( 0 \right) = x_{0} ,f\left( 0 \right) = 0,x \in {\mathbb{R}}^{n} $$
(1)

where \(x = \left[ {x_{1} ,x_{2} , \cdots ,x_{n} } \right]^{T} \in {\mathbb{R}}^{n}\) is a state vector, and \(f\left( {x\left( t \right)} \right):{\mathbb{R}}^{n} \to {\mathbb{R}}^{n}\) is a possibly discontinuous vector. If there exists a continuously differentiable, positive definite function \(V\left( x \right)\), real numbers \(\delta_{1} \in \left( {0,1} \right)\) and \(\delta_{2} > 0\) such that \(\dot{V}\left( x \right) + \delta_{2} V^{{\delta_{1} }} \left( x \right) \le 0\). Then, the origin of system (1) is finite-time stable, and system (1) converges to zero in finite time \(T \le \frac{1}{{\delta_{2} \left( {1 - \delta_{1} } \right)}}V^{{1 - \delta_{1} }} \left( {x_{0} } \right)\).

2.2 Problem formulation

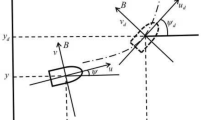
The movement of an MSV on a horizontal surface is shown in Fig. 1. First, the inertial and fixed coordinate systems are defined. The earth-fixed inertial frame (EF) system is fixed on Earth, and the origin \(O_{e}\) is set as the fixed point. The \(O_{e} X_{e}\)-axis points to the north, and the \(O_{e} Y_{e}\)-axis points to the east. The coordinate origin \(O\) of the body-fixed frame (BF) is taken as the geometric center point of the MSV structure as shown in Fig. 1. The \(OX\)-axis points in front of the MSV. The \(OY\)-axis points to the right of the MSV.

Fig. 1
figure 1

Motion of the MSV

Full size image

Ignoring motion of roll, pitch and heave, the nonlinear equation of three degrees of freedom in the presence of disturbances and ocean currents can be expressed as [41]:

$$ \dot{n} = J\left( \psi \right)\upsilon + \upsilon_{r} $$
(2)
$$ M\dot{\upsilon } + C\left( \upsilon \right)\upsilon + D\left( \upsilon \right)\upsilon = s\left( \tau \right) + d $$
(3)

In the above expressions, \(n = \left[ {x,y,\psi } \right]^{T} \in {\mathbb{R}}^{3}\) is the actual track position and yaw angle of the MSV in the EF. \(\upsilon = \left[ {u,v,r} \right]^{T} \in {\mathbb{R}}^{3}\) is the actual track velocity of the MSV in the BF, where \(u\) and \(v\) denote the forward and transverse velocities, and \(r\) denotes the yaw angular velocity. \(\upsilon_{r} = \left[ {u_{r} ,v_{r} ,0} \right]^{T}\)\(\in {\mathbb{R}}^{3}\) is the vector representing the time-varying ocean currents. The matrix \(J\left( \psi \right)\) is a rotational matrix defined as

$$ J\left( \psi \right) = \left[ {\begin{array}{*{20}c} {\cos \psi } & { - \sin \psi } & 0 \\ {\sin \psi } & {\cos \psi } & 0 \\ 0 & 0 & 1 \\ \end{array} } \right] $$
(4)

Note the property \(J^{ - 1} \left( \psi \right) = J^{T} \left( \psi \right)\). \(M = M^{T} \in {\mathbb{R}}^{3 \times 3}\) is a positive definite inertia matrix, \(C\left( \upsilon \right) \in {\mathbb{R}}^{3 \times 3}\) is the Coriolis/Centripetal matrix and \(D\left( \upsilon \right) \in {\mathbb{R}}^{3 \times 3}\) is the damping matrix. \(d = \left[ {d_{1} ,d_{2} ,d_{3} } \right]^{T} \in {\mathbb{R}}^{3}\) denotes the unknown bounded time-varying external disturbances induced by winds and waves. \(s\left( \tau \right) = \left[ {s_{1} \left( {\tau_{1} } \right),s_{2} \left( {\tau_{2} } \right),s_{3} \left( {\tau_{3} } \right)} \right]^{T} \in {\mathbb{R}}^{3}\) is the system input of the saturation, which is described as:

$$ s_{i} \left( {\tau_{i} } \right) = \left\{ \begin{gathered} \tau_{i\max } ,{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} if\tau_{i} > \tau_{i\max } \hfill \\ \tau_{i} ,{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} if\tau_{i\min } \le \tau_{i} \le \tau_{i\max } \hfill \\ \tau_{i\min } ,{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} if\tau_{i} < \tau_{i\min } \hfill \\ \end{gathered} \right.,\left( {i = 1,2,3} \right) $$
(5)

where \(\tau = \left[ {\tau_{1} ,\tau_{2} ,\tau_{3} } \right]^{T} \in {\mathbb{R}}^{3}\) is the desired input to the actuator without considering input saturation, \(\tau_{i\max }\) and \(\tau_{i\min }\) are the known upper and lower bounds of \(\tau_{i}\), respectively.

Remark 1

The relationship between the applied control \(s_{i} \left( {\tau_{i} } \right)\) and the control input \(\tau_{i}\) has sharp corners when \(\tau_{i} = \tau_{i\max }\) and \(\tau_{i} = \tau_{i\min }\). Thus, the backstepping technique cannot be directly applied theoretically [42, 43].

Since the saturation model (5) cannot be directly used for backstepping design, we employ a new model to describe the saturation nonlinearity instead of model (5). The model for representing the asymmetric saturation nonlinearity with smooth form is defined as:

$$ s_{i} \left( {\tau_{i} } \right) = \tau_{iM} \times erf\left( {\frac{\sqrt \pi }{{2\tau_{iM} }}\tau_{i} } \right),i = 1,2,3 $$
(6)

where \(\tau_{iM} = {{\left( {\tau_{i\max } + \tau_{i\min } } \right)} \mathord{\left/ {\vphantom {{\left( {\tau_{i\max } + \tau_{i\min } } \right)} {2 + }}} \right. \kern-\nulldelimiterspace} {2 + }}\left( {{{\left( {\tau_{i\max } - \tau_{i\min } } \right)} \mathord{\left/ {\vphantom {{\left( {\tau_{i\max } - \tau_{i\min } } \right)} 2}} \right. \kern-\nulldelimiterspace} 2}} \right)sign\left( {\tau_{i} } \right)\), and \(erf\left( \cdot \right)\) is a Gaussian error function, defined as:

$$ erf\left( x \right) = \frac{2}{\sqrt \pi }\int_{0}^{x} {e^{{ - t^{2} }} } dt $$
(7)

Figure 2 shows that (6) indeed guarantees the saturation limitation with smooth form, where \(\tau_{f\max } { = }5.5\),\(\tau_{f\min } = - 3\), and the input signal \(\tau_{f} = 10\sin (1.5t)\).

Fig. 2
figure 2

Saturation functions

Full size image

Remark 2

The values \(\tau_{i\max }\) and \(\tau_{i\min }\) can be easily adjusted to different upper and lower bounds in model (6). If \(\left| {\tau_{i\max } } \right| \ne \left| {\tau_{i\min } } \right|\), the asymmetric saturation actuator is obtained, while \(\left| {\tau_{i\max } } \right| = \left| {\tau_{i\min } } \right|\) denotes symmetric saturation model.

To facilitate the trajectory tracking control design later, define \(\Delta s\tau { = }s\left( \tau \right){ - }\tau\). Then, the dynamic model (3) changes to

$$ M\dot{\upsilon } + C\left( \upsilon \right)\upsilon + D\left( \upsilon \right)\upsilon = \Delta s\tau { + }\tau + d $$
(8)

The control objective is to design a robust trajectory tracking control law \(\tau\) for dynamic systems (2) and (8) with input saturation (6). The position and yaw angle \(n\) of the MSV can track an arbitrary smooth reference trajectory \(n_{d}\), while it is guaranteed that all the signals of the resulting closed-loop trajectory tracking system of the MSV remain bounded.

To facilitate the discussion and analysis, the following assumptions are made.

Assumption 1

The actual control input \(s\left( \tau \right)\) is bounded; therefore, \(\Delta s\tau\) values are bounded and exist as a positive constant such that \(\left\| {\Delta s\tau } \right\| \le \Delta_{M}\).

Assumption 2

The time-varying ocean currents \(\upsilon_{r}\) are assumed to be irrotational, the changing rate is bounded and a positive constant exists such that \(\left\| {\dot{\upsilon }_{r} } \right\| \le \overline{\dot{\upsilon }}_{r}\). The disturbances \(d\) are unknown and time-varying yet bounded, and their first derivatives are also bounded such that \(\left\| {\dot{d}} \right\| \le \overline{\dot{d}}\), where \(\overline{\dot{d}}\) is an unknown constant.

Assumption 3

The desired smooth reference signal \(n_{d} = \left[ {x_{d} ,y_{d} ,\psi_{d} } \right]^{T} \in {\mathbb{R}}^{3}\) is bounded, and its corresponding time derivatives \(\dot{n}_{d}\) and \(\ddot{n}_{d}\) are bounded. In other words, the desired trajectory is in the compact set \(\Omega_{d} = \left( {\left[ {n_{d}^{T} ,\dot{n}_{d}^{T} ,\ddot{n}_{d}^{T} } \right]^{T} } \right.\left. {\left| {\left\| {n_{d} } \right\|^{2} { + }\left\| {\dot{n}_{d} } \right\|^{2} + \left\| {\ddot{n}_{d} } \right\|^{2} \le N_{0} } \right.} \right)\), where \(N_{0}\) is a positive constant.

Remark 3

For a given practical MSV, when input saturation occurs, if the difference between the desired control input \(\tau\) and the actual control input \(s\left( \tau \right)\) is infinite, the system will be uncontrollable, and Assumption 1 is reasonable [44]. The ocean current and disturbances must be bounded, which is also practical in actual situations. It should be noted that all these bounds \(\overline{\upsilon }_{r}\) and \(\overline{d}\) are not required for implementing the proposed trajectory tracking controller. These bounds are used only for analytical purposes.

3 Main results

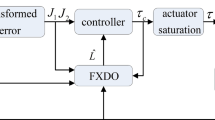
This section presents a robust trajectory tracking control algorithm design for MSV systems with uncertain disturbances and input saturation. We utilize a finite-time disturbance observer to estimate external environmental disturbances, and use an adaptive method to compensate for the effects of unknown time-varying ocean currents and saturation problems, and utilize a tan-type BLF to design robust trajectory tracking controller. Finally, the stability of the closed-loop system is analyzed by the Lyapunov stability theory.

3.1 Finite-time disturbance observer design

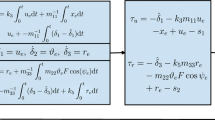
Based on the finite-time disturbance observer in [45] for a general nonlinear system, we construct a nonlinear observer to estimate the unknown environmental disturbance \(d\). The proposed observer is designed as:

$$ M\dot{\hat{\upsilon }} = s\left( \tau \right) - C\left( \upsilon \right)\upsilon - D\left( \upsilon \right)\upsilon + \hat{d} $$
(9)

where \(\hat{\upsilon }\) is the observed value of the velocity \(\upsilon\), and \(\hat{d}\) is the observed value of disturbance \(d\). A new variate is defined as:

$$ \mu = M\left( {\upsilon - \hat{\upsilon }} \right) $$
(10)

Then, the update of \(\hat{d}\) is given as

$$ \hat{d} = K_{b1} sig^{{\rho_{1} }} \left( \mu \right) + K_{b2} \int {sig^{{\rho_{2} }} \left( \mu \right)dt} $$
(11)

where \(K_{b1}\) and \(K_{b2} \in {\mathbb{R}}^{3 \times 3}\) are positive definite diagonal matrixes to be designed; \(\rho_{1}\), and \(\rho_{2}\) are constants to be designed that satisfy \(0.5 \le \rho_{1} < 1\) and \(\rho_{2} = 2\rho_{1} - 1\), respectively. The time derivative of (10) and substituting (11) is given as

$$ \begin{gathered} \dot{\mu } = d - \hat{d} \hfill \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} = d - K_{b1} sig^{{\rho_{1} }} \left( \mu \right) - K_{b2} \int {sig^{{\rho_{2} }} \left( \mu \right)dt} \hfill \\ \end{gathered} $$
(12)

Considering the following transformation of coordinates

$$ p = \left[ {p_{1} ,p_{2} } \right]^{T} = \left[ {\mu ,\gamma } \right]^{T} $$
(13)

where \(\gamma = d - K_{b2} \int {sig^{{\rho_{2} }} \left( \mu \right)dt}\), system (12) can then be rewritten as

$$ \dot{p}_{1} = p_{2} - K_{b1} sig^{{\rho_{1} }} \left( {p_{1} } \right) $$
(14)
$$ \dot{p}_{2} = \dot{d} - K_{b2} sig^{{\rho_{2} }} \left( {p_{1} } \right) $$
(15)

Therefore, the following theorem holds.

Theorem 1

Consider the MSV system in (2) and (3) under Assumption 1–2; applying the FTDO (finite-time disturbance observer) constructed by (9) and (11) with appropriate gains, the states \(p_{1}\) and \(p_{2}\) in the auxiliary system in (14) and (15) are finite-time uniformly ultimately bounded (UUB) stable. Then, \(\dot{p}_{1}\) will converge to a small region of the origin in a finite time, which also means that the observation error converges to zero in a finite time.

Proof

Consider the following Lyapunov function candidate:

$$ V_{o} = 0.5\vartheta^{T} P\vartheta $$
(16)

where the vector \(\vartheta\) and positive definite matrix \(P\) are selected as follows:

$$ \vartheta = \left[ {\begin{array}{*{20}c} {sig^{{\rho_{1} }} \left( {p_{1} } \right)} \\ {p_{2} } \\ \end{array} } \right],P = \left[ {\begin{array}{*{20}c} {{{2K_{b2} } \mathord{\left/ {\vphantom {{2K_{b2} } {\rho_{1} }}} \right. \kern-\nulldelimiterspace} {\rho_{1} }} + K_{b1}^{2} } & { - K_{b1} } \\ { - K_{b1} } & {2I_{3 \times 3} } \\ \end{array} } \right] $$
(17)

Note that the considered Lyapunov candidate (16) is continuous and differentiable everywhere except \(p = \left\{ {\left( {p_{1} ,p_{2} } \right)|p_{1} = 0_{3 \times 1} } \right\}\); it is positively definite and radically unbounded. Hence, the follows that \(V_{o}\) satisfies

$$ 0.5\lambda_{\min } \left( P \right)\left\| \vartheta \right\|^{2} \le V_{o} \le 0.5\lambda_{\max } \left( P \right)\left\| \vartheta \right\|^{2} $$
(18)

where

$$ \left\| \vartheta \right\|^{2} = \left\| {p_{1} } \right\|^{{2\rho_{1} }} + p_{2}^{T} p_{2} $$
(19)

From (19), one can obtain

$$ \left\| {p_{1} } \right\|^{{\rho_{1} - 1}} \ge \left\| \vartheta \right\|^{{\frac{{\rho_{1} - 1}}{{\rho_{1} }}}} $$
(20)

Furthermore, the differential of the Lyapunov function (16) is given as

$$ \begin{gathered} \dot{V}_{o} = - \left\| {p_{1} } \right\|^{{\rho_{1} - 1}} \vartheta^{T} Q\vartheta + \vartheta^{T} h\dot{d} \hfill \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \le - \lambda_{\min } \left( Q \right)\left\| {p_{1} } \right\|^{{\rho_{1} - 1}} \left\| \vartheta \right\|^{2} + \overline{\dot{d}}\left\| \vartheta \right\|\left\| h \right\| \hfill \\ \end{gathered} $$
(21)

where

$$ Q = K_{b1} \left[ {\begin{array}{*{20}c} {K_{b2} + \rho_{1} K_{b1}^{2} } & { - \rho_{1} K_{b1} } \\ { - \rho_{1} K_{b1} } & {\rho_{1} I_{3 \times 3} } \\ \end{array} } \right],h = \left[ {\begin{array}{*{20}c} { - K_{b1} } \\ {2I_{3 \times 3} } \\ \end{array} } \right] $$
(22)

Substituting (20) into (21) gives

$$ \dot{V}_{o} \le - \kappa \left\| \vartheta \right\|^{{\frac{{\rho_{1} + \rho_{2} }}{{\rho_{1} }}}} $$
(23)

The parameter \(\kappa\) obtained from the above inequation is defined as

$$ \kappa = \lambda_{\min } \left( Q \right) - \frac{{\overline{\dot{d}}\left\| h \right\|}}{{\left\| \vartheta \right\|^{{\frac{{\rho_{2} }}{{\rho_{1} }}}} }} $$
(24)

To make \(\kappa > 0\), consider the following inequation:

$$ \left\| \vartheta \right\| > \left( {\frac{{\overline{\dot{d}}\left\| h \right\|}}{{\lambda_{\min } \left( Q \right)}}} \right)^{{\frac{{\rho_{1} }}{{\rho_{2} }}}} $$
(25)

According to inequations (18) and (25), expression (23) is bounded and can be rewritten as

$$ \dot{V}_{o} \le - C_{o} V_{o}^{l} $$
(26)

where \(l = \frac{{\rho_{1} + \rho_{2} }}{{2\rho_{1} }}\), and \(C_{o} = \left[ {\kappa \left( {0.5\lambda_{\min } \left( P \right)} \right)^{{\frac{{\rho_{1} + \rho_{2} }}{{ - 2\rho_{1} }}}} } \right]\). Then, \(0 \le l < 1\) and \(C_{o} > 0\). According to Lemma 1, the finite-time stability can be guaranteed, the auxiliary system (14) and (15) will converge to the region in a finite time, and the region is

$$ \left\| \vartheta \right\| \le \left( {\frac{{\overline{\dot{d}}\left\| h \right\|}}{{\lambda_{\min } \left( Q \right)}}} \right)^{{\frac{{\rho_{1} }}{{\rho_{2} }}}} $$
(27)

Practically, if the suitable parametric design matrixes \(K_{b1}\) and \(K_{b2}\) are selected, the inequation \({{\overline{\dot{d}}\left\| h \right\|} \mathord{\left/ {\vphantom {{\overline{\dot{d}}\left\| h \right\|} {\lambda_{\min } \left( Q \right)}}} \right. \kern-\nulldelimiterspace} {\lambda_{\min } \left( Q \right)}} < 1\) holds. Then, since \({{\rho_{1} } \mathord{\left/ {\vphantom {{\rho_{1} } {\rho_{2} }}} \right. \kern-\nulldelimiterspace} {\rho_{2} }}\) is sufficiently large, \(\left\| \vartheta \right\|\) is sufficiently small in a finite time, and we can select parametric design matrixes \(K_{b1}\) and \(K_{b2}\) such that

$$ K_{b1} > 0,K_{b2} > {{\overline{\dot{d}}^{2} \left\| h \right\|^{2} } \mathord{\left/ {\vphantom {{\overline{\dot{d}}^{2} \left\| h \right\|^{2} } {\rho_{1} K_{b1}^{2} }}} \right. \kern-\nulldelimiterspace} {\rho_{1} K_{b1}^{2} }} $$
(28)

This completes the proof.

Remark 4

If the fraction power \(\rho_{1} = 0.5\) is designed, the FTDO has a strong robustness property, and ensures that update (12) converges to the origin (\(\vartheta = 0\) and \(\dot{\vartheta } = 0\)) in a finite time.

3.2 Estimation of ocean currents

In the following, an adaptive estimate law is proposed for the accurate estimation of unknown time-varying ocean currents. The adaptive estimate law is designed at the kinematic level and has a simple structure. In addition, this method can achieve the stability of the entire system by combining the adaptive law and kinetic control law.

From (2), the position dynamics can be described by

$$ \left\{ \begin{gathered} \dot{x} = u\cos \psi - v\sin \psi + u_{r} \hfill \\ \dot{y} = u\sin \psi + v\cos \psi + v_{r} \hfill \\ \end{gathered} \right. $$
(29)

Define variables \(\hat{u}_{r}\) and \(\hat{v}_{r}\) as the estimation values of \(u_{r}\) and \(v_{r}\), respectively. Thus, a nonlinear adaptive estimate law is constructed as follows:

$$ \left\{ \begin{gathered} \dot{\hat{x}} = u\cos \psi - v\sin \psi + \hat{u}_{r} - l_{1} \tilde{x} \hfill \\ \dot{\hat{y}} = u\sin \psi + v\cos \psi + \hat{v}_{r} - l_{2} \tilde{y} \hfill \\ \end{gathered} \right. $$
(30)

where \(\tilde{x} = \hat{x} - x\) and \(\tilde{y} = \hat{y} - y\) are estimation errors,\(l_{1} \in {\mathbb{R}}\) and \(l_{2} \in {\mathbb{R}}\) are positive constants, and the updated \(\hat{u}_{r}\) and \(\hat{v}_{r}\) are given as

$$ \left\{ \begin{gathered} \dot{\hat{u}}_{r} = \Upsilon_{x} \left[ { - \tilde{x} + k_{x} \left( {\hat{u}_{rf} - \hat{u}_{r} } \right)} \right] \hfill \\ \dot{\hat{v}}_{r} = \Upsilon_{y} \left[ { - \tilde{y} + k_{y} \left( {\hat{v}_{rf} - \hat{v}_{r} } \right)} \right] \hfill \\ \end{gathered} \right. $$
(31)

where \(\hat{u}_{rf}\) and \(\hat{v}_{rf}\) are low-pass filter weight estimates of \(\hat{u}_{r}\) and \(\hat{v}_{r}\) given by

$$ \left\{ \begin{gathered} \dot{\hat{u}}_{rf} = \Upsilon_{rx} \left( {\hat{u}_{r} - \hat{u}_{rf} } \right) \hfill \\ \dot{\hat{v}}_{rf} = \Upsilon_{ry} \left( {\hat{v}_{r} - \hat{v}_{rf} } \right) \hfill \\ \end{gathered} \right. $$
(32)

where \(k_{x} \in {\mathbb{R}}\), \(k_{y} \in {\mathbb{R}}\), \(\Upsilon_{x} \in {\mathbb{R}}\), \(\Upsilon_{y} \in {\mathbb{R}}\), \(\Upsilon_{rx} \in {\mathbb{R}}\) and \(\Upsilon_{ry} \in {\mathbb{R}}\) are all positive constants. The resulting error dynamics of \(\tilde{x}\) and \(\tilde{y}\) can be described by

$$ \left\{ \begin{gathered} \dot{\tilde{x}} = - l_{1} \tilde{x} + \tilde{u}_{r} \hfill \\ \dot{\tilde{y}} = - l_{2} \tilde{y} + \tilde{v}_{r} \hfill \\ \end{gathered} \right. $$
(33)

where \(\tilde{u}_{r} = \hat{u}_{r} - u_{r}\) and \(\tilde{v}_{r} = \hat{v}_{r} - v_{r}\).

The following theorem holds.

Theorem 2

For the MSV kinematic dynamic system (29) under Assumption 2, applying the adaptive estimate law constructed by (30), (31) and (32) with the appropriate control gain parameters can guarantee the estimation errors \(\tilde{x}\), \(\tilde{y}\), \(\tilde{u}_{r}\), and \(\tilde{v}_{r}\) to be UUB stable.

Proof

Consider the following Lyapunov function candidate:

$$ V_{r} = 0.5(\tilde{x}^{2} + \tilde{y}^{2} + \Upsilon_{x}^{ - 1} \tilde{u}_{r}^{2} + \Upsilon_{y}^{ - 1} \tilde{v}_{r}^{2} {\kern 1pt} + k_{x} \Upsilon_{rx}^{ - 1} \tilde{u}_{rf}^{2} + k_{y} \Upsilon_{ry}^{ - 1} \tilde{v}_{rf}^{2} ) $$
(34)

where \(\tilde{u}_{rf} = \hat{u}_{rf} - u_{r}\) and \(\tilde{v}_{rf} = \hat{v}_{rf} - v_{r}\). Its time derivative of (34) along (33) can be described by

$$ \dot{V}_{r} = - l_{1} \tilde{x}^{2} - l_{2} \tilde{y}^{2} - \left( {\tilde{u}_{r} \Upsilon_{x}^{ - 1} + k_{x} \Upsilon_{rx}^{ - 1} \tilde{u}_{rf} } \right)\dot{u}_{r} - \left( {\tilde{v}_{r} \Upsilon_{y}^{ - 1} + k_{y} \Upsilon_{ry}^{ - 1} \tilde{v}_{rf} } \right)\dot{v}_{r} + \tilde{u}_{r} k_{x} \left( {\hat{u}_{rf} - \hat{u}_{r} } \right) + \tilde{v}_{r} k_{y} \left( {\hat{v}_{rf} - \hat{v}_{r} } \right) + \tilde{u}_{rf} k_{x} \left( {\hat{u}_{r} - \hat{u}_{rf} } \right) + \tilde{v}_{rf} k_{y} \left( {\hat{v}_{r} - \hat{v}_{rf} } \right) $$
(35)

Using Young’s inequality, the following inequalities hold:

$$ \left\{ \begin{gathered} \left| { - \left( {\tilde{u}_{r} \Upsilon_{x}^{ - 1} + k_{x} \Upsilon_{rx}^{ - 1} \tilde{u}_{rf} } \right)\dot{u}_{r} } \right| \le \left( {\Upsilon_{x}^{ - 1} + k_{x} \Upsilon_{rx}^{ - 1} } \right)\tilde{u}_{rM} \overline{\dot{u}}_{r} \hfill \\ \left| { - \left( {\tilde{v}_{r} \Upsilon_{y}^{ - 1} + k_{y} \Upsilon_{ry}^{ - 1} \tilde{v}_{rf} } \right)\dot{v}_{r} } \right| \le \left( {\Upsilon_{y}^{ - 1} + k_{y} \Upsilon_{ry}^{ - 1} } \right)\tilde{v}_{rM} \overline{\dot{v}}_{r} \hfill \\ 2k_{x} \tilde{u}_{r} \tilde{u}_{rf} \le k_{x} \tilde{u}_{r}^{2} + k_{x} \tilde{u}_{rf}^{2} \hfill \\ 2k_{y} \tilde{v}_{r} \tilde{v}_{rf} \le k_{y} \tilde{v}_{r}^{2} + k_{y} \tilde{v}_{rf}^{2} \hfill \\ \end{gathered} \right. $$
(36)

where \(\tilde{u}_{rM} = \max \left\{ {\tilde{u}_{r} ,\tilde{u}_{rf} } \right\} \in {\mathbb{R}}\),\(\tilde{v}_{rM} = \max \left\{ {\tilde{v}_{r} ,\tilde{v}_{rf} } \right\} \in {\mathbb{R}}\), \(\overline{\dot{u}}_{r} \in {\mathbb{R}}\) and \(\overline{\dot{v}}_{r} \in {\mathbb{R}}\) are positive constants. Then, we have

$$ \dot{V}_{r} \le - l_{1} \tilde{x}^{2} - l_{2} \tilde{y}^{2} + \varepsilon_{0} $$
(37)

where \(\varepsilon_{0} = \left( {\Upsilon_{x}^{ - 1} + k_{x} \Upsilon_{rx}^{ - 1} } \right)\tilde{u}_{rM} \overline{\dot{u}}_{r} + \left( {\Upsilon_{y}^{ - 1} + k_{y} \Upsilon_{ry}^{ - 1} } \right)\tilde{v}_{rM} \overline{\dot{v}}_{r}\). Note that \(\tilde{x} \ge \sqrt {{{\varepsilon_{0} } \mathord{\left/ {\vphantom {{\varepsilon_{0} } {l_{1} }}} \right. \kern-\nulldelimiterspace} {l_{1} }}}\) and \(\tilde{y} \ge \sqrt {{{\varepsilon_{0} } \mathord{\left/ {\vphantom {{\varepsilon_{0} } {l_{2} }}} \right. \kern-\nulldelimiterspace} {l_{2} }}}\) render \(\dot{V}_{r} < 0\). It follows that \(\tilde{x}\) and \(\tilde{y}\) are UUB, which implies that \(\tilde{u}_{r}\) and \(\tilde{v}_{r}\) are also UUB. The proof is complete.

Remark 5

In [24, 46], a nonlinear observer was proposed to identify constant ocean currents. In [47], reduced-order linear extended state observers were developed to estimate the unknown time-varying ocean current velocities. In this paper, we address time-varying ocean currents using an adaptive estimation method, and its simple structure is close to actual conditions.

3.3 Robust nonlinear control design

In this subsection, we use a backstepping technique to develop a robust trajectory tracking control law that combines a finite-time disturbance observer and an adaptive estimation law of ocean currents. Here, a tan-type BLF is utilized to achieve the tracking error constraints, thus improving control robustness, and an auxiliary dynamic system is employed to address input saturation. The whole design process consists of the following two steps.

Step 1: Define the dynamic tracking error vectors \(z_{1} \in {\mathbb{R}}^{3}\) and \(z_{2} \in {\mathbb{R}}^{3}\) as

$$ z_{1} = n - n_{d} $$
(38)
$$ z_{2} = \upsilon - \alpha $$
(39)

where \(\alpha\) is the virtual control function. Substitute the tracking errors into MSV dynamics systems (2) and (8), and the closed-loop system is translated as

$$ \left\{ \begin{gathered} \dot{z}_{1} = J\left( {z_{2} + \alpha } \right) + \upsilon_{r} - \dot{n}_{d} \hfill \\ \dot{z}_{2} = M^{ - 1} \left( {\Delta s\tau + \tau - C\left( \upsilon \right)\upsilon - D\left( \upsilon \right)\upsilon + d} \right) - \dot{\alpha } \hfill \\ \end{gathered} \right. $$
(40)

To improve the robustness of the trajectory tracking control, we expect the tracking error \(z_{1}\) to remain in the prescribed bound. Therefore, we transform the control problem to the constraint of \(\left\| {z_{1} } \right\|\). Furthermore, a tan-type BLF is proposed as follows [48]:

$$ V_{b} = \frac{{k_{b}^{2} }}{\pi }\tan \left( {\frac{{\pi z_{1}^{T} z_{1} }}{{2k_{b}^{2} }}} \right) $$
(41)

where \(k_{b}\) is the time-varying bound of \(\left\| {z_{1} } \right\|\) and \(\left\| {z_{1} \left( 0 \right)} \right\| < k_{b} \left( 0 \right)\).

Remark 6

If the initial value of \(\left\| {z_{1} } \right\|\) satisfies \(\left\| {z_{1} \left( 0 \right)} \right\| < k_{b} \left( 0 \right)\), the Lyapunov function \(V_{b}\) is bounded; with the condition of \(\mathop {\lim }\limits_{{\left\| {z_{1} } \right\| \to k_{b} }} \frac{{k_{b}^{2} }}{\pi }\tan \left( {\frac{{\pi z_{1}^{T} z_{1} }}{{2k_{b}^{2} }}} \right) = \infty\), it can be inferred that \(\left\| {z_{1} } \right\|\) will not exceed \(k_{b}\).

Remark 7

If \(\left\| {z_{1} } \right\|\) is not required to be constrained on the system tracking error, we will have \(k_{b} \to \infty\), and the tan-type BLF (41) has \(\mathop {\lim }\limits_{{k_{b} \to \infty }} \frac{{k_{b}^{2} }}{\pi }\tan \left( {\frac{{\pi z_{1}^{T} z_{1} }}{{2k_{b}^{2} }}} \right) = \frac{1}{2}z_{1}^{T} z_{1}\), which is a commonly used quadratic form and means that the constraint function is infinite. Therefore, the proposed control law is also applicable to be unconstrained conditions.

Then, differentiating \(V_{b}\) with respect to time, we can obtain

$$ \dot{V}_{b} = \frac{{2k_{b} \dot{k}_{b} }}{\pi }\tan \left( {\frac{{\pi z_{1}^{T} z_{1} }}{{2k_{b}^{2} }}} \right) - \frac{{\dot{k}_{b} }}{{k_{b} }}\frac{{z_{1}^{T} z_{1} }}{{\cos^{2} \left( {\frac{{\pi z_{1}^{T} z_{1} }}{{2k_{b}^{2} }}} \right)}}{\kern 1pt} + \frac{{z_{1}^{T} \left[ {J\left( {z_{2} + \alpha } \right) + \upsilon_{r} - \dot{n}_{d} } \right]}}{{\cos^{2} \left( {\frac{{\pi z_{1}^{T} z_{1} }}{{2k_{b}^{2} }}} \right)}} $$
(42)

Let \(K_{e} = \sup_{t} \sqrt {\left( {\frac{{\dot{k}_{b} }}{{k_{b} }}} \right)^{2} + \ell }\) and \(\Gamma = {{z_{1}^{T} } \mathord{\left/ {\vphantom {{z_{1}^{T} } {\cos^{2} \left( {\frac{{\pi z_{1}^{T} z_{1} }}{{2k_{b}^{2} }}} \right)}}} \right. \kern-\nulldelimiterspace} {\cos^{2} \left( {\frac{{\pi z_{1}^{T} z_{1} }}{{2k_{b}^{2} }}} \right)}}\), where \(\ell\) is a small positive constant. From (42), one has

$$ \dot{V}_{b} < 2K_{e} \frac{{k_{b}^{2} }}{\pi }\tan \left( {\frac{{\pi z_{1}^{T} z_{1} }}{{2k_{b}^{2} }}} \right) + K_{e} z_{1}^{T}\Gamma +\Gamma ^{T} J\left( {z_{2} + \alpha } \right) +\Gamma ^{T} \left( {\upsilon_{r} - \dot{n}_{d} } \right) $$
(43)

Design the virtual control function \(\alpha\) as follows:

$$ \alpha = J^{ - 1} \left[ { - K_{e} z_{1} - K_{d} \tanh \left( \Gamma \right) - \hat{\upsilon }_{r} + \dot{n}_{d} - \left( {2K_{e} + K_{1} } \right)\frac{{k_{b}^{2} }}{\pi }\frac{{z_{1} }}{{2z_{1}^{T} z_{1} }}\sin \left( {\frac{{\pi z_{1}^{T} z_{1} }}{{k_{b}^{2} }}} \right)} \right] $$
(44)

where \(\hat{\upsilon }_{r} = \left[ {\hat{u}_{r} ,\hat{v}_{r} ,0} \right]^{T} \in {\mathbb{R}}^{3}\) is the ocean current estimation value; and \(K_{1}\) and \(K_{d}\) are positive constants. Here, the additional term \(K_{d} \tanh \left( \Gamma \right)\) is used to cancel out the unknown term \(\Gamma ^{T} \tilde{\upsilon }_{r}\), \(\tilde{\upsilon }_{r} = \hat{\upsilon }_{r} - \upsilon_{r}\).

Consider a Lyapunov function as

$$ V_{1} = V_{b} + V_{r} $$
(45)

Substituting (44) into (43), we can obtain

$$ \dot{V}_{1} \le - K_{1} \frac{{k_{b}^{2} }}{\pi }\tan \left( {\frac{{\pi z_{1}^{T} z_{1} }}{{2k_{b}^{2} }}} \right) + \Gamma^{T} Jz_{2} + \left\| {\Gamma^{T} } \right\|_{1} \overline{\tilde{\upsilon }}_{r} - K_{d} \Gamma^{T} \tanh \left( \Gamma \right) - l_{1} \tilde{x}^{2} - l_{2} \tilde{y}^{2} + \varepsilon_{0} $$
(46)

Note that

$$ \left| { - \Gamma^{T} \tilde{\upsilon }_{r} } \right| \le \left\| {\Gamma^{T} } \right\|_{1} \overline{\tilde{\upsilon }}_{r} $$
(47)

where \(\overline{\tilde{\upsilon }}_{r}\) is an ocean current estimation error max value. When time goes to infinity, the estimation error value will converge to a small constant, and by introducing inequality \(\left| \partial \right| - \partial \tanh \left( \partial \right) \le 0.2785\) for a given variable \(\partial \in {\mathbb{R}}\), the following inequality holds:

$$ \left\| {\Gamma^{T} } \right\|_{1} \le \Gamma^{T} \tanh \left( \Gamma \right) + 0.8335 $$
(48)

It follows that (46) can be further put into

$$ \dot{V}_{1} \le - K_{1} \frac{{k_{b}^{2} }}{\pi }\tan \left( {\frac{{\pi z_{1}^{T} z_{1} }}{{2k_{b}^{2} }}} \right) + \varepsilon_{0} - l_{1} \tilde{x}^{2} - l_{2} \tilde{y}^{2} + \Gamma^{T} Jz_{2} - \left( {K_{d} - \overline{\tilde{\upsilon }}_{r} } \right)\Gamma^{T} \tanh \left( \Gamma \right) + 0.8335\overline{\tilde{\upsilon }}_{r} $$
(49)

Select \(K_{d} > \overline{\tilde{\upsilon }}_{r}\) such that

$$ \begin{gathered} \dot{V}_{1} \le - K_{1} \frac{{k_{b}^{2} }}{\pi }\tan \left( {\frac{{\pi z_{1}^{T} z_{1} }}{{2k_{b}^{2} }}} \right) - l_{1} \tilde{x}^{2} - l_{2} \tilde{y}^{2} \hfill \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} + \Gamma^{T} Jz_{2} + \varepsilon_{1} \hfill \\ \end{gathered} $$
(50)

where \(\varepsilon_{1} { = }0.8335\overline{\tilde{\upsilon }}_{r} { + }\varepsilon_{0}\).

Step 2: Consider a Lyapunov function as follows:

$$ V_{2} = V_{1} + 0.5z_{2}^{T} Mz_{2}, $$
(51)

and its time derivative with (51) and (8) satisfies

$$ \begin{gathered} \dot{V}_{2} \le - K_{1} \frac{{k_{b}^{2} }}{\pi }\tan \left( {\frac{{\pi z_{1}^{T} z_{1} }}{{2k_{b}^{2} }}} \right) - l_{1} \tilde{x}^{2} - l_{2} \tilde{y}^{2} {\kern 1pt} + \Gamma^{T} Jz_{2} + \varepsilon_{1} \hfill \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} + z_{2}^{T} \left( {\Delta s\tau + \tau - C\left( \upsilon \right)\upsilon - D\left( \upsilon \right)\upsilon + d - M\dot{\alpha }} \right) \hfill \\ \end{gathered} $$
(52)

To address the input saturation, an auxiliary dynamic system is constructed as follows:

$$ \dot{\xi } = - K_{f} \xi - S(\xi )\xi \frac{{\left| {z_{2}^{T} \Delta s\tau } \right| + 0.5\Delta s\tau^{T} \Delta s\tau}}{\xi^T \xi } + \Delta s\tau $$
(53)

where \(\xi = \left[ {\xi_{1} ,\xi_{2} ,\xi_{3} } \right]^{T} \in {\mathbb{R}}^{3}\) is the state vector of the auxiliary dynamic system, \(K_{f} \in {\mathbb{R}}^{3 \times 3}\) is a positive definite design matrix and the smooth switching function \(S(\xi )\) is given by [49]

$$ S\left( \xi \right) = \left\{ \begin{gathered} 0,{\kern 1pt} \quad {\kern 1pt} \left\| \xi \right\| \le s_{a} \hfill \\ 1 - \cos \left( {\frac{\pi }{2}\sin \left( {\frac{\pi }{2}\frac{{\left\| \xi \right\|^{2} - s_{a}^{2} }}{{s_{b}^{2} - s_{a}^{2} }}} \right)} \right),\quad {\text{otherwise}} \hfill \\ 1,{\kern 1pt} \quad \left\| \xi \right\| \ge s_{b} \hfill \\ \end{gathered} \right. $$
(54)

where \(s_{a}\) and \(s_{b}\) are arbitrarily small positive design constants, which are introduced to avoid the singularity of (53) when \(\left\| \xi \right\|\) approaches zero.

Design the robust trajectory tracking control law as follows

$$ \tau = - J^{T} \Gamma - K_{2} z_{2} + C\left( \upsilon \right)\upsilon + D\left( \upsilon \right)\upsilon + M\dot{\alpha } - \hat{d} + K_{s} \xi $$
(55)

where \(K_{2} \in {\mathbb{R}}^{3 \times 3}\) and \(K_{s} \in {\mathbb{R}}^{3 \times 3}\) are positive definite design matrixes.

Theorem 3

Consider the closed-loop dynamics (2) and (8), the robust trajectory tracking control law (55), the finite-time disturbance observer (9) and (11), the adaptive estimate law (30), (31) and (32) and the auxiliary dynamic system (53) with uncertain disturbances and input saturations under Assumptions 1–3. Then, there exist appropriate design parameters such that all the signals in the closed-loop control system are semi-globally uniformly ultimately bounded (SGUUB) with bounded initial conditions, and the tracking error converges to a small neighborhood of zero. In addition, the tracking error constraints \(\left\| {z_{1} } \right\| \le k_{b} \left( t \right)\) are not violated when subjected to low-frequency disturbances.

Proof

Consider a new Lyapunov function as follows:

$$ V_{3} = V_{2} + 0.5\xi^{T} \xi $$
(56)

Differentiating \(V_{3}\) with respect to time and using (52), (53) and (55), we have

$$ \begin{gathered} \dot{V}_{3} \le - K_{1} \frac{{k_{b}^{2} }}{\pi }\tan \left( {\frac{{\pi z_{1}^{T} z_{1} }}{{2k_{b}^{2} }}} \right) - l_{1} \tilde{x}^{2} - l_{2} \tilde{y}^{2} {\kern 1pt} + \varepsilon_{1} \hfill \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} - z_{2}^{T} K_{2} z_{2} + z_{2}^{T} \Delta s\tau + z_{2}^{T} \dot{\mu } + z_{2}^{T} K_{s} \xi \hfill \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} - {\kern 1pt} \xi^{T} K_{f} \xi - S\left( \xi \right)\left( {\left| {z_{2}^{T} \Delta s\tau } \right| + 0.5\Delta s\tau^{T} \Delta s\tau } \right) + \xi^{T} \Delta s\tau \hfill \\ \end{gathered} $$
(57)

Using Young’s inequality, the following inequalities hold:

$$ \left\{ \begin{gathered} z_{2}^{T} \Delta s\tau \le 0.5z_{2}^{T} z_{2} + 0.5\Delta s\tau^{T} \Delta s\tau \hfill \\ z_{2}^{T} \dot{\mu } \le 0.5z_{2}^{T} z_{2} + 0.5\dot{\mu }^{2} \hfill \\ z_{2}^{T} K_{s} \xi \le 0.5z_{2}^{T} z_{2} + 0.5\lambda_{\min } \left( {K_{s}^{2} } \right)\xi^{T} \xi \hfill \\ \xi^{T} \Delta s\tau \le 0.5\xi^{T} \xi + 0.5\Delta s\tau^{T} \Delta s\tau \hfill \\ \end{gathered} \right. $$
(58)

In Sect. 3.1, we have proven that \(\dot{\mu }\) converges to zero in a finite time; then, we have

$$ \begin{aligned} \dot{V}_{3} & \le - K_{1} \frac{{k_{b}^{2} }}{\pi }\tan \left( {\frac{{\pi z_{1}^{T} z_{1} }}{{2k_{b}^{2} }}} \right) - l_{1} \tilde{x}^{2} - l_{2} \tilde{y}^{2} {\kern 1pt} + \varepsilon_{1} {\kern 1pt} \\ & \quad - \left( {\lambda_{\min } \left( {K_{2} } \right) - 1} \right)z_{2}^{T} z_{2} - \lambda_{\min } {\kern 1pt} \left( {K_{f} - 0.5K_{s}^{2} - 0.5I_{3 \times 3} } \right)\xi^{T} \xi \\ & \quad - \left| {z_{2}^{T} \Delta s\tau } \right|\left( {S\left( \xi \right) - sign\left( {z_{2}^{T} \Delta s\tau } \right)} \right) + 0.5\Delta s\tau^{T} \Delta s\tau \left( {1 - S\left( \xi \right)} \right) \\ \end{aligned} $$
(59)

Thus, for \(\left\| \xi \right\| \ge s_{b}\) that is \(S\left( \xi \right) = 1\), we have

$$ \begin{aligned} \dot{V}_{3} & \le - K_{1} \frac{{k_{b}^{2} }}{\pi }\tan \left( {\frac{{\pi z_{1}^{T} z_{1} }}{{2k_{b}^{2} }}} \right) - l_{1} \tilde{x}^{2} - l_{2} \tilde{y}^{2} {\kern 1pt} + \varepsilon_{1} {\kern 1pt} \\ & \quad {\kern 1pt} - \left( {\lambda_{\min } \left( {K_{2} } \right) - 1} \right)z_{2}^{T} z_{2} - \lambda_{\min } {\kern 1pt} \left( {K_{f} - 0.5K_{s}^{2} - 0.5I_{3 \times 3} } \right)\xi^{T} \xi \\ \end{aligned} $$
(60)

Otherwise, when \(S\left( \xi \right) < 1\), (59) becomes

$$ \dot{V}_{3} \le - K_{1} \frac{{k_{b}^{2} }}{\pi }\tan \left( {\frac{{\pi z_{1}^{T} z_{1} }}{{2k_{b}^{2} }}} \right) - l_{1} \tilde{x}^{2} - l_{2} \tilde{y}^{2} + \varepsilon_{1} + \Delta_{M}^{2} - \left( {\lambda_{\min } \left( {K_{2} } \right) - 1.5} \right)z_{2}^{T} z_{2} - \lambda_{\min } \left( {K_{f} - 0.5K_{s}^{2} - 0.5I_{3 \times 3} } \right)\xi^{T} \xi $$
(61)

Let \(\varepsilon = \varepsilon_{1} + \Delta_{M}^{2}\); from the above inequality, either \(\left\| {z_{1} } \right\| \ge \sqrt {\frac{{2k_{b}^{2} }}{\pi }\arctan \left( {\frac{\varepsilon \pi }{{K_{1} k_{b}^{2} }}} \right)}, \, \left\| {z_{2} } \right\| \ge \sqrt {{\varepsilon \mathord{\left/ {\vphantom {\varepsilon {\left( {\lambda_{\min } \left( {K_{2} } \right) - 1.5} \right)}}} \right.} {\left( {\lambda_{\min } \left( {K_{2} } \right) - 1.5} \right)}}}, \, \left\| \xi \right\| \ge \sqrt {{\varepsilon \mathord{\left/ {\vphantom {\varepsilon {\lambda_{\min } \left( {K_{f} - 0.5K_{s}^{T} K_{s} - 0.5I_{3 \times 3} } \right)}}} \right.} {\lambda_{\min } {\kern 1pt} \left( {K_{f} - 0.5K_{s}^{T} K_{s} - 0.5I_{3 \times 3} } \right)}}}, \, \left\| {\tilde{x}} \right\| \ge \sqrt {{\varepsilon \mathord{\left/ {\vphantom {\varepsilon {l_{1} }}} \right.} {l_{1} }}} \) or \(\left\| {\tilde{y}} \right\| \ge \sqrt {{\varepsilon \mathord{\left/ {\vphantom {\varepsilon {l_{2} }}} \right. \kern-\nulldelimiterspace} {l_{2} }}}\) such that \(\dot{V}_{3} < 0\). This proves that all the signals in the closed-loop system are SGUUB. Moreover, we have

$$ V_{b} = \frac{{k_{b}^{2} }}{\pi }\tan \left( {\frac{{\pi z_{1}^{T} z_{1} }}{{2k_{b}^{2} }}} \right) \le V_{3} < V_{3} \left( 0 \right) $$
(62)

Furthermore, we have \(\left\| {z_{1} \left( t \right)} \right\| \le k_{b} \left( t \right)\), which implies that the position tracking error constraints \(\left\| {n - n_{d} } \right\| \le k_{b} \left( t \right)\) are satisfied. This completes the proof.

Remark 8

According to Theorem 3 and Remark 6, the bounded initial condition and \(\left\| {z_{1} \left( 0 \right)} \right\| < k_{b} \left( 0 \right)\) are satisfied, and the proposed control scheme can guarantee that the closed-loop system is SGUUB. From the above proof process analysis, if the control parameters \(k_{b}\) and \(K_{1}\) are sufficiently small and large, respectively, \(\left\| {z_{1} } \right\| \ge \sqrt {\frac{{2k_{b}^{2} }}{\pi }\arctan \left( {\frac{\varepsilon \pi }{{K_{1} k_{b}^{2} }}} \right)}\) can be guaranteed; hence, the selection of parameters \(k_{b}\) and \(K_{1}\) can adjust the performance of location tracking; the control gain matrix \(K_{2}\) is selected to be large enough to guarantee \(\left\| {z_{2} } \right\| \ge \sqrt {{\varepsilon \mathord{\left/ {\vphantom {\varepsilon {\left( {\lambda_{\min } \left( {K_{2} } \right) - 1.5} \right)}}} \right. \kern-\nulldelimiterspace} {\left( {\lambda_{\min } \left( {K_{2} } \right) - 1.5} \right)}}}\), which can adjust the performance of velocity tracking; the control parameters \(l_{1}\) and \(l_{2}\) are selected to be large enough to guarantee \(\left\| {\tilde{x}} \right\| \ge \sqrt {{\varepsilon \mathord{\left/ {\vphantom {\varepsilon {l_{1} }}} \right. \kern-\nulldelimiterspace} {l_{1} }}}\),\(\left\| {\tilde{y}} \right\| \ge \sqrt {{\varepsilon \mathord{\left/ {\vphantom {\varepsilon {l_{2} }}} \right. \kern-\nulldelimiterspace} {l_{2} }}}\), which can adjust the performance of ocean current identification and ensure control robustness; the parameters \(K_{f}\) and \(K_{s}\) are selected to ensure that \(\lambda_{\min } {\kern 1pt} \left( {K_{f} - 0.5K_{s}^{T} K_{s} - 0.5I_{3 \times 3} } \right)\) is large, but in a practical system, if \(K_{f}\) is too large, violent oscillations will occur, and if \(K_{s}\) is too small, the compensation input will be too small, and the system control effect is not obvious. Therefore, the control parameter selection requires additional attempts to obtain better control performance.

Remark 9

The proposed control scheme mainly depends on the state feedback, and the control parameter selection is not easy. Therefore, the state observers and intelligent algorithms, such as high-gain observers, second-order sliding mode observers, state predictive observers [50], fuzzy logic [51], and neural network [52], will be considered to further remove restrictions.

4 Simulation results

In this section, simulation examples are provided to illustrate the effectiveness of the proposed robust trajectory tracking controller for MSVs with uncertain disturbances and input saturations. The vessel model parameters can be found in Table 1 [53].

Table 1 Dynamic parameters of the vessel model
Full size table

In the earth-fixed frame, the reference trajectories are given as follows:

$$ \left\{ {\begin{array}{*{20}l} {x_{d} = 4\sin \left( {0.02t} \right)} \hfill \\ {y_{d} = 2.5\left( {1 - \cos \left( {0.02t} \right)} \right)} \hfill \\ {\psi _{d} = 0.02t} \hfill \\ \end{array} } \right. $$
(63)

The time-varying ocean current model is assumed as

$$ \left\{ \begin{gathered} u_{r} = 0.3\sin (0.2t) \hfill \\ v_{r} = 0.3\cos (0.2t) \hfill \\ \end{gathered} \right. $$
(64)

The low-frequency disturbances are described by

$$ \left\{ \begin{gathered} d_{1} = 1 + 5\cos (0.1\pi t) + 5\cos (0.2\pi t) + 4\cos (0.3\pi t) \hfill \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} + 4\cos (0.4\pi t) + 3\cos (0.5\pi t + {\pi \mathord{\left/ {\vphantom {\pi 3}} \right. \kern-\nulldelimiterspace} 3}) \hfill \\ d_{2} = 2 + 5\cos (0.1\pi t) + 5\cos (0.2\pi t) + 4\cos (0.3\pi t) \hfill \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} + 4\cos (0.4\pi t) + 3\cos (0.5\pi t) \hfill \\ d_{3} = 3 + 5\cos (0.1\pi t + {\pi \mathord{\left/ {\vphantom {\pi 3}} \right. \kern-\nulldelimiterspace} 3}) + 5\cos (0.15\pi t + {\pi \mathord{\left/ {\vphantom {\pi 6}} \right. \kern-\nulldelimiterspace} 6}) \hfill \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} + 4\cos (0.2\pi t) \hfill \\ \end{gathered} \right. $$
(65)

The prescribed tracking error bound \(k_{b} \left( t \right)\) is selected as

$$ k_{b} \left( t \right) = 2e^{ - t} + 0.8 $$
(66)

The initial conditions are chosen as \(n\left( 0 \right) = \left[ {0.5,1.3, - 0.012} \right]^{T}\) and \(\upsilon \left( 0 \right) = \left[ {0.8,0.8, - 0.1} \right]^{T}\). The control parameters of the FTDO are chosen as \(K_{b1} = diag\{ 10,10,10\}\), \(K_{b2} = diag\{ 10,10,10\}\), \(\rho_{1} = 0.75\) and \(\rho_{2} = 0.5\), the parameters of the estimated ocean current and the adaptive law are chosen as \(l_{1} = 3\), \(l_{2} = 3\), \(\Upsilon_{x} = 10\), \(\Upsilon_{y} = 10\), \(k_{x} = 0.1\), \(k_{y} = 0.1\), \(\Upsilon_{rx} = 2\) and \(\Upsilon_{ry} = 2\) and the other parameters are chosen as \(K_{1} = 5\), \(K_{e} = 1.1\), \(K_{d} = 1\), \(K_{2} = diag\{ 150,150,150\}\), \(K_{s} = diag\{ 3,3,2.8\}\), \(K_{f} = diag\{ 5,5,5\}\), \(s_{a} = 0.1\) and \(s_{b} = 1\). The upper and lower bounds of the control input are set as \(\tau_{\max } = [300,290,20]^{T}\)\(^{T}, a\)nd \(\tau_{\min } = [ - 280, - 280, - 25]^{T}\). The control scheme is shown in Fig. 3.

Fig. 3
figure 3

Structure of the proposed robust tracking trajectory control method

Full size image

The simulation results of the robust trajectory tracking controller are shown in Figs.4–7. Figure 4 presents that \(n\) can track the reference trajectory \(n_{d}\) with high accuracy, while Fig. 5 shows that there are slight deviations in the tracking of \(\upsilon\), especially \(u\). We can find that the tracking error \(z_{1}\) and \(z_{2}\) can quickly converge to zero and fluctuate in a very small range close to zero, as shown in Figs.6 and 7. Figure 8 shows that FTDOs (9) and (11) can rapidly estimate the complex external low-frequency disturbances with high accuracy, which conforms to Theorem 1. Figure 9 shows that the adaptive laws (30), (31) and (32) estimate the time-varying ocean current with high accuracy, which conforms to Theorem 2. The smooth form (6) and auxiliary dynamic system (53) used to handle the input saturation results are shown in Fig. 10.

Fig. 4
figure 4

Position tracking of the proposed method

Full size image
Fig. 5
figure 5

Velocity tracking of the proposed method

Full size image
Fig. 6
figure 6

Position tracking error of the proposed method

Full size image
Fig. 7
figure 7

Velocity tracking error of the proposed method

Full size image
Fig. 8
figure 8

Time-varying disturbance estimation of FTDO

Full size image
Fig. 9
figure 9

Time-varying ocean current estimation of adaptive law

Full size image
Fig. 10
figure 10

Control input using auxiliary compensation of the proposed method

Full size image

In addition, we select the previous two work results and compare them with the results of our proposed method. Compared with the simulation in [29], a nonlinear disturbance observer is employed to improve the control robustness. In [30], a composite-error-based extended state observer is employed to estimate the low-frequency disturbances and use the disturbance rejection control law. The above two control laws and the selected parameters of the controller are shown in Table 2. The initial states are all the same.

Table 2 Control methods and gain parameters of the vessel
Full size table

First, the disturbance observation error comparisons are shown in Fig. 11. It is clear that the observation error of the proposed disturbance observer is smaller than those of the other two methods. Second, for the position track error \(z_{1}\), as shown in Fig. 12, we can see that the position error of the proposed method relatively quickly converges to zero and still has a small error when it is subjected to disturbance; in addition, the tracking error constraints \(\left\| {n - n_{d} } \right\| \le k_{b} \left( t \right)\) are not violated, which conforms to Theorem 3. Finally, we provide a floor plan for comparison in Fig. 13 and similarly find that the proposed method offers a better performance.

Fig. 11
figure 11

Time-varying disturbance estimation error of [29, 30] and the proposed method

Full size image
Fig. 12
figure 12

Euclidean norm of position tracking error of [29, 30] and the proposed method

Full size image
Fig. 13
figure 13

Actual and reference trajectories in \(xy\)-plane of [29, 30] and the proposed method

Full size image

Remark 10

Compared with the three results, the other two methods only focus on the disturbances of kinetics, while we consider the disturbances of kinetics and kinematics. Moreover, under the difficult conditions of input saturation, the proposed method still exhibits stronger robustness.

5 Conclusions

This research investigates robust control strategies for the trajectory tracking of MSVs subjected to uncertain disturbances and input saturations. The FTDO and adaptive estimation law are employed to estimate the external environmental disturbances. A smooth input saturation nonlinear model is denoted by a Gaussian error function, and auxiliary dynamic systems are employed to compensate for the input saturation. A tan-type barrier Lyapunov function is combined with a backstepping technique to design a robust trajectory tracking controller. All the signals of the closed-loop system are proven to be SGUUB in bounded initial conditions, and the tracking error converges to a small neighborhood of the origin. Comparative simulations are used to evaluate the performance of the proposed controller with respect to the current literature. In addition, the lack of state information and the optimization of control parameters in practical situations present a considerable challenge. Further work will be required to solve these problems and to verify the proposed methods by experiments in practice.