Adaptive dynamic surface control for cooperative path following of marine surface vehicles with input saturation

Abstract

This paper considers the cooperative path following problem of multiple marine surface vehicles subject to input saturation, unknown dynamical uncertainty and unstructured ocean disturbances, and partial knowledge of the reference velocity. The control design is categorized into two envelopes. Path following for each vehicle amounts to reducing an appropriately defined geometric error. Vehicles coordination is achieved by exchanging the path variables, as determined by the communications topology adopted. The control design is developed with the aid of the neural network-based dynamic surface control (DSC) technique, an auxiliary design, and a distributed estimator. The key features of the developed controllers are as follows. First, the neural network-based adaptive DSC technique allows for handling the unknown dynamical uncertainty and ocean disturbances without the need for explicit knowledge of the model, and at the same time simplify the cooperative path following controllers by introducing the first-order filters. Second, input saturations are incorporated into the cooperative path following design, and the stability of the modified control solution is verified. Third, the amount of communications is reduced effectively due to the distributed speed estimator, which means the global knowledge of the reference speed is relaxed. Under the proposed controllers, all signals in the closed-loop system are guaranteed to be uniformly ultimately bounded. Simulation results validate the performance and robustness improvement of the proposed strategy.

1 Introduction

During the past few years, there has been a growing interest in the development of multiple vehicles for a number of scientific and commercial mission scenarios. The relevant applications include deep space imaging using multiple satellite telescopes, aerial imaging and surveillance using multiple aircraft, coordinated control of land robots, and seismic imaging of the seabed using a fleet of marine surface vessels [1–7]. To perform many of these tasks, several methods have been proposed, ranging from cooperative target tracking [8], cooperative trajectory tracking [9, 10], to cooperative path following [11–14]. In particular, the objective of cooperative path following is to steer a group of vehicles along predefined paths while keeping a desired spatial formation.

Recently, cooperative path following problem of marine surface vehicles has been widely studied. A variety of approaches to this problem have been reported in the literature, using a wide range of analytic tools. For instance, in [11], a passivity-based approach for cooperative path following is developed where it allows the designer to construct filters that preserve the passivity properties of the closed-loop system. This additional flexibility is capable of improving the system performance and robustness. In [15], the path following and formation control problem for a group of marine surface vessels in the presence of unknown ocean currents is solved by combining the line-of-sight guidance with adaptive control technique. In [20], the problem of temporary communication losses is addressed by putting together the path following and coordination strategies as a cascade system form. A key feature of the cooperative path following controllers in [2, 11, 13, 14, 20, 23] is that they are designed based on a backstepping technique [16–19]. A major drawback in the traditional backstepping design is the problem of computational complexity, which is caused by the repeated differentiations of virtual controls. In [25], a dynamic surface control (DSC) technique is proposed to eliminate this problem by introducing a first-order filtering of the synthetic input. In [21], the NN-based DSC approach is proposed for adaptive tracking control of strict-feedback systems with arbitrary uncertain nonlinearities. In [22], the NN-based DSC technique is employed to solve the leader-follower formation control problem of autonomous surface vehicles with uncertain local dynamics and uncertain leader dynamics, which leads to a much simpler formation controller. However, such technique has not been explored for cooperative path following problem of marine surface vehicles.

In practice, the actuator saturation as one of the most important non-smooth nonlinearities usually appears in many industry control system. This problem is of great importance because almost all practical control systems have limited input amplitude. The actuator constraints can severely degrade the closed-loop system performance, and therefore must be taken into account in the controller design. During the past few years, the input saturation problem of nonlinear systems has drawn great attention. Analysis and design of control systems with input saturation have been reported in [26] for tracking control of uncertain MIMO nonlinear systems, in [27] for position mooring control of a marine surface vessel, and in [28] for tracking control of an ocean surface vessel. From a practical perspective, it is meaningful to consider the cooperative path following of multiple marine surface vessels with input constraints.

On the other hand, a major assumption in cooperative path following design of [6, 7, 11–13, 20, 23, 24] is the global knowledge of the reference velocity, which may not be known to all vehicles for security reasons. In order to eliminate the need of reference speed known to all the vehicles, one option is to employ the distributed control strategy [29]. In [30], a leader-follower problem for a multi-agent system under a switching interconnection topology is considered. The distributed observers design allows an active leader to be followed in an unknown velocity. In [31], an algorithm for distributed estimation of the active leaders unmeasurable state variables is presented. A neighbor-based local controller together with a neighbor-based state-estimation rule is developed for each agent.

Motivated by the above observations [21, 22, 26–31], this paper considers the cooperative path following problem of multiple marine surface vehicles subject to input saturation, unknown dynamical uncertainty and ocean disturbances induced by unknown wind, waves and ocean currents, and partial knowledge of the reference velocity. The control designs to this problem, which unfolds into two basic aspects. First, in order to force each marine surface vehicle to follow a predefined path, an NN adaptive path following controller is designed based on the DSC technique in the presence of input saturation. Second, with the analytic tool of graph theory, the speed and path variables are synchronized to each vehicle owing to the proposed synchronization control law where the distributed speed estimate strategy is incorporated. Based on Lyapunov analysis, it is proved that with the developed algorithms, all signals in the closed-loop system are uniformly ultimately bounded (UUB). The contributions of this paper are summarized as follows. (i) The NN-based DSC technique is firstly employed to solve the cooperative path following problem of marine surface vehicles with unknown dynamical uncertainty and ocean disturbances, which leads to a much simpler controller than traditional backstepping-based design. (ii) The input saturation is incorporated into the cooperative path following design to cope with physical constraints. (iii) A distributed speed estimator is proposed, by which the restriction on the common reference speed being available to all cooperating vehicles is explicitly relaxed.

This paper is organized as follows: Section 2 introduces some preliminaries and gives the problem formulation. Section 3 presents the cooperative path following controllers design and stability analysis. Section 4 provides the simulation results to illustrate the proposed controllers. Section 5 concludes this article.

2 Preliminaries and problem formulation

2.1 Notation

The notation used in this paper is quite standard. ${{\mathbb {R}}^{n}}$ denotes the $n$-dimensional Euclidean Space. ${{\lambda }_{\min }}\text {(}\cdot \text {)}$, ${{\lambda }_{2}}\text {(}\cdot \text {)}$, and ${{\lambda }_{\max }}\text {(}\cdot \text {)}$ denote the smallest, the second smallest, and the biggest eigenvalue of a matrix, respectively. $\left\| \cdot \right\|$, ${{\left\| \cdot \right\| }_{F}}$, and $\hbox {tr}\text {(}\cdot \text {)}$ represent the Euclidean norm, the Frobenius norm, and the trace of a matrix, respectively. $\text {diag}[b_1,\ldots ,b_n]$ represents a diagonal matrix with scalars $b_1,\ldots ,b_n$ on the diagonal. ${{\mathbf {1}}_{n}}\in {{\mathbb {R}}^{n}}$ denotes a column vector with all entries equal to one.

2.2 Graph theory

An undirected graph $\mathcal {G}=\mathcal {G}(\mathcal {V},\mathcal {E})$ consists of a finite set $\mathcal {V}=\{1,2,\ldots ,n\}$ of $n$ vertices and a finite set $\mathcal {E}$ of $m$ pairs of vertices $\{i,j\}\in \mathcal {E}$ named edges. If $\{i,j\}$ belongs to $\mathcal {E}$, then $i$ and $j$ are said to be adjacent. A path from $i$ to $j$ is a sequence of distinct vertices called adjacent. If there is a path between any two vertices, then the graph $\mathcal {G}$ is said to be connected. The adjacency matrix of the graph $\mathcal {G}$, denoted by $\mathcal {A}=[a_{ij}]\in \mathbb {R}^{n\times n}$, is a square matrix with rows and columns indexed by the vertices, such that ${{a}_{ij}}$ equals one if $\{j,i\}\in \mathcal {E}$ and zero otherwise. The degree matrix $\mathcal {D}=[d_{ij}]\in \mathbb {R}^{n\times n}$ of the graph $\mathcal {G}$ is a diagonal matrix where ${{d}_{ij}}$ equals to the number of adjacent vertices of vertex $i$. The Laplacian associated with the graph $\mathcal {G}$ is defined as $L=\mathcal {D}-\mathcal {A}$. If the graph $\mathcal {G}$ is connected, then zero is an eigenvalue of $L$, and all nonzero eigenvalues are positive. This implies that for a connected undirected graph, there exists a matrix $G\in {{\mathbb {R}}^{n\times (n-1)}}$ such that $L=G{{G}^{\mathrm{{T}}}}$, where rank $G=n-1$.

Lemma 1

If $\mathcal {G}$ is a connected undirected graph, then there exists a positive definite matrix $P$ such that ${{\theta }^{\mathrm{{T}}}}L\theta ={{s}^{\mathrm{{T}}}}Ps$, where $\theta =[\theta _1,\ldots ,\theta _n]^\mathrm{{T}}\in {{\mathbb {R}}^{n}}$, $s=[s_1,\ldots ,s_n]^\mathrm{{T}}\in {{\mathbb {R}}^{n}}$, ${{s}_{i}}=\sum _{i=1}^{n}{{{a}_{ij}}({{\theta }_{i}}-{{\theta }_{j}})}$.

Proof

The proof can be found in [32], and thus omitted here for brevity.

2.3 Neural networks

In the sequel, we will make use of the universal approximation property of a linear-in-parameter neural network to estimate the unknown parts of the given system. The neural networks take the form of ${{W}^{\mathrm{{T}}}}\sigma (\xi )$, where $W\in {{\mathbb {R}}^{\ell \times m}}$ is called weight matrix, with $\ell$ being the number of neural network nodes, and $\sigma (\xi )\in {{\mathbb {R}}^{\ell }}$ is a vector valued function, with $\xi \in {{\mathbb {R}}^{q}}$ being the neural network input vector. Denote the components of $\sigma (\xi )$ by ${{\rho }_{l}}(\xi ),l=1,\ldots ,\ell$, and ${{\rho }_{l}}(\xi )$ is a basis function. Typical examples of the function ${{\rho }_{l}}(\xi )$ are sigmoid, ${{\rho }_{l}}(\xi )=\frac{1}{1+\exp (-p\xi )}$, gaussian ${{\rho }_{l}}(\xi )=\exp (-\xi ^2 )$, and hyperbolic tangent ${{\rho }_{l}}(\xi )=\frac{\exp (\xi )-\exp (-\xi )}{\exp (\xi )+\exp (-\xi )}$. According to the approximation property of the neural networks [33–37], given a continuous real-valued function $f(\xi ):\varOmega \rightarrow \mathbb {R}^m$, with $\varOmega \in {{\mathbb {R}}^{q}}$ a compact set, and any ${{\varepsilon }_{\mathrm{{M}}}}>0$, for some sufficiently large integer $\ell$, there exists ${{\left\| W \right\| }_{F}}\le {{W}_{\mathrm{{M}}}}$, such that the neural network ${{W}^{\mathrm{{T}}}}\sigma (\xi )$ can approximate the given function $f(\xi )$ as

$$\begin{aligned} f(\xi )={{W}^{\mathrm{{T}}}}\sigma (\xi )+\varepsilon , \end{aligned}$$

(1)

where $\varepsilon$ represents the network reconstruction error and satisfies $\Vert \varepsilon \Vert \le \varepsilon _{\mathrm{{M}}}$.

2.4 Problem formulation

Consider a group of $n$ marine surface vehicles with the $i$th vehicle dynamics described by Morten and Fossen [38]

$$\begin{aligned}&{{\dot{\eta }}_{i}}=J_i({{\psi }_{i}}){{\nu }_{i}},\end{aligned}$$

(2)

$$\begin{aligned}&{{M}_{i}}{{\dot{\nu }}_{i}}={{\tau }_{i}}-{{C}_{i}}({{\nu }_{i}}){\nu }_{i}-{{D}_{i}}({{\nu }_{i}}){\nu }_{i}-{{\Delta }_{i}}({{\nu }_{i}})+\tau _{iw}(t),\nonumber \\ \end{aligned}$$

(3)

where ${{\eta }_{i}}={{[{{x}_{i}},{{y}_{i}},{{\psi }_{i}}]}^{\mathrm{{T}}}}\in {{\mathbb {R}}^{3}}$ represents the position-altitude vector in the earth-fixed reference frame as shown in Fig. 1. ${{\nu }_{i}}={{[{{u}_{i}},{{v }_{i}},{{r}_{i}}]}^{\mathrm{{T}}}}\in {{\mathbb {R}}^{3}}$ denotes the velocity vector in the body-fixed reference frame. ${{\tau }_{i}}={{[{{\tau }_{iu}},{{\tau }_{iv}},{{\tau }_{ir}}]}^{\mathrm{{T}}}}\in {{\mathbb {R}}^{3}}$ is the control input vector with ${{\tau }_{iu}}$ being the surge force, ${{\tau }_{iv}}$ being the sway force, and ${{\tau }_{ir}}$ being the yaw moment. ${{M}_{i}}=M_{i}^{\mathrm{{T}}}\in \mathbb {R}^{3\times 3}$ is the system inertia matrix. ${{C}_{i}}\in \mathbb {R}^{3\times 3}$ is the skew-symmetric matrix of Coriolis. ${{D}_{i}}\in \mathbb {R}^{3\times 3}$ is the nonlinear damping matrix. ${{\Delta }_{i}}\in \mathbb {R}^{3}$ represents the unmodeled dynamics. ${{\tau }_{iw}}(t)={{[{{\tau }_{iuw}},{{\tau }_{ivw }},{{\tau }_{irw}}]}^{\mathrm{{T}}}}\in {{\mathbb {R}}^{3}}$ denotes the time-varying ocean disturbance induced by wind and waves satisfying $|{{\tau }_{iw}}(t)|\le {\tau }_{iwM}$, where ${\tau }_{iwM}\in {{\mathbb {R}}^{3}}$ is a positive constant vector. The rotation matrix $J_i({\psi }_{i})$ is given by

$$\begin{aligned} J_i({{\psi }_{i}})=\left[ \begin{array}{ccc} \cos {{\psi }_{i}} &{} -\sin {{\psi }_{i}} &{} 0 \\ \sin {{\psi }_{i}} &{} \cos {{\psi }_{i}} &{} 0 \\ 0 &{} 0 &{} 1 \end{array} \right] . \end{aligned}$$

(4)

Fig. 1

Inertial and body-fixed coordinate frames

Consider that the input $\tau _i$ is subject to the following constraints

$$\begin{aligned} -{{\tau }_{i\min }}\le {{\tau }_{i}}\le {{\tau }_{i\max }}, \end{aligned}$$

(5)

where ${{\tau }_{i\min }}={{[{{\tau }_{i\min u}},{{\tau }_{i\min v}},{{\tau }_{i\min r}}]}^{\mathrm{{T}}}}\in {{\mathbb {R}}^{3}}$ is the known lower limit of input saturation constraints, ${{\tau }_{i\max }}={{[{{\tau }_{i\max u}},{{\tau }_{i\max v}},{{\tau }_{i\max r}}]}^{\mathrm{{T}}}}\in {{\mathbb {R}}^{3}}$ is the known upper limit of input saturation constraints. Thus, the control input $\tau _i$ is defined by

$$\begin{aligned} {{\tau }_{i}}=\left\{ \begin{array}{l@{\quad }l} {{\tau }_{i\max }}, &{} \text {if} \ {{\tau }_{i0}}>{{\tau }_{i\max }} \\ {{\tau }_{i0}}, &{} \text {if} \ -{{\tau }_{i\min }}\le {{\tau }_{i0}}\le {{\tau }_{i\max }} \\ -{{\tau }_{i\min }}, &{} \text {if} \ {{\tau }_{i0}}<-{{\tau }_{i\min }} \end{array} \right. \end{aligned}$$

(6)

where ${{\tau }_{i0}}={{[{{\tau }_{i0u}},{{\tau }_{i0v}},{{\tau }_{i0r}}]}^{\mathrm{{T}}}}\in {{\mathbb {R}}^{3}}$ is the control command to be designed in the presence of input saturation constraints.

The control objective of this paper is stated as follows.

Cooperative Path Following Problem. Let ${\eta }_{id}({{\theta }_{i}})={{[{{x}_{id}}({{\theta }_{i}}),{{y}_{id}}({{\theta }_{i}}),{{\psi }_{id}}({{\theta }_{i}})]}^{\mathrm{{T}}}}\in {{\mathbb {R}}^{3}},$ $i=1,\ldots ,n,$ be a series of desired paths parameterized by continuous variables ${{\theta }_{i}}\in \mathbb {R}$. Suppose that each ${{\eta }_{id}}({{\theta }_{i}})$ is sufficiently smooth, and its second derivative $\eta _{id}^{\theta _{i}^{2}}$ is bounded, i.e., given any positive number ${{\delta }_{i1}}$, the set ${{\varOmega }_{i1}}=\big \{{{\big [\eta _{id}^{\mathrm{{T}}}, \eta {{_{id}^{{\theta }_{i}{\mathrm{{T}}}}}}, \eta {{_{id}^{\theta _{i}^{2}{\mathrm{{T}}}}}}\big ]^{\mathrm{{T}}}}}: \Vert {{\eta }_{id}}{{\Vert }^{2}}+\Vert \eta _{id}^{{{\theta }_{i}}}{{\Vert }^{2}}+\Vert \eta _{id}^{\theta _{i}^{2}}{{\Vert }^{2}}\le {{\delta }_{i1}}\big \}$ is compact, where ${{(\cdot )}^{{{\theta }_{i}}}}=(\partial (\cdot )/\partial {{\theta }_{i}})$ and ${{(\cdot )}^{\theta _{i}^{2}}}=({{\partial }^{2}}(\cdot )/\partial \theta _{i}^{2})$, $|| \eta _{id}^{{{\theta }_{i}}} ||\le \eta _{dM}^{\theta }$ with $\eta _{dM}^{\theta }$ a positive constant. Design a controller $\tau _{i0}$ such that all signals in the closed-loop networked system are UUB, and

• (i) each vehicle converges to the desired geometric path, i.e.,

  $$\begin{aligned} \underset{t\rightarrow \infty }{\mathop {\lim }}\,\,\,\left\| {{\eta }_{i}}-{{\eta }_{id}} \right\| \le {{\epsilon }_{i1}}, \end{aligned}$$

  (7)

• (ii) and speed is synchronized, i.e.,

  $$\begin{aligned} \underset{t\rightarrow \infty }{\mathop {\lim }}\,\left\| {\dot{\theta }_{i}}-{v}_{0} \right\| \le {{\epsilon }_{i2}}, \end{aligned}$$

  (8)

• (iii) and all path variables are synchronized, i.e.,

  $$\begin{aligned} \underset{t\rightarrow \infty }{\mathop {\lim }}\,\left\| {{\theta }_{i}}-{{\theta }_{j}} \right\| \le {{\epsilon }_{i3}}, \end{aligned}$$

  (9)

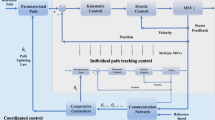
where ${{\epsilon }_{i1}},{{\epsilon }_{i2}},{{\epsilon }_{i3}}\in \mathbb {R}$ are some small constants, and ${v}_{0}\in \mathbb {R}$ is a constant reference speed which assigned by the virtual leader. The control architecture is shown in Fig. 2.

Fig. 2

Control architecture

3 Cooperative path following controller design

3.1 Individual path following design

In this subsection, individual path following controllers will be derived by employing the NN-based DSC technique. The synchronization control law and distributed speed estimate strategy for cooperative path following will be derived in the next subsection.

Step 1. The error variables are defined as

$$\begin{aligned} {{z}_{i1}}&= {{J}_{i}}^{\mathrm{{T}}}({{\eta }_{i}}-{{\eta }_{id}}),\end{aligned}$$

(10)

$$\begin{aligned} \tilde{v}_{id}&= {\hat{v}_{id}}-{v}_{0},\end{aligned}$$

(11)

$$\begin{aligned} {{\omega }_{is}}&= {{\dot{\theta }}_{i}}-{\hat{v}_{id}}, \end{aligned}$$

(12)

where $\hat{v}_{id}\in \mathbb {R}$ is the estimate of common reference speed ${v}_{0}$. Differentiating ${{z}_{i1}}$ with respect to time and using (2), (11) and (12) yield

$$\begin{aligned} {{\dot{z}}_{i1}}=&-rS{{z}_{i1}}+{{\nu }_{i}}-{{J}_{i}}^{\mathrm{{T}}}\left[ \eta _{id}^{{{\theta }_{i}}}\left( {\hat{v}_{id}}+{{\omega }_{is}}\right) \right] , \end{aligned}$$

(13)

where $S$ is defined as

$$\begin{aligned} S=\begin{bmatrix} 0&-1&0 \\ 1&0&0 \\ 0&0&0 \\ \end{bmatrix}. \end{aligned}$$

(14)

To stabilize (13), choose a virtual control law ${{\alpha }_{i}}$ as

$$\begin{aligned} {{\alpha }_{i}}=-{{K}_{i1}}{{z}_{i1}}+{{J}_{i}}^{\mathrm{{T}}}\eta _{id}^{{{\theta }_{i}}}{\hat{v}_{id}}, \end{aligned}$$

(15)

where ${{K}_{i1}}=\mathrm{{diag}}[{k}_{i1}]\in {{\mathbb {R}}^{3\times 3}}$ is a diagonal matrix and its diagonal elements are positive constants. The update law for ${\hat{v}_{id}}$ will be specified in the next subsection, because it is supported by the information exchanges between its neighbors.

Consider a scalar function

$$\begin{aligned} {{V}_{i1}}=\frac{1}{2}z_{i1}^{\mathrm{{T}}}{{z}_{i1}} \end{aligned}$$

(16)

whose time derivative along (13) and (15) is

$$\begin{aligned} {{\dot{V}}_{i1} }=-z_{i1}^{\mathrm{{T}}}{{K}_{i1}}{{z}_{i1}}+z_{i1}^{\mathrm{{T}}}(\nu _i-\alpha _i)-z_{i1}^{\mathrm{{T}}}{{J}_{i}}^{\mathrm{{T}}}\eta _{id}^{{{\theta }_{i}}}{{\omega }_{is}}. \end{aligned}$$

(17)

Introduce a new state variable ${{{\bar{\nu }}_{id}}}\in {{\mathbb {R}}^{3}}$ and let ${{\alpha }_{i}}$ pass through a first-order filter with a time constant $\rho \in \mathbb {R}$

$$\begin{aligned} \rho {{\dot{\bar{\nu }}}_{id}}+{{{\bar{\nu }}_{id}}}={{\alpha }_{i}}. \end{aligned}$$

(18)

Let ${{q}_{i}}={{{\bar{\nu }}_{id}}}-{{\alpha }_{i}}$ and ${{z}_{i2}}={{\nu }_{i}}-{{{\bar{\nu }}_{id}}}$. Then, define the second scalar function

$$\begin{aligned} V_{i2}=V_{i1}+\frac{1}{2}q_{i}^{2}. \end{aligned}$$

(19)

Invoking (17), the time derivative of (19) is given by

$$\begin{aligned} {{\dot{V}}_{i2} }&=-z_{i1}^{\mathrm{{T}}}{{K}_{i1}}{{z}_{i1}}+z_{i1}^{\mathrm{{T}}}({{z}_{i2}}+q_{i})-z_{i1}^{\mathrm{{T}}}{{J}_{i}}^{\mathrm{{T}}}\eta _{id}^{{{\theta }_{i}}}{{\omega }_{is}}\nonumber \\&\qquad +q_{i}^\mathrm{{T}}\dot{q}_{i}. \end{aligned}$$

(20)

Step 2. For convenience of constraint effect analysis of the input saturation, the following auxiliary design system is given by

$$\begin{aligned} {{\dot{\pi }}_{i}}=-{{K}_{\pi _i }}{{\pi }_{i}}-\frac{\left| z_{i2}^{\mathrm{{T}}}{{{\tilde{\tau }}}_{i}} \right| +\frac{1}{2}\tilde{\tau }_{i}^{\mathrm{{T}}}{{{\tilde{\tau }}}_{i}}}{{{\left\| {{\pi }_{i}} \right\| }^{2}}}{{\pi }_{i}}+{{\tilde{\tau }}_{i}}, \end{aligned}$$

(21)

where ${{\pi }}_{i}\in {{\mathbb {R}}^{3}}$ is the state of the auxiliary design system. $\tilde{\tau }_{i}={\tau }_{i}-{\tau }_{i0}$, ${{K}_{\pi _i}}\in {{\mathbb {R}}^{3\times 3}}$ is a diagonal matrix, and its diagonal elements are positive constants. The control command ${\tau }_{i0}$ will be designed next.

Taking the time derivative of ${{z}_{i2}}$ along (3) gives

$$\begin{aligned} {{M}_{i}}{{\dot{z}}_{i2}}&={{\tau }_{i}}-{{C}_{i}}({{\nu }_{i}}){{\nu }_{i}}-{{D}_{i}}({{\nu }_{i}}){{\nu }_{i}}-{{\Delta }_{i}}({{\nu }_{i}}) \nonumber \\&+\tau _{iw}(t)-{{M}_{i}}{{\dot{\bar{\nu }}}_{id}}, \end{aligned}$$

(22)

Consider the third scalar function as

$$\begin{aligned} {{V}_{i3}}={{V}_{i2}}+\frac{1}{2}{{\pi }}_{i}^{\mathrm{{T}}}{{\pi }}_{i}+\frac{1}{2}{z_{i2}^{\mathrm{{T}}}}{{M}_{i}}{{z}_{i2}}, \end{aligned}$$

(23)

and its time derivative along (20), (22) and (21) can be written as

$$\begin{aligned} {{\dot{V}}_{i3}}&\le -\,z_{i1}^{\mathrm{{T}}}{{K}_{i1}}{{z}_{i1}}-z_{i1}^{\mathrm{{T}}}{{J}^{\mathrm{{T}}}}\eta _{id}^{{{\theta }_{i}}}{{\omega }_{is}}+q_{i}^\mathrm{{T}}\dot{q}_{i}+z_{i1}^{\mathrm{{T}}}{q}_{i}\nonumber \\&-\,\pi _{i}^{\mathrm{{T}}}({{K}_{\pi _i }}-\frac{1}{2}{{I}_{3\times 3}}){{\pi }_{i}}-\left| z_{i2}^{\mathrm{{T}}}{{{\tilde{\tau }}}_{i}} \right| \nonumber \\&+\,z_{i2}^{\mathrm{{T}}}[{{z}_{i1}}-{{C}_{i}}({{\nu }_{i}}){{\nu }_{i}}-{{D}_{i}}({{\nu }_{i}}){{\nu }_{i}}-{{\Delta }_{i}}({{\nu }_{i}})\nonumber \\&-\,{{M}_{i}}{{\dot{\bar{\nu }}}_{id}}+{{\tau }_{i}}]+\left| z_{i2}^{\mathrm{{T}}}\tau _{iw}(t)\right| . \end{aligned}$$

(24)

Substituting $\tau _i=\tilde{\tau }_{i}+\tau _{i0}$ into (24) and using the inequality $|{{{\chi } }_{1}}|-{{{\chi } }_{2}}\text {tanh}({{{\chi } }_{1}}/{{{\chi } }_{2}})\le 0.2478{{{\chi } }_{2}}$ with ${{{\chi } }_{1}}, {{{\chi } }_{2}}\in \mathbb {R}$, one has

$$\begin{aligned} {{\dot{V}}_{i3}}&\le -\,z_{i1}^{\mathrm{{T}}}{{K}_{i1}}{{z}_{i1}}-z_{i1}^{\mathrm{{T}}}{{J}^{\mathrm{{T}}}}\eta _{id}^{{{\theta }_{i}}}{{\omega }_{is}}\nonumber \\&+\,q_{i}^\mathrm{{T}}\dot{q}_{i}+z_{i1}^{\mathrm{{T}}}{q}_{i}-\pi _{i}^{\mathrm{{T}}}\left( {{K}_{\pi _i }}-\frac{1}{2}{{I}_{3\times 3}}\right) {{\pi }_{i}}\nonumber \\&-\left| z_{i2}^{\mathrm{{T}}}{{{\tilde{\tau }}}_{i}} \right| +z_{i2}^{\mathrm{{T}}}\left[ {{z}_{i1}} -f_i(\cdot )+\tilde{\tau }_{i}+\tau _{i0}\right] \nonumber \\&+\,0.2478\delta ^\mathrm{{T}}{\tau }_{iwM}. \end{aligned}$$

(25)

where $\delta =[\delta _{1}, \delta _2, \delta _3]^\mathrm{{T}}$ with ${{\delta }_{1}},$ ${{\delta }_{2}},$ and ${{\delta }_{3}}$ being very small scalars. $f_i(\cdot )$ is written as

$$\begin{aligned} {{f}_{i}}(\cdot )&= {{C}_{i}}({{\nu }_{i}}){{\nu }_{i}}+{{D}_{i}}({{\nu }_{i}}){{\nu }_{i}}\nonumber \\&+{{\Delta }_{i}}({{\nu }_{i}})+{{M}_{i}}{{\dot{\bar{\nu }}}_{id}}-\text {tanh}({{z}_{i2}}){{\tau }_{iwM}}, \end{aligned}$$

(26)

where $\text {tanh}({{z}_{i2}})=\text {diag}[\tanh \frac{{{(z_{i2}^{\mathrm{{T}}})}_{11}}}{{{\delta }_{1}}},\text {tanh}\frac{{{(z_{i2}^{\mathrm{{T}}})}_{12}}}{{{\delta }_{2}}},\tanh \frac{{{(z_{i2}^{\mathrm{{T}}})}_{13}}}{{{\delta }_{3}}}]$.

Consider a desired control command ${{\tau }_{i0}}$ as

$$\begin{aligned} {{\tau }_{i0}}=-{{z}_{i1}}-{{K}_{i2}}({{z}_{i2}}-\pi _i)+{{f}_{i}}(\cdot ), \end{aligned}$$

(27)

where ${{K}_{i2}}=\hbox {diag}[{k}_{i2}]\in {{\mathbb {R}}^{3\times 3}}$ is a diagonal matrix, and its diagonal elements are positive constants. In practice, ${{f}_{i}}(\cdot )$ is very hard to obtain accurately. Hence, the controller (27) cannot be implemented. To overcome this problem, a neural network is employed to approximate $f_i(\cdot )$ as follows

$$\begin{aligned} {{f}_{i}}(\cdot )=W_{i}^{\mathrm{{T}}}\sigma ({{\xi }_{i}})+{{\varepsilon }_{i}}, \end{aligned}$$

(28)

where ${{\xi }_{i}}={{[1,\nu _{i}^{\mathrm{{T}}},{{\dot{\bar{\nu }}}_{id}^\mathrm{{T}}}]^{\mathrm{{T}}}}} \in \mathbb {R}^7$ is the NN input; $W_{i}$ is the NN weight; ${{\varepsilon }_{i}}$ is the approximation error satisfying $\Vert {\varepsilon }_{i}\Vert \le \varepsilon _{iM}$ with $\varepsilon _{iM}$ being a positive constant.

Select a control command ${{\tau }_{i0}}$ as

$$\begin{aligned} {{\tau }_{i0}}=-{{z}_{i1}}-{{K}_{i2}}({{z}_{i2}}-\pi _i)+\hat{W}_{i}^{\mathrm{{T}}}\sigma ({{\xi }_{i}}), \end{aligned}$$

(29)

where $\hat{W}_{i}$ is an estimate of $W_i$ and is updated as

$$\begin{aligned} {{\dot{\hat{W}}}_{i}}={{\varGamma }_{W}}\left[ -\sigma \left( {{\xi }_{i}}\right) z_{i2}^{\mathrm{{T}}}-{{k}_{{{W}}}}{{\hat{W}}_{i}}\right] , \end{aligned}$$

(30)

where ${{\varGamma }_{W}}\in {{\mathbb {R}}}$ and ${{k }_{{{W}}}}\in {{\mathbb {R}}}$ are positive constants.

Substituting (29) into (25) yields

$$\begin{aligned} {{{\dot{V}}}_{i3}}&\le -\,z_{i1}^{\mathrm{{T}}}{{K}_{i1}}{{z}_{i1}}-z_{i2}^{\mathrm{{T}}}{{K}_{i2}}{{z}_{i2}}+q_{i}^\mathrm{{T}}\dot{q}_{i}+z_{i1}^{\mathrm{{T}}}{q}_{i}\nonumber \\&-\,\pi _{i}^{\mathrm{{T}}}\left( {{K}_{\pi _i }}-\frac{1}{2}{{I}_{3\times 3}}\right) {{\pi }_{i}} +z_{i2}^{\mathrm{{T}}}{{K}_{i2}}{{\pi }_{i}}\nonumber \\&+\,z_{i2}^{\mathrm{{T}}}\left[ \tilde{W}_{i}^{\mathrm{{T}}}\sigma ({{\xi }_{i}})-{\varepsilon }_{i}\right] +0.2478{{\delta }^{\mathrm{{T}}}}{\tau }_{iwM}-\mu _i{{\omega }_{is}},\nonumber \\ \end{aligned}$$

(31)

where ${{\mu }_{i}}={z}_{i1}^{\mathrm{{T}}}{{J}_{i}}^{\mathrm{{T}}}\eta _{id}^{{{\theta }_{i}}}$ and ${{\tilde{W}}_{i}}={{\hat{W}}_{i}}-{{W}_{i}}$.

Define the fourth scalar function as

$$\begin{aligned} {{V}_{i4}}={{V}_{i3}}+\frac{1}{2}\hbox {tr}\left( {{\tilde{W}}_{i}}^{\mathrm{{T}}}\varGamma _{{{W}}}^{-1}{{\tilde{W}}_{i}}\right) , \end{aligned}$$

(32)

whose time derivative along (30) and (31) is

$$\begin{aligned} {{{\dot{V}}}_{i4}}&\le -\,z_{i1}^{\mathrm{{T}}}{{K}_{i1}}{{z}_{i1}}-z_{i2}^{\mathrm{{T}}}{{K}_{i2}}{{z}_{i2}}+q_{i}^\mathrm{{T}}\dot{q}_{i}+z_{i1}^{\mathrm{{T}}}{q}_{i}\nonumber \\&-\,\pi _{i}^{\mathrm{{T}}}\left( {{K}_{\pi _i }}-\frac{1}{2}{{I}_{3\times 3}}\right) {{\pi }_{i}}\nonumber \\&+\,z_{i2}^{\mathrm{{T}}}{{K}_{i2}}{{\pi }_{i}}-{{k}_{{{W}}}}\hbox {tr}\left( \tilde{W}_{i}^{\mathrm{{T}}}{{\hat{W}}_{i}}\right) -z_{i2}^{\mathrm{{T}}}{{\varepsilon }_{i}}\nonumber \\&+\,0.2478{{\delta }^{\mathrm{{T}}}}{{\tau }_{iwM}}-\mu _i{{\omega }_{is}}. \end{aligned}$$

(33)

3.2 Cooperative path following design

Cooperative control strategies for multiple vehicles are supported by the communications network over which the vehicles exchange information. Because more than one vehicle is involved, the path variables and speed should be synchronized to each vehicle, in order to maintain the desired formation. We assume that the vehicles can exchange relative path variables information using the network infrastructure. To satisfy the constraints imposed by the communication network, the synchronization control law for the vehicle $i$ can only depend on its own local states and on the information exchanged with its neighbors. Furthermore, since not all the vehicles can obtain the value of common reference speed, some of them have to estimate it throughout the process. Let $\mathcal {N}_i$ be the set of labels of those vehicles that are neighbors of vehicle $i$, $\mathcal {N}_0$ be the set of labels of those vehicles that are neighbors of the virtual leader. In such a way, the common reference speed assigned by a virtual leader is available to only one or one subset of vehicles, so the speed estimate strategy is distributed. The amount of communications is reduced effectively due to the distributed speed estimate strategy. To this end, choose the following synchronization control law with an auxiliary state ${{\gamma }_{i}}$ as

$$\begin{aligned} {{\omega }_{is}}&=-k _{i3}^{-1}\left[ \sum \limits _{_{j\in {{\mathcal {N}}_{i}}}}{{{a}_{ij}}({{\theta }_{i}}-{{\theta }_{j}})}+{{\mu }_{i}}\right] -{{\gamma }_{i}}, \nonumber \\ {{{\dot{\gamma }}}_{i}}&=-({{k}_{i3}}+{{k}_{i4}}){{\gamma }_{i}}-\sum \limits _{_{j\in {{\mathcal {N}}_{i}}}}{{{a}_{ij}}({{\theta }_{i}}-{{\theta }_{j}})}-{{\mu }_{i}}, \end{aligned}$$

(34)

where ${k}_{i3}\in \mathbb {R}$ and ${k}_{i4}\in \mathbb {R}$ are positive constants; ${a}_{ij}$ has been defined in Sect. 2.2. The distributed speed update law is designed as

$$\begin{aligned} {{\dot{\hat{v}}}_{id}}\!=\!-{k}_{i5}\!\sum \limits _{j\in {{\mathcal {N}}_{i}}}{{{a}_{ij}}({{{\hat{v}}}_{id}}\!-\!{{{\hat{v}}}_{jd}})}-{k}_{i6}\!\sum \limits _{i\in {{\mathcal {N}}_{0}}}{{{b}_{i}}({{{\hat{v}}}_{id}}\!-\!{{v}_{0}})}, \end{aligned}$$

(35)

where ${k_{i5}}\in \mathbb {R}$ and ${k_{i6}}\in \mathbb {R}$ are positive constants. $b_{i}$ is the connection weight between vehicle $i$ and the virtual leader, $b_{i}=1$ if the virtual leader is available to $i$th vehicle and $b_{i}=0$ otherwise. Let $\omega _{s}=[\omega _{1s},\ldots ,\omega _{ns}]^\mathrm{{T}}\in {{\mathbb {R}}^{n}}$, $\mu =[{{\mu }_{1}},\ldots ,{{\mu }_{n}}]^{\mathrm{{T}}}\in {{\mathbb {R}}^{n}}$, $\gamma =[\gamma _{1},\ldots ,\gamma _{n}]^\mathrm{{T}}\in {{\mathbb {R}}^{n}}$, ${K_{3}}=\hbox {diag}[{k_{i3}}]\in {{\mathbb {R}}^{n\times n}}$, ${K_{4}}=\hbox {diag}[{k_{i4}}]\in {{\mathbb {R}}^{n\times n}}$, ${K_{5}}=\hbox {diag}[{k_{i5}}]\in {{\mathbb {R}}^{n\times n}}$, ${K_{6}}=\hbox {diag}[{k_{i6}}]\in {{\mathbb {R}}^{n\times n}}$, $\hat{v}_d =[\hat{v}_{1d},\ldots ,\hat{v}_{nd}]^{\mathrm{{T}}}\in {{\mathbb {R}}^{n}}$. Then, (34) can be written as

$$\begin{aligned} \dot{\theta }&={\hat{v}_{d}}-{K_{3}^{-1}}(L\theta +\mu )-\gamma ,\nonumber \\ \dot{\gamma }&=-({{K}_{3}}+{{K}_{4}})\gamma -L\theta -\mu , \end{aligned}$$

(36)

(35) can be written as

$$\begin{aligned} {{\dot{\hat{v}}}_{d}}=-\mathcal {L}{{\hat{v}}_{d}}+{K_{6}}\mathcal {B}{{v}_{0}}{{\mathbf {1}}_{n}}, \end{aligned}$$

(37)

where $\mathcal {L}={K_{5}}L+{K_{6}}\mathcal {B}$, $\mathcal {B}=\hbox {diag}[b_1,\ldots ,b_n]\in {{\mathbb {R}}^{n\times n}}$. Because the fixed undirected graph is connected, and at lease one $b_i$ is nonzero, so $\mathcal {L}$ is symmetric positive definite. Noting that $\tilde{v}_{d}={\hat{v}_{d}}-{v}_{0}{{\mathbf {1}}_{n}}$, then we have

$$\begin{aligned} {{\dot{\tilde{v}}}_{d}}=-\mathcal {L}{{\tilde{v}}_{d}}. \end{aligned}$$

(38)

Consider the fifth scalar function as

$$\begin{aligned} {{V}}=\frac{1}{2}{{\theta }^{\mathrm{{T}}}}L\theta +\frac{1}{2}{{\gamma }^{\mathrm{{T}}}}\gamma +\frac{1}{2}{\tilde{v}_{d}^\mathrm{{T}}}{\tilde{v}_{d}} +\sum \limits _{i=1}^{n}{{{V}_{i4}}}, \end{aligned}$$

(39)

and its time derivative along (33), (36), and (38) is

$$\begin{aligned} {{\dot{V}}}&\le -\omega _{s}^{\mathrm{{T}}}{K_3}{{\omega }_{s}}-{{\gamma }^{\mathrm{{T}}}}{K_4}\gamma -\tilde{v}_{d}^{\mathrm{{T}}}\mathcal {L}{{\tilde{v}}_{d}}\nonumber \\&+\sum \limits _{i=1}^{n} \left[ -z_{i1}^{\mathrm{{T}}}{{K}_{i1}}{{z}_{i1}}-{z_{i2}^{\mathrm{{T}}}{{K}_{i2}}{{z}_{i2}}}+q_{i}^\mathrm{{T}}\dot{q}_{i}+z_{i1}^{\mathrm{{T}}}{q}_{i}\right. \nonumber \\&-\pi _{i}^{\mathrm{{T}}}\left( {{K}_{\pi _i }}-\frac{1}{2}{{I}_{3\times 3}}\right) {{\pi }_{i}}+z_{i2}^{\mathrm{{T}}}{{K}_{i2}}{{\pi }_{i}}\nonumber \\&\left. -{{k}_{{{W}}}}\hbox {tr}\left( \tilde{W}_{i}^{\mathrm{{T}}}{{\hat{W}}_{i}}\right) -z_{i2}^{\mathrm{{T}}}{{\varepsilon }_{i}}+0.2478{{\delta }^{\mathrm{{T}}}}{{\tau }_{iwM}}\right] .\nonumber \\ \end{aligned}$$

(40)

3.3 Stability analysis

Theorem 1

Consider a network of marine surface vehicles with the vehicles dynamics given in (2) and (3). Suppose the communication network is undirected and connected. Design the control law (29), NN adaptive law (30), synchronization control law (36), and distributed speed update law (37). Then, given any positive number ${\delta }_{i2}$, for all initial conditions satisfying ${{\varOmega }_{i2}}=\{{{[{{z}_{i1}},{{z}_{i2}},{{\tilde{W}}_{i}},q_{i},\tilde{v}_{id}]^{\mathrm{{T}}}: V \le {{\delta }_{i2}}}}\}$, there exist ${{K}_{i1}},{{K}_{i2}},{{\varGamma }_{W}},{{k}_{W}},\rho ,{K_3}$, ${K_4}$, ${K_5}$, and ${K_6}$; such all signals in the closed-loop system are UUB, and the path following error ${{\eta }_{i}}-{{\eta }_{id}}$, speed tracking error ${\dot{\theta }_{i}}-{v}_{0}$, and path variable coordination error ${{\theta }_{i}}-{{\theta }_{j}}$ satisfy (7), (8) and (9), respectively.

Proof

Taking the time derivative of $q_{i}$ along (18), we have

$$\begin{aligned} {{{\dot{q}}}_{i}}&=-\frac{{{q}_{i}}}{\rho }+B_i\left( {{z}_{i1}},{{z}_{i2}},{{\omega }_{is}},{{q}_{i}},{{\eta }_{id}},\eta _{id}^{{{\theta }_{i}}},\eta _{id}^{\theta _{i}^{2}}\right) , \end{aligned}$$

(41)

where $B_{i}(\cdot )$ is a continuous function. Since for any ${{\delta }_{i1}}$ and ${{\delta }_{i2}}$, the sets ${{\varOmega }_{i1}}$ and ${{\varOmega }_{i2}}$ are compact, ${{\varOmega }_{i1}}\times {{\varOmega }_{i2}}$ is also compact. Hence, $B_{i}(\cdot )$ has a maximum $B_{iM}$ on ${{\varOmega }_{i1}}\times {{\varOmega }_{i2}}$. Furthermore, using Young’s inequality yields

$$\begin{aligned}&q_{i}^{\mathrm{{T}}}{{\dot{q}}_{i}}\le -\frac{{{\left\| {{q}_{i}} \right\| }^{2}}}{\rho }+\frac{B_{iM}^{2}{{\left\| {{q}_{i}} \right\| }^{2}}}{2\varpi _i }+\frac{\varpi _i }{2} ,\nonumber \\&z_{i2}^{\mathrm{{T}}}{{K}_{i2}}{{\pi }_{i}}\le \frac{1}{2}{{\lambda }_{\min }}^{2}({{K}_{i2}}){{\left\| {{z}_{i2}} \right\| }^{2}}+\frac{1}{2}{{\left\| {{\pi }_{i}} \right\| }^{2}} ,\nonumber \\&-{{k}_{{{W}}}}\hbox {tr} \left( {{\tilde{W}}_{i}}^{\mathrm{{T}}}{{\hat{W}}_{i}}\right) \le -\frac{{{k}_{{{W}}}}}{2}\Vert {{\tilde{W}}_{i}}\Vert _{F}^{2}+\frac{{{k}_{{{W}}}}}{2}\Vert {{{W}}_{i}}\Vert _{F}^{2},\nonumber \\&\left| z_{i1}^{\mathrm{{T}}}{{q}_{i}} \right| \le \frac{1}{2}{{\left\| z_{i1} \right\| }^{2}} +\frac{1}{2}{{\left\| {{q}_{i}} \right\| }^{2}},\nonumber \\&- z_{i2}^{\mathrm{{T}}}{{\varepsilon }_{i}} \le \frac{1}{2}{{\left\| z_{i2} \right\| }^{2}} +\frac{1}{2}{{\left\| {{\varepsilon }_{iM}} \right\| }^{2}}, \end{aligned}$$

(42)

where $\varpi _i\in {{\mathbb {R}}}$ is a positive constant. Then, (40) can be rewritten as

$$\begin{aligned} {{{\dot{V}}}}&\le -{{\lambda }_{\min }}(K_3){{\left\| {{\omega }_{s}} \right\| }^{2}}-{{\lambda }_{\min }}(K_4){{\left\| \gamma \right\| }^{2}}\nonumber \\&-{{\lambda }_{\min }}(\mathcal {L}){{\left\| \tilde{v}_{d} \right\| }^{2}}+\sum \limits _{i=1}^{n}\left[ {{{-\left( {{\lambda }_{\min }}({{K}_{i1}})-\frac{1}{2}\right) }}}{{\left\| {{z}_{i1}} \right\| }^{2}}\right. \nonumber \\&-\left[ {{\lambda }_{\min }}({{K}_{i2}})-\frac{1}{2}{{\lambda }_{\min }}^{2}({{K}_{i2}})-\frac{1}{2}\right] {{\left\| {{z}_{i2}} \right\| }^{2}}\nonumber \\&-\left( \frac{1}{\rho }-\frac{1}{2}-\frac{B_{iM}^{2}}{2\varpi _i }\right) \left\| q_{i}\right\| ^{2}-\left[ {{\lambda }_{\min }}\left( {{K}_{\pi _i }}-\frac{1}{2}{{I}_{3\times 3}}\right) \right. \nonumber \\&\left. -\frac{1}{2}]{{\left\| {{\pi }_{i}} \right\| }^{2}}-\frac{{{k}_{{{W}}}}}{2}\Vert {{{\tilde{W}}}_{i}}{{\Vert }_{F}^{2}}\right] +{H}_{i}, \end{aligned}$$

(43)

where ${{H}_{i}}=\sum \limits _{i=1}^{n}[0.2478{{\delta }^{\mathrm{{T}}}}{{\tau }_{iwM}}+\frac{1}{2}{{k}_{W}}\Vert {{{W}}_{i}}\Vert _{F}^{2}+\frac{1}{2}{{\left\| {{\varepsilon }_{iM}} \right\| }^{2}}+\frac{1}{2}\varpi _i ]$. Choose ${{\lambda }_{\min }}(\mathcal {L})>0$, ${{\lambda }_{\min }}({{K}_{i1}})-\frac{1}{2}>0$, ${{\lambda }_{\min }}({{K}_{i2}})-\frac{1}{2}{{\lambda }_{\min }}^{2}({{K}_{i2}})-\frac{1}{2}>0$, $\frac{1}{\rho }-\frac{1}{2}-\frac{B_{iM}^{2}}{2\varpi _i }>0$, ${{\lambda }_{\min }}({{K}_{\pi _i }}-\frac{1}{2}{{I}_{3\times 3}})-\frac{1}{2}>0$ and note that, $\left\| {{\omega }_{s}} \right\| >\sqrt{\frac{{{{H}_{i}}}}{{{\lambda }_{\min }}({K_3})}}$, $\left\| \gamma \right\| >\sqrt{\frac{{{{H}_{i}}}}{{{\lambda }_{\min }}({K_4})}}$, $\left\| \tilde{v}_{d} \right\| >\sqrt{\frac{{{{H}_{i}}}}{{{\lambda }_{\min }}(\mathcal {L})}}$, $\left\| {{z}_{i1}} \right\| >\sqrt{\frac{{{{H}_{i}}}}{{{\lambda }_{\min }}({{K}_{i1}})-\frac{1}{2}}}$, $\left\| {{z}_{i2}} \right\| >\sqrt{\frac{{{{H}_{i}}}}{{{\lambda }_{\min }}({{K}_{i2}})-\frac{1}{2}{{\lambda }_{\min }}^{2}({{K}_{i2}})-\frac{1}{2}}}$, ${{|| {{{\tilde{W}}}_{i}} ||}_{F}}>\sqrt{\frac{2{{{H}_{i}}}}{{{k}_{W}}}}$, $\left\| q_{i}\right\| >\sqrt{\frac{2\rho \varpi _i {{{H}_{i}}}}{2\varpi _i -\rho \varpi _i -\rho B_{iM}^{2} }}$, or $\left\| {{\pi }_{i}} \right\| >\sqrt{\frac{{{{H}_{i}}}}{{{\lambda }_{\min }}({{K}_{\pi _i }}-\frac{1}{2}{{I}_{3\times 3}})-\frac{1}{2}}}$ renders $\dot{V}<0$. This proves that all signals in the closed-loop system are UUB. Moreover, when $t\rightarrow \infty$, the path following error ${{\eta }_{i}}-{{\eta }_{id}}$ and along-path speed tracking error ${\dot{\theta }_{i}}-{\hat{v}_{id}}$ satisfy (7) and (8) with ${{\epsilon }_{i1}}, {{\epsilon }_{i2}}$ taken as ${{\epsilon }_{i1}}=\sqrt{\frac{{{{{H}_{i}}}}}{{{\lambda }_{\min }}({{K}_{i1}})-\frac{1}{2}}}$, ${{\epsilon }_{i2}}=\sqrt{\frac{{{{H}_{i}}}}{{{\lambda }_{\min }}(K_3)}}$. Let $s=L\theta$, from (36) we have

$$\begin{aligned} \left\| s \right\| \le {{\epsilon }_{is}}, \end{aligned}$$

(44)

where ${{\epsilon }_{is}}=\sqrt{{\epsilon _{i1}^{2}(\eta {{_{idM}^{{{\theta }_{i}}}})^{2}}}}+{{\lambda }_{\max }}({K_3})\left( \sqrt{\frac{{{{H}_{i}}}}{{{\lambda }_{\min }}({K_3})}}+\sqrt{\frac{{{{H}_{i}}}}{{{\lambda }_{\min }}({K_4})}}\right)$. In addition, since $\frac{1}{2}{{\lambda }_{2}}(L)\left\| \theta -Ave(\theta ){{\mathbf {1}}_{n}} \right\| ^{2}\le \frac{1}{2}{{\theta }^{\mathrm{{T}}}}L\theta$, where $Ave(\theta )=\frac{1}{n}\sum _{i=1}^{n}{{{\theta }_{i}}}$ [39], then by Lemma 1 we further obtain

$$\begin{aligned} \frac{1}{2}{{\lambda }_{2}}(L){{\left\| \theta -Ave(\theta ){{\mathbf {1}}_{n}} \right\| }^{2}}\le \frac{1}{2}{{s }^{\mathrm{{T}}}}Ps. \end{aligned}$$

(45)

It follows from (44) that the inequality (9) is satisfied with ${{\epsilon }_{i3}}=\sqrt{\frac{{{\lambda }_{\max }}(P)}{{{\lambda }_{2}}(L)}}{{\epsilon }_{is}}$, i.e., ${{\theta }_{i}}\rightarrow {{\theta }_{j}}\rightarrow Ave(\theta )$.

This concludes the proof.$\square$

Remark 1

By incorporating the DSC technique, the proposed design leads to a much simpler cooperative path following controller than the traditional backstepping-based design. In fact, using the traditional backstepping-based method, the derivative of virtual control ${{\dot{\alpha }}_{i}}={{K}_{i1}}\big \{rS{{z}_{i1}}-{{\nu }_{i}}-J_{i}^{\mathrm{{T}}}\big [\eta _{id}^{{{\theta }_{i}}}({\hat{v}_{id}} +{{\omega }_{is}})\big ]-\dot{J}_{i}^{\mathrm{{T}}}\eta _{id}^{{{\theta }_{i}}}{\hat{v}_{id}}-J_{i}^{\mathrm{{T}}}\eta _{id}^{\theta _{i}^{2}}{\hat{v}_{id}}\big \}$ would have to appear in the control algorithm. As a result, the expression of $\tau _{i}$ would be much more complicated.

Remark 2

In contrast to the previous works [6, 7, 11–13, 20, 23, 24], the cooperative path following problem in the presence of the input saturation and partial knowledge of reference velocity is considered in this paper. Moreover, the proposed NN-based DSC technique results in much simpler cooperative path following controllers than the backstepping-based design.

4 Simulation example

In this section, an example is given to illustrate the proposed controllers. In our simulation study, we consider the model of Cybership II from [40], and some model uncertainty and time-varying disturbances are introduced.

Consider a group of five vehicles with a communication network that induces a graph with the Laplacian matrix $L=\left[ \begin{matrix} 1 &{} -1 &{} 0 &{} 0 &{} 0 \\ -1 &{} 2 &{} -1 &{} 0 &{} 0 \\ 0 &{} -1 &{} 2 &{} -1 &{} 0 \\ 0 &{} 0 &{} -1 &{} 2 &{} -1 \\ 0 &{} 0 &{} 0 &{} -1 &{} 1 \\ \end{matrix} \right]$, $\mathcal {B}=\hbox {diag}[1,0,0,1,0]$. The basis function ${{\rho }_{l}}(\xi )$ is chosen as the commonly used hyperbolic tangent function, ${{\rho }_{l}}(\xi )=\frac{\exp (\xi )-\exp (-\xi )}{\exp (\xi )+\exp (-\xi )}$. The initial velocities are ${{u}_{i}}(0)={{v}_{i}}(0)=0\,\hbox {m}/\hbox {s}$, ${{r}_{i}}(0)=0\,\hbox {rad}/\hbox {s}$. The NN adaptive law parameters are chosen as ${{k}_{{{W}}}}=1,{{\varGamma }_{{{W}}}}=100$. The controller gains are selected as ${{K}_{i1}}=\hbox {diag}[1,1,1]$, ${{K}_{i2}}=\hbox {diag}[60,70,8]$, ${{K}_{\pi _i}}=\hbox {diag}[200,200,200]$, $K_3=\hbox {diag}[1,1,1]$, $K_4=\hbox {diag}[1,1,1]$. The filter time constant is chosen as $\rho =0.05$. The uncertainty of five vehicles is given as ${{\Delta }_{i}}({{\nu }_{i}})={{[v_{i}^{3}+0.03u_{i},u_{i}r_i+0.02u_{i},u_{i}r_i+0.2r_i^{2}]}^{\mathrm{{T}}}}$ and $\tau _{iw}=[v_i^3+0.06u_i+0.001\sin (t),u_ir_i+0.1u_i+0.001\sin (t),0.4u_ir_i+v_i^2+0.001\sin (t)]^\mathrm{{T}}$.

The lower and upper limits of input saturation constraints are chosen as $\tau _{i \min u}=-9.2\,\mathrm{{N}}$, $\tau _{i\max u}=9.2\,\hbox {N}, \tau _{i\min v}=-4.5\,\hbox {N}, \tau _{i\max v}=4.5\,\hbox {N}, \tau _{i\min r}=-3\,\hbox {Nm}, \tau _{i\max r}=3\,\hbox {Nm}.$

Fig. 3

Desired and actual vehicles paths

Figure 3 shows the tracking performance of five vehicles, where the desired paths are denoted by dotted line, and the actual paths are denoted by solid line. As can be observed that the vehicles remain within a small neighborhood of the desired path despite the disturbances. To verify the learning ability of NN, the NN approximation performance of vehicle 2 is shown in Fig. 4, where $f_{2u}(\cdot )$, $f_{2v}(\cdot )$, and $f_{2r}(\cdot )$ denote the vehicle 2’s uncertainty in the surge, sway, and yaw direction, respectively, and $\mathrm{{NN}}_{2u}$, $\mathrm{{NN}}_{2v}$, and $\mathrm{{NN}}_{2r}$ are the corresponding neural network outputs. We can verify the uncertainty is efficiently compensated for by NN. The path variables coordination errors are shown in Fig. 5. Figure 6 shows that the control input signals of vehicle 3 are bounded within $\pm 9.2\,\mathrm{{N}}$ and $\pm 4.5\,\mathrm{{N}}$, which we have set as the saturation limits. Figure 7 shows that the speed information is well estimated by the proposed distributed speed estimate strategy, while vehicles 2, 3, and 5 do not obtain the common reference speed $v_0=0.1$.

Fig. 4

Neural network approximation performance

Fig. 5

Path variables coordination errors

Fig. 6

Control input

Fig. 7

Speed estimate of vehicles 2, 3, 5

5 Conclusions

This paper addressed the cooperative path following problem of multiple marine surface vehicles in the presence of input saturation, unknown functional uncertainty, time-varying environmental disturbances, and partial knowledge of the reference velocity. The cooperative path following controllers are devised based on the NN-based DSC technique, the auxiliary design, and the distributed velocity estimator. It has been shown that the closed-loop signals under the proposed algorithm are UUB, and the compact set to which the error signals converge can be made small through appropriate choosing of control parameters. Simulation results demonstrated the effectiveness of the proposed control approaches.