Nonlinear observer-based adaptive output feedback tracking control of underactuated ships with input saturation

Abstract

This paper focuses on adaptive robust output feedback tracking control of an underactuated ship considering input saturation and unavailable velocities. First, a nonlinear observer is designed for the estimation of velocities and the backstepping method is combined with the dynamic surface control (DSC) technique to stabilize the tracking errors and solve the problem of complexity explosion inherent. Then, an adaptive algorithm is designed to estimate the upper bound of external disturbances. In particular, the hyperbolic tangent function and an auxiliary system are used to compensate for the input saturation. Finally, According to the Lyapunov stability theory, all closed-loop signals are uniformly ultimately bounded (UUB). Simulation results and comparisons show the effectiveness and superiority of the designed controller.

1 Introduction

With the rapid development of modern control theory and the advancement of intelligent control technology, some results have been achieved in complex motion control of underactuated ships [1] with multiple degrees of freedom. Unlike normal ship systems, underactuated ships are controlled only by the yaw moment of the rudder and the surge force of the propeller, so the research into underactuated ships is challenging. Moreover, because underactuated ships also have the disadvantages of strong inertia, time delay [2], and nonlinear nonlinearity [3], it is very difficult to achieve an accurate controller design. Besides, in actual navigation, the ships are vulnerable to external disturbances such as wind, waves, and currents, which will affect the motion state of the ship and cause the ship to deviate from its original course. In summary, it is meaningful to design an accurate underactuated ship controller.

In recent years, scholars have done a lot of research on the motion control of underactuated ships. Do et al. [4] used the backstepping method and Lyapunov’s direct method to design the trajectory tracking control of underactuated ships. However, in the design of the backstepping method, it is necessary to derive the virtual control laws, which causes an “explosion of complexity”. In [5,6,7], the dynamic surface control technique (DSC) was added to the backstepping, which avoided the “differential explosion” caused by the derivation of the virtual control rate and simplified the computational complexity.

In the actual sea conditions, unknown disturbances such as wind, waves and currents are inevitable, so the influence of external disturbances needs to be considered in the design of the controller. To eliminate the influence of external time-varying disturbances on ship course keeping, Liu et al. [8] designed a controller based on an adaptive sliding mode control method and a nonlinear disturbance observer, which can maintain the ship course effectively and have strong robustness against disturbances. Recently, to overcome the drawback of dependence on the model certainties, Sun et al. [9] proposed a non-deterministic adaptive control method to approximate the model uncertainties. In [10], the influence of external disturbances and the model uncertainties were eliminated by designing a fuzzy robust controller.

In general, the system status is the premise condition for controller design. However, the ship velocities are often unpredictable due to the influence of measurement noise [11], only the position and heading of the ship are measured. In [12,13,14], to overcome the problem of unknown velocities, output feedback control was applied to the design of the controller. In [15], a high-gain observer (HGO) was proposed to reconstruct the velocities from the measured position and heading of the ship. Ngongi et al. [16] proposed a dynamic positioning controller by integrating the HGO, the DSC technique, and the backstepping method. Considering unmeasured velocities and uncertainty parameters of the ship, a high gain observer [17, 18] provided an estimation of the ship velocities and a radial basis function (RBF) neural network compensated for the ship uncertainties. Compared with the state feedback [4], In [15,16,17,18], the design of the output feedback controllers only required position information. But the HGO has one obvious disadvantage, which is easy to generate oscillation and make the system crash. The HGO causes the peaking phenomenon [19], which leads to unexpected control performance and even system instability. Moreover, for underactuated ships, the design method of the HGO is not simple to apply directly. There is seldom research on the application of observers to underactuated ships. In [20], considering the external environment disturbances, an output feedback control law based on a linear observer is designed for the path tracking of underactuated ships. Do et al. [21] proposed a state and output feedback controller which introduces a new nonlinear observer to observe the unmeasured ship velocities. It was more robust compared with the linear controller. In [22], the unknown velocities were estimated by designing a nonlinear extended state observer which can be applied to both fully-actuated and underactuated ships.

However, the problem of ship input saturation is not considered in the above references. In the actual control process, because of the limit on system hardware and the requirement of safe driving, it is necessary to avoid the control inputs exceeding the executable range of the actuator. Therefore, input saturation [23] must be taken into account in the controller design. There are many references to input saturation in tracking control [24], position control [25], and path following control [26]. In [23], a global tracking controller was designed for underactuated ships with input and velocity constraints. To achieve dynamic positioning of the ship with disturbances and input saturation, Hu et al. [25] used a disturbance observer to estimate external disturbances and introduced the auxiliary system to solve the problem of input saturation. An adaptive control strategy of neural network (NN) based on line-of-sight (LOS) method was proposed in [26, 27]. The rudder angle with input saturation was compensated by an auxiliary system, and NN was used to approximate the model uncertainties so that the designed controller had strong robustness. The Nussbaum-type function can compensate for the time-varying nonlinear terms arising from input saturation. In [28, 29], a novel control scheme was proposed by incorporating the Nussbaum gain technique into backstepping.

Inspired by the above research, to achieve the trajectory tracking of an underactuated ship considering input saturation, unavailable velocities and unknown external disturbances, we propose an adaptive output feedback control strategy. First, a nonlinear observer is designed for the estimation of unknown ship velocities and the backstepping method is combined with the DSC technique to stabilize the tracking errors to a small neighborhood of the origin. Then, the adaptive technique is introduced to estimate the upper bound of external disturbances. The hyperbolic tangent function is introduced in the design process of control laws and the auxiliary system is also adopted to deal with the problem of input saturation. Finally, the “BAY CLASS” remote patrol ship is used as the control target. Moreover, circular and sine shapes are selected as the desired tracking trajectory to verify the effectiveness of the designed controller. The main contributions are as follows:

• (1) The backstepping combined with the DSC technique solves the problem of “explosion of complexity” and avoids the singular value problem caused by the typical backstepping technique.

• (2) The unmeasured velocities of the ship are estimated by introducing a nonlinear observer. A nonlinear feedback function is employed to design the observer that can effectively avoid system saturation. The Unmeasured velocities can be constructed from the position-heading measurement and the observer can suppress the noise very well.

• (3) Due to the input saturation, the hyperbolic tangent function is employed to approximate the saturation function and an auxiliary system is introduced to compensate for the influence of input saturation.

The rest of this paper is organized as follows. Sect. 2 presents the problem formulation. In Sect. 3, the nonlinear observer is introduced to estimate ship velocities. Sect. 4 introduces the DSC and the backstepping techniques in controller design. In Sect. 5, the stability analysis for the designed controller. Sect. 6 completes the simulation analysis. Sect. 7 is the conclusion.

2 Problem formulation

Consider the existence of external disturbances, the kinematics and dynamics [30] of underactuated ships are described by the following differential equations:

$$\begin{aligned} \begin{array}{c} {\varvec{{\dot{\eta }}}} = {\varvec{R}}(\psi ){\varvec{\upsilon }} \\ {\varvec{M}}{\varvec{{\dot{\upsilon }}}} = - {\varvec{C}}({\varvec{\upsilon }} ){\varvec{\upsilon }} - {\varvec{D}}({\varvec{\upsilon }} ){\varvec{\upsilon }} + {\varvec{\tau }} + {\varvec{{\tau _w}}} \end{array} \end{aligned}$$

(1)

where the vectors ${\varvec{\eta }} = {\left[ {x,y,\psi } \right] ^{\mathrm{{T}}}}$ and ${\varvec{\upsilon }} = {\left[ {u,v,r} \right] ^{\mathrm{{T}}}}$ denote the position (x, y), heading $\psi$, and the surge u, sway v, and yaw r velocities of the ship in the earth-fixed frame and the body-fixed frame. The rotation matrix in yaw ${{\varvec{R}}(\psi ) }= \left[ {\begin{array}{*{20}{c}} {\cos \psi }&{}{ - sin\psi }&{}0\\ {sin\psi }&{}{\cos \psi }&{}0\\ 0&{}0&{}1 \end{array}} \right]$ describes the kinematic equation of motion, and satisfies ${{{\varvec{R}}^{ - 1}}(\psi )= {{\varvec{R}}^{\mathrm{{T}}}}(\psi )}$. The expression for Coriolis and centripetal matrix is ${{\varvec{C}}({\varvec{\upsilon }} )} = \left[ {\begin{array}{*{20}{c}} 0&{}0&{}{ - {m_{22}}v}\\ 0&{}0&{}{{m_{11}}u}\\ {{m_{22}}v}&{}{ - {m_{11}}u}&{}0\end{array}} \right]$. The ship inertia matrix ${\varvec{M}}=diag\left[ {{m_{11}},{m_{22}},{m_{33}}} \right]$ includes added mass forces and moments. The hydrodynamic damping coefficients ${{\varvec{D}}({\varvec{\upsilon }} )} = diag\left[ {{d_{11}},{d_{22}},{d_{33}}} \right]$ consists of ${d_{11}}\left( \upsilon \right) = {d_{u1}} + {d_{u2}}\vert u \vert$, ${d_{22}}\left( \upsilon \right) = {d_{v1}} + {d_{v2}}\vert v \vert$ and ${d_{33}}\left( \upsilon \right) = {d_{r1}} + {d_{r2}}\vert r \vert$. The control inputs $\tau = {\left[ {p({\tau _u}),0,p({\tau _r})} \right] ^{\mathrm{{T}}}}$ consists of the surge force $\tau _u$ and yaw moment $\tau _r$. The time-varying disturbances of the external environmental is ${\tau _w} = {\left[ {{\tau _{wu}},{\tau _{wv}},{\tau _{wr}}} \right] ^{\mathrm{{T}}}}$.

In the actual motion of the ship, due to the limit of propeller rotational speed and the requirement of safety, the surge force provided by the ship propeller and the yaw moment generated by the rudder are bounded which is expressed as follows:

$$\begin{aligned} p({\tau _i}) = sat({\tau _i}) = \left\{ {\begin{array}{*{20}{c}} {{\mathop {\mathrm{sgn}}} ({\tau _i}){{N_j}},\vert {\tau _i}\vert \ge {{N_j}}}\\ {{\tau _i},\vert {{\tau _i}}\vert < {{N_j}}} \end{array}} \right. \end{aligned}$$

(2)

where ${\tau _i} = \left( {{\tau _u}, {\tau _r}} \right)$, ${M_j}\left( {j = 1,2} \right)$ is the bound value of control input. To make the control input $p({\tau _i})$ has the nonlinear smooth characteristic, the hyperbolic tangent function is used to approximate the boundary function. The expression is as follows:

$$\begin{aligned} G({\tau _i}) = {{N_j}}\tan (\frac{{{\tau _i}}}{{{\xi _j}}}) = {{N_j}}\frac{{{e^{{\tau _j}/{\xi _j}}} - {e^{ - {\tau _i}/{\xi _j}}}}}{{{e^{{\tau _i}/{\xi _j}}} + {e^{ - {\tau _i}/{\xi _j}}}}} \end{aligned}$$

(3)

where ${\xi _j}{(j = 1,2)}$ is the positive design parameter. The generated error function is as follows:

$$\begin{aligned} \rho ({\tau _i}) = sat({\tau _i}) - G({\tau _i}) \end{aligned}$$

(4)

where $\rho ({\tau _i})$ is a bounded function and its bound value is expressed as follows:

$$\begin{aligned} \vert {\rho ({\tau _i})} \vert = \vert {sat\left( {{\tau _i}} \right) - G({\tau _i})}\vert \le {{{N_j}}}(1 - \tanh (1)) \end{aligned}$$

(5)

Assumption 1

For the desired trajectory $\left( {{x_d},{y_d}} \right)$ of ship, its first derivative $\left( {{{\dot{x}}_{d}},{{\dot{y}}_{d}}} \right)$ and second derivative $\left( {{{\ddot{x}}_{d}},{{\ddot{y}}_{d}}} \right)$ exist and bounded.

Assumption 2

The external disturbances ${\tau _{wu}}$, ${\tau _{wv}}$, and ${\tau _{wr}}$ acting on the underactuated ships are time-varying disturbances, and satisfy $\left| {{\tau _{wu}}} \right| \le \tau _{wu}^*$, $\left| {{\tau _{wv}}} \right| \le \tau _{wv}^*$, and $\left| {{\tau _{wr}}} \right| \le \tau _{wr}^*$. where $\tau _{wu}^* > 0$, $\tau _{wv}^* > 0$ and $\tau _{wv}^* > 0$ denote the upper bound of the external disturbances which are unknown constants.

Assumption 3

To facilitate the calculation and design of the controller, a simplified ship dynamics equation is used, where the inertia matrix is simplified to a diagonal matrix and the damping matrix is retained as a first-order linear and second-order non-linear damping matrix. The specific model assumptions are as follows: (a) the center of gravity coincides with the center of buoyancy ; (b) the mass distribution of the ship is homogeneous, and the ship is rigid body; (c) the heave, pitch, and roll motions are neglected; (d) The shape of the ship is symmetrical from front to back and side to side; (e) the shape structure of the vehicle is symmetrical regarding three plane of symmetrical.

3 Nonlinear observer

To eliminate the Coriolis and centripetal forces ${\varvec{C(\upsilon )}}{{\varvec{\upsilon }}}$ in Eq. 1 and facilitate the design of the nonlinear observer, a state transition matrix is introduced as follows:

$$\begin{aligned} {{\varvec{X}} = {\varvec{Q}}({\varvec{\eta }}){\varvec{\upsilon }}} \end{aligned}$$

(6)

where, $Q(\eta ) \in {R^{3 \times 3}}$ is the generalized matrix.

Combine Eq. 1 and Eq. 6, the time derivative of X is

$$\begin{aligned}&{\varvec{\dot{X} }}= \left( {{\varvec{\dot{Q}}}({\varvec{\eta }} ){\varvec{\upsilon }} - {\varvec{Q}}({\varvec{\eta }} ){{\varvec{M}}^{ - 1}}{\varvec{C}}({\varvec{\upsilon }} ){\varvec{\upsilon }} } \right) \nonumber \\&\quad - {\varvec{Q}}({\varvec{\eta }} ){{\varvec{M}}^{ - 1}}{\varvec{D}}({\varvec{\upsilon }}){{\varvec{Q}}^{ - 1}}({\varvec{\eta }} ){\varvec{X}} + {\varvec{Q}}({\varvec{\eta }} ){{\varvec{M}}^{ - 1}}\left( {{\varvec{\tau }} + {\varvec{{\tau _w}}}} \right) \end{aligned}$$

(7)

For ${{\varvec{\dot{{Q}}}}({\varvec{\eta }} ){\varvec{\upsilon }} - {\varvec{Q}}({\varvec{\eta }} ){{\varvec{M}}^{ - 1}}{\varvec{C}}({\varvec{\upsilon }} ){\varvec{\upsilon }} = 0}$, we have

$$\begin{aligned} {{\varvec{Q}}({\varvec{\eta }} )} = \left[ {\begin{array}{*{20}{c}} \displaystyle {cos\psi }&{}{ - \frac{{{m_{22}}}}{{{m_{11}}}}\sin \psi }&{}0\\ \displaystyle {\sin \psi }&{}{\frac{{{m_{22}}}}{{{m_{11}}}}cos\psi }&{}0\\ {\frac{{{m_{11}}}}{{{m_{33}}}}E({\varvec{{\eta }}} )}&{}{\frac{{{m_{22}}}}{{{m_{33}}}}F({\varvec{{\eta }}} )}&{}1 \end{array}} \right] \end{aligned}$$

(8)

where

$$\begin{aligned} \begin{array}{l} E(\eta ) = x\sin \psi - y\cos \psi \\ F(\eta ) = x\cos \psi + y\sin \psi \end{array} \end{aligned}$$

(9)

It can be obtained from the above equations that ${\left| {{\varvec{Q({\varvec{\eta }})}}} \right| }= {m_{22}} \cdot {m_{11}}^{ - 1} > 0$ , so ${{{\varvec{Q}}({\varvec{\eta }})}}$ is a global positive definite matrix.

Substitute Eq. 8 into Eq. 7 and combine with the ship model in Eq. 1, we can get

$$\begin{aligned}&\begin{array}{l} {\varvec{{\dot{\eta }}}} = {\varvec{R}}(\psi ){{\varvec{Q}}^{ - 1}}({\varvec{\eta }} ){\varvec{X}} \end{array} \end{aligned}$$

(10a)

$$\begin{aligned}&\begin{array}{l} {\varvec{{\dot{X}}}} = - {{\varvec{D_\eta }} }({\varvec{\eta }} ){\varvec{X}}+ {\varvec{Q}}({\varvec{\eta }} ){{\varvec{M}}^{ - 1}}\left( {{\varvec{\tau }} + {{\varvec{\tau _w}}}} \right) \end{array} \end{aligned}$$

(10b)

where, ${{\varvec{D_\eta }} }({\varvec{\eta }} ) ={\varvec{ Q}}({\varvec{\eta }} ){{\varvec{M}}^{ - 1}}{\varvec{D}}({\varvec{\upsilon }}){{\varvec{Q}}^{ - 1}}({\varvec{\eta }} )$

Therefore, the nonlinear observer is designed as follows :

$$\begin{aligned}&\begin{array}{l} {\varvec{\dot{{\hat{\eta }}} }} = {\varvec{R}}(\psi ){{\varvec{Q}}^{ - 1}}({\varvec{\eta }} ){\varvec{{\hat{X}}}} + {\varvec{{K_{01}}}}{{\varvec{G_1}}}({\varvec{{\tilde{\eta }}}} ) \end{array} \end{aligned}$$

(11a)

$$\begin{aligned}&\begin{array}{l} {\varvec{\dot{{\hat{X}}} }}= - {\varvec{{D_\eta }}}({\varvec{\eta }} ){\varvec{{\hat{X}} }}+{\varvec{ Q}}({\varvec{\eta }} ){{\varvec{M}}^{ - 1}}\left( {{\varvec{\tau }} + {{\varvec{\tau _w}}}} \right) + {\varvec{{K_{02}}}}{{\varvec{G_2}}}({\varvec{{\tilde{\eta }}}} ) \end{array} \end{aligned}$$

(11b)

where, ${{{\varvec{{\hat{\eta }}}}}}$ and ${{\varvec{{\hat{X}}}}}$ are the observation values of ${\varvec{\eta }}$ and ${\varvec{X}}$. ${\varvec{{K_{01}}}}$ and ${\varvec{{K_{02}}}}$ are the gain matrixes of the observer, and ${\varvec{{\tilde{\eta }}}} = {\varvec{\eta }} - {\varvec{{\hat{\eta }}}}$ is the position observation error of the nonlinear observer. Nonlinear feedback functions ${\varvec{{G_1}}}({\varvec{{\tilde{\eta }}}} )$ and ${\varvec{{G_2}}}({\varvec{{\tilde{\eta }}}} )$ satisfy

$$\begin{aligned} { {{\varvec{{\tilde{\eta }}}} ^{\mathrm{T}}}{{\varvec{G_i}}}({\varvec{{\tilde{\eta }}}} )} \ge 0,(i = 1,2) \end{aligned}$$

(12)

Select the nonlinear functions as

$$\begin{aligned}&\begin{array}{l} {{{\varvec{G_1}}({\varvec{{\tilde{\eta }}}} )}} = {\left[ {\begin{array}{*{20}{c}} {{g_1}({\tilde{x}})}&{}{{g_1}({\tilde{y}})}&{}{{g_1}({\tilde{\psi }} )} \end{array}} \right] ^{\mathrm{{T}}}}\\\;\;\;\;\;\;\; = {\left[ {\begin{array}{*{20}{c}} {{{\left| {{\tilde{x}}} \right| }^{1/2}}{\mathop {\mathrm{sign}}\nolimits } (\tilde{x})}&{}{{{\left| {{\tilde{y}}} \right| }^{1/2}}{\mathop {\mathrm{sign}}\nolimits } ({\tilde{y}})}&{}{{{\left| {{\tilde{\psi }} } \right| }^{1/2}}{\mathop {\mathrm{sign}}\nolimits } ({\tilde{\psi }} )} \end{array}} \right] ^{\mathrm{{T}}}}\\ \end{array} \end{aligned}$$

(13a)

$$\begin{aligned}&\begin{array}{l} {{\varvec{{G_2}}}({\varvec{{\tilde{\eta }}}} )} = {\left[ {\begin{array}{*{20}{c}} {{g_2}({\tilde{x}})}&{}{{g_2}({\tilde{y}})}&{}{{g_2}({\tilde{\psi }} )} \end{array}} \right] ^T}\\ = {\left[ {\begin{array}{*{20}{c}} {{{\left| {{\tilde{x}}} \right| }^{1/4}}{\mathop {\mathrm{sign}}\nolimits } (\tilde{x})}&{}{{{\left| {{\tilde{y}}} \right| }^{1/4}}{\mathop {\mathrm{sign}}\nolimits } ({\tilde{y}})}&{}{{{\left| {{\tilde{\psi }} } \right| }^{1/4}}{\mathop {\mathrm{sign}}\nolimits } ({\tilde{\psi }} )} \end{array}} \right] ^{\mathrm{{T}}}} \end{array} \end{aligned}$$

(13b)

The functions have the property of “small error but large gain, large error but small gain”.

Define the observation error ${\varvec{{\tilde{X}}}} ={\varvec{ X}} - {\varvec{{\hat{X}}}}$ and combine Eq. 10 with Eq. 12

$$\begin{aligned}&\begin{array}{l} {\varvec{\dot{{\tilde{\eta }}}}} = {\varvec{R}}(\psi ){{\varvec{Q}}^{ - 1}}({\varvec{\eta }} ){\varvec{{\tilde{X}}}} - {\varvec{{K_{01}}}}{\varvec{{G_1}}}({\varvec{{\tilde{\eta }}}} ) \end{array} \end{aligned}$$

(14a)

$$\begin{aligned}&\begin{array}{l} {\varvec{\dot{{\tilde{X}}}}} = - {\varvec{{D_\eta }}}({\varvec{\eta }} ){\varvec{{\tilde{X}}}} - {\varvec{{K_{02}}}}{\varvec{{G_2}}}({\varvec{{\tilde{\eta }}}} ) \end{array} \end{aligned}$$

(14b)

where, ${{\varvec{{\tilde{\eta }}}}} = {\left[ {{\tilde{x}},{\tilde{y}},{\tilde{\psi }} } \right] ^{\mathrm{{T}}}}$, ${{\varvec{{\tilde{X}} }}}= {\left[ {{{\tilde{x}}_1},{{{\tilde{x}}}_2},{{{\tilde{x}}}_3}} \right] ^{\mathrm{{T}}}}$.

Select Lyapunov function

$$\begin{aligned} {V_0} = \frac{1}{2}{\varvec{G_2}}{({\varvec{{\tilde{\eta }}}} )^{\mathrm{{T}}}}{\varvec{p_{01}}}{\varvec{{\tilde{\eta }}}} + \frac{1}{2}{{\varvec{\tilde{X}}}^{\mathrm{{T}}}}{\varvec{p_{02}}}{\varvec{{\tilde{X}}}} \end{aligned}$$

(15)

The time derivative of $V_0$ is

$$\begin{aligned} {{\dot{V}}_0}=\;& {} {\varvec{G_2}}{{\varvec{({\tilde{\eta }} )}}^{\mathrm{{T}}}}{\varvec{p_{01}}}{\varvec{\dot{\tilde{\eta }}}} + {{{\varvec{{\tilde{X}}}}}^T}{\varvec{p_{02}}}{\varvec{{\dot{{\tilde{X}}}}}}\nonumber \\=\;& {} {\varvec{{G_2}}}{({\varvec{{\tilde{\eta }}}} )^{\mathrm{{T}}}}{\varvec{p_{01}}}\left( {{\varvec{R}}(\psi ){{\varvec{Q}}^{ - 1}}({\varvec{\eta }} ){\varvec{{\tilde{X}}}} - {\varvec{{K_{01}}}}{\varvec{{G_1}}}({\varvec{{\tilde{\eta }} }})} \right) \nonumber \\&\quad + {{{\varvec{{\tilde{X}}}}}^{\mathrm{{T}}}}{\varvec{p_{02}}}\left( { - {{\varvec{D_\eta }} }({\varvec{\eta }} ){\varvec{{\tilde{X}} }}- {\varvec{{K_{02}}}}{\varvec{{G_2}}}({\varvec{{\tilde{\eta }}}} )} \right) \nonumber \\=\;& {} {\varvec{{G_2}}}{({\varvec{{\tilde{\eta }}}} )^{\mathrm{{T}}}}{\varvec{p_{01}}}{\varvec{R}}({\varvec{\eta }} ){{\varvec{Q}}^{ - 1}}({\varvec{\eta }} ){\varvec{{\tilde{X}} }}- \nonumber \\&\quad {\varvec{{G_2}}}{({\varvec{{\tilde{\eta }}}} )^{\mathrm{{T}}}}{\varvec{p_{01}}}{{\varvec{K_{01}}}}{\varvec{{G_1}}}({\varvec{{\tilde{\eta }}}} ) - {{{\varvec{{\tilde{X}}}}}^{\mathrm{{T}}}}{\varvec{p_{02}}}{{\varvec{D_\eta }} }({\varvec{\eta }} ){\varvec{{\tilde{X}}}}\nonumber \\&\quad - {{{\varvec{\tilde{X}}}}^{\mathrm{{T}}}}{\varvec{p_{02}}}{{\varvec{K_{02}}}}{\varvec{{G_2}}}({\varvec{{\tilde{\eta }}}} ) \end{aligned}$$

(16)

Let ${{\varvec{Q_{01}}}} = {{\varvec{K_{01}}}}^{\mathrm{{T}}}{\varvec{p_{01}}} + {\varvec{p_{01}}}{{\varvec{K_{01}}}}$ and ${{\varvec{Q_{02}}}} = {{\varvec{D_\eta }}}^{\mathrm{{T}}}({\varvec{\eta }} ){\varvec{p_{02}}} + {\varvec{p_{02}}}{{\varvec{D_\eta }} }({\varvec{\eta }} )$, where ${{\varvec{Q_{01}}}}$, ${{\varvec{Q_{02}}}}$, ${{\varvec{p_{01}}}}$, ${{\varvec{p_{02}}}}$ and ${{\varvec{D_\eta }} }({\varvec{\eta }} )$ are positive definite matrixes, which satisfy

$$\begin{aligned} { {\left( {{\varvec{R}}(\psi ){{\varvec{Q}}^{ - 1}}({\varvec{\eta }} )} \right) ^{\mathrm{{T}}}}{\varvec{p_{01}}} - {\varvec{p_{02}}}{{\varvec{K_{02}}}} = 0} \end{aligned}$$

(17)

From Eq. 12 and Eq. 13, we can get

$$\begin{aligned} {{\dot{V}_0}} = - \frac{1}{2}{{\varvec{G_2}}}{({\varvec{{\tilde{\eta }}}} )^{\mathrm{{T}}}}{{\varvec{Q_{01}}}}{\varvec{{G_1}}}({\varvec{{\tilde{\eta }}}} ) - \frac{1}{2}{{\varvec{{\tilde{X}}}}^{\mathrm{{T}}}}{{\varvec{Q_{02}}}}{\varvec{{\tilde{X}} }}< 0 \end{aligned}$$

(18)

According to Lyapunov analysis, it can be known that the nonlinear observer designed in Eq. 6 is asymptotical stable. Define the velocity estimator ${{\varvec{{\hat{\upsilon }} }}}= {\left[ {{{{\hat{u}}}_o},{{{\hat{v}}}_o},{{{\hat{r}}}_o}} \right] ^{\mathrm{{T}}}}$ where ${{\hat{u}}_o}$, ${{\hat{v}}_o}$, and ${{\hat{r}}_o}$ are the estimation values of u, u and r respectively and satisfies

$$\begin{aligned} {{\varvec{{\hat{\upsilon }} }} = {{\varvec{Q}}^{ - 1}}({\varvec{\eta }} ){\varvec{{\hat{X}}}}} \end{aligned}$$

(19)

The observation error ${{\varvec{{\tilde{\upsilon }}}} = {\varvec{\upsilon }} - {\varvec{{\hat{\upsilon }}}} } = {\left[ {{\tilde{u}},{\tilde{v}},{\tilde{r}}} \right] ^{\mathrm{{T}}}}$ is defined as follows:

$$\begin{aligned} {{\varvec{{\tilde{\upsilon }} }} = {{\varvec{Q}}^{ - 1}}({\varvec{\eta }} ){\varvec{{\tilde{X}}}}} \end{aligned}$$

(20)

In summary, the observer model of the ships kinematics and dynamics shown in Eq. 1 can be expressed as

$$\begin{aligned}&\begin{array}{l} {\varvec{\dot{{\hat{\eta }}}}} = {\varvec{R(\psi )}}{\varvec{{\hat{\upsilon }}}} + {\varvec{{K_{01}}}}{\varvec{{G_1}}}({\varvec{{\tilde{\eta }}}} ) \end{array} \end{aligned}$$

(21a)

$$\begin{aligned}&\begin{array}{l} {\varvec{M}}{\varvec{\dot{{\hat{\upsilon }}}}} = - {\varvec{C}}({\varvec{{\hat{\upsilon }} }}){\varvec{{\hat{\upsilon }} }} - {\varvec{D}}({\varvec{{\hat{\upsilon }}}}){\varvec{{\hat{\upsilon }}}} + {\varvec{\tau }} + {\varvec{{\tau _w}}} + {\varvec{M}}{{\varvec{Q}}^{ - 1}}{{\varvec{K_{02}}}}{{\varvec{G_2}}}({\varvec{{\tilde{\eta }}}} ) \end{array} \end{aligned}$$

(21b)

where, ${{{\varvec{K_{01}}}}} = diag({k_{01}},{k_{01}},{k_{01}})$ and ${{\varvec{{K_{02}}}}= {\left( {{\varvec{R}}(\psi ){{\varvec{Q}}^{ - 1}}} \right) ^{\mathrm{{T}}}}}$.

4 Controller design for trajectory tracking

4.1 Coordinate transformation and auxiliary system

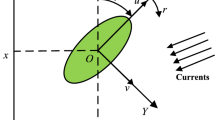
{I} is the earth-fixed frame and {B} is the body-fixed frame in Fig. 1. The variables ${x_{\mathrm{{d}}}}$ and ${y_{\mathrm{{d}}}}$ are the desired positions of the ship. The variable ${\psi _{\mathrm{{d}}}}$ is the virtual ship heading angle. The variables ${u_{\mathrm{{d}}}}$, ${v_{\mathrm{{d}}}}$, and ${r_{\mathrm{{d}}}}$ are virtual ship surge, sway, and yaw velocities. The variables ${x_{\mathrm{{e}}}}$, and ${y_{\mathrm{{e}}}}$ are the position errors in the earth-fixed frame. The variables ${e_x}$ and ${e_y}$ are position errors in the body-fixed frame.

Fig. 1

Earth-fixed frame and body-fixed frame

To facilitate the controller design, this paper will transform the position errors ${x_{\mathrm{{e}}}}$ and ${y_{\mathrm{{e}}}}$ into ${e_x}$ and ${e_y}$. Define the position and heading angle errors of the earth-fixed frame as

$$\begin{aligned} \left\{ {\begin{array}{*{20}{l}} {x_e} = x - {x_d}\\ {y_e} = y - {y_d}\\ {\psi _e} = \psi - {\psi _d} \end{array}} \right. \end{aligned}$$

(22)

where ${\psi _d} = arctan\left( {\frac{{{{\dot{y}}_d}}}{{{{\dot{x}}_d}}}} \right)$. The ship attitude of relative desired trajectory can be determined with ${\psi _e}$.

The position errors in body-fixed frame are obtained by coordinate frame transformation

$$\begin{aligned} \left[ {\begin{array}{*{20}{c}} {{e_x}}\\ {{e_y}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {cos\psi }&{}{sin\psi }\\ { - sin\psi }&{}{cos\psi } \end{array}} \right] \left[ {\begin{array}{*{20}{c}} {{x_e}}\\ {{y_e}} \end{array}} \right] \end{aligned}$$

(23)

From Eq. 23, we have $\left[ {\begin{array}{*{20}{c}} {{x_e}}\\ {{y_e}} \end{array}} \right] = {\left[ {\begin{array}{*{20}{c}} {cos\psi }&{}{sin\psi }\\ { - sin\psi }&{}{cos\psi } \end{array}} \right] ^{{\mathrm{- }}1}}\left[ {\begin{array}{*{20}{c}} {{e_x}}\\ {{e_y}} \end{array}} \right]$. If $\left\{ {\begin{array}{*{20}{c}} {{e_x}(t) = 0}\\ {{e_y}(t) = 0} \end{array}} \right.$, then $\left\{ {\begin{array}{*{20}{c}} {{x_e}(t) = 0}\\ {{y_e}(t) = 0} \end{array}} \right.$. Therefore, it is only necessary to design the control laws so that the tracking errors ${e_x}$ and ${e_y}$ quickly converge to a small neighborhood of the origin. From Eq. 1 and Eq. 23, the derivative of ${e_x}$ and ${e_y}$ are

$$\begin{aligned}&\begin{array}{l} {\dot{e}_x} = - {{\hat{u}}_o} + Ucos{\psi _e} + r{e_y} \end{array} \end{aligned}$$

(24a)

$$\begin{aligned}&\begin{array}{l} {\dot{e}_y} = - {{\hat{v}}_o} + Usin{\psi _e} - r{e_x} \end{array} \end{aligned}$$

(24b)

where $U = \sqrt{\dot{x}_d^2 + \dot{y}_d^2}$. Define the resultant velocity error as $\alpha = Usin{\psi _e}$, which can effectively avoid the singular value problems caused by the initial state constraints.

Define the velocity errors as

$$\begin{aligned} \left\{ {\begin{array}{*{20}{l}} {u_e} = {{\hat{u}}_o} - {u_d} \\ {\alpha _e} = \alpha - {\alpha _d}\\ {r_e} = {{\hat{r}}_o} - {r_d} \end{array}} \right. \end{aligned}$$

(25)

At the same time, to reduce the influence of the input constraints, An auxiliary system is introduced to compensate velocity errors ${u_e}$ and ${r_e}$. Design the auxiliary system as

$$\begin{aligned}&\begin{array}{l} {\dot{q}_1} = - {k_6}{q_1} + \frac{1}{{{m_{11}}}}\left[ {G\left( {{\tau _u}} \right) - {\tau _u}} \right] \end{array} \end{aligned}$$

(26a)

$$\begin{aligned}&\begin{array}{l} {\dot{q}_2} = - {k_7}{q_2} + \frac{1}{{{m_{33}}}}\left[ {G\left( {{\tau _r}} \right) - {\tau _r}} \right] \end{array} \end{aligned}$$

(26b)

where ${k_6}$ and ${k_7}$ are the positive design parameters, ${q_1}$ and ${q_2}$ are the states of auxiliary system. Redefine the corrected velocity errors as

$$\begin{aligned}&\begin{array}{l} {{\bar{u}}_e} = {u_e} - {q_1} \end{array} \end{aligned}$$

(27a)

$$\begin{aligned}&\begin{array}{l} {{\bar{r}}_e} = {r_e} - {q_2} \end{array} \end{aligned}$$

(27b)

4.2 Controller design

The process of controller design can be divided into four steps, including stabilizing position errors ${e_x}$ and ${e_y}$, stabilizing ${{\bar{u}}_e}$, stabilizing ${\alpha _e}$ and stabilizing ${{\bar{r}}_e}$ .

Step 1::

Stabilizing the position errors ${e_x}$ and ${e_y}$. Consider the following Lyapunov function as follows:

$$\begin{aligned} {V_1} = \frac{1}{2}\left( {e_x^2 + e_y^2} \right) \end{aligned}$$

(28)

The time derivative of $V_1$ is

$$\begin{aligned} {{\dot{V}}_1}&= {e_x}{{\dot{e}}_x} + {e_y}{{\dot{e}}_y}\nonumber \\&= \left( { - {{\hat{u}}_o} + {U}\cos {\psi _e}} \right) {e_x} + \left( { - {{\hat{v}}_o} + \alpha } \right) {e_y} \end{aligned}$$

(29)

Choose virtual control ${u_d}$ and ${\alpha _d}$ as follows:

$$\begin{aligned}&{u_d} = {U}cos{\psi _e} + {k_1}{e_x} \end{aligned}$$

(30a)

$$\begin{aligned}&{\alpha _d} = {{\hat{v}}_o} - {k_2}{e_y} \end{aligned}$$

(30b)

where ${k_1}$ and ${k_2}$ are positive design parameters.

Step 2::

Stabilizing ${{\bar{u}}_e}$. Consider the following Lyapunov function

$$\begin{aligned} {V_2} = {V_1} + \frac{1}{2}{\bar{u}}_e^2 \end{aligned}$$

(31)

The time derivative of $V_2$ is

$$\begin{aligned} {{\dot{V}}_2}&= {{\dot{V}}_1} + {{{\bar{u}}}_e}(\dot{{\hat{u}}}_o - {{\dot{u}}_d} - {{\dot{q}}_1})\nonumber \\&= {{\dot{V}}_1} + {{{\bar{u}}}_e}\left[ {\frac{1}{{{m_{11}}}}\left( {{m_{22}}{{\hat{v}}_o}{{\hat{r}}_o} - {d_{u1}}{{\hat{u}}_o} - {d_{u2}}{{\hat{u}}_o} \vert {{\hat{u}}_o}\vert + } \right. } \right. {\tau _u}+\nonumber \\&\quad \left. {\left. {{\mathrm{+ }}\rho \left( {{\tau _u}} \right) + {\tau _{wu}}} \right) - {{\dot{u}}_d} + {k_6}{q_1}} \right] \end{aligned}$$

(32)

To avoid repeatedly differentiating the virtual control ${u_{d}}$, which will lead to the “explosion of complexity”, the DSC technique is introduced [31]. Introduce a first-order filter ${{\varvec{X_d}}}= \left[ {{\hat{u}},{\hat{\alpha }} ,{\hat{r}}} \right]$ and let ${{\varvec{\nu }}} = \left[ {{u_{\mathrm{{d}}}},{\alpha _d},{r_d}} \right]$ pass through it

$$\begin{aligned} T{{\varvec{\dot{X}_d}} + {\varvec{X_d}}{\mathrm{= }}\nu , {\varvec{\dot{X}_d}}(0) = {\varvec{\nu }}} (0) \end{aligned}$$

(33)

According to the Eq. 33, we have

$$\begin{aligned} {{\varvec{\dot{X}_d}}}= \left( {{{\varvec{\nu }} - {\varvec{X_d}}}} \right) /T \end{aligned}$$

(34)

where T is the filter time constant. Define the output error of this filter as

$$\begin{aligned} {{\varvec{Y}}} = {{\varvec{X_d}} - {\varvec{\nu }}} \end{aligned}$$

(35)

The time derivative of ${\varvec{Y}}$ is

$$\begin{aligned} {{\varvec{\dot{Y}}} = {\varvec{\dot{X}_d}} - {\varvec{{\dot{\nu }} }} = - \frac{{\varvec{Y}}}{T} + {{\varvec{\beta _1}}}}\left( {{{\dot{x}}_d},{{\ddot{x}}_d},{{\dot{y}}_d},{{\ddot{y}}_d},} \right. \nonumber \\ \left. {{e_x},{{\dot{e}}_x},{e_y},{{\dot{e}}_y},{\psi _e},{{{\dot{\psi }} }_e},{{{\dot{\psi }} }_d},{{\ddot{\psi }}_d},{\alpha _e},{{{\dot{\alpha }} }_e}} \right) \end{aligned}$$

(36)

where ${\varvec{{\beta _1}}}$ is continuous function. The surge force is designed as

$$\begin{aligned} {\tau _u} =&m_{11}^{}\left( {{{\dot{{\hat{u}}}}} - {k_6}{q_1} - {k_3}{{{\bar{u}}}_e} - \frac{{{u_e}{e_x}}}{{\sqrt{{{{\bar{u}}}_e}^2{\mathrm{+ }}\beta } }}} \right) - m_{22}^{}{{\hat{v}}_o}{{\hat{r}}_o}\nonumber \\&+ {d_{u1}}{{\hat{u}}_o} +{d_{u2}}{{\hat{u}}_o} \vert {{\hat{u}}_o}\vert - {\hat{\tau }} _{wu}^* \phi \left( {{{{\bar{u}}}_e}} \right) \end{aligned}$$

(37)

where $\phi \left( {{{{\bar{u}}}_e}} \right) = \tanh \left( {{{\bar{u}}_e}/{\iota _1}} \right)$, ${k_3}$, ${k_6}$, ${\iota _1}$ and $\beta$ are positive design parameters, and ${\hat{\tau }} _{wu}^*$ is upper bound of the external disturbance. Design the parameter adaptive law as

$$\begin{aligned} \dot{{\hat{\tau }}} _{wu}^* = {\gamma _1}\left[ {{{{\bar{u}}}_e}\phi \left( {{{{\bar{u}}}_e}} \right) - {\sigma _1}\left( {{\hat{\tau }} _{wu}^* - \tau _{wu}^0} \right) } \right] \end{aligned}$$

(38)

where ${\gamma _1}$ and ${\sigma _1}$ are the positive design parameters, and $\tau _{wu}^0$ is a prior estimation value of ${\hat{\tau }} _{wu}^*$. Substitute Eq. 37 into Eq. 32

$$\begin{aligned} {{\dot{V}}_2} =&- {k_1}e_x^2 - {k_2}e_y^2 - {k_3}{\bar{u}}_e^2 + {\alpha _e}{e_y}{\mathrm{+ }}{\mu _1} + \tau _{wu}^{\mathrm{{*}}}\nonumber \\&- {\hat{\tau }} _{wu}^*\phi \left( {{{{\bar{u}}}_e}} \right) \end{aligned}$$

(39)

where ${\mu _1} = - \displaystyle \frac{{{{\bar{u}}_e}{u_e}{e_x}}}{{\sqrt{{\bar{u}}_e^2 + \beta } }}{\mathrm{+ }}{u_e}{e_x}$.

Step 3::

Stabilizing ${\alpha _e}$. Consider the following Lyapunov function

$$\begin{aligned} {V_3} = {V_2} + \frac{1}{2}\alpha _e^2 \end{aligned}$$

(40)

The time derivative of $V_3$ is

$$\begin{aligned} {\dot{V}_3} = {\dot{V}_2} + {{\dot{\alpha }} _e}{\alpha _e} \end{aligned}$$

(41)

where ${{\dot{\alpha }} _e} = {\dot{U}}sin{\psi _e} + {U}cos{\psi _e}\left( {{{{\dot{\psi }} }_d} - {{\hat{r}}_o}} \right) - {{\dot{\alpha }}_d}$. To avoid the $\cos \left( {{\psi _e}} \right)$ appearing in the denominator when designing ${r_d}$, redefine ${\mathop {r}\limits ^{\frown }} = r\cos \left( {{\psi _e}} \right)$. Design the virtual control ${\mathop {r}\limits ^{\frown }} _{\mathrm{{d}}}$ as

$$\begin{aligned} {\mathop {r}\limits ^{\frown }}_{d} = {{\dot{\psi }} _d}\left( {\cos \left( {{\psi _e}} \right) - 1} \right) + {r_d} \end{aligned}$$

(42)

Choose the virtual control ${r_d}$ as follows:

$$\begin{aligned} {r_d} = {{\dot{\psi }} _d} + \frac{{{e_y} + {k_4}{\alpha _e} - {\dot{\alpha }_d} + {\dot{U}}sin{\psi _e}}}{{{U}}} \end{aligned}$$

(43)

In Eq. 43, $\cos \left( {{\psi _e}} \right)$ does not appear in the denominator of ${r_d}$, which avoid the influence of ${\psi _e} = \displaystyle \frac{\pi }{2}$. The error variable is defined as follows:

$$\begin{aligned} {\mathop {r}\limits ^{\frown }}_{e} = {\mathop {r}\limits ^{\frown }}- {\mathop {r}\limits ^{\frown }}_{d} \end{aligned}$$

(44)

Substitute Eq. 42 into Eq. 44, we can get

$$\begin{aligned} {\mathop {r}\limits ^{\frown }}_{e}&= {r_e}\cos \left( {{\psi _e}} \right) + \left( {\cos \left( {{\psi _e}} \right) - 1} \right) \left( {{r_d} - {{{\dot{\psi }} }_d}} \right) \nonumber \\&= {r_e}\cos \left( {{\psi _e}} \right) + \delta \end{aligned}$$

(45)

where $\delta = \left( {\cos \left( {{\psi _e}} \right) - 1} \right) \left( {{r_d} - {{{\dot{\psi }} }_d}} \right)$. Substitute Eq. 42–45 into Eq. 41

$$\begin{aligned} {{\dot{V}}_3} =&- {k_1}e_x^2 - {k_2}e_y^2 - {k_3}{\bar{u}}_e^2 - {k_4}\bar{\alpha _e}^2 + \tau _{wu}^{\mathrm{{*}}} \nonumber \\&- {\hat{\tau }} _{wu}^*\phi \left( {{{{\bar{u}}}_e}} \right) + {\mu _1} + {U}{r_e}{\alpha _e}\cos \left( {{\psi _e}} \right) + {U}{\alpha _e}\delta \end{aligned}$$

(46)

Step 4::

Consider the following Lyapunov function to stabiliz ${{\bar{r}}_e}$.

$$\begin{aligned} {V_4} = {V_3} + \frac{1}{2}{\bar{r}}_e^2 \end{aligned}$$

(47)

The time derivative of $V_4$ is

$$\begin{aligned} {{\dot{V}}_4}&= {{\dot{V}}_3} + {{{\bar{r}}}_{e}}\left( {\dot{{\hat{r}}}_o - \dot{{\hat{r}}} - {{\dot{q}}_2}} \right) \nonumber \\&= {{\dot{V}}_3} + {{{\bar{r}}}_{e}}\left\{ {\frac{1}{{{m_{33}}}}\left[ {{\tau _r} + \left( {{m_{11}} - {m_{22}}} \right) {{\hat{u}}_o}{{\hat{v}}_o}} \right. } \right. \nonumber \\&\quad \left. { - {d_{r3}}{{\hat{r}}_o}- {d_{r3}}{{\hat{r}}_o}\vert {{\hat{r}}_o}\vert + \rho \left( {{\tau _r}} \right) } \right] \left. { - \dot{{\hat{r}}} + {k_7}{q_2}} \right\} \end{aligned}$$

(48)

The yaw moment is designed as

$$\begin{aligned} {\tau _r} =&m_{33}^{}( - {k_5}{{{\bar{r}}}_e} + \dot{{\hat{r}}} - {k_7}{q_2} - \frac{{{U}{\alpha _e}{r_e}\cos {\psi _e}}}{{\sqrt{{\bar{r}}_e^2 + \beta } }})\nonumber \\&- (m_{11}^{} - m_{22}^{}){{\hat{u}}_o}{{\hat{v}}_o} + {d_{r3}}{{\hat{r}}_o}+ {d_{r3}}{{\hat{r}}_o}\vert {{\hat{r}}_o}\vert - {\hat{\tau }} _{wr}^*\phi \left( {{{{\bar{r}}}_e}} \right) \end{aligned}$$

(49)

where $\phi \left( {{{{\bar{r}}}_e}} \right) = \tan \left( {{{\bar{r}}_e}/{\iota _2}} \right)$, ${\iota _2}$, ${k_5}$ and ${k_7}$ are positive design parameters, and ${\hat{\tau }} _{wr}^*$ is upper bound of the external disturbance $\tau _{w{\mathrm{r}}}^*$.

Design parameter adaptive law as

$$\begin{aligned} \dot{{\hat{\tau }}} _{wr}^* = {\gamma _2}\left[ {{{{\bar{r}}}_e}\phi \left( {{{{\bar{r}}}_e}} \right) - {\sigma _2}\left( {{\hat{\tau }} _{wr}^* - \tau _{wr}^0} \right) } \right] \end{aligned}$$

(50)

where ${\gamma _2}$ and ${\sigma _2}$ are positive design parameters, and $\tau _{w{\mathrm{r}}}^0$ is a prior estimation of $\hat{\tau }_{w{\mathrm{r}}}^*$.

Substitute Eq. 49 into Eq. 48, we have

$$\begin{aligned} {{\dot{V}}_4} =&- {k_1}e_x^2 - {k_2}e_y^2 - {k_3}{\bar{u}}_e^2 - {k_4}\bar{\alpha _e}^2 - {k_5}\bar{r_e}^2 \nonumber \\&- {\hat{\tau }} _{wu}^*\phi \left( {{{{\bar{u}}}_e}} \right) + \tau _{wu}^{\mathrm{{*}}}- {\hat{\tau }} _{wr}^*\phi \left( {{{{\bar{r}}}_e}} \right) + \tau _{wr}^{\mathrm{{*}}}\nonumber \\&+ {U}{\alpha _e}\delta + {\mu _1} + {\mu _2} \end{aligned}$$

(51)

where ${\mu _2} = - \displaystyle \frac{{{U}{\alpha _e}{r_e}{{{\bar{r}}}_e}\cos {\psi _e}}}{{\sqrt{{\bar{r}}_e^2 + \beta } }}{\mathrm{+ }}{U}{\alpha _e}{r_e}\cos {\psi _e}$.

Remark 1

The reference [5] ignored the unavailable velocities, which did not conform with the practical engineering case. This paper introduces the nonlinear observer to estimate velocities.

Remark 2

The reference [18] did not take input saturation into account in the process of controller design. When the control inputs exceed the safe range, it will cause damage to the actuator. Therefore, this paper introduces the saturation function. At the same time, an auxiliary system is introduced to reduce the influence of input saturation.

5 System stability analysis

Theorem 1

Consider the mathematical model of underactuated ships in Eq. 1 with external disturbances and the unavailable velocities, under the control of Eq. 37 and Eq. 49 and parameter adaptive laws of Eq. 38 and Eq. 50. If the assumption 1 and 2 are satisfied, all signals in the closed-loop system are uniformly ultimately bounded (UUB) by the reasonable design of the parameters.

Proof

Consider the following Lyapunov function

$$\begin{aligned} V = {V_4} + \frac{1}{2}{{{\varvec{Y}}^{\mathrm{T}}{\varvec{Y}}}} + \frac{1}{{2{\gamma _1}}}{\tilde{\tau }} _{wu}^{*2} + \frac{1}{{2{\gamma _2}}}{\tilde{\tau }} _{wr}^{*2} \end{aligned}$$

(52)

where ${{\tilde{\tau }} ^{\mathrm{{*}}}}_{{\mathrm{wr}}} = {{\hat{\tau }} ^{\mathrm{{*}}}}_{{\mathrm{wr}}} - \tau _{{\mathrm{wr}}}^{\mathrm{{*}}}$ and ${\tilde{\tau }^{\mathrm{{*}}}}_{{\mathrm{wu}}} = {{\hat{\tau }} ^{\mathrm{{*}}}}_{{\mathrm{wu}}} - \tau _{{\mathrm{wu}}}^{\mathrm{{*}}}$ are the disturbances estimation error.

The time derivative of V is

$$\begin{aligned} \dot{V} =&{\dot{V}_4} + {{{\varvec{Y}}^{\mathrm{T}}}{{\varvec{\dot{Y}}}}} + \frac{1}{{{\gamma _1}}}\dot{{\hat{\tau }}} _{wu}^*{\tilde{\tau }} _{wu}^* + \frac{1}{{{\gamma _2}}}\dot{{\hat{\tau }}} _{wr}^*{\tilde{\tau }} _{wr}^* \end{aligned}$$

(53)

For given positive parameters $B_0$ and $I_0$, consider the following compact sets

$$\begin{aligned} \begin{array}{c} {\Omega _d} = \left\{ {\left( {{x_{\mathrm{{d}}}},{{\dot{x}}_d},{{\ddot{x}}_d},{y_{\mathrm{{d}}}},{{\dot{y}}_d},{{\ddot{y}}_d}} \right) :} \right. \\ \left. {x_d^2 + \dot{x}_d^2 + \ddot{x}_d^2 + y_d^2 + \dot{y}_d^2 + \ddot{y}_d^2 \le {B_0}} \right\} \\ {\Omega _1} = \left\{ {\left( {{e_x},{e_y},{{{\bar{u}}}_e},{\alpha _e},{{{\bar{r}}}_e},Y,{{{\tilde{\tau }} }^{\mathrm{{*}}}}_{wu},{{{\tilde{\tau }} }^{\mathrm{{*}}}}_{wr}} \right) :} \right. \left. {V \le {I_0}} \right\} \end{array} \end{aligned}$$

${\Omega _d} \times {\Omega _1}$ is also a compact set. ${\beta _1}$ on the compact set ${\Omega _d} \times {\Omega _1}$ has maximum ${N_u}$, so

$$\begin{aligned} {{{\varvec{Y}}^{\mathrm{T}}}{\varvec{\dot{{ Y}}}}} \le - \frac{{{{{\varvec{Y}}^\mathrm{T}}{{\varvec{Y}}}}}}{T} + \omega {{{\varvec{Y}}^{\mathrm{T}}}{{\varvec{Y}}}} + \frac{{N_u^2}}{{4\omega }} \end{aligned}$$

(54)

where $\omega$ is positive design parameter. Substitute Eqs. 51, 54 into Eq. 53, we have

$$\begin{aligned} \dot{V} \le&- {k_1}e_x^2 - {k_2}e_y^2 - {k_3}{\bar{u}}_e^2 - {k_4}\alpha _e^2 - {k_5}{\bar{r}}_e^2\nonumber \\&+ \tau _{wu}^*[\left| {{{{\bar{u}}}_e}} \right| - {{{\bar{u}}}_e}\phi \left( {{{{\bar{u}}}_e}} \right) ] + \tau _{wr}^*\left[ {\left| {{{{\bar{r}}}_e}} \right| - {{{\bar{r}}}_e}\phi \left( {{{{\bar{r}}}_e}} \right) } \right] \nonumber \\&+ {\sigma _1}\left( {\tau _{wu}^* - {\hat{\tau }} _{wu}^*} \right) \left( {{\hat{\tau }} _{wu}^* - \tau _{wu}^0} \right) + {U}{\alpha _e}\delta \nonumber \\&+ {\sigma _2}\left( {\tau _{wr}^* - {\hat{\tau }} _{wr}^*} \right) \left( {{\hat{\tau }} _{wr}^* - \tau _{wr}^0} \right) + {\mu _1} + {\mu _2}\nonumber \\&- \left( {\frac{1}{T} - \omega } \right) {{{\varvec{Y}}^{\mathrm{T}}}{{\varvec{Y}}} }+ \frac{{N_u^2}}{{4\omega }} + 1 \end{aligned}$$

(55)

Consider the following inequalities

$$\begin{aligned} \begin{array}{c} \left( {\tau _{wu}^* - {\hat{\tau }} _{wu}^*} \right) \left( {{\hat{\tau }} _{wu}^* - \tau _{wu}^0} \right) \\ \le - \displaystyle \frac{1}{2}{\left( {{\hat{\tau }} _{wu}^* - \tau _{wu}^*} \right) ^2} + \displaystyle \frac{1}{2}{\left( {\tau _{wu}^* - \tau _{wu}^0} \right) ^2} \end{array} \end{aligned}$$

(56)

Similarly,

$$\begin{aligned} \begin{array}{c} \left( {\tau _{wr}^* - {\hat{\tau }} _{wr}^*} \right) \left( {{\hat{\tau }} _{wr}^* - \tau _{wr}^0} \right) \\ \le - \frac{1}{2}{\left( {{\hat{\tau }} _{wr}^* - \tau _{wr}^*} \right) ^2} + \displaystyle \frac{1}{2}{\left( {\tau _{wr}^* - \tau _{wr}^0} \right) ^2} \end{array} \end{aligned}$$

(57)

Applying the lemma of [27], for any ${\varepsilon _j} > 0$, ${\varpi _j} \in {\mathrm{R}}\left( {j = 1,2} \right)$, there is $0 \le \left| {{\varpi _j}} \right| - {\varpi _j}\tan \left( {{\varpi _j}/{\varepsilon _j}} \right) \le 0.2785{\varepsilon _j}.$

Substitude Eqs. 56, 57 into Eq. 55, we can get

$$\begin{aligned} \dot{V} \le&- {k_1}e_x^2 - {k_2}e_y^2 - {k_3}{\bar{u}}_e^2 - {k_4}\alpha _e^2 - {k_5}{\bar{r}}_e^2\nonumber \\&- \left( {\frac{1}{T} - \omega } \right) {{{\varvec{Y}}^{\mathrm{T}}}{\varvec{Y}}} - \frac{{{\sigma _1}}}{2}{\left( {{\hat{\tau }} _{wu}^* - \tau _{wu}^*} \right) ^2}\nonumber \\&- \frac{{{\sigma _2}}}{2}{\left( {{\hat{\tau }} _{wr}^* - \tau _{wr}^*} \right) ^2}+ 0.2785{\varepsilon _1}\tau _{wu}^* + 0.2785{\varepsilon _2}\tau _{wr}^*\nonumber \\&+ \frac{{{\sigma _1}}}{2}{\left( {\tau _{wu}^* - \tau _{wu}^0} \right) ^2} + \frac{{{\sigma _2}}}{2}{\left( {\tau _{wr}^* - \tau _{wr}^0} \right) ^2}\nonumber \\&+ \frac{{N_u^2}}{{4\omega }} + {U}{\alpha _e}\delta + {\mu _1} + {\mu _2} + 1\nonumber \\&= - \mu V + C \end{aligned}$$

(58)

where

$$\begin{aligned} \begin{array}{c} \mu = \min \left\{ {2{k_1},2{k_2},2{k_3},2{k_4},2{k_5},} \right. \\ \left. {2\left( {1/T - \omega } \right) ,{\sigma _1},{\sigma _2}} \right\} \end{array} \end{aligned}$$

$$\begin{aligned} C =\;&0.2785{\varepsilon _1}\tau _{wu}^* + 0.2785{\varepsilon _2}\tau _{wr}^* \\&+ \frac{{{\sigma _1}}}{2}{\left( {\tau _{wu}^* - \tau _{wu}^0} \right) ^2}+ \frac{{{\sigma _2}}}{2}{\left( {\tau _{wr}^* - \tau _{wr}^0} \right) ^2}\\&+ \frac{{N_u^2}}{{4{\omega }}} + {U}{\alpha _e}\delta + {\mu _1} + {\mu _2} + 1 \\&\left( {1/T - \omega } \right)> 0,2{k_3} - 1> 0,2{k_5} - 1 > 0 \end{aligned}$$

So

$$\begin{aligned} 0 \le V\left( t \right) \le \frac{C}{\mu } + \left[ {V\left( 0 \right) - \frac{C}{\mu }} \right] {e^{ - \mu t}} \end{aligned}$$

(59)

From Eq. 59, it gives

$$\begin{aligned} \mathop {\lim }\limits _{t \rightarrow \infty } V = \frac{C}{\mu } \end{aligned}$$

(60)

Eq. 60 means that the upper bound of ${V}\left( t \right)$ convergence value is ${C}/{\mu }$. According to Eq. 55, the ship control system signals ${e_x}$, ${e_{\mathrm{{y}}}}$, ${{\bar{u}}_e}$, ${\alpha _e}$, ${{\bar{r}}_e}$, ${\varvec{Y}}$, ${\tilde{\tau }} _{wu}^*$, ${\tilde{\tau }} _{wr}^*$ are uniformly ultimately bounded (UUB). Thus, ${x_e}$ and ${y_e}$ are bounded, which can determine all error signals in the closed-loop system are UUB. $\square$

6 Simulation results

In this section, we carry out the simulations of the circular and sine trajectories to demonstrate the effectiveness of the designed controller by a ship named “BAY CLASS” [32]. The ship has a length of 38 m, a mass of $m = 118 \times {10^3}\mathrm{kg}$ ,and other parameters are shown in Table 1. The control parameters are shown in Table 2.

Table 1 Model parameters of ship simulation

Table 2 Control parameters of ship simulation

The force and moment of external environmental disturbances are taken as:

$$\begin{aligned} \left[ {\begin{array}{*{20}{c}} {{\tau _{wu}}}\\ {{\tau _{wv}}}\\ {{\tau _{wr}}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {1 \times {{10}^5}\left( {\sin \left( {0.2t} \right) + \cos \left( {0.5t} \right) } \right) }\\ {1 \times {{10}^2}\left( {\sin \left( {0.1t} \right) + \cos \left( {0.4t} \right) } \right) }\\ {1 \times {{10}^6}\left( {\sin \left( {0.5t} \right) + \cos \left( {0.3t} \right) } \right) } \end{array}} \right] \end{aligned}$$

To further illustrate the superiority of the proposed method, we evaluated the tolerance of the algorithm to noise velocity of measurement, the ship’s velocity with measurement noise is $\upsilon = \upsilon + \Xi$, where the power of band-limited white noise $\Xi$ is ${\left[ {0.01,0.001,0.001} \right] ^{\mathrm{{T}}}}$ and its sample time is set as ${\left[ {0.1,0.1,0.5} \right] ^\mathrm{{T}}}$. In this case, we performed simulations with the same control parameters and initial conditions. Furthermore, simulation comparisons are taken with the benchmark method (without nonlinear observer and input saturation).

6.1 Simulation of circular trajectory

Set the desired trajectory: ${x_d}{\mathrm{= }}300{\mathrm{*}}\sin \left( {0.03t} \right)$, ${y_d}{\mathrm{= }}300$ ${\mathrm{*}}\sin \left( {0.03t} \right)$. The initial values of the ship are given to be x(0)=0m, y(0)=0m, $\psi$=0.3rad, u(0)=0m/s, v(0)=0m/s, r(0)=0rad/s.

Fig. 2

Actual and desired trajectories of ship in xy-plane

Fig. 3

The curves of ship position

Fig. 4

The surge, sway and yaw velocities of ship

Fig. 5

The comparison curves of control inputs

Fig. 6

External environmental disturbances and its upper bound

Fig. 2 shows the simulation diagram of circular trajectory tracking and Fig. 3 shows the position of the ship. We can see from the two figures that the proposed method enables the ship to accurately track the desired trajectory. However, the ship of the comparison method without the nonlinear observer is shifted during tracking due to measurement noise interference. Fig. 4 shows the real values, the actual measurements, and the observer estimation values of ship velocities. From the figure, it can be obtained that due to the influence of the measurement noise, the measurements of velocities without the nonlinear observer produces a large error, which affects the tracking accuracy of the ship. However, the proposed method can suppress the noise very well and the velocities estimates are very accurate. From Fig. 5, we can see the comparison curves of control laws. In the early stages of tracking, the control inputs of the proposed method satisfies the input saturation. Therefore, the effectiveness of the designed compensation system can be seen in the fact that the system is still stable in the presence of input saturation. However, the control inputs of the compared methods without the nonlinear observer does not meet the input saturation requirement and the control input varies considerably due to noise, which tends to increase the physical losses of the actuator. Fig. 6 illustrates the upper bound estimation of external disturbances. we can see that the upper bound of the disturbances is well approximated by the proposed method, but the comparison method has a large deviation in the approximation process due to the noise. Thus the designed controller has great robustness against the external disturbances.

6.2 Sine tracking simulation

To further demonstrate the effectiveness of the designed controller in this paper, the circular trajectory is changed to the sine trajectory: ${x_d}=3\mathrm {*}t$, ${y_d}=200\mathrm {*}\sin \left( {0.03t}\right)$. The initial values of the ship are given to be x(0)=0m, y(0)=0m, $\psi$=0rad, u(0)=0m/s, v(0)=0m/s, r(0)=0rad/s.

Fig. 7

Actual and desired trajectories of ship in xy-plane

Fig. 8

The curves of ship position

Fig. 9

The surge, sway and yaw velocities of ship

Fig. 10

The comparison curves of control inputs

Fig. 11

External environmental disturbances and its upper bound

In Fig. 7 and Fig. 8, the simulation diagram of sine trajectory tracking and ship positions are shown. We can see from the two figures that the proposed method enables the ship to accurately track the desired trajectory. However, the ship of the comparison method without the nonlinear observer is shifted during tracking due to the measurement noise interference. From Fig. 9, we can see the real values, the actual measurements, and the observer estimation values of ship velocities. It can be obtained that due to the influence of the measurement noise, the measurements of velocities without the nonlinear observer produce a large error, which affects the tracking accuracy of the ship. However, the proposed method can suppress the noise very well and the velocities estimates are very accurate. Fig. 10 shows the comparison curves of control laws. In the early stages of tracking, the control inputs of the proposed method satisfies the input saturation. Therefore, the effectiveness of the designed compensation system can be seen in the fact that the system is still stable in the presence of input saturation. However, the control inputs of the compared methods without the nonlinear observer do not meet the input saturation requirement and the control input varies considerably due to noise, which tends to increase the physical losses of the actuator. In Fig. 11, we can see that the upper bound of the disturbances is well approximated by the proposed method, but the comparison method has a large deviation in the approximation process due to the noise. Thus the designed controller has a great robustness against the external disturbances.

7 Conclusion

Aiming at the trajectory tracking control problem of the underactuated ship with input saturation, an adaptive output feedback DSC trajectory tracking controller is designed in this paper. The control laws are designed by the backstepping technique which stabilizes the position errors and velocity errors in the body-fixed frame. Through the Lyapunov stability theory, all error signals in the control laws are UUB. Using the “BAY CLASS” patrol boat as the controlled object, the trajectory tracking simulations are performed for both circular and sine trajectories. The simulation results show that the designed controller has strong robustness to the external disturbances by introducing the adaptive technique. The observer is designed with a nonlinear gain function to estimate unavailable velocities, which can effectively resolve the contradiction between the dynamic quality and control accuracy of the system. The DSC technique is employed which can reduce the computational complexity of the control algorithm. Furthermore, both hyperbolic tangent function and auxiliary system are used to deal with input saturation, which can provide effective theoretical guidance for engineering practice. In the following study, we will consider the error-constrained problem of the ship and limit the position and velocity errors of the ship to allow for accurate tracking.