Bifurcation of a modified railway wheelset model with nonlinear equivalent conicity and wheel–rail force

Abstract

This paper presents the bifurcation behaviors of a modified railway wheelset model to explore its instability mechanisms of hunting motion. Equivalent conicity data measured from China high-speed railway vehicle are used to modify the wheelset model. Firstly, the relationships between longitudinal stiffness, lateral stiffness, equivalent conicity and critical speed are taken into account by calculating the real parts of the eigenvalues of the Jacobian matrix and Hurwitz criterion for the corresponding linear model. Secondly, measured equivalent conicity data are fitted by a nonlinear function of the lateral displacement rather than are considered as a constant as usual. Nonlinear wheel–rail force function is used to describe the wheel–rail contact force. Based on these modifications, a modified railway wheelset model with nonlinear equivalent conicity and wheel–rail force is set up, and then, some instability mechanisms of China high-speed train vehicle are investigated based on Hopf bifurcation, fold (limit point) bifurcation of cycles, cusp bifurcation of cycles, Neimark–Sacker bifurcation of cycles and 1:1 resonance. In particular, fold bifurcation of cycles can produce a vast effect on the hunting motion of the modified wheelset model. One of the main reasons leading to hunting motion is due to the fold bifurcation structure of cycles, in which stable limit cycles and unstable limit cycles may coincide, and multiple nested limit cycles appear on a side of fold bifurcation curve of cycles. Unstable hunting motion mainly depends on the coexistence of equilibria and limit cycles and their positions; if the most outward limit cycle is stable, then the motion of high-speed vehicle should be safe in a reasonable range. Otherwise, if the initial values are chosen near the most outward unstable limit cycle or the system is perturbed by noises, the high-speed vehicle will take place unstable hunting motion and even lead to serious train derailment events. Therefore, in order to control hunting motions, it may be the easiest way in theory to guarantee the coexistence of the inner stable equilibrium and the most outward stable limit cycle in a wheelset system.

1 Introduction

Hunting motion is a kind of self-excited vibration of wheelset, bogie or carbody, and it is a dynamic combination of lateral movement and yaw rotation [1, 2]. The occurrence of hunting motion often depends on multiple factors such as speed, stiffness and damping of the spring, wheel tread slope, creepage and other parameters [2,3,4,5,6]. Among them, the critical speed is defined by a critical point, where the real parts of a pair of eigenvalues of ordinary differential equations (ODEs) are zero; meanwhile, the real parts of the other eigenvalues are negative. In other words, this critical threshold of hunting motion is defined by Hopf bifurcation of nonlinear ODEs [1, 7]. Above those thresholds, the motion can increase the load of vehicle components, damage tracks and wheels and potentially cause derailment [8, 9]. Analyzing the bifurcations about hunting motion of a modified railway wheelset system based on varying lateral parameters helps ones to understand the complex dynamical behaviors of wheelset when it is in the process of high-speed running.

Over the past decades, some numerical simulation software, such as SIMPACK, has been applied to calculate critical speed, vibration frequency, amplitude and stable/unstable limit cycles of a bogie frame under different conditions [10]. The equivalent relation between limit cycles and safety limits is mainly discussed by numerical simulations in [11].

Bogoliubov averaging method is used to deal with the hunting oscillatory problem [12, 13]. Ahmadian et al. studies Hopf bifurcations and concludes that the critical hunting speed from the nonlinear analysis is less than the linear critical speed [12]. The nonlinearities in the primary suspension and flange contact may contribute significantly to the hunting behaviors. In [13], Hopf bifurcation is studied in a bogie model, in which nonlinear yaw damper and lateral wheel/rail contact are considered. Their research shows that yaw stiffness has a major effect on hunting velocity, and more gauge clearance and increasing the rail lateral stiffness can reduce the hunting amplitude. In addition, averaging method is used to obtain the amplitude of the limit cycle.

Fig. 1

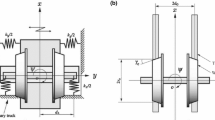
Sketch map of wheelset and part of parameters revised based on [22]

Stability analyses of nonconservative mechanical systems are developed in engineering [14, 15]. The center manifold theorem and the normal form theory are the bases of analyzing stability and bifurcation of high-dimensional discrete and continuous-time nonlinear systems [16, 17]. The Hopf bifurcations of a semi-carbody and a bogie system are discussed in [18]. The supercritical and subcritical Hopf bifurcations are distinguished by the first Lyapunov coefficient $\hbox {Re}(c_1(0))$, and numerical shooting method is used to verify their theoretical results. A lateral direction model of a railway wheelset with two degrees of freedom is taken into account in [19]. Therein, the center manifold theory is used to simplify the dimensionality of the system, and the normal form theory is used to derive a symbolic expression of a parameter, which can also be used to determine the Hopf bifurcation type. Their results show that the lateral linear stiffness has two effects on the critical speed and the nonlinear stability against disturbance. In [20], a two-parameter bifurcation analysis of limit cycles of a simplified railway wheelset model is investigated. Some complex instability mechanisms of wheelset are explored like the supercritical and subcritical Hopf bifurcation, general Hopf bifurcation, period-doubling bifurcation and Neimark–Sacker bifurcation of cycles.

For the conical tread, the wheelset tread can be regarded as a cone before contacting the two sides of rail. Thus, the tread slope is usually considered a constant. But for the worn profile tread or the wheel–rail contact point out of the straight line section of the tread, the equivalent conicity of the wheelset, i.e., the slope of the taper tread, is no longer a constant. It is correlated with the lateral displacement of the wheelset. In view of these points, one of the main contributions of this paper is to fit a nonlinear function to describe the equivalent conicity varying with lateral displacement based on the real data from China high-speed train vehicle. Therefore, some new more complex instability mechanisms of wheelset system can be revealed compared with the system with a constant equivalent conicity of wheelset. The wheel–rail contact force is another important effect related to lateral displacement between flange and track. There exists a gap between them. The wheel–rail contact force states that the rail will push against the wheel by the rail lateral stiffness if the flange contacts a side of track because of lateral displacement.

In particular, the novelty of this paper is to present the instability mechanisms of this modified system with a nonlinear equivalent conicity function, that is, the stable equilibrium loses its stability via a Hopf bifurcation. And then, Hopf bifurcation curve is divided into a supercritical branch and a subcritical branch by a generalized Hopf bifurcation point, and the stable and the unstable limit cycles appear, respectively. The detailed fold bifurcation of cycles and cusp bifurcation of cycles, Neimark–Sacker bifurcation of cycles and 1:1 resonance points are detected by numerical simulation on a two-parameter plane, respectively. These results show that the instability mechanism of China high-speed train vehicle is mainly due to the interaction among multiple interwinded stable limit cycles and unstable limit cycles. In order to control the hunting motion, the easiest way in theory is to guarantee the coexistence of stable equilibrium and stable limit cycle in a wheelset system. The numerical simulations in this paper are mainly carried out by the software package MATCONT [20, 21].

The layout of this paper is as follows: In Sect. 2, the effects of lateral stiffness, longitudinal stiffness and equivalent conicity on critical speed are discussed in linear wheelset model. In Sect. 3, firstly, the nonlinear equivalent conicity function associated with lateral displacement is introduced. Secondly, on the parameter plane of longitudinal stiffness and speed, the critical instability mechanism is discussed by using the supercritical (subcritical) Hopf bifurcation, limit point bifurcation of cycles and cusp bifurcation of cycles. Thirdly, lateral stiffness is taken into account, and the related Neimark–Sacker bifurcation of cycles and 1:1 resonance points are detected by numerical simulation. And finally, Sect. 4 concludes this paper.

2 The stability of the linear wheelset model

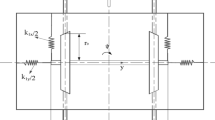
Figure 1a, b shows the top view of the wheelset, the springs and the steel rails. The origin O is located at the geometrical center of the wheelset. The coordinate x denotes the direction along the train running. The direction of right movement of the wheelset is defined as the positive direction of the y-axis. The z-axis that is not drawn is perpendicular to the horizontal plane of the track.

2.1 Linear wheelset model

By Newton’s the second law in translational motion and rotation direction, respectively, the model can be expressed as the following form [23]:

$$\begin{aligned} \left\{ \begin{array}{l} m\frac{\mathrm{d}^2y}{\mathrm{d}t^2}=-\,\frac{2\kappa _y}{v}\frac{\mathrm{d}y}{\mathrm{d}t}-K_x\left( \frac{l_0}{l_1}-1\right) y\\ -K_yy+2\kappa _y\psi ,\\ I\frac{\mathrm{d}^2\psi }{\mathrm{d}t^2}=-\,\frac{2d_0^2\kappa _x}{v}\frac{\mathrm{d}\psi }{\mathrm{d}t}-\frac{2d_0\kappa _x\lambda }{r_0}y-K_xd_1^2\psi , \\ \end{array} \right. \end{aligned}$$

(1)

where the variable y is the lateral displacement and $\psi$ is the yaw angle. The physical significance and values of the parameters are listed in Table 1. All the values of parameters are positive. The longitudinal (lateral) stiffness $K_x$ ($K_y$) includes the longitudinal (lateral) stiffness of primary springs and the nodal point longitudinal (lateral) stiffness of axle box rotary arm. Linear Carter theory is used to calculate the creep coefficient in order to eliminate its nonlinear effect. The vertical springs in this system are in a compression state because the weights of the car body and the bogie are on them.

Table 1 Values of the parameters in this paper

Equation (1) can be written in a matrix form:

$$\begin{aligned} \mathbf {M}\ddot{\mathbf {y}}+\mathbf {C}{\dot{\mathbf {y}}}+\mathbf {Ky}=0, \end{aligned}$$

(2)

where

$$\begin{aligned} {\mathbf {M}}= & {} \left( \begin{array}{cc} m &{} 0\\ 0 &{} I\\ \end{array} \right) , {\mathbf {C}}= \left( \begin{array}{cc} \frac{2\kappa _y}{v} &{} 0\\ 0 &{} \frac{2d_0^2\kappa _x}{v}\\ \end{array} \right) ,\\ {\mathbf {K}}= & {} \left( \begin{array}{cc} K_x\left( \frac{l_0}{l_1}-1\right) +K_y &{} -2\kappa _y\\ \frac{2d_0\kappa _x\lambda }{r_0} &{} K_xd_1^2\\ \end{array} \right) , {\mathbf {y}}= \left( \begin{array}{cc} y\\ \psi \\ \end{array} \right) . \end{aligned}$$

Let $x_1=y$, $x_2={\dot{y}}$, $x_3=\psi$, $x_4={\dot{\psi }}$, then Eq. (1) becomes

$$\begin{aligned} \left\{ \begin{array}{l} \dot{x_1}=x_2, \\ \dot{x_2}=-\,\frac{K_x}{m}\left( \frac{l_0}{l_1}-1\right) x_1-\frac{K_y}{m}x_1\\ \qquad \quad -\frac{2\kappa _y}{mv}x_2+\frac{2\kappa _y}{m}x_3,\\ \dot{x_3}=x_4, \\ \dot{x_4}=-\,\frac{2d_0\kappa _x\lambda }{Ir_0}x_1-\frac{K_xd_1^2}{I}x_3-\frac{2d_0^2\kappa _x}{Iv}x_4.\\ \end{array} \right. \end{aligned}$$

(3)

where $x_1=y$ is the lateral displacement of the wheelset, $x_2={\dot{y}}$ is the velocity of lateral motion, $\dot{x_2}$ is the acceleration of lateral motion, $x_3=\psi$ is the yaw angle of wheelset, $x_4={\dot{\psi }}$ is the angular velocity of yaw motion, and $\dot{x_4}$ is the angular acceleration. In this paper, we use $V~{(\hbox {km}/\hbox {h})}$ to show the speed in figures.

The Jacobian matrix of Eq. (3) at the unique equilibrium origin O is given by

$$\begin{aligned} J_O=\left( \begin{array}{cccc} 0 &{} 1 &{} 0 &{} 0\\ d_{21} &{} d_{22} &{} d_{23} &{} 0 \\ 0 &{} 0 &{} 0 &{} 1\\ d_{41} &{} 0 &{} d_{43} &{} d_{44}\\ \end{array} \right) , \end{aligned}$$

(4)

where

$$\begin{aligned} d_{21}= & {} -\,\frac{K_x}{m}\left( \frac{l_0}{l_1}-1\right) -\frac{K_y}{m}, d_{22} =-\,\frac{2\kappa _y}{mv}, d_{23}=\frac{2\kappa _y}{m},\\ d_{41}= & {} -\,\frac{2d_0\kappa _x\lambda }{Ir_0}, d_{43}=-\,\frac{K_xd_1^2}{I}, d_{44}=-\,\frac{2d_0^2\kappa _x}{Iv}. \end{aligned}$$

and $d_{21}, d_{22}, d_{41}, d_{43}, d_{44}<0$, $d_{23}>0$. The eigenvalues of Eq. (4) $\mu _i$ satisfy:

$$\begin{aligned}&\mu _i^4-(d_{22}+d_{44})\mu _i^3-(d_{21}+d_{43}-d_{22}d_{44})\mu _i^2\nonumber \\&\quad +\,(d_{21}d_{44}+d_{22}d_{43})\mu _i+d_{21}d_{43}-d_{23}d_{41}=0,\nonumber \\&\qquad ~(i=1,2,3,4). \end{aligned}$$

(5)

Then, the stability of the wheelset system can be described by the following description [16, 17]:

For a linear wheelset system ${\dot{X}}=F(X)$, $X \in R^4$, if the characteristic polynomial has two pairs of complex roots $\mu _{1,2}=\alpha _{1}\pm i\omega _1$, $\mu _{3,4}=\alpha _{2}\pm i\omega _2$, and $\alpha _1<\alpha _2$, $\omega _i\ne 0$, $\alpha _i,\omega _i\in R ~(i=1,2)$,

Case 1: If $\alpha _1,\alpha _2<0$, then the system is exponentially stable;

Case 2: If $\alpha _1<0$ and $\alpha _2=0$, then the system is at a critical condition between stability and instability;

Case 3: If $\alpha _2>0$, then the system is strictly unstable.

Remark 1

A linear system is stable only when all the real parts of eigenvalues are negative. The imaginary parts of eigenvalues show the rates of rotation. If the wheelset system is nonlinear, then Case 2 is a necessary condition of Hopf bifurcation. Hopf bifurcation and other codimension-one/two bifurcations show the critical instability mechanisms of hunting motion form the point of mathematical model.

2.2 Critical speeds calculated by linear wheelset model

Fig. 2

The $\lambda -V$ parameter planes when we fix a $K_y=8.96~\hbox {MN}/\hbox {m}$, and $K_x=2.96,4.96,6.96,8.96~\hbox {MN}/\hbox {m}$; and b $K_x=8.96~\hbox {MN}/\hbox {m}$, $K_y=2.96,8.96,14.96,20.96~\hbox {MN}/\hbox {m}$, respectively. c, d show evolving eigenvalues $\mu _{3,4}=\alpha _{2} \pm i\omega _2$ when the parameter V varies near the critical points, $\lambda =0.1271$ and the stiffness parameters are the same as those in a, b (the other pair of eigenvalues that have smaller real parts are not shown in this paper). (Color figure online)

Fig. 3

a1, a2 Phase diagrams of the limit cycle when $x_0=(0.01,0.05,0.007,0.5)$, $K_x=8.96~\hbox {MN}/\hbox {m}$, $K_y=8.96~\hbox {MN}/\hbox {m}$, $V_0=536.634923~\hbox {km}/\hbox {h}$; b1–b4 show the stable equilibrium when $K_x=8.96~\hbox {MN}/\hbox {m}$, $K_y=8.96~\hbox {MN}/\hbox {m}$, $V_-=520~\hbox {km}/\hbox {h}$; c1–c4 Waveforms corresponding to a1, a2, d1–d4 describe the unstable equilibrium when $K_x=8.96~\hbox {MN}/\hbox {m}$, $K_y=8.96~\hbox {MN}/\hbox {m}$, $V_+=550~\hbox {km}/\hbox {h}$. (Color figure online)

The critical speed of train operation is defined by the boundary point between the positive and the negative real parts of eigenvalues of linear ordinary differential equation. Figure 2a, b shows critical speed curves under seven stiffness conditions. The red curves in Fig. 2a, b are the same. For Fig. 2a, we fix $K_y=8.96~\hbox {MN}/\hbox {m}$ and make $K_x=2.96,4.96,6.96,8.96~\hbox {MN}/\hbox {m}$ to judge the effect of longitudinal stiffness on the critical speed. For Fig. 2b, we fix $K_x=8.96~\hbox {MN}/\hbox {m}$ and make $K_y=2.96,8.96,14.96,20.96~\hbox {MN}/\hbox {m}$ to judge the effect of lateral stiffness on the critical speed. For each curve in Fig. 2a, b, the equilibria on the curve correspond to closed curves, on which $x_1$, $x_2$, $x_3$ and $x_4$ oscillate at a constant amplitude and frequency. Take $(K_x,K_y,\lambda )=(8.96,8.96,0.1271)$ (a point on the red curve in Fig. 2a) as an example, the phase diagrams in $x_1-x_2$ and $x_1-x_3$ are in Fig. 3a1, a2. The phase diagram in $x_3-x_4$ has the same closed curve as in $x_1-x_2$. The waveforms are shown in Fig. 3c1–c4 when the initial point is chosen as $x_0=(0.01,0.05,0.007,0.5)$, and the eigenvalues corresponding to the critical point $V_0=536.634923~\hbox {km}/\hbox {h}$ (the green $*$ in Fig. 2a) are as follows:

$$\begin{aligned} \mathbf {\mu }(V_0)= & {} \left( \begin{array}{cccc} \mu _{1}(V_0)\\ \mu _{2}(V_0)\\ \mu _{3}(V_0)\\ \mu _{4}(V_0)\\ \end{array} \right) =\left( \begin{array}{cccc} -\,61.5026\\ -\,61.5026\\ 0\\ 0\\ \end{array} \right) \nonumber \\&+\,i\left( \begin{array}{cccc} 90.8747\\ -\,90.8747\\ 89.7127\\ -\,89.7127\\ \end{array} \right) . \end{aligned}$$

(6)

The real parts of the third and the fourth eigenvalues increase to 0. The equilibria corresponding to the parameters below a curve are stable, and it implies that the wheelset can be stabilized to the origin in a limited time if an initial lateral or yaw displacement/angle, speed and acceleration are given in a reasonable range. Stable equilibria are shown in Fig. 3b1–b4 when $V_-=520~\hbox {km}/\hbox {h}$ (the blue $*$ in Fig. 2a). And for Fig. 3d1–d4 when $V_+=550~\hbox {km}/\hbox {h}$ (the red $*$ in Fig. 2a), the equilibria of the upper curve are unstable. In the above three cases, the vibration frequencies of wheelset are all about 14 Hz.

There are two pairs of eigenvalues $\mu _{1,2}=\alpha _{1}\pm i\omega _1$, $\mu _{3,4}=\alpha _{2}\pm i\omega _2$ ($\alpha _1<\alpha _2$, $\omega _i\ne 0$) in this wheelset system. We show evolving eigenvalues $\mu _{3,4}=\alpha _{2} \pm i\omega _2$ in Fig. 2c, d when the parameter V varies near the critical points, $\lambda =0.1271$ and the stiffness parameters are the same as those in Fig. 2a, b. Once $\hbox {Re}(\mu _{3,4})=0$, the critical speeds are obtained, accordingly: $V_0=536.634923$ (red), 476.872437 (blue),428.155705 (magenta) and $384.701298~\hbox {km}/\hbox {h}$ (green) in Fig. 2c; $V_0=554.296633$ (dark blue), 536.634923 (red), 565.303816 (cyan) and $635.487135~\hbox {km}/\hbox {h}$ (purple) in Fig. 2d, respectively.

Figure 2a, b also implies that: (1) For each curve at its condition, the critical speed decreases with a ratio inversely proportional to the equivalent conicity. (2) Under the same equivalent conicity, the critical speed increases evenly with the increase in longitudinal stiffness at a fixed lateral stiffness as in Fig. 2a. (3) If the longitudinal stiffness is fixed as shown in Fig. 2b, the critical speed increases with the increase in the lateral stiffness for $\lambda >0.17$. When $\lambda <0.17$, four curves intersect as the following laws: Among the four curves, the curve with the minimum critical speed (i.e., the curve on the bottom of the four curves) is cyan, red and blue curves, respectively, as the equivalent conicity increases. It shows that the larger the equivalent conicity, the smaller the critical speed and the smaller the lateral stiffness required for instability. Taking the dark blue curve ($K_y=2.96~\hbox {MN}/\hbox {m}$) as a reference, the intersection points of the dark blue one and the red ($K_y=8.96~\hbox {MN}/\hbox {m}$), the cyan ($K_y=14.96~\hbox {MN}/\hbox {m}$), the purple ($K_y=20.96~\hbox {MN}/\hbox {m}$) ones turn left sequentially. It demonstrates that the minimum lateral stiffness $K_y=2.96~\hbox {MN}/\hbox {m}$ will gradually turn from the worst to the best stiffness condition as the equivalent conicity decreases. In other words, the wheelsets have the lowest critical speed when $\lambda >0.16$, and the wheelsets have the highest critical speed when $\lambda <0.08$.

Proposition

At the critical curves, the relationship between $\lambda$ and other parameters is:

$$\begin{aligned} \lambda= & {} \left( r_0I^2K_x^2d_0^2\kappa _x\kappa _yl_0^2v^2-2r_0I^2K_x^2d_0^2\kappa _x\kappa _yl_0l_1v^2 \right. \nonumber \\&+\,r_0I^2K_x^2d_0^2\kappa _x\kappa _yl_1^2v^2+2r_0I^2K_xK_yd_0^2\kappa _x\kappa _yl_0l_1v^2\nonumber \\&-\,2r_0I^2K_xK_yd_0^2\kappa _x\kappa _yl_1^2v^2+r_0I^2K_y^2d_0^2\kappa _x\kappa _yl_1^2v^2\nonumber \\&-\,2r_0IK_x^2d_0^2d_1^2\kappa _x\kappa _yl_0l_1mv^2\nonumber \\&+\,2r_0IK_x^2d_0^2d_1^2\kappa _x\kappa _yl_1^2mv^2\nonumber \\&-\,2r_0IK_xK_yd_0^2d_1^2\kappa _x\kappa _yl_1^2mv^2+4r_0IK_xd_0^4\kappa _x^2\kappa _y^2l_0l_1\nonumber \\&-\,4r_0IK_xd_0^4\kappa _x^2\kappa _y^2l_1^2+4r_0IK_xd_0^2d_1^2\kappa _x\kappa _y^3l_1^2\nonumber \\&+\,4r_0IK_yd_0^4\kappa _x^2\kappa _y^2l_1^2+r_0K_x^2d_0^2d_1^4\kappa _x\kappa _yl_1^2m^2v^2\nonumber \\&+\,4r_0K_xd_0^6\kappa _x^3\kappa _yl_0l_1m-4r_0K_xd_0^6\kappa _x^3\kappa _yl_1^2m\nonumber \\&+\,4r_0K_xd_0^4d_1^2\kappa _x^2\kappa _y^2l_1^2m\nonumber \\&+\left. \,4r_0K_yd_0^6\kappa _x^3\kappa _yl_1^2m\right) /\left( 4I^2d_0\kappa _x\kappa _y^3l_1^2v^2 \right. \nonumber \\&+\left. \,8Id_0^3\kappa _x^2\kappa _y^2l_1^2mv^2+4d_0^5\kappa _x^3\kappa _yl_1^2m^2v^2\right) . \end{aligned}$$

(7)

Proof

Let $a_0=1$, $a_1=-(d_{22}+d_{44})$, $a_2=-(d_{21}+d_{43}-d_{22}d_{44})$, $a_3=d_{21}d_{44}+d_{22}d_{43}$, $a_4=d_{21}d_{43}-d_{23}d_{41}$ in Eq. (5). Then,

$$\begin{aligned} \begin{array}{{l@{~}l}} \Delta _1&{}=a_1=-(d_{22}+d_{44}), \\ \Delta _2&{}=\left| \begin{array}{cccc} a_1 &{} a_0 \\ a_3 &{} a_2 \end{array}\right| = \left| \begin{array}{cccc} -(d_{22}+d_{44}) &{} 1 \\ d_{21}d_{44}+d_{22}d_{43} &{} -(d_{21}+d_{43}-d_{22}d_{44}) \end{array}\right| \\ &{} = d_{21}d_{22}+d_{43}d_{44}-d_{22}^2d_{44}-d_{22}d_{44}^2, \\ \Delta _3&{}=\left| \begin{array}{cccc} a_1 &{} a_0 &{} 0 \\ a_3 &{} a_2 &{}a_1 \\ G0 &{} a_4 &{}a_3 \\ \end{array}\right| = \left| \begin{array}{cccc} -(d_{22}+d_{44}) &{} 1 &{} 0 \\ d_{21}d_{44}+d_{22}d_{43} &{} -(d_{21}+d_{43}-d_{22}d_{44}) &{} -(d_{22}+d_{44}) \\ 0 &{} d_{21}d_{43}-d_{23}d_{41} &{} d_{21}d_{44}+d_{22}d_{43} \\ \end{array} \right| \\ &{}=d_{21}^2d_{22}d_{44}-d_{21}d_{22}^2d_{44}^2-2d_{21}d_{22}d_{43}d_{44}-d_{21}d_{22}d_{44}^3-d_{22}^3d_{43}d_{44}-d_{22}^2d_{43}d_{44}^2\\ &{}\quad +\,d_{23}d_{41}d_{22}^2+d_{22}d_{43}^2d_{44}+2d_{23}d_{41}d_{22}d_{44}+d_{23}d_{41}d_{44}^2,\\ \Delta _4&{}=\left| \begin{array}{cccc} a_1 &{} a_0 &{} 0 &{} 0 \\ a_3 &{} a_2 &{}a_1 &{} a_0 \\ 0 &{} a_4 &{} a_3 &{} a_2 \\ 0 &{} 0 &{} 0 &{} a_4 \\ \end{array}\right| \\ &{}=\left| \begin{array}{cccc} -(d_{22}+d_{44}) &{} 1 &{} 0 &{} 0 \\ d_{21}d_{44}+d_{22}d_{43} &{} -(d_{21}+d_{43}-d_{22}d_{44}) &{} -(d_{22}+d_{44}) &{} 1 \\ 0 &{} d_{21}d_{43}-d_{23}d_{41} &{} d_{21}d_{44}+d_{22}d_{43} &{} -(d_{21}+d_{43}-d_{22}d_{44}) \\ 0 &{} 0 &{} 0 &{} d_{21}d_{43}-d_{23}d_{41} \\ \end{array}\right| \\ &{}=(d_{21}d_{43}-d_{23}d_{41})\Delta _3=a_4\Delta _3. \end{array} \end{aligned}$$

(8)

According to Hurwitz criterion, due to $\Delta _1>0, \Delta _2>0, a_4>0, \Delta _4=a_4\Delta _3$, if $\Delta _3>0$, then $\hbox {Re}(\mu _i)<0~(i=1,2,3,4)$, the system is asymptotically stable. The mathematical expression formula of critical curves Eq. (7) can be calculated by $\Delta _3=0$. $\square$

The red curve in Fig. 2a, b is

$$\begin{aligned} \lambda (v)=\frac{13923463053770920541266236145664 v^2 + 3320207897823869867491786743980490752}{1285167037943443173173456808181760 v^2} \end{aligned}$$

(9)

under its parameter conditions. Other critical curves can be obtained similarly by substituting parameters into Eq. (7).

Fig. 4

Raw data, Gaussian fitting curve Eq. (10) and its simplification form Eq. (11) about the equivalent conicity $\lambda$ and the lateral displacement y. (Color figure online)

3 Bifurcation mechanism based on nonlinear equivalent conicity and wheel–rail contact force

3.1 Measured equivalent conicity function and nonlinear wheelset model

In general, the equivalent conicity is regarded as a constant. In reality, the parameter of equivalent conicity $\lambda$ is related to the lateral displacement y of wheelset, which is a state variable in differential equations. We choose the equivalent conicity data measured from the high-speed train CRH380 on Beijing–Shanghai railway after 100,900 km’ wearing. The software package Curve Fitting Tool (cftool) in MATLAB is used to fit the function relation between the equivalent conicity and the lateral displacement. We obtain that

$$\begin{aligned} \begin{array}{r@{~}l} &{}\lambda =\lambda _0(y)\\ &{}\quad =0.7099\exp \left[ -((y-0.009884)/0.001472)^2\right] \\ &{}\qquad +\,0.6979\exp \left[ -((y+0.009873)/0.001444)^2\right] \\ &{}\qquad +\,2.319\times 10^{14}\exp \left[ -((y+18.3)/3.095)^2\right] . \end{array}\nonumber \\ \end{aligned}$$

(10)

Then, its simplification form is as follows:

$$\begin{aligned} \lambda (y)= & {} 0.7\exp \left[ -\left( \frac{y-0.01}{0.00145}\right) ^2\right] \nonumber \\&+0.7\exp \left[ -\left( \frac{y+0.01}{0.00145}\right) ^2\right] +0.1358. \end{aligned}$$

(11)

The raw data and the fitting curve are shown in Fig. 4. The reason for selecting exponential function to fit the data is based on the following facts: (1) The function Eq. (10) fits very well with the original data: The sum of squares due to error is SSE = 0.02767, coefficient of determination is R-square = 0.9948, adjusted R-square = 0.9945, and root mean squared error is RMSE = 0.01572; (2) the trend of function is consistent with the data. There is no opposite fluctuation in $y\in [-0.010,0.010]~\hbox {m}$; (3) polynomial function and sine function can fit it a little better (because the SSE and RMSE will be smaller, and the R-square and adjusted R-square will be closer to (1)). $\lambda (y)$ fitted by polynomial function or sine function can obtain the same bifurcations and parameter planes as those obtained by exponential function fitting. Variable step size method in MATCONT can reduce the concern about discrete method. But the polynomial and sine functions make the structure of ODE unsuitable to make numerical calculation, which will be terminated since the step size is too small whatever the discrete methods and maximum step sizes are chosen; (4) it is reasonable to consider the variation regularity closing to the origin and to neglect the equivalent conicity for $|y|>0.010~\hbox {m}$. In order to obtain accurate radius of limit cycles, we directly substitute Eq. (11) into Eq. (13) rather than truncate the higher-order term of the Taylor’s expanded formula of Eq. (11); (5) furthermore, the constant term of $\lambda (y)$ can be considered as a value of $\lambda$ in model (3). Equations (10) and (11) are close to each other. They cause the same bifurcation phenomena in the present wheelset model by our test.

The wheel–rail contact force is considered as a simplified piecewise linear function, as the black dashed lines in Fig. 5, the rail will push against the wheel if $|y|\ge 0.008~\hbox {m}$ while no affect between them if $|y|< 0.008~\hbox {m}$ [12, 24,25,26]. It is usually expressed by a nonlinear wheel–rail force function as $F_T(y)=\alpha _1y^3+\alpha _2y^5$ [18, 27] for the sake of smoothing, so that the wheel–rail contact force is described by a nonlinear function as the red curve shown in Fig. 5.

Fig. 5

Wheel–rail contact force. (Color figure online)

Therefore, the wheelset model with nonlinear equivalent conicity and wheel–rail contact force can be described by a nonlinear ordinary differential equations as follows:

$$\begin{aligned} \left\{ \begin{array}{l} m\frac{\mathrm{d}^2y}{\mathrm{d}t^2}=-\,\frac{2\kappa _y}{v}\frac{\mathrm{d}y}{\mathrm{d}t}-K_x\left( \frac{l_0}{l_1}-1\right) y\\ \qquad \qquad \;\, -K_yy+2\kappa _y\psi -F_T(y), \\ I\frac{\mathrm{d}^2\psi }{\mathrm{d}t^2}=-\,\frac{2d_0^2\kappa _x}{v}\frac{\mathrm{d}\psi }{\mathrm{d}t}-\frac{2d_0\kappa _x\lambda (y)}{r_0}y-K_xd_1^2\psi . \\ \end{array} \right. \end{aligned}$$

(12)

Similarly to the linear equation, let $x_1=y$, $x_2={\dot{y}}$, $x_3=\psi$, $x_4={\dot{\psi }}$, then

$$\begin{aligned} \left\{ \begin{array}{l} \dot{x_1}=x_2, \\ \dot{x_2}=-\,\frac{K_x}{m}\left( \frac{l_0}{l_1}-1\right) x_1-\frac{K_y}{m}x_1\\ \qquad \quad -\frac{2\kappa _y}{mv}x_2+\frac{2\kappa _y}{m}x_3-\frac{F_T(x_1)}{m},\\ \dot{x_3}=x_4, \\ \dot{x_4}=-\,\frac{2d_0\kappa _x\lambda (x_1)}{Ir_0}x_1-\frac{K_xd_1^2}{I}x_3-\frac{2d_0^2\kappa _x}{Iv}x_4.\\ \end{array} \right. \end{aligned}$$

(13)

The stability and the bifurcations of the trivial equilibrium O of this system are discussed in the following.

3.2 Bifurcation of the cycles about the longitudinal stiffness $K_x$ and the speed V

Fig. 6

Hopf bifurcation curve and limit point bifurcation of cycles about the longitudinal stiffness $K_x$ and the speed V when $K_y=10.96~\hbox {MN}/\hbox {m}$. (Color figure online)

The longitudinal stiffness $K_x$ and the operating speed V are considered as two parameters, in order to explore their effects on the stability of train operation. In Fig. 6, Hopf bifurcation, limit point bifurcation of cycles and cusp bifurcation of cycles happen when $K_y=10.96~\hbox {MN}/\hbox {m}$ in the region $(K_x,V)=[9.0,10.7]\times [520,580]$.

3.2.1 The supercritical/subcritical Hopf bifurcation

The blue curve in Fig. 6 is a Hopf bifurcation curve, on which the point GH: $(K_x,V){=}(10.413634,566.5220)$ implies a generalized Hopf bifurcation point. The subcritical and supercritical Hopf bifurcation curves are, respectively, on the left and the right sides of the point GH, and the second Lyapunov coefficient of GH is $l_2=-\,37.5146$. Below the subcritical Hopf bifurcation curve $H^-$, the equilibria are stable and surrounded by unstable limit cycles, and unstable equilibria appear up to the curve $H^-$. Below the supercritical Hopf bifurcation curve $H^+$, the equilibria are also stable. Unstable equilibria appear up to the supercritical Hopf bifurcation curve $H^+$ and surrounded by stable limit cycles. The red curve shows the fold/limit point bifurcation of cycles, on which a cusp bifurcation point of cycles CPC: $(K_x,V)=(9.416860,532.4951)$ exists as a boundary of limit point bifurcation of cycles with normal form coefficient $c(0)=854.4763$. Subcritical Hopf bifurcation curve $H^-$ and the upper half of limit point bifurcation curve of cycles intersect at point $P_1$. Then, we divide the values of $K_x$ into four parts by point CPC, $P_1$ and GH.

Fig. 7

Limit point bifurcation of cycles when $K_y=10.96~\hbox {MN}/\hbox {m}$, $K_x=9.1, 9.7, 9.9, 10.413634~{(\hbox {GH})\hbox {MN}/\hbox {m}}$, respectively. The blue curves denote stable limit cycles, and the magenta and the pink curves indicate unstable limit cycles. (Color figure online)

3.2.2 Fold/limit point bifurcation structure of cycles

Limit point bifurcation of cycles for $K_y=10.96\,\hbox {MN}/\hbox {m}$ is shown in Fig. 7a–d, which explain the bifurcation diagram in Fig. 6 by four specific bifurcation structures. We fix $K_x=9.1$, 9.7, 9.9, $10.413634~{(\hbox {GH}) \hbox {MN}/\hbox {m}}$, respectively. The z-axis represents the speed range near the bifurcation curves, and abscissa $x_1$ and ordinate $x_2$ are used to display the limit cycles on the 2D subspace. The blue closed curves denote stable limit cycles, and the magenta and the pink curves indicate unstable limit cycles. The equilibria below the point H are stable, and the upper equilibria are unstable.

Figure 7a is a bifurcation diagram for $K_x=9.1~\hbox {MN}/\hbox {m}$ that on the left of point CPC. Speed V is considered as a single parameter, and Hopf bifurcation happens at point H: $V=527.4349~\hbox {km}/\hbox {h}$ with the first Lyapunov coefficient $l_1=7.4072$. Stable equilibria are bounded by unstable limit cycles when $V<527.4349~\hbox {km}/\hbox {h}$. If the initial point is inside the unstable limit cycle, the wheelset is balanced to the origin in finite time. The radius of limit cycle decreases with the increasing speed. Once the speed exceeds point H, no initial point can make the wheelset stable.

For Fig. 7b, supercritical Hopf bifurcation point H: $V=544.3795~\hbox {km}/\hbox {h}$ has the first Lyapunov coefficient $l_1=3.8482$ when $K_x=9.7~\hbox {MN}/\hbox {m}$. Besides unstable limit cycles appearing at $V<544.3795~\hbox {km}/\hbox {h}$, two limit point bifurcations of cycles are detected at $\hbox {LPC}_1$: $V=542.4787~\hbox {km}/\hbox {h}$ with the normal form coefficient $c(0)=-5.7258$, and $\hbox {LPC}_2$: $V=543.2090~\hbox {km}/\hbox {h}$ with the normal form coefficient $c(0)=49.7624$. These results illustrate that a stable limit cycle and an unstable limit cycle coincide at a critical state. In other words, an unstable limit cycle, a stable limit cycle and another unstable limit cycle are outside the stable equilibrium one by one when the speed is fixed between $\hbox {LPC}_1$ and $\hbox {LPC}_2$.

Fig. 8

Waveforms for different initial values in Fig. 6b. Fix $K_x=9.7~\hbox {MN}/\hbox {m}$, $K_y=10.96~\hbox {MN}/\hbox {m}$, $V=543~\hbox {km}/\hbox {h}$, which is between $\hbox {LPC}_1$ and $\hbox {LPC}_2$. There are two unstable limit cycles, a stable limit cycle and a stable equilibrium. The initial values are $x_1=0.001~\hbox {m}$, $x_2=0.001~\hbox {m}/\hbox {s}$. a A stable equilibrium for $x_3=0.001~\hbox {rad}$, $x_4=0.01~\hbox {s}^{-1}$; b an unstable limit cycle for $x_3=0.003~\hbox {rad}$, $x_4=0.06~\hbox {s}^{-1}$; c a stable limit cycle for $x_3=0.006~\hbox {rad}$, $x_4=0.06~\hbox {s}^{-1}$; d an unstable limit cycle for $x_3=0.007~\hbox {rad}$, $x_4=0.07~\hbox {s}^{-1}$, respectively. (Color figure online)

Different initial values near each equilibrium/limit cycle are given, and the waveform diagrams are drawn in Fig. 8 accordingly. When $K_x=9.7~\hbox {MN}/\hbox {m}$, $K_y=10.96~\hbox {MN}/\hbox {m}$ and $V=522.5~\hbox {km}/\hbox {h}$, and the initial variables are taken as $x_1=0.001~\text {m}$, $x_2=0.001~\hbox {m}/\hbox {s}$:

• (1) For $x_3=0.001~\text {rad}$, $x_4=0.01~\text {s}^{-1}$ which is near the origin O, it takes about 70 s to stop the hunting vibration. This is much longer than that used to stabilize the linear system.

• (2) The initial point with $x_3=0.003~\text {rad}$, $x_4=0.06~\text {s}^{-1}$ is close to the small unstable limit cycle. In this situation, the lateral displacement and the yaw angle increase gradually to a stable limit cycle after more than $30\text {s}'$ staying on the unstable limit cycle.

• (3) In Fig. 8c, the wheelset converges to a hunting vibration at a fixed displacement/angle when $x_3=0.006~\text {rad}$, $x_4=0.06~\text {s}^{-1}$. This stable limit cycle is the one in Fig. 7b.

• (4) And for the unstable limit cycle in the outermost, the initial values $x_3=0.007~\text {rad}$, $x_4=0.07~\text {s}^{-1}$ tend to the unstable limit cycle firstly, but expand outward rapidly to another bigger cycle, which may be produced by a bifurcation that is not within a reasonable parameter range.

Figure 7c for $K_x=9.9~\hbox {MN}/\hbox {m}$ has a higher critical speed at Hopf bifurcation point H: $V=550.3513~\hbox {km}/\hbox {h}$ with the first Lyapunov coefficient $l_1=2.7316$; one limit point bifurcation of cycles is below to the point H: $\text {LPC}_1$: $V=549.3634~\hbox {km}/\hbox {h}$ with normal form coefficient $c(0)=-4.4459$, and the other is up to H: $\text {LPC}_2$: $V=551.1587~\hbox {km}/\hbox {h}$, normal form coefficient $c(0)=7.8777$. Comparing with Fig. 7b, c has a new range $V\in [550.3513,551.1587)$ between H and $\text {LPC}_2$, where there is a stable limit cycle and an unstable limit cycle outside the unstable equilibrium.

When $K_x\ge 10.413634~\hbox {MN}/\hbox {m (GH)}$, the curve $\hbox {LPC}_1$ coincides with the supercritical Hopf bifurcation curve $H^+$. The supercritical Hopf bifurcation and the limit point bifurcation of cycles are shown in Fig. 7d if we fix $K_x= 10.413634~\hbox {MN}/\hbox {m}$. The Hopf bifurcation point appears at H: $V=566.5219~\hbox {km}/\hbox {h}$ with the first Lyapunov coefficient $l_1=8.8580\times 10^{-7}$ which can be regarded as zero. At parameter $V=566.5219~\hbox {km}/\hbox {h}$, the normal form coefficient $c(0)=-3.4385\times 10^{-4}$ of $\hbox {LPC}_1$ is also almost zero. Therefore, a stable and an unstable limit cycles are outside the unstable equilibrium for $566.5219~\hbox {km}/\hbox {h}<V<573.0105~\hbox {km}/\hbox {h}$. $\hbox {LPC}_2$ has the normal form coefficient $c(0)=154.9663$ which is not closed to zero.

From the actual train operation point of view, stable equilibria are the most desirable, such that the train can still gradually tend to the direction parallel to the tracks once the track irregularities occur in the neighborhood of the equilibria. However, for the differential equations with nonlinear factors, there is usually an unstable limit cycle outside the stable equilibrium. It implies that a larger external disturbance will make the train run beyond the unstable limit cycle and even derail. Nevertheless, if there is another stable limit cycle outside the unstable one, then the former can restrict the region of hunting motion, such as the cases between $\hbox {LPC}_1$ and $\hbox {LPC}_2$ in Fig. 7b, or the cases between $\hbox {LPC}_1$ and H in Fig. 7c. It will greatly increase the safety of train operation. Conversely, even if a stable limit cycle arises from the supercritical Hopf bifurcation, the unstable equilibrium is still not desirable; otherwise, the train will always be in a state of hunting and cannot proceed paralleling along the tracks. Consequently, the existence of both a stable equilibrium and a stable limit cycle is the most desirable critical condition to restrict the region of hunting motion that beyond the limits of safe operation. The corresponding instability region is the triangle inside the points $P_1$, CPC and GH in Fig. 6, i.e., a longitudinal stiffness between CPC and GH.

In addition, the boundary between stable equilibria and unstable equilibria in Fig. 6 is almost a straight line and two branches of limit point bifurcation curve of cycles are near the Hopf bifurcation curve. They imply that the effect of longitudinal stiffness on critical is essentially linear in both linear and nonlinear system. Only when the longitudinal stiffness $K_x$ is greater than $9.4~\hbox {MN}/\hbox {m~(CPC)}$, the bifurcation of cycles will occur. Otherwise, it will go through the critical speed and directly destabilize.

3.3 Stability determined by Lyapunov exponents

In order to calculate the stability of systems and to describe the rates that every variables tend to be convergent or divergent, we calculate Lyapunov exponents in several cases. Lyapunov numbers measure the average per step rates of separation from the current orbit along each orthogonal direction. A Lyapunov exponent is the natural logarithm of a Lyapunov number. Thus, stable equilibria have negative Lyapunov exponents; the Lyapunov exponents of asymptotically periodic orbits are zero; unstable equilibria for linear system and chaotic orbits for nonlinear system have positive Lyapunov exponents [28]. In this section, Euler method with implicit midpoint scheme is used to discrete systems Eqs. (3) and (13), since it is a symmetric method and basically makes the discrete system maintain the same structure with the original system [29].

Fig. 9

Lyapunov exponents correspond to linear wheelset system in a and nonlinear wheelset system in b; c different $\lambda (y)$ determined by parameter a; d Lyapunov exponents about parameter a corresponding to nonlinear wheelset system. All the three initial points are $(x_1,x_2,x_3,x_4)=(1.0,0.1,0.1,0.1)$, which is not near the origin O. (Color figure online)

Figure 9a shows a Lyapunov exponent diagram for linear reduced system Eq. (3). The red and the blue curves (the upper) are almost overlapped, and the orange and the purple curves (the lower) are also overlapped. This phenomenon indicates that the stabilized/destabilized rates of lateral displacement y and lateral speed ${\dot{y}}$ are the same. The same phenomenon also happens in yaw angle $\psi$ and yaw angular velocity ${\dot{\psi }}$. It may imply that the characteristic roots of the Jacobian matrix of the system Eq. (3) are two pairs of complex numbers. When the running speed is fixed at $V=400~\hbox {km}/\hbox {h}$, linear system Eq. (3) becomes unstable at about $\lambda =0.22$ with positive Lyapunov exponents.

Figure 9b takes the same parameter values as Fig. 7b. The maximum Lyapunov exponents are all almost zero when $V\in [540,545]$. The system is absolutely unstable when $V\in [545,600]$. From the orange and the purple curves, they show that the convergence rates of $x_1$ and $x_2$ are fluctuant. Symmetry phenomenon is caused by two pairs of conjugate complex eigenvalues of Jacobian matrix.

Fig. 10

a Hopf bifurcation curve and limit point bifurcation curve of cycles about the lateral stiffness $K_y$ and the speed V when $K_x=10.0~\hbox {MN}/\hbox {m}$; b–f bifurcation structures for $K_y=9.0, 9.914016\hbox {(GH)}, 11.2, 11.8, 13.5~\hbox {MN}/\hbox {m}$, respectively. The blue curves denote stable equilibria and limit cycles, the red dashed line denotes unstable equilibria, and the magenta and the pink curves indicate unstable limit cycles. (Color figure online)

Table 2 Bifurcation values corresponding to Fig. 10b–f

Fig. 11

a Hopf bifurcation curve and limit point bifurcation curve of cycles about the longitudinal stiffness $K_x$ and the lateral stiffness $K_y$. Fix $V=500~\hbox {km}/\hbox {h}$. b The limit point bifurcation surface of cycles. (Color figure online)

Fig. 12

Bifurcation structures of cycles for $V=500~\hbox {km}/\hbox {h}$, a $K_x=8.555~\hbox {MN}/\hbox {m}$, b $K_x=8.553385~{(\hbox {CPC}) \hbox {MN}/\hbox {m}}$, respectively. The maximum step size is 1.0 (color figure online)

Fig. 13

Bifurcation structures of cycles for $V=500~\hbox {km}/\hbox {h}$, $K_x=8.555~\hbox {MN}/\hbox {m}$, the maximum step size is 1.0 corresponding to Fig. 12a. Views from different angles are shown in this figure: a limit cycles in variable space $(x_1,x_2,x_3)$; b limit cycles in variable space $(x_1,x_2,x_4)$. (Color figure online)

Fig. 14

Bifurcation structures of cycles for $V=500~\hbox {km}/\hbox {h}$, $K_x=8.553385~{(\hbox {CPC}) \hbox {MN}/\hbox {m}}$, the maximum step size is 1.0 corresponding to Fig. 12b. Views from different angles are shown in this figure: a–f limit cycles in variable space $(x_1,x_2,x_3)$; g–p limit cycles in variable space $(x_1,x_2,x_4)$. The red and the green rings express the limit point bifurcation of cycles and the NS bifurcation of cycles, respectively. (Color figure online)

Fig. 15

a The NS bifurcation curve of cycles is almost coincident with the limit point bifurcation curve of cycles. There are some 1:1 resonance points on the NS bifurcation curve. b The orbits when the initial point is $(x_1,x_2,x_3,x_4)=(-\,0.005,0.05,0.01,0.2)$ and parameters $K_x=8.555762~\hbox {MN}/\hbox {m}$, $K_y=5.915434~\hbox {MN}/\hbox {m}$ (the blue curve) and $K_x=8.551702~\hbox {MN}/\hbox {m}$, $K_y=8.298495~\hbox {MN}/\hbox {m}$ (the red curve), respectively. The maximum step size is 1.0. (Color figure online)

To analyze Eq. (11), we introduce a parameter a such that

$$\begin{aligned} \lambda (y,a)= & {} 0.7\exp \left\{ -\left( \frac{y-0.01}{a}\right) ^2\right\} \nonumber \\&+\,0.7\exp \left\{ -\left( \frac{y-0.01}{a}\right) ^2\right\} +0.1358\nonumber \\ \end{aligned}$$

(14)

for the convenience of understanding the effect of function $\lambda (y,a)$ on the system (13). For example, Fig. 9c shows the blue curve for $a=0.00145$ and the red curve for $a=0.004$. If a is taken from $a\in [0.00145,0.004]$, then function curves of $\lambda (y,a)$ are taken in the yellow region. The maximum Lyapunov exponents shown in Fig. 9d are almost zero. It demonstrably indicates that the system almost converges to limit cycles when $V=543~\hbox {km}/\hbox {h}$ if a initial point far away from origin is chosen. The initial points in Fig. 9a, c, d are all $(x_1,x_2,x_3,x_4)=(1.0,0.1,0.1,0.1)$, which are not very close to the origin O, so that the Lyapunov exponents can describe the global stability of the system. We discuss the effect of parameter a by computing the maximum Lyapunov exponents rather than the critical speed of system, because different parameters a cannot change critical speed at equilibrium O, and the maximum Lyapunov exponents give the average orbit states in phase space.

3.4 Similar bifurcations about the lateral stiffness $K_y$ and the speed V

In this section, a two-parameter bifurcation plane about lateral stiffness and speed is shown in Fig. 10a when $K_x=10~\hbox {MN}/\hbox {m}$. The blue and the red curves represent Hopf bifurcation curve and fold bifurcation curve of cycles, respectively. The general Hopf bifurcation point GH: $(K_y,V)=(9.914016,552.7460)$ with $l_2=-43.4422$ has the minimum critical speed on the Hopf bifurcation curve. A value of $K_y$ on the left side of point GH and one on the right side can cause the same critical speed.

Taking the point GH as a dividing point, the supercritical Hopf bifurcations happen on the left of point GH and the subcritical Hopf bifurcations happen on the right side. The coordinate of cusp bifurcation point of cycles is CPC: $(K_y,V)=(12.499200,552.8033)$ and $c(0)=987.2905$. The bifurcation structures corresponding to different $K_y$ are shown in Fig. 10b–f, and their bifurcation values are listed in Table 2. $l_1$, $c_1(0)$ and $c_2(0)$ denote the first Lyapunov coefficient of Hopf bifurcation point, normal form coefficients of $\hbox {LPC}_1$ and $\hbox {LPC}_2$, respectively. The normal form coefficient less than 0 indicates that the cycle representing fold bifurcation is the minimum value of a paraboloid going upward. Conversely, a positive normal form coefficient indicates that fold bifurcation cycle is the maximum value of a paraboloid going downward. If the curve $\hbox {LPC}$ coincides with the point GH, the normal form coefficient is equal to 0.

3.5 Bifurcations of cycles about the longitudinal and the lateral stiffness

If the longitudinal and the lateral stiffness are considered as parameters, while speed is fixed at $V=500~\hbox {km}/\hbox {h}$, and Hopf bifurcation curve and limit point bifurcation of cycles are shown in Fig. 11a. The right upper part of the blue Hopf bifurcation curve in Fig. 11a corresponds to stable equilibria.

3.5.1 Cusp bifurcation of cycles

The information of generalized Hopf bifurcation and cusp bifurcation is as follows: GH: $(K_x,K_y)=(8.555763,5.875175)$ with $l_2=-81.59077$, CPC: $(K_x,K_y)=(8.553385,8.475153)$ with $c(0)=660.4899$. Figure 11b shows the cusp bifurcation of cycles on a three-dimension space $(K_x,K_y,x_1)$. The magenta and the blue lines denote the diameters of cycles. They are the boundaries where the stable and the unstable limit cycles encounter. In other words, they are the projections of curve $\hbox {LPC}$ on one-dimensional phase space $x_1$. Starting from point GH, their radius gradually increases.

A phenomenon related to numerical simulation is observed: When numerical calculation is used to show the bifurcation of cycles, the limit cycles will be drawn repeatedly between two Hopf bifurcation points. For example, when the longitudinal stiffness is fixed at $K_x=8.555~\hbox {MN}/\hbox {m}$ which is between points CPC and GH, two Hopf bifurcation points in Fig. 12a are as follows: $H_1$: $K_y=5.648453~\hbox {MN}/\hbox {m}$, the first Lyapunov coefficient $l_1=-0.7389$; $H_2$: $K_y=6.099804~\hbox {MN}/\hbox {m}$, the first Lyapunov coefficient $l_1=0.7163$. Unstable equilibria (the red dashed line) exist between the two Hopf bifurcation points. Two limit point bifurcation points of cycles are found through the forward/backward numerical calculation starting from any Hopf bifurcation point as an initial point. $\hbox {LPC}_1$: $K_y=7.109678~\hbox {MN}/\hbox {m}$, normal form coefficient $c(0)=-3.6837$; $\hbox {LPC}_2$: $K_y=6.099806~\hbox {MN}/\hbox {m}$, normal form coefficient $c(0)=1.0825$. Both the forward and the backward numerical calculations can cause a loop between two Hopf bifurcation points: $H_1{\mathop {\longrightarrow }\limits ^{\hbox {ULC}}}\hbox {LPC}{\mathop {\longrightarrow }\limits ^{\hbox {SLC}}}H_2 {\mathop {\longrightarrow }\limits ^{\hbox {SLC}}} \hbox {LPC} {\mathop {\longrightarrow }\limits ^{\hbox {ULC}}} H_1 {\mathop {\longrightarrow }\limits ^{\hbox {ULC}}} \hbox {LPC} {\mathop {\longrightarrow }\limits ^{\hbox {SLC}}}H_2...$ (Here, ULC denotes magenta unstable limit cycles, and SLC denotes green stable limit cycles). It is caused by the overlap of the inferior branch of curve $\hbox {LPC}$ and the Hopf bifurcation curve. The green stable limit cycles are the largest range of stable hunting motion. The bifurcation structures are drawn in the three-dimensional phase space in Fig. 13. The limit cycles are all in a plane.

3.5.2 NS (Neimark–Sacker) bifurcation of cycles and 1:1 resonance

Figure 12b shows the bifurcation structure of cycles when parameters are fixed at $V=500~\hbox {km}/\hbox {h}$, $K_x=8.553385~\hbox {MN}/\hbox {m (CPC)}$, and the maximum step size is 1.0.

The structures of limit point bifurcation of cycles and NS bifurcation of cycles are drawn in the three-dimensional phase space in Fig. 14. Trajectories of limit cycles from different angles are shown in Fig. 14a–p. The red and the green rings express the limit point bifurcation and the NS bifurcation of cycles, respectively. The cycles inside the green cycle NS $(K_y=8.372094~\hbox {MN}/\hbox {m})$ are all on a plane. But the cycles outside NS warp in 3D-space. The warped limit cycles demonstrate that there exist complex spatial relations between the lateral and the yaw movements during one period of hunting motion. NS bifurcation of cycles only appears when the maximum step size h>0.99. Therefore, NS bifurcation of cycles may be not the nature behavior of the system itself, but some complex dynamic behavior may appear when the continuous system is inappropriately discretized.

In addition, the NS bifurcation curve and some 1:1 resonance points are drawn in Fig. 15a if the maximum step size is 1.0. The phase diagrams of 1:1 resonance points are shown in Fig. 15b.

4 Conclusions

In this paper, firstly, the effects of longitudinal stiffness, the lateral stiffness and the equivalent conicity on the critical speed are discussed by calculating the real parts of the eigenvalues of the Jacobian matrix and Hurwitz criterion of a linear wheelset model.

Secondly, our research shows that the critical speed decreases with a ratio inversely proportional to the equivalent conicity. Furthermore, for the same equivalent conicity, the critical speed increases with the increase in longitudinal stiffness at a fixed lateral stiffness. In addition, if the longitudinal stiffness is fixed, then the critical speed increases with the increase in lateral stiffness when $\lambda >0.17$. When $\lambda <0.17$, the smaller the equivalent conicity is, the lesser the lateral stiffness $K_y=2.96~\hbox {MN}/\hbox {m}$ will gradually change from the worst condition into the best condition compared with the other lateral stiffness.

Thirdly, nonlinear equivalent conicity related to the lateral displacement has been introduced into the system according to actual test data measured from the high-speed train CRH380 on Beijing–Shanghai railway after $100{,}900~\hbox {km}'$ wearing. Nonlinear wheel–rail force function is used to describe the wheel–rail contact force. On the parameter plane of longitudinal/lateral stiffness and velocity, the Hopf bifurcation curve is the boundary between the stable and the unstable equilibria. The supercritical/subcritical Hopf bifurcation implies the existence of stable/unstable limit cycles. On the basis of generalized Hopf bifurcation, the fold bifurcation of cycles indicates the existence of multiple limit cycles. Thus, disturbances will make the movement of trains to converge or diverge at different limit cycles. Neimark–Sacker bifurcations of cycles and 1:1 resonances are detected by numerical simulation when the maximum step size $h>0.99$.

Fourthly, fold bifurcation of cycles is an important bifurcation, which can explain the complex behaviors in the hunting motion of the wheelset model with nonlinear equivalent conicity and wheel–rail contact force. Our research demonstrates that one of the main reasons leading to hunting motion is the fold (limit point) bifurcation structure of cycles, and this is because there may exist multiple limit cycles on a side of fold bifurcation curve of cycles, at which stable limit cycles and unstable limit cycles may coincide. If the most outward limit cycle is stable, then the motion of high-speed vehicle should be safe in a reasonable range. Otherwise, if the initial values are chosen near the most outward unstable limit cycle or the system is perturbed by stronger noises, the high-speed vehicle will take place unstable hunting motion and even lead to serious train derailment events. Therefore, in order to control a hunting motion, it may be the easiest way in theory to guarantee the coexistence of stable equilibrium and stable limit cycle in a wheelset system.

Fifthly, the corresponding parameter value at $\hbox {LPC}$ can be regarded as a critical threshold concerning on the existence and disappearance of limit cycles as shown in Figs. 7 and 11. The cusp bifurcation point as shown in Fig. 11b is also a critical value at which the $\hbox {LPC}$ will appear or disappear.

Sixthly, the computation of Lyapunov exponents shows that the variation of steepness of equivalent conicity function may produce little effect on the bifurcation type of the wheelset model with nonlinear equivalent conicity and wheel–rail contact force.

Finally, it is noted that much attention should be paid on the step size in discretizing a continuous-time ordinary differential equation. This is because if a relatively small step size is used to discretize a continuous-time system, the numerical results as shown in Fig. 13 demonstrate that all limit cycles appear on the same plane, which is a kind of hunting motion coupled by evenly lateral and yaw movement in two directions, while if the step size is relatively larger, then the corresponding numerical simulations as shown in Fig. 14 present another feature, in which the interwinded limit cycles show that this is a kind of more complex unevenly hunting motion than the regular vibration in two directions, and at the same time, there will appear numerous 1:1 resonance points. In addition, it is still a tough task to investigate the instability mechanisms of this modified system using the approximate analytical method, especially for more bifurcations of nested limit cycles. It will be our future research direction to give a complete picture of rich dynamic behavior using some approximate analytical method that stays behind the hunting motion rather than only using numerical simulations.