1 Introduction

Various physical phenomenon occurring around us can be modeled in the form of nonlinear models [1,2,3]. So, nonlinear equations are of utmost importance to study. While working with these nonlinear models, we come to know about the underlying process and the importance of parameters involved which cannot be understood at a cursory look on the model. It is important to observe that a completely integrable nonlinear model equation has extensive practical application from both mathematical and physical point of view [4, 5]. In addition to this, the study of nonlinear and supernonlinear traveling waves [6], solitons, water waves and shock waves, etc., has experienced a revolution over past few decades. For a complete scenario of a model equation, the qualitative behavior of the model equation is very important along with the exact traveling wave solutions. Recently, the qualitative behavior of a singular nonlinear equation of second class was studied and sufficient conditions were established for the existence of propagation wave solutions [7, 8]. In 2012, the bifurcation analysis of KP–MEW equation was reported [9].

In the present study, we deal with Sharma–Tasso–Olver (STO) equation of the form

$$\begin{aligned} u_{t}+a\left( u^{3}\right) _{x}+b\left( u^{2}\right) _{xx}+cu_{xxx}=0, \end{aligned}$$
(1)

which is an odd ordered hierarchy of the well-known Burger’s equation which produces shock wave solutions [10].

In the recent years, many researchers tried to explore Eq. (1) in various directions which include the fractional sub-equation method [11], first integral method [12], the sine–cosine method [13], Lucas Ricatti expansion method [14], etc. Also, many researchers used variety of transformations like Cole–Hopf transformation, fractional complex transform [15] and Darboux transformation [16, 17]. In addition to this, using Hirota’s direct method, fission and fusion of solitary wave solutions are obtained by using B\(\ddot{a}\)cklund transformation [16, 18]. While coming to the higher dimensional studies, we come across [19, 20]. During the literature survey of STO equation, limited detail on the solution schemes based on \({1}/{G^{^{\prime }}}\) expansion method, Kudryashov method, Runge–Kutta fourth-order and Fourier spectral scheme is available. Also, there is hardly any study performed on the behavior of nonlinear and supernonlinear traveling waves for STO equation (1).

In the present study, we make several investigations to have a detailed study of the nature of solutions so obtained. Our study includes \({1}/{G^{^{\prime }}}\) expansion method, Kudryashov method, Runge–Kutta fourth-order and Fourier spectral scheme. All these have been detailed in the proceeding sections. Furthermore, we investigate the bifurcation behavior of nonlinear and supernonlinear traveling waves of STO equation (1) applying bifurcation theory of planar dynamical systems [21,22,23].

This paper is organized as: After introductory part, Sect. 2 is dedicated to exact solutions of STO equation in hand. This part includes \({1}/{G^{^{\prime }}}\) expansion method and modified Kudryashov method. In Sect. 3, we obtain components of conservation law using multiplier method. After having an analytical view, we proceed for the numerical aspect in Sect. 4. In Sect. 5, we study bifurcation behavior of traveling wave solutions of STO equation. In Sect. 6, final conclusion is drawn followed by the list of references used for the study.

2 Exact solutions of Sharma–Tasso–Olver equation

We consider Sharma–Tasso–Olver (STO) equation (1) for the calculation of the exact solution with \({1}/{G^{^{\prime }}}\) expansion method [24] and modified Kudryashov method [25]. We apply the wave transformation of the form \(\xi =x-vt\) on Eq. (1). This will transform the nonlinear STO equation into another nonlinear ODE as given below

$$\begin{aligned} -vu^{\prime }+3au^{2}u^{\prime }+2b\left( u^{\prime }\right) ^{2}+2buu^{\prime \prime }+cu^{\prime \prime \prime }=0. \end{aligned}$$
(2)

2.1 \({1}/{G^{^{\prime }}}\) expansion method

Using balance equation method we obtain \(m=1\). Now the solution will take the following form

$$\begin{aligned} u(\xi )=u=a_{0}+a_{1}\left( \frac{1}{G^{^{\prime }}}\right) , \end{aligned}$$
(3)

where \(a_{0}\) and \(a_{1}\) are the constants to be determine and \({1}/{G^{^{\prime }}}\) is expressed as

$$\begin{aligned} \frac{1}{G^{^{\prime }}}=\frac{\lambda }{-\mu +\lambda c_{1}\left[ \text{ cosh }\left( \lambda \xi \right) -\text{ sinh }\left( \lambda \xi \right) \right] }, \end{aligned}$$
(4)

where \(c_{1}\), \(\lambda \) and \(\mu \) are constants. Also, \(G^{^{\prime }}\) satisfy the differential equation

$$\begin{aligned} G^{^{\prime \prime }}=-\mu -\lambda G^{^{\prime }}. \end{aligned}$$
(5)

Substituting the values of u and its derivatives in Eq. (2) and comparing the different powers of \({1}/{G^{^{\prime }}}\), we obtain the following system

$$\begin{aligned}&\left( \frac{1}{G^{^{\prime }}}\right) ^{4} :3aa_{1}^{3}\mu +6ba_{1}^{2}\mu ^{2}+6ca_{1}\mu ^{3}=0, \nonumber \\&\left( \frac{1}{G^{^{\prime }}}\right) ^{3} :3aa_{1}^{3}\lambda +6aa_{0}a_{1}^{2}\mu \nonumber \\&\qquad +10ba_{1}^{2}\mu \lambda + 4a_{0}a_{1}b\mu ^{2}+12a_{1}c\lambda \mu ^{2}=0,\nonumber \\&\left( \frac{1}{G^{^{\prime }}}\right) ^{2} :6aa_{0}a_{1}{}^{2}\lambda +4ba_{1}{}^{2}\lambda ^{2}-a_{1}\mu \nonumber \\&\quad +3aa_{0}^{2}a_{1}\mu +6ba_{0}a_{1}\mu \lambda +7ca_{1}\mu \lambda ^{2}=0, \nonumber \\&\left( \frac{1}{G^{^{\prime }}}\right) :-a_{1}v\lambda +3aa_{0}^{2}a_{1}\lambda \nonumber \\&\quad +2ba_{0}a_{1}\lambda ^{2}+ca_{1}\lambda ^{3}=0. \end{aligned}$$
(6)

Solving the above system, we obtain

Set 1:

$$\begin{aligned} a_{0}= & {} \dfrac{\lambda (-b+\sqrt{b^{2}-2ac})}{2a},\end{aligned}$$
(7)
$$\begin{aligned} a_{1}= & {} \dfrac{\mu (-b+\sqrt{b^{2}-2ac})}{a}, \end{aligned}$$
(8)
$$\begin{aligned} v= & {} \dfrac{\lambda ^{2}(b^{2}-ac-b\sqrt{b^{2}-2ac})}{2a}, \end{aligned}$$
(9)

Set 2:

$$\begin{aligned} a_{0}= & {} -\dfrac{\lambda (b+\sqrt{b^{2}-2ac})}{2a}, \end{aligned}$$
(10)
$$\begin{aligned} a_{1}= & {} -\dfrac{\mu (b+\sqrt{b^{2}-2ac})}{a}, \end{aligned}$$
(11)
$$\begin{aligned} v= & {} \dfrac{\lambda ^{2}(b^{2}-ac+b\sqrt{b^{2}-2ac})}{2a}, \end{aligned}$$
(12)

Now putting the values of \(a_{0},a_{1}\) and v in Eq. (3), we get

From set 1:

$$\begin{aligned} u_{1}= & {} \dfrac{\lambda (-b+\sqrt{b^{2}-2ac})}{2a}\nonumber \\&+\left[ \dfrac{\mu (-b+\sqrt{ b^{2}-2ac})}{a}\right] \left( \dfrac{1}{G^{^{\prime }}}\right) , \end{aligned}$$
(13)

where

$$\begin{aligned} \dfrac{1}{G^{^{\prime }}}=\dfrac{\lambda }{-\mu +\lambda c_{1}[\text{ cosh } (\lambda (x-vt))-\text{ sinh }(\lambda (x-vt))]}, \end{aligned}$$
(14)

and

$$\begin{aligned} v=\dfrac{\lambda ^{2}(b^{2}-ac-b\sqrt{b^{2}-2ac})}{2a}. \end{aligned}$$
(15)

From set 2:

$$\begin{aligned} u_{2}= & {} -\dfrac{\lambda (b+\sqrt{b^{2}-2ac})}{2a}\nonumber \\&-\left[ \dfrac{\mu (b+\sqrt{ b^{2}-2ac})}{a}\right] \left( \dfrac{1}{G^{^{\prime }}}\right) , \end{aligned}$$
(16)

where

$$\begin{aligned} \dfrac{1}{G^{^{\prime }}}=\dfrac{\lambda }{-\mu +\lambda c_{1}[\text{ cosh } (\lambda (x-vt))-\text{ sinh }(\lambda (x-vt))]}, \end{aligned}$$
(17)

and

$$\begin{aligned} v=\dfrac{\lambda ^{2}(b^{2}-ac+b\sqrt{b^{2}-2ac})}{2a}. \end{aligned}$$
(18)
Fig. 1
figure 1

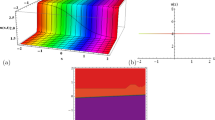
The 3D surfaces of the solution Eq. (13) for different values of \(\lambda \), when \(t=0\), \(a=-1\), \(b=-3\), \(c=-1\), \(c_{1}=10\) and \(\mu =5\)

Full size image
Fig. 2
figure 2

The 3D surfaces of solution Eq. (27) for different values of d, when \(t=0\), \(a=-1\), \(b=-3\), \(c=1\) and \(\sigma =5\)

Full size image
Fig. 3
figure 3

The 3D surfaces of solution Eq. (27) for different values of d, when \(t=0\), \(a=1\), \(b=-5\), \(c=3\) and \(\sigma =2\)

Full size image

The 3D surfaces of the solution Eq. (13) are showed for different values of \(\lambda \) in Fig. 1.

2.2 Modified Kudryashov method

Using balance equation method, we obtain \(m=1\). Therefore, solution will take the form as

$$\begin{aligned} u(\xi )=a_{0}+a_{1}Q\left( \xi \right) . \end{aligned}$$
(19)

Substitute Eq. (19) in Eq. (2) and equating the coefficients of different powers of \(Q\left( \xi \right) \), it gives

$$\begin{aligned}&\left[ Q\left( \xi \right) \right] ^{1} :-3aa_{0}^{2}a_{1}\left( \ln \sigma \right) \nonumber \\&\quad +2a_{0}a_{1}b\left( \ln \sigma \right) ^{2}-\left( \ln \sigma \right) ^{3}a_{1}c+a_{1}v\left( \ln \sigma \right) =0,\nonumber \\&\left[ Q\left( \xi \right) \right] ^{2} :3aa_{0}^{2}a_{1}\left( \ln \sigma \right) \nonumber \\&\quad -6aa_{0}a_{1}^{2}\left( \ln \sigma \right) -6a_{0}a_{1}b\left( \ln \sigma \right) ^{2}+4a_{1}^{2}b\left( \ln \sigma \right) ^{2}\nonumber \\&\quad +7a_{1}c\left( \ln \sigma \right) ^{3}-a_{1}v\left( \ln \sigma \right) =0,\nonumber \\&\left[ Q\left( \xi \right) \right] ^{3} :6aa_{0}a_{1}^{2}\left( \ln \sigma \right) -3aa_{1}^{3}\left( \ln \sigma \right) \nonumber \\&\quad +4a_{0}a_{1}b\left( \ln \sigma \right) ^{2}-10a_{1}^{2}b\left( \ln \sigma \right) ^{2}\nonumber \\&\quad -12a_{1}c\left( \ln \sigma \right) ^{3}=0, \nonumber \\&\left[ Q\left( \xi \right) \right] ^{4} :3aa_{1}^{3}\left( \ln \sigma \right) +6a_{1}^{2}b\left( \ln \sigma \right) ^{2}\nonumber \\&\quad +6a_{1}c\left( \ln \sigma \right) ^{3}=0. \end{aligned}$$
(20)

where \(\sigma \) is a positive constant.

By solving the above system, we get sets of unknowns as follows:

Set 1:

$$\begin{aligned} v= & {} \frac{\left( \ln \sigma \right) \left[ b\sqrt{\left( \ln \sigma \right) ^{2}\left( b^{2}-2ac\right) }+\left( \ln \sigma \right) \left( b^{2}-2ac\right) \right] }{2a},\nonumber \\ \end{aligned}$$
(21)
$$\begin{aligned} a_{0}= & {} \frac{b\left( \ln \sigma \right) +\sqrt{\left( \ln \sigma \right) ^{2}\left( b^{2}-2ac\right) }}{2a}, \end{aligned}$$
(22)
$$\begin{aligned} a_{1}=-\frac{b\left( \ln \sigma \right) +\sqrt{\left( \ln \sigma \right) ^{2}\left( b^{2}-2ac\right) }}{a}, \end{aligned}$$
(23)

Set 2:

$$\begin{aligned} v= & {} \frac{\left( \ln \sigma \right) \left[ -b\sqrt{\left( \ln \sigma \right) ^{2}\left( b^{2}-2ac\right) }+\left( \ln \sigma \right) \left( b^{2}-2ac\right) \right] }{2a},\nonumber \\ \end{aligned}$$
(24)
$$\begin{aligned} a_{0}= & {} \frac{b\left( \ln \sigma \right) -\sqrt{\left( \ln \sigma \right) ^{2}\left( b^{2}-2ac\right) }}{2a}, \end{aligned}$$
(25)
$$\begin{aligned} a_{1}= & {} \frac{-b\left( \ln \sigma \right) +\sqrt{\left( \ln \sigma \right) ^{2}\left( b^{2}-2ac\right) }}{a}, \end{aligned}$$
(26)

Now the exact solutions of the nonlinear equation are:

From set 1:

$$\begin{aligned} u_{1}\left( \xi \right)= & {} \frac{b\left( \ln \sigma \right) +\sqrt{\left( \ln \sigma \right) ^{2}\left( b^{2}-2ac\right) }}{2a}\nonumber \\&-\frac{b\left( \ln \sigma \right) + \sqrt{\left( \ln \sigma \right) ^{2}\left( b^{2}-2ac\right) }}{a}\nonumber \\&\quad \left( \frac{1}{ 1+d\sigma ^{\xi }}\right) . \end{aligned}$$
(27)

From set 2:

$$\begin{aligned} u_{2}\left( \xi \right)= & {} \frac{b\left( \ln \sigma \right) -\sqrt{\left( \ln \sigma \right) ^{2}\left( b^{2}-2ac\right) }}{2a}\nonumber \\&+\frac{-b\left( \ln \sigma \right) \sqrt{\left( \ln \sigma \right) ^{2}\left( b^{2}-2ac\right) }}{a}\nonumber \\&\quad \left( \frac{1}{ 1+d\sigma ^{\xi }}\right) . \end{aligned}$$
(28)

where d is a constant.

The 3D surfaces of the solution Eq. (27) are illustrated for different values of d in Figs. 2, 3.

3 Conservation laws with multiplier method

In this section, we study the conservation laws of STO equation (1) of the form

$$\begin{aligned} u_{t}+a\left( u^{3}\right) _{x}+b\left( u^{2}\right) _{xx}+cu_{xxx}=0, \end{aligned}$$
(29)

with multiplier method [26]. Consider the \(zero^{th}\) order multiplier of the form \(\Lambda _{1}\left( t,x,u\right) \). It yields the following determining system

$$\begin{aligned}&\left( \Lambda _{1}\right) _{t}=0\nonumber \\&\left( \Lambda _{1}\right) _{x}=0\nonumber \\&\left( \Lambda _{1}\right) _{x}=0\nonumber \\&\left( \Lambda _{1}\right) _{u_{x}}=0\nonumber \\&\left( \Lambda _{1}\right) _{u_{xx}}=0. \end{aligned}$$
(30)

Solution of this system is

$$\begin{aligned} \Lambda _{1}\left( t,x,u\right) =c_{1}, \end{aligned}$$
(31)

where \(c_{1}\) is the arbitrary constant. Hence, the components conservation law for Eq. (1) are

$$\begin{aligned} c_{t}&=u, \nonumber \\ c_{x}&=au^{3}+2buu_{x}+cu_{xx}. \end{aligned}$$
(32)

4 Fourier transform method

Consider the equation

$$\begin{aligned} u_t + a(u^3)_x + b(u^2)_{xx} + c u_{xxx} = 0. \end{aligned}$$
(33)

initial condition \(u(x, 0) = f(x)\).

Here, we are interested to integrate Eq. (33) using Fourier transforms [27, 28]. The Fourier transform for any w(x), \(x\in \mathbb {R}\) can be defined by

$$\begin{aligned} \hat{w} (\xi ) = \int _{-\infty }^{\infty } e^{-i\xi x} w(x)\mathrm{d}x,\quad \xi \in \mathbb {R}, \end{aligned}$$
(34)

and its inverse can be defined by

$$\begin{aligned} w (x) = \frac{1}{2\pi }\int _{-\infty }^{\infty } e^{i\xi x} \hat{w}(\xi )\mathrm{d}x,\quad x\in \mathbb {R}. \end{aligned}$$
(35)

Here, \(\hat{w}(\xi )\) is the amplitude density of w(x) at wave number \(\xi \). For simplicity we define the Fourier transform operator by the \(\hat{w} (\xi ) = \mathcal {F}\{w\}\) and the inverse Fourier transform operator by \(\hat{w} (x) = \mathcal {F}^{-1}\{w\}(k)\). Applying Fourier transform on (33) for the spatial variable, we get

$$\begin{aligned} \hat{u}_t + \frac{iak}{2} \left( \widehat{u}\right) ^3 - b k^2 \left( \widehat{u}\right) ^2 - c i k^3 \hat{u} = 0, \end{aligned}$$
(36)

where \(\mathcal {F}\{u\}= \hat{u}\). The resulting time-dependent ODE (36) is a stiff one. To reduce the higher-order linear term, we again apply the following variable transformation defining

$$\begin{aligned} \hat{U} = e^{-i c k^3 t} \hat{u}. \end{aligned}$$
(37)

Here,

$$\begin{aligned} e^{-i c k^3 t} \hat{u}_t = \hat{U}_t + i c k^3 \hat{U}. \end{aligned}$$
(38)

Thus, with the variable transformation (36) can be written as

$$\begin{aligned} \hat{U}_t + \frac{ia}{2} e^{-i c k^3 t} k \left( \widehat{u}\right) ^3 - b e^{-i c k^3 t} k^2 \left( \widehat{u}\right) ^2 = 0. \end{aligned}$$
(39)

With the above-mentioned transformation, we can discretize Eq. (36) by

$$\begin{aligned}&\hat{U}_t + \frac{ia}{2} e^{-ick^3 t} k \mathcal {F}\left[ \mathcal {F}^{-1}\left( e^{i c k^3 t} \hat{U} \right) \right] ^3 \nonumber \\&\quad -\, b e^{-ick^3 t} k^2 \mathcal {F}\left[ \mathcal {F}^{-1}\left( e^{i c k^3 t} \hat{U} \right) \right] ^2 = 0, \end{aligned}$$
(40)

with the initial function we obtain

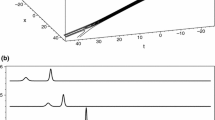
$$\begin{aligned} \mathcal {F}\{u(x, 0)\} = \mathcal {F}\{f(x)\}. \end{aligned}$$
(41)

Then, we apply standard Runge–Kutta 4 scheme for differential equation (40) subject to initial condition (41). Here, one may use any standard implicit/semi-implicit scheme for time integration. Here, the exact detail of the Fourier transformations, its accuracy results and accuracy of time integration schemes are well known [29,30,31]. In Fig. 4, we plot the solution of Eq. (40).

Fig. 4
figure 4

\( u_0(x) = \text{ sech } (10 x)\), with \(a = -1\), \(b = -3\) and \(c= -3\)

Full size image

In Fig. 5, we plot the solution of Eq. (40) with a different set of parameters.

Fig. 5
figure 5

\( u_0(x) = \text{ sech } (10 x)\) (left), and \( u_0(x) = (1/2)\text{ sech }[20(x+1)]+ \text{ sech }(10x) +.05\text{ sech }[20(x-1)]\) (right) with \(a=b=c=3\)

Full size image

5 Bifurcation behavior

In this section, we study bifurcation behavior of nonlinear and supernonlinear traveling waves of STO equation (1). For this purpose, we have transformed STO equation (1) to an ordinary differential equation (2) using traveling wave transformation \(\xi =x-vt\), where v is the velocity of the traveling wave in the positive direction of the x-axis. Then, integrating equation (2) with respect to \(\xi \), one can obtain

$$\begin{aligned} -vu+au^3+2buu^{\prime }+cu^{\prime \prime }=0. \end{aligned}$$
(42)

System (42) can be expressed as a nonlinear planar dynamical system given by

$$\begin{aligned} \left\{ \begin{array}{ll} u^{\prime }=z, \\ z^{\prime }=\frac{1}{c}u(v-au^2)-\frac{2b}{c}uz. \end{array} \right. \end{aligned}$$
(43)

It is important to note that phase portraits of a dynamical system can vary significantly depending on the number of equilibrium points and number of enveloped separatrix layers [6]. Any orbit in the phase portrait of a dynamical system represents one wave solution for the corresponding nonlinear evolution equation. For classification of different orbits in the phase portrait, we use following notations: SNPO\(_{m,n}\) for supernonlinear periodic orbit [6], NHO\(_{m,n}\) for nonlinear homoclinic orbit, and NHTO\(_{m,n}\) for nonlinear heteroclinic orbit, where m is the number of equilibrium points enveloped by the orbit and n is the number of separatrix layers enveloped by the orbit.

Fig. 6
figure 6

Phase portraits of nonlinear dynamical system (43) for a \(a=0.2, b=0.02, c=0.3, v=0.2\), and b \(a=0.2, b=0.02, c=-0.3, v=0.2\)

Full size image
Fig. 7
figure 7

Phase portraits of nonlinear dynamical system (43) for a \(a=0.2, b=0, c=0.3, v=0.2\), and b \(a=0.2, b=0, c=-0.3, v=0.2\)

Full size image
Fig. 8
figure 8

a Supernonlinear periodic wave, and b stable oscillatory wave of STO equation (1) with same parametric values as Fig. 6a

Full size image
Fig. 9
figure 9

a Supernonlinear periodic wave, and b nonlinear periodic wave of STO equation (1) with same parametric values as Fig. 7a

Full size image
Fig. 10
figure 10

a Shock waves, and b nonlinear periodic wave of STO equation (1) with same parametric values as Fig. 7b

Full size image

The bifurcation theory of planar dynamical systems [21,22,23] plays an important role in the study of nonlinear dynamical system (43). Let \(u(\xi )\) be a continuous solution of (1) for \(\xi \in \mathbb {R}\) with \(\lim _{\xi \rightarrow +\infty } u(\xi )=\alpha \) and \(\lim _{\xi \rightarrow -\infty } u(\xi )=\beta \). Then, \(u(\xi )\) is called a nonlinear solitary wave solution if \(\alpha =\beta \). In general, a solitary wave solution of system (1) corresponds to a nonlinear homoclinic orbit (NHO\(_{1,0}\)) of nonlinear dynamical system (43). A nonlinear periodic orbit (NPO\(_{1,0}\)) of nonlinear dynamical system (43) corresponds to a nonlinear periodic traveling wave solution of system (1). A supernonlinear periodic orbit (SNPO\(_{m,n}\)) of nonlinear dynamical system (43) corresponds to a supernonlinear periodic traveling wave solution of system (1). Hence for the investigation of all possible bifurcations of nonlinear solitary waves, nonlinear shock wave, nonlinear periodic waves and supernonlinear periodic waves of nonlinear system (1), we need to find all nonlinear homoclinic orbits, nonlinear periodic orbits, nonlinear heteroclinic orbits and supernonlinear periodic orbits of nonlinear dynamical system (43), which depend on the parameters a, b, c and v involved in system (43). When \(a>0\), then there exist three equilibrium points of nonlinear dynamical system (43) at \(E_0(u_0,0)\), \(E_1(u_1,0)\), and \(E_2(u_2,0)\), with \(u_0=0\), \(u_1=\sqrt{\frac{v}{a}}\), and \(u_2=-\sqrt{\frac{v}{a}}\). Let \(M(u_e,z_e)\) be the coefficient matrix of the linearized system of (43) at an equilibrium point \((u_e,z_e)\). Also let \(J=\)det\((M(u_e,z_e))\), \(T_1=\)trace\((M(u_e,z_e))\) and \(T_2=(\)trace\( (M(u_e,z_e)))^2\). Then, \((u_e,z_e)\) is a saddle point if \(J<0\), a center point if \(J>0,T_1=0\), a cusp if \(J=0\) and Poincar\(\acute{e}\) index of \((u_e,z_e)\) is zero, a node if \(J>0\) and \(T_2-4J>0\).

Based on the above qualitative analysis, we present all possible phase portraits of nonlinear dynamical system (43) in Figs. 6 and 7 and all possible traveling wave solutions of STO equation (1) in Figs. 8, 9 and 10. In Fig. 6a, we depict phase portrait of the nonlinear dynamical system (43) for \(a=0.2, b=0.02, c=0.3\) and \(v=0.2\). This phase portrait contains a family of supernonlinear periodic orbits (SNPO\(_{3,1}\)) which envelope three equilibrium points \(E_0(u_0,0)\), \(E_1(u_1,0)\), and \(E_2(u_2,0)\), where \(E_0(u_0,0)\) is a saddle point and there are two stable spirals at \(E_1(u_1,0)\), and \(E_2(u_2,0)\). There is also a nonlinear homoclinic orbit (NHO\(_{2,0}\)) at the equilibrium point \(E_0(u_0,0)\) enclosing the stable spirals at \(E_1(u_1,0)\), and \(E_2(u_2,0)\). In Fig. 6b, phase portrait of nonlinear dynamical system (43) is shown for \(a=0.2, b=0.02, c=-0.3\) and \(v=0.2\). This phase portrait contains a pair of nonlinear heteroclinic orbits (NHTO\(_{1,0}\)) joining two saddle points \(E_1(u_1,0)\) and \(E_2(u_2,0)\). Furthermore, this pair of NHTO\(_{1,0}\) envelope the center \(E_0(u_0,0)\) surrounded by a family of nonlinear periodic orbits (NPO\(_{1,0}\)).

In Fig. 7a, we manifest phase portrait of the nonlinear dynamical system (43) for \(a=0.2, b=0, c=0.3\) and \(v=0.2\). This phase portrait contains a family of supernonlinear periodic orbits (SNPO\(_{3,1}\)) which envelope three equilibrium points \(E_0(u_0,0)\), \(E_1(u_1,0)\) and \(E_2(u_2,0)\), where \(E_0(u_0,0)\) is a saddle point and \(E_1(u_1,0)\) and \(E_2(u_2,0)\) are centers. There is also a pair of nonlinear homoclinic orbits (NHO\(_{1,0}\)) at saddle point \(E_0(u_0,0)\) surrounding the centers \(E_1(u_1,0)\) and \(E_2(u_2,0)\). Furthermore, there are two families of nonlinear periodic orbits (NPO\(_{1,0}\)) about centers \(E_1(u_1,0)\), and \(E_2(u_2,0)\). In Fig. 7b, phase portrait of the nonlinear dynamical system (43) is shown for \(a=0.2, b=0, c=-0.3\) and \(v=0.2\). This phase portrait contains a pair of nonlinear heteroclinic orbits (NHTO\(_{1,0}\)) joining two saddle points \(E_1(u_1,0)\) and \(E_2(u_2,0)\). Furthermore, this pair of NHTO\(_{1,0}\) envelope the center \(E_0(u_0,0)\) which is surrounded by a family of nonlinear periodic orbits (NPO\(_{1,0}\)).

In Fig. 8a, b, we show supernonlinear periodic wave and nonlinear periodic wave of STO equation (1) with same parametric values as Fig. 7a corresponding to the supernonlinear periodic orbit (SNPO\(_{3,1}\)) enveloped three equilibrium points \(E_0(u_0,0)\), \(E_1(u_1,0)\) and \(E_2(u_2,0)\), and stable spiral at the equilibrium point \(E_1(u_1,0)\) of dynamical system (43) in the phase portrait Fig. 6a.

In Fig. 9a, b, we present supernonlinear periodic wave and stable oscillatory wave of the Sharma–Tasso–Olver (STO) equation (1) with same parametric values as Fig. 7a corresponding to the supernonlinear periodic orbit (SNPO\(_{3,1}\)) enveloped three equilibrium points \(E_0(u_0,0)\), \(E_1(u_1,0)\) and \(E_2(u_2,0)\), and nonlinear periodic orbit about the equilibrium point \(E_1(u_1,0)\) of the dynamical system (43) in the phase portrait Fig. 7a.

In Fig. 10a, b, we manifest nonlinear shock waves and nonlinear periodic wave of STO equation (1) with same parametric values as Fig. 7b corresponding to the nonlinear heteroclinic orbits (NHTO\(_{1,0}\)) joining the equilibrium points \(E_1(u_1,0)\) and \(E_2(u_2,0)\) enveloped the equilibrium point \(E_0(u_0,0)\), and nonlinear periodic orbit (NPO\(_{1,0}\)) about the equilibrium point \(E_0(u_0,0)\) of the dynamical system (43) in the phase portrait Fig. 7b.

6 Conclusion

In this work, we applied \({1}/{G^{^{\prime }}}\) expansion and modified Kudryashov method in a satisfactory way to get the exact solutions of Sharma–Tasso–Olver equation. For numerical analysis, we combined Runge–Kutta fourth-order and Fourier spectral technique and developed a mixed scheme for the numerical study of STO equation. Since spectral methods expand the solution in trigonometric series resulting into higher-order technique and Runge–Kutta produces improved accuracy, we extract these qualities for a mixed scheme. Graphical and numerical consequences are introduced to fetch the useful information about the dynamical behavior of the Sharma–Tasso–Olver equation. From the output, we observe that the scheme is quite simple and effective which can be further used to handle a variety of other nonlinear problems. Using bifurcation theory of planar dynamical systems, we successfully studied the bifurcation behavior of nonlinear and supernonlinear traveling waves of STO equation through numerical simulation. It was seen that STO equation underpins nonlinear solitary wave, periodic wave, shock wave, stable oscillatory wave and most paramount two types of supernonlinear periodic waves.