1 Introduction

Hypersonic flight vehicles (HFVs) have spurred considerable attention owing to its promising prospect for a reliable and cost-efficient access to near-space for both civilian and military applications [1, 2]. To capture all of the potential effects on HFVs controllability, we must take into consideration aerodynamics, aerodynamic heating, and flexible airframe, as well as the interactions among these disciplines. For this reason, the vehicle model we developed is highly coupled and nonlinear. This makes hypersonic flight control a challenging research area. Moreover, owing to the inconstant of the vehicle characteristics including aerodynamics and thrust level with varying flight conditions, significant uncertainties affect the vehicle model [3,4,5,6,7]. Besides, HFVs usually experience extreme aerothermal loads that cause dynamic forces and moments to rapidly change, which further increase the model uncertainties.

The nonlinear and coupled motion model for HFVs implies that the vehicle model is completely nonaffine in the control inputs (For example, “\({\dot{x}}=f(x,u)\)” is nonaffine and “\(\dot{x}=g(x)+F(x)u\)” is affine, where x is the state, u is the control input, f(), g() and F() are given functions.). Noting that it is extreme difficult to directly design controls using such a highly coupled nonaffine system, lots of efforts are made to simplify HFV’s nonaffine models as affine ones, followed by affine control designs for HFVs [8,9,10,11,12,13]. In [14, 15], simplified affine models are firstly constructed applying the input/output linearization technique based on Lie derivative notations, and then affine sliding mode controllers are presented for HFVs to provide robust tracking of reference trajectories. Moreover, under rigorous assumptions/restrictions, HFVs’ motion models are directly simplified as affine ones of the formulations \({\dot{y}}_i =f_i (y_i )+g_i (y_i )u_i \) (\(f_i ()\) and \(g_i ()\ne 0\) are given functions, \(u_i \) and \(y_i \) are the control input and state, respectively.) [16,17,18,19], on this basis, various affine control methodologies are addressed. However, model simplifications mean that we neglect certain key dynamic characteristics of HFVs, probably resulting in invalidation of control systems [20]. Besides, additional techniques have to be attached to improve these controllers’ robust performance against system uncertainties especially the ones caused by model simplifications.

Noticing the fact that HFVs’ motion models are nonlinear in the control inputs, nonaffine control designs for them also spur considerable interests. In [21], an indirect nonaffine control method is investigated, that is, the HFV’s nonaffine model is firstly equivalently converted into an affine one by adding and subtracting the same term \(k_{i}u_{i}\) (\(u_{i}\) is the control input, and \(k_{i}\) is a positive constant to be designed.) in each subsystem of HFV’s model, and then an affine controller is devised. Another indirect nonaffine control strategy [22, 23] is exploited by transforming the nonaffine motion model into an affine one based on Mean Value Theorem, which yields an unknown control direction problem that is handed by introducing a Nussbaum-type function.

Despite excellent tracking performance obtained by the previous studies, it is worth pointing out that there is still a considerable lack of effort in direct nonaffine control designs. Therefore, in this paper, we propose a novel direct nonaffine control methodology for HFVs. The special contributions are as summarized follows.

  1. (1)

    A direct nonaffine hybrid control is presented based on the invertible theory, which avoids model simplifications and exhibits fine practicability and reliability.

  2. (2)

    To guarantee the addressed hybrid controllers with satisfactory robustness against pragmatic uncertainties, fuzzy wavelet neural networks (FWNNs) are applied to estimate unknown flight dynamics. Furthermore, the computational costs for online learning parameters are reduced by developing modified regulation laws.

  3. (3)

    In contrast to the existing methods, larger stable region of the closed-loop control system is achieved owing to the developed robust terms.

The rest of this paper is structured as follows. Problem formulations are presented in Sect. 2. Section 3 shows the design procedure of hybrid controller. Simulation results are given in Sect. 4, and the conclusions are shown in Sect. 5.

2 Problem formulation

2.1 Vehicle model

In this study, we use a longitudinal motion model developed by Parker, formulated as [7]

$$\begin{aligned}&{\dot{V}}=T\cos (\theta -\gamma )/m-D/m-g\sin \gamma \end{aligned}$$
(1)
$$\begin{aligned}&{\dot{h}}=V\sin \gamma \end{aligned}$$
(2)
$$\begin{aligned}&{\dot{\gamma }}=L/(mV)+T\sin (\theta -\gamma )/(mV)\nonumber \\&\qquad -\,(g/V)\cos \gamma \end{aligned}$$
(3)
$$\begin{aligned}&{\dot{\theta }}=Q \end{aligned}$$
(4)
$$\begin{aligned}&{\dot{Q}}=(M+{\tilde{\psi }}_1 {\ddot{\eta }}_1 +{\tilde{\psi }}_2 {\ddot{\eta }}_2 )/I_{\mathrm{yy}} \end{aligned}$$
(5)
$$\begin{aligned}&k_1 {\ddot{\eta }}_1 =-\,2\zeta _1 \omega _1 {\dot{\eta }}_1 -\omega _1^2 \eta _1 +N_1 \nonumber \\&\qquad \,\quad -{\tilde{\psi }}_1 M/I_{\mathrm{yy}} -\tilde{\psi }_1 {\tilde{\psi }}_2 {\ddot{\eta }}_2 /I_{\mathrm{yy}} \end{aligned}$$
(6)
$$\begin{aligned}&k_2 {\ddot{\eta }}_2 =-\,2\zeta _2 \omega _2 {\dot{\eta }}_2 -\omega _2^2 \eta _2 +N_2 -{\tilde{\psi }}_2 M/I_{\mathrm{yy}} \nonumber \\&\qquad \,\quad -\tilde{\psi }_2 {\tilde{\psi }}_1 {\ddot{\eta }}_1 /I_{\mathrm{yy}} \end{aligned}$$
(7)

In the above model, velocity V, altitude h, flight-path angle \(\gamma \), pitch angle \(\theta \) and pitch rate Q are the rigid body states, \(\eta _{1}\) and \(\eta _{2 }\) are the flexible states. The attack angle \(\alpha =\theta -\gamma \). The thrust force T, drag force D, lift force L, pitching moment M and the generalized force \(N_{1}\) and \(N_{2}\) are defined as [7]

$$\begin{aligned}&T\approx \beta _1 \left( {h,{\bar{q}}} \right) \varPhi \alpha ^{3}+\beta _2 \left( {h,{\bar{q}}} \right) \alpha ^{3}\\&\qquad +\beta _3 \left( {h,{\bar{q}}} \right) \varPhi \alpha ^{2}+\beta _4 \left( {h,{\bar{q}}} \right) \alpha ^{2} \\&\qquad +\beta _5 \left( {h,{\bar{q}}} \right) \varPhi \alpha +\beta _6 \left( {h,{\bar{q}}} \right) \alpha \\&\qquad +\beta _7 \left( {h,{\bar{q}}} \right) \varPhi +\beta _8 \left( {h,{\bar{q}}} \right) , \\&D\approx {\bar{q}}SC_\mathrm{D}^{\alpha ^{2}} \alpha ^{2}+\,{\bar{q}}SC_\mathrm{D}^\alpha \alpha +{\bar{q}}SC_\mathrm{D}^{\delta _\mathrm{e}^2 } \delta _\mathrm{e}^2 \\&\qquad \ +\,{\bar{q}}SC_\mathrm{D}^{\delta _\mathrm{e} } \delta _\mathrm{e} +{\bar{q}}SC_\mathrm{D}^0 ,\\&M\approx z_\mathrm{T} T+{\bar{q}}S{\bar{c}}C_{M,\alpha }^{\alpha ^{2}} \alpha ^{2}+{\bar{q}}S{\bar{c}}C_{M,\alpha }^\alpha \alpha +{\bar{q}}S{\bar{c}}C_{M,\alpha }^0 \\&\qquad +\,{\bar{q}}S{\bar{c}}c_\mathrm{e} \delta _\mathrm{e} , \\&L\approx {\bar{q}}SC_\mathrm{L}^\alpha \alpha +{\bar{q}}SC_\mathrm{L}^{\delta _\mathrm{e} } \delta _\mathrm{e} +{\bar{q}}SC_\mathrm{L}^0 ,\\&N_1 =N_1^{\alpha ^{2}} \alpha ^{2}+N_1^\alpha \alpha +N_1^0 ,\\&N_2 =N_2^{\alpha ^{2}} \alpha ^{2}+N_2^\alpha \alpha +N_2^{\delta _\mathrm{e} } \delta _\mathrm{e} +N_2^0 , \quad {\bar{q}}={{\bar{\rho }}V^{2}}/2, \\&{\bar{\rho }}={\bar{\rho }}_0 \exp \left( {-{\left( {h-h_0 } \right) }/{h_\mathrm{s} }} \right) , \end{aligned}$$

where the control inputs \(\varPhi \) and \(\delta _{\mathrm{e}}\) denote fuel equivalence ratio and elevator angular deflection, respectively. For more detailed definitions of other parameters and coefficients, the reader could refer to [7] or Nomenclature

Remark 1

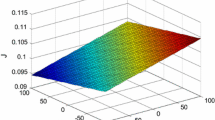
Some sample plots [7] of aerodynamic data derived from the above vehicle model are shown in Fig. 1. Obviously, the HFVs’ model is completely nonaffine, which is due to that the above motion model contains these nonlinear terms “\(\delta _\mathrm{e}^2 \),” “\(\alpha ^{3}\)” and “\(\alpha ^{2}\).” (For back-stepping designs, \(\alpha \) is treated as a virtual control input.) For this reason, in what follows, we directly employ the vehicle nonaffine model to devise controllers. Furthermore, to represent the entire model’s features, the pole-zero map [7] is depicted in Fig. 2.

Fig. 1
figure 1

The responses of drag, lift and moment along with the varying of \(\alpha \) and \(\delta _e \). a The response of drag. b, the response of lift, c the response of moment

Full size image

2.2 Control objective

To facilitate the subsequent control designs, the motion model of HFVs is formally decomposed into the velocity subsystem (i.e., Eq. (1)) and the altitude subsystem (i.e., Eqs. (2)–(5)).

The velocity subsystem (1) is rewritten as a succinct nonaffine formulation:

$$\begin{aligned} \left\{ {\begin{array}{l} {\dot{V}}=f_V (V,\varPhi ) \\ y_V =V \\ u_V =\varPhi \\ \end{array}} \right. \end{aligned}$$
(8)

where \(f_V (V,\varPhi )\) is an unknown differentiable function; \(u_V \) and \(y_V \) are the control input and output of velocity subsystem, respectively.

Building upon the previous studies [22, 23], the altitude subsystem (3)–(5) can be transformed as the following nonaffine form:

$$\begin{aligned} \left\{ {\begin{array}{l} {\dot{z}}_1 =z_2 \\ {\dot{z}}_2 =z_3 \\ {\dot{z}}_3 =F_h ({\varvec{ x}},\delta _\mathrm{e} ) \\ y_h =z_1 =\gamma \\ u_h =\delta _\mathrm{e} \\ \end{array}} \right. \end{aligned}$$
(9)

where \(F_h ({\varvec{x}}, \delta _\mathrm{e} )\) is an unknown differentiable function and \({\varvec{x}}=[\gamma ,\theta ,Q]^{\mathrm{T}}\in \mathfrak {R}^{3}\); \(u_h \) and \(y_h \) mean the control input and output of altitude subsystem, respectively.

The pursued control objective is that velocity V and altitude h follow their reference trajectories \(V_{\mathrm{ref}}\) and \(h_{\mathrm{ref}}\) in the presence of parametric uncertainties by developing direct nonaffine hybrid controllers \(\varPhi \) and \(\delta _{\mathrm{e}}\).

2.3 FWNN approximate

FWNN is combined wavelet theory with fuzzy logic and neural networks (NNs). Because fuzzy logics can improve wavelet neural approximation performance, FWNN exhibits excellent performance and global approximation [24, 25]. Thus, we employ it as an accurate function approximator in this study.

For the simplify of formulation, by employing a singleton fuzzifier, product inference and weighted average defuzzifier, the output of FWNN can be described as

$$\begin{aligned} y={\varvec{W}}^{\mathrm{T}}{\varvec{\psi }} ({\varvec{\ell }} ) \end{aligned}$$
(10)

where \({\varvec{\ell }} =[\ell _1 ,\ell _2 ,\cdots ,\ell _n ]^{\mathrm{T}}\in \mathfrak {R}^{n}\) is the input vector and \({\varvec{W}}^{\mathrm{T}}=[w_1 ,w_1 ,\cdots ,w_N ]^{\mathrm{T}}\in \mathfrak {R}^{N}\) is the weight matrix; \({\varvec{\psi }} ({\varvec{\ell }} )=[{{\psi }} _1 ({\varvec{\ell }} ), \psi _2 ({\varvec{\ell }} ),\cdots ,\psi _N ({\varvec{\ell }} )]^{\mathrm{T}}\) is the fuzzy wavelet basis function vector and \(\psi _j ()\) has the following formulation:

$$\begin{aligned} \psi _j ={\prod _{i=1}^n {g_{ji} (\ell _i )} \phi _j }\Bigg /{\sum _{j=1}^N {\phi _j } } \end{aligned}$$
(11)

where \(g_{ji} (\ell _i )=1-b_{ji}^2 (\ell _i -c_{ji} )^{2}\) and \(\phi _j =\prod \nolimits _{i=1}^n {\mu _{A_{ji} } (\ell _i )} \) is the firing strength with the membership function \(\mu _{A_{ji} } (\ell _i )\) given by \(\mu _{A_{ji} } (\ell _i )=\exp (-\,b_{ji}^2 (\ell _i -c_{ji} )^{2})\); \(b_{ji} \) and \(c_{ji} \) are dilation and translation parameters, respectively.

Fig. 2
figure 2

Pole-zero maps of the Jacobian linearization of the adopted HFV model. Inputs \(u=[\varPhi , \delta _\mathrm{e}]\), outputs \(y=[V, \gamma \)]

Full size image

Traditionally, Taylor expansion linearization technique is usually applied to convert the nonlinear fuzzy wavelet basis function into a partially linear function of \(\psi _j \), \(b_{ji} \) and \(c_{ji} \) [24]. Then, parameters \(\psi _j \), \(b_{ji} \) and \(c_{ji} \) are all online regulated for the sake of achieving desired approximation performance. This leads to high computational burden and reduces the real-time performance of control system. Therefore, an advanced learning scheme is adopted to directly turn \(\varphi =\left\| {{\varvec{\psi }} ({\varvec{\ell }} )} \right\| ^{2}\) by setting appropriate values for \(b_{ji} \) and \(c_{ji} \). In this way, there is only one learning parameter \(\varphi \). Thus, the online computational load is low.

3 Hybrid control design

3.1 Velocity control design

Assumption 1

[21] \(\partial f_V (V,\varPhi )/\partial \varPhi \) is continuous and positive.

Define velocity tracking error \({\tilde{V}}=V-V_{\mathrm{ref}} \). Then using (8), \(\dot{{\tilde{V}}}\) is derived as

$$\begin{aligned} \dot{{\tilde{V}}}={\dot{V}}-{\dot{V}}_{\mathrm{ref}} =f_V (V,\varPhi )-\dot{V}_{\mathrm{ref}} \end{aligned}$$
(12)

From (12), a hybrid pseudocontrol \(\upsilon _V \) is developed as

$$\begin{aligned} \upsilon _V =\hat{{f}}_V (V,\varPhi ) \end{aligned}$$
(13)

where \(\hat{{f}}_V (V,\varPhi )\) denotes the approximate of \(f_V (V,\varPhi )\). Define the inversion error \(\delta _V =f_V (V,\varPhi )- \hat{{f}}_V (V,\varPhi )\) and then Eq. (12) becomes

$$\begin{aligned} \dot{{\tilde{V}}}=\delta _V +\hat{{f}}_V (V,\varPhi )-{\dot{V}}_{\mathrm{ref}} \end{aligned}$$
(14)

Assumption 2

It is concluded from Assumption 1 that \(\partial \hat{{f}}_V (V,\varPhi )/\partial \varPhi \) also is continuous and positive.

The hybrid controller \(\upsilon _V \) is designed as

$$\begin{aligned} \upsilon _V =\upsilon _{V1} +\upsilon _{V2} -\upsilon _{V3} +\upsilon _{V4} \end{aligned}$$
(15)

where \(\upsilon _{V1} ={\dot{V}}_{\mathrm{ref}} \) and \(\upsilon _{V2} =-K_{V1} {\tilde{V}}-K_{V2} \int _0^t {\tilde{V}}(\tau )\hbox {d}\tau \); \(K_{V1} \in \mathfrak {R}^{+}\) and \(K_{V2} \in \mathfrak {R}^{+}\) are constants to be chosen; \(\upsilon _{V4} \) is a robust term and \(\upsilon _{V3} \) will be devised to cancel \(\delta _V \).

The control input \(\varPhi \) is derived from (13) as follows

$$\begin{aligned} \varPhi =\hat{{f}}_V^{-1} (V,\upsilon _V ) \end{aligned}$$
(16)

Substituting (13) and (15) into (14), we have

$$\begin{aligned} \dot{{\tilde{V}}}= & {} \delta _V +\upsilon _V -{\dot{V}}_{\mathrm{ref}} \nonumber \\= & {} \delta _V +\upsilon _{V1} +\upsilon _{V2} -\upsilon _{V3} +\upsilon _{V4} -{\dot{V}}_{\mathrm{ref}} \nonumber \\= & {} -K_{V1} {\tilde{V}}-K_{V2} \int _0^t {{\tilde{V}}(\tau )\hbox {d}\tau } +\delta _V -\upsilon _{V3} +\upsilon _{V4}\nonumber \\ \end{aligned}$$
(17)

with

$$\begin{aligned}&\delta _V -\upsilon _{V3} =f_V (V,\hat{{f}}_V^{-1} (V,\upsilon _{V1} {+}\upsilon _{V2} {-}\upsilon _{V3} {+}\upsilon _{V4} ))\nonumber \\&\qquad \quad -\hat{{f}}(V,\hat{{f}}_V^{-1} (V,\upsilon _{V1} {+}\upsilon _{V2} {-}\upsilon _{V3} {+}\upsilon _{V4} ))-\upsilon _{V3} \nonumber \\&\quad =f_V (V,\hat{{f}}_V^{-1} (V,\upsilon _{V1} +\upsilon _{V2} -\upsilon _{V3} +\upsilon _{V4} ))\nonumber \\&\qquad \quad -\upsilon _{V1} -\upsilon _{V2} -\upsilon _{V4} \end{aligned}$$
(18)

By defining \(\upsilon _{Vl}\, \buildrel \Delta \over = \,\upsilon _{V1} +\upsilon _{V2} \) and \(\upsilon _V^*\,\buildrel \Delta \over = \, \hat{{f}}_V (V,f_V^{-1} (V,\upsilon _{Vl} ))\), we obtain \(f_V^{-1} (V,\upsilon _{Vl} )=\hat{{f}}_V^{-1} (V,\upsilon _V^*)\Rightarrow \upsilon _{Vl} =f_V (V,\hat{{f}}_V^{-1} (V,\upsilon _V^*))\). Then, Eq. (18) becomes

$$\begin{aligned} \delta _V -\upsilon _{V3}= & {} f_V (V,\hat{{f}}_V^{-1} (V,\upsilon _V ))-\upsilon _{Vl} -\upsilon _{V4} \nonumber \\= & {} f_V (V,\hat{{f}}_V^{-1} (V,\upsilon _V ))\nonumber \\&-f_V (V,\hat{{f}}_V^{-1} (V,\upsilon _V^*))-\upsilon _{V4} \end{aligned}$$
(19)

By Mean Value Theorem, Eq. (19) is further rewritten as

$$\begin{aligned}&\delta _V -\upsilon _{V3} =f_V (V,\hat{{f}}_V^{-1} (V,\upsilon _V ))\nonumber \\&\qquad \quad -f_V (V,\hat{{f}}_V^{-1} (V,\upsilon _V^*))-\upsilon _{V4} \nonumber \\&\quad =f_V ({\bar{\upsilon }}_V )(\upsilon _V -\upsilon _V^*)-\upsilon _{V4} \nonumber \\&\quad =f_V ({\bar{\upsilon }}_V )(\upsilon _{Vl} -\upsilon _{V3} +\upsilon _{V4} \nonumber \\&\qquad -\hat{{f}}_V (V,f_V^{-1} (V,\upsilon _{Vl} )))-\upsilon _{V4} \nonumber \\&\quad =f_V ({\bar{\upsilon }}_V )({\bar{\upsilon }}_{Vl} -\upsilon _{V3} +\upsilon _{V4} )-\upsilon _{V4} \end{aligned}$$
(20)

where \({\bar{\upsilon }}_{Vl} =\upsilon _{Vl} -\hat{{f}}_V (V,f_V^{-1} (V,\upsilon _{Vl} ))=f_V (V,\hat{{f}}_V^{-1} (V,\upsilon _V^*))-\upsilon _V^*\) is an unknown term; \(f_V ({\bar{\upsilon }}_V )= \left. {\frac{\partial f_V }{\partial \varPhi }\frac{\partial \varPhi }{\partial \upsilon _V }} \right| _{\upsilon _V ={\bar{\upsilon }}_V } =\left. {\frac{\partial f_V }{\partial \varPhi }\frac{\partial \hat{{f}}_V }{\partial \varPhi }} \right| _{\varPhi =\hat{{f}}_V^{-1} (V,{\bar{\upsilon }}_V )} >0\) and \({\bar{\upsilon }}_V =\theta _V \upsilon _V +(1-\theta _V )\upsilon _V^*\) with \(\theta _V \in [0,1]\).

Substituting (20) into (17) yields

$$\begin{aligned} \dot{{\tilde{V}}}= & {} -K_{V1} {\tilde{V}}-K_{V2} \int _0^t {\tilde{V}(\tau )\hbox {d}\tau } +f_V ({\bar{\upsilon }}_V )({\bar{\upsilon }}_{Vl} \nonumber \\&-\upsilon _{V3} )+f_V ({\bar{\upsilon }}_V )\upsilon _{V4} \end{aligned}$$
(21)

If \({\bar{\upsilon }}_{Vl} \) is known, we can set \(\upsilon _{V3} ={\bar{\upsilon }}_{Vl} \) to stabilize (8). However, \({\bar{\upsilon }}_{Vl} \) is usually unknown and hereon we employ one FWNN to approximate it. Based on the universal approximation theorem [24, 25], there must exist an ideal weight vector \({\varvec{W}}_V^{*} \in \mathfrak {R}^{N}\) such that

$$\begin{aligned} {\bar{\upsilon }}_{Vl} ={\varvec{W}}_V^{\mathrm{*T}} {\varvec{\psi }} _V ({\varvec{\ell }} _V )+\varepsilon _V \end{aligned}$$
(22)

where \({\varvec{\ell }} _V =V\) is the input of FWNN and \({\varvec{\psi }} _V ({\varvec{\ell }} _V )\) has the same formulation as (11); \(\varepsilon _V \) is an approximation error and there is a constant \(\varepsilon _{V{\mathrm{M}}} \in \mathfrak {R}^{+}\) such that \(|\varepsilon _V |\le \varepsilon _{V{\mathrm{M}}} \).

Define \(\varphi _V =\left\| {{\varvec{W}}_V^*} \right\| ^{2}\in \mathfrak {R}\) and \(\upsilon _{V3} \) is devised as

$$\begin{aligned} \upsilon _{V3} =\frac{1}{2}{\tilde{V}}\hat{{\varphi }}_V {\varvec{\psi }} _V^\mathrm{T} ({\varvec{\ell }} _V ){\varvec{\psi }} _V ({\varvec{\ell }} _V ) \end{aligned}$$
(23)

where \(\hat{{\varphi }}_V \) denotes the estimate of \(\varphi _V \).

For the single online parameter \(\hat{{\varphi }}_V \), we design the following adaptive law:

$$\begin{aligned} \dot{\hat{{\varphi }}}_V =\frac{\eta _V }{2}\tilde{V}^{2}{\varvec{\psi }} _V^\mathrm{T} ({\varvec{\ell }} _V ){\varvec{\psi }} _V ({\varvec{\ell }} _V )-2\hat{{\varphi }}_V \end{aligned}$$
(24)

with \(\eta _V \in \mathfrak {R}^{+}\).

Employing (22) and (23), \({\bar{\upsilon }}_{Vl} -\upsilon _{V3} \) equals to

$$\begin{aligned}&{\bar{\upsilon }}_{Vl} -\upsilon _{V3} ={\varvec{W}}_V^{\mathrm{*T}} {\varvec{\psi }} _V ({\varvec{\ell }} _V )+\varepsilon _V \nonumber \\&\quad \qquad -\frac{1}{2}\tilde{V}\hat{{\varphi }}_V {\varvec{\psi }} _V^\mathrm{T} ({\varvec{\ell }} _V ){\varvec{\psi }} _V ({\varvec{\ell }}_V ) \end{aligned}$$
(25)

Considering (25), Eq. (21) becomes

$$\begin{aligned} \dot{{\tilde{V}}}= & {} -\,K_{V1} {\tilde{V}}-K_{V2} \int _0^t {\tilde{V}(\tau )\hbox {d}\tau } \nonumber \\&+f_V ({\bar{\upsilon }}_V ){\varvec{W}}_V^{\mathrm{*T}} {\varvec{\psi }} _V ({\varvec{\ell }} _V )+f_V ({\bar{\upsilon }}_V )\varepsilon _V \nonumber \\&-\frac{1}{2}f_V ({\bar{\upsilon }}_V ){\tilde{V}}\hat{{\varphi }}_V {\varvec{\psi }} _V^\mathrm{T} ({\varvec{\ell }} _V ){\varvec{\psi }} _V ({\varvec{\ell }} _V )\nonumber \\&+f_V ({\bar{\upsilon }}_V )\upsilon _{V4} \end{aligned}$$
(26)

The robust term \(\upsilon _{V4} \) is chosen as

$$\begin{aligned} \upsilon _{V4} =-\frac{{\tilde{V}}}{2\rho _V^2 } \end{aligned}$$
(27)

where \(\rho _V \in \mathfrak {R}^{+}\) is a constant to be selected.

Taking into consideration (27), it is derived from (26) that

$$\begin{aligned} \dot{{\tilde{V}}}= & {} -K_{V1} {\tilde{V}}-K_{V2} \int _0^t {\tilde{V}(\tau )\hbox {d}\tau }\nonumber \\&+f_V ({\bar{\upsilon }}_V ){\varvec{W}}_V^{\mathrm{*T}} {\varvec{\psi }} _V ({\varvec{\ell }} _V )+f_V ({\bar{\upsilon }}_V )\varepsilon _V \nonumber \\&-\frac{1}{2}f_V ({\bar{\upsilon }}_V ){\tilde{V}}\hat{{\varphi }}_V {\varvec{\psi }} _V^\mathrm{T} ({\varvec{\ell }} _V ){\varvec{\psi }} _V ({\varvec{\ell }} _V )\nonumber \\&-f_V ({\bar{\upsilon }}_V )\frac{{\tilde{V}}}{2\rho _V^2 } \end{aligned}$$
(28)

Theorem 1

Consider the closed-loop system consisting of plant (8) under Assumptions 1 and 2 with controller (15) and adaptive law (24). Then, all the signals involved are semi-globally uniformly ultimately bounded.

Proof

Define estimate error \({\tilde{\varphi }}_V =\hat{{\varphi }}_V -\varphi _V \).

Define the following Lyapunov function:

$$\begin{aligned} V_V =\frac{{\tilde{V}}^{2}}{2}+\frac{K_{V2} }{2}\left( {\int _0^t {{\tilde{V}}(\tau )\hbox {d}\tau } } \right) ^{2}+\frac{{\bar{f}}_V {\tilde{\varphi }}_V^2 }{2\eta _V } \end{aligned}$$
(29)

where \({\bar{f}}_V \in \mathfrak {R}^{+}\) is a constant to be ingeniously selected such that \({\bar{f}}_V \le f_V ({\bar{\upsilon }}_V )\)when \({\tilde{\varphi }}_V \dot{{\tilde{\varphi }}}_V \ge 0\) or else \({\bar{f}}_V >f_V ({\bar{\upsilon }}_V )\). We further have \({{\bar{f}}_V {\tilde{\varphi }}_V \dot{\tilde{\varphi }}_V }/{\eta _V }\le {f_V ({\bar{\upsilon }}_V )\tilde{\varphi }_V \dot{{\tilde{\varphi }}}_V }/{\eta _V }\).

The time derivative of \(V_V \) is given by

$$\begin{aligned} {\dot{V}}_V= & {} {\tilde{V}}\dot{{\tilde{V}}}+K_{V2} {\tilde{V}}\int _0^t {{\tilde{V}}(\tau )\hbox {d}\tau } +\frac{{\bar{f}}_V }{\eta _V }{\tilde{\varphi }}_V \dot{{\tilde{\varphi }}}_V \nonumber \\\le & {} {\tilde{V}}\dot{{\tilde{V}}}+K_{V2} {\tilde{V}}\int _0^t {{\tilde{V}}(\tau )\hbox {d}\tau } \nonumber \\&+\frac{f_V ({\bar{\upsilon }}_V )}{\eta _V }\tilde{\varphi }_V \dot{\hat{{\varphi }}}_V \end{aligned}$$
(30)

Substituting (24) and (28) into (30) leads to

$$\begin{aligned} {\dot{V}}_V\le & {} -K_{V1} {\tilde{V}}^{2}+f_V ({\bar{\upsilon }}_V ){\tilde{V}}{\varvec{W}}_V^{\mathrm{*T}} {\varvec{\psi }} _V ({\varvec{\ell }} _V )\nonumber \\&+f_V ({\bar{\upsilon }}_V ){\tilde{V}}\varepsilon _V \nonumber \\&-\frac{1}{2}f_V ({\bar{\upsilon }}_V ){\tilde{V}}^{2}\hat{{\varphi }}_V {\varvec{\psi }} _V^\mathrm{T} ({\varvec{\ell }} _V ){\varvec{\psi }} _V ({\varvec{\ell }} _V ) \nonumber \\&-f_V ({\bar{\upsilon }}_V )\frac{{\tilde{V}}^{2}}{2\rho _V^2 }\nonumber \\&+\frac{1}{2}f_V ({\bar{\upsilon }}_V ){\tilde{V}}^{2}{\tilde{\varphi }}_V {\varvec{\psi }} _V^\mathrm{T} ({\varvec{\ell }} _V ){\varvec{\psi }} _V ({\varvec{\ell }} _V )\nonumber \\&-\frac{2f_V ({\bar{\upsilon }}_V ){\tilde{\varphi }}_V \hat{{\varphi }}_V }{\eta _V } \nonumber \\= & {} -K_{V1} {\tilde{V}}^{2}+f_V ({\bar{\upsilon }}_V )\tilde{V}{\varvec{W}}_V^{\mathrm{*T}} {\varvec{\psi }} _V ({\varvec{\ell }} _V )\nonumber \\&+f_V ({\bar{\upsilon }}_V )\tilde{V}\varepsilon _V \nonumber \\&-\frac{1}{2}f_V ({\bar{\upsilon }}_V ){\tilde{V}}^{2}\varphi _V {\varvec{\psi }} _V^\mathrm{T} ({\varvec{\ell }} _V ){\varvec{\psi }} _V ({\varvec{\ell }} _V )\nonumber \\&-f_V ({\bar{\upsilon }}_V )\frac{{\tilde{V}}^{2}}{2\rho _V^2 }\nonumber \\&-\frac{2f_V ({\bar{\upsilon }}_V ){\tilde{\varphi }}_V \hat{{\varphi }}_V }{\eta _V } \end{aligned}$$
(31)

Notice that \({\tilde{V}}{\varvec{W}}_V^{\mathrm{*T}} {\varvec{\psi }} _V ({\varvec{\ell }} _V )\le \frac{{\tilde{V}}^{2}}{2}\left\| {{\varvec{W}}_V^{\mathrm{*T}} {\varvec{\psi }} _V ({\varvec{\ell }} _V )} \right\| ^{2}+\frac{1}{2}=\frac{{\tilde{V}}^{2}}{2}\left\| {{\varvec{W}}_V^\mathrm{*} } \right\| ^{2}\left\| {{\varvec{\psi }} _V ({\varvec{\ell }} _V )} \right\| ^{2}+\frac{1}{2}=\frac{{\tilde{V}}^{2}}{2}\varphi _V {\varvec{\psi }} _V^T ({\varvec{\ell }} _V ){\varvec{\psi }} _V ({\varvec{\ell }} _V ) +\frac{1}{2}\), \(2\tilde{\varphi }_V \hat{{\varphi }}_V \ge {\tilde{\varphi }}_V^2 -\varphi _V^2 \) and \(\tilde{V}\varepsilon _V \le \left| {{\tilde{V}}} \right| \varepsilon _{VM} =2\left| {\frac{{\tilde{V}}}{2}} \right| \varepsilon _{VM} \le \frac{{\tilde{V}}^{2}}{4}+\varepsilon _{VM}^2 \). Therefore, inequality (31) becomes

$$\begin{aligned} {\dot{V}}_V\le & {} -K_{V1} {\tilde{V}}^{2}-\frac{f_V ({\bar{\upsilon }}_V ){\tilde{\varphi }}_V^2 }{\eta _V }+\frac{f_V ({\bar{\upsilon }}_V ){\tilde{V}}^{2}}{4}\nonumber \\&-f_V ({\bar{\upsilon }}_V )\frac{\tilde{V}^{2}}{2\rho _V^2 }+\frac{f_V ({\bar{\upsilon }}_V )\varphi _V^2 }{\eta _V }+\frac{1}{2}f_V ({\bar{\upsilon }}_V )\nonumber \\&+f_V ({\bar{\upsilon }}_V )\varepsilon _{VM}^2 \end{aligned}$$
(32)

Setting \(\rho _V =\sqrt{2}\), we have

$$\begin{aligned} {\dot{V}}_V\le & {} -K_{V1} {\tilde{V}}^{2}-\frac{f_V ({\bar{\upsilon }}_V ){\tilde{\varphi }}_V^2 }{\eta _V }+\frac{f_V ({\bar{\upsilon }}_V )\varphi _V^2 }{\eta _V }\nonumber \\&+\frac{1}{2}f_V ({\bar{\upsilon }}_V )+f_V ({\bar{\upsilon }}_V )\varepsilon _{VM}^2 \end{aligned}$$
(33)

Define the following compact sets:

$$\begin{aligned}&\Omega _{{\tilde{V}}} =\left\{ {\tilde{V}}\left| \left| {{\tilde{V}}} \right| \right. \right. \nonumber \\&\left. \left. \le \sqrt{{\left( {\frac{f_V ({\bar{\upsilon }}_V )\varphi _V^2 }{\eta _V }+\frac{1}{2}f_V ({\bar{\upsilon }}_V )+f_V ({\bar{\upsilon }}_V )\varepsilon _{VM}^2 } \right) }/{K_{V1} }} \right. \right\} \nonumber \\&\Omega _{{\tilde{\varphi }}_V } =\left\{ {{\tilde{\varphi }}_V \left| {\left| {{\tilde{\varphi }}_V } \right| \le \sqrt{{\left( {\frac{\varphi _V^2 }{\eta _V }+\frac{1}{2}+\varepsilon _{VM}^2 } \right) }/{\left( {\frac{1}{\eta _V }} \right) }}} \right. } \right\} \nonumber \\ \end{aligned}$$
(34)

If \({\tilde{V}}\notin \Omega _{{\tilde{V}}} \) or \({\tilde{\varphi }}_V \notin \Omega _{{\tilde{\varphi }}_V } \), we have \({\dot{V}}_V <0\). Hence, \({\tilde{V}}\) and \({\tilde{\varphi }}_V \) are semi-globally uniformly ultimately bounded. Moreover, by choosing adequately large \(K_{V1} \), the velocity tracking error \({\tilde{V}}\) can be arbitrarily small. This completes the proof. \(\square \)

3.2 Altitude control design

Assumption 3

[21] \(\partial F_h ({{\varvec{x}}},\delta _\mathrm{e} )/\partial \delta _\mathrm{e} \) is continuous and positive.

Define altitude tracking error \({\tilde{h}}=h-h_{\mathrm{ref}} \) and the reference command \(\gamma _\mathrm{d} =\arcsin \big ( -\,\kappa _h {\tilde{h}}/V+{\dot{h}}_{\mathrm{ref}} /V \big )\) with \(\kappa _h \in \mathfrak {R}^{+}\). When \(\gamma \rightarrow \gamma _{\mathrm{d}}\), we have \(\kappa _h \dot{{\tilde{h}}}=-\,{\tilde{h}}\), that is, \(\dot{{\tilde{h}}}\tilde{h}=-\,{{\tilde{h}}^{2}}/{\kappa _h }\le 0\) and \({\tilde{h}}\) can converge to zero when \(t\rightarrow \infty \). In what follows, the design objective becomes to let \(\gamma \rightarrow \gamma _{\mathrm{d}}\) by devising a hybrid control \(\delta _{\mathrm{e}}\).

Define flight-path angle tracking error \(e_{h}\) and error function \(E_{h}\) as

$$\begin{aligned} \left\{ {\begin{array}{l} e_h =\gamma -\gamma _\mathrm{d} =z_1 -\gamma _\mathrm{d} \\ E_h =\left( {\frac{\hbox {d}}{\hbox {d}t}+\mu _h } \right) ^{3}\int _0^t {e_h {(}\tau \hbox {)d}\tau } \\ \end{array}} \right. \end{aligned}$$
(35)

where \(\mu _h \in \mathfrak {R}^{+}\) and the polynomial (\(s+ \mu _{h})^{3}\) is Hurwitz.

Define

$$\begin{aligned} \left\{ {\begin{array}{l} \xi _1 ={\dot{e}}_h \\ \xi _2 ={\dot{\xi }}_1 \\ \xi _3 ={\dot{\xi }}_2 \\ \end{array}} \right. \end{aligned}$$
(36)

Invoking (35) and (36), \({\dot{E}}_h \) is given by

$$\begin{aligned} {\dot{E}}_h= & {} \xi _3 +3\mu _h \xi _2 +3\mu _h^2 \xi _1 +\mu _h^3 e_h \nonumber \\= & {} F_h ({{\varvec{x}}},\delta _\mathrm{e} )-{\dddot{\gamma }}_\mathrm{d} +3\mu _h \xi _2 +3\mu _h^2 \xi _1 +\mu _h^3 e_h \end{aligned}$$
(37)

We design the following hybrid pseudocontrol \(\upsilon _h \):

$$\begin{aligned} \upsilon _h =\hat{{F}}_h ({{\varvec{x}}},\delta _\mathrm{e} ) \end{aligned}$$
(38)

where \(\hat{{F}}_h ({{\varvec{x}}},\delta _\mathrm{e} )\) represents the estimate of \(F_h ({{\varvec{x}}},\delta _\mathrm{e} )\) and the estimation error is formulated as \(\delta _h = F_h ({{\varvec{x}}},\delta _\mathrm{e} )-\hat{{F}}_h ({{\varvec{x}}},\delta _\mathrm{e} )\). Then Eq. (37) is rewritten as

$$\begin{aligned} {\dot{E}}_h =\delta _h +\hat{{F}}_h ({{\varvec{x}}},\delta _\mathrm{e} )-{\dddot{\gamma }}_\mathrm{d} +3\mu _h \xi _2 +3\mu _h^2 \xi _1 +\mu _h^3 e_h \end{aligned}$$
(39)

Assumption 4

Based on Assumption 3, we have that \(\partial \hat{{F}}_h ({{\varvec{x}}},\delta _\mathrm{e} )/\partial \delta _\mathrm{e} \) is continuous and positive.

We design the hybrid controller \(\upsilon _h \) as

$$\begin{aligned} \upsilon _h =\upsilon _{h1} +\upsilon _{h2} -\upsilon _{h3} +\upsilon _{h4} \end{aligned}$$
(40)

where \(\upsilon _{h1} ={\dddot{\gamma }}_\mathrm{d} \) and \(\upsilon _{h2} =-K_h E_h -(3\mu _h \xi _2 +3\mu _h^2 \xi _1 +\mu _h^3 e_h )\); \(K_h \in \mathfrak {R}^{+}\) is a chosen parameter and \(\upsilon _{h3} \) will be developed to handle \(\delta _h \); \(\upsilon _{h4} \) is a robust term to be designed.

From (38), we can directly achieve the following altitude control effort:

$$\begin{aligned} \delta _\mathrm{e} =\hat{{F}}_h^{-1} ({{\varvec{x}}},\upsilon _h ) \end{aligned}$$
(41)

Using (38) and (40), it is derived from (39) that

$$\begin{aligned} {\dot{E}}_h= & {} \delta _h +\upsilon _{h1} +\upsilon _{h2} -\upsilon _{h3} +\upsilon _{h4} -{\dddot{\gamma }}_\mathrm{d}\nonumber \\&+3\mu _h \xi _2 +3\mu _h^2 \xi _1 +\mu _h^3 e_h \nonumber \\= & {} -K_h E_h +\delta _h -\upsilon _{h3} +\upsilon _{h4} \end{aligned}$$
(42)

with

$$\begin{aligned}&\delta _h -\upsilon _{h3} =F_h ({{\varvec{x}}},\hat{{F}}_h^{-1} ({{\varvec{x}}},\upsilon _{h1} +\upsilon _{h2} -\upsilon _{h3} +\upsilon _{h4} )) \nonumber \\&\qquad -\hat{{F}}_h ({{\varvec{x}}},\hat{{F}}_h^{-1} ({{\varvec{x}}},\upsilon _{h1} +\upsilon _{h2} -\upsilon _{h3} +\upsilon _{h4} ))-\upsilon _{h3} \nonumber \\&\quad =F_h ({{\varvec{x}}},\hat{{F}}_h^{-1} ({{\varvec{x}}},\upsilon _{h1} +\upsilon _{h2} -\upsilon _{h3} +\upsilon _{h4} ))\nonumber \\&\qquad -\upsilon _{h1} -\upsilon _{h2} -\upsilon _{h4} \end{aligned}$$
(43)

Define \(\upsilon _{hl} \,\buildrel \Delta \over = \,\upsilon _{h1} +\upsilon _{h2} \) and \(\upsilon _h^*\,\buildrel \Delta \over = \, \hat{{F}}_h ({{\varvec{x}}},F_h^{-1} ({{\varvec{x}}},\upsilon _{hl} ))\). Then, we obtain \(\upsilon _{hl} =F_h ({{\varvec{x}}},\hat{{F}}_h^{-1} ({{\varvec{x}}},\upsilon _h^*))\). Thus, Eq. (43) becomes

$$\begin{aligned}&\delta _h -\upsilon _{h3} =F_h ({{\varvec{x}}},\hat{{F}}_h^{-1} ({{\varvec{x}}},\upsilon _h ))-\upsilon _{hl} -\upsilon _{h4} \nonumber \\&\quad =F_h ({{\varvec{x}}},\hat{{F}}_h^{-1} ({{\varvec{x}}},\upsilon _h ))-F_h ({{\varvec{x}}},\hat{{F}}_h^{-1} ({{\varvec{x}}},\upsilon _h^*))-\upsilon _{h4}\nonumber \\ \end{aligned}$$
(44)

Employing Mean Value Theorem, we further get

$$\begin{aligned} \delta _h -\upsilon _{h3}= & {} F_h ({{\varvec{x}}},\hat{{F}}_h^{-1} ({{\varvec{x}}},\upsilon _h ))\nonumber \\&-F_h ({{\varvec{x}}},\hat{{F}}_h^{-1} ({{\varvec{x}}},\upsilon _h^*))-\upsilon _{h4} \nonumber \\= & {} F_h ({\bar{\upsilon }}_h )(\upsilon _h -\upsilon _h^*)-\upsilon _{h4} \nonumber \\= & {} F_h ({\bar{\upsilon }}_h )(\upsilon _{hl} -\upsilon _{h3} +\upsilon _{h4} \nonumber \\&-\hat{{F}}_h ({{\varvec{x}}},F_h^{-1} ({{\varvec{x}}},\upsilon _{hl} )))-\upsilon _{h4} \nonumber \\= & {} F_h ({\bar{\upsilon }}_h )({\bar{\upsilon }}_{hl} -\upsilon _{h3} +\upsilon _{h4} )-\upsilon _{h4} \end{aligned}$$
(45)

where \({\bar{\upsilon }}_{hl} =\upsilon _{hl} -\hat{{F}}_h ({{\varvec{x}}},F_h^{-1} ({{\varvec{x}}},\upsilon _{hl} ))=F_h ({{\varvec{x}}},\hat{{F}}_h^{-1} ({{\varvec{x}}},\upsilon _h^*))-\upsilon _h^*\) is an unknown term; \(F_h ({\bar{\upsilon }}_h )= \quad \left. {\frac{\partial F_h }{\partial \delta _\mathrm{e} }\frac{\partial \delta _\mathrm{e} }{\partial \upsilon _h }} \right| _{\upsilon _h ={\bar{\upsilon }}_h } =\left. {\frac{\partial F_h }{\partial \delta _\mathrm{e} }\frac{\partial \hat{{F}}_h }{\partial \delta _\mathrm{e} }} \right| _{\delta _\mathrm{e} =\hat{{F}}_h^{-1} ({{\varvec{x}}},\upsilon _h )} >0\) and \({\bar{\upsilon }}_h =\theta _h \upsilon _h +(1-\theta _h )\upsilon _h^*\) with \(\theta _h \in [0,1]\).

Substituting (45) into (42) yields

$$\begin{aligned} {\dot{E}}_h =-K_h E_h +F_h ({\bar{\upsilon }}_h )({\bar{\upsilon }}_{hl} -\upsilon _{h3} )+F_h ({\bar{\upsilon }}_h )\upsilon _{h4}\nonumber \\ \end{aligned}$$
(46)

To cancel \({\bar{\upsilon }}_{hl} \), we define \(\upsilon _{h3} ={\bar{\upsilon }}_{hl} \). Owing to the fact that \({\bar{\upsilon }}_{hl} \) cannot be calculated since it is unknown, we also introduce one FWNN to approximate it.

$$\begin{aligned} {\bar{\upsilon }}_{hl} ={\varvec{W}}_h^{\mathrm{*T}} {\varvec{\psi }} _h ({\varvec{\ell }} _h )+\varepsilon _h \end{aligned}$$
(47)

where \({\varvec{\ell }} _h ={\varvec{x}}\) is the input vector of FWNN and \({\varvec{W}}_h^\mathrm{*} \in \mathfrak {R}^{N}\) is an ideal weight vector; the formulation of \({\varvec{\psi }} _h ({\varvec{\ell }} _h )\) is the same as (11); \(\varepsilon _h \) is the approximation error and there exists a constant \(\varepsilon _{h{\mathrm{M}}} \in \mathfrak {R}^{+}\) such that \(|\varepsilon _h |\le \varepsilon _{h{\mathrm{M}}} \).

We select the following \(\upsilon _{h3} \):

$$\begin{aligned} \upsilon _{h3} =\frac{1}{2}E_h \hat{{\varphi }}_h {\varvec{\psi }} _h^\mathrm{T} ({\varvec{\ell }} _h ){\varvec{\psi }} _h ({\varvec{\ell }} _h ) \end{aligned}$$
(48)

where \(\hat{{\varphi }}_h \) denotes the estimation of \(\varphi _h =\left\| {{\varvec{W}}_h^*} \right\| ^{2}\in \mathfrak {R}\) and its adaptive law is designed as

$$\begin{aligned} \dot{\hat{{\varphi }}}_h =\frac{\eta _h }{2}E_h^2 {\varvec{\psi }} _h^\mathrm{T} ({\varvec{\ell }} _h ){\varvec{\psi }} _h ({\varvec{\ell }} _h )-2\hat{{\varphi }}_h \end{aligned}$$
(49)

with \(\eta _h \in \mathfrak {R}^{+}\).

Based on (47) and (48), \(\delta _h -\upsilon _{h3} \) is described as

$$\begin{aligned} {\bar{\upsilon }}_{hl} -\upsilon _{h3} ={\varvec{W}}_h^{\mathrm{*T}} {\varvec{\psi }} _h ({\varvec{\ell }} _h )+\varepsilon _h -\frac{1}{2}E_h \hat{{\varphi }}_h {\varvec{\psi }} _h^\mathrm{T} ({\varvec{\ell }} _h ){\varvec{\psi }} _h ({\varvec{\ell }} _h ) \end{aligned}$$
(50)

Then Eq. (46) leads to

$$\begin{aligned} {\dot{E}}_h= & {} -K_h E_h +F_h ({\bar{\upsilon }}_h ){\varvec{W}}_h^{\mathrm{*T}} {\varvec{\psi }} _h ({\varvec{\ell }} _h )+F_h ({\bar{\upsilon }}_h )\varepsilon _h \nonumber \\&-\frac{1}{2}F_h ({\bar{\upsilon }}_h )E_h \hat{{\varphi }}_h {\varvec{\psi }} _h^\mathrm{T} ({\varvec{\ell }} _h ){\varvec{\psi }} _h ({\varvec{\ell }} _h )+F_h ({\bar{\upsilon }}_h )\upsilon _{h4}\nonumber \\ \end{aligned}$$
(51)

The robust term \(\upsilon _{h4} \) is chosen as

$$\begin{aligned} \upsilon _{h4} =-\frac{E_h }{2\rho _h^2 } \end{aligned}$$
(52)

where \(\rho _h \in \mathfrak {R}^{+}\) is a constant to be designed.

Substituting (52) into (51), we obtain

$$\begin{aligned} {\dot{E}}_h= & {} -K_h E_h +F_h ({\bar{\upsilon }}_h ){\varvec{W}}_h^{\mathrm{*T}} {\varvec{\psi }} _h ({\varvec{\ell }} _h )+F_h ({\bar{\upsilon }}_h )\varepsilon _h \nonumber \\&-\frac{1}{2}F_h ({\bar{\upsilon }}_h )E_h \hat{{\varphi }}_h {\varvec{\psi }} _h^\mathrm{T} ({\varvec{\ell }} _h ){\varvec{\psi }} _h ({\varvec{\ell }} _h )-F_h ({\bar{\upsilon }}_h )\frac{E_h }{2\rho _h^2 }\nonumber \\ \end{aligned}$$
(53)

Theorem 2

Consider the closed-loop system consisting of plant (3) under Assumptions 3 and 4 with controller (40) and adaptive law (49). Then, all the signals involved are semi-globally uniformly ultimately bounded.

Proof

Define estimate error \({\tilde{\varphi }}_h =\hat{{\varphi }}_h -\varphi _h \).

Define the following Lyapunov function:

$$\begin{aligned} V_h =\frac{E_h^2 }{2}+\frac{{\bar{F}}_h {\tilde{\varphi }}_h^2 }{2\eta _h } \end{aligned}$$
(54)

where \({\bar{F}}_h \in \mathfrak {R}^{+}\) is a constant to be ingeniously chosen such that \({\bar{F}}_h \le F_h ({\bar{\upsilon }}_h )\)when \({\tilde{\varphi }}_h \dot{{\tilde{\varphi }}}_h \ge 0\) or else \({\bar{F}}_h >F_h ({\bar{\upsilon }}_h )\). Then, we get \({\bar{F}}_h {\tilde{\varphi }}_h \dot{{\tilde{\varphi }}}_h /\eta _h \le F_h ({\bar{\upsilon }}_h ){\tilde{\varphi }}_h \dot{{\tilde{\varphi }}}_h /\eta _h \).

Taking time derivative along (54), \({\dot{V}}_h \) is given by

$$\begin{aligned} {\dot{V}}_h =E_h {\dot{E}}_h +\frac{{\bar{F}}_h }{\eta _h }\tilde{\varphi }_h \dot{{\tilde{\varphi }}}_h \le E_h {\dot{E}}_h +\frac{F_h ({\bar{\upsilon }}_h )}{\eta _h }{\tilde{\varphi }}_h \dot{\hat{{\varphi }}}_h \end{aligned}$$
(55)

By utilizing (49) and (53), \({\dot{V}}_h \) further becomes

$$\begin{aligned}&{\dot{V}}_h \le -K_h E_h^2 +F_h ({\bar{\upsilon }}_h )E_h {\varvec{W}}_h^{\mathrm{*T}} {\varvec{\psi }} _h ({\varvec{\ell }} _h )\nonumber \\&\qquad \quad +F_h ({\bar{\upsilon }}_h )E_h \varepsilon _h -\frac{1}{2}F_h ({\bar{\upsilon }}_h )E_h^2 \hat{{\varphi }}_h {\varvec{\psi }} _h^\mathrm{T} ({\varvec{\ell }} _h ){\varvec{\psi }} _h ({\varvec{\ell }} _h ) \nonumber \\&\qquad \quad -F_h ({\bar{\upsilon }}_h )\frac{E_h^2 }{2\rho _h^2 }+\frac{1}{2}F_h ({\bar{\upsilon }}_h )E_h^2 {\tilde{\varphi }}_h {\varvec{\psi }} _h^\mathrm{T} ({\varvec{\ell }} _h ){\varvec{\psi }} _h ({\varvec{\ell }} _h )\nonumber \\&\qquad \quad -\frac{2F_h ({\bar{\upsilon }}_h ){\tilde{\varphi }}_h \hat{{\varphi }}_h }{\eta _h } \nonumber \\&\quad =-K_h E_h^2 +F_h ({\bar{\upsilon }}_h )E_h {\varvec{W}}_h^{\mathrm{*T}} {\varvec{\psi }} _h ({\varvec{\ell }} _h )+F_h ({\bar{\upsilon }}_h )E_h \varepsilon _h \nonumber \\&\qquad -\frac{1}{2}F_h ({\bar{\upsilon }}_h )E_h^2 \varphi _h {\varvec{\psi }} _h^\mathrm{T} ({\varvec{\ell }} _h ){\varvec{\psi }} _h ({\varvec{\ell }} _h )\nonumber \\&\qquad -F_h ({\bar{\upsilon }}_h )\frac{E_h^2 }{2\rho _h^2 }-\frac{2F_h ({\bar{\upsilon }}_h )\tilde{\varphi }_h \hat{{\varphi }}_h }{\eta _h } \end{aligned}$$
(56)

Because \(E_h {\varvec{W}}_h^{\mathrm{*T}} {\varvec{\psi }} _h ({\varvec{\ell }} _h )\le \frac{E_h^2 }{2}\left\| {{\varvec{W}}_h^{\mathrm{*T}} {\varvec{\psi }} _h ({\varvec{\ell }} _h )} \right\| ^{2}+\frac{1}{2}=\frac{E_h^2 }{2}\left\| {{\varvec{W}}_h^\mathrm{*} } \right\| ^{2}\left\| {{\varvec{\psi }} _h ({\varvec{\ell }} _h )} \right\| ^{2}+\frac{1}{2}=\frac{E_h^2 }{2}\varphi _h {\varvec{\psi }} _h^T ({\varvec{\ell }} _h ){\varvec{\psi }} _h ({\varvec{\ell }} _h )+\frac{1}{2}\), \(2{\tilde{\varphi }}_h \hat{{\varphi }}_h \ge {\tilde{\varphi }}_h^2 -\varphi _h^2 \) and \(E_h \varepsilon _h \le \left| {E_h } \right| \varepsilon _{hM} =2\left| {\frac{E_h }{2}} \right| \varepsilon _{hM} \le \frac{E_h^2 }{4}+\varepsilon _{hM}^2 \), Eq. (56) is further calculated as

$$\begin{aligned} {\dot{V}}_h\le & {} -K_h E_h^2 +F_h ({\bar{\upsilon }}_h )\nonumber \\&\times \left[ {\frac{E_h^2 }{2}\varphi _h {\varvec{\psi }} _h^T ({\varvec{\ell }} _h ){\varvec{\psi }} _h ({\varvec{\ell }} _h )+\frac{1}{2}} \right] \nonumber \\&+F_h ({\bar{\upsilon }}_h )\left( {\frac{E_h^2 }{4}+\varepsilon _{hM}^2 } \right) \nonumber \\&-\frac{1}{2}F_h ({\bar{\upsilon }}_h )E_h^2 \varphi _h {\varvec{\psi }} _h^\mathrm{T} ({\varvec{\ell }} _h ){\varvec{\psi }} _h ({\varvec{\ell }} _h )\nonumber \\&-F_h ({\bar{\upsilon }}_h )\frac{E_h^2 }{2\rho _h^2 }-\frac{F_h ({\bar{\upsilon }}_h )}{\eta _h }\left( {{\tilde{\varphi }}_h^2 -\varphi _h^2 } \right) \nonumber \\= & {} -K_h E_h^2 -\frac{F_h ({\bar{\upsilon }}_h )}{\eta _h }\tilde{\varphi }_h^2 +\frac{F_h ({\bar{\upsilon }}_h )E_h^2 }{4}\nonumber \\&-F_h ({\bar{\upsilon }}_h )\frac{E_h^2 }{2\rho _h^2 }+F_h ({\bar{\upsilon }}_h )\varepsilon _{hM}^2 \nonumber \\&+\frac{F_h ({\bar{\upsilon }}_h )}{\eta _h }\varphi _h^2 +\frac{F_h ({\bar{\upsilon }}_h )}{2} \end{aligned}$$
(57)

Let \(\rho _h =\sqrt{2}\) and then we conclude from (57) that

$$\begin{aligned} {\dot{V}}_h\le & {} -K_h E_h^2 -\frac{F_h ({\bar{\upsilon }}_h )}{\eta _h }{\tilde{\varphi }}_h^2 +F_h ({\bar{\upsilon }}_h )\varepsilon _{hM}^2 \nonumber \\&+\frac{F_h ({\bar{\upsilon }}_h )}{\eta _h }\varphi _h^2 +\frac{F_h ({\bar{\upsilon }}_h )}{2} \end{aligned}$$
(58)

Define the following compact sets:

$$\begin{aligned}&\Omega _{E_h } =\left\{ {E_h \left| {\left| {E_h } \right| \le \sqrt{{\left( {F_h ({\bar{\upsilon }}_h )\varepsilon _{hM}^2 +\frac{F_h ({\bar{\upsilon }}_h )}{\eta _h }\varphi _h^2 +\frac{F_h ({\bar{\upsilon }}_h )}{2}} \right) }/{K_h }}} \right. } \right\} \nonumber \\&\Omega _{{\tilde{\varphi }}_h } =\left\{ {{\tilde{\varphi }}_h \left| {\left| {{\tilde{\varphi }}_h } \right| \le \sqrt{{\left( {\varepsilon _{hM}^2 +\frac{\varphi _h^2 }{\eta _h }+\frac{1}{2}} \right) }/{\left( {\frac{1}{\eta _h }} \right) }}} \right. } \right\} \end{aligned}$$
(59)

If \(E_h \notin \Omega _{E_h }\) or \({\tilde{\varphi }}_h \notin \Omega _{{\tilde{\varphi }}_h } \), then \({\dot{V}}_h <0\). Hence, \(E_h \) and \({\tilde{\varphi }}_h \) are semi-globally uniformly ultimately bounded. Furthermore, when we design infinitely large \(K_h \), the velocity tracking error can converge to an arbitrarily small value. This is the end of the proof. \(\square \)

Remark 2

For each subsystem, only one FWNN is applied to approximate the unknown term. Hence, disturbance rejection performance is guaranteed for the addressed controller and meanwhile the computational costs are low.

Remark 3

The existing studies [10, 20,21,22,23] require that all the control design parameters \(K_{V1} \) and \(K_h \) must be greater than unknown positive constants. In this paper, novel roust terms \(\upsilon _{V4} \) and \(\upsilon _{h4} \) are developed such that \(K_{V1} \in \mathfrak {R}^{+}\) and \(K_h \in \mathfrak {R}^{+}\) can ensure the stability of closed-loop control system, which infers that larger stable regions than the previous methodologies [10, 20,21,22,23] are achieved in this study.

4 Simulation results

This section presents the simulation test of the proposed hybrid controller (HB) in comparison with a traditional back-stepping control (TBC) approach [26] to show its superiority in velocity and altitude tracking performance. The input vectors of FWNNs are \({\varvec{\ell }} _V =V\) and \({\varvec{\ell }} _h ={\varvec{x}}=[\gamma ,\theta ,Q]^{\mathrm{T}}\) with \(V\in [7700\hbox { ft}/\hbox {s}\), \(8700\hbox { ft}/\hbox {s}]\), \(\gamma \in [-\,5^{\circ }, 5^{\circ }]\), \(\theta \in [-10^{\circ }, 10^{\circ }]\), \(Q\in [-10^{\circ }/\hbox {s}, 10^{\circ }/\hbox {s}]\). Other design parameters are chosen as: \(K_{V1} =0.5\), \(K_{V2} =0.8\), \(\eta _V =0.1\), \(\kappa _h =12\), \(\mu _h =7\), \(K_h =50\), \(\eta _h =25\), N=10. To test the robustness performance, we suppose that all the aerodynamic coefficients (i.e., \(C_\mathrm{T}^0 \), \(C_\mathrm{T}^{\alpha ^{i}} \), \(C_\mathrm{D}^{\delta _\mathrm{e}^i } \), \(C_\mathrm{D}^{\alpha ^{i}} \), \(C_\mathrm{D} ^0 \), \(C_\mathrm{L}^{\delta _\mathrm{e} } \), \(C_\mathrm{L}^\alpha \), \(C_\mathrm{L}^0 \), \(C_{M,\alpha }^0 \), \(C_{M,\alpha }^{\alpha ^{i}} \), \(c_\mathrm{e} \), \(N_1^0 \), \(N_1^{\alpha ^{i}} \), \(N_2^{\alpha ^{i}} \), \(N_2^0 \), \(N_2^{\delta _\mathrm{e} } \) and \(\beta _j \left( {h,{\bar{q}}} \right) \), where i=1,2, j=1,2, ..., 8.) are uncertain. A maximum uniform variation within 40% of the nominal value is considered by defining

$$\begin{aligned} C=\left\{ {{\begin{array}{ll} {C_0 ,}&{} 0\hbox { s}\le t\le 50\hbox { s} \\ {C_0 \left[ {1+0.4\sin (0.1\uppi t)} \right] ,}&{} {\hbox {else}} \\ \end{array} }} \right. \end{aligned}$$
(60)

where C represents the value of uncertain coefficient mentioned above and \(C_{0}\) means the nominal value of C.

The obtained simulation results, presented in Figs. 3, 4, 5, 6, 7 8, show that the proposed control strategy can provide better tracking of reference commends in contrast to TBC in the presence of seriously parametric uncertainties. Figures 3 and 4 reveal that velocity tracking error and altitude tracking error obtained by HB are smaller than the ones provided by TBC, and this superiority is more obvious when parameters are uncertain (\(50\hbox { s}<t\le 80\hbox { s})\). Hence, the exploit controller exhibits better robustness performance than TBC. For both controllers, Figs. 5 and 6 show that the responses of \(\varPhi \) and \(\delta _{\mathrm{e}}\), \(\gamma \), \(\theta \) and Q are smooth and there is no high frequency chattering. It is noticed from Fig. 7 that the flexible states of applying HC are smoother than utilizing TBC. The estimations of \(||{\varvec{W}}_V^\mathrm{*} ||\) and \(||{\varvec{W}}_h^\mathrm{*} ||\), presented in Fig. 8, indicate that \(||\hat{{{\varvec{W}}}}_V ||\) and \(||\hat{{{\varvec{W}}}}_h ||\) can turn themselves along with the variations of uncertain parameters, which means that desired FWNN approximations are achieved and robustness performance can be guaranteed for the studied controllers.

Fig. 3
figure 3

Velocity tracking performance

Full size image
Fig. 4
figure 4

Altitude tracking performance

Full size image
Fig. 5
figure 5

Control inputs

Full size image
Fig. 6
figure 6

Attitude angles

Full size image
Fig. 7
figure 7

The flexible states

Full size image
Fig. 8
figure 8

Estimations of \(||{\varvec{W}}_V^\mathrm{*} ||\) and \(||{\varvec{W}}_h^\mathrm{*} ||\)

Full size image

5 Conclusions

This study investigates a direct nonaffine hybrid controller for HFVs. For velocity subsystem and altitude subsystem, direct nonaffine controllers are addressed without model simplifications, extending the previous indirect nonaffine control approaches. By a fusion of FWNN approximation and pseudocontrol strategy, both the nonaffine dynamics and parametric uncertainties are well handled. Further, advanced regulation laws are exploited for online learning parameters to reduce computational load and guarantee real-time performance. In addition, the stable regions of closed-loop control system are broadened via exploiting robust terms. Finally, numerical simulation results are presented to validate the effectiveness and superiority of the developed control scheme.