1 Introduction

As a strategic near-space weapon, air-breathing hypersonic vehicles (AHVs) have seen significant developments in the past decade. Flight control design for AHVs is a challenging and meaningful research area since control systems should deal with system uncertainties, complicated couplings and model nonlinearities [1, 2]. Thereby, the control gains usually are completely unknown due to system uncertainties, which results in a problem of unknown control direction [3, 4]. In particular, traditional affine control methodologies are inadequate to handle such vehicles whose motion models presenting non-affine formulations. In addition, special requirements of transient performance are also needed for AHV’s control systems owing to the maneuver at hypersonic speeds [5,6,7].

It is well known that devising efficient control approaches for AHVs is very important to complete multiple flight tasks over a wide range of flight envelopes. But varying flight environments, unknown external disturbances, and unavoidable modeling uncertainties make robust flight control design for AHVs a challenging task [8, 9]. By addressing a robust tracking issue of AHVs subject to uncertainties and disturbances, an inaccuracy model-based asymptotic tracking controller is exploited based on an affine model of AHVs without using high-order time derivatives of vehicle states [10]. To weaken the undesired high-frequency chattering that may stimulate vehicle’s flexible modes, a high-order sliding mode control design is presented for AHVs to provide robust tracking of reference trajectories, while avoiding traditional robust controllers’ conservatism [1]. Furthermore, a terminal sliding mode control method is investigated for AHVs to achieve fast tracking of velocity and altitude commands in the presence of parametric uncertainties and unknown disturbances [11]. For an AHV with multiple disturbances, a hybrid control frame incorporating fuzzy approximation and disturbance observer is studied to reject multiple source disturbances, which guarantees the addressed controller with better practicality than the ones that only considers single type of disturbance [12]. By employing neural networks to estimate unknown dynamics, a low computational controller is developed for a constrained AHV, and simulation results prove the tracking performance of that strategy despite of uncertainties, disturbances, and control input constraints [13, 14]. In [2], an active disturbance rejection control strategy is proposed for AHVs’ tracking system, and extended state observers are constructed to estimate uncertainties for the sake of further enhancing the controller’s robustness.

It has been proved that the altitude dynamics of AHVs is easy to be rewritten as a strict feedback formulation, which makes the recursive back-stepping design realizable [15,16,17]. On the basis of a newly designed nonlinear disturbance observer, a robust back-stepping control scheme is developed to steer velocity and altitude to track their reference commands, and meanwhile the problem of “explosion of terms” caused by back-stepping design is handled by a tracking differentiator [18]. The control approach exploited in [19] is to combine back-stepping with sliding mode control such that the addressed controller for AHVs with mismatched uncertainties can provide robust tracking of reference trajectories. Owing to the excellent capability of nonlinearity approximation, neural networks are incorporated with back-stepping design procedure, based on which an adaptive nonlinear controller is devised for AHVs [20]. Though the tracking performance and robustness of that scheme are validated by numerical simulations in the presence of system uncertainties and external disturbances, too many neural networks and online learning parameters are required to guarantee the robustness and convergence, which yields high computational load and results in certain control time delay. For this reason, great efforts are made to reduce the required neural networks via a model transformation [14, 18, 21, 22] and also to decrease the utilized online learning parameters based on advanced algorithms [22,23,24].

Though excellent tracking performance can be achieved by the above-mentioned control methodologies, there are still some shortcomings to these approaches [1, 8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24]. A fatal one is that these controllers are devised using simplified affine models, which harms their application validity in practice since AHVs’ motion models are completely non-affine [25, 26]. Another is that it is difficult for these control methods to guarantee prescribed output tracking performance especially transient performance for AHVs’ hypersonic maneuver. In this paper, we propose a new tracking controller with prescribed performance for AHVs based on non-affine models using the back-stepping design procedure, capable of guaranteeing prescribed performance for tracking errors. The special contributions are summarized as follows.

  1. 1.

    The addressed controller directly stems from a non-affine model of AHVs, which avoids inappropriate model simplifications under rigorous assumptions and guarantees controllers with practicality.

  2. 2.

    Prescribed output tracking quality is achieved for AHVs via prescribed performance control.

  3. 3.

    The presented control approach is independent on accurate vehicle models and function estimations. Thus its disturbance rejection ability is fine and the computational cost is low.

The rest of this study is outlined as follows. The motion model of AHVs is formulated in Sect. 2, and the preliminary knowledge of prescribed performance is briefly explained in Sect. 3. In Sect. 4, prescribed performance back-stepping controllers are devised and the convergence of closed-loop control system is proved. Simulation results are shown in Sect. 5, and finally conclusions are presented in Sect. 6.

2 Problem formulation

2.1 Vehicle model

The longitudinal motion model considered in this paper is formulated as [25, 26]

$$\begin{aligned}&\dot{V}={T\cos \left( {\theta -\gamma } \right) }/m-D/m-g\sin \gamma \end{aligned}$$
(1)
$$\begin{aligned}&\dot{h}=V\sin \gamma \end{aligned}$$
(2)
$$\begin{aligned}&\dot{\gamma }=L/({mV})+{T\sin \left( {\theta -\gamma } \right) }/({mV})-g\cos \gamma \end{aligned}$$
(3)
$$\begin{aligned}&\dot{\theta } = Q \end{aligned}$$
(4)
$$\begin{aligned}&\dot{Q}={\left( {M+\tilde{\psi }_1 \ddot{\eta }_1 +\tilde{\psi }_2 \ddot{\eta }_2 } \right) }/{I_{{yy}} } \end{aligned}$$
(5)
$$\begin{aligned}&k_1 \ddot{\eta }_1 =-2\zeta _1 \omega _1 \dot{\eta }_1 -\omega _1^2 \eta _1 +N_1 -{\tilde{\psi }_1 M}/{I_{{yy}} }\nonumber \\&\quad -{\tilde{\psi }_1 \tilde{\psi }_2 \ddot{\eta }_2 }/{I_{{yy}} } \end{aligned}$$
(6)
$$\begin{aligned}&k_2 \ddot{\eta }_2 =-2\zeta _2 \omega _2 \dot{\eta }_2 -\omega _2^2 \eta _2 +N_2 \nonumber \\&\quad -\,{\tilde{\psi }_2 M}/{I_{{yy}} }-{\tilde{\psi }_2 \tilde{\psi }_1 \ddot{\eta }_1 }/{I_{{yy}} }. \end{aligned}$$
(7)

The above vehicle model consists of five rigid body states (velocity V, altitude h, flight-path angle \(\gamma \), pitch angle \(\theta \), and pitch rate Q) and two flexible states ( \(\eta \) \(_{1}\) and \(\eta \) \(_{2})\). The attack angle \(\alpha =\theta -\gamma \). T, D, L, M, \(N_{1}\) and \(N_{2}\) denote thrust force, drag force, lift force, pitching moment, the first generalized force, and the second generalized force, respectively. Their details are as follows [26]

$$\begin{aligned}&T\approx \beta _1 \left( {h,\bar{{q}}} \right) \varPhi \alpha ^{3}+\beta _2 \left( {h,\bar{{q}}} \right) \alpha ^{3}+\beta _3 \left( {h,\bar{{q}}} \right) \varPhi \alpha ^{2}\\&\quad +\,\beta _4 \left( {h,\bar{{q}}} \right) \alpha ^{2} \\&\quad +\,\beta _5 \left( {h,\bar{{q}}} \right) \varPhi \alpha +\beta _6 \left( {h,\bar{{q}}} \right) \alpha +\beta _7 \left( {h,\bar{{q}}} \right) \varPhi \\&\quad +\,\beta _8 \left( {h,\bar{{q}}} \right) , \\&D\approx \, \bar{{q}}SC_D^{\alpha ^{2}} \alpha ^{2}+\bar{{q}}SC_D^\alpha \alpha +\bar{{q}}SC_D^{\delta _\mathrm{e}^2 } \delta _\mathrm{e}^2\\&\quad +\,\bar{{q}}SC_D^{\delta _\mathrm{e} } \delta _\mathrm{e} +\bar{{q}}SC_D^0 ,\\&M\approx z_\mathrm{T} T+\bar{{q}}S\bar{{c}}C_{M,\alpha }^{\alpha ^{2}} \alpha ^{2}+\bar{{q}}S\bar{{c}}C_{M,\alpha }^\alpha \alpha +\bar{{q}}S\bar{{c}}C_{M,\alpha }^0 \\&\quad +\,\bar{{q}}S\bar{{c}}c_\mathrm{e} \delta _\mathrm{e} ,\\&L\approx \bar{{q}}SC_L^\alpha \alpha +\bar{{q}}SC_L^{\delta _\mathrm{e} } \delta _\mathrm{e} +\bar{{q}}SC_L^0 , \\ \quad&N_1 =N_1^{\alpha ^{2}} \alpha ^{2}+N_1^\alpha \alpha +N_1^0 ,\\&N_2 =N_2^{\alpha ^{2}} \alpha ^{2}+N_2^\alpha \alpha +N_2^{\delta _\mathrm{e} } \delta _\mathrm{e} +N_2^0 , \quad \bar{{q}}={\bar{{\rho }}V^{2}}/2,\\&\bar{{\rho }}=\bar{{\rho }}_0 \exp \left( {-{\left( {h-h_0 } \right) }/{h_\mathrm{s} }} \right) , \end{aligned}$$

where fuel equivalence ratio \(\varPhi \) and elevator angular deflection \(\delta \) \(_\mathrm{e}\) are the control inputs, and they occur implicitly in Eqs. (1)–(7). For more detailed definitions of other parameters and coefficients, the reader could refer to [25, 26].

Remark 1

Traditionally, only the rigid body states are measured and used for control designs, while the flexible states are treated as system uncertainties that are coped with by the controller’s robustness [14,15,16].

2.2 Control objective

The control goal sought is to devise non-affine prescribed performance controllers \(\varPhi \) and \(\delta \) \(_\mathrm{e}\) via back-stepping for AHVs such that velocity V and altitude h track their reference commands \(V_\mathrm{ref}\) and \(h_\mathrm{ref}\) in the presence of parametric uncertainties. Meanwhile, all closed-loop signals are bounded, and the transient property’s tracking performance and the steady-state error are characterized by performance functions.

3 Prescribed performance

By prescribed performance, we mean that the tracking error e evolves strictly within predefined decaying bounds as follows:

$$\begin{aligned} -{\delta }\rho (t)<e<\bar{{\delta }}\rho (t), \end{aligned}$$
(8)

where the performance function \(\rho (t)=\left( {\rho _0 -\rho _\infty } \right) e^{-lt}+\rho _\infty >0\) is bounded and strictly positive decreasing with the property \(\rho _\infty \le \rho (t)\le \rho _0 \); \(\rho _0>\rho _\infty >0\), \(l>0\), \(0<\bar{{\delta }}<1\), \(0<{\delta }<1\) are design parameters.

If e remains within the adjustable neighborhood of (8), the maximum overshoot of e is prescribed less than \(\max \left\{ {\bar{{\delta }}\rho _0 ,{\delta }\rho _0 } \right\} \), and the steady value \(e(\infty )\) is no more than \(\max \left\{ {\bar{{\delta }}\rho _\infty ,{\delta }\rho _\infty } \right\} \). Thus, both transient performance and steady-state performance of e are guaranteed by choosing appropriate design parameters for (8).

Noting that it is hard to directly design controllers using inequality constraint (8), a transformed function \(\varPsi \left( {\varepsilon (t)} \right) =\frac{\bar{{\delta }}e^{\varepsilon (t)}-{\delta }e^{-\varepsilon (t)}}{e^{\varepsilon (t)}+e^{-\varepsilon (t)}}\) is applied to convert (8) into the following formulation.

$$\begin{aligned} e=\varPsi \left( {\varepsilon (t)} \right) \rho (t), \end{aligned}$$
(9)

where \(\varepsilon (t)\) is a transformed error.

Since \(\mathop {\lim }\nolimits _{\varepsilon (t)\rightarrow +\infty } \varPsi \left( {\varepsilon (t)} \right) =\bar{{\delta }}\) and \(\mathop {\lim }\nolimits _{\varepsilon (t)\rightarrow -\infty } \varPsi \left( {\varepsilon (t)} \right) =-{\delta }\), (9) is equivalent to (8). Furthermore, \(\varPsi \left( {\varepsilon (t)} \right) \in \left( {-{\delta },\bar{{\delta }}} \right) \) is bounded and strictly increasing.

From (9), we have

$$\begin{aligned} \varepsilon (t)=\varPsi ^{-1}\left( {\varepsilon (t)} \right) =\frac{1}{2}\ln \left( {\frac{e/{\rho (t)}+{\delta }}{\bar{{\delta }}-e/{\rho (t)}}} \right) . \end{aligned}$$
(10)

\(\dot{\varepsilon }(t)\) is derived as

$$\begin{aligned} \dot{\varepsilon }(t)=r\left[ {\dot{e}-e\frac{\dot{\rho }(t)}{\rho (t)}} \right] {,} \end{aligned}$$
(11)

with

$$\begin{aligned} \dot{\rho }(t)= & {} -l\left( {\rho _0 -\rho _\infty } \right) e^{-lt}\in \left[ {-l\left( {\rho _0 -\rho _\infty } \right) ,0} \right] ,\\ r= & {} \frac{1}{2\rho (t)}\left[ {\frac{1}{e/{\rho (t)}+{\delta }}-\frac{1}{e/{\rho (t)}-\bar{{\delta }}}} \right] \\= & {} \frac{1}{2\rho (t)}\left[ \frac{1}{{\varPsi \left( {\varepsilon (t)} \right) \rho (t)}/{\rho (t)}+{\delta }}\right. \\&\quad -\,\left. \frac{1}{{\varPsi \left( {\varepsilon (t)} \right) \rho (t)}/{\rho (t)}-\bar{{\delta }}} \right] \\= & {} \frac{1}{2\rho (t)}\left[ {\frac{1}{\varPsi \left( {\varepsilon (t)} \right) +{\delta }}-\frac{1}{\varPsi \left( {\varepsilon (t)} \right) -\bar{{\delta }}}} \right] . \end{aligned}$$

Noticing the fact that \(0<\rho _\infty \le \rho (t)\le \rho _0 \) and \(\varPsi \left( {\varepsilon (t)} \right) \in \left( {-{\delta },\bar{{\delta }}} \right) \), r is bounded and satisfies \(r\ge \frac{1}{2\rho _0 }\left( {\frac{1}{{\delta }}+\frac{1}{\bar{{\delta }}}} \right) >0\).

4 Controller design

Based on the analyses of [22, 23], we decompose the motion model of AHVs into the velocity subsystem (i.e., Eq. (1)) and the altitude subsystem (i.e., Eqs. (2)–(5)) for the simplicity of control design.

4.1 Velocity controller design

According to the timescale principle [3], the velocity is slower dynamics compared with the altitude and attitude angles. When velocity varies, the altitude and attitude angles are considered to reach their steady constants. Thus, the velocity subsystem can be expressed as the following non-affine formulation.

$$\begin{aligned} \left\{ {\begin{array}{l} \dot{V}=\varphi _V (V,\varPhi ) \\ u_V =\varPhi \\ y_V =V \\ \end{array}} \right. \end{aligned}$$
(12)

where \(\varphi _V (V,\varPhi )\) is a continuous unknown function, \(u_V \) and \(y_V \) are the control input and output of velocity subsystem, respectively.

By mean value theorem [27], (12) further becomes

$$\begin{aligned} \left\{ {\begin{array}{l} \dot{V}=\beta _{V1} (V)+\beta _{V2} (V)\varPhi \\ u_V =\varPhi \\ y_V =V \\ \end{array}} \right. \end{aligned}$$
(13)

with \(\beta _{V2} (V)=\frac{\partial \varphi _V (V,\varPhi _*)}{\partial \varPhi _*}\ne 0\), \(\varPhi _*\in (0,\varPhi )\).

Remark 2

\(\beta _{V2} (V)\ne 0\) is the controllability condition of (13). There is no need of priori knowledge about sign of \(\beta _{V2} (V)\) that may not be easily obtained in practice.

Assumption 1

[28] The reference command \(V_{ref}\) and its time derivative \(\dot{V}_\mathrm{ref} \) are bounded. That is, there exist positive constants \(\bar{{V}}_\mathrm{ref} \) and \(\bar{{\dot{V}}}_\mathrm{ref} \) such that \(\left| {V_\mathrm{ref} } \right| \le \bar{{V}}_\mathrm{ref} \) and \(\left| {\dot{V}_\mathrm{ref} } \right| \le \bar{{\dot{V}}}_\mathrm{ref} \).

Define velocity tracking error \(e_V \)

$$\begin{aligned} e_V =V-V_\mathrm{ref} \end{aligned}$$
(14)

Employ a performance function \(\rho _V (t)=\big ( \rho _{V0}-\rho _{V\infty } \big )e^{-l_V t}+\rho _{V\infty } \) to constrain \(e_V \)

$$\begin{aligned} -{\delta }_V \rho _V (t)<e_V <\bar{{\delta }}_V \rho _V (t) \end{aligned}$$
(15)

where \(\rho _{V0} >0\), \(\rho _{V\infty } >0\), \(l_V >0\), \(0<{\delta }_V <1\), \(0<\bar{{\delta }}_V <1\) are design parameters and satisfy \(\rho _{V0} >\rho _{V\infty } \), \(-{\delta }_V \rho _{V0}<e_V (0)<\bar{{\delta }}_V \rho _{V0} \), \(\rho _{V\infty } \le \rho _V (t)\le \rho _{V0} \).

We transform (15) as

$$\begin{aligned} e_V =\varPsi _V \left( {\varepsilon _V (t)} \right) \rho _V (t) \end{aligned}$$
(16)

where \(\varPsi _V \left( {\varepsilon _V (t)} \right) =\frac{\bar{{\delta }}_V e^{\varepsilon _V (t)}-{\delta }_V e^{-\varepsilon _V (t)}}{e^{\varepsilon _V (t)}+e^{-\varepsilon _V (t)}}\in \left( {-{\delta }_V ,\bar{{\delta }}_V } \right) \) is a transformed function, \(\varepsilon _V (t)\) is a transformed error, and its formulation is

$$\begin{aligned} \varepsilon _V (t)=\varPsi _V^{-1} \left( {\varepsilon _V (t)} \right) =\frac{1}{2}\ln \left( {\frac{{e_V }/{\rho _V (t)}+{\delta }_V }{\bar{{\delta }}_V -{e_V }/{\rho _V (t)}}} \right) . \end{aligned}$$
(17)

Taking time derivative along (17) leads to

$$\begin{aligned}&\dot{\varepsilon }_V (t)=r_V \left[ {\dot{e}_V -e_V \frac{\dot{\rho }_V (t)}{\rho _V (t)}} \right] \nonumber \\&\quad =r_V \left[ {\beta _{V1} (V)+\beta _{V2} (V)\varPhi -\dot{V}_\mathrm{ref} -e_V \frac{\dot{\rho }_V (t)}{\rho _V (t)}} \right] \nonumber \\ \end{aligned}$$
(18)

with \(r_V =\frac{1}{2\rho _V (t)}\left[ {\frac{1}{{e_V }/{\rho _V (t)}+{\delta }_V }-\frac{1}{{e_V }/{\rho _V (t)}-\bar{{\delta }}_V }} \right] \ge \frac{1}{2\rho _{V0} }\left( {\frac{1}{{\delta }_V }+\frac{1}{\bar{{\delta }}_V }} \right) >0\), \(\dot{\rho }_V (t)=-l_V \left( {\rho _{V0} -\rho _{V\infty } } \right) e^{-l_V t} \in \left[ {-l_V \left( {\rho _{V0} -\rho _{V\infty } } \right) ,0} \right) \).

From the fact that \(e_V =\varPsi _V \left( {\varepsilon _V (t)} \right) \rho _V (t)\), we obtain \(e_V =V-V_\mathrm{ref} =\varPsi _V \left( {\varepsilon _V (t)} \right) \rho _V (t)\), that is, \(V=\varPsi _V \left( {\varepsilon _V (t)} \right) \rho _V (t)+V_\mathrm{ref} \). Then (18) becomes

$$\begin{aligned} \dot{\varepsilon }_V (t)= & {} r_V \left[ \beta _{V1} (\varPsi _V \left( {\varepsilon _V (t)} \right) \rho _V (t)+V_\mathrm{ref} )\right. \nonumber \\&\quad +\,\left. \beta _{V2} (V)\varPhi -\dot{V}_\mathrm{ref} \right. \nonumber \\&\quad -\,\left. \varPsi _V \left( {\varepsilon _V (t)} \right) \rho _V (t)\frac{\dot{\rho }_V (t)}{\rho _V (t)} \right] \nonumber \\&=r_V \left[ \beta _{V1} (\varPsi _V \left( {\varepsilon _V (t)} \right) \rho _V (t)+V_\mathrm{ref} )\right. \nonumber \\&\quad +\,\left. \beta _{V2} (V)\varPhi -\dot{V}_\mathrm{ref} -\varPsi _V \left( {\varepsilon _V (t)} \right) \dot{\rho }_V (t) \right] .\nonumber \\ \end{aligned}$$
(19)

Define Lyapunov function

$$\begin{aligned} L_V =\frac{\varepsilon _V^2 (t)}{2} \end{aligned}$$
(20)

Invoking (19), \(\dot{L}_V \) is derived as

$$\begin{aligned} \dot{L}_V= & {} \varepsilon _V (t)\dot{\varepsilon }_V (t) \nonumber \\&=\varepsilon _V (t)r_V \left[ \beta _{V1} (\varPsi _V \left( {\varepsilon _V (t)} \right) \rho _V (t)\right. \nonumber \\&\quad +\,\left. V_\mathrm{ref} )+\beta _{V2} (V)\varPhi -\dot{V}_\mathrm{ref}\right. \nonumber \\&\quad -\,\left. \varPsi _V \left( {\varepsilon _V (t)} \right) \dot{\rho }_V (t) \right] \nonumber \\&=\varepsilon _V (t)r_V \beta _{V2} (V)\varPhi \nonumber \\&\quad +\,\varepsilon _V (t)r_V \left[ \beta _{V1} (\varPsi _V \left( {\varepsilon _V (t)} \right) \rho _V (t)+V_\mathrm{ref} )\right. \nonumber \\&\quad -\,\left. \dot{V}_\mathrm{ref} -\varPsi _V \left( {\varepsilon _V (t)} \right) \dot{\rho }_V (t) \right] . \end{aligned}$$
(21)

The boundedness of \(\varPsi _V \left( {\varepsilon _V (t)} \right) \), \(\rho _V (t)\) and \(V_\mathrm{ref} \) leads to that \(\beta _{V1} (\varPsi _V \left( {\varepsilon _V (t)} \right) \rho _V (t)+V_\mathrm{ref} )\) is also bounded. Thereby, there is a positive constant \(\bar{{\beta }}_{V1} \) such that \(\left| {\beta _{V1} (\varPsi _V \left( {\varepsilon _V (t)} \right) \rho _V (t)+V_\mathrm{ref} )} \right| \le \bar{{\beta }}_{V1} \). Then \(\dot{L}_V \) becomes

$$\begin{aligned} \dot{L}_V \le \varepsilon _V (t)r_V \beta _{V2} (V)\varPhi +\left| {\varepsilon _V (t)} \right| r_V \Sigma _V \end{aligned}$$
(22)

with \(\Sigma _V \!=\!\bar{{\beta }}_{V1} \!+\!\bar{{\dot{V}}}_\mathrm{ref} +\max \{{\delta }_V ,\bar{{\delta }}_V \}l_V \left( {\rho _{V0} -\rho _{V\infty } } \right) >0\).

The control law \(\varPhi \) is chosen as

$$\begin{aligned} \left\{ {\begin{array}{l} \varPhi =N_V \left( {\xi _V } \right) \left[ {\kappa _{V1} \varepsilon _V (t)+\frac{\kappa _{V2} r_V \varepsilon _V (t)}{2}} \right] \\ \dot{\xi }_V =\kappa _{V1} r_V \varepsilon _V^2 (t)+\frac{\kappa _{V2} r_V^2 \varepsilon _V^2 (t)}{2} \\ \end{array}} \right. \end{aligned}$$
(23)

where \(N_V \left( {\xi _V } \right) =e^{\xi _V^2 }\cos ({\pi }\xi _V /2)\) is a Nussbaum function [3, 4]; \(\kappa _{V1} \), \(\kappa _{V2} >0\) are design parameters.

Substituting \(\varPhi \) into (22), we get

$$\begin{aligned} \dot{L}_V\le & {} \varepsilon _V (t)r_V \beta _{V2} (V)N_V \left( {\xi _V } \right) \nonumber \\&\left[ {\kappa _{V1} \varepsilon _V (t)+\frac{\kappa _{V2} r_V \varepsilon _V (t)}{2}} \right] +\left| {\varepsilon _V (t)} \right| r_V \Sigma _V.\nonumber \\ \end{aligned}$$
(24)

By Young’s inequality, we obtain \(\left| {\varepsilon _V (t)} \right| r_V \Sigma _V \le \frac{\kappa _{V2} }{2}r_V^2 \varepsilon _V^2 (t)+\frac{\Sigma _V^2 }{2\kappa _{V2} }\). Then (24) becomes

$$\begin{aligned}&\dot{L}_V \le \varepsilon _V (t)r_V \beta _{V2} (V)N_V \left( {\xi _V } \right) \nonumber \\&\quad \left[ {\kappa _{V1} \varepsilon _V (t)+\frac{\kappa _{V2} r_V \varepsilon _V (t)}{2}} \right] +\frac{\kappa _{V2} }{2}r_V^2 \varepsilon _V^2 (t)+\frac{\Sigma _V^2 }{2\kappa _{V2} } \nonumber \\&\quad =\kappa _{V1} \varepsilon _V^2 (t)r_V \beta _{V2} (V)N_V \left( {\xi _V } \right) \nonumber \\&\qquad +\,\frac{\kappa _{V2} }{2}r_V^2 \varepsilon _V^2 (t)\left[ {\beta _{V2} (V)N_V \left( {\xi _V } \right) +1} \right] \nonumber \\&\qquad +\,\frac{\Sigma _V^2 }{2\kappa _{V2} } +\kappa _{V1} \varepsilon _V^2 (t)r_V -\kappa _{V1} \varepsilon _V^2 (t)r_V \nonumber \\&\quad =\kappa _{V1} \varepsilon _V^2 (t)r_V \left[ {\beta _{V2} (V)N_V \left( {\xi _V } \right) +1} \right] \nonumber \\&\qquad +\,\frac{\kappa _{V2} }{2}r_V^2 \varepsilon _V^2 (t)\left[ {\beta _{V2} (V)N_V \left( {\xi _V } \right) +1} \right] \nonumber \\&\qquad +\,\frac{\Sigma _V^2 }{2\kappa _{V2} }-\kappa _{V1} \varepsilon _V^2 (t)r_V \nonumber \\&\quad =\left[ {\kappa _{V1} \varepsilon _V^2 (t)r_V +\frac{\kappa _{V2} }{2}r_V^2 \varepsilon _V^2 (t)} \right] \nonumber \\&\qquad \, \times \left[ {\beta _{V2} (V)N_V \left( {\xi _V } \right) +1} \right] +\frac{\Sigma _V^2 }{2\kappa _{V2} }-\kappa _{V1} \varepsilon _V^2 (t)r_V \nonumber \\&\quad =-\kappa _{V1} r_V \varepsilon _V^2 (t)+\left[ {\beta _{V2} (V)N_V \left( {\xi _V } \right) +1} \right] \dot{\xi }_V +\frac{\Sigma _V^2 }{2\kappa _{V2} } \nonumber \\&\quad \le -\iota _V L_V +\left[ {\beta _{V2} (V)N_V \left( {\xi _V } \right) +1} \right] \dot{\xi }_V +\frac{\Sigma _V^2 }{2\kappa _{V2} } \end{aligned}$$
(25)

with \(\iota _V =\frac{\kappa _{V1} }{\rho _{V0} }\left( {\frac{1}{{\delta }_V }+\frac{1}{\bar{{\delta }}_V }} \right) \).

Being multiplied by \(e^{\iota _V t}\) on both sides of (25), we have

$$\begin{aligned}&\frac{\hbox {d}}{\hbox {d}t}\left( {L_V e^{\iota _V t}} \right) \le \beta _{V2} (V)N_V \left( {\xi _V } \right) \dot{\xi }_V e^{\iota _V t}+\dot{\xi }_V e^{\iota _V t}\nonumber \\&\qquad +\,\frac{\Sigma _V^2 }{2\kappa _{V2} }e^{\iota _V t}. \end{aligned}$$
(26)

Integrating (26) over [0, t] yields

$$\begin{aligned}&0\le L_V \le L_V (0)+e^{-\iota _V t}\nonumber \\&\quad \times \, \int _0^t {\beta _{V2} (V)N_V \left( {\xi _V } \right) \dot{\xi }_V e^{\iota _V \tau }\hbox {d}\tau } \nonumber \\&\quad +\,e^{-\iota _V t}\int _0^t {\dot{\xi }_V e^{\iota _V \tau }\hbox {d}\tau } +\int _0^t {\frac{\Sigma _V^2 }{2\kappa _{V2} }e^{-\iota _V \left( {t-\tau } \right) }\hbox {d}\tau } \end{aligned}$$
(27)

Since \(\int _0^t {\frac{\Sigma _V^2 }{2\kappa _{V2} }e^{-\iota _V \left( {t-\tau } \right) }\hbox {d}\tau } =\frac{\Sigma _V^2 }{2\kappa _{V2} }\frac{1}{\iota _V }\left( {1-e^{-\iota _V t}} \right) \in \left[ {0,\frac{\Sigma _V^2 }{2\kappa _{V2} }\frac{1}{\iota _V }} \right) \), we know that \(\int _0^t {\frac{\Sigma _V^2 }{2\kappa _{V2} }e^{-\iota _V \left( {t-\tau } \right) }\hbox {d}\tau } \) is bounded. Thus, (27) becomes

$$\begin{aligned}&0 \le L_V \le L_{V0} \!+\!e^{-\iota _V t}\int _0^t {\beta _{V2} (V)N_V \left( {\xi _V } \right) \dot{\xi }_V e^{\iota _V \tau }\hbox {d}\tau } \nonumber \\&\qquad +\,e^{-\iota _V t}\int _0^t {\dot{\xi }_V e^{\iota _V \tau }\hbox {d}\tau } \end{aligned}$$
(28)

with\(L_{V0} =L_V (0)+\frac{\Sigma _V^2 }{2\kappa _{V2} }\frac{1}{\iota _V }\).

By Lemmas 1 and 2 presented in [29], we know that \(L_V \), \(e^{-\iota _V t}\int _0^t {\beta _{V2} (V)N_V \left( {\xi _V } \right) \dot{\xi }_V e^{\iota _V \tau }\hbox {d}\tau } \) and \(e^{-\iota _V t}\int _0^t {\dot{\xi }_V e^{\iota _V \tau }\hbox {d}\tau } \) are bounded. Hence all the closed-loop signals are bounded, and there exists a positive constant \(\bar{{\varepsilon }}_V \) such that \(\left| {\varepsilon _V (t)} \right| \le \bar{{\varepsilon }}_V \). The inversion transformation of (17) is \(\frac{{e_V }/{\rho _V (t)}+{\delta }_V }{\bar{{\delta }}_V -{e_V }/{\rho _V (t)}}=e^{2\varepsilon _V (t)}\), which yields \(e_V =\frac{\bar{{\delta }}_V e^{2\varepsilon _V (t)}-{\delta }_V }{1+e^{2\varepsilon _V (t)}}\rho _V (t)\). Finally, we have \(-{\delta }_V \rho _V (t)<\frac{\bar{{\delta }}_V e^{-2\bar{{\varepsilon }}_V }-{\delta }_V }{1+e^{-2\bar{{\varepsilon }}_V }}\rho _V (t)\le e_V \le \quad \frac{\bar{{\delta }}_V e^{2\bar{{\varepsilon }}_V }-{\delta }_V }{1+e^{2\bar{{\varepsilon }}_V }}\rho _V (t)<\bar{{\delta }}_V \rho _V (t)\). Thus the prescribed performance for \(e_V \) is guaranteed.

4.2 Altitude controller design

Define altitude tracking error \(e_h \) as

$$\begin{aligned} e_h =h-h_\mathrm{ref} \end{aligned}$$
(29)

Define a performance function \(\rho _h (t)=\left( {\rho _{h0} -\rho _{h\infty } } \right) e^{-l_h t}+\rho _{h\infty } >0\) to constrain \(e_h \).

$$\begin{aligned} -{\delta }_h \rho _h (t)<e_h <\bar{{\delta }}_h \rho _h (t) \end{aligned}$$
(30)

where \(\rho _{h0} >0\), \(\rho _{h\infty } >0\), \(l_h >0\), \(0<{\delta }_h <1\), \(0<\bar{{\delta }}_h <1\) are design parameters and satisfy \(\rho _{h0} >\rho _{h\infty } \), \(-{\delta }_h \rho _{h0}<e_h (0)<\bar{{\delta }}_h \rho _{h0} \), \(\rho _{h\infty } \le \rho _h (t)\le \rho _{h0} \).

Define transformed error \(\varepsilon _h (t)\) as

$$\begin{aligned} \varepsilon _h (t)=\frac{1}{2}\ln \left( {\frac{{e_h }/{\rho _h (t)}+{\delta }_h }{\bar{{\delta }}_h -{e_h }/{\rho _h (t)}}} \right) \end{aligned}$$
(31)

The command of \(\gamma \) is selected as

$$\begin{aligned} \gamma _\mathrm{d} =\arcsin \left[ {\frac{-\mu _h \varepsilon _h (t)+\dot{h}_\mathrm{ref} +{\dot{\rho }_h (t)e_h }/{\rho _h (t)}}{V}} \right] \end{aligned}$$
(32)

where \(\mu _h >0\) is a design parameter, \(\dot{\rho }_h (t)=-l_h \left( {\rho _{h0} -\rho _{h\infty } } \right) e^{-l_h t}\).

If \(\gamma \) \(\rightarrow \) \(\gamma \) \(_{d}\), the corresponding dynamics for \(\varepsilon _h (t)\) is derived as

$$\begin{aligned} \mu _h \dot{\varepsilon }_h (t)+\varepsilon _h (t)=0 \end{aligned}$$
(33)

Thus \(\varepsilon _h (t)\) is bounded, and there exists a positive constant \(\bar{{\varepsilon }}_h \) such that \(\left| {\varepsilon _h (t)} \right| \le \bar{{\varepsilon }}_h \). The inversion transformation of (31) is \(\frac{{e_h }/{\rho _h (t)}+{\delta }_h }{\bar{{\delta }}_h -{e_h }/{\rho _h (t)}}=e^{2\varepsilon _h (t)}\), from which we have \(e_h =\frac{\bar{{\delta }}_h e^{2\varepsilon _h (t)}-{\delta }_h }{1+e^{2\varepsilon _h (t)}}\rho _h (t)\). Finally, we obtain \(-{\delta }_h \rho _h (t)<\frac{\bar{{\delta }}_h e^{-2\bar{{\varepsilon }}_h }-{\delta }_h }{1+e^{-2\bar{{\varepsilon }}_h }}\rho _h (t)\le e_h \le \frac{\bar{{\delta }}_h e^{2\bar{{\varepsilon }}_h }-{\delta }_h }{1+e^{2\bar{{\varepsilon }}_h }}\rho _h (t)< \quad \bar{{\delta }}_h \rho _h (t)\).

(1) Model transformation

By the timescale principle [3], attitude angles are faster dynamics compared with the velocity. When attitude angles vary, the velocity is considered to keep a constant. Thus, the altitude subsystem can be formulated as the following non-affine model.

$$\begin{aligned} \left\{ {\begin{array}{l} \dot{x}_1 =\varphi _{h1} (x_1 ,x_2 ) \\ \dot{x}_2 =x_3 \\ \dot{x}_3 =\varphi _{h3} (\mathbf{x},\delta _\mathrm{e} ) \\ u_h =\delta _\mathrm{e} \\ y_h =x_1 \\ \end{array}} \right. \end{aligned}$$
(34)

where \(\varphi _{h1} (x_1 ,x_2 )\), \(\varphi _{h3} (\mathbf{x},\delta _\mathrm{e} )\) are continuous unknown functions; \(u_h \) and \(y_h \) are the control input and output of altitude subsystem, respectively; \(x_1 =\gamma \), \(x_2 =\theta \), \(x_3 =Q, \mathbf{x}=[x_1, x_2, x_3]\)

Define \(z_1 =x_1 \), \(z_2 =\dot{z}_1 =\dot{x}_1 =\varphi _{h1} (x_1 ,x_2 )\). Then we have

$$\begin{aligned} \dot{z}_2&=\frac{\partial \varphi _{h1} (x_1 ,x_2 )}{\partial x_1 }\dot{x}_1 +\frac{\partial \varphi _{h1} (x_1 ,x_2 )}{\partial x_2 }\dot{x}_2 \nonumber \\&=\frac{\partial \varphi _{h1} (x_1 ,x_2 )}{\partial x_1 }\varphi _{h1} (x_1 ,x_2 )+\frac{\partial \varphi _{h1} (x_1 ,x_2 )}{\partial x_2 }x_3 \nonumber \\&\buildrel \Delta \over = F_{h1} (\mathbf{x}) \end{aligned}$$
(35)

Define \(z_3 =\dot{z}_2 =F_{h1} (\mathbf{x})\), and the time derivative of \(z_3 \) is

$$\begin{aligned} \dot{z}_3&\!=\frac{\partial F_{h1} (\mathbf{x})}{\partial x_1 }\dot{x}_1 +\frac{\partial F_{h1} (\mathbf{x})}{\partial x_2 }\dot{x}_2 +\frac{\partial F_{h1} (\mathbf{x})}{\partial x_3 }\dot{x}_3 \nonumber \\&=\frac{\partial F_{h1} (\mathbf{x})}{\partial x_1 }\varphi _{h1} (x_1 ,x_2 )+\frac{\partial F_{h1} (\mathbf{x})}{\partial x_2 }x_3 \nonumber \\&\quad +\,\frac{\partial F_{h1} (\mathbf{x})}{\partial x_3 }\varphi _{h3} (\mathbf{x},\delta _\mathrm{e} )=\frac{\partial F_{h1} (\mathbf{x})}{\partial x_1 }\varphi _{h1} (x_1 ,x_2 ) \nonumber \\&\quad +\,\frac{\partial F_{h1} (\mathbf{x})}{\partial x_2 }x_3 +\frac{\partial F_{h1} (\mathbf{x})}{\partial x_3 }\varphi _{h3} (\mathbf{x},\delta _\mathrm{e} ) \nonumber \\&\buildrel \Delta \over = \varGamma _h (z_3 ,\delta _\mathrm{e} ) \end{aligned}$$
(36)

Finally, we obtain the following formulation

$$\begin{aligned} \left\{ {\begin{array}{l} \dot{z}_1 =z_2 \\ \dot{z}_2 =z_3 \\ \dot{z}_3 =\varGamma _h (z_3 ,\delta _\mathrm{e} ) \\ u_h =\delta _\mathrm{e} \\ y_h =z_1 =x_1 =\gamma \\ \end{array}} \right. \end{aligned}$$
(37)

Utilizing mean value theorem [27], (37) becomes

$$\begin{aligned} \left\{ {\begin{array}{l} \dot{z}_1 =z_2 \\ \dot{z}_2 =z_3 \\ \dot{z}_3 =\varGamma _{h0} (z_3 ,0)+\varGamma _{h1} (z_3 ,\delta _\mathrm{e}^*)\delta _\mathrm{e} \\ u_h =\delta _\mathrm{e} \\ y_h =z_1 =x_1 =\gamma \\ \end{array}} \right. \end{aligned}$$
(38)

where \(\varGamma _{h1} (z_3 ,\delta _\mathrm{e}^*)=\frac{\partial \varGamma _h (z_3 ,\delta _\mathrm{e}^*)}{\varGamma _h (z_3 ,\delta _\mathrm{e}^*)}\ne 0,\delta _\mathrm{e}^*\in \left( {0,\delta _\mathrm{e} } \right) \); \(\varGamma _{h0} (z_3 ,0)\) is a continuous unknown function.

Remark 3

\(\varGamma _{h1} (z_3 ,\delta _\mathrm{e}^*)\ne 0\) is the controllability condition of (38), and the strict restriction on the sign of \(\varGamma _{h1} (z_3 ,\delta _\mathrm{e}^*)\) is released.

(2) Prescribed performance back-stepping controller design

Step 1 :

Define tracking error \(e_{h1} \)

$$\begin{aligned} e_{h1} =z_1 -z_{\mathrm{1d}} =z_1 -\gamma _\mathrm{d} \end{aligned}$$
(39)

Define a performance function \(\rho _{h1} (t)\!=\!\left( {\rho _{h10} -\rho _{h1\infty } } \right) e^{-l_{h1} t}+\rho _{h1\infty } >0\) to constrain \(e_{h1} \)

$$\begin{aligned} -{\delta }_{h1} \rho _{h1} (t)<e_{h1} <\bar{{\delta }}_{h1} \rho _{h1} (t) \end{aligned}$$
(40)

where \(\rho _{h10} >0\), \(\rho _{h1\infty } >0\), \(l_{h1} >0\), \(0<{\delta }_{h1} <1\), \(0<\bar{{\delta }}_{h1} <1\) are design parameters and satisfy \(\rho _{h10} >\rho _{h1\infty } \), \(-{\delta }_{h1} \rho _{h10}<e_{h1} (0)<\bar{{\delta }}_{h1} \rho _{h10} \), \(\rho _{h1\infty } \le \rho _{h1} (t)\le \rho _{h10} \).

We convert (40) into the following formulation

$$\begin{aligned} e_{h1} =\varPsi _{h1} \left( {\varepsilon _{h1} (t)} \right) \rho _{h1} (t) \end{aligned}$$
(41)

where \(\varPsi _{h1} \left( {\varepsilon _{h1} (t)} \right) \!=\!\frac{\bar{{\delta }}_{h1} e^{\varepsilon _{h1} (t)}-{\delta }_{h1} e^{-\varepsilon _{h1} (t)}}{e^{\varepsilon _{h1} (t)}+e^{-\varepsilon _{h1} (t)}}\in \left( {-{\delta }_{h1} ,\bar{{\delta }}_{h1} } \right) \) is a transformed function and \(\varepsilon _{h1} (t)\) is a transformed error. From (41), we get the formulation of \(\varepsilon _{h1} (t)\)

$$\begin{aligned} \varepsilon _{h1} (t)=\varPsi _{h1}^{-1} \left( {\varepsilon _{h1} (t)} \right) =\frac{1}{2}\ln \left( {\frac{{e_{h1} }/{\rho _{h1} (t)}+{\delta }_{h1} }{\bar{{\delta }}_{h1} -{e_{h1} }/{\rho _{h1} (t)}}} \right) . \end{aligned}$$
(42)

Furthermore, \(\dot{\varepsilon }_{h1} (t)\) is derived as

$$\begin{aligned} \dot{\varepsilon }_{h1} (t)= & {} r_{h1} \left[ {\dot{e}_{h1} -e_{h1} \frac{\dot{\rho }_{h1} (t)}{\rho _{h1} (t)}} \right] \nonumber \\&=r_{h1} \left[ {\dot{z}_1 -\dot{\gamma }_\mathrm{d} -e_{h1} \frac{\dot{\rho }_{h1} (t)}{\rho _{h1} (t)}} \right] \nonumber \\&=r_{h1} \left[ {z_2 -\dot{\gamma }_\mathrm{d} -e_{h1} \frac{\dot{\rho }_{h1} (t)}{\rho _{h1} (t)}} \right] \end{aligned}$$
(43)

where \(r_{h1} =\frac{1}{2\rho _{h1} (t)}\left[ \frac{1}{{e_{h1} }/{\rho _{h1} (t)}+{\delta }_{h1} }\right. \left. -\frac{1}{{e_{h1} }/{\rho _{h1} (t)}-\bar{{\delta }}_{h1} } \right] \ge \frac{1}{2\rho _{h10} {\delta }_{h1} }+\frac{1}{2\rho _{h10} \bar{{\delta }}_{h1} }>0\).

The virtual control law is designed as

$$\begin{aligned} z_{\hbox {2d}} =-k_{h1} \varepsilon _{h1} (t)+\dot{\gamma }_\mathrm{d} +e_{h1} \frac{\dot{\rho }_{h1} (t)}{\rho _{h1} (t)} \end{aligned}$$
(44)

where \(k_{h1} >0\) is a design parameter, \(\dot{\rho }_{h1} (t)=-l_{h1} \left( {\rho _{h10} -\rho _{h1\infty } } \right) e^{-l_{h1} t}\).

Step 2 :

Define tracking error \(e_{h2} \)

$$\begin{aligned} e_{h2} =z_2 -z_{\hbox {2d}} \end{aligned}$$
(45)

Construct a performance function \(\rho _{h2} (t)=\left( \rho _{h20}\right. \left. -\rho _{h2\infty } \right) e^{-l_{h2} t}+\rho _{h2\infty } >0\) to constrain \(e_{h2} \)

$$\begin{aligned} -{\delta }_{h2} \rho _{h2} (t)<e_{h2} <\bar{{\delta }}_{h2} \rho _{h2} (t) \end{aligned}$$
(46)

where \(\rho _{h20} >0\), \(\rho _{h2\infty } >0\), \(l_{h2} >0\), \(0<{\delta }_{h2} <1\), \(0<\bar{{\delta }}_{h2} <1\) are design parameters and satisfy \(\rho _{h20} >\rho _{h2\infty } \), \(-{\delta }_{h2} \rho _{h20}<e_{h2} (0)<\bar{{\delta }}_{h2} \rho _{h20} \), \(\rho _{h2\infty } \le \rho _{h2} (t)\le \rho _{h20} \).

Equation (46) is further converted into the following formulation

$$\begin{aligned} e_{h2} =\varPsi _{h2} \left( {\varepsilon _{h2} (t)} \right) \rho _{h2} (t) \end{aligned}$$
(47)

where \(\varPsi _{h2} \left( {\varepsilon _{h2} (t)} \right) \!=\!\frac{\bar{{\delta }}_{h2} e^{\varepsilon _{h2} (t)}-{\delta }_{h2} e^{-\varepsilon _{h2} (t)}}{e^{\varepsilon _{h2} (t)}+e^{-\varepsilon _{h2} (t)}}\in \left( {-{\delta }_{h2} ,\bar{{\delta }}_{h2} } \right) \) is a transformed function and \(\varepsilon _{h2} (t)\) is a transformed error. From (47), we have

$$\begin{aligned} \varepsilon _{h2} (t)=\varPsi _{h2}^{-1} \left( {\varepsilon _{h2} (t)} \right) =\frac{1}{2}\ln \left( {\frac{{e_{h2} }/{\rho _{h2} (t)}+{\delta }_{h2} }{\bar{{\delta }}_{h2} -{e_{h2} }/{\rho _{h2} (t)}}} \right) . \end{aligned}$$
(48)

The time derivative of \(\varepsilon _{h2} (t)\) is

$$\begin{aligned} \dot{\varepsilon }_{h2} (t)= & {} r_{h2} \left[ {\dot{e}_{h2} -e_{h2} \frac{\dot{\rho }_{h2} (t)}{\rho _{h2} (t)}} \right] \nonumber \\&=r_{h2} \left[ {\dot{z}_2 -\dot{z}_{\hbox {2d}} -e_{h2} \frac{\dot{\rho }_{h2} (t)}{\rho _{h2} (t)}} \right] \nonumber \\&=r_{h2} \left[ {z_3 -\dot{z}_{\hbox {2d}} -e_{h2} \frac{\dot{\rho }_{h2} (t)}{\rho _{h2} (t)}} \right] \end{aligned}$$
(49)

where \(r_{h2} =\frac{1}{2\rho _{h2} (t)}\left[ {\frac{1}{{e_{h2} }/{\rho _{h2} (t)}+{\delta }_{h2} }-\frac{1}{{e_{h2} }/{\rho _{h2} (t)}-\bar{{\delta }}_{h2} }} \right] \ge \frac{1}{2\rho _{h20} }\left( {\frac{1}{{\delta }_{h2} }+\frac{1}{\bar{{\delta }}_{h2} }} \right) >0\).

The virtual control law is devised as

$$\begin{aligned} z_{\hbox {3d}} =-k_{h2} \varepsilon _{h2} (t)+\dot{z}_{\hbox {2d}} +e_{h2} \frac{\dot{\rho }_{h2} (t)}{\rho _{h2} (t)} \end{aligned}$$
(50)

where \(k_{h2} >0\) is a design parameter, \(\dot{\rho }_{h2} (t)=-l_{h2} \left( {\rho _{h20} -\rho _{h2\infty } } \right) e^{-l_{h2} t}\).

Step 3 :

Define tracking error \(e_{h3} \)

$$\begin{aligned} e_{h3} =z_3 -z_{\hbox {3d}} \end{aligned}$$
(51)

Devise a performance function \(\rho _{h3} (t)=\left( \rho _{h30}\right. \left. -\rho _{h3\infty } \right) e^{-l_{h3} t}+\rho _{h3\infty } >0\) to constrain \(e_{h3} \)

$$\begin{aligned} -{\delta }_{h3} \rho _{h3} (t)<e_{h3} <\bar{{\delta }}_{h3} \rho _{h3} (t) \end{aligned}$$
(52)

with \(\rho _{h30} >0\), \(\rho _{h3\infty } >0\), \(l_{h3} >0\), \(0<{\delta }_{h3} <1\), \(0<\bar{{\delta }}_{h3} <1\) being design parameters and satisfying \(\rho _{h30} >\rho _{h3\infty } \), \(-{\delta }_{h3} \rho _{h30}<e_{h3} (0)<\bar{{\delta }}_{h3} \rho _{h30} \), \(\rho _{h3\infty } \le \rho _{h3} (t)\le \rho _{h30} \).

We transform (52) into an equivalent formulation

$$\begin{aligned} e_{h3} =\varPsi _{h3} \left( {\varepsilon _{h3} (t)} \right) \rho _{h3} (t) \end{aligned}$$
(53)

where \(\varPsi _{h3} \left( {\varepsilon _{h3} (t)} \right) =\frac{\bar{{\delta }}_{h3} e^{\varepsilon _{h3} (t)}-{\delta }_{h3} e^{-\varepsilon _{h3} (t)}}{e^{\varepsilon _{h3} (t)}+e^{-\varepsilon _{h3} (t)}}\in \left( {-{\delta }_{h3} ,\bar{{\delta }}_{h3} } \right) \) is a transformed function and \(\varepsilon _{h3} (t)\) is a transformed error. The inversion of (53) is as follows

$$\begin{aligned} \varepsilon _{h3} (t)=\varPsi _{h3}^{-1} \left( {\varepsilon _{h3} (t)} \right) =\frac{1}{2}\ln \left( {\frac{{e_{h3} }/{\rho _{h3} (t)}+{\delta }_{h3} }{\bar{{\delta }}_{h3} -{e_{h3} }/{\rho _{h3} (t)}}} \right) . \end{aligned}$$
(54)

\(\dot{\varepsilon }_{h3} (t)\) is derived as

$$\begin{aligned}&\dot{\varepsilon }_{h3} (t)=r_{h3} \left[ {\dot{e}_{h3} -e_{h3} \frac{\dot{\rho }_{h3} (t)}{\rho _{h3} (t)}} \right] \nonumber \\&\quad =r_{h3} \left[ {\dot{z}_3 -\dot{z}_{\hbox {3d}} -e_{h3} \frac{\dot{\rho }_{h3} (t)}{\rho _{h3} (t)}} \right] \nonumber \\&\quad =r_{h3} \left[ {\varGamma _{h0} (z_3 ,0)+\varGamma _{h1} (z_3 ,\delta _\mathrm{e}^*)\delta _\mathrm{e} -\dot{z}_{\hbox {3d}} -e_{h3} \frac{\dot{\rho }_{h3} (t)}{\rho _{h3} (t)}} \right] \nonumber \\&\quad =r_{h3} \left[ \varGamma _{h0} (z_3 ,0)+\varGamma _{h1} (z_3 ,\delta _\mathrm{e}^*)\delta _\mathrm{e} -\dot{z}_{\hbox {3d}}\right. \nonumber \\&\quad \quad -\,\left. \varPsi _{h3} \left( {\varepsilon _{h3} (t)} \right) \rho _{h3} (t)\frac{\dot{\rho }_{h3} (t)}{\rho _{h3} (t)} \right] \nonumber \\&\quad =r_{h3} \left[ \varGamma _{h0} (z_3 ,0)+\varGamma _{h1} (z_3 ,\delta _\mathrm{e}^*)\delta _\mathrm{e} -\dot{z}_{\hbox {3d}}\right. \nonumber \\&\quad \quad -\,\left. \varPsi _{h3} \left( {\varepsilon _{h3} (t)} \right) \dot{\rho }_{h3} (t) \right] \end{aligned}$$
(55)

with \(r_{h3} =\frac{1}{2\rho _{h3} (t)}\left[ {\frac{1}{{e_{h3} }/{\rho _{h3} (t)}+{\delta }_{h3} }-\frac{1}{{e_{h3} }/{\rho _{h3} (t)}-\bar{{\delta }}_{h3} }} \right] \ge \frac{1}{2\rho _{h30} }\left( {\frac{1}{{\delta }_{h3} }+\frac{1}{\bar{{\delta }}_{h3} }} \right) >0\).

Define Lyapunov function

$$\begin{aligned} L_h =\frac{\varepsilon _{h1}^2 (t)}{2}+\frac{\varepsilon _{h2}^2 (t)}{2}+\frac{\varepsilon _{h3}^2 (t)}{2}. \end{aligned}$$
(56)

Employing (43), (49) and (55), \(\dot{L}_h \) is

$$\begin{aligned}&\dot{L}_h =\varepsilon _{h1} (t)\dot{\varepsilon }_{h1} (t)+\varepsilon _{h2} (t)\dot{\varepsilon }_{h2} (t)+\varepsilon _{h3} (t)\dot{\varepsilon }_{h3} (t) \nonumber \\&\quad =\varepsilon _{h1} (t)r_{h1} \left[ {z_2 -\dot{\gamma }_\mathrm{d} -e_{h1} \frac{\dot{\rho }_{h1} (t)}{\rho _{h1} (t)}} \right] \nonumber \\&\qquad +\,\varepsilon _{h2} (t)r_{h2} \left[ {z_3 -\dot{z}_{\hbox {2d}} -e_{h2} \frac{\dot{\rho }_{h2} (t)}{\rho _{h2} (t)}} \right] \nonumber \\&\qquad +\,\varepsilon _{h3} (t)r_{h3} \left[ \varGamma _{h0} (z_3 ,0)+\varGamma _{h1} (z_3 ,\delta _\mathrm{e}^*)\delta _\mathrm{e} -\dot{z}_{\hbox {3d}} \right. \nonumber \\&\qquad -\,\left. \varPsi _{h3} \left( {\varepsilon _{h3} (t)} \right) \dot{\rho }_{h3} (t) \right] \nonumber \\&\quad =\varepsilon _{h1} (t)r_{h1} \left[ {e_{h2} +z_{\hbox {2d}} -\dot{\gamma }_\mathrm{d} -e_{h1} \frac{\dot{\rho }_{h1} (t)}{\rho _{h1} (t)}} \right] \nonumber \\&\qquad +\,\varepsilon _{h3} (t)r_{h3} \varGamma _{h1} (z_3 ,\delta _\mathrm{e}^*)\delta _\mathrm{e} +\varepsilon _{h3} (t)r_{h3} \nonumber \\&\qquad \times \, \left[ \varGamma _{h0} (z_3 ,0)-\dot{z}_{\hbox {3d}}\right. \nonumber \\&\qquad -\,\left. \varPsi _{h3} \left( {\varepsilon _{h3} (t)} \right) \dot{\rho }_{h3} (t) \right] . \end{aligned}$$
(57)

Substituting (44) and (50) into (57) leads to

$$\begin{aligned} \dot{L}_h= & {} \varepsilon _{h1} (t)r_{h1} \left[ {e_{h2} -k_{h1} \varepsilon _{h1} (t)} \right] +\varepsilon _{h2} (t)r_{h2} \nonumber \\&\times \,\left[ {e_{h3} -k_{h2} \varepsilon _{h2} (t)} \right] \nonumber \\&+\,\varepsilon _{h3} (t)r_{h3} \left[ \varGamma _{h0} (z_3 ,0)+\varGamma _{h1} (z_3 ,\delta _\mathrm{e}^*)\delta _\mathrm{e} -\dot{z}_{\hbox {3d}}\right. \nonumber \\&-\,\left. \varPsi _{h3} \left( {\varepsilon _{h3} (t)} \right) \dot{\rho }_{h3} (t) \right] \nonumber \\= & {} \varepsilon _{h1} (t)r_{h1} \left[ {\varPsi _{h2} \left( {\varepsilon _{h2} (t)} \right) \rho _{h2} (t)-k_{h1} \varepsilon _{h1} (t)} \right] \nonumber \\&+\,\varepsilon _{h2} (t)r_{h2} \left[ {\varPsi _{h3} \left( {\varepsilon _{h3} (t)} \right) \rho _{h3} (t)-k_{h2} \varepsilon _{h2} (t)} \right] \nonumber \\&+\,\varepsilon _{h3} (t)r_{h3} \varGamma _{h1} (z_3 ,\delta _\mathrm{e}^*)\delta _\mathrm{e} +\varepsilon _{h3} (t)r_{h3} \left[ \varGamma _{h0} (z_3 ,0)\right. \nonumber \\&-\,\left. \dot{z}_{\hbox {3d}} -\varPsi _{h3} \left( {\varepsilon _{h3} (t)} \right) \dot{\rho }_{h3} (t) \right] \nonumber \\= & {} r_{h1} \left[ {\varPsi _{h2} \left( {\varepsilon _{h2} (t)} \right) \rho _{h2} (t)\varepsilon _{h1} (t)-k_{h1} \varepsilon _{h1}^2 (t)} \right] \nonumber \\&+\,r_{h2} \left[ {\varPsi _{h3} \left( {\varepsilon _{h3} (t)} \right) \rho _{h3} (t)\varepsilon _{h2} (t)-k_{h2} \varepsilon _{h2}^2 (t)} \right] \nonumber \\&+\,\varepsilon _{h3} (t)r_{h3} \varGamma _{h1} (z_3 ,\delta _\mathrm{e}^*)\delta _\mathrm{e} \nonumber \\&+\,\varepsilon _{h3} (t)r_{h3} \left[ \varGamma _{h0} (\varPsi _{h3} \left( {\varepsilon _{h3} (t)} \right) \rho _{h3} (t)\right. \nonumber \\&+\,\left. z_{\hbox {3d}} ,0)-\dot{z}_{\hbox {3d}} -\varPsi _{h3} \left( {\varepsilon _{h3} (t)} \right) \dot{\rho }_{h3} (t) \right] \end{aligned}$$
(58)

It is easy to conclude that there exists a positive constant \(\Sigma _h \) such that \(\left| \varGamma _{h0} (\varPsi _{h3} \left( {\varepsilon _{h3} (t)} \right) \rho _{h3} (t)+z_{\hbox {3d}} ,0)\right. \left. -\dot{z}_{\hbox {3d}} -\varPsi _{h3} \left( {\varepsilon _{h3} (t)} \right) \dot{\rho }_{h3} (t) \right| \le \Sigma _h \). Furthermore, \(\rho _{h2\infty } \le \rho _{h2} (t)\le \rho _{h20} \),

$$\begin{aligned}&\rho _{h3\infty } \le \rho _{h3} (t)\le \rho _{h30} , \quad r_{h1} \ge \frac{1}{2\rho _{h10} }\left( {\frac{1}{{\delta }_{h1} }+\frac{1}{\bar{{\delta }}_{h1} }} \right)>0,\\&r_{h2} \ge \frac{1}{2\rho _{h20} }\left( {\frac{1}{{\delta }_{h2} }+\frac{1}{\bar{{\delta }}_{h2} }} \right) >0,\\&\varPsi _{h2} \left( {\varepsilon _{h2} (t)} \right) =\frac{\bar{{\delta }}_{h2} e^{\varepsilon _{h2} (t)}-{\delta }_{h2} e^{-\varepsilon _{h2} (t)}}{e^{\varepsilon _{h2} (t)}+e^{-\varepsilon _{h2} (t)}}\in \left( {-{\delta }_{h2} ,\bar{{\delta }}_{h2} } \right) , \\&\varPsi _{h3} \left( {\varepsilon _{h3} (t)} \right) =\frac{\bar{{\delta }}_{h3} e^{\varepsilon _{h3} (t)}-{\delta }_{h3} e^{-\varepsilon _{h3} (t)}}{e^{\varepsilon _{h3} (t)}+e^{-\varepsilon _{h3} (t)}}\in \left( {-{\delta }_{h3} ,\bar{{\delta }}_{h3} } \right) . \end{aligned}$$

Then (58) becomes

$$\begin{aligned} \dot{L}_h\le & {} r_{h1} \left[ {\bar{{\delta }}_{h2} \rho _{h20} \left| {\varepsilon _{h1} (t)} \right| -k_{h1} \varepsilon _{h1}^2 (t)} \right] \nonumber \\&+\,r_{h2} \left[ {\bar{{\delta }}_{h3} \rho _{h30} \left| {\varepsilon _{h2} (t)} \right| -k_{h2} \varepsilon _{h2}^2 (t)} \right] \nonumber \\&+\,\varepsilon _{h3} (t)r_{h3} \varGamma _{h1} (z_3 ,\delta _\mathrm{e}^*)\delta _\mathrm{e} +\left| {\varepsilon _{h3} (t)} \right| r_{h3} \Sigma _h \nonumber \\= & {} r_{h1} \left| {\varepsilon _{h1} (t)} \right| \left[ {\bar{{\delta }}_{h2} \rho _{h20} -k_{h1} \left| {\varepsilon _{h1} (t)} \right| } \right] \nonumber \\&+\,r_{h2} \left| {\varepsilon _{h2} (t)} \right| \left[ {\bar{{\delta }}_{h3} \rho _{h30} -k_{h2} \left| {\varepsilon _{h2} (t)} \right| } \right] \nonumber \\&+\,\varepsilon _{h3} (t)r_{h3} \varGamma _{h1} (z_3 ,\delta _\mathrm{e}^*)\delta _\mathrm{e} +\left| {\varepsilon _{h3} (t)} \right| r_{h3} \Sigma _h. \end{aligned}$$
(59)

Finally, the actual control law \(\delta _\mathrm{e} \) is chosen as

$$\begin{aligned} \left\{ {\begin{array}{l} \delta _\mathrm{e} =N_{h3} \left( {\xi _{h3} } \right) \left[ {\kappa _{h31} \varepsilon _{h3} (t)+\frac{\kappa _{h32} r_{h3} \varepsilon _{h3} (t)}{2}} \right] \\ \dot{\xi }_{h3} =\kappa _{h31} r_{h3} \varepsilon _{h3}^2 (t)+\frac{\kappa _{h32} r_{h3}^2 \varepsilon _{h3}^2 (t)}{2} \\ \end{array}} \right. \end{aligned}$$
(60)

where \(N_{h3} \left( {\xi _{h3} } \right) =e^{\xi _{h3}^2 }\cos ({\uppi }\xi _{h3} /2)\) is a Nussbaum function [3,4]; \(\kappa _{h31} \), \(\kappa _{h32} >0\) are design parameters.

Invoking (60), (59) becomes

$$\begin{aligned}&\dot{L}_h \le r_{h1} \left| {\varepsilon _{h1} (t)} \right| \left[ {\bar{{\delta }}_{h2} \rho _{h20} -k_{h1} \left| {\varepsilon _{h1} (t)} \right| } \right] \nonumber \\&\qquad +\,r_{h2} \left| {\varepsilon _{h2} (t)} \right| \left[ {\bar{{\delta }}_{h3} \rho _{h30} -k_{h2} \left| {\varepsilon _{h2} (t)} \right| } \right] \nonumber \\&\qquad +\,\varepsilon _{h3} (t)r_{h3} \varGamma _{h1} (z_3 ,\delta _\mathrm{e}^*)N_{h3} \left( {\xi _{h3} } \right) \left[ \kappa _{h31} \varepsilon _{h3} (t)\right. \nonumber \\&\qquad +\,\left. \frac{\kappa _{h32} r_{h3} \varepsilon _{h3} (t)}{2} \right] +\left| {\varepsilon _{h3} (t)} \right| r_{h3} \Sigma _h. \end{aligned}$$
(61)

Based on Young’s inequality, we get \(\left| {\varepsilon _{h3} (t)} \right| r_{h3} \Sigma _V \le \frac{\kappa _{h32} }{2}r_{h3}^2 \varepsilon _{h3}^2 (t)+\frac{\Sigma _h^2 }{2\kappa _{h32} }\). Then (61) further becomes

$$\begin{aligned} \dot{L}_h\le & {} r_{h1} \left| {\varepsilon _{h1} (t)} \right| \left[ {\bar{{\delta }}_{h2} \rho _{h20} -k_{h1} \left| {\varepsilon _{h1} (t)} \right| } \right] \nonumber \\&+\,r_{h2} \left| {\varepsilon _{h2} (t)} \right| \left[ {\bar{{\delta }}_{h3} \rho _{h30} -k_{h2} \left| {\varepsilon _{h2} (t)} \right| } \right] \nonumber \\&+\,\varepsilon _{h3} (t)r_{h3} \varGamma _{h1} (z_3 ,\delta _\mathrm{e}^*)N_{h3} \left( {\xi _{h3} } \right) \nonumber \\&\left[ {\kappa _{h31} \varepsilon _{h3} (t)+\frac{\kappa _{h32} r_{h3} \varepsilon _{h3} (t)}{2}} \right] \nonumber \\&+\,\frac{\kappa _{h32} }{2}r_{h3}^2 \varepsilon _{h3}^2 (t)+\frac{\Sigma _h^2 }{2\kappa _{h32} } \nonumber \\= & {} r_{h1} \left| {\varepsilon _{h1} (t)} \right| \left[ {\bar{{\delta }}_{h2} \rho _{h20} -k_{h1} \left| {\varepsilon _{h1} (t)} \right| } \right] \nonumber \\&+\,r_{h2} \left| {\varepsilon _{h2} (t)} \right| \left[ {\bar{{\delta }}_{h3} \rho _{h30} -k_{h2} \left| {\varepsilon _{h2} (t)} \right| } \right] \nonumber \\&+\,\varGamma _{h1} (z_3 ,\delta _\mathrm{e}^*)N_{h3} \left( {\xi _{h3} } \right) \nonumber \\&\times \left[ {\kappa _{h31} r_{h3} \varepsilon _{h3}^2 (t)+\frac{\kappa _{h32} r_{h3}^2 \varepsilon _{h3}^2 (t)}{2}} \right] \nonumber \\&+\,\frac{\kappa _{h32} }{2}r_{h3}^2 \varepsilon _{h3}^2 (t)+\frac{\Sigma _h^2 }{2\kappa _{h32} } \nonumber \\= & {} r_{h1} \left| {\varepsilon _{h1} (t)} \right| \left[ {\bar{{\delta }}_{h2} \rho _{h20} -k_{h1} \left| {\varepsilon _{h1} (t)} \right| } \right] \nonumber \\&+\,r_{h2} \left| {\varepsilon _{h2} (t)} \right| \left[ {\bar{{\delta }}_{h3} \rho _{h30} -k_{h2} \left| {\varepsilon _{h2} (t)} \right| } \right] \nonumber \\&+\,\varGamma _{h1} (z_3 ,\delta _\mathrm{e}^*)N_{h3} \left( {\xi _{h3} } \right) \dot{\xi }_{h3} \nonumber \\&+\,\frac{\kappa _{h32} }{2}r_{h3}^2 \varepsilon _{h3}^2 (t)+\frac{\Sigma _h^2 }{2\kappa _{h32} } \nonumber \\= & {} r_{h1} \left| {\varepsilon _{h1} (t)} \right| \left[ {\bar{{\delta }}_{h2} \rho _{h20} -k_{h1} \left| {\varepsilon _{h1} (t)} \right| } \right] \nonumber \\&+\,r_{h2} \left| {\varepsilon _{h2} (t)} \right| \left[ {\bar{{\delta }}_{h3} \rho _{h30} -k_{h2} \left| {\varepsilon _{h2} (t)} \right| } \right] \nonumber \\&+\,\varGamma _{h1} (z_3 ,\delta _\mathrm{e}^*)N_{h3} \left( {\xi _{h3} } \right) \dot{\xi }_{h3} \nonumber \\&-\,\kappa _{h31} r_{h3} \varepsilon _{h3}^2 (t)+\kappa _{h31} r_{h3} \varepsilon _{h3}^2 (t)\nonumber \\&+\,\frac{\kappa _{h32} }{2}r_{h3}^2 \varepsilon _{h3}^2 (t)+\frac{\Sigma _h^2 }{2\kappa _{h32} } \nonumber \\= & {} r_{h1} \left| {\varepsilon _{h1} (t)} \right| \left[ {\bar{{\delta }}_{h2} \rho _{h20} -k_{h1} \left| {\varepsilon _{h1} (t)} \right| } \right] \nonumber \\&+\,r_{h2} \left| {\varepsilon _{h2} (t)} \right| \left[ {\bar{{\delta }}_{h3} \rho _{h30} -k_{h2} \left| {\varepsilon _{h2} (t)} \right| } \right] \nonumber \\&-\,\kappa _{h31} r_{h3} \varepsilon _{h3}^2 (t)+\varGamma _{h1} (z_3 ,\delta _\mathrm{e}^*)\nonumber \\&\times N_{h3} \left( {\xi _{h3} } \right) \dot{\xi }_{h3} +\dot{\xi }_{h3} +\frac{\Sigma _h^2 }{2\kappa _{h32} } \end{aligned}$$
(62)

If \(\left| {\varepsilon _{h1} (t)} \right| \le {\bar{{\delta }}_{h2} \rho _{h20} }/{k_{h1} }\) and \(\left| {\varepsilon _{h2} (t)} \right| \le {\bar{{\delta }}_{h3} \rho _{h30} }/{k_{h2} }\), then \(\varepsilon _{h1} (t)\) and \(\varepsilon _{h2} (t)\) are bounded. Else if \(\left| {\varepsilon _{h1} (t)} \right| >{\bar{{\delta }}_{h2} \rho _{h20} }/{k_{h1} }\) and \(\left| {\varepsilon _{h2} (t)} \right| >{\bar{{\delta }}_{h3} \rho _{h30} }/{k_{h2} }\), we obtain \(r_{h1} \left| {\varepsilon _{h1} (t)} \right| \left[ {\bar{{\delta }}_{h2} \rho _{h20} -k_{h1} \left| {\varepsilon _{h1} (t)} \right| } \right] <0\) and \(r_{h2} \left| {\varepsilon _{h2} (t)} \right| \left[ {\bar{{\delta }}_{h3} \rho _{h30} -k_{h2} \left| {\varepsilon _{h2} (t)} \right| } \right] <0\). Moreover, we easily know that there exist adequately small constants\(0<\kappa _{H1} <r_{h1} k_{h1} \)and\(0<\kappa _{H2} <r_{h2} k_{h2} \)such that \(r_{h1} \left| {\varepsilon _{h1} (t)} \right| \left[ {\bar{{\delta }}_{h2} \rho _{h20} -k_{h1} \left| {\varepsilon _{h1} (t)} \right| } \right] +\kappa _{H1} \varepsilon _{h1}^2 (t)<0\) and \(r_{h2} \left| {\varepsilon _{h2} (t)} \right| \left[ {\bar{{\delta }}_{h3} \rho _{h30} -k_{h2} \left| {\varepsilon _{h2} (t)} \right| } \right] +\kappa _{H2} \varepsilon _{h2}^2 (t)<0\). Thus (62) becomes

$$\begin{aligned}&\dot{L}_h \le r_{h1} \left| {\varepsilon _{h1} (t)} \right| \left[ {\bar{{\delta }}_{h2} \rho _{h20} -k_{h1} \left| {\varepsilon _{h1} (t)} \right| } \right] \nonumber \\&\qquad +\kappa _{H1} \varepsilon _{h1}^2 (t)-\kappa _{H1} \varepsilon _{h1}^2 (t) +r_{h2} \left| {\varepsilon _{h2} (t)} \right| \nonumber \\&\qquad \left[ {\bar{{\delta }}_{h3} \rho _{h30} -k_{h2} \left| {\varepsilon _{h2} (t)} \right| } \right] +\kappa _{H2} \varepsilon _{h2}^2 (t)-\kappa _{H2} \varepsilon _{h2}^2 (t) \nonumber \\&\qquad -\,\kappa _{h31} r_{h3} \varepsilon _{h3}^2 (t)+\varGamma _{h1} (z_3 ,\delta _\mathrm{e}^*)\nonumber \\&\qquad \times N_{h3} \left( {\xi _{h3} } \right) \dot{\xi }_{h3} +\dot{\xi }_{h3} +\frac{\Sigma _h^2 }{2\kappa _{h32} } \nonumber \\&\quad \le -\kappa _{H1} \varepsilon _{h1}^2 (t)-\kappa _{H2} \varepsilon _{h2}^2 (t)-\kappa _{h31} r_{h3} \varepsilon _{h3}^2 (t) \nonumber \\&\qquad +\varGamma _{h1} (z_3 ,\delta _\mathrm{e}^*)N_{h3} \left( {\xi _{h3} } \right) \dot{\xi }_{h3} +\dot{\xi }_{h3} +\frac{\Sigma _h^2 }{2\kappa _{h32} } \nonumber \\&\quad \le -\iota _h L_h +\varGamma _{h1} (z_3 ,\delta _\mathrm{e}^*)N_{h3} \left( {\xi _{h3} } \right) \dot{\xi }_{h3} +\dot{\xi }_{h3}\nonumber \\&\qquad +\,\frac{\Sigma _h^2 }{2\kappa _{h32} } \end{aligned}$$
(63)

with \(\iota _h =\min \left\{ {2\kappa _{H1} ,2\kappa _{H2} ,\frac{\kappa _{h31} }{\rho _{h30} }\left( {\frac{1}{{\delta }_{h3} }+\frac{1}{\bar{{\delta }}_{h3} }} \right) } \right\} \).

Being multiplied by \(e^{\iota _h t}\) on both sides of (63) leads to

$$\begin{aligned}&\frac{\hbox {d}}{\hbox {d}t}\left( {L_h e^{\iota _h t}} \right) \le \varGamma _{h1} (z_3 ,\delta _\mathrm{e}^*)N_{h3} \left( {\xi _{h3} } \right) \dot{\xi }_{h3} e^{\iota _h t}\nonumber \\&\qquad +\dot{\xi }_{h3} e^{\iota _h t}+\frac{\Sigma _h^2 }{2\kappa _{h32} }e^{\iota _h t} \end{aligned}$$
(64)

Integrating (64) over [0, t], we obtain

$$\begin{aligned} 0\le & {} L_h \le L_h (0)+e^{-\iota _h t}\nonumber \\&\times \int _0^t {\varGamma _{h1} (z_3 ,\delta _\mathrm{e}^*)N_{h3} \left( {\xi _{h3} } \right) \dot{\xi }_{h3} e^{\iota _h \tau }\hbox {d}\tau } \nonumber \\&+e^{-\iota _h t}\int _0^t {\dot{\xi }_{h3} e^{\iota _h \tau }\hbox {d}\tau } +\int _0^t {\frac{\Sigma _h^2 }{2\kappa _{h32} }e^{-\iota _h \left( {t-\tau } \right) }\hbox {d}\tau }\nonumber \\ \end{aligned}$$
(65)

Noticing \(\int _0^t {\frac{\Sigma _h^2 }{2\kappa _{h32} }e^{-\iota _h \left( {t-\tau } \right) }\hbox {d}\tau } =\frac{\Sigma _h^2 }{2\kappa _{h32} }\frac{1}{\iota _h }\left( {1-e^{-\iota _h t}} \right) \in \left[ {0,\frac{\Sigma _h^2 }{2\kappa _{h32} }\frac{1}{\iota _h }} \right) \), we know that \(\int _0^t {\frac{\Sigma _h^2 }{2\kappa _{h32} }e^{-\iota _h \left( {t-\tau } \right) }\hbox {d}\tau } \) is bounded. Furthermore, (65) becomes

$$\begin{aligned}&0\le L_h \le L_{h0} +e^{-\iota _h t}\int _0^t \varGamma _{h1} (z_3 ,\delta _\mathrm{e}^*)\nonumber \\&\qquad \times \, N_{h3} \left( {\xi _{h3} } \right) \dot{\xi }_{h3} e^{\iota _h \tau }\hbox {d}\tau +e^{-\iota _h t}\int _0^t {\dot{\xi }_{h3} e^{\iota _h \tau }\hbox {d}\tau } \end{aligned}$$
(66)

with \(L_{h0} =L_h (0)+\frac{\Sigma _h^2 }{2\kappa _{h32} }\frac{1}{\iota _h }\).

Invoking Lemmas 1 and 2 presented in [29], we have that \(L_h \), \(e^{-\iota _h t}\int _0^t {\varGamma _{h1} (z_3 ,\delta _\mathrm{e}^*)N_{h3} \left( {\xi _{h3} } \right) \dot{\xi }_{h3} e^{\iota _h \tau }\hbox {d}\tau } \) and \(e^{-\iota _h t}\int _0^t {\dot{\xi }_{h3} e^{\iota _h \tau }\hbox {d}\tau } \) are all bounded. Thus, all the closed-loop signals are bounded. From the boundedness of \(\varepsilon _i (t),i=h1 ,h2 ,h3 \), we know that there exist positive constant \(\bar{{\varepsilon }}_i ,i=h1 ,h2 ,h3 \) such that \(\left| {\varepsilon _i (t)} \right| \le \bar{{\varepsilon }}_i ,i=h1, h2, h3 \). Further, the inversions of \(\varepsilon _i (t),i=h1 ,h2 ,h3 \) are \(\frac{{e_i }/{\rho _i (t)}+{\delta }_i }{\bar{{\delta }}_i -{e_i }/{\rho _i (t)}}=e^{2\varepsilon _i (t)}, \quad i=h1 ,h2 ,h3 \). That is, \(e_i =\frac{\bar{{\delta }}_i e^{2\varepsilon _i (t)}-{\delta }_i }{1+e^{2\varepsilon _i (t)}}\rho _i (t),i=h1 ,h2 ,h3 \), which leads to \(-{\delta }_i \rho _i (t)<\frac{\bar{{\delta }}_i e^{-2\bar{{\varepsilon }}_i }-{\delta }_i }{1+e^{-2\bar{{\varepsilon }}_i }}\rho _i (t) \quad \le e_i \le \frac{\bar{{\delta }}_i e^{2\bar{{\varepsilon }}_i }-{\delta }_i }{1+e^{2\bar{{\varepsilon }}_i }}\rho _i (t)<\bar{{\delta }}_i \rho _i (t),i=h1 ,h2 ,h3 \). Obviously, the prescribed performance for \(e_{h1} \), \(e_{h2} \) and \(e_{h3} \) is guaranteed.

The design procedure of velocity and altitude controllers is completed. The structure of the addressed control approach is presented in Fig. 1.

Fig. 1
figure 1

The structure of the proposed control strategy

Full size image

Remark 4

It is apparent that the developed control laws (23), (44), (50) and (60) do not rely on vehicle models, which guarantees the control system with satisfactory robustness against uncertainties.

Remark 5

The above analysis reveals that prescribed output tracking performance for tracking errors \(e_V \), \(e_h \), \(e_{h1} \), \(e_{h2} \) and \(e_{h3} \) is achieved by selecting appropriate design parameters for (15), (30), (40), (46) and (52).

Remark 6

The addressed control laws (23), (44), (50) and (60) are designed based on non-affine models (12) and (37) only using equal transformations from (12), (37) to (13), (38), on the basis of which the proposed control methodology presents good practicality because there is no need of model simplification.

Fig. 2
figure 2

Velocity tracking performance

Full size image
Fig. 3
figure 3

Velocity tracking error

Full size image
Fig. 4
figure 4

Altitude tracking performance

Full size image
Fig. 5
figure 5

Altitude tracking error

Full size image
Fig. 6
figure 6

The response of \(e_{h1}\)

Full size image
Fig. 7
figure 7

The response of \(e_{h2}\)

Full size image
Fig. 8
figure 8

The response of \(e_{h3}\)

Full size image
Fig. 9
figure 9

The response of \(\gamma \)

Full size image
Fig. 10
figure 10

The response of \(\theta \)

Full size image
Fig. 11
figure 11

The response of Q

Full size image
Fig. 12
figure 12

The control input \(\varPhi \)

Full size image
Fig. 13
figure 13

The control input \(\delta \) \(_\mathrm{e}\)

Full size image

5 Simulation results

In this section, the effectiveness of presented control strategy is verified through simulation. Moreover, to show the superiority, the investigated controller is compared with a dynamic surface control-based neural control scheme proposed in [20]. The design parameters are chosen as follows: \(\rho _{V0} =10\), \(\rho _{V\infty } =1.5\), \(l_V =0.05\), \({\delta }_V =\bar{{\delta }}_V =0.9\), \(\kappa _{V1} =-15\), \(\kappa _{V2} =0.5\), \(\rho _{h0} =0.4\), \(\rho _{h\infty } =0.1\), \(l_h =0.05\), \({\delta }_h =\bar{{\delta }}_h =0.5\), \(\mu _h =15\), \(\rho _{h10} =0.087\), \(\rho _{h1\infty } =0.026\), \(l_{h1} =0.1\), \({\delta }_{h1} =\bar{{\delta }}_{h1} =0.5\), \(k_{h1} =0.02\), \(\rho _{h20} =0.087\), \(\rho _{h2\infty } =0.026\), \(l_{h2} =0.1\), \({\delta }_{h2} =\bar{{\delta }}_{h2} =0.5\), \(k_{h2} =0.02\), \(\rho _{h30} =0.087\), \(\rho _{h3\infty } =0.026\), \(l_{h3} =0.1\), \({\delta }_{h3} =\bar{{\delta }}_{h3} =0.5\), \(\kappa _{h31} =-40\), \(\kappa _{h32} =0.5\). Moreover, all the model coefficients in (1)–(7) are assumed to be uncertain by defining \(C=C_0 \left[ {1+0.3\sin (0.05\pi t)} \right] \), where C denotes the value of uncertain coefficient and \(C_{0}\) is the normal value of C.

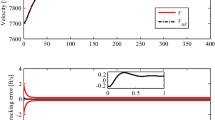
The tracking performance of the presented control approach is depicted in Figs. 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12 and 13. Figures 2, 3, 4, 5, 6, 7 and 8 show that all the tracking errors are forced to fall within prescribed boundaries in the presence of parametric uncertainties. Thus, the pursued control objective is achieved. Further, it is observed from Figs. 3, 4 and 5 that velocity and altitude tracking error converge to zero faster when using the proposed controllers than by employing the strategy of [20], which indicates that better transient performance can be provided by the addressed controller than by the one presented in [20]. Besides, the responses of attitude angles and control inputs, as shown in Figs. 9, 10, 11, 12 and 13, reveal that these variables are bounded and vary without high-frequency chattering. To sum up, the addressed control approach can provide robust tracking of velocity and altitude commands with better transient performance in comparison with the control method of [20].

6 Conclusions

In this paper, a prescribed performance controller is exploited for AHVs within the back-stepping framework. The control laws are devised utilizing non-affine models. Prescribed boundaries are constructed by introducing performance functions to constrain tracking errors. Desired transient performance is guaranteed for control systems. The presented control method does not need accurate models or the signs of control gains. Both the robustness and practicality of the controller are fine. The stability of the closed-loop control system is proved via Lyapunov synthesis. Finally, the tracking performance and superiority of the design is validated by numerical simulation results.