Dynamics analysis of 2-DOF complex planar mechanical system with joint clearance and flexible links

Abstract

Joint clearance and flexible links are two important factors that affect the dynamic behaviors of planar mechanical system. Traditional dynamics studies of planar mechanism rarely take into account both influence of revolute clearance and flexible links, which results in lower accuracy. And many dynamics studies mainly focus on simple mechanism with clearance, the study of complex mechanism with clearance is a few. In order to study dynamic behaviors of two-degree-of-freedom (DOF) complex planar mechanical system more precisely, the dynamic analyses of the mechanical system with joint clearance and flexibility of links are studied in this work. Nonlinear dynamic model of the 2-DOF nine-bar mechanical system with revolute clearance and flexible links is built by Lagrange and finite element method (FEM). Normal and tangential force of the clearance joint is built by the Lankarani–Nikravesh and modified Coulomb’s friction models. The influences of clearance value and driving velocity of the crank on the dynamic behaviors are researched, including motion responses of slider, contact force, driving torques of cranks, penetration depth, shaft center trajectory, Phase diagram, Lyapunov exponents and Poincaré map of clearance joint and slider are both analyzed, respectively. Bifurcation diagrams under different clearance values and different driving velocities of cranks are also investigated. The results show that clearance joint and flexibility of links have a certain impact on dynamic behavior of mechanism, and flexible links can partly decrease dynamic response of the mechanical system with clearance relative to rigid mechanical system with clearance.

1 Introduction

The planar mechanical system will be more faster and lighter in the future and need for higher operational precision [1, 2]. Deformation of the members increased under inertia load, which causes the error between real motion and ideal motion. Elasticity of component has a relatively high influence on precision and stability of the mechanical system. The traditional method of considering the component as a rigid body cannot meet the requirements of modern machinery. Thus, elastic deformation of the links cannot be avoided in the process of movement, and the flexibility of the links should be considered in the dynamic study. As we all know, due to some errors appearing in manufacturing and assembling, existence of clearance is unavoidable, it has a negative influence on dynamic performances of mechanical system, and the clearances of the joints are main reason of instability and vibration. Impact at the clearance joint would cause vibration, fatigue, and noise, the contact force reduces lifetime, and performance and operational accuracy of mechanism generally results in a different response from desired response. Hence, in order to research the dynamic behavior of the planar mechanical system more precisely, the dynamic analysis of the mechanical system with clearance and flexible links should be investigated.

In the recent decades, many studies have been developed to research the influences of clearance joint on dynamic behaviors of rigid mechanical system [3,4,5,6]. However, many previous works mainly focused on the dynamics of a simple mechanism. Erkaya et al. [7] researched influences of the clearances on the noise and the vibration characteristics of the mechanical system. Clearance of revolute joint has been regarded as the massless virtual link, the continuous contact mode between bearing and shaft in joint connection is adopted. Muvengei et al. [8] investigated dynamic characteristics of planar rigid crank-slider mechanism owing to two revolute joints clearance. The influences on dynamic behavior of mechanism and nine simultaneous motion modes of two clearance joints are also researched. Megahed et al. [9] introduced the influence of revolute clearance joint on the dynamic characteristics of the slider-crank mechanism. The slider-crank mechanism with one and two clearance are both considered and studied. Bai et al. [10] studied the dynamic performances of a planar mechanism contain revolute clearance joints by adopting a computational method. Contact force model is built by adopting a novel-type nonlinear contact force model, and the modified Coulomb friction model is utilized to think about friction influence. Tan et al. [11] built the equations of motion of a slider-crank mechanism with single clearance joint and two revolute clearance joints by using the Newton–Euler method with improved Coulomb friction force model and modified contact force model. Baumgarte stabilization method has been utilized to heighten stability of numerical. Wang et al. [12] proposed a non-penetration method of frictional contact to model revolute clearances of a rigid slider-crank. Marques et al. [13] proposed the new method to build spatial joints with axial and radial clearance of the rigid slider-crank mechanism. Newton–Euler method is utilized to model dynamic equation. Varedi et al. [14] put forward an optimization approach based on PSO to decrease the undesirable influences of revolute clearance joints for a slider–crank mechanism. Yaqubi et al. [15] analyzed nonlinear dynamic behaviors of the rigid mechanism by Poincaré maps and bifurcation diagrams and developed a control scheme providing continuous contact in revolute clearance joints in order to obtain a more stable dynamic performance. Rahmanian et al. [16] investigated nonlinear dynamic performance of the rigid slider-crank mechanism containing the clearance. Dynamic equations are derived in consideration of clearance joint, which exists between connecting rod and end slider. Bifurcation diagrams are researched with changing clearance values under various driving speed. Flores  [17] introduced and analyzed the general method of dynamic modeling and analysis of multi-rigid body system containing multiple revolute clearance joints. The nonlinear characteristics of crank-slider mechanism are studied by phase diagrams and Poincaré maps.

Fig. 1

a Revolute joint with clearance, b Modes of the journal motion inside the bearing

So far, most previous studies rarely considered the effect of joint clearance and flexible links together on dynamic behaviors of mechanical system, and mainly concentrate upon the dynamics of the simple mechanism. Erkaya et al. [18] researched conventional and compliant mechanism with clearance joints and compare the impact of revolute clearance joint. Pseudo-rigidbody model of the slider-crank has been built. For various clearance sizes and operating velocity, dynamic behaviors of the slider-crank are analyzed by using ADAMS. Chen et al. [19] discussed impact of the clearance value, driving velocity, link flexibility on dynamic behavior of the slider-crank mechanism by experiment and ADAMS. Erkaya et al. [20] discussed dynamics of the spatial partly compliant slider–crank mechanism with revolute joint clearance. Results indicated that clearances bring about chaotic phenomenon on dynamic exports of the spatial slider–crank mechanism. Marques et al. [21] conducted a research on dynamic behavior of the spatial four bars mechanism containing spherical clearances. The mechanism with spherical clearance has been taken as the object to research the impacts of different clearance values, different friction force models and different friction coefficients. Abdallah et al. [22] discussed dynamic performances of slider-crank mechanism contain flexible links and a multiple revolute joint clearances. The model of the mechanism of the simulation test is carried out by the ADAMS software. Erkaya et al. [23] researched dynamic behaviors of the four bars mechanism containing revolute clearance and flexible links, clearance exists in joint has been taken as the virtual massless rod. Yang et al. [24] proposed a novel method of calculation for the dynamic performance study of mechanism with revolute clearances joints by using vector form intrinsic FEM. Li et al. [25] carried out a numerically research on dynamic behavior of mechanism contain multiple revolute clearance joints and studied the influence of harmonic drive and flexible components on dynamic performance of the planar slider–crank with various locations of one joint clearance and two joint clearances. Erkaya et al. [26] conducted both experimental and numerical analysis to study the influences of revolute clearance joint for rigid mechanism and flexible mechanism. Yaqubi et al. [27] analyzed nonlinear dynamic behaviors and control of a slider-crank mechanism considering the influences of clearance joint and flexible link. In order to keep continuous contact, control scheme has been presented. The motion state of the connecting rod is also studied by the Poincare map and the bifurcation diagram. Wang et al. [28] discussed the nonlinear dynamics characteristics of a planar mechanism consider flexibility of links and revolute clearance joint in the research. The bifurcation diagrams, phase diagrams, and Poincaré map of the slider-crank mechanism are also studied systematically.

On basis of the previous studies, the effects of clearance joint and flexible body on dynamic behavior are independently investigated rather than being considered simultaneously in the same mechanism. The effects of clearance joint and flexible links on nonlinear dynamic behavior are rarely investigated. The study objects are mainly focus on simple mechanisms, and a few studies on complex mechanism [29]. Therefore, the aim of this paper is to study the dynamic behaviors of 2-DOF complex planar mechanical system with revolute clearance joint and flexible links, thus analyzing and forecasting the dynamic behavior of multi-link mechanism and multi- degree-of-freedom mechanism. The dynamic behavior of ideal rigid mechanism, the rigid mechanism with clearance, and the flexible mechanism with clearance are also compared with each other in this paper. The arrangements of the article are as follows. In Sect. 2, model of joint clearance and contact force of joint clearance are both built. In Sect. 3, rigid body dynamics model of the 2-DOF nine-bar mechanism considering clearance is set up. In Sect. 4, nonlinear dynamic model of the 2-DOF nine-bar mechanical system with revolute clearance and flexible linkages is built by Lagrange and FEM. In Sect. 5, the influences of clearance value and driving velocity on dynamic behaviors have been researched. Dynamic responses are researched thoroughly, and nonlinear characteristics of the mechanism with revolute clearance and flexible links are studied by phase diagram, Poincaré map, Lyapunov exponent, and bifurcation diagram.

Fig. 2

a Joints contact force, b Revolute joint with clearance

2 Modeling of joint clearance and contact force

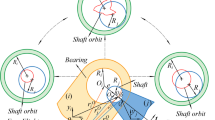
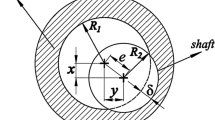
A planar revolute clearance joint is shown in Fig. 1a. The radii of the bearing and the shaft are $R_1$ and $R_2$. $R_1 -R_2$ is used as the value of clearance r. The shaft and bearing could move relative to each other unconstrained owing to the revolute clearance. These might lead to randomness of mechanism. Therefore, there are three different modes of the shaft, which are as follows: the free flight, the impact, and the continuous contact mode, as shown in Fig. 1b.

It is remarkable that the contact force consist of the normal contact force $F_n$ and the tangential contact force $F_t$ between the shaft and bearing, as shown in Fig. 2a.

$$\begin{aligned} F=F_n +F_t, \quad \left\{ {\begin{array}{lll} \delta <0,&{}F=0&{}\text {free flight mode} \\ \delta =0,&{}F\ne 0&{}\text {continuous contact mode} \\ \delta >0,&{}F\ne 0&{} \text {impact mode} \\ \end{array}} \right. \nonumber \\ \end{aligned}$$

(1)

Here $\delta$ is the penetration depth between the shaft and the bearing as depicted in Fig. 2b and is given as

$$\begin{aligned} \delta =e-r \end{aligned}$$

(2)

where e represents value of clearance vector between shaft center and bearing center, $e=\sqrt{x^{2}+y^{2}}$. x and y represent displacement of shaft inside bearing in X direction and Y direction, as shown in Fig. 2b.

The L-N normal contact force as a nonlinear viscoelastic model, it is well conformity to and experimental outcome, and it is suitable for the general mechanical contact collision question with high recovery coefficient, especially for the relatively small energy dissipation in the process of collision. Therefore, it is more efficient while the recovery coefficient is close to unity. This model not only involves the energy loss in collision process, but also considers the material properties, local elastic deformation, and velocity of collision, etc. This model is widely applied to the dynamic studies of the mechanical multiple body system with clearance thanks to simplicity of its contact force model, the resulting ease of calculation, applicability to the impact in mechanical multi-body system, fast convergence and straightforward for numerical integration algorithm [30, 31].

$$\begin{aligned} F_n =K\delta ^{n}+D{\dot{\delta }} \end{aligned}$$

(3)

where K represents generalized stiffness parameter, relying on physical properties of contact surfaces and its geometry, D represents hysteresis damping coefficient, and n is a constant, relying on contact surface’s material characteristics.

$$\begin{aligned} K=\frac{4}{3(\sigma _1 +\sigma _2 )}\sqrt{\frac{R_1 R{ }_2}{R_1 +R_2 }} \end{aligned}$$

(4)

where $\sigma _1$ and $\sigma _2$ are $\sigma _1 =\frac{1-\nu _1 ^{2}}{E_1 }$, $\sigma _2 =\frac{1-\nu _2 ^{2}}{E_2 }$, $\nu _1$ and $\nu _2$ are Poisson’s ratio of bearing and shaft, respectively. $E_1$ and $E_2$ represent elastic modulus of bearing and shaft. The radius is negative for the concave surfaces and positive for the convex surface.

Fig. 3

Schematic diagram of mechanism with single clearance joint

Hysteresis damping coefficient is expressed as

$$\begin{aligned}&D=\frac{3(1-c_e ^{2})}{4}\delta ^{n} \end{aligned}$$

(5)

$$\begin{aligned}&F_n =K\delta ^{n}\left[ 1+\frac{3(1-c_e ^{2})}{4}\frac{\dot{\delta }}{{\dot{\delta }}^{*}}\right] \end{aligned}$$

(6)

where ${\dot{\delta }}$ is penetration velocity, $\dot{\delta }=\frac{x{\dot{x}}+y{\dot{y}}}{\sqrt{x^{2}+y^{2}}}$. $\dot{\delta }^{*}$ represents the initial impact velocity, if $\delta \left( {t_n } \right) \delta \left( {t_{n+1} } \right) \le 0$,$\delta \left( {t_n } \right) <0$ and $\delta \left( {t_{n+1} } \right) >0$, the penetration velocity at $t_{n+1}$ moment is $\dot{\delta }^{*}$.

It is also known that, when tangential velocity is near to zero, the numerical definition of the original Coulomb’s friction method is very difficult, then a modified Coulomb’s friction method proposed by Ambrosio can be written as follows [32]

$$\begin{aligned} F_t =-c_f c_d F_N \frac{v_t }{\left| {v_t } \right| } \end{aligned}$$

(7)

where $c_f$ is friction coefficient, $c_d$ represents the dynamic correction coefficient, and

$$\begin{aligned} c_d =\left\{ {\begin{array}{l@{\quad }l} 0,&{}\left| {v_t } \right| <v_0 \\ \frac{\left| {v_t } \right| -v_0 }{v_1 -v_0 },&{}v_0 \le \left| {v_t } \right| \le v_1 \\ 1,&{}\left| {v_t } \right| >v_1 \\ \end{array}} \right. \end{aligned}$$

(8)

where $v_0$ and $v_1$ are the given bounds for the tangential velocity.

The contact force of the revolute pair with clearance can be expressed as

$$\begin{aligned} f=F_n {{\varvec{n}}}+F_t{{\varvec{t}}} =[f_x~~ f_y ]^{T} \end{aligned}$$

(9)

where $f_x$and $f_y$represent component of contact force of the shaft to the bearing in the X and Y direction, respectively.

3 Rigid body dynamic model of 2-DOF nine-bar mechanism with clearance

A 2-DOF nine-bar mechanism is composed of nine sections which are the frame, crank 1, link 2, link 3, crank 4, rocker 6, triangular panel 7, link 8 and slider 9. Link 5 is a part of the frame. The DOF of mechanism is two, the crank 1 and the crank 4 are driven by two motors, respectively. The schematic diagram of 2-DOF nine-bar mechanism is shown in Fig. 3a.

The crank 1 and link 2 are connected through the revolute clearance joint. The schematic diagram of 2-DOF nine-bar mechanism with clearance is shown in Fig. 3b. Local enlargement of clearance joint is also shown in Fig. 3b. Motion pairs of the mechanism are made up of revolute pairs and translational pair, and the number of revolute pair of the mechanism is largest. Therefore, it is more representative to study the revolute clearance of the mechanism.

It’s remarkable that a revolute clearance joint introduces two additional DOFs which contain horizontal and vertical displacements of center of shaft correspond to bearing center. Generalized coordinates of the rigid mechanism are selected as follows: $x,y,\theta _1,\theta _4$.

According to the Lagrange equation, the dynamic model of nine-bar mechanism with revolute clearance is given by

$$\begin{aligned} \frac{d}{dt}\left( \frac{\partial T}{\partial {\dot{q}}_j }\right) -\frac{\partial T}{\partial q_j }+\frac{\partial U}{\partial q_j }=Q_j~ (j=x,y,1,4)\nonumber \\ \end{aligned}$$

(10)

where $T,U,Q_j$ represent kinetic energy, potential energy and general force, respectively.

$q_j$ is generalized coordinate.

3.1 Kinetic energy of mechanism with revolute clearance

The expression of the kinetic energy of the 2-DOF nine-bar mechanism can be expressed as

$$\begin{aligned} T=\frac{1}{2}{\mathop {\sum }\limits _{\begin{array}{c} i=1\\ i\ne 1,4,5,6 \end{array}}^9} {m_i v_{si}^2 } +\frac{1}{2}{\mathop {\sum }\limits _ {\begin{array}{c} i=1\\ i\ne 5,9 \end{array}} ^9} {J_i {\dot{\theta }}_i^2 } \end{aligned}$$

(11)

From Eq. (11), the kinetic energy of the 2-DOF nine-bar mechanism is given by

$$\begin{aligned} T= & {} \frac{1}{2}J_{11} {\dot{\theta }}_1 ^{2}+\frac{1}{2}J_{22} \dot{\theta }_2 ^{2}+\frac{1}{2}J_{33} {\dot{\theta }}_3 ^{2}+\frac{1}{2}J_{44} {\dot{\theta }}_4 ^{2}+\frac{1}{2}J_{55} \dot{\theta }_6 ^{2}\nonumber \\&\quad +\,\frac{1}{2}J_{66} {\dot{\theta }}_7 ^{2}+\frac{1}{2}J_{77} {\dot{\theta }}_8 ^{2}+\frac{1}{2}m_9 \dot{S}_9 ^{2}\nonumber \\&\quad +\,\frac{1}{2}m_2 ({\dot{x}}^{2}+{\dot{y}}^{2})+m_2 L_1 {\dot{\theta }}_1 ({\dot{y}}\cos \theta _1 -{\dot{x}}\sin \theta _1 )\nonumber \\&\quad +\,m_2 L_1 L_{s2} \cos (\theta _1 -\theta _2 ){\dot{\theta }}_1 {\dot{\theta }}_2 \nonumber \\&\quad +\,m_2 L_{s2} {\dot{\theta }}_2 ({\dot{y}}\cos \theta _2 -{\dot{x}}\sin \theta _2 )\nonumber \\&\quad +\,m_3 L_4 L_{s3} \cos (\theta _3 -\theta _4 )\dot{\theta }_3 {\dot{\theta }}_4 \nonumber \\&\quad +\,m_7 L_6 L_{s71} \cos (\theta _6 -\theta _7 -\beta ){\dot{\theta }}_6 {\dot{\theta }}_7 \nonumber \\&\quad +\,m_8 L_6 L_{72} \cos (\theta _6 -\theta _7 -\beta _{12} )\dot{\theta }_6 {\dot{\theta }}_7 \nonumber \\&\quad +\,m_8 L_6 L_{s8} \cos (\theta _6 -\theta _8 ){\dot{\theta }}_6 {\dot{\theta }}_8 \nonumber \\&\quad +\,m_8 L_{72} L_{s8} \cos (\theta _7 +\beta _{12} -\theta _8 ){\dot{\theta }}_7 \dot{\theta }_8 \end{aligned}$$

(12)

where $J_{11} =J_1 +m_2 L_1 ^{2}$, $J_{22} =J_2 +m_2 L_{s2} ^{2}$, $J_{33} =J_3 +m_3 L_{s3} ^{2}$, $J_{44} =J_4 +m_3 L_4 ^{2}$, $J_{55} =J_6 +m_7 L_6 ^{2}+m_8 L_6 ^{2}$, $J_{66} =J_7 +m_7 L_{s71} ^{2}+m_8 L_{72} ^{2}$, $J_{77} =J_8 +m_8 L_{s8} ^{2}$, $J_i$ is inertia moment of member i, $m_i$ is the mass of member i, $L_{si}$ represents distance from center of mass of linkage to front hinge, $\theta _i$ and $S_9$ represent the rotation angle of each member and the displacement of slider 9, when the mechanism contains clearance, respectively. ${\dot{\theta }}_i$ and $\dot{S}_9$ represent angular speed of each component and velocity of slider 9, while mechanism contain clearance.

3.2 Potential energy of mechanism with revolute clearance

The potential energy of the 2-DOF nine-bar mechanism is written as

$$\begin{aligned} U={\mathop {\sum }\limits _{\begin{array}{c} i=1\\ i\ne 5 \end{array}}^9} {m_i gx_{si} } \end{aligned}$$

(13)

where $x_{si}$ is centroid coordinate in X direction of component i.

3.3 Generalized force of mechanism with revolute clearance

The generalized force of 2-DOF nine-bar mechanism with clearance can be expressed as

$$\begin{aligned} Q_j ={\mathop {\sum }\limits _{\begin{array}{c} i=1\\ i\ne 5 \end{array}}^9} \left( F_i \frac{\partial r_i }{\partial q_j } +M_i \frac{\partial \theta _i }{\partial q_j }\right) \end{aligned}$$

(14)

where $F_i$ is equivalent force and $M_i$ is external torque acting on body i, respectively. $r_i$ is the position vector of component i.

The general force can be expressed as

$$\begin{aligned} \left\{ {\begin{array}{l} Q_x =F_t R_2 a_1 -f_x \\ Q_y =F_t R_2 a_2 -f_y \\ Q_1 =M_1 +F_t R_2 -f_x L_1 \sin \theta _1 +f_y L_1 \cos \theta _1 \\ Q_4 =M_4 +F_t R_2 \\ \end{array}} \right. \end{aligned}$$

(15)

where $F_t$ represents tangential contact force of bearing acting on the shaft of revolute clearance joint, respectively. $f_x$ and $f_y$ represent contact force of shaft acting on the bearing of revolute clearance joint in the X and Y direction, respectively. $M_1$,$M_4$ represent driving torque of crank 1 and crank 4, respectively.

Equations (12), (13) and (15) are brought into the Eq. (10), and the second-order nonlinear differential equations (Eq. 16) with variable coefficients are derived. Through MATLAB programming, Runge–Kutta method of the MATLAB is adopted to calculate differential equations

$$\begin{aligned} \left\{ {\begin{array}{l} {\ddot{x}}=f_1 (t,x,y,{\dot{x}},{\dot{y}}) \\ {\ddot{y}}=f_2 (t,x,y,{\dot{x}},{\dot{y}}) \\ \end{array}} \right. \end{aligned}$$

(16)

4 Elastic dynamic model with clearance by Lagrange and FEM

The position constraint of the hinge joint is relieved due to the existence of the clearance, so that the elastic members linked by the clearance pair is independent. The constraint action at the hinge is achieved by constraining force that is equivalent to external force acting on component and could be obtained from Sect. 2. Taking the 2-DOF nine-bar mechanism as an object, elastic dynamic model is built by adopting Lagrange and FEM.

4.1 Model of beam element

Structural diagram of beam unit is shown in Fig. 4. $\bar{{x}}o\bar{{y}}$ is rotating coordinate. Lateral displacement and longitudinal displacement of beam unit at any point can be expressed by $W\left( {x_i ,t} \right)$ and $V\left( {x_i ,t} \right)$, respectively.

$$\begin{aligned} \left\{ \!{\begin{array}{l} W\left( {x_i ,t} \right) =N_{iA}^T u_i \\ V\left( {x_i ,t} \right) =N_{iB}^T u_i \\ \end{array}} \right. \end{aligned}$$

(17)

where $u_i$ is generalized coordinate vector for unit, and $u_i =\left[ {{\begin{array}{llllll} {u_1 }&{} {u_2 }&{} {u_3 }&{} {u_4 }&{} {u_5 }&{} {u_6 } \\ \end{array} }} \right] ^{T}$

$$\begin{aligned} \left\{ \!\begin{array}{l} N_{iA} =\left[ {{\begin{array}{llllll} 0&{} {\mu _2 }&{} {\mu _3 }&{} 0&{} {\mu _5 }&{} {\mu _6 } \\ \end{array} }} \right] ^{T} \\ N_{iB} =\left[ {{\begin{array}{llllll} {\mu _1 }&{} 0&{} 0&{} {\mu _4 }&{} 0&{} 0 \\ \end{array} }} \right] ^{T} \\ \end{array}\right. \end{aligned}$$

(18)

where $\mu _1 =1-\bar{{e}}$, $\mu _2 =1-3\bar{{e}}^{2}+2\bar{{e}}^{3}$, $\mu _3 =l_i \left( {\bar{{e}}-2\bar{{e}}^{2}+\bar{{e}}^{3}} \right)$, $\mu _4 =\bar{{e}}$, $\mu _5 =3\bar{{e}}^{2}-2\bar{{e}}^{3}$

$\mu _6 =l_i \left( {\bar{{e}}^{3}-\bar{{e}}^{2}} \right) , \bar{{e}}$ is relative coordinates of beam element, $\bar{{e}}={x_i }/{l_i }$. $l_i$is the unit length.

Fig. 4

Beam unit and unit generalized coordinate

4.2 Dynamic model of beam element

4.2.1 Kinetic energy of beam element

Assuming that each element’s mass is concentrated on the axis, kinetic energy of beam element can be expressed as

$$\begin{aligned} E_k =\frac{1}{2}\int _0^{l_i } {\rho \bar{{A}}\left[ {\left( {\frac{\mathrm{d}W_a \left( {x_i ,t} \right) }{\mathrm{d}t}} \right) ^{2}+\left( {\frac{\mathrm{d}V_a \left( {x_i ,t} \right) }{\mathrm{d}t}} \right) ^{2}} \right] } \mathrm{d}x\nonumber \\ \end{aligned}$$

(19)

where $\rho$ represents density of beam unit. $\bar{{A}}$ represents cross-sectional area of beam unit. $W_a \left( {x_i ,t} \right)$ and $V_a \left( {x_i ,t} \right)$, respectively, represent absolute lateral displacement and absolute longitudinal displacement of beam element at any point.

$$\begin{aligned} \left\{ {\begin{array}{l} W_a \left( {x_i ,t} \right) =W_r \left( {x_i ,t} \right) +W\left( {x_i ,t} \right) \\ V_a \left( {x_i ,t} \right) =V_r \left( {x_i ,t} \right) +V\left( {x_i ,t} \right) \\ \end{array}} \right. \end{aligned}$$

(20)

where $W_r \left( {x_i ,t} \right)$ and $V_r \left( {x_i ,t} \right)$ are rigid motion displacement in $\bar{{x}}$ and $\bar{{y}}$ direction.

Simplifying Eq. (19), then,

$$\begin{aligned} E_k =\frac{1}{2}{\dot{u}}_{ia}^T \bar{{m}}_i {\dot{u}}_{ia} \end{aligned}$$

(21)

where $\bar{{m}}_i$ represents mass matrix of uint, ${\dot{u}}_{ia}$ is absolute velocity, ${\dot{u}}_{ia} ={\dot{u}}_{ir} +{\dot{u}}_i$,${\dot{u}}_{ir}$ is velocity of rigid element, it can be obtained through the dynamic model of the rigid body with clearance, $\dot{u}_i$ represents first-order derivative of unit generalized coordinate $u_i$.

$$\begin{aligned} \bar{{m}}_i =\int _0^{l_i } {\left[ {\rho \bar{{A}}\left( {N_{iA}^T N_{iA} +N_{iB}^T N_{iB} } \right) } \right] } \mathrm{d}x \end{aligned}$$

(22)

4.2.2 Deformation energy of beam element

When the beam element happen elastic deformation, the element is subjected to the axial force and the bending moment. The total deformation energy of unit includes bending, the compression and the tension deformation energy.

$$\begin{aligned} E_p= & {} \frac{1}{2}\int _0^{l_i } {EI\left( {\frac{\partial ^{2}W\left( {x_i ,t} \right) }{\partial x^{2}}} \right) ^{2}} \mathrm{d}x\nonumber \\&+\frac{1}{2}\int _0^{l_i } {E\bar{{A}}\left( {\frac{\partial V\left( {x_i ,t} \right) }{\partial x}} \right) ^{2}} \mathrm{d}x \end{aligned}$$

(23)

where E is elasticity modulus. I represents inertia moment of cross section.

Simplifying Eq. (23), we can get

$$\begin{aligned} E_p =\frac{1}{2}{\dot{u}}_i ^{T}\bar{{k}}_i {\dot{u}}_i \end{aligned}$$

(24)

where $\bar{{k}}_i$ is stiffness matrix of unit.

$$\begin{aligned} \bar{{k}}_i =E\bar{{A}}\int _0^{l_i } {{\dot{N}}_{iA}^T {\dot{N}}_{iA} \mathrm{d}x} +EI\int _0^{l_i } {{\ddot{N}}_{iB}^T {\ddot{N}}_{iB} \mathrm{d}x} \end{aligned}$$

(25)

4.2.3 Dynamic equations of beam element

Equations (21) and (24) are put into the Lagrange equation $\frac{d}{dt}\left( {\frac{\partial E_k }{\partial \dot{u}_i }} \right) -\frac{\partial E_k }{\partial u_i }+\frac{\partial E_p }{\partial u_i }=\bar{{f}}_e$, the dynamic model of beam element in rotating coordinate system could be expressed as

$$\begin{aligned} \bar{{m}}_i {\ddot{u}}_i +\bar{{k}}_i u_i =f_a +p_a +q_a \end{aligned}$$

(26)

where $f_a$ is the generalized external force array of every unit, containing the contact force due to the revolute clearance joint. $p_a$ represents force array of contact element caused by connecting beam element. $q_a$ represents rigid inertial force array, and $q_a =-\,\bar{{m}}{\ddot{u}}_{ir}$,${\ddot{u}}_{ir}$ is acceleration of rigid element contain joint clearance, ${\ddot{u}}_i$ is second-order derivative of unit generalized coordinate $u_i$.

In order to assemble unit’s dynamic equations into the system’s dynamic equation, a new generalized coordinate array of the unit $U_{ie}$ has been introduced, $U_{ie} =\left[ {{\begin{array}{llll} {U_1 }&{} {U_2 }&{} \cdots &{} {U_6 } \\ \end{array} }} \right] ^{T}$. The relationship between $U_{ie}$ and generalized coordinates $u_i$ of unit can be expressed

$$\begin{aligned} u_i =R_i U_{ie} \end{aligned}$$

(27)

where $R_i$ is the coordinate transformation matrix.

Dynamic equation of beam element in absolute coordinate system is as follows

$$\begin{aligned} {\tilde{m}}_i {\ddot{U}}_{ie} +{\tilde{c}}_i {\dot{U}}_{ie} +\tilde{k}_i U_{ie} =f_e \end{aligned}$$

(28)

where ${\tilde{m}}_i =R_i^T \bar{{m}}_i R_i$, ${\tilde{c}}_i =2R_i^T \bar{{m}}_i {\dot{R}}_i$, ${\tilde{k}}_i =R_i^T \bar{{m}}_i \ddot{R}_i +R_i^T \bar{{k}}_i R_i$, $f_e =R_i^T f_a +R_i^T p_a +R_i^T q_a$.

Fig. 5

Triangular panel

Table 1 Dimensions and mass properties for the 2-DOF nine-bar mechanism

Table 2 Moment of inertia for the 2-DOF nine-bar mechanism

Table 3 Clearance joints’ parameters

4.3 Dynamic equations of system

Crank is treated as the cantilever beam, and slider is used as a rigid member. As shown in Fig. 5, triangular panel 7 could be divided into three parts, that are $L_{71}$,$L_{72}$ and $L_{73}$. Crank 1, link 2, link 3, crank 4, $L_{71}$, $L_{72}$, $L_{73}$, rocker 6 and link 8 are, respectively, divided into $n_1$,$n_2$,$n_3$,$n_4$,$n_5$,$n_6$,$n_7$,$n_8$ and $n_9$ units. Their corresponding generalized coordinates obtained by constraint condition are $U^{1},U^{2},U^{3},U^{4},U^{5},U^{6},U^{7},U^{8}$and $U^{9}$, respectively.

$$\begin{aligned} U^{1}= & {} \left[ U_{1\left( 2 \right) 1} U_{1\left( 2 \right) 2} U_{1\left( 2 \right) 3} U_{1\left( 2 \right) 4} U_{1\left( 2 \right) 5} U_{1\left( 2 \right) 6}\cdots \right. \\&\quad \left. U_{1\left( {n1} \right) 1} U_{1\left( {n1} \right) 2} U_{1\left( {n1} \right) 3} U_{1\left( {n1} \right) 4} U_{1\left( {n1} \right) 5} U_{1\left( {n1} \right) 6} \right] ^{T} \\ U^{2}= & {} \left[ U_{1\left( {n1} \right) 4} U_{1\left( {n1} \right) 5} U_{2\left( 1 \right) 3} U_{2\left( 1 \right) 4} U_{2\left( 1 \right) 5} U_{2\left( 1 \right) 6}\cdots \right. \\&\quad \left. U_{2\left( {n2} \right) 1} U_{2\left( {n2} \right) 2} U_{2\left( {n2} \right) 3} U_{2\left( {n2} \right) 4} U_{2\left( {n2} \right) 5} U_{2\left( {n2} \right) 6} \right] ^{T} \\ U^{4}= & {} \left[ U_{4\left( 2 \right) 1} U_{4\left( 2 \right) 2} U_{4\left( 2 \right) 3} U_{4\left( 2 \right) 4} U_{4\left( 2 \right) 5} U_{4\left( 2 \right) 6} \cdots \right. \\&\quad \left. U_{4\left( {n4} \right) 1} U_{4\left( {n4} \right) 2} U_{4\left( {n4} \right) 3} U_{4\left( {n1} \right) 4} U_{4\left( {n4} \right) 5} U_{4\left( {n4} \right) 6} \right] ^{T} \\ U^{3}= & {} \left[ U_{3\left( {n4} \right) 4} U_{3\left( {n4} \right) 5} U_{3\left( 1 \right) 3} U_{3\left( 1 \right) 4} U_{3\left( 1 \right) 5} U_{3\left( 1 \right) 6} \cdots \right. \\&\quad \left. U_{3\left( {n3} \right) 1} U_{3\left( {n3} \right) 2} U_{3\left( {n3} \right) 3} U_{2\left( {n2} \right) 4} U_{2\left( {n2} \right) 5} U_{3\left( {n3} \right) 6} \right] ^{T} \\ U^{5}= & {} \left[ U_{2\left( {n2} \right) 4} U_{2\left( {n2} \right) 5} U_{73\left( 1 \right) 3} U_{73\left( 1 \right) 4} U_{73\left( 1 \right) 5} U_{73\left( 1 \right) 6}\cdots \right. \\&\quad \left. U_{73\left( {n5} \right) 1} U_{73\left( {n5} \right) 2} U_{73\left( {n5} \right) 3} U_{73\left( {n5} \right) 4} U_{73\left( {n5} \right) 5} U_{73\left( {n5} \right) 6} \right] ^{T} \\ U^{6}= & {} \left[ U_{2\left( {n2} \right) 4} U_{2\left( {n2} \right) 5} U_{73\left( 1 \right) 3} U_{71\left( 1 \right) 4} U_{71\left( 1 \right) 5} U_{71\left( 1 \right) 6}\cdots \right. \\&\quad \left. U_{71\left( {n6} \right) 1} U_{71\left( {n6} \right) 2} U_{71\left( {n6} \right) 3} U_{71\left( {n6} \right) 4} U_{71\left( {n6} \right) 5} U_{71\left( {n6} \right) 6} \right] ^{T} \\ U^{7}= & {} \left[ U_{73\left( {n5} \right) 4} U_{73\left( {n5} \right) 5} U_{73\left( {m5} \right) 6} U_{72\left( 1 \right) 4} U_{72\left( 1 \right) 5} U_{72\left( 1 \right) 6} \cdots \right. \\&\quad \left. U_{72\left( {n7} \right) 1} U_{72\left( {n7} \right) 2} U_{72\left( {n7} \right) 3} U_{71\left( {n6} \right) 4} U_{71\left( {n6} \right) 5} U_{71\left( {n6} \right) 6} \right] ^{T} \\ U^{8}= & {} \left[ U_{71\left( {n6} \right) 4} U_{71\left( {n6} \right) 5} U_{6\left( 1 \right) 3} U_{6\left( 1 \right) 4} U_{6\left( 1 \right) 5} U_{6\left( 1 \right) 6} \cdots \right. \\&\quad \left. U_{6\left( {n8} \right) 1} U_{6\left( {n8} \right) 2} U_{6\left( {n8} \right) 3} U_{6\left( {n8} \right) 6} \right] ^{T} \\ U^{9}= & {} \left[ U_{73\left( {n5} \right) 4} U_{73\left( {n5} \right) 5} U_{8\left( 1 \right) 3} U_{8\left( 1 \right) 4} U_{8\left( 1 \right) 5} U_{8\left( 1 \right) 6} \cdots \right. \\&\quad \left. U_{8\left( {n9} \right) 1} U_{8\left( {n9} \right) 2} U_{8\left( {n9} \right) 3} U_{8\left( {n9} \right) 4} U_{8\left( {n9} \right) 6} \right] ^{T} \end{aligned}$$

The system generalized coordinate array U consists of $U^{1}\cdots U^{9}$, the relationship between $U_{ie}$ and generalized coordinates U of system is written as

$$\begin{aligned} U_{ie} =B_i U \end{aligned}$$

(29)

where $B_i$ is coordinate harmony matrix.

The dynamic equation of the system is as follows

$$\begin{aligned} M{\ddot{U}}+\bar{{C}}{\dot{U}}+KU=F_e \end{aligned}$$

(30)

where $M=\sum _{i=1}^{N_e } {B_i^T {\tilde{m}}_i B_i }$, $K=\sum _{i=1}^{N_e } {B_i^T {\tilde{k}}_i B_i }$, $F=\sum _{i=1}^{N_e } {B_i^T f_e }$, $C=\sum _{i=1}^{N_e } {B_i^T {\tilde{c}}_i B_i } +\zeta _1 M+\zeta _2 K$, $\zeta _1$ and $\zeta _2$ are damping scale coefficients,$N_e$ is total quantity of units.

4.4 Numerical solution of dynamic equation

The dynamic equation (Eq. 30) is a strongly coupled and strongly nonlinear differential equations. In this paper, the Newmark algorithm and fourth-order Runge–Kutta method are utilized to solve dynamic equations. The concrete solution process is as follows:

• (1) Rigid dynamic model of mechanism with clearance is solved by fourth-order Runge–Kutta method, and the displacement, velocity, acceleration of the each component and the contact force generated by the clearance revolute joint on the first time step are obtained.

• (2) The relevant quantities obtained in step (1) are brought into elastic dynamic model. The elastic deformation, inertia force, and inertia moment of each component brought about by elastic deformation are calculated by Newmark algorithm.

• (3) The inertia force and the moment of inertia caused by the elastic deformation motion are taken into step (1), and the relative quantities in the next integral step are solved.

• (4) Step (1)–(3) are repeated for the next operation, and then the whole movement of the system is got finally.

Fig. 6

Acceleration of slider a modified Coulomb friction model; b LuGre model

Fig. 7

Driving torque of crank 1 a modified Coulomb friction model; b LuGre model

Fig. 8

Driving torque of crank 4 a modified Coulomb friction model; b LuGre model

5 Simulations and results

5.1 System parameters of 2-DOF nine-bar mechanism

The system parameters for the 2-DOF nine-bar mechanism are shown in Tables 1, 2 and 3.

Fig. 9

Displacement of slider, a clearance = 0.05 mm; b clearance = 0.5 mm

Fig. 10

Velocity of slider a clearance = 0.05 mm; b clearance = 0.5 mm

5.2 The influence of different friction model on dynamic response

In this section, the driving speeds of two cranks are set as $\omega _1 =-\,2.5 \pi \left( {\text {rad/s}} \right) , \omega _4 =2.5\pi \left( \text {rad/s} \right)$, the clearance of joint is both set as 0.5 mm. In order to study difference between the friction models, the effects of modified Coulomb friction model and LuGre model on the dynamic response of rigid body mechanism are both studied, containing driving torques and acceleration of slider. By using LuGre model on 2-DOF nine-bar mechanism, friction force of clearance is considered not to have a discontinuity at zero slip speed, it is capable of capturing the Stribeck and stiction effects [32, 33]. From Figs. 6, 7 and 8, it is shown that, the effects of modified Coulomb friction model and LuGre model on mechanism dynamics for this mechanism are principally at the same, time point of collision is in general agreement. There are some differences in the peak magnitude of dynamic response, when the LuGre model is used, the peak magnitude of dynamic response is higher than that of modified Coulomb friction model.

5.3 The influence of clearance value on dynamic behavior

5.3.1 The influence of clearance value on dynamic response

The influence of the clearance values on dynamic behavior of the 2-DOF nine-bar mechanism is studied in this section. The crank 1 and crank 4 are modeled as a driving component with the rotate speed of $\omega _1 =-2\pi \left( {\text {rad/s}} \right) , \omega _4 =2\pi \left( {\text {rad/s}} \right)$, respectively. Clearance value is regarded as 0.05 and 0.5 mm. The kinematic characteristics of slider are shown in Figs. 9, 10 and 11, which contain displacement, velocity and acceleration of end slider. The driving torque of the crank 1 and the crank 4 is displayed in Figs. 12 and 13. Contact force, penetration depth and shaft center trajectory curve of clearance joint are shown in Figs. 14, 15 and 16.

Fig. 11

Acceleration of slider, a clearance = 0.05 mm; b clearance = 0.5 mm

Fig. 12

Driving torque of crank 1, a clearance = 0.05 mm; b clearance = 0.5 mm

Fig. 13

Driving torque of crank 4, a clearance = 0.05 mm; b clearance = 0.5 mm

Fig. 14

Contact force of the clearance joint, a clearance = 0.05 mm; b clearance = 0.5 mm

Fig. 15

Penetration depth, a clearance = 0.05 mm; b clearance = 0.5 mm

Fig. 16

Shaft center trajectory, a clearance = 0.05 mm; b clearance = 0.5 mm

Fig. 17

Phase diagram in X direction of clearance joint, a clearance = 0.05 mm; b clearance = 0.5 mm

Fig. 18

Phase diagram in Y direction of clearance joint, a clearance = 0.05 mm; b clearance = 0.5 mm

With regard to the rigid mechanism contain clearance joint, the magnitude of the dynamic response of the mechanism is obviously higher than that of mechanism do not have clearance, and the fluctuation influences the mechanism’s accuracy and stability. According to Figs. 9 and 10, the displacement and velocity of the slider are less influenced and close to the ideal state. As shown in Figs. 11, 12 and 13, the acceleration of slider and driving torques of two cranks are susceptible to the clearance and produce greater vibration. From Figs. 11, 12, 13 and  14, the time point of the acceleration and driving torques vibration is approximately the same as vibration of the contact force at the revolute clearance joint.

Comparing with two different clearance values, the dynamic response of large clearance value is deteriorated severely than small clearance value, the peak value of the dynamic response of the larger clearance value is much larger than the low clearance value, and the vibration is more strong, it can be confirmed through velocity, acceleration of slider, contact force, and driving torques curves. As shown in Fig. 16a, b, which correspond to Fig. 15a, b, there are more free flight motions in shaft center trajectory with larger clearance, its shaft center trajectory more chaos, so the collision is more serious than the low clearance value.

As seen from Figs. 9, 10, 11, 12, 13, 14, 15 and 16, it is a clear difference between flexible and rigid mechanism outputs. For flexible mechanism with revolute clearance, the peak value of contact force of flexible mechanism at revolute clearance joint is small than the rigid mechanism. The proper elastic deformation of the links could assimilate energy and reduce the separation times between the elements of joint, which makes vibration of the slider acceleration and driving torques of cranks decrease obviously, peak value of the driving torques of cranks are same decreased, the mechanism’s stability and accuracy are both enhanced. As shown in Fig. 16a, b, center trajectory of flexible mechanism is close to ideal state, and the free flight motion is obviously reduced. It is same to Fig. 15a, b, the penetration depth of flexible mechanism is also improved than rigid one. The flexible link in the mechanism with clearance joint has a more obvious effect on alleviating vibration characteristic compared to the mechanism with rigid mechanism with clearance joint. The main reason is that the elastic link can properly absorb the vibration due to the clearance and make the dynamic response of the mechanism tends to be stable.

Fig. 19

Poincaré map in X direction of clearance joint, a clearance = 0.05 mm; b clearance = 0.5 mm

Fig. 20

Poincaré map in Y direction of clearance joint, a clearance = 0.05 mm; b clearance = 0.5 mm

5.3.2 The influence of clearance value on nonlinear characteristics

It is well known that mechanism with clearance joint and flexible links is a typical nonlinear dynamical system; the chaotic phenomena and the bifurcation exist in mechanical system, and then chaos phenomena and bifurcation analysis should be researched. When the clearance value is 0.05 mm, the phase diagrams of the X and Y directions at the revolute clearance joint are shown in Figs. 17a and 18a. When the clearance size of joint is 0.5 mm, the phase diagrams of the X and Y directions at the revolute clearance joint are shown in Figs. 17b and 18b. As can be seen from Figs. 17 and 18, when clearance is 0.05 and 0.5 mm, phase diagrams are both chaotic and disordered, so they are all in the state of the chaos. From Figs. 17 and 18, when clearance value of joint increases, phase of mechanism becomes more and more disorder, and phase diagrams have the trend of expansion, chaos phenomenon existed in the joint is more obvious.

Figures 19 and 20 show the Poincaré maps of the mechanism with clearance and flexible rods when the clearance value are 0.05 and 0.5 mm, respectively. As can be seen from Figs. 19 and 20, the Poincaré maps is chaotic, each point is scattered in the diagrams, the mapping points are not repeated, which shows that mechanism has no periodic solution, and the mechanism is in chaos. Compared with Figs. 19 and  20, while the size of clearance increases, the Poincaré map has an expansion trend, and chaos phenomenon increases obviously.

The Lyapunov exponent can be used effectively as a strong criterion for determining whether system is in chaos. When largest Lyapunov exponent (LLE) is less than zero, system is in periodic motion. When LLE is greater than zero, system corresponds to chaotic motion.

Lyapunov exponents of clearance joint are shown in Figs. 21 and 22, while clearance value is 0.05 and 0.5 mm. From Figs. 21 and 22, when clearance value is 0.05 mm, the LLE in X and Y direction are C 0.0111 and 0.0656, when clearance size is 0.5 mm, the LLE in X and Y direction are 0.4226 and 0.1088. Because the LLE are all greater than zero, so the mechanism is in chaos.

Fig. 21

Lyapunov exponent in X direction of clearance joint, a clearance = 0.05 mm; b clearance = 0.5 mm

Fig. 22

Lyapunov exponent in Y direction of clearance joint, a clearance = 0.05 mm; b clearance = 0.5 mm

In order to further develop impact of revolute joint clearance on dynamic behavior, the bifurcation behavior is observed with the change in clearance values. The clearance sizes ranged from 0.01 to 0.5 mm are selected to research bifurcation phenomena. The bifurcation diagrams with varying clearance values in X and Y direction of elastic mechanism with joint clearance are shown in Fig. 23a, b, respectively. With increase in clearance value of joint, chaotic phenomenon of clearance joint is more serious, the mechanism is more unstable. According to above study, clearance of joint is the important element to affect the responses of mechanism.

Fig. 23

Bifurcation diagram of clearance joint with varying clearance. a Poincaré map in X direction. b Poincaré map in Y direction

The phase diagram, Poincaré map, Lyapunov exponent and bifurcation diagram of slider are shown in Figs. 24, 25, 26 and 27. It can be seen from phase diagram that, when clearance value is 0.5 mm, the phase diagram of the end slider is more larger than the phase diagram of the end slider while the clearance value is 0.05 mm. It can be known from Lyapunov exponent and Poincaré map that, the Poincaré map of clearance value 0.05 and 0.5 mm are all independent points, the LLE of the clearance value 0.05 and 0.5 mm are $-\,0.0221$ and $-\,0.0135$, which are all less than zero, so it can be judged that the slider is in periodic motion. According to Figs. 23 and 27, when clearance size changed from 0.01 to 0.5 mm, although the motion state of the clearance joint is changed from periodic motion to chaotic motion shown in Fig. 23, but the end slider’s motion state is always in periodic motion shown in Fig. 27. Because of the stable region of mechanism with single clearance is larger, so slider is not sensitive to chaos phenomenon.

Fig. 24

Phase diagram of slider, a clearance = 0.05 mm; b clearance = 0.5 mm

Fig. 25

Poincaré map of slider, a clearance = 0.05 mm; b clearance = 0.5 mm

Fig. 26

Lyapunov exponent of slider, a clearance = 0.05 mm; b clearance = 0.5 mm

Fig. 27

Bifurcation diagram of slider with varying clearance

5.4 The influence of driving speeds of the cranks on dynamic behavior

5.4.1 The influence of driving speed of crank on dynamic response

The speed of crank 1 and the speed of crank 4 are same in value and opposite in direction. Two groups of the driving speed of the crank 1 and the crank 4 are researched, that are $\omega _1 =-\,0.5\pi \left( {\text {rad/s}} \right) , \omega _4 =0.5\pi \left( {\text {rad/s}} \right)$ and $\omega _1 =-\,2.5\pi \left( {\text {rad/s}} \right) , \omega _4 =2.5\pi \left( {\text {rad/s}} \right)$. The clearance value is set as 0.5 mm. The velocity and the acceleration of slider are depicted in Figs. 28 and 29. The driving torque of crank 1 and crank 4 are shown in Figs. 30 and 31. Contact force and shaft center trajectory curve of clearance joint is shown in Figs. 32 and 33.

Fig. 28

Velocity of slider a $\omega _1 =-\,0.5\pi \left( {\text {rad/s}} \right) , \omega _4 =0.5\pi \left( {\text {rad/s}} \right)$; b $\omega _1 =-\,2.5\pi \left( {\text {rad/s}} \right) , \omega _4 =2.5\pi \left( {\text {rad/s}} \right)$

Fig. 29

Acceleration of slider a $\omega _1 =-\,0.5\pi \left( {\text {rad/s}} \right) , \omega _4 =0.5\pi \left( {\text {rad/s}} \right)$; b $\omega _1 =-\,2.5\pi \left( {\text {rad/s}} \right) , \omega _4 =2.5\pi \left( {\text {rad/s}} \right)$

Fig. 30

Driving torque of crank 1. a $\omega _1 =-\,0.5\pi \left( {\text {rad/s}} \right) , \omega _4 =0.5\pi \left( {\text {rad/s}} \right)$; b $\omega _1 =-\,2.5\pi \left( {\text {rad/s}} \right) , \omega _4 =2.5\pi \left( {\text {rad/s}} \right)$

Fig. 31

Driving torque of crank 4. a $\omega _1 =-\,0.5\pi \left( {\text {rad/s}} \right) , \omega _4 =0.5\pi \left( {\text {rad/s}} \right)$; b $\omega _1 =-\,2.5\pi \left( {\text {rad/s}} \right) , \omega _4 =2.5\pi \left( {\text {rad/s}} \right)$

Fig. 32

Contact force, a $\omega _1 =-\,0.5\pi \left( {\text {rad/s}} \right) , \omega _4 =0.5\pi \left( {\text {rad/s}} \right)$; b $\omega _1 =-\,2.5\pi \left( {\text {rad/s}} \right) , \omega _4 =2.5\pi \left( {\text {rad/s}} \right)$

Fig. 33

Shaft center trajectory a $\omega _1 =-\,0.5\pi \left( {\text {rad/s}} \right) , \omega _4 =0.5\pi \left( {\text {rad/s}} \right)$; b $\omega _1 =-\,2.5\pi \left( {\text {rad/s}} \right) , \omega _4 =2.5\pi \left( {\text {rad/s}} \right)$

Fig. 34

Phase diagram in X direction of clearance joint. a $\omega _1 =-\,0.5\pi \left( {\text {rad/s}} \right) , \omega _4 =0.5\pi \left( {\text {rad/s}} \right)$, b $\omega _1 =-\, 2 .5\pi \left( {\text {rad/s}} \right) , \omega _4 = 2 .5\pi \left( {\text {rad/s}} \right)$

Fig. 35

Phase diagram in Y direction of clearance joint. a $\omega _1 =-\,0.5\pi \left( {\text {rad/s}} \right) , \omega _4 =0.5\pi \left( {\text {rad/s}} \right)$, b $\omega _1 =-\, 2 .5\pi \left( {\text {rad/s}} \right) , \omega _4 = 2 .5\pi \left( {\text {rad/s}} \right)$

From Fig. 28, while the driving speeds of cranks are $\omega _1 =-\,0.5\pi \left( {\text {rad/s}} \right)$ and $\omega _{\mathrm{4}} =0.5\pi \left( {\text {rad/s}} \right)$, the velocity curve with clearance basically conforms to the ideal state, and when the driving speed are $\omega _1 =-\,2.5\pi \left( {\text {rad/s}} \right)$and $\omega _{\mathrm{4}} =2.5\pi \left( {\text {rad/s}} \right)$, the speed curve has obvious vibration. From Figs. 29, 30, 31 and 32, it could be seen that peak magnitude of acceleration of slider, the driving torques of cranks and the contact force at clearance joint all increase significantly with increase in driving speeds. Because driving velocity is larger, collision between shaft and bearing is more severe, so the dynamic response will produce greater fluctuation and peak value. As shown in Fig. 33, when driving speeds of the driving cranks are high, the shaft center trajectory appears more free flight state and is very chaotic. When the driving speed of driving cranks are low, the shaft center trajectory is in the continuous contact state.

Fig. 36

Poincaré map in X direction of clearance joint. a $\omega _1 =-\,0.5\pi \left( {\text {rad/s}} \right) , \omega _4 =0.5\pi \left( {\text {rad/s}} \right)$, b $\omega _1 =-\, 2 .5\pi \left( {\text {rad/s}} \right) , \omega _4 = 2 .5\pi \left( {\text {rad/s}} \right)$

Fig. 37

Poincaré map in Y direction of clearance joint. a $\omega _1 =-\,0.5\pi \left( {\text {rad/s}} \right) , \omega _4 =0.5\pi \left( {\text {rad/s}} \right)$, b $\omega _1 =-\, 2 .5\pi \left( {\text {rad/s}} \right) , \omega _4 = 2 .5\pi \left( {\text {rad/s}} \right)$

Fig. 38

Lyapunov exponent in X direction of clearance joint. a $\omega _1 =-\,0.5\pi \left( {\text {rad/s}} \right) , \omega _4 =0.5\pi \left( {\text {rad/s}} \right)$, b $\omega _1 =-\, 2 .5\pi \left( {\text {rad/s}} \right) , \omega _4 = 2 .5\pi \left( {\text {rad/s}} \right)$

Fig. 39

Lyapunov exponent in Y direction of clearance joint. a $\omega _1 =-\,0.5\pi \left( {\text {rad/s}} \right) , \omega _4 =0.5\pi \left( {\text {rad/s}} \right)$, b $\omega _1 =-\, 2 .5\pi \left( {\text {rad/s}} \right) , \omega _4 = 2 .5\pi \left( {\text {rad/s}} \right)$

Fig. 40

Bifurcation diagram of clearance joint with varying driving speed. a Poincaré map in X direction. b Poincaré map in Y direction

From Figs. 28, 29 30, 31, 32 and 33, it can know that, characteristics of the kinematic and the dynamic for rigid mechanism and flexible mechanism are quite different. The effect of the flexible rods are quite visible. When driving speeds are $\omega _1 =-\,0.5\pi \left( {\text {rad/s}} \right)$ and $\omega _{\mathrm{4}} =0.5\pi \left( {\text {rad/s}} \right)$, the dynamic behavior of elastic mechanism with clearance are almost same as the dynamic response in the ideal state, there is a small distinction. And especially for the high driving velocity, influences are more visible. The peak value of the dynamic behaviors of the flexible mechanism with clearance is smaller than that of the rigid mechanism with clearance. And the shaft center trajectory of the elastic mechanism is also improved. The flexibility of components improve dynamic behaviors of mechanism. The flexible links behave as a spring and damper to assimilate the energy caused by clearance joint, and reduce the vibration frequency and vibration amplitude.

5.4.2 The influence of driving speed on nonlinear characteristics

When driving speeds are $\omega _1 =-\,0.5\pi \left( {\text {rad/s}} \right) , \omega _4 =0.5\pi \left( {\text {rad/s}} \right)$, the phase diagrams of the X and Y directions at the revolute clearance joint of flexible mechanism are shown in Figs. 34a and 35a. When driving speeds are $\omega _1 =-\,2.5\pi \left( {\text {rad/s}} \right) , \omega _4 =2.5\pi \left( {\text {rad/s}} \right)$, the phase diagrams of the X and Y directions at the revolute clearance joint of flexible mechanism are shown in Figs. 34b and 35b. Their corresponding Poincaré maps are shown in Figs. 36 and 37. And Lyapunov exponents are shown in Figs. 38 and 39.

From Figs. 34, 35, 36, 37, 38 and 39, when driving speeds are $\omega _1 =-\,0.5\pi \left( {\text {rad/s}} \right) , \omega _4 =0.5\pi \left( {\text {rad/s}} \right)$, the phase diagrams in X and Y direction of clearance joint are both closed curve, the Poincaré maps in X and Y direction of clearance joint are both an independent point, the LLE in X and Y direction of clearance joint are $-\,0.0026$ and $-\,0.0187$, which are both less than zero, so they are all in periodic motion. From Figs. 34, 35, 36, 37, 38 and 39, when the driving speeds are $\omega _1 =-\,2.5\pi \left( {\text {rad/s}} \right) , \quad \omega _4 =2.5\pi \left( {\text {rad/s}} \right)$, the phase diagrams in X and Y direction of clearance joint are both disorderly curve, mapping point of the Poincaré maps in X and Y direction of clearance joint are scattered, and mapping points do not repeat each other, the LLE in X and Y direction of clearance joint are 0.6890 and 0.1868, which are both greater than zero. It shows that the mechanism has no periodic solution and the joint with clearance is in chaotic.

Fig. 41

Phase diagram of slider, a $\omega _1 =-\,0.5\pi \left( {\text {rad/s}} \right) , \omega _4 =0.5\pi \left( {\text {rad/s}} \right)$; b $\omega _1 =-\,2.5\pi \left( {\text {rad/s}} \right) , \omega _4 =2.5\pi \left( {\text {rad/s}} \right)$

Fig. 42

Poincaré map of slider, a $\omega _1 =-\,0.5\pi \left( {\text {rad/s}} \right) , \omega _4 =0.5\pi \left( {\text {rad/s}} \right)$; b $\omega _1 =-\,2.5\pi \left( {\text {rad/s}} \right) , \omega _4 =2.5\pi \left( {\text {rad/s}} \right)$

Fig. 43

Lyapunov exponent of slider. a $\omega _1 =-\,0.5\pi \left( {\text {rad/s}} \right) , \omega _4 =0.5\pi \left( {\text {rad/s}} \right)$; b $\omega _1 =-\,2.5\pi \left( {\text {rad/s}} \right) , \omega _4 =2.5\pi \left( {\text {rad/s}} \right)$

The bifurcation diagrams of revolute clearance joint in X and Y direction with varying driving speed of cranks are shown in Fig. 40a, b. It can be drew from the diagrams that, when the interval of driving speed of crank 4 is $\left[ {0.5\pi ,1.6\pi } \right] \left( {\text {rad/s}} \right) ,$and corresponding driving speed of crank 1 is $\left[ {-\,0.5\pi ,-\,1.6\pi } \right] \left( {\text {rad/s}} \right) ,$ the mechanism is in a periodic state. The driving speed of crank 4 starts from $1.65\pi \left( {\text {rad/s}} \right)$(The driving speed of crank 1 starts from $-\,1.65\pi \left( {\text {rad/s}} \right) )$, with increase in crank velocity, the chaos at the clearance joint becomes more and more serious.

The driving speeds of the crank 1 and the crank 4 are considered as $\omega _1 =-\,0.5\pi \left( {\text {rad/s}} \right) , \omega _4 =0.5\pi \left( {\text {rad/s}} \right)$ and $\omega _1 =-\,2.5\pi \left( {\text {rad/s}} \right) , \omega _4 =2.5\pi \left( {\text {rad/s}} \right)$, respectively. The phase diagram, Poincaré map, Lyapunov exponent and bifurcation diagram of slider are shown in Figs. 41, 42, 43 and44. When the driving speeds are $\omega _1 =-\,0.5\pi \left( {\text {rad/s}} \right) , \omega _4 =0.5\pi \left( {\text {rad/s}} \right)$, the phase diagram of the slider is a closed curve, while the driving speeds are $\omega _1 =-\,2.5\pi \left( {\text {rad/s}} \right) , \omega _4 =2.5\pi \left( {\text {rad/s}} \right)$, the phase diagram of end slider occurs obvious fluctuations. The corresponding Poincaré maps are shown in Fig. 42, which are both independent points. Corresponding Lyapunov exponents are shown in Fig. 43, its LLE are $-\,0.0106$ and $-\,0.0021$, which are both less than zero. Therefore, the motion state of end slider is periodic motion. According to Figs. 34b, 35b, 36b, 37b, 38b and 39b, although clearance joint is in chaos, the slider is not in chaotic motion. According to Fig. 44, it can be observed that slider is all in periodic motion. Compared with Figs. 40 and 44, when clearance joint is chaotic, slider is not necessarily to do chaotic motion. The reason is that the stable region of mechanism with single clearance is larger. The single clearance has less effect on the chaotic state of the end slider.

Fig. 44

Bifurcation diagram of slider with varying driving speed

6 Conclusions and future works

Based on previous studies, the effects of clearance joint and flexible body on dynamic behavior are independently investigated rather than being considered simultaneously in the same mechanism. Nonlinear dynamic behavior of 2-DOF nine-bar mechanism with clearance in flexible system is studied in this paper. The nonlinear dynamic model of 2-DOF nine-bar mechanical system with revolute clearance and flexible links is built by Lagrange and FEM combining with Lankarani–Nikravesh and modified Coulomb’s friction models.

On basis of the numerical simulations, it could be concluded that there are sizeable changes in mechanical response owing to the influence of clearance. Main functional parameters were researched in this work, namely, the clearance value and the driving velocities of cranks. The fluctuation of the dynamic response all increase with the clearance value under the same driving speed. Compared with low driving velocity, the high driving speed exhibits a more deteriorated response of mechanism. With the increase in clearance size and driving speeds of cranks, peak magnitude of slider acceleration, the contact force at the clearance joint and driving torque of cranks are all increased, stability of the mechanism has also weakened.

For the case of flexibility of links, flexible links can partly decrease dynamic response of the mechanical system with clearance relative to rigid mechanical system with clearance, the peak magnitude of acceleration of slider, the contact force at the clearance joint and the driving torque of cranks decreased obvious, the shaft trajectories at rigid mechanism is much more chaotic than that of flexible mechanism, dynamic response of flexible mechanism with clearance is closer to the ideal state than that of rigid mechanism with clearance. Flexibility of rod has a damping effect for the mechanism. The main reason is that the flexible links can properly absorb the vibration due to the clearance and make the dynamic response of the mechanism tends to be stable.

It can be observed that flexible system with revolute clearance joint is well known as nonlinear dynamic system, and it exhibits a chaotic response under the certain conditions. In this paper, the nonlinear characteristics of elastic mechanisms with clearances are studied comprehensively and systematically. The phase diagrams, Poincaré portraits, Lyapunov exponents, and bifurcation diagrams of the clearance joint are researched. Under the same driving velocity of cranks, chaos of clearance joint becomes more and more serious with the increase in the clearance value. Under the same clearance value, with the increase in driving speeds of cranks, the motion state of clearance joint gradually changes from the periodic motion to the chaotic motion. Nonlinear characteristics of slider are also researched. It is shown that, because of the stable region of mechanism with single clearance is larger, although the joint with clearance is in chaos, slider isn’t in chaotic motion. In future works, Friction, wear, experimental work in the flexible mechanism with multiple clearances could be investigated, and this work will be also extended to the 3D models.