1 Introduction

Revolute pair and translational pair are the important connecting parts of the planar mechanism. Due to manufacturing tolerance and wear, revolute pair and translational pair are not perfect, and there will be some clearances [1,2,3,4,5,6,7]. Clearances will affect dynamic response and result in significant deviation between the expected behavior and the actual results. When the mechanism moves too fast or the cross-sectional area is too small, a certain elastic deformation of the components will be produced. The impact phenomenon related to clearance and the vibration phenomenon related to elastic deformation of components directly affect the service life of mechanism. In addition, joint clearance and elastic deformation of components are the key factors leading to chaos in multi-body system. The chaotic quantization of mechanical system not only helps to understand the nonlinear nature of the system, but also helps to rationalize the control parameters. Besides, the treatment of kinematic pair clearance and elastic deformation of components is a complex and important problem [8,9,10,11,12,13,14]. Therefore, it is necessary to research in detail the coupling action between flexible member and clearance, and the influence of this coupling effect on nonlinear dynamics.

Revolute pair is the most common kinematic pair in planar mechanism. Its clearance will influence the mechanism’s stability, which has attracted the attention of many scholars [15,16,17,18,19,20,21,22]. Chen et al. [23] derived a dynamic model of six bars rigid mechanism containing revolute clearance. Marques et al. [24] considered the comprehensive influences related to radial and axial displacement, and proposed a method of dynamic modeling of 3D rotating clearance. Wan et al. [25] built computational dynamic equation of momentum wheel assembly by considering the influencing factors such as flexibility and clearance. Based on fractal theory, Li et al. [26] established a new stiffness coefficient model considering the surface roughness, which considered the elastic, elastic–plastic and plastic deformations of the asperities of the contact surface. Bai et al. [27] introduced a 3D rotating clearance joint modeling method, and its application in satellite antenna system was studied. Alshaer et al. [28] discussed influence of lubrication clearance on motion characteristic and force condition of mechanism. Xu et al. [29]. studied the wear characteristic of rotating clearance pair through numerical simulation and experiment.

Any component is an elastomer with different rigidity, and the flexibility of member seriously affects the mechanism’s stability. Therefore, many scholars have studied the coupling effect between the revolute clearance pair and elastic deformation of components [30,31,32,33,34,35,36,37]. Pi et al. [38] proposed a unified geometric model of clearance pair within the framework of iso-geometric analysis (IGA). Numerical simulation was carried out for different flexible mechanism, and their dynamic responses were analyzed in detail. Jiang et al. [39] used the transverse and torsional spring system to describe the dynamics of connected beams containing two clearances, and proposed an improved numerical method to solve dynamic equations by Newmark integral method. Chen et al. [40] researched the effect of operating parameters on dynamics of high-precision mechanism with clearance through mathematical statistical parameters. Xiang et al. [41] studied dynamic of robot manipulator considering parameter uncertainty and clearance. Based on Chebyshev polynomial method, interval algorithm was utilized to calculate the dynamic response of mechanism. Li et al. [42] comprehensively studied effect of clearance and friction coefficient on dynamic of plane deployable structure composed of shear like elements. Chen et al. [43] put forward a novel contact force entropy weight method to evaluate the influences of different clearances and angular velocities on contact force. Chen et al. [44] proposed a dynamic modeling method considering plane rotating clearance pair, elastic deformation and large-scale motion. Li et al. [45] researched dynamic and wear characteristics of solar cell array system containing the revolute clearance and solid coating.

The translational pair is an important connecting part of end effector of planar mechanism, and its clearance seriously affects the motion characteristic of the mechanism, which has been studied by some scholars. Stoenescu et al. [46] discussed the dynamic of planar rigid linkage containing sliding joint clearance and studied the effect of driving velocity and recovery coefficient on chaotic characteristics. Wu et al. [47] proposed an improved model to evaluate the contact force generated by translational clearance, and numerically studied a rigid-body double crank mechanism considering translational clearance. Flores et al. [48] used multiple friction unilateral constraints to model the clearance of translational pair, and proposed and discussed a dynamic modeling approach for crank slider with translational clearance joint. Qian et al. [49] built a 3D translational pair model with clearance, studied the motion between the guide rail and slider. Flores et al. [50] established dynamic equation containing single translational clearance, and the effects of four clearance sizes on mechanism were compared.

The combined action of revolute clearance and translational clearance can more accurately predict mechanism’s dynamics. Chen et al. [51] established the rigid dynamic equation containing multiple clearances by LMD. Wang et al. [52] built rigid dynamic equation of crank slider mechanism with both rotating clearance pair and translational clearance pair. Wu et al. [53] introduced the compound action of translational clearance and rotational clearance on the dynamic of plane rigid crank slider mechanism with correlation dimension and bifurcation.

To sum up, the researches on dynamic behavior of mechanisms with clearance mainly focused on dynamic behavior of rigid / rigid flexible coupling mechanisms with revolute clearance pair, rigid mechanisms with translational clearance pair and rigid mechanisms with mixed clearances. There are few studies on the influence of the hybrid clearance composed of revolute clearance and translational clearance on dynamic response and chaos of rigid flexible coupling MLM. Therefore, the main innovation of this paper is to propose an accurate dynamic modeling method of MLM considering the coupling effects of revolute clearance, translational clearance and flexibility of the component, and study its dynamic response and chaotic characteristics.

The main arrangements are as follows: in the second section, the models of revolute clearance, translational clearance and flexible member are built, and the accurate nonlinear dynamic model of MLM considering the coupling action of revolute clearance, translational clearance and elastic deformation of member is established. In the third section, dynamic response and chaotic characteristics of rigid-flexible coupling MLM with revolute clearance and translational clearance are analyzed. The experimental platform of six-bar mechanism is built to verify the correctness of theoretical model. Sect 3 gives some conclusions.

2 Dynamic model of rigid-flexible coupling MLM with revolute clearance and translational clearance

2.1 Clearance model of revolute pair

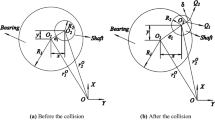
Clearance model of revolute joint and motion state of clearance shaft in bearing are shown in Fig. 1. Oi and Oj are the center of bearing and shaft, respectively. Ri is the bearing radius and Rj is the shaft radius. Qi is the impact point of the bearing during the collision, and Qj is the impact point on the shaft during the collision.

Fig. 1
figure 1

Clearance model of revolute pair

Full size image

The eccentric position vector between bearing and shaft is

$$ e = r_{j}^{O} - r_{i}^{O} $$
(1)

The relative embedded depth between bearing and shaft is

$$ \delta_{R} = e - c_{R} $$
(2)

where e is magnitude of eccentric position vector, \(e = \sqrt {e^{T} e}\); c is clearance value between bearing and shaft, cR = Ri–Rj.

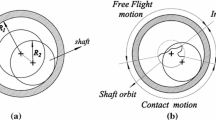
Motion state of the clearance pair can be determined according to the relative penetration depth

$$ \left\{ {\begin{array}{*{20}l} {\delta _{R} > 0,} \hfill & {{\text{impact}}\;{\text{state}}} \hfill \\ {\delta _{R} = 0,} \hfill & {{\text{continue}}\;{\text{contact}}\;{\text{state}}} \hfill \\ {\delta _{R} < 0,} \hfill & {{\text{free}}\;{\text{flight}}\;{\text{state}}} \hfill \\ \end{array} } \right. $$
(3)

Collision detection at the clearance can be carried out by monitoring the embedded depth. When two components of pair are in contact, the embedded depth has a positive value, while in free flight mode, the symbol is opposite. The change of contact status between shaft and bearing is [42]

$$ \delta_{R} \left( {t_{n} } \right)\delta_{R} \left( {t_{n + 1} } \right) < 0 $$
(4)

When \(\delta_{R} \left( {t_{n} } \right)\delta_{R} \left( {t_{n + 1} } \right) < 0\), \(\delta_{R} \left( {t_{n} } \right) < 0\) and \(\delta_{R} \left( {t_{n + 1} } \right) > 0\), at this moment, motion state changes from free flight state to impact state. When \(\delta_{R} \left( {t_{n} } \right)\delta_{R} \left( {t_{n + 1} } \right) < 0\), \(\delta_{R} \left( {t_{n} } \right) > 0\) and \(\delta_{R} \left( {t_{n + 1} } \right) < 0\), at this moment, motion state changes from impact state to free flight state.

Because the Lankarani–Nikravesh model considers the elastic properties and energy dissipation of the colliding object, it is widely used to describe the local collision contact phenomenon, it can be expressed as [11]

$$ F_{n} = K\delta_{R}^{n} + D\dot{\delta }_{R} $$
(5)

Fn is normal contact force, K is stiffness coefficient, D is damping coefficient of contact collision, and \(\dot{\delta }_{R}\) is relative velocity of contact collision.

Stiffness coefficient of the contact object is [27]

$$ K = \frac{{4E_{i} E_{j} }}{{3\left( {E_{i} \left( {1 - \nu_{i}^{2} } \right) + E_{j} \left( {1 - \nu_{j}^{2} } \right)} \right)}}\left( {\frac{{R_{i} R_{j} }}{{R_{i} - R_{j} }}} \right)^{\frac{1}{2}} $$
(6)

where \(\nu_{k} (k = i,j)\) and \(E_{k} (k = i,j)\) are Poisson's ratio and Young's modulus of bearing and shaft, respectively.

Damping coefficient is expressed as

$$ D = \frac{{3K\left( {1 - c_{e}^{2} } \right)\delta_{R}^{1.5} }}{{4\dot{\delta }_{R}^{\left( - \right)} }} $$
(7)

where ce is coefficient of recovery, \(\dot{\delta }_{R}^{\left( - \right)}\) is initial relative velocity.

In addition, the friction between shaft and bearing surface is a complex nonlinear factor of clearance pair. In order to accurately describe friction, the modified Coulomb friction model is adopted [54]

$$ F_{t} = - \mu_{d} c_{d} F_{n} \frac{{v_{t} }}{{\left| {v_{t} } \right|}} $$
(8)

where \(\mu_{d}\) is frictional coefficient; \(c_{d}\) is correction factor; it can be expressed as

$$ c_{d} = \left\{ \begin{gathered} 0{\kern 1pt} ,{\kern 1pt} {\kern 1pt} {\kern 1pt} \left| {v_{t} } \right| < v_{0} \hfill \\ \frac{{\left| {v_{t} } \right| - v_{0} }}{{v_{1} - v_{0} }}{\kern 1pt} ,{\kern 1pt} {\kern 1pt} {\kern 1pt} v_{0} \le \left| {v_{t} } \right| \le v_{1} \hfill \\ {\kern 1pt} 1{\kern 1pt} ,{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \left| {v_{t} } \right| > v_{1} \hfill \\ \end{gathered} \right. $$
(9)

where \(v_{0}\) and \(v_{1}\) are given tolerances for the tangential velocity, \(v_{0}\) = 0.0001 m/s and \(v_{1}\) = 0.001 m/s [44]. When \({\kern 1pt} \left| {v_{t} } \right| < v_{0}\), the value of \(c_{d}\) is 0; When \(v_{0} \le \left| {v_{t} } \right| \le v_{1}\), the value of \(c_{d}\) is \(\frac{{\left| {v_{t} } \right| - v_{0} }}{{v_{1} - v_{0} }}\); When \({\kern 1pt} \left| {v_{t} } \right| > v_{1}\), the value of \(c_{d}\) is 1.

2.2 Clearance model of translational pair

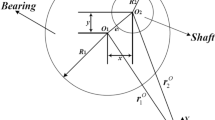
The clearance model of translational pair is shown in Fig. 2. Length and width of slider are LT and WT, respectively, the width of guide rail is HT, the clearance value of the translational pair is

$$ c_{T} = \frac{{H_{T} - W_{T} }}{2} $$
(10)
Fig. 2
figure 2

The clearance model of translational pair

Full size image

The analysis model of translational clearance is shown in Fig. 3. The slider and the guild rail are represented by m and n. As shown in Fig. 3, Am, Bm, Cm and Dm are the four corners of the slider, and An, Bn, Cn and Dn are the points closest to the corner of slider on the guide rail. The point A is taken as an example for detailed modeling and analysis. The position vector of any point H is

$$ \varvec{r}_{i}^{H} = \varvec{r}_{i} + \varvec{A}_{i} \varvec{s}_{i}^{H} \left( {i = m,n} \right){\kern 1pt} $$
(11)

where ri is position vector of the centroid of component i, Ai is transformation matrix, SiH is position vector of any point H.

Fig. 3
figure 3

Analytical model of translational clearance

Full size image

Position vector between Am point and the An point can be expressed as

$$ \varvec{\delta }_{T} = \varvec{r}_{n}^{A} - \varvec{r}_{m}^{A} $$
(12)

Normal vector of guide rail surface is

$$ \varvec{n}_{T} = \left( {\begin{array}{*{20}c} {t_{T}^{y} } & { - t_{T}^{x} } \\ \end{array} } \right)^{T} $$
(13)

where tTx and tTy are the components of tangential vector tT in the X and Y directions, respectively.

When there is a collision between two component, the condition of collision between slider and guide rail is [11]

$$ \varvec{n}_{T}^{T} \varvec{\delta}_{T} lt; 0 $$
(14)

As shown in Fig. 4a, when the two adjacent corners of slider are in contact with guide rail, collision force acts on the centroid of embedded area, it can be expressed as [50, 52]

$$ F_{T}^{n} = K_{T} \delta_{T} $$
(15)
$$ K_{T} = \frac{{aE_{m} E_{n} }}{{0.475\left( {E_{n} \left( {1 - \nu_{m}^{2} } \right) + E_{m} \left( {1 - \nu_{n}^{2} } \right)} \right)}} $$
(16)

where \(\delta_{T} = \sqrt {\delta_{T}^{T} \delta_{T} }\),\(a\) is half of the circumference of rectangular contact surface, \(E_{k} (k = m,n)\) and \(\nu_{k} (k = m,n)\) are elastic modulus and Poisson's ratio of slider and guide rail, respectively.

Fig. 4
figure 4

Contact mode of translational clearance

Full size image

As shown in Fig. 4b, when one or two opposite corners of slider are in contact with guide rail surface, contact force can be expressed as [51]

$$ F_{T}^{n} = K_{T} \delta_{T}^{n} + D_{T} \dot{\delta }_{T} $$
(17)
$$ K_{T} = \frac{{4E_{m} E_{n} \sqrt {R_{mn} } }}{{3\left( {E_{n} \left( {1 - \nu_{m}^{2} } \right) + E_{m} \left( {1 - \nu_{n}^{2} } \right)} \right)}} $$
(18)

where Rmn is radius of curvature of slider corner, DT is damping coefficient, \(D_{T} = \frac{{3K_{T} \left( {1 - c_{e}^{2} } \right)\delta_{T}^{1.5} }}{{4\dot{\delta }^{\left( - \right)} }}\).

The modified Coulomb friction model is also applied to describe the friction of translational clearance, as shown in Eq. (8).

2.3 Flexible beam element model

Flexible beam element model is built by ANCF, as shown in Fig. 5. The position vector of any point on element is

$$ r = \left( {\begin{array}{*{20}c} {r_{x} } & {r_{y} } \\ \end{array} } \right)^{T} = \left( \begin{gathered} a_{0} + a_{1} x + a_{2} x^{2} + a_{3} x^{3} \hfill \\ b_{0} + b_{1} x + b_{2} x^{2} + b_{3} x^{3} \hfill \\ \end{gathered} \right) = S_{{\text{f}}} q_{{\text{f}}} $$
(19)

where Sf is shape function.

$$ {\varvec{S}}_{f} = \left( {S_{f}^{1} {\varvec{I}},S_{f}^{2} {\varvec{I}},S_{f}^{3} {\varvec{I}},S_{f}^{4} {\varvec{I}}} \right) $$
(20)

where I is the element matrix; \(S_{f}^{1} = 1 - 3\zeta^{2} + 2\zeta^{3}\), \(S_{f}^{2} = l\left( {\zeta - 2\zeta^{2} + \zeta^{3} } \right)\), \(S_{f}^{3} = 3\zeta^{2} - 2\zeta^{3}\),\(S_{f}^{4} = l\left( { - \zeta^{2} + \zeta^{3} } \right)\), \(\zeta { = }{x \mathord{\left/ {\vphantom {x l}} \right. \kern-\nulldelimiterspace} l}\), l is length of flexible beam element, qf is the generalized coordinates of the flexible beam element.

Fig. 5
figure 5

Flexible beam element model

Full size image

qf can be expressed as [31]

$$ \begin{gathered} \varvec{q}_{f} = \left( {q_{f1} ,q_{f2} ,q_{f3} ,q_{f4} ,q_{f5} ,q_{f6} ,q_{f7} ,q_{f8} } \right)^{T} \hfill \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} = \left( {r_{ix} ,r_{iy} ,\frac{{\partial r_{ix} }}{\partial x},\frac{{\partial r_{iy} }}{\partial x},r_{jx} ,r_{jy} ,\frac{{\partial r_{jx} }}{\partial x},\frac{{\partial r_{jy} }}{\partial x}} \right)^{T} \hfill \\ \end{gathered} $$
(21)

where \(\left( {r_{ix} ,r_{iy} } \right)\) and \(\left( {r_{jx} ,r_{jy} } \right)\) are the position vectors of nodes i and j, respectively; \(\left( {\frac{{\partial r_{ix} }}{\partial x},\frac{{\partial r_{iy} }}{\partial x}} \right)\) and \(\left( {\frac{{\partial r_{jx} }}{\partial x},\frac{{\partial r_{jy} }}{\partial x}} \right)\) represent slope vectors in the tangential direction of the axis.

Kinetic energy of flexible beam element is

$$ \varvec{T}_{f} = \frac{1}{2}\int_{V} {\rho \dot{\varvec{r}}^{T} \dot{\varvec{r}}dV} = \frac{1}{2}\dot{\varvec{q}}_{f}^{T} \left( {\int_{V} {\rho \varvec{S}_{f}^{T} \varvec{S}_{f} dV} } \right)\dot{\varvec{q}}_{f} = \frac{1}{2}\dot{q}_{f}^{T} \varvec{M}_{f} \dot{\varvec{q}}_{f} $$
(22)

where Mf is mass matrix, \(M_{f} = \int_{V} {\rho S_{f}^{T} S_{f} dV}\). ρ and V are the density and volume.

The element elastic force of flexible beam is [45]

$$ \varvec{F}_{f} = \frac{{\partial \varvec{U}_{f} }}{{\partial \varvec{q}_{f} }} = \frac{{\partial \left( {\varvec{U}_{t} + \varvec{U}_{l} } \right)}}{{\partial \varvec{q}_{f} }} = \varvec{F}_{f}^{t} + \varvec{F}_{f}^{l} = K_{f}^{t} \varvec{q}_{f} + K_{f}^{l} \varvec{q}_{f} $$
(23)

where \({\varvec{U}}_{f}\), \({\varvec{F}}_{f}^{t}\), \({\varvec{F}}_{l}^{t}\), \({\varvec{K}}_{f}^{t}\) and \({\varvec{K}}_{f}^{l}\) represent the total strain energy, bending elastic force, axial elastic force, bending stiffness and axial stiffness of flexible beam element, respectively.

According to the theory of continuum mechanics, the total strain energy of the element includes bending strain energy and axial tensile strain energy, which can be expressed as [34]

$$ \varvec{U}_{f} = \varvec{U}_{l} + \varvec{U}_{t} = \frac{1}{2}\int_{0}^{l} {E_{f} A_{f} \varepsilon_{f}^{2} {\text{d}}x} + \frac{1}{2}\int_{0}^{l} {E_{f} I_{f} \kappa_{f}^{2} } {\text{d}}x $$
(24)

where Ef, Af, εf, If and \(\kappa_{f}\) are the Young’s modulus, cross-sectional area, strain and area moment of inertia and curvature, respectively.

The bending stiffness and the axial stiffness of the flexible beam element are

$$ K_{f}^{t} = \int_{0}^{l} {E_{f} I_{f} S^{\prime\prime T}_{f} S^{\prime\prime}_{f} {\text{d}}x} $$
(25)
$$ \varvec{K}_{l}^{t} = \int_{0}^{l} {E_{f} A_{f} \varepsilon_{f} \overline{\varvec{S}}_{f} {\text{d}}x} $$
(26)

where \(\overline{S}_{f} = S_{f}^{\prime T} S^{\prime}_{f}\).

The flexible beam element equation can be expressed as [54]

$$ \varvec{M}_{f} \ddot{\varvec{q}}_{f} + \varvec{F}_{f} = \varvec{Q}_{f} $$
(27)

where Qf is the generalized external force.

2.4 Establishment of nonlinear dynamic model of rigid-flexible coupling MLM considering revolute clearance and translational clearance

2.4.1 Description of structural features

The schematic diagram of six-bar mechanism is shown in Fig. 6. The mechanism is composed of frame, crank 1 (L1), connecting rod 2 (L2), connecting rod 3 (L3), connecting rod 4 (L4) and slider 5 (S5). L1 and L2 are connected by revolute joint A. L4 and S5 are connected by translational pair B. L3 and frame are connected by revolute joint C. L2, L3 and L4 are connected by compound hinge D. L4 and slider are connected by revolute joint E. The compound hinge D can be regarded as a combination of two revolute pairs (D1 and D2). L2 and L4 are connected by the revolute pair D1, and L3 and L4 are connected by revolute pair D2. Six-bar mechanism can be better applied to the main transmission mechanism of multi-link press.

Fig. 6
figure 6

The schematic diagram of six-bar mechanism

Full size image

As the slider is the end effector of the whole mechanism, the cooperation between the slider and the guide rail is an important factor affecting the dynamic and accuracy for whole mechanism. Therefore, translational clearance B needs to be considered. At the same time, revolute pair A is directly related to the driving member for it is an important connecting part between crank 1 and rod 2. Therefore, it is necessary to pay attention to the revolute clearance pair A between crank 1 and connecting rod 2. In addition, L2, L3 and L4 are regarded as flexible members for they are longer and more prone to elastic deformation. L1 is considered a rigid member for its short length and high stiffness. Similarly, the slider is regarded as a rigid member for its high stiffness. Therefore, it is very necessary to study dynamic model of MLM considering the coupling action of revolute clearance, translational clearance and flexibility of component. The schematic diagram of rigid-flexible coupling six-bar mechanism with revolute clearance and translational clearance is shown in Fig. 7.

Fig. 7
figure 7

The schematic diagram of mechanism with revolute clearance and translational clearance

Full size image

2.4.2 Rigid-flexible coupling dynamic model with revolute clearance and translational clearance

Velocity and acceleration constraint equation can be expressed as [23]

$$ \Phi_{q} \dot{q} = - \Phi_{t} \equiv \upsilon $$
(28)
$$ \Phi_{q} \ddot{q} = - \left( {\Phi_{q} \dot{q}} \right)_{q} \dot{q} - 2\Phi_{qt} \dot{q} - \Phi_{tt} \equiv \gamma $$
(29)

where \(\Phi_{q}\) is Jacobian matrix, \(\Phi_{q} = {{\partial \Phi } \mathord{\left/ {\vphantom {{\partial \Phi } {\partial q}}} \right. \kern-\nulldelimiterspace} {\partial q}}\). \(\dot{q}\) and \(\ddot{q}\) are generalized velocity vector and acceleration vector, respectively. \(\Phi_{qt} = {{\partial \Phi_{q} } \mathord{\left/ {\vphantom {{\partial \Phi_{q} } {\partial t}}} \right. \kern-\nulldelimiterspace} {\partial t}}\), \(\Phi_{t} = {{\partial \Phi } \mathord{\left/ {\vphantom {{\partial \Phi } {\partial t}}} \right. \kern-\nulldelimiterspace} {\partial t}}\), \(\Phi_{tt} = {{d\Phi_{t} } \mathord{\left/ {\vphantom {{d\Phi_{t} } {dt}}} \right. \kern-\nulldelimiterspace} {dt}}\).

Based on LMD, the rigid-flexible coupling dynamic equation containing clearances is [55]

$$ \overline{M}_{f} \ddot{q} + \Phi_{q}^{T} \lambda + \overline{F}_{f} = \overline{Q}_{f} $$
(30)

where \(\overline{M}_{f}\), \(\lambda\), \(\overline{F}_{f}\) and \(\overline{Q}_{f}\) are the mass matrix, Lagrange multiplier, elastic force and generalized force of system, respectively.

Baumgarte stabilization technology is used to suppress the acceleration constraint conflict by feedback the position and velocity constraint conflict [24, 47, 56, 57], dynamic equation can be written as

$$ \left( {\begin{array}{*{20}c} {M_{f} } & {\Phi_{q}^{T} } \\ {\Phi_{q} } & 0 \\ \end{array} } \right)\left( \begin{gathered} {\ddot{q}} \hfill \\ \lambda \hfill \\ \end{gathered} \right) = \left( {\begin{array}{*{20}c} {Q_{f} - F_{f} } \\ {\gamma - 2\alpha \dot{\Phi } - \beta^{2} \Phi } \\ \end{array} } \right) $$
(31)

3 Nonlinear dynamics behavior analysis of rigid-flexible coupling MLM with revolute clearance and translational clearance

3.1 Structural parameters of system

Geometric and inertial parameters are shown in Table 1. Clearance simulation parameters and flexible rod parameters are shown in Table 2.

Table 1 Geometric and inertial parameters
Full size table
Table 2 Clearance simulation parameters and flexible rod parameters
Full size table

3.2 Dynamic response analysis of rigid-flexible coupling MLM with multiple clearances

As shown in Fig. 6, the six-bar mechanism has four revolute pairs, one compound hinge and one translational pair. The revolute pair at point O is used to connect the crank and the motor. The revolute pair at point O is usually subject to interference treatment, and generally no clearance will be generated. Therefore, the clearance is not considered for the revolute pair at O, and the clearances are considered for other kinematic pairs, including revolute clearances A, C and E, compound clearance hinge D, and translational clearance pair B. The clearance values and driving velocity are 0.1 mm and 150 rpm, respectively. Dynamic response diagrams are shown in Figs.8, 9, 10, 11, 12.

Fig. 8
figure 8

Displacement

Full size image
Fig. 9
figure 9

Velocity

Full size image
Fig. 10
figure 10

Acceleration

Full size image
Fig. 11
figure 11

Driving torque

Full size image
Fig. 12
figure 12

Trajectory of clearance pair

Full size image

From the displacement, velocity and acceleration curves, the displacement and velocity are less sensitive to the clearance and flexible component, and the displacement curve almost coincides with the ideal curve, and the velocity curve has a weak vibration near the ideal curve, while the acceleration curve produces a more violent vibration and produces some obvious peaks. The driving torque curve shows that the sensitivity of the torque to the clearance and the flexible rod is also large, and some obvious peaks also appear.

The trajectory diagram shows that the movement of shaft in the bearing and the movement of the slider in the guide rail are disordered. As for the clearance of the revolute pairs, the disorder of the shaft movement in the bearing at the clearance A is greater, and the embedding depth of the shaft in the bearing is greater. When the revolute clearances A, C and E, compound clearance hinge D, translational clearance pair B are all considered, the nonlinear degree of the dynamic equation is greater and its solving speed is relatively slower. Since the research on the nonlinear characteristics requires a lot of data, in order to facilitate the research on the nonlinear characteristics in the following chapters, the following chapters mainly consider the revolute clearance A and translational clearance B.

3.3 Dynamic response analysis and chaos identification of rigid-flexible coupling MLM with revolute clearance and translational clearance

3.3.1 Dynamic response analysis

In order to fully understand the effect of coupling action of revolute clearance pair, translational clearance pair and the flexible component on the mechanism, dynamic response is analyzed in detail, including motion characteristics curve, driving torque curve and center trajectory curve at clearance pair, as shown in Figs. 13, 14, 15, 16, 17, 18, respectively. The clearance value of clearance pair and driving speed of crank are 0.5 mm and 150 rpm, respectively.

Fig. 13
figure 13

Displacement

Full size image
Fig. 14
figure 14

Velocity

Full size image
Fig. 15
figure 15

Acceleration

Full size image
Fig. 16
figure 16

Driving torque

Full size image
Fig. 17
figure 17

Trajectory of revolute clearance joint

Full size image
Fig. 18
figure 18

Trajectory of translational clearance joint

Full size image

From the dynamic response diagram, the coupling action of revolute clearance, translational clearance and elastic deformation of components has a greater impact on acceleration and torque, but less on displacement and velocity. The displacement is almost consistent with the curve under the ideal condition. Through the local enlarged view, there are small fluctuations in velocity, while the acceleration and torque have violent vibration and more peaks. The central trajectory curve is the real motion trajectory of the shaft and the slider when the mechanism runs for 200 cycles. It can be seen that the coupling action of clearance and component flexibility intensifies the collision between the two components at the kinematic pair with clearance, which leads to the instability of the motion state at clearance pair.

3.3.2 Chaos identification

In order to study the effect of revolute clearance, translational clearance and elastic deformation of components on nonlinear characteristics, chaos identification is carried out through phase diagram, Poincaré map and LLE, as shown in Figs. 19, 20, respectively. LLEs of revolute clearance and translational clearance are shown in Table 3.

Fig. 19
figure 19

Phase diagram and Poincaré map

Full size image
Fig. 20
figure 20

LLE

Full size image
Table 3 LLE of clearance joints
Full size table

Through the phase diagram and Poincaré map, it can be qualitatively determined that the revolute clearance pair is in the chaotic motion state in the X and Y directions, and the translational clearance pair is in the chaotic motion state in the X direction, and the translational clearance pair is in the periodic motion state along the Y direction. Because when LLE is greater than 0, mechanism is in chaotic motion state, and when LLE is less than 0, mechanism is in periodic motion state. LLE can quantitatively determine that the revolute clearance pair is in chaotic motion state in X and Y directions, the translational clearance pair is in chaotic motion state in X direction, and the translational clearance pair is in periodic motion state along Y direction.

3.4 Influence of different clearance values on nonlinear dynamic behavior of rigid-flexible coupling MLM with revolute clearance and translational clearance

3.4.1 Analysis of dynamic response

Two clearance values are selected to study the effect of clearance sizes on dynamic response, which are 0.1 mm and 0.4 mm, respectively. The speed of the driving member is 150 rpm. Dynamic response diagrams are shown in Figs. 21, 22, 23, 24, 25, 26.

Fig. 21
figure 21

Displacement

Full size image
Fig. 22
figure 22

Velocity

Full size image
Fig. 23
figure 23

Acceleration

Full size image
Fig. 24
figure 24

Driving torque

Full size image
Fig. 25
figure 25

Trajectory of the shaft in the bearing

Full size image
Fig. 26
figure 26

Trajectory of the slider in the guild rail

Full size image

According to the displacement and velocity curves, displacement and velocity are less affected by the coupling action of clearance and flexible member, but the local enlarged diagram shows that the greater the clearance value, the more obvious impact on mechanism. It is obvious from the acceleration curve and torque curve that the larger the clearance value is, the greater the vibration peak value of response is and the more unstable the mechanism is. In addition, acceleration curve shows that the smaller the clearance value, the faster the response vibration frequency, which is mainly caused by the more collision times between the slider and guide rail. The maximum peak value of dynamic response under different clearance sizes is shown in Table 4. The center trajectory diagram shows that the larger the clearance value, the more chaotic the motion state of shaft in the bearing and slider in the guide rail.

Table 4 The maximum peak value of dynamic response under different clearance values
Full size table

3.4.2 Analysis of nonlinear characteristics

The influence of two clearance values (0.1 mm and 0.4 mm) on the chaotic characteristics is analyzed through the phase diagram and Poincaré map, as shown in Figs. 27, 28, respectively. The bifurcation diagram varying with clearance value is shown in Fig. 29, and the value area of the clearance value is [0 mm, 1 mm].

Fig. 27
figure 27

Phase diagram

Full size image
Fig. 28
figure 28

Poincaré map

Full size image
Fig. 29
figure 29

Bifurcation diagram varying with clearance value

Full size image

With the increase of clearance value, the area of phase diagram of revolute clearance pair in the X and Y directions and phase diagram of translational clearance pair in the X direction also increase, their corresponding Poincaré maps also diffuse, and the chaotic phenomenon of the revolute clearance pair in the X and Y directions and translational clearance pair in the X direction are strengthened. The movement of slider in the Y direction is weakly affected by the clearance value. Through the local enlarged diagram of the phase diagram, the phase diagram also becomes chaotic with the increase of the clearance value, but the Poincaré map is always an isolated point, which shows that the slider moves periodically in the Y direction. According to the bifurcation diagram, with the increase of the clearance value, the chaotic phenomenon of revolute clearance pair in the X and Y directions and the translational clearance pair in the X direction are gradually enhanced, and the chaotic phenomenon of translational clearance pair in the X direction is stronger than that of the revolute clearance pair in the X and Y directions. The movement of slider in the Y direction is less affected by the clearance value and flexibility of component, so it is always in the state of periodic movement.

3.5 Influence of different speeds on nonlinear dynamic behavior of rigid-flexible coupling MLM with revolute clearance and translational clearance

3.5.1 Analysis of dynamic response

Two different speeds of driving member are selected to research the effect of various speeds on dynamic response, which are 30 rpm and 60 rpm, respectively. The clearance sizes of revolute pair and translational pair are both 0.2 mm. The dynamic response diagrams are shown in Figs. 30, 31, 32, 33, 34, 35.

Fig. 30
figure 30

Displacement of slider

Full size image
Fig. 31
figure 31

Velocity of slider

Full size image
Fig. 32
figure 32

Acceleration of slider

Full size image
Fig. 33
figure 33

Driving torque

Full size image
Fig. 34
figure 34

Trajectory of revolute clearance joint

Full size image
Fig. 35
figure 35

Trajectory of translational clearance joint

Full size image

Because the sensitivity of displacement to driving speed is not high, there is no obvious fluctuation in displacement curve. The speed curve shows that the speed curve fluctuates significantly around the ideal curve as the driving speed increases. As shown in acceleration curve and driving torque curve, the acceleration and torque are greatly affected by driving speed. The faster the driving speed is, the greater peak value of the response is, and the more unstable the mechanism is. The maximum peak value of dynamic response under different driving speeds is shown in Table 5. The center trajectory diagrams show that the smaller the driving speed, the closer the trajectory of shaft and trajectory of the slider are to the ideal curve, and the smaller the influence of clearance pairs and flexibility of component on dynamic response.

Table 5 The maximum peak value of dynamic response under different driving speeds
Full size table

3.5.2 Analysis of nonlinear characteristics

Phase diagram and Poincaré map shown in Figs. 36, 37 compare and analyze the effect of driving speeds on chaotic characteristics. With the increase of the driving speed, the area of phase diagram at revolute clearance and translational clearance expands and the degree of confusion increases. With the increase of the driving speed, the area of point of Poincaré mapping of the rotating clearance pair in the X and Y directions and the point of Poincaré mapping of translational clearance pair in the X direction expand and the degree of dispersion strengthens. However, the point of Poincaré mapping of translational clearance pair in the Y direction has always been a point. It can be seen that the driving speed has little effect on motion state of slider in the Y direction. As shown in the bifurcation diagrams of the rotating clearance pair in the X and Y directions and the bifurcation diagram of the translational clearance pair in the X direction(Figs. 38a, b and c), with the increase of the driving speed, the chaos becomes more and more serious and the mechanism becomes more unstable. The bifurcation diagram of translational clearance pair in the Y direction has not changed and has been in the state of periodic motion.

Fig. 36
figure 36

Phase diagram

Full size image
Fig. 37
figure 37

Poincaré map

Full size image
Fig. 38
figure 38

Bifurcation diagram varying with driving velocity

Full size image

3.6 Virtual simulation verification

The virtual simulation model of six-bar mechanism is established through ADAMS, considering the revolute clearance pair A and translational clearance pair B, and the component flexibility of components 2, 3 and 4. The clearance value of clearance pair and driving speed of crank are 0.5 mm and 150 rpm, respectively. The dynamic response comparison diagrams corresponding to MATLAB and ADAMS are shown in Figs. 39, 40, 41, 42. Through the comparative analysis of MATLAB curve and ADAMS curve, the displacement curve and speed curve of the mechanism almost coincide, but the acceleration and torque curve deviate to a certain extent, which have basically the same trend. The main reason is that the modeling methods and solving methods of the two software are different, which leads to the deviation of the dynamic response. Therefore, it can be generally considered that theoretical model is correct.

Fig. 39
figure 39

Displacement

Full size image
Fig. 40
figure 40

Velocity

Full size image
Fig. 41
figure 41

Acceleration

Full size image
Fig. 42
figure 42

Driving torque

Full size image

3.7 Test verification

In order to verify the correctness of theoretical model, test platform as shown in Fig. 43 is built. The motion characteristic of the slider of the test platform are measured by acceleration sensor, acceleration sensor is shown in Fig. 44. Data acquisition card shown in Fig. 45 plays a role of connecting signal detection element and computer, and it is the key component to ensure the working performance of the whole system.

Fig. 43
figure 43

Test platform

Full size image
Figs. 44
figure 44

Acceleration sensor

Full size image
Figs. 45
figure 45

Data acquisition card

Full size image

The clearance size of revolute pair A and the translational pair B are both set 0.3 mm, as shown in Figs. 46, 47. The diameter of ideal pin is 15 mm. Length of the cross section of ideal slider is 50 × 100mm2. The driving speed is set 60 rpm. When the mechanism has revolute clearance A and translational clearance B, the comparison between theoretical results and experimental results is shown in Fig. 48.

Figs. 46
figure 46

Shaft(clearance = 0.3 mm)

Full size image
Figs. 47
figure 47

Slider(clearance = 0.3 mm)

Full size image
Fig. 48
figure 48

The comparison between the theoretical result and the experimental result

Full size image

From the comparison between theoretical results and experimental results, the trend of theoretical result and experimental result is basically consistent, but there are certain differences in the vibration frequency and peak value. The main reason is that friction between components and the lubrication between slider and guide rail will lead to errors. And then, the correctness of the theoretical model can be basically verified.

4 Conclusion

Based on the dynamic of flexible multi-body system, considering the coupling effects of revolute clearance, translational clearance and elastic deformation of components, an accurate dynamic model of multi-body linkage mechanism is proposed.

  1. (1)

    Based on ANCF and RPCM, a six-link accurate dynamic model considering the coupling effects of revolute clearance, translational clearance and elastic deformation of components is established by using LMD.

  2. (2)

    Dynamic response and chaos identification of rigid-flexible coupling mechanism with revolute clearance and translational clearance are researched. It is found that the accuracy and stability of the mechanism are affected by the coupling effects of revolute clearance pair, translational clearance pair and elastic deformation of components. The chaotic state is determined qualitatively and quantitatively by phase diagram, Poincaré map and LLE. It is found that there is chaos in the mechanism.

  3. (3)

    Influences of different clearance values and driving speeds on nonlinear dynamic behavior of rigid-flexible coupling mechanism with revolute clearance and translational clearance are analyzed. With the increase of clearance value and driving speed, the stability and accuracy of mechanism decrease, the chaos of the revolute clearance in the X and Y direction and translational clearance in the X direction increases gradually, and the chaos of translational clearance in the Y direction has been in periodic motion.

  4. (4)

    The dynamic modeling method is compared and verified by ADAMS. The correctness of theoretical model is further verified by building an experimental platform.