1 Introduction

Stock markets are often considered to be complex dynamical systems with lots of complex factors from internal and external environments [1,2,3]. In order to clarify their potential mechanisms, all kinds of models, techniques and theoretical methods have been developed to characterize financial dynamics from different aspects [4,5,6,7]. Recently, many tools and approaches have been introduced to investigate the features of multifractality, power-law and complexity successfully [8,9,10]. Among them, the complexity is a measure of completeness of a market and has been the concern of many researchers. Meanwhile, the irreversibility, as an important aspect of complexity, is closely related to predictability. Since there is a conceptual relationship between predictability and efficiency, it can be considered that reversible time series are less predictable than irreversible ones. In this sense, the ranking of companies based on stock price irreversibility could provide relevant information for traders and optimal portfolio designs [11]. On the other hands, according to the degree of reversibility of each company varies over time, periods of financial turmoil can be easily identified and distinguished from periods of financial stability if we use the irreversibility values of each company. Nowadays, various measures of complexity were developed to compare time series and distinguish regular (e.g., periodic), chaotic, and random behavior [12, 13]. It can be very helpful to analyze the complexity with the concept of entropy because of its ability on capturing the uncertainty and disorder of the time series without imposing any constraints on the theoretical probability distribution [2, 14]. A range of entropy-based approaches attract much attention and there have been some successful attempts such as transfer entropy [15], sample entropy [16] and permutation entropy [17] These methods are constructed based on quantifying the regularity of a time series, and initially aimed at estimating the system complexity of stock markets [18, 19].

Topological entropy (TE), first introduced by Adler et al. for compact dynamical systems in 1965 [20], is an important invariant of topological conjugacy and it can be used to describe the complexity of a single map acting on a compact metric space [3, 21]. Later, Dinaburg and Rufus Bowen gave a different, weaker definition, which clarified the meaning of the topological entropy: for a system given by an iterated function, the topological entropy characterizes the total exponential complexity of the orbit structure with a single number [21,22,23]. Moreover, the TE is a numerical measure that determines the dynamical complexity of a topological dynamical system, which describes the rate of hidden information in chaotic orbits with time and controls the ergodicity [24, 25]. This method also has been successfully applied to some substitution sequences, and got a satisfying result [26]. Inspired by these theories and applications, we consider that dynamical aspects of time series derived from stock markets may be analyzed by means of the topological entropy.

In recent years, the study of dynamics of group actions has absorbed some researchers interests. Walczak et al. gave the concept of geometric entropy (GE) for group actions in 1988, which can be viewed as a generalization of topological entropy of a single group [27]. In the field of dynamical systems, the geometric entropy of the continuous map is further proposed [28, 29]. Influenced by this theory, but also to apply this theory to finite discrete time series time series, we redefine the geometric entropy based on the coarse-grained method, and use it to analyze the characteristics of various time series.

Meanwhile, we notice that diverse symbolic methods have been used for the physiological time series [14, 30, 31]. Enlightened by this adhibition, but also to facilitate the calculation of the value of topological entropy and geometric entropy, we introduce the horizontal visibility algorithm, which is a simple and well-defined tool for measuring time series irreversibility [32, 33]. This is an original time series symbolic method proposed recently, which makes use of graph theoretical concepts. On the other hand, it is also based on the mapping of a time series to a graph and subsequent analysis of the associated graph properties.

The reminder of the paper is organized as follows. In the following section, we present the topology entropy and the geometric entropy. In Sect. 3, we briefly introduce the horizontal visibility graph approach and a measure of time series irreversibility based on TE. Section 4 describes the database used in this paper and obtained symbolic series. Furthermore, we explore TE and GE to analyze simulated data and six groups of stock time series in Sect. 5. Finally, we offer concluding remarks in Sect. 6.

2 Methodologies

2.1 Topological entropy

Topological entropy (TE) is known as measuring the complexity of a single map acting on a compact metric space [23], and it has been applied to the substitution sequences successfully [26]. For the time being, we leave substitutions, to consider more generally, sequences with terms in a finite alphabet A. A way to measure the degree of irregularity of such a sequence y, is to detect the behavior of the sequence:

$$\begin{aligned} P(n)=|\varOmega _{n}|\quad \forall n \ge 1 \end{aligned}$$
(1)

where \(\varOmega _{n}\) denotes the set of all words in y of length n and P(n) is the number of different words of \(\varOmega _{n}\). Thus the growth of P(n) gives information about the randomness of the sequence y. For example, let us assume that we start with the sequence \(y=\{2, 3, 1, 2, 3, 4, 6\}\). If we set n to be 2, we can combine the elements in sequence y to get all words of length 2: {23, 31, 12, 23, 34, 46}. And then we can know that the value of P(2) is 5. Furthermore, through a series of simple proofs, it is not difficult to find the following two properties about P(n) are true [26]:

  1. (a)

    \(P(n+1)=P(n)\), for some \(n \ge 1\);

  2. (b)

    \(P(n)\le n\), for some \(n \ge 1\).

The topological entropy of the substitution sequences is defined as this equation [21]: \(h=\overline{\lim }_{n \rightarrow \infty } \frac{log_{k}P(n)}{n}\) , where \(k=|A|\). Hence, \(0 \le h \le 1\) and sequence with entropy 0 are said to be established.

Motivated by the definition of the TE under the substitution sequences, we consider a finite time series \(\{X_t\}_{t=1}^N\). First, we choose a symbolic method to transform this time series \(\{X_t\}_{t=1}^N=\{x_1,x_2,\dots ,x_N\}\) into a symbolic sequence \(\{Y_t\}_{t=1}^N=\{y_1,y_2,\dots ,y_N\}\). At the same time, Let k be the number of different alphabets of \(\{Y_t\}\). Next, we still use P(n) to represent the number of different word sets with length of n. And it is easy to find that \(P(N)=1\). Hence, the topological entropy (\(h_{n}\)) of time series can be similarly constructed by using following formula:

$$\begin{aligned} h_{n}=\frac{\log _{k}P(n)}{n}\quad (1 \le n \le N) \end{aligned}$$
(2)

According to the knowledge of permutation and combination, we can speculate that the maximum of P(n) is \(k^{n}\). At the moment, the TE can reach the maximum 1, whereas there is no doubt that the TE (\(h_N\)) reaches the minimize 0 when the value of n is N.

2.2 Geometric entropy

Geometric entropy is based on the application of TE, which is proposed by Walczak et al. [27]. Before introducing the GE for time series, we first briefly review the multiscale theory [9, 34, 35]. For a given discrete time series \(\{X_t\}_{t=1}^N\), coarse-grained time series are constructed by averaging the data points within nonoverlapping windows of increasing length q [36]. The coarse-grained time series \(\{u_{j}^{(q)}\}\) is defined as:

$$\begin{aligned} u_{j}^{(q)}=\frac{1}{q}\sum _{i=(j-1)q+1}^{jq} x_{i} , \quad 1 \le j \le \frac{N}{q} \end{aligned}$$
(3)

For scale one (\(q=1\)), the time series \(\{u^{(1)}\}\) is the original series. Then, for each given q, the original series is divided into \(\frac{N}{q}\) coarse-grained time series.

In the light of the multiscale theory and the original definition of geometric entropy given by Walczak, the GE for time series is proposed and can be described in the following steps:

  1. Step 1:

    Consider a time series \(\{X_t\}_{t=1}^N \), where N denotes the length of this series. Then, we construct the coarse-grained time series \(\{u_{j}^{(q)}\}\) by the Formula 3.

  2. Step 2:

    Transform the coarse-grained time series \(\{u_{j}^{(q)}\}\) into symbolic series \(\{Y_{t}\} (1\le t\le \frac{N}{q})\).

  3. Step 3:

    Calculate TE of each symbolic coarse-grained time series as a function of scale factor q.

  4. Step 4:

    For each scale factor q, we define the geometric entropy \((G_{q})\) as the following formula:

$$\begin{aligned} G_{q}=\sum _{n=1}^{N_{q}} \frac{\log _{k}P(n)}{n} \end{aligned}$$
(4)

where \(N_{q}=\frac{N}{q}\).

3 A symbolic approach for measuring time series irreversibility

3.1 The horizontal visibility graph

For calculating the value of TE and GE, we first need to transform a complex time series into a set of simple sequences, which is called a symbolic process [31]. In this paper, we use the horizontal visibility graph to symbolize the time series [11, 37]. The horizontal visibility graph (HVg) was introduced by L. Lacasa as a irreversibility measure for real-valued time series and defined as follows [32]: let \(\{X_t\}_{t=1}^N\) be a real-valued time series of N data. The algorithm assigns each datum of the series to a node in the horizontal visibility graph. Then, two nodes i and j in the graph are connected if one can draw a horizontal line in the time series joining \(x_{i}\) and \(x_{j}\) that does not intersect any intermediate data height. Therefore, i and j are two connected nodes if the following geometrical criterion is fulfilled within the time series:

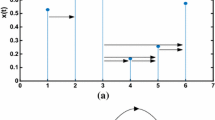
$$\begin{aligned} x_{i},x_{j}>x_{n},\quad \forall n|i<n<j \end{aligned}$$
(5)

However, these can be made directed by assigning to the links the time arrow naturally induced by the node ordering. Accordingly, the degree sequence of the HVg (which assigns to each node its degree or number of edges) thus splits into an in-going degree sequence \(\{Y_t^\mathrm{in}\}_{t=1}^N\), where \( y_t^\mathrm{in}\) is the in-going degree of node t, and an out-going degree sequence \(\{Y_t^\mathrm{out}\}_{t=1}^N\), where \( y_t^\mathrm{out}\) is the out-going degree of node t. Figure 1 shows an example to show the progressing of this symbolic approach.

Fig. 1
figure 1

Graphical illustration of the HVg method. In the figure, we plot a simple time series \(\{X_t\}=\{4,2,5,6,4,7,3\}\). Each datum in the series is mapped to a node in the graph. Arrows, describing allowed directed visibility, link nodes. In this method, each node has an in-going degree \(y^\mathrm{in}\), which accounts for the number of links with past nodes, and an out-going degree \(y^\mathrm{out}\) , which in turn accounts for the number of links with future nodes. Hence, we finally get two groups of symbolic time series: \(\{Y_t^\mathrm{in}\}=\{0,1,2,1,1,2,1\}\) and \(\{Y_t^\mathrm{out}\}=\{2,1,1,2,1,1,0\}\). Moreover, there is no doubt that \( y_1^\mathrm{in}\) and \( y_N^\mathrm{out}\)are zero for any time series

Full size image

3.2 Quantifying irreversibility

Through the above-mentioned part of the symbolization method, each set of data can be converted into two sets of symbolic sequences \(\{Y_t^\mathrm{in}\}_{t=1}^N\) and \(\{Y_t^\mathrm{out}\}_{t=1}^N\). Therefore, for each group of time series, using the topological entropy calculation method referred in Sect. 2.1, we can get two sets of entropy:\(\{h_n^\mathrm{in}\}\) and \(\{h_n^\mathrm{out}\}\). Inspired by the definition of the normalized directionality index introduced in [13], we propose a measure called normalized index(\(R_g\)) to quantify the time series irreversibility. It is given by

$$\begin{aligned} R_g=\frac{\left| h_n^\mathrm{in}-h_n^\mathrm{out}\right| }{h_n^\mathrm{in}+h_n^\mathrm{out}} \end{aligned}$$
(6)

This approach, on the one hand, can eliminate the effects of dimensions and increase the comparability between different data. On the other hand, by means of Formula 6, we can easily conclude that the greater the value of \(R_g\), the higher the degree of irreversibility.

Fig. 2
figure 2

Daily price returns for N225, STI, HIS, NASDAQ, S&P500 and TD stock indices

Full size image

4 Data

The analyzed data set consists of two parts: simulated time series and stock time series. The Chaos has captured the fancy of many financial economists. The attractiveness of chaotic dynamics is its ability to generate large movements which appear to be random, with greater frequency than linear models [38]. The simplest chaotic mapping operator, which was brought to the attention of scientists in 1976, is the logistic map [39].

$$\begin{aligned} x_{t+1}=rx_{t}(1-x_{t}) \end{aligned}$$
(7)

where \(x_t\) is the t-th chaotic number, t denotes the iteration number and r is parameter. Logistic mapping includes all the properties of chaotic systems, such as self-similarity, ergodicity, semi-random motion, and sensitivity to initial conditions. A detailed explanation about chaotic properties can be found in [40]. On the other hand, the Logistic map can provide more diversity than randomly selected initial solutions [41]. Besides, when \(r\in [3.5,4]\), the data generated by this map exactly exhibit chaotic behavior. In the study of the complexity of the dynamic system, many scholars often use logistic map as simulated data for experimental analysis [10, 39, 42,43,44,45,46,47,48,49]. Consequently, in this paper, we also use the logistic map as simulated time series to conduct experiment. We analyze six groups of time series with different value of r and the length of each group is 2500. (In the next section, we will verify that the experimental results are not affected by the length of the time series.) Meanwhile, we control the parameter \(r\in [3.5,4]\) in this paper to get time series with chaotic behavior.

As for the stock time series, we analyze the daily records of six indices: three Asia indices: N225, STI and HSI and three America indices: NASDAQ, S&P500 and TD. Because different stock markets have different opening dates, we exclude the asynchronous datum and then reconnect the remaining parts of the original series to obtain the same length time series. As a result, the total of the closing price recorded from January 4, 2000, to August 18, 2016, is 4097 days. Let \(s_{t}\) denote the closing price of stock market on day t. For characterizing these financial time series accurately, we investigate the financial time series using the daily return \(x_{t}\), which is calculated as its logarithmic difference, \(x_{t}=\log (s_{t})-\log (s_{t-1})\). Figure 2 presents the daily price returns of six stock markets.

In this paper, we desire to reveal the dynamics of TE and GE on the symbolic series of different data. Thus, these time series are transformed into their corresponding symbolic series by the HVg introduced in Sect. 3.1. NASDAQ is taken as an example illustrating the visibility approach to symbolic dynamics and is shown in Fig. 3. For observing the transformation clearly, Fig. 3 only shows the first 100 closing prices for example.

Fig. 3
figure 3

NASDAQ symbolic series of HVg. Only the first 100 closing prices of NASDAQ are displayed for clear observation

Full size image

5 Analysis and results

5.1 Analysis of simulated data

In order to more vividly display the change trend of topological entropy, we use six groups of simulated data with different parameter r through the logistic map and set the maximum value of n to 50 (the meaning of n is the same as it in Sect. 2.1). First, we transform these data into symbolized time series by the HVg introduced in Sect. 3.1. After symbolization, every group of data is transformed into two kinds of symbolized sequences. Consequently, we finally get two kinds of TE: \(h_n^\mathrm{in}\) and \(h_n^\mathrm{out}\) (see Fig. 4). From Fig. 4 we find that, whether the in-going degree sequence or the out-going degree sequence, the TE for all these time series decreases with the value of n increasing. Meanwhile, in order to illustrate the effect of data length on experimental results, we use the parameter \(r=3.75\) as an example to analyze the trend of topological entropy under different length of data(see Fig. 5). From the figure, we find that in spite of the different length of the time series, their topological entropy changes in the trend are almost no distinction. Hence, we are easily able to draw a conclusion that the results of topological entropy is not affected by the length of time series. Furthermore, since the geometric entropy is the generalization of the topological entropy, we can also sum up that the geometric entropy results are not affected by the time series length.

Fig. 4
figure 4

Topological entropy for six groups of simulated data with different parameter r through the logistic map. The black line represents the TE of in-going degree, while the red line is the TE of out-going degree. (Color figure online)

Full size image
Fig. 5
figure 5

Topological entropy for \(r=3.75\) through the logistic map. Lines of different colors represent different length of time series. (Color figure online)

Full size image
Fig. 6
figure 6

Simulated data irreversibility based the value of TE

Full size image
Fig. 7
figure 7

Geometric entropy for six groups of simulated data with different parameter r through the logistic map. The left is the result of GE on in-going degree, and the right is about out-going degree

Full size image
Fig. 8
figure 8

Topological entropy for two symbolic series of six stock time series. The left represents the in-going degree and the right represents the out-going degree

Full size image
Fig. 9
figure 9

Topological entropy for N225 through the logistic map. Lines of different colors represent different length of time series. (Color figure online)

Full size image
Fig. 10
figure 10

Financial time series irreversibility based the value of TE

Full size image
Fig. 11
figure 11

GE results of different stock markets on in-going degree

Full size image
Fig. 12
figure 12

GE results of different stock markets on out-going degree

Full size image

On the basis of the TE results, we can further quantify the irreversibility of these time series according to Formula 6, and Fig. 6 presents this result. From Figs. 4 and 6, although the trend of the topological entropy based on the in-going degree sequence and the out-going degree sequence seems to be little different, the Formula 6 can help us to study the differences in depth and further expose the irreversibility of different time series. Through the analysis of Fig. 6, we find that when n is greater than 20, the irreversibility of each time series turns to be stable. Moreover, to our surprise, after stabilization, \(r = 3.6\) and \(r = 3.85\) have the same degree of irreversibility, and higher than the other four time series. As well, the irreversibility of \(r = 3.75\) is the lowest.

Next, we apply the GE method to six groups of simulated time series mentioned in Sect. 3.1 for detecting the characteristics of GE intuitively. Figure 7 including two graphs displays the results of GE on in-going degree sequence and out-going degree sequence, respectively. From the figure, we can clearly discover that at different scales q, the GE method can distinguish the simulated sequence between different parameters r, especially the GE on out-going degree, which reflects that GE is an efficient way to differentiate the statistical properties of different time series and expose the interrelationships between them.

Fig. 13
figure 13

TE results of surrogate data generated by randomizing the different financial time series

Full size image
Fig. 14
figure 14

TE results of row data and surrogate data from different financial market when \(n=10\). The left one represents the in-going degree and the other is out-going degree

Full size image
Fig. 15
figure 15

TE results of row data and surrogate data from different financial market when \(n=15\). The left one represents the in-going degree and the other is out-going degree

Full size image
Fig. 16
figure 16

TE results of row data and surrogate data from different parameter r of the logistic map when \(n=10\). The left one represents the in-going degree and the other is out-going degree

Full size image
Fig. 17
figure 17

TE results of row data and surrogate data from different parameter r of the logistic map when \(n=10\). The left one represents the in-going degree and the other is out-going degree

Full size image
Fig. 18
figure 18

Irreversibility of surrogate data generated by randomizing the different financial time series based on the TE results

Full size image
Fig. 19
figure 19

GE results of surrogate data generated by randomizing the different financial time series

Full size image

5.2 Application to financial time series

In this section, we first perform TE methods on financial time series and discuss the similarities of different stock markets. Simultaneously, based on the results of topological entropy, we further compare the irreversibility of these financial data. And then, we also employ the GE method to the America and Asia market and analyze their differences and correlation. Additionally, in order to strengthen the rationality of the conclusion, we test the method proposed on surrogate data generated by randomizing the financial time series.

5.2.1 TE analysis on financial time series

Firstly, TE method based on the symbolic series is applied to investigate the complexity of six stock time series: N225, STI, HIS, NASDAQ, S&P500 and TD. In the same way, we also choose the maximum value of n to 50 for observing the variance tendency of TE more visually.

Figure 8 displays \(h_n^\mathrm{in}\) and \(h_n^\mathrm{out}\) of these six stock time series, respectively. According to our observation, it is relatively easy to find that although these data come from different stock markets, they have similar variance tendency of the TE, which is consistent with the results of simulated data. Consequently, the TE is an efficient way to detect the system complexity and similarity from different financial time series. Moreover, combined with the TE theory, we can assume that the n of the Formula 2 actually represents the data length per unit time. With the increase in n, the information loss per time unit about the state of the system, that is the value of TE, is reduced. Consequently, this result also reflects the characteristic of the TE, namely with the increase in the amount of data, the information loss per time unit about the state of the system is reduced. On the other side, similarly, we choose N225 as an example to discuss the relationship between topological entropy and time series length. From Fig. 9, we can see that the result is consistent with that of the simulated data, that is, the result of topological entropy is hardly affected by the length of financial time series. Furthermore, based on the intrinsic relation between topological entropy and geometric entropy, it can be deduced that the results of geometric entropy are also not influenced by the data length.

Afterward, we compare the irreversibility of the six groups of financial time series (see Fig. 10). As anticipated, when n is big enough, the irreversibility of time series tends to be stable, which is similar to the result of simulated data. Furthermore, after the irreversibility stabilized, it is noticeable that the irreversibility of HSI and STI is the strongest, while the irreversibility of TD is the weakest. This feature also points out that the characteristic of HIS is more similar to STI. Based on the ranking of financial time series irreversibility, we can provide information for traders and the optimal portfolio design. It is also worth emphasizing that, depending on the degree of reversibility of each financial index, over time, if we use the irreversibility value of each financial index, the financial turmoil can easily identify and distinguish financial stability [11].

5.2.2 GE application to different stock markets

In this subsection, we investigate six stock markets employing GE method. To comprehensively characterize the complexity, we choose the range of scales from 1 to 10, since the complexity is different on different scales. Likewise, we always get two kinds of symbolic series after Step 2 introduced in Sect. 2.2, so we will discuss the GE results of these two symbolic time series, respectively.

In Fig. 11, numbers in x-axis stand for the value of scale q and y label represents the GE value of in-going degree. First of all, we find that the value of GE decreases with scale factor increasing for all cases, which indicates that the complexity of each stock market decreases over the time scale. Furthermore, through observing the plots carefully, some interesting characteristics are displayed after comparison:

  1. 1.

    For scale one, the NASDAQ series are assigned the highest value of GE, the S&P500 series and the TD series are assigned the lowest, while the values of the Asia series are almost converge at a point between them.

  2. 2.

    The entropy of the America markets is higher than the N225 and the STI series when q is 2, nevertheless, the entropy of the STI and the HSI are greater than the America markets when q is 5. Moreover, since \(q \ge 4\), the entropy of the S&P500 is bigger than the N225, and when q is between 5 and 9, the entropy of S&P500 is smaller than the STI.

  3. 3.

    As for scale 10, the entropy of the America time series converges at a point and is assigned the highest, whereas the entropy of the Asia is assigned the lowest.

With respect to the GE results of different stock markets on out-going degree (see Fig. 12), it also can be seen that as scale q increases, the GE of each time series decreases. Besides, for scale 10, the entropy of NASDAQ and TD are at the lowest point, which is in contrast to the results of the GE on in-going degree. What is worthy mentioning is that the GE of Asia intersects at the same point which distributes between the Americas. When q is 5 to 8, the entropy of the TD series is bigger than the N225, but when q is 3, 4, 9 and 10, the result is universe.

To sum up, some new conclusions are gotten by the new characteristics we detected in the comparison. The GE method can distinguish different stock markets well and it is a precise way to quantify the complexity and correlation of different financial time series.

5.2.3 Test on surrogate data generated by randomizing the financial time series

In this subsection, in order to further validate our conclusions, we test TE and GE on surrogate data generated by randomizing the financial time series. The results are shown in Figs. 13, 14, 15, 16, 17, 18, and 19.

Table 1 The TE results of NASDAQ time series and surrogate data under in-going degree
Full size table
Table 2 The TE results of NASDAQ time series and surrogate data under out-going degree
Full size table

From Fig. 13, we find that, after randomizing the financial time series, the overall trend of their topological entropy is similar to that before the disruption, that is, the topological entropy from different markets decreases with the increase in n. But, there are still some internal differences between the surrogate data and the raw data. As a validation, we choose NASDAQ as an example to compare the changes of the topological entropy of the raw data and that of the data after disruption. In order to make the comparison more obvious, we select some n and list the topological entropy corresponding to every n (see Tables 1, 2). After comparing and analyzing, we can see that in spite of the similar overall trend, the TE values under different n of the surrogate data are different from that of the raw data. Additionally, we select \(n=10\) and \(n=15\), respectively, and compare the TE values between row data and surrogate data from different financial market (see Figs. 14, 15). From the figure, we can easily find that, for the chosen n, there are significant differences between the TE values of the time series from different financial markets. There is no doubt that the reason for this phenomenon is that we have destroyed the temporal correlations of original time series. Besides, we also carry out same experiments on the simulated data generated by the logistic map, as shown in Figs. 16 and 17 and get similar conclusions. This also further reflects the fact that topological entropy is an effective way indeed to expose the similarity of time series from different markets.

Then we analyze the irreversibility of the randomized time series (see Fig. 18). When n is greater than 10, the irreversibility of time series tends to be stable, which is similar to the raw data result. However, when the irreversibility is stationary, the irreversibility of the different surrogate time series is different from the results of raw data. For instance, the irreversibility of NASDAQ is similar to that of S&P500, and is higher than that of the other four time series. Moreover, N225 and STI have similar irreversibility levels, and their irreversibility is the weakest in these six surrogate time series. These results farther confirm that we propose a time series irreversibility measure based on topological entropy—\(R_g\), which is a reasonable way to compare the irreversibility of different time series.

Furthermore, we apply the GE to randomized financial time series (see Fig. 19). Since the internal properties of the randomized time series may change, there are some differences between these results and those of the financial time series before the disruption. But by comparing the analysis of Fig. 19, the results also verify the conclusions we have in the previous section, that is, the GE method can distinguish different stock markets well and it can quantify the complexity and correlation of different financial time series effectively.

6 Conclusion

To characterize the total exponential complexity of the orbit structure with a single number, the topological entropy was proposed and also has been successfully applied to substitution sequences. On the other hand, with the development of the study of group actions, many researchers attach much interest in the geometric entropy of the continuous map. Inspired by these theories and applications, this paper changes the perspective of research and improves these classical methods to apply them to time series (discrete dynamical system). In summary, we first introduce topological entropy based on time series, which is the most important for smooth dynamical system. Then, we also account for geometric entropy based on a finite time series successfully. For a further validation, we apply TE and GE to an original symbolic method, i.e., horizontal visibility graph and construct a measure of time series irreversibility combined with the results of TE. In addition, we conduct experiments on a logistic map and stock time series from different markets to detect the properties of these entropies. Moreover, we test these methods on the surrogate data generated by randomizing the financial time series to ulteriorly examine the conclusions.

As far as we know, due to the inherent nonlinearity and nonstationary characteristics of financial stock market price time series, it is significant to study the complexity of financial time series. Nowadays, many methods have been developed to quantify the complexity of financial time series from different markets, most of which are based on the purpose of distinguishing the complexity of different time series. However, for deeper exploration on the characteristic of financial dynamics system, it is not enough to just study the differences of financial time series. It is also important to discuss the regularity and similarity between different time series. The topology entropy described in this paper is from this point of view. Results are shown that the TE value of financial time series decreases with the value of n increasing, which is consistent with the results of simulated data. These characteristics prove that TE can effectively analyze the similarity of different time series, on the other hand, there is no doubt that it is an effective way to quantify the changes of complexity for stock market data and reflects the regularity dynamical changes well. In addition, they are able to demonstrate the physical meaning of TE, namely the loss of the information about the system state per time unit reduces as the amount of data increases. Besides, we have experimentally demonstrated that both TE results and GE results are not affected by the length of time series.

On the basis of the TE results, we quantify the time series irreversibility, and make a comparison between different time series. According to the comparison results, the simulation time series and the financial time series have a common characteristic, that is, when n reaches a certain value, the time series irreversibility tends to be stable. Once it remains stable, we can easily compare the irreversibility of different time series. For instance, from the results of the analysis on the financial time series irreversibility, it can be concluded that the irreversibility of HSI and STI is stronger than that of other stock markets after n reaches 10. All these findings are more valuable. We know that stock market price prediction is regarded as one of the most challenging tasks of financial time series prediction, while the irreversibility is very useful for the predictability of time series. Our approach can effectively distinguish the irreversibility of different time series, and then can be used to explore their predictability, which will also be an important focus in our further study.

In accordance to the analysis of the GE results, we find out that the financial time series under different markets have a common phenomenon that is the value of geometric entropy decreases as the scale factor q increases. This phenomenon reflects the fact that, although different financial time series have significant internal structural differences, their complexity decreases with the increase of coarse-grain degree. Furthermore, after comparing the results of the simulated data and financial time series from America and Asia, we discover that geometrical entropy can well distinguish various time series at different scales. Consequently, it is a fine way to do some otherness study of different time series. Beyond all that, results of the test on surrogate data generated by randomizing the financial time series further strengthen our summing-up.

In fact, TE and GE can analyze the features of different time series from different angles. They are both proper tools for investigating the similarity and correlation among time series. Additionally, TE and GE can also be applied to other time series of multifarious fields to detect complex behaviors. All in all, there are still meaningful aspects that need further discussion.