Directed vector visibility graph from multivariate time series: a new method to measure time series irreversibility

Abstract

As a practical tool, visibility graph provides a different perspective to characterize time series. In this paper, we present a new visibility algorithm called directed vector visibility graph and combine it with the Kullback–Leibler divergence to measure the irreversibility of multivariable time series. T directed vector visibility algorithm converts the time series into a directed network. Subsequently, the ingoing and outgoing degree distributions of the directed network can be got to calculate the Kullback–Leibler divergence, which will be applied to assess the level of irreversibility of the time series. This is a simple and effective method without any special symbolic process. The numerical results from various types of systems are used to validate that this method can accurately distinguish reversible time series from those irreversible ones. Finally, we employ this method to estimate the irreversibility of financial time series and the results show that our method is efficient to analyze the financial time series irreversibility.

1 Introduction

For a time series $X\left( t \right)$, if the series $\{ X(t_{1} ), \ldots ,X(t_{N} )\}$ and $\{ X(t_{N} ), \ldots ,X(t_{1} )\}$ possess the identical joint probability distribution for any $N$, in other words, if its statistical properties will not change with the reversal of time, this time series will be regarded as reversible time series [1]. Statistically speaking, the reversible time series has the same probability as its reversed time series. From the perspective of physics, the second law of thermodynamics defines the unidirectionality of time for the first time. Time irreversibility means that when time is reversed, the system cannot return to the past state. The stationary transformations of some nonlinear sequences, Gaussian linear processes and Fourier transform substitutions of Gaussian processes all belong to reversible processes. On the contrary, the irreversibility of time series means that the given dynamic system has nonlinear properties, which is related to dissipative chaos and non-Gaussian stochastic processes [2, 3].

In the past few decades, many different irreversible measures have been proposed [4,5,6,7,8,9,10,11,12,13,14,15]. However, on the one hand, the reversibility test of time series can merely analyze the irreversibility of time series qualitatively rather than quantitatively. On the other hand, most of the studies mainly focus on the irreversibility of time series in the low-dimensional phase space at a single scale. Therefore, researchers have gradually proposed some statistics which can be used to quantitatively measure irreversibility and extended the irreversible measurement index to high-dimensional and multiscale analysis [16,17,18,19,20,21,22]. At present, researchers believe that the time series irreversibility can reflect the dynamic characteristics of the system and the directionality of time series; they also find that the irreversibility is related to physical dissipation [23, 24]. An effective method to characterize it is the Kullback–Leibler divergence $\left( {KLD} \right)$[25]. Later, some methods, which measure time series irreversibility by using the difference of probability distribution between positive and inverse order, were proposed one after another [26,27,28,29]. Lacasa et al. mapped the time series into a network and applied $KLD$ to estimate the irreversibility of the univariate time series [30]. By comparing the degree distributions of positive and inverse time series, the level of irreversibility of this time series was reflected. Theoretically, the visibility graph provides a new method to characterize time series and this method does not need to set up the symbolic conditions in advance. It has been extended and applied to the financial field [31, 32], fluid dynamics [33, 34] and medical research [35]. However, this method is not suitable for multivariate time series.

Since the algorithm of mapping a time series into a complex network and using graph theory to explore the characteristics of time series, most researches have focused on the analysis of univariate time series. What is exciting is that Ren et al. [36] proposed the vector visibility graph $\left( {VVG} \right)$ for multivariable time series, which provides a way to transform the multivariable time series into a directed complex network. As an effective method to convert a multivariate time series into a graph, $VVG$ is a practical tool to analyze multivariate time series from the perspective of graph theory. The multivariate time series are mapped into a directed complex network, while each multidimensional data vector is regarded as one node and the visibility between the corresponding data vectors determines the connection of the network. According to these facts, we propose the directed vector visibility algorithm. The multivariate time series are mapped into a graph, and the properties of the association graph are analyzed. More accurately, we apply the $KLD$, which is calculated by the $ingoing$ and $outgoing$ degree distributions of the time series, to measure the time series irreversibility. Based on the numerical results, we confirm that it is a convenient and powerful method to measure the irreversibility of time series.

The rest of the paper is arranged as follows. Section 2 shows the methods of the directed vector visibility graph, the $KLD$ and provides a simple proof of this method for uncorrelated stochastic series. Later, we introduce the multiscale method and give the definition of $KLD_{\tau }$. In Sect. 3 , we apply the new proposed method to analyze several different classes of processes and verify its validity. Section 4 first introduces some other statistics and then displays the practical application of financial time series. Finally, the conclusions are given in Sect. 5 .

2 Methodology

2.1 2.1 Directed vector visibility graph

Visibility algorithm family is a set of methods which convert time series into networks on the basis of geometric criteria [37, 38]. The principle of these methods is to map the information contained in time series into another mathematical structure, so that the effective tools of graph theory can be applied to describe time series from the different angle.

Here, we use the algorithms of horizontal visibility graph [38] and vector visibility graph [36] for reference and introduce the new method, which is defined as follows:

For a $m$-dimensional time series $X_{t} = \{ x_{t}^{i} \}_{i = 1}^{m}$ and the length of each dimension is N, map the multivariate time series into a vector space, then we will gain a sequence of vectors $\left\{ {\vec{X}_{t} } \right\}$, where $\vec{X}_{t} = [x_{t}^{1} , x_{t}^{2} , \ldots x_{t}^{m}$]. For any two vectors ($\vec{X}_{a} {\text{ and }}\vec{X}_{b}$) in the vector sequence, the projection from $\vec{X}_{a} {\text{ to }}\vec{X}_{b}$ is defined as follows:

$$\left| {\left| {\vec{X}_{b}^{a} } \right|} \right| = \frac{{\mathop \sum \nolimits_{i = 1}^{m} x_{a}^{i} x_{b}^{i} }}{{\sqrt {\mathop \sum \nolimits_{i = 1}^{m} x_{a}^{i} x_{a}^{i} } }}$$

(2.1)

and $\left| {\left| {\vec{X}_{a} } \right|} \right| = \sqrt {\mathop \sum \limits_{i = 1}^{m} x_{a}^{i} x_{a}^{i} }$. Each vector in the vector sequence is regarded as one node in the network, and the visibility criteria for vectors can be shown as follows:

Any two vectors $\vec{X}_{a} {\text{ and }}\vec{X}_{b}$ will he the directed visibility from $\vec{X}_{a} {\text{ to }}\vec{X}_{b}$, if the arbitrary vector $\vec{X}_{c}$ situated between them fulfills:

$$\left| {\left| {\vec{X}_{a} } \right|} \right|,\left| {\left| {\vec{X}_{b}^{a} } \right|} \right| > \left| {\left| {\vec{X}_{c}^{a} } \right|} \right|$$

(2.2)

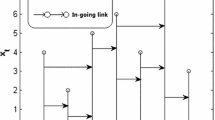
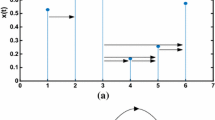
where $t_{a} < t_{c} < t_{b}$,$\left| {\left| {\vec{X}_{b}^{a} } \right|} \right|$ and $\left| {\left| {\vec{X}_{c}^{a} } \right|} \right|$ is the projection from $\vec{X}_{b}$ and $\vec{X}_{c}$ to $\vec{X}_{a}$. Then, we obtain a directed link from the node standing for $\vec{X}_{a}$ to the node standing for $\vec{X}_{b}$ in the network. Therefore, the directed complex network named directed vector visibility graph $\left( {DVV_{g} } \right)$ can be defined. The number of connections of node $t$ linked to other past nodes $t^{^{\prime}} \left( {t^{\prime } < t} \right)$ is expressed by the $ingoing$ degree $k_{{{\text{in}}}} \left( t \right)$. On the contrary, the number of connections of node $t$ linked to other future nodes $t^{\prime } \left( {t^{\prime \prime } > t} \right)$ is expressed by the $outgoing$ degree $k_{{{\text{out}}}} \left( t \right)$. The degree $k\left( t \right)$ of the node $t$ includes these two parts: the $ingoing$ degree $k_{{{\text{in}}}} \left( t \right)$ and the $outgoing$ degree $k_{out} \left( t \right)$, that is to say, $k\left( t \right) = k_{in} \left( t \right) + k_{out} \left( t \right)$.

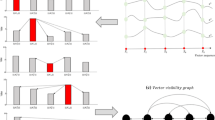
Figure 1 displays the procedures from the multivariate time series to its $DVV_{g}$. The degree distribution of the $DVV_{g}$ refers to the probability of any node with degree $k$. The $outgoing$ and $ingoing$ degree distributions of a $DVV_{g}$ are, respectively, defined as the probability distributions of $k_{{{\text{out}}}}$ and $k_{{{\text{in}}}}$, where $P_{{{\text{out}}}} \left( k \right) \equiv P\left( {k_{{{\text{out}}}} = k} \right)$ and $P_{{{\text{in}}}} \left( k \right) \equiv P\left( {k_{{{\text{in}}}} = k} \right)$.

Fig. 1

Procedures from the multivariate time series ($m = 3,N = 5$) to a directed vector visibility graph. a Each vector corresponds to a node after mapping the time series into the vector space. b The link from a node to others is determined on the basis of the visibility criteria between vectors. c The corresponding directed vector visibility graph

2.2 Kullback–Leibler divergence via ${\text{ DVV}}_{g}$

The premise of the work is that the information contained in the $ingoing$ and $outgoing$ degree distributions can indicate the irreversibility of time series. More accurately, this can be determined by the distance between the $ingoing$ and $outgoing$ degree distributions in the first-order approximation.

The distance between the $ingoing$ and $outgoing$ degree distributions can be shown by the Kullback–Leibler divergence $\left( {KLD} \right)$[25]. In information theory, $KLD$ (or known as relative entropy) is proposed as an asymmetric measure of the difference between two probability distributions. Given the random variable $x$ with two probability distributions $p\left( x \right)$ and $q\left( x \right)$, $KLD$ with $p\left( x \right)$ and $q\left( x \right)$ is given as follows:

$${\text{KLD}}\left( {{\text{pq}}} \right) = \mathop \sum \limits_{x \in X} p\left( x \right)\log \frac{p\left( x \right)}{{q\left( x \right)}}$$

(2.3)

which is equal to zero if and only if the two probability distributions $p\left( x \right)$ and $q\left( x \right)$ are equal. Otherwise, the ${\text{ KLD }}$ is greater than zero.

Theoretically, the information contained in the $outgoing$ degree distribution $k_{{{\text{out}}}}$ is enough to distinguish the reversible time series from the irreversible ones. The probability corresponding to the $outgoing$ degree distribution of the time-reversed time series is equal to the probability corresponding to the $ingoing$ degree distribution of the actual process, that is to say, $P_{{k_{{{\text{out}}}} }} (k\left| {\left\{ {X\left( t \right)} \right\}_{t = N, \ldots ,1} )} \right. = P_{{k_{in} }} (k\left| {\left\{ {X\left( t \right)} \right\}_{t = 1, \ldots ,N} )} \right.$. The $KLD$ between $P_{{{\text{out}}}} \left( k \right)$ and $P_{{{\text{in}}}} \left( k \right)$ is written as:

$$D\left[ {P_{out} \left( k \right)P_{in} \left( k \right)} \right] = \mathop \sum \limits_{k} P_{out} \left( k \right)\log \frac{{P_{out} \left( k \right)}}{{P_{in} \left( k \right)}}$$

(2.4)

${\text{KLD }}$ is equal to zero, if and only if, the probability distribution of both the $ingoing$ and the $outgoing$ degrees of the series is the same, i.e., $P_{{{\text{in}}}} \left( k \right) = P_{{{\text{out}}}} \left( k \right)$. Otherwise, it is positive. The time series is reversible if and only if $P_{{k_{{{\text{in}}}} }} (k\left| {\left\{ {X\left( t \right)} \right\}_{t = 1, \ldots ,N} )} \right. = P_{{k_{in} }} (k\left| {\left\{ {X\left( t \right)} \right\}_{t = N, \ldots ,1} ) = P_{{k_{out} }} (k\left| {\left\{ {X\left( t \right)} \right\}_{t = 1, \ldots ,N} )} \right.} \right.$, that is, the distribution of $ingoing$ degree is the same as that of $outgoing$ degree. In other words, if the ${\text{KLD }}$ between the $ingoing$ and $outgoing$ degree distributions gradually inclines to zero with the increase in series size, it means that the time series is reversible. However, if the ${\text{KLD }}$ converges to a finite positive value, the time series is considered to be irreversible. Different from other measures applied to evaluate the irreversibility of time series [27, 39,40,41], the ${\text{KLD }}$ has the statistical significance. Concretely, $KLD$ is a measure of “distinguishability.” The more distinguishable $P_{{{\text{out}}}} \left( k \right)$ and $P_{{{\text{in}}}} \left( k \right)$ are from each other, the more the $KLD$ deviates from 0, which means that the time series is more irreversible. Therefore, we use the value of ${\text{KLD }}$ to reflect the degree of irreversibility of the time series.

Most of the previous methods for estimating the irreversibility of time series generally started with a local symbolization of the sequence, and the occurrences of word from the forward- and reverse-symbolized series are statistically analyzed [42, 43]. As a result, the irreversibility of time series is related to the difference between the word statistics of the forward- and reverse-symbolized series. If we only take advantage of the information contained in the series $\left\{ {k_{{{\text{out}}}} \left( t \right)} \right\}_{t = 1, \ldots ,N}$ and $\left\{ {k_{{{\text{in}}}} \left( t \right)} \right\}_{t = 1, \ldots ,N}$, $KLD$ can also be regarded as a symbolization. Nevertheless, unlike other methods, this method does not need specific parameters and considers the global information. From a statistical mechanics point of view, ${\text{KLD}}$ can not only determine the irreversibility of the time series obtained from the non-equilibrium processes, but also can be used to measure its average entropy production [2, 17, 44,45,46].

Next, we give a simple proof of our proposed algorithm. Here, we only show the $ingoing$ and $outgoing$ degree distributions obtained from the uncorrelated stochastic series and confirm that they are equal under the condition of infinite size series.

Theorem

Let $X_{t} = \{ x_{t}^{i} \}_{i = 1,t = - \infty , \ldots ,\infty }^{m}$ be a bi-infinite vector sequence of independent and identically distributed random variables obtained from the continuous probability density $f\left( {x^{1} ,x^{2} , \ldots ,x^{m} } \right)$. Then, the distribution of both the $ingoing$ and the $outgoing$ degrees of its ${\text{DVV}}_{g}$ are.

$$P_{{{\text{in}}}} \left( k \right) = P_{{{\text{out}}}} \left( k \right) = \left( {1/2} \right)^{k} ,k = 1,2,3, \ldots$$

(2.5)

Proof

For the convenience of proof, we choose $m = 3.$ Let $X_{0}$ be an arbitrary datum. The probability that the vector visibility of $X_{0}$ is interrupted by the datum $X_{1}$ on its right is independent of $f\left( {x^{1} ,x^{2} ,x^{3} } \right),$

$$\begin{aligned} \Phi_{1} & = \int {\int {\int\limits_{ - \infty }^{\infty } {f\left( {x_{0}^{1} ,x_{0}^{2} ,x_{0}^{3} } \right)dx_{0} } } } \int {\int {\int\limits_{{x_{0}^{1} x_{1}^{1} + x_{0}^{2} x_{1}^{2} + x_{0}^{3} x_{1}^{3} > \mathop \sum \limits_{i = 1}^{3} \left( {x_{0}^{i} } \right)^{2} }}^{\infty } {f\left( {x_{1}^{1} ,x_{1}^{2} ,x_{1}^{3} } \right)} } } dx_{1} \\ = \int {\int {\int\limits_{ - \infty }^{\infty } {f\left( {x_{0}^{1} ,x_{0}^{2} ,x_{0}^{3} } \right)} } } \left[ {1 - F\left( {x_{0}^{1} ,x_{0}^{2} ,x_{0}^{3} } \right)} \right]dx_{0} = \frac{1}{2}, \\ \end{aligned}$$

where

$$F\left( {x_{0}^{1} ,x_{0}^{2} ,x_{0}^{3} } \right) = \int {\int {\int\limits_{ - \infty }^{{\sqrt {\mathop \sum \limits_{i = 1}^{3} \left( {x_{0}^{i} } \right)^{2} } }} {f\left( {x^{1} ,x^{2} ,x^{3} } \right){\text{d}}x} } }$$

The probability $P\left( k \right)$ of the datum $X_{0}$ being able to see $k$ data accurately can be established as

$$P\left( k \right) = Q\left( k \right)\Phi_{1} = \frac{1}{2}Q\left( k \right),$$

(2.6)

where $Q\left( k \right)$ is the probability of $X_{0}$ at least seeing $k$ data. $Q\left( k \right)$ can be recurrently computed by

$$Q\left( k \right) = Q\left( {k - 1} \right)\left( {1 - \Phi_{1} } \right) = \frac{1}{2}Q\left( {k - 1} \right),$$

(2.7)

Because the arbitrary datum $X_{0}$ can see at least the first adjacent node to its right, $Q\left( 1 \right) = 1$. The following expression can be got

$$Q\left( k \right) = \left( \frac{1}{2} \right)^{k - 1},$$

(2.8)

which together with Eq. (2.6) derives the proof. A similar derivation makes available for the ingoing case.

It is worth noting that the above result is not affected by the probability density $f\left( {x^{1} ,x^{2} , \ldots ,x^{m} } \right)$. It holds not only for Gaussian or uniform distribution time series, but also for arbitrary independent and identically distributed random variables with a continuous distribution $f\left( {x^{1} ,x^{2} , \ldots ,x^{m} } \right)$.

2.3 ${KLD}_{\tau }$of multivariate multiscale time series

In order to better understand the intrinsic characteristics of multivariate system, we introduce the multiscale method. Given a $m$-dimensional time series ${X}_{t}=$ with the length of each dimension equaling to $N$, we define ${\text{KLD}}_{\tau }$ as follows:

Step 1 For the scale factor $\tau$, the original time series is divided into non-overlapping windows of length $\tau$[14]. We gain the coarse-grained $m$-dimensional time series $Y_{k}^{\tau } = y_{{i,k_{i} = 1}}^{\tau m}$ as

$$y_{j,k}^{\tau } = \frac{1}{\tau }\mathop \sum \limits_{{t = \left( {k - 1} \right)\tau + 1}}^{k\tau } x_{t}^{i} ,1 \le k \le \frac{N}{\tau }$$

(2.9)

Step 2 Get the $DVV_{g}$ transformed from the coarse-grained $m$-dimensional time series $Y_{k}^{\tau }$.

Step 3 Compute the ${\text{KLD}}_{\tau }$ by the $ingoing$ and $outgoing$ degree distributions corresponding to the $DVV_{g}$.

3 Analyses and results of synthetic data

In this section, we choose several types of systems: uncorrelated stochastic series, correlated stochastic series, dissipative chaotic systems and conservative chaotic systems, to evaluate the degree of irreversibility of their multivariate time series by our new proposed method and Table 1 contains the numerical results.

• (a) Uncorrelated stochastic series

• (b) Three-dimensional random series

Here, we generate a trivariate time series, where all the data channels are observations of mutually independent time series extracted from the uniform distribution $U\left[ {0,1} \right]$.

• (b) Correlated stochastic series

• (c) Two-dimensional time series generated by normal distribution

Table 1 Values of the KLD corresponding to time series of 0.7 × 10⁵ data generated by reversible and irreversible processes

In order to obtain the correlated stochastic series, we consider the bivariate normal distribution $N\left( {0,0,1,2,0.8} \right)$ as an example of linearly correlated stochastic processes.

• (c) Dissipative Chaotic systems

• (3) Chen system [47]

  $$\left[ \begin{gathered} x^{\prime} = a\left( {y - x} \right) \hfill \\ y^{\prime} = \left( {c - a} \right)x - xz + cy \hfill \\ z^{\prime} = xy - bz \hfill \\ \end{gathered} \right.$$

  (3.1)

Parameter values: $a = 35, b = 3$ and $c = 28$;

initial conditions: $x_{0} = 0,y_{0} = 1.001$ and $z_{0} = 0$.

• (4) Duffing system [48]

  $$\left[ \begin{gathered} x^{\prime} = y \hfill \\ y^{\prime} = - x - x^{3} - ky + f\cos z \hfill \\ z^{\prime} = 1 \hfill \\ \end{gathered} \right.$$

  (3.2)

Parameter values: $k = 0.1$ and $f = 80$;

initial conditions: $x_{0} = 0,y_{0} = 0$ and $z_{0} = 1$.

• (5) Holmes–Duffing system [48]

  $$\left[ \begin{gathered} x^{\prime} = y \hfill \\ y^{\prime} = x - x^{3} - ky + f\cos z \hfill \\ z^{\prime} = 1 \hfill \\ \end{gathered} \right.$$

  (3.3)

Parameter values: $k = 0.1$ and $f = 80$;

initial conditions: ${x}_{0}=0,{y}_{0}=0$ and ${z}_{0}=1$.

• (6) Lorenz system [49]

  $$\left[ \begin{gathered} x^{\prime} = s\left( {y - x} \right) \hfill \\ y^{\prime} = rx - y - xz \hfill \\ z^{\prime} = xy - bz \hfill \\ \end{gathered} \right.$$

  (3.4)

Parameter values: $s = 10, r = 28$ and $b = 8/3$;

initial conditions: $x_{0} = 10,y_{0} = 1$ and $z_{0} = 0$.

• (7) L $\ddot{u}$ system [50]

  $$\left[ \begin{gathered} x^{\prime} = a\left( {y - x} \right) \hfill \\ y^{\prime} = - xz + cy \hfill \\ z^{\prime} = xy - bz \hfill \\ \end{gathered} \right.$$

  (3.5)

Parameter values: $a = 36, b = 3$ and $c = 20$;

initial conditions: $x_{0} = 0,y_{0} = 1.001$ and $z_{0} = 0$.

• (8) R $\ddot{o}$ ssler system [51]

  $$\left[ \begin{gathered} x^{\prime} = - y - z \hfill \\ y^{\prime} = x + ay \hfill \\ z^{\prime} = b + z\left( {x - c} \right) \hfill \\ \end{gathered} \right.$$

  (3.6)

Parameter values: $a = 0.2, b = 0.4$ and $c = 5.7$;

initial conditions: $x_{0} = 1,y_{0} = 0$ and $z_{0} = 0$

• (d) Conservative Chaotic systems

(9) Sprott-A system [52]

$$\left[ \begin{gathered} x^{\prime} = y \hfill \\ y^{\prime} = - x + yz \hfill \\ z^{\prime} = 1 - y^{2} \hfill \\ \end{gathered} \right.$$

(3.7)

initial conditions: $x_{0} = 0.1,y_{0} = 0.1$ and $z_{0} = 0.1$.

Figure 2 shows the $ingoing$ and $outgoing$ degree distributions of the $DVV_{g}$ corresponding to the multivariate time series with the size $N = 0.7 \times 10^{5}$. We can discover that expect the time series from the Lorenz system, their $ingoing$ and $outgoing$ degree distributions are almost indistinguishable. And their specific numerical values of $KLD$ are given in Table 1 and each of them is very close to 0. It indicates that these time series, which are generated from uncorrelated stochastic series, correlated stochastic series and conservative chaotic systems, respectively, are all reversible time series. And those time series generated from dissipative chaotic systems are irreversible.

Fig. 2

The ingoing and outgoing degree distributions of the DVVg corresponding to the multivariate time series of $0.7 \times 10^{5}$ data points from: a the uniform distribution $U\left[ {0,1} \right]$; b the two-dimensional normal distribution $N\left( {0,0,1,2,0.8} \right);$ c the Lorenz system; d the Sprott-A system $.$

The change of $KLD$ corresponding to different multivariate time series with gradually increasing series size $N$ is plotted in Fig. 3. With the increase in series size, the $KLD$ of reversible time series tends to zero, while the $KLD$ of irreversible time series converges to a positive value. Therefore, we can say that the deviation between $KLD$ of reversible time series and zero is caused by the finite size effect.

Fig. 3

Semi-log plot of KLD of the graph corresponding to the multivariate time series as a function of the series size N (points are the average of several realizations). a the uniform distribution$U\left[ {0,1} \right]$; b the two-dimensional normal distribution $N\left( {0,0,1,2,0.8} \right)$$;$c the Lorenz system; d the Sprott-A system $.$

In fact, the research on the influence of series length to $KLD$ is similar to the multiscale analysis of time series, but the structure of the coarse-grained time series may be different from that of the original time series. Therefore, the $KLD_{\tau }$ of coarse-grained sequence obtained from the original sequence on a large scale is different from that of a short sequence segment of the real original sequence. Figure 4 exhibits the $KLD_{\tau }$ of nine simulation series with the length of $N = 10^{4}$ on scale $\tau \in \left[ {1,20} \right]$. For uncorrelated stochastic series, correlated stochastic series and conservative chaotic systems, their $KLD_{\tau }$ increases slightly with the increase in scale $\tau,$ respectively, but each of them is still very close to 0 on any scale. For dissipative chaotic systems, their $KLD_{\tau },$ respectively, shows the downward trend with the increase in scale $\tau$ and tends to 0. However, the change trend of $KLD_{\tau }$ with the increase in scale $\tau$ is different from that obtained from simply shortening the length of time series. Therefore, we can consider that the coarse-grained process changes the internal structure of the system, which may have an influence on the degree of its internal irreversibility. Nevertheless, for the reversible time series, even if the coarse-grained process changes the internal structure of the system, the coarse-grained sequence is still in a random state, so it is still reversible.

Fig. 4

Irreversibility measures $KLD_{\tau }$ of nine simulated series as a function of $\tau$ with $\tau \in \left[ {1,20} \right].$

4 Analyses and results of financial time series

Stock markets reflect the development of the national economy and also display the economic development and social stability of countries. The commonly used parameters to reflect the fluctuation of stock market are stock trading price and stock trading volume. Here, we use the proposed new irreversible method to analyze the financial time series. The daily closing price and volume of twenty-one stock indices from 2005 to 2019 are gathered from the Web site https://finance.yahoo.com/, and these stock indices are divided into three different regions: Americas, Europe and Asia & Pacific. The exact information of 21 stock indices is shown in Table 2.

Table 2 World stock indices

Because of the non-stationarity of financial time series, we remove the unwanted data firstly and then use logarithmic price difference as proxies for volatility of stock indices, which is given by

$$x_{n} = \log (S_{n} ) - \log (S_{n - 1} )$$

(4.1)

where $S_{n}$ is the closing price of $n$ th trading day.

For volume, we firstly standardize the data to maintain data consistency. Next, we also select the logarithmic volume difference to handle the standardized data for the sake of weakening the diversity between them.

So as to precisely measure the time irreversibility, we provide Score [s], which is the average of the annual irreversibility value to assess the time irreversibility of a given stock index $s$[53].

$${\text{Score}}\left[ s \right] = \frac{1}{15}\mathop \sum \limits_{{{\text{year}} = 2005}}^{2019} {\text{KLD}}_{{{\text{year}}}}^{s}$$

(4.2)

Furthermore, we calculate several other statistics of the irreversibility. The standard deviation $sd$ is established as

$${\text{sd}} = \left( {\frac{1}{14}\mathop \sum \limits_{{{\text{year}} = 2005}}^{2019} ({\text{KLD}}_{{{\text{year}}}} - \overline{{{\text{KLD}}}} )^{2} } \right)^{\frac{1}{2}}$$

(4.3)

where

$${ }\overline{{{\text{KLD}}}} = \frac{1}{15}\mathop \sum \limits_{{{\text{year}} = 2005}}^{2019} {\text{KLD}}_{{{\text{year}}}}$$

(4.4)

And the coefficient of variation C_v is given by

$$C_{v} = \frac{{\text{ sd}}}{{\overline{{{\text{KLD}}}} }}$$

(4.5)

the third central moment $v_{3}$ is defined as

$$v_{3} = \frac{1}{15}\mathop \sum \limits_{{{\text{year}} = 2005}}^{2019} ({\text{KLD}}_{{{\text{year}}}} - \overline{{{\text{KLD}}}} )^{3}$$

(4.6)

the skewness $\beta_{s}$ is expressed as

$$\beta_{s} = \frac{{v_{3} }}{{{\text{sd}}^{3} }}$$

(4.7)

In the synthetic data analysis, we find that $KLD$ can distinguish the irreversible multivariate time series from the reversible ones. However, it can be realized that in the process of financial time series analysis, it cannot well reflect the irreversibility of these multivariate time series as shown in Fig. 5. Here, we only give three different stock markets, respectively, from Americas, Europe and Asia & Pacific. The difference between the distribution of their $ingoing$ and $outgoing$ degree is not very obvious. Therefore, we consider using ${\text{KLD}}_{\tau }$ to analyze the irreversibility of stock indices on different scales. Figure 6 illustrates the volatility of ${\text{KLD}}_{\tau }$ of each stock index on scale $\tau \in \left[ {1,10} \right]$. As the scale increases, the coarse-grained time series becomes shorter, and the ${\text{KLD}}_{\tau },$ respectively, shows the increasing trend. However, from the results of synthetic data, we know that the ${\text{KLD}}_{\tau }$ of irreversible time series decreases with the increase in scale and tends to 0, while the ${\text{ KLD}}_{\tau }$ of reversible time series is very close to 0 on any scale. By comparing the results of ${\text{KLD}}_{\tau }$ of the simulated series given in Fig. 4, we can obtain that the value of ${\text{KLD}}_{\tau }$ of each stock index series is relatively small, but it is not strictly close to 0, which is different from that of reversible time series. Therefore, we believe that financial time series are multiscale irreversibility.

Fig. 5

The $ingoing$ and $outgoing$ degree distributions of the ${\text{DVV}}_{g}$ corresponding to the multivariate time series of data points from each region: Americas, Europe and Asia & Pacific

As we can see from Fig. 6, the stock indices from Americas fluctuate sharply at $\tau = 6\& 8$, while the stock indices from Europe fluctuate greatly at $\tau = 7$. However, the stock indices from Asia & Pacific are scattered and it does not fluctuate particularly violently on any scale. These facts are a little different from the situation in Fig. 7, which exhibits the volatility of ${\text{ KLD}}_{\tau }$ averaged for all stock indices from each region on scale $\tau \in \left[ {1,10} \right]$. The curve of world reaches its maximum at $\tau = 7$ and has a significant drop at $\tau = 8$. Except for the curve from Americas, the curves from Europe and Asia & Pacific reach the maximum at $\tau = 7$ and decrease at $\tau = 8$. Curve of Americas shows a downward trend at $\tau = 7\& 8$. Because the statistical characteristics of time series irreversibility can reflect the dynamic characteristics of the system, these facts make us consider periodicity. When we handle the time series with scale factor $\tau = 7$, we regard the information of 7 days as a whole, and the information of the next trading day may be identical with that of the first day. Similarly, the scale factor $\tau = 8$ can also be the periodic signal. Owing to the effect of uncertain factors such as the level of development and system mechanism, the periodicity of different stock markets tends to be distinguishing.

Fig. 6

Irreversibility measures ${\text{KLD}}_{\tau }$ of 21 stock indices as a function of $\tau$ with $\tau \in \left[ {1,10} \right].$

These points obtained from the score and its average annual volatility of the irreversibility corresponding to each stock index are shown in Fig. 8. And the standard deviation of the price log-returns of one year is regarded as the proxy for volatility of stock indices. As is known to all, the degree of stability of financial stock indices is generally reflected by its annual volatility. If the two statistics are related, the points in the scatter plot will tend to a smooth curve rather than being as scattered as the plot showing here. Therefore, we can come to a conclusion from Fig. 8 that there is no correlation between the irreversibility and volatility, which implies that we take the time irreversibility as a new statistical measure to research the properties of financial time series is reasonable. In order to further explore the irreversibility of financial time series, some other statistics, such as the standard deviation ${\text{sd}}$, the coefficient of variation $C_{v}$, the third central moment $v_{3}$ and the skewness $\beta_{s}$ are computed.

Fig. 7

Irreversibility measures ${\text{KLD}}_{\tau }$ $C_{{{\text{MMJS}}}}$ $C_{{{\text{MMJS}}}}$ averaged over all the stock indices from each region: Americas, Europe and Asia & Pacific

Figure 9 presents the relation between the coefficient of variation $C_{v}$ and its standard deviation ${\text{sd }}$ of the irreversibility of each stock index. The coefficient of variation is a statistic to measure the variation degree of variables, which is not only impacted by the level of dispersion of variables, but also under the influence of the average of variables. As Fig. 9 shows, the standard deviation of irreversibility approximatively tends to be proportional to the coefficient of variation. It indicates that the average of variables, which is displayed by the average of the annual irreversibility, may have a negligible effect on its coefficient of variation. Consequently, we can replace the standard deviation with the coefficient of variation to explore the potential qualities of financial time series.

Fig. 8

The plot of points generated by the score and its average annual volatility of the irreversibility of each stock index

Figure 10 manifests the points plotted by the skewness $\beta_{s}$ and its third central moment $v_{3}$ of the irreversibility of 21 stock indices, respectively. Skewness is the statistic, which reflects the asymmetry of the probability distribution of a random variable with respect to its mean value. By viewing Fig. 10, it can be realized that the skewness values of most points are between − 0.6 and 1. Besides, the third central moment corresponding to them is less than others and all close to 0. It suggests that the skewness can express the irreversibility alone. Ranking each stock index according to its score, we can discover that the distributions of the points corresponding to the top two stock indices and the bottom one are all outstanding.

Fig. 9

The plot of points generated by the coefficient of variation $C_{v}$ and its standard deviation ${\text{sd }}$ of the irreversibility of each stock index

To better analyze the financial time series, we investigate the irreversibility of all stock indices in different years and plot the points generated by the skewness $\beta_{s}$ and its third central moment $v_{3}$ of the irreversibility of each year in Fig. 11. Due to the essential difference between financial crisis period and economic stable period, we try to make use of the new proposed method to distinguish them. As we all know, one of the most serious financial crises in the history was triggered by the American subprime mortgage crisis in 2007 and the financial crisis broke out in 2008. The global economy began to recover gradually in 2011. As shown in Fig. 11, it is obvious that the two points corresponding to 2007 and 2008 are deviated from most points, but the points of other two years are also distinguished from most of them. In order to make a more detailed analysis, the location of points given by the skewness $\beta_{s}$ and its third central moment $v_{3}$ of each year from three different regions is displayed in Fig. 12.

Fig. 10

The plot of points generated by the skewness $\beta_{s}$. and its third central moment $v_{3}$. of the irreversibility of each stock index

Fig. 11

The plot of points generated by the skewness $\beta_{s}$ and its third central moment $v_{3}$ of the irreversibility of different years

Fig. 12

The plots of points generated by the skewness $\beta_{s}$ and its third central moment $v_{3}$ of the irreversibility of different years from each region: Americas, Europe and Asia & Pacific

From Fig. 12, we realize that 2015 is a special year for Americas and Asia & Pacific, while for Europe, 2012 presents different characteristics from other years. As a matter of fact, the stock indices from Americas, such as $BVSP$,$GSPTSE$ and $RUT$, did show greater volatility in 2015 than in other years, while $DJI$ and $GSPC$ from Americas did not show significant fluctuations in the whole year, but both had pretty large fluctuations in several months. And the stock indices from Asia & Pacific, such as $N225$, $BSESN$,$SSE$ and $HSI$, all fluctuated sharply from 2014 to 2015. For the whole stock indices from Europe, they were basically in a sustained upward phase in 2012.

5 Conclusions

In this paper, we introduce a new method to measure the irreversibility of multivariate time series. By mapping multivariate time series into the directed vector visibility graph $\left( {{\text{DVV}}_{g} } \right)$, we measure the level of irreversibility of the time series by using the value of Kullback–Leibler divergence ${ }\left( {{\text{KLD}}} \right)$, which is calculated by the $ingoing$ and $outgoing$ degree distributions corresponding to the ${\text{DVV}}_{g}$.

In order to validate the effectiveness of this method, we select uncorrelated stochastic series, correlated stochastic series, dissipative chaotic systems and conservative chaotic systems, and evaluate the degree of irreversibility of their multivariate time series. The results show that when the time series is reversible, their $ingoing$ and $outgoing$ degree distributions are almost indistinguishable and their specific numerical values of ${\text{KLD }}$ are all very close to 0. The deviation between the ${\text{KLD }}$ of reversible time series and zero is caused by the finite size effect, while the irreversible time series converges to an asymptotical nonzero positive value with the increase in series size.

Later, to further investigate the internal structure of the system, we utilize the multiscale method to analyze the irreversibility of time series. For the reversible time series, their ${\text{KLD}}_{\tau }$ are close to 0 at all scales, while the ${\text{KLD}}_{\tau }$ of irreversible time series decreases and tends to 0 with the increase in scale. Therefore, we consider that the coarse-grained process changes the internal structure of the system, which may have an influence on the degree of its internal irreversibility. However, for the reversible time series, even if the coarse-grained process changes the internal structure of the system, the coarse-grained time series is still in a random state and its irreversibility is low.

Finally, this method is applied to stock markets. We choose 21 stock indices and, respectively, divide them into three groups on account of different regions. Through experimental analysis, we believe that the financial time series are multiscale irreversibility. To better evaluate the irreversibility of financial time series, we introduce some other statistics and recognize that the new method can be used to identify the special financial periods.

On the whole, the new irreversible method is an effective way to measure the irreversibility of multivariate time series.