1 Introduction

The advent of gradation technique in materials initiated the beginning of an era of advanced class of structural materials known as functionally graded (FG) materials [1,2,3,4,5,6,7,8,9]. Being free of the disadvantages that conventional laminated composite materials suffer from, FG materials possess outstanding characteristics such as high ratio of strength and stiffness to weight, high thermal resistance, low maintenance cost. Functionally graded structures such as beams [10] and plates [11,12,13,14] can be divided into two groups, depending on the gradient variation being through the thickness or along the length. For the latter case, i.e. the axial functionally graded (AFG) beams, the variation of material properties (density and elastic modulus) along the length of the beam are governed by specified functions. In addition to the non-uniform mechanical properties, an AFG beam can possess a varying cross-sectional area, i.e. it can be tapered along its length. These features allow the utilisation of AFG tapered beams in many mechanical and civil engineering applications, as well as automotive and robotic industries.

The complex behaviour of beams made up of FG materials has attracted the attention of engineers and researchers in the last decades. The main body of the literature is dedicated to FG beams which are graded along the thickness. The analysis of the AFG beams, on the other hand, is a relatively newer field; in what follows, only the investigations on AFG beams are reviewed. Linear and nonlinear studies are the two common class of studies conducted on the vibrations of AFG beams. The literature on the first class (i.e. linear analysis) is quite large; however, the studies on nonlinear AFG beams are limited.

Starting with linear investigations in the literature, Huang and Li [15] presented a new approach for the free vibration analysis of AFG beams; they examined transverse vibrations and the natural frequencies. In another study, Hein and Feklistova [16] examined the free oscillations of AFG beams and obtained their natural frequencies of making use of Haar wavelets by neglecting the axial vibrations. The transverse forced oscillations of an AFG beam when subjected to a moving load were examined by Şimşek et al. [17], who obtained the vibration amplitude versus the moving force frequency. The Timoshenko beam theory was employed by Huang et al. [18] in order to analyse the effect of different boundary conditions on the natural frequencies of AFG beams. Rajasekaran [19] employed the differential quadrature technique along with a differential transformation for the free oscillation analysis of AFG beams which resulted in the evaluation of natural frequencies. A closed-form solution for vibration behaviour of AFG Timoshenko beam was developed by Sarkar and Ganguli [20], who provided the results for a fixed–fixed beam. Both the forced and free linear vibrations of AFG Timoshenko beam resting on a viscoelastic foundation were investigated by Calim [21].

Fig. 1
figure 1

Schematic representation of an axially functionally graded tapered beam subject to distributed static and dynamic loads in the transverse direction

Full size image

Extension of the investigations to include nonlinearities was performed in few studies. Shahba et al. [22] examined the stability (buckling) and free transverse vibrations of AFG Timoshenko tapered beam. Kein [23] developed the couple equations of motion of a tapered AFG beam and obtained the static bending behaviour. The nonlinear natural frequencies of a vibrating AFG beam were obtained by Kumar et al. [24] via a free vibration analysis. The nonlinear free vibrations of an AFG microscale beam was investigated by Şimşek [25], utilising He’s variational method. In another study, Shafiei et al. [26] used the method of the generalised differential quadrature method and direct iterative method to examine the nonlinear free oscillations of a non-uniform AFG microscale beam.

The current study is the first which conducts a nonlinear forced transverse-longitudinal static and dynamic analysis of a nonlinear AFG Euler–Bernoulli beam. To this end, the nonlinear equations of motion in transverse and longitudinal directions are derived with the aid of Hamilton’s principle. Sufficient number of symmetric and asymmetric modes are considered in the Galerkin discretisation procedure in order to ensure converged results. A well-optimised numerical scheme is developed to handle the complex high-dimensional system with different sources of nonlinearities arising from large deformation of the beam, non-uniform distribution of material properties, and non-uniform cross section. The fundamental natural frequency of the system is obtained and compared with published results in the literature. Extensive numerical simulations are conducted to highlight the effect of different system parameters on the nonlinear static and dynamic characteristics of the system; the importance of employing a high-dimensional is also highlighted. For the first time, the nonlinear static and dynamic asymmetric responses of the system are investigated. The results are presented in the form of nonlinear static deflection curves as well as nonlinear frequency–amplitude diagrams.

2 Equations of motion and method of solution

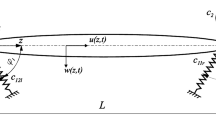
An extensible AFG tapered beam subject to a distributed harmonic excitation load is shown in Fig. 1, with the axial coordinate x and the transverse one z; y denotes the direction of the width of the beam. The beam is of length L, the constant thickness h, and a varying width b(x), associated with the tapered geometry, resulting in varying second area moment I(x) and the cross-sectional area A(x). Furthermore, the material properties of the beam such as the density \(\rho (x)\) and the modulus of elasticity E(x) vary along the longitudinal direction (i.e. x-axis), from a material 1 at the left-hand end to material 2 at the right-hand end. The beam exhibits two motions, namely the transverse motion denoted by w(x, t) and the longitudinal one represented by \(u(x, t)-t\) represents time. Furthermore, an external load in the form of \(F_0 \left( x \right) +F_1 \left( x \right) \cos \left( {\omega t} \right) \) is applied to the AFG beam in the transverse direction, with \(\omega \) being the forcing frequency, \(F_{1}(x)\) being the dynamic forcing amplitude, and \(F_{0}(x)\) being the static forcing amplitude.

As already mentioned, it is assumed that the geometrical and the material properties of the AFG beam vary exponentially and continuously along the longitudinal direction; in the present study, these parameters are governed by the following expressions

$$\begin{aligned} E\left( x \right)= & {} (E_{R} -E_{L} )\left( \frac{x}{L}\right) ^{n}+E_{L},\nonumber \\ \rho \left( x \right)= & {} (\rho _{R} -\rho _{L} ) \left( \frac{x}{L}\right) ^{n}+\rho _{L},\nonumber \\ b\left( x \right)= & {} (b_{R} -b_{L} ) \left( \frac{x}{L}\right) ^{n}+b_{L},\nonumber \\ h_{R}= & {} h_{L} =h, \end{aligned}$$
(1)

where L and R subscripts correspond to the values of parameters at the left and right ends of the beam, respectively; n represents the gradient index which determines the variation profile along the length of the beam.

Employing the Euler–Bernoulli beam theory, the displacement field components of a generic point in the beam, represented by \(u_x\), \(u_y\), and \(u_z\), in the x, y and z directions, respectively, can be written as

$$\begin{aligned} u_x \left( {x,z,t} \right)= & {} u\left( {x,t} \right) -z\frac{\partial w\left( {x,t} \right) }{\partial x},\nonumber \\ u_y \left( {x,z,t} \right)= & {} 0,\nonumber \\ u_z \left( {x,z,t} \right)= & {} w\left( {x,t} \right) . \end{aligned}$$
(2)

The axial strain is given by

$$\begin{aligned} \varepsilon _{{\textit{xx}}} =\frac{\partial u}{\partial x}+\frac{1}{2}\left( {\frac{\partial w}{\partial x}} \right) ^{2}-z\frac{\partial ^{2}w}{\partial x^{2}}. \end{aligned}$$
(3)

Hence, the potential energy becomes

$$\begin{aligned} U= & {} \frac{1}{2}\int _V {\left\{ {E\left( x \right) \left[ {\frac{\partial u}{\partial x}+\frac{1}{2}\left( {\frac{\partial w}{\partial x}} \right) ^{2}-z\frac{\partial ^{2}w}{\partial x^{2}}} \right] ^{2}} \right\} \mathrm{d}v} \nonumber \\= & {} \frac{1}{2}\int _0^L \left\{ E\left( x \right) A\left( x \right) \left[ {\frac{\partial u}{\partial x}+\frac{1}{2}\left( {\frac{\partial w}{\partial x}} \right) ^{2}} \right] ^{2}\right. \nonumber \\&\qquad \qquad \left. +E\left( x \right) I\left( x \right) \left[ {\frac{\partial ^{2}w}{\partial x^{2}}} \right] ^{2} \right\} \mathrm{d}x, \end{aligned}$$
(4)

where

$$\begin{aligned} A\left( x \right)= & {} b\left( x \right) h, \nonumber \\ I\left( x \right)= & {} \frac{1}{12}b\left( x \right) h^{3}, \end{aligned}$$
(5)

The kinetic energy of the AFG tapered beam can be formulated as

$$\begin{aligned} KE= & {} \frac{1}{2}\int \limits _v {\rho \left( x \right) \left\{ {\left( {\frac{\partial u}{\partial t}-z\frac{\partial ^{2}w}{\partial t\partial x}} \right) ^{2}+\left( {\frac{\partial w}{\partial t}} \right) ^{2}} \right\} } \mathrm{d}v \nonumber \\= & {} \frac{1}{2}\int _0^L \left\{ \rho \left( x \right) A\left( x \right) \left( {\frac{\partial u}{\partial t}} \right) ^{2}+\rho \left( x \right) I\left( x \right) \left( {\frac{\partial ^{2}w}{\partial t\partial x}} \right) ^{2}\right. \nonumber \\&\qquad \left. +\,\rho \left( x \right) A\left( x \right) \left( {\frac{\partial w}{\partial t}} \right) ^{2} \right\} \mathrm{d}x , \end{aligned}$$
(6)

The virtual work done the damping, with damping coefficient \(c_{d}\), as well as the external force in the transverse direction is obtained by

$$\begin{aligned} \delta W_D= & {} -c_d \int _0^L {\left( {\frac{\partial u}{\partial t}\delta u+\frac{\partial w}{\partial t}\delta w} \right) \mathrm{d}x} . \nonumber \\ \delta W_{{\textit{EF}}}= & {} \int _0^L {\left[ {F_0 \left( x \right) +F_1 \left( x \right) \cos \left( {\omega t} \right) } \right] } \delta w \mathrm{d}x. \end{aligned}$$
(7)

Inserting the expression given in Eqs. (4), (6), and (7) into Hamilton’s principle given by

$$\begin{aligned} \int _{t_1 }^{t_2 } {\left( {\delta {\textit{KE}} -\delta U+\delta W_{{\textit{EF}}} +\delta W_D } \right) } \mathrm{d}t=0, \end{aligned}$$
(8)

and integrating by parts over the length of the AFG tapered beam and time, and setting the coefficients of \(\delta u\) and \(\delta w\) equal to zero, the following partial differential equations governing the motion are obtained

$$\begin{aligned}&\rho \left( x \right) A\left( x \right) \frac{\partial ^{2}w}{\partial t^{2}}-\rho \left( x \right) I\left( x \right) \frac{\partial ^{4}w}{\partial t^{2}\partial x^{2}}+c_d \frac{\partial w}{\partial t}\nonumber \\&\quad -\left[ {f_0 +f_1 \cos \left( {\omega t} \right) } \right] +\frac{\partial ^{2}}{\partial x^{2}}\left[ {E\left( x \right) I\left( x \right) } \right] \frac{\partial ^{2}w}{\partial x^{2}}\nonumber \\&\quad +\,2\frac{\partial }{\partial x}\left[ {E\left( x \right) I\left( x \right) } \right] \frac{\partial ^{3}w}{\partial x^{3}}+E\left( x \right) I\left( x \right) \frac{\partial ^{4}w}{\partial x^{4}} \nonumber \\&\quad -\frac{\partial }{\partial x}\left[ {E\left( x \right) A\left( x \right) } \right] \left[ {\frac{\partial w}{\partial x}\frac{\partial u}{\partial x}+\frac{1}{2}\left( {\frac{\partial w}{\partial x}} \right) ^{3}} \right] \nonumber \\&\quad -E\left( x \right) A\left( x \right) \left[ {\frac{\partial ^{2}w}{\partial x^{2}}\frac{\partial u}{\partial x}+\frac{\partial w}{\partial x}\frac{\partial ^{2}u}{\partial x^{2}}+\frac{3}{2}\left( {\frac{\partial w}{\partial x}} \right) ^{2}\frac{\partial ^{2}w}{\partial x^{2}}} \right] =0, \nonumber \\ \end{aligned}$$
(9)
$$\begin{aligned}&\rho \left( x \right) A\left( x \right) \frac{\partial ^{2}u}{\partial t^{2}}+c_d \frac{\partial u}{\partial t}\nonumber \\&\quad -\frac{\partial }{\partial x}\left[ {E\left( x \right) A\left( x \right) } \right] \left[ {\frac{\partial u}{\partial x}+\frac{1}{2}\left( {\frac{\partial w}{\partial x}} \right) ^{2}} \right] \nonumber \\&\quad -E\left( x \right) A\left( x \right) \left[ {\frac{\partial ^{2}u}{\partial x^{2}}+\frac{\partial ^{2}w}{\partial x^{2}}\frac{\partial w}{\partial x}} \right] =0, \end{aligned}$$
(10)

in which the substitutions \(F_0 \left( x \right) =f_0\) and \(F_1 \left( x \right) =f_1\) are made in Eq. (9); the boundary conditions for the clamped–clamped beam are (at \(x=0, L)\)

$$\begin{aligned} w=0, \frac{\partial w}{\partial x}=0, u=0. \end{aligned}$$
(11)

Considering the geometrical and material characteristics of the left-hand end of the AFG tapered beam as a reference, the following dimensionless parameters are introduced

$$\begin{aligned}&x^{*}=\frac{x}{L}, \left( {w^{*},u^{*}} \right) =\frac{\left( {w,u} \right) }{h},\nonumber \\&A^{*}\left( x \right) =\frac{A\left( x \right) }{A_{L} }, I^{*}\left( x \right) =\frac{I\left( x \right) }{I_{L}}, \nonumber \\&E^{*}\left( x \right) =\frac{E\left( x \right) }{E_{\mathrm{Steel}} }, \rho ^{*}\left( x \right) =\frac{\rho \left( x \right) }{\rho _{\mathrm{Steel}}},\nonumber \\&\eta =\frac{L}{h}, \left( {f_0^*,f_1^*} \right) = \frac{\left( {f_0 ,f_1 } \right) L^{4}}{E_{\mathrm{Steel}} I_{L} h}, \nonumber \\&t^{*}=t\sqrt{\frac{E_{\mathrm{Steel}} I_{L} }{\rho _{\mathrm{Steel}} A_{L} L^{4}}},\nonumber \\&\Omega =\omega \sqrt{\frac{\rho _{\mathrm{Steel}} A_{L} L^{4}}{E_{\mathrm{Steel}} I_{L}}},\nonumber \\&c_d^{*}=c_d \sqrt{\frac{L^{4}}{E_{\mathrm{Steel}} I_{L} \rho _{\mathrm{Steel}} A_{L} }}, \end{aligned}$$
(12)

In which the subscript L stands for the left-hand end. These parameters are substituted into Eqs. (9)–(10) and the asterisk notation is disregarded for brevity; the following nonlinear dimensionless equations for the transverse and longitudinal motions can then be obtained

$$\begin{aligned}&\rho \left( x \right) A\left( x \right) \frac{\partial ^{2}w}{\partial t^{2}} -\frac{1}{12\eta ^{2}}\rho \left( x \right) I\left( x \right) \frac{\partial ^{4}w}{\partial t^{2}\partial x^{2}}\nonumber \\&\quad +\,c_d \frac{\partial w}{\partial t}-\left[ {f_0 +f_1 \cos \left( {\Omega t} \right) } \right] \nonumber \\&\quad +\frac{\partial ^{2}}{\partial x^{2}}\left[ {E\left( x \right) I\left( x \right) } \right] \frac{\partial ^{2}w}{\partial x^{2}}+2\frac{\partial }{\partial x}\left[ {E\left( x \right) I\left( x \right) } \right] \frac{\partial ^{3}w}{\partial x^{3}}\nonumber \\&\quad +\,E\left( x \right) I\left( x \right) \frac{\partial ^{4}w}{\partial x^{4}} \nonumber \\&\quad -12\frac{\partial }{\partial x}\left[ {E\left( x \right) A\left( x \right) } \right] \left[ \eta \frac{\partial w}{\partial x}\frac{\partial u}{\partial x} +\frac{1}{2}\left( {\frac{\partial w}{\partial x}} \right) ^{3} \right] \nonumber \\&\quad -12E\left( x \right) A\left( x \right) \left[ \eta \frac{\partial ^{2}w}{\partial x^{2}}\frac{\partial u}{\partial x}+\eta \frac{\partial w}{\partial x}\frac{\partial ^{2}u}{\partial x^{2}}\right. \nonumber \\&\left. \qquad \qquad \qquad \qquad \qquad +\frac{3}{2}\left( {\frac{\partial w}{\partial x}} \right) ^{2}\frac{\partial ^{2}w}{\partial x^{2}} \right] =0, \end{aligned}$$
(13)
$$\begin{aligned}&\rho \left( x \right) A\left( x \right) \frac{\partial ^{2}u}{\partial t^{2}}+c_d \frac{\partial u}{\partial t}\nonumber \\&\quad -12\frac{\partial }{\partial x}\left[ {E\left( x \right) A\left( x \right) } \right] \left[ {\eta ^{2}\frac{\partial u}{\partial x}+\frac{\eta }{2}\left( {\frac{\partial w}{\partial x}} \right) ^{2}} \right] \nonumber \\&\quad -12E\left( x \right) A\left( x \right) \left[ {\eta ^{2}\frac{\partial ^{2}u}{\partial x^{2}}+\eta \frac{\partial ^{2}w}{\partial x^{2}}\frac{\partial w}{\partial x}} \right] =0, \end{aligned}$$
(14)

Equations (13) and (14) are discretised via the Galerkin modal decomposition technique; to this end, the displacements are assumed as

$$\begin{aligned} w(x,t)= & {} \sum _{k=1}^M {\varphi _k (x)q_k (t),}\nonumber \\ u(x,t)= & {} \sum _{k=1}^Q {\xi _k (x)r_k (t),} \end{aligned}$$
(15)

where \(q_k (t)\) and \(r_k (t)\) represent the kth generalised coordinates for the transverse and the axial motions, respectively; \(\varphi _k\) and \(\xi _k\) denote the kth eigenfunction for the transverse and longitudinal displacement of a clamped–clamped beam.

Substitution of the assumed displacements, i.e. Eq. (15), into Eqs. (13) and (14), and the application of the Galerkin method yields

$$\begin{aligned}&\sum _{j=1}^M {\left[ {\int _0^1 {\rho A \varphi _i \varphi _j \mathrm{d}x} } \right] } \ddot{q}_j \nonumber \\&\quad -\frac{1}{12\eta ^{2}}\sum _{j=1}^M {\left[ {\int _0^1 {\rho I \varphi _i {{\varphi }}''_j \mathrm{d}x} } \right] } \ddot{q}_j \nonumber \\&\quad +c_d \sum _{j=1}^M {\left( {\int _0^1 {\varphi _i \varphi _j \mathrm{d}x} } \right) } \dot{q}_j -\left[ {f_0 +f_1 \cos \left( {\Omega t} \right) } \right] \int _0^1 {\varphi _i \mathrm{d}x}\nonumber \\&\quad +\sum _{j=1}^M {\left[ {\int _0^1 {\left( {{E}''I+2{E}'{I}'+E{I}''} \right) \varphi _i {{\varphi }}''_j \mathrm{d}x} } \right] } q_j \nonumber \\&\quad +2\sum _{j=1}^M {\left[ {\int _0^1 {\left( {{E}'I+{E}{I}'} \right) \varphi _i {{\varphi }}'''_j \mathrm{d}x} } \right] } q_j\nonumber \\&\quad +\sum _{j=1}^M {\left( {\int _0^1 {EI \varphi _i {{{{\varphi }}}}''''_j \mathrm{d}x} } \right) } q_j \nonumber \\&\quad -12\eta \sum _{j=1}^Q \sum _{k=1}^M \left[ \int _0^1 {\left( {{E}'A+E{A}'} \right) \varphi _i {\xi }'_j {\varphi }'_k \mathrm{d}x} \right. \nonumber \\&\left. \quad +\int _0^1 {EA \varphi _i {\xi }'_j {\varphi }''_k \mathrm{d}x} +\int _0^1 {EA \varphi _i {\xi }''_j {\varphi }'_k \mathrm{d}x} \right] r_j q_k \nonumber \\&\quad -6\sum _{j=1}^M \sum _{k=1}^M \sum _{l=1}^M \left[ \int _0^1 {\left( {{E}'A+E{A}'} \right) \varphi _i {\varphi }'_j {\varphi }'_k {\varphi }'_l \mathrm{d}x}\right. \nonumber \\&\left. \quad +3\int _0^1 {EA \varphi _i {\varphi }'_j {\varphi }'_k {\varphi }''_l \mathrm{d}x} \right] q_j q_k q_l =0,\qquad \quad i={1, 2,\ldots , }M,\nonumber \\ \end{aligned}$$
(16)
$$\begin{aligned}&\sum _{j=1}^Q {\left( {\int _0^1 {\rho A \xi _i \xi _j dx} } \right) } \ddot{r}_j +c_d \sum _{j=1}^Q {\left( {\int _0^1 {\xi _i \xi _j \mathrm{d}x}} \right) } \dot{r}_j \nonumber \\&\quad -12\eta ^{2}\sum _{j=1}^Q {\left[ {\int _0^1 {\left( {{E}'A+E{A}'} \right) \xi _i {\xi }'_j \mathrm{d}x} +\int _0^1 {EA \xi _i {\xi }''_j \mathrm{d}x} } \right] } r_j \nonumber \\&\quad -6\eta \sum _{j=1}^M \sum _{k=1}^M \left[ \int _0^1 {\left( {{E}'A+E{A}'} \right) \xi _i {\varphi }'_j {\varphi }'_k \mathrm{d}x} \right. \nonumber \\&\quad \left. +2\int _0^1 {EA \xi _i {\varphi }'_j {\varphi }''_k \mathrm{d}x} \right] q_j q_k =0\qquad i={1, 2,\ldots , }Q, \end{aligned}$$
(17)

where the prime and dot notations represent \(\partial /{\partial x}\) and \(\partial /{\partial t}\), respectively. The discretised model given in Eqs. (16) and (17) is solved employing a continuation technique [27, 28]. The number of the degrees of freedom of the system is \(M+Q\); setting \(M=Q=10\) gives a system with 20 degrees of freedom.

3 Numerical results

The numerical results are presented and discussed in this section by constructing: (1) the plots of the variations of system properties along the length, (2) the nonlinear static deflection curves, and (3) the nonlinear dynamic frequency–amplitude diagrams. The effects of different system parameters are examined. In the present study, the AFG system is established by mixing Steel of \(E_{{\text {Steel}}} =210\) GPa and \(\rho _{{\text {Steel}}} =7800\,\hbox {kg/m}^{3}\), and Alumina of \(E_{\mathrm{Alumina}} =390\) GPa and \(\rho _{\mathrm{Alumina}} =3960\,\hbox {kg/m}^{3}\); the material changes from pure Steel in the left-hand end to pure Alumina in the right-hand end.

3.1 Property profiles

Figure 2 depicts the variation of Young’s modulus of the AFG beam with respect to the length for different values of the gradient index n; as seen in this figure, this relation is linear for n equal to unity and for the rest of values of n, the Young’s modulus varies exponentially (nonlinearly) along the length. Moreover, one can conclude that, for large values of the gradient index (i.e. reaching the pure Steel case), Young’s modulus decreases for a large portion of the length of the beam; for instance, for \(n=10\), the Young’s modulus of the AFG beam is close to 210 GPa for almost 70% of the length—a reverse scenario is observed for small values of n (i.e. reaching purely Alumina case).

The variation of the density of the beam along the length of the AFG beam is illustrated in Fig. 3 for different values of n. A behaviour similar to Fig. 2 is seen here where at larger values of n the density of the beam is closer to that of the Steel, and for smaller values of n it is closer to density of Alumina.

Fig. 2
figure 2

Young’s modulus variations with respect to the length of the AFG beam for different values of n

Full size image
Fig. 3
figure 3

Density variations with respect to the length of the AFG beam for different values of n

Full size image
Fig. 4
figure 4

Nonlinear static deflection configuration of the AFG tapered beam for several static forcing amplitudes; \(n=0.5\)

Full size image
Fig. 5
figure 5

Nonlinear static deflection configuration of the AFG beam for several values of the gradient index; \(f_{0}=800\)

Full size image

3.2 Nonlinear static deflection

The nonlinear static simulations are conducted by setting \(f_{1}=0\) and obtaining the static deflection of the AFG beam for different static forcing amplitude \(f_{0}\). The numerical results are obtained for an AFG beam of \(h_{{L}} = h_{{R}} =h=0.1\,\hbox {m}\), \(L/h=100, b_{{R}}/h =6\), and \(b_{{L}}/h=2\). The nonlinear static deflection of the system is obtained for various forcing amplitudes as well as different values of the gradient index n, and plotted in Figs. 4 and 5, respectively.

Figure 4 shows the nonlinear static bending profile of the AFG beam for several static forcing amplitudes; \(n=5\). As seen, the static deflection curve is not symmetric with respect to the x axis; for all cases, the maximum transverse deflection occurs in the vicinity of \(x=0.45\). As the static forcing amplitude is increased, the location of the maximum transverse deflection is shifted slightly towards the beam midpoint; in particular, the maximum deflection occurs at \(x=0.4506\) when \(f_{0}=200\), while it occurs at 0.4518, 0.4531, and 0.4543 at \(f_{0}=400\), 600, and 800, respectively. Furthermore, it is worth noting that the amount of increase in the deflection amplitude becomes less at larger forcing amplitudes, i.e. large deflections, showing that the induced tension due to stretching of the centreline increases nonlinearly at large static deflections.

The effect of the gradient index on the nonlinear static deflection profile is depicted in Fig. 5; \(f_{0}=800\). It is seen that at very small values of n, i.e. 0.1, the AFG beam shows almost symmetric response, with the maximum amplitude occurring at \(x=0.4869\). However, as the value of the gradient index is increased, for the range examined here, the asymmetry in the system becomes stronger. In fact, for \(n=0.5\), 1.0, and 2.0, the maximum static deflection occurs at \(x=0.4556\), 0.4406, and 0.4380, respectively; this slight shift in the location of the maximum deflection is visible in Fig. 5.

3.3 Nonlinear dynamic response

The results of the nonlinear dynamic numerical simulations are presented in this section for an AFG beam with the same mechanical and geometrical properties as in Sect. 3.2. In all the results of this section, the static forcing amplitude \(f_{0}\) is set to zero and the modal damping ratio is set to \(\zeta =0.015\).

Figure 6 illustrates the frequency response curves of the extensible AFG tapered beam with \(n=5, f_{1}=30.0\), and \(\zeta =0.015\); the dimensionless linear natural frequency is obtained as \(\omega _{1}=27.4733\). Although the schematic figure (i.e. Fig. 1) shows the symmetric boundary conditions (i.e. clamped condition at both ends), the asymmetric mode shapes (here \(q_{2}\) for the transverse motion and \(r_{1}\) for the axial one) are activated due to asymmetric distribution of the materials constituents as well as the change of the width along the length of the beam; these asymmetric modes are equal to zero for a symmetric system. Comparing subfigures (b) and (c) shows that the maximum amplitude of the second generalised coordinate, \(q_{2}\), is close to 0.1 which is considerably larger than that of the third generalised coordinate, \(q_{3}\), indicating the presence of a strong asymmetry. Such asymmetric behaviour necessitates employment of a high-dimensional discretised model by retaining a large number of modes in order to obtain reliable results. Furthermore, Fig. 6 shows that the AFG beam exhibits two saddle-node bifurcations at \(\Omega / \omega _{1}= 1.3430\) and \(\Omega /\omega _{1}= 1.0950\) representing a hardening-type resonance. More specifically, increasing the excitation frequency, at the first saddle-node bifurcation (i.e. point A), the system jumps from one stable attractor of higher amplitude to another stable attractor of smaller amplitude; a reverse scenario is seen at point B.

Fig. 6
figure 6

Frequency–amplitude curves of the AFG tapered beam: a–c the maximum amplitudes of the first, second, and third generalised coordinates of the transverse motion, respectively, and d the maximum amplitude of the first generalised coordinate of the axial motion. \(n=5, b_{R} = 6b_{L}\), \(f_{1}=30.0\), and \(\zeta =0.015\)

Full size image

Another important response of the AFG system is plotted in Fig. 7; this figure shows the force–response amplitude plots of the AFG tapered beam when \(n=5\), \(\Omega /\omega _{1}= 1.2\), and \(\zeta =0.015\). The system shows two saddle-node bifurcations; in particular, increasing the excitation amplitude results in the occurrence of the first saddle-node bifurcation at \(f_{1}= 96.718\) (point A) where the amplitude of vibrations jumps abruptly to a larger value; as the excitation amplitude decreases from large values, another saddle-node bifurcation takes place at \(f_{1}=19.585\) (point B), where a sudden decrease in the amplitude of the vibration occurs. The wide bistable region ranging from points A to B indicates a strong nonlinear behaviour of the AFG tapered beam, caused by the presence of geometric nonlinearities and nonlinear material property distributions.

Fig. 7
figure 7

Force–response curves of the AFG tapered beam: a–c the maximum amplitudes of the first, second, and third generalised coordinates of the transverse motion, respectively, and d the maximum amplitude of the first generalised coordinate of the axial motion. \(n=5\), \(b_{R}= 6b_{L}\), \(\Omega /\omega _{1}=1.2\), and \(\zeta =0.015\)

Full size image
Fig. 8
figure 8

Frequency–amplitude curves of the AFG tapered beam for different values of n (\(n=50.0\), 5.0, 1.0, and 0.5): a–c the maximum amplitudes of the first, second, and third generalised coordinates of the transverse motion, respectively, and d the maximum amplitude of the first generalised coordinate of the axial motion. \(b_{R} = 6b_{L}\), \(f_{1}=30.0\), and \(\zeta =0.015\)

Full size image
Fig. 9
figure 9

Frequency–response curves of the AFG tapered beam for different tapered status: a–c the maximum amplitudes of the first, second, and third generalised coordinates of the transverse motion, respectively, and d the maximum amplitude of the first generalised coordinate of the axial motion. \(n=5.0\), \(f_{1}=30.0\), and \(\zeta =0.015\)

Full size image

Figure 8 highlights the effect of the gradient index on the resonance behaviour of the AFG tapered beam, when \(f_{1}=30.0\), and \(\zeta =0.015\), and \(b_{{R}}=6b_{{L}}\). The figure shows that as the gradient index increases from 0.5, i.e. a beam dominantly made of Alumina, to 50.0, i.e. a beam dominantly made of Steel, the oscillation amplitude increases accordingly for the first generalised coordinate of the transverse motion, i.e. subfigure (a); furthermore, the increased gradient index results in smaller natural frequency, which causes a shift in the resonance region to the left in the frequency axis. The effect of gradient index on asymmetric modes, i.e. \(q_{2}\) and \(r_{1}\), on the other hand, is different. As seen in subfigures (b) and (d), by increasing n from 0.5 to 1, the contribution of the asymmetric generalised coordinates (i.e. \(q_{2}\) and \(r_{1})\) in the response becomes stronger; note that for \(n=0.5\), the maximum amplitude of \(q_{2}\) is close to 0.1 which is quite comparable with the amplitude of \(q_{1}\), showing the presence of a strong asymmetry in the system. For a moderately large value of the index gradient (i.e. \(n=5\)), the system still displays a strong asymmetric behaviour. However, by increasing the gradient index to \(n=50\), the amplitudes of \(q_{2}\) and \(r_{1}\) reduce substantially while the amplitude of the \(q_{1}\) increases; this shows that the response of the system becomes closer to that of a symmetric system.

Figure 9 depicts the effect of the variation of the width of the beam for different tapered ratios; in particular, four different tapered ratios are considered. i.e. \(b_{{R}}=b_{{L}}\), \(b_{{R}}=2b_{{L}}\), \(b_{{R}}=4b_{{L}}\), and \(b_{{R}}=6b_{{L}}\), and the corresponding frequency–amplitude diagrams are compared. Other dimensionless parameters of the AFG tapered beam are selected as \(n=5.0\), \(f_{1}=30.0\), and \(\zeta =0.015\). As seen in this figure, the largest amplitude of the first generalised coordinate of the transverse motion is designated to the case \(b_{{R}}=b_{{L}}\) (i.e. a beam with uniform width); as the tapered ratio increases, the area of the dominantly Alumina region increases which in turn decreases the amplitude of the first generalised coordinate of the transverse motion. However, the scenario is reverse for the second generalised coordinate of the transverse motion as well as the first one of the axial motion. More specifically, by increasing the \(b_{{R}}/b_{{L}}\) ratio, the amplitude of the \(q_{2}\) motion increases substantially, while the amplitude of the \(q_{1}\) motion decreases; this shows that the asymmetry in the system substantially increases by increasing the \(b_{{R}}/b_{{L}}\) ratio. On the frequency point of view, the largest resonance frequency, as well as natural frequency, is associated with the case \(b_{{R}}=6b_{{L}}\). It is worth mentioning that although for the case \(b_{{R}}=b_{{L}}\) the AFG beam is uniform along its length, the asymmetric generalised coordinates (\(q_{2}\) and \(r_{1})\) are still activated due to the non-uniform material distribution along the length of the beam; however, this case possesses the smallest amplitude of the asymmetric generalised coordinates (\(q_{2}\) and \(r_{1})\) among the cases studied here. As seen in subfigure (c), the behaviour of the third generalised coordinate is clearly different for the case \(b_{{R}}=b_{{L}}\), where the system possesses uniform cross section.

4 Conclusions

The nonlinear forced static and dynamic responses of a tapered AFG beam have been investigated in this paper. The kinetic and potential energies as well as the work done by the damping and the external harmonic load were derived and implemented in the Hamilton’s principle. Nonlinear equations of motion in transverse and longitudinal direction were obtained in order to predict the large deformations of the AFG tapered beam. Exponential distributions were employed to formulate expressions for the geometrical and material properties of the AFG tapered beam. To examine the system response numerically, first, the Galerkin technique, along with adequate number of symmetric and asymmetric modes, was employed to discretise the system; next, a continuation scheme was employed in order to conduct numerical simulations. Computations were carried out to examine the effect of different parameters on the nonlinear static and dynamic responses of the system. The following conclusions were drawn from the numerical results:

  1. (1)

    The nonlinear static deflection of the AFG tapered beam shows the presence of a strong asymmetry in the response of the system; furthermore, the induced tension due to centreline stretching becomes much stronger at larger deflection amplitudes, which in turn increases the resistance of the system to the applied load.

  2. (2)

    By increasing the gradient index in the range of 0.1 to 2.0, the asymmetry in the system becomes stronger, causing the maximum static deflection to occur at locations further from the midpoint.

  3. (3)

    The nonlinear frequency–amplitude and force–amplitude plots of the AFG tapered beam show two jumps (saddle-node bifurcations).

  4. (4)

    In contrast to symmetric systems, the asymmetric mode shapes contribute to the response of the system due to non-uniform cross-sectional area of the tapered geometry and non-homogeneous material properties of the AFG beam along the length.

  5. (5)

    The nonlinear dynamic results showed that the amplitude of the second generalised coordinate of the transverse motion is comparable to that of the first generalised coordinate; this highlights the importance of employing a high-dimensional model with a large number of degrees of freedom.

  6. (6)

    As the gradient index increases, the vibration amplitude increases accordingly for the first generalised coordinate of the transverse motion and the resonance region shifts to the smaller values of the frequency; however, a mixed behaviour is seen for the second generalised coordinate as the gradient index is increased. In particular, increasing the gradient index from small values to moderately large values results in strengthened asymmetric behaviour; however, beyond a certain value of the gradient index, the asymmetry becomes weaker.

  7. (7)

    Although one of the sources of asymmetry eliminates for the case of uniform cross section (i.e. \(b_{{R}}=b_{{L}})\), the asymmetric generalised coordinates have nonzero value due to the asymmetric distribution of the materials constituents.

  8. (8)

    Due to increased \(b_{{R}}/b_{{L}}\) ratio, the amplitude of the first generalised coordinate of the transverse motion decreases, while that of the second generalised coordinate increases substantially; this shows that the asymmetry in the AFG tapered beam depends strongly on the \(b_{{R}}/b_{{L}}\) ratio.