1 Introduction

Dynamic behavior of stepped beam-like elements is of practical interest in many engineering applications, including civil, aerospace, shipbuilding and automobile engineering. Long span bridges, tall buildings, spacecraft antennae, rotor blades and robot arm manipulators can be modeled with beam-like elements.

In a dynamical environment, steps in cross-section and in material properties affect the natural frequencies. This situation may cause resonance if the changed frequency is close to the working frequency. It is crucial to predict the change in the frequency, as well as the mode shape.

The classical Bernoulli–Euler beam theory adequately predicts the frequencies of vibration of lower modes of slender beams. The governing characteristic differential equation of a non-uniform beam is a fourth order ordinary differential equation in the flexural displacement with variable coefficients. Many authors have performed analysis of vibration of stepped beams based on this theory. [1–10]. Among them, in 2010 the paper by Mao et al. [10] presents free vibrations of stepped homogeneous beams by Adomain decomposition method.

For Timoshenko beams, the governing characteristic differential equations are two differential equations coupled in terms of the flexural displacement and the angle of rotation which results from bending [11–15]. Free vibration of homogeneous stepped Timoshenko beam studies have been presented in [14, 15] among other papers. Various previous studies have been reported for beams made of AFG materials [11, 16–19] with a continuous variation of the cross-sectional area (tapered beams) [11, 16, 19] and with constant cross-sectional area [17, 18]. Exact solution for the behavior of vibrating Timoshenko beams with variable coefficients does not exist, then the problem must be analyzed by approximate procedures. Differential quadrature method, DQM, is a useful technique to solve the governing equations directly. Early references on the DQM can be found in Bellman and Casti [20], Bert and Malik [21], Laura and Gutiérrez [22] and more recent development and applications can be found in [6, 14, 15, 19, 23–26] among many others. In particular, Karami et al. [14] developed an accurate differential quadrature element method based on the theory of shear deformable beams. They employed it to analyze beams with non-uniform or discontinuous geometry and other complexities.

A recent literature survey on free vibration of stepped beams of functionally graded materials revealed that not many papers cover this topic. In particular to the authors’ knowledge, there are no natural frequency data in the literature for axially functionally graded, AFG, Timoshenko beams with stepped changes in material properties and in cross-sectional area.

In the present paper a different point of view that adds the effect of the material inhomogeneity to the stepped change geometry is modeled for free vibration of Timoshenko beams with elastic boundary conditions. Functionally graded material properties are assumed to vary along the beam in a linear, quadratic or cubic fashion in each beam element, with an abrupt discontinuity at the stepped change geometry. The study considers the accuracy and convergence of the DQM as applied to the study of free transverse vibration of stepped beams of AFG materials.

2 Theory

2.1 Axially functionally graded material properties

In the present paper the free vibration of stepped AFG Timoshenko beams with different combinations of boundary conditions is analyzed.

The beam could have stepped jumps in cross-sectional area and in material properties. In order to obtain the dynamic response, the beam is discretized into elements or subdomains depending on the geometrical and material discontinuities.

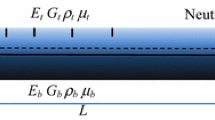
The inhomogeneous material [27], with gradient compositional variation of the constituents, varies in the longitudinal direction of the beam. Properties of AFG materials, like mass density ρ, Young’s modulus E, shear modulus G, continuously vary in the axial direction.

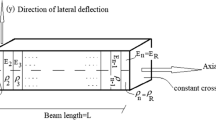
A generic material property \( P(\bar{x}) \) [16] is assumed to vary along the beam axis \( \bar{x} \) with a power law relation, Fig. 1:

Fig. 1
figure 1

Power law relation of AFG material properties. \( x = {{\bar{x}} \mathord{\left/ {\vphantom {{\bar{x}} L}} \right. \kern-0pt} L} \); P b /P a  < 1

Full size image
$$ P(\bar{x}) = P_{a} + (P_{b} - P_{a} )\left( {\frac{{\bar{x}}}{L}} \right)^{n} , $$
(1)

where P a and P b are properties of material “a” and material “b”, respectively. They are the constituents of the inhomogeneous material of the beam; n is the material non-homogeneity parameter and \( P(\bar{x}) \) is a typical material property such as ρ, E or G. The percentage content of material “a” increases as n increases. When n = 1 the composition changes linearly through the length L, while n = 1/2 or n = 2 corresponds to a quadratic distribution, and so on. In general, any value n outside the range (1/3, 3) is not desired [27] because such a functionally graded material would contain too much of one of the constituents. (When n = 1/3 or 3, one constituent has the 75 % of the total AFG material.)

2.2 The Timoshenko beam theory for AFG beams with stepped changes

Figure 2 presents the stepped Timoshenko beam of length L with elastic restrains at both ends. Cartesian global coordinate system \( \bar{x}\,\bar{y}\,\bar{z} \) is adopted at the left hand end of the beam and the local coordinate systems are at the left hand end of each beam element k. The global \( \bar{x} \) and local \( \bar{x}_{k} \) axes are coincident; both are normal to the beam cross-section and pass through section’s barycenter. The beam model is discretized in N e subdomains or elements, depending on the geometrical and material discontinuities.

Fig. 2
figure 2

Stepped beam with elastic restrains

Full size image

Following the Timoshenko beam theory, [28, 29], the axial and shear strains could be expressed as:

$$ \varepsilon = \varepsilon_{x} \cong - y\theta^{{\prime }} + \frac{1}{2}\left( {w^{{\prime }} } \right)^{2} ;\quad \gamma = \gamma_{xy} = w^{{\prime }} - \theta , $$
(2)

where \( w = w(\bar{x},t) \) is the flexural displacement of the beam neutral axes in the \( \bar{y} \) direction and \( \theta = \theta (\bar{x},t) \) is the cross-section rotation about the \( \bar{z} \) axis. (Prime mark indicates derivative with respect to the spatial coordinate.)

The potential energy due to flexure stretching and shear:

$$ U_{1} = \int_{A} {\int_{0}^{L} {\frac{{(E\varepsilon^{2} + G\gamma^{2} )}}{2}} } \;d\bar{x}\;dA = \frac{1}{2}\int_{0}^{L} {EI(\theta^{{\prime }} )^{2} } d\bar{x} + \frac{1}{2}\int_{0}^{L} {\kappa AG(w^{{\prime }} - \theta )^{2} } d\bar{x} + C_{1} , $$

where C 1 is a constant [28], \( E = E(\bar{x}) \) is the Young modulus, \( G = G(\bar{x}) \) is the shear modulus. The area and the second moment of area of beam cross section are noted as \( A = A(\bar{x}) \) and \( I = I(\bar{x}) \). The coefficient κ is the shear correction factor.

The energy due to the elastic supports at beam’s ends:

$$ U_{2} = \frac{1}{2}\left( {k_{{W_{1} }} w_{{_{1} }}^{2} + k_{{\Psi_{1} }} \theta_{{_{1} }}^{2} + k_{{W_{Ne} }} w_{{_{Ne} }}^{2} + k_{{\Psi_{Ne} }} \theta_{{_{Ne} }}^{2} } \right), $$

where \( k_{{W_{1} }} ,\;k_{{W_{Ne} }} \) and \( k_{{\Psi_{1} }} ,\;k_{{\Psi_{Ne} }} \) are constants of the elastic restrains, w 1, w Ne are the displacements in the \( \bar{y} \) direction and θ 1, θ Ne are the section rotation at beam ends.

Considering the energies for the k subdomains and summing them to the energies of the elastic supports, the total potential energy is given by:

$$ \begin{aligned} U & = \frac{1}{2}\sum\limits_{k = 1}^{{N_{e} }} {\left\{ {\int_{0}^{{L_{k} }} {\left[ {EI(\theta^{{\prime }} )^{2} + \kappa AG\left( {w^{{\prime }} - \theta } \right)^{2} } \right]_{k} } d\bar{x}_{k} } \right\}} + C_{1} \\ & \quad + \frac{1}{2}\left( {k_{{W_{1} }} w_{{_{1} }}^{2} + k_{{\Psi_{1} }} \theta_{{_{1} }}^{2} + k_{{W_{Ne} }} w_{{_{Ne} }}^{2} + k_{{\Psi_{Ne} }} \theta_{{_{Ne} }}^{2} } \right). \\ \end{aligned} $$
(3)

The expression of the kinetic energy is derived from the velocity components of a point at a distance \( \bar{y} \) from the neutral axis. The velocity components in the \( \bar{x} \), \( \bar{y} \) and \( \bar{z} \) directions are expressed as:

$$ V_{x} = - \bar{y}\dot{\theta };\quad V_{y} = 0;\quad V_{z} = \dot{w} $$
(4)

and the kinetic energy T of the beam is given by:

$$ T = \int_{0}^{L} {\int_{A} {\frac{{\left( {V_{x}^{2} + V_{y}^{2} + V_{z}^{2} } \right)}}{2}\rho \;dA\;d\bar{x} = \frac{1}{2}\sum\limits_{k = 1}^{{N_{e} }} {\left\{ {\int_{0}^{{L_{k} }} {\left[ {\rho I(\dot{\theta })^{2} + \rho A(\dot{w})^{2} } \right]_{k} } d\bar{x}_{k} + C_{2} } \right\}} } } , $$
(5)

where C 2 is a constant and \( \rho = \rho (\bar{x}) \) is the material’s density. Superimposed dot indicates differentiation with respect to time t.

The governing differential equations of motion are derived applying Hamilton’s principle that states that \(\int_{{t_{1} }}^{{t_{2} }} {\left( {T - U} \right)} dt \) taken between two specified times t 1 and t 2 is stationary for a dynamic trajectory, then:

$$ \delta \int_{{t_{1} }}^{{t_{2} }} {\left( {T - U} \right)} dt = 0. $$
(6)

When the system vibrates in one of its normal modes, the flexional displacement w and the section rotation θ can be written as:

$$ w = \bar{W}\;e^{i\omega t} ;\quad \theta = \bar{\Psi }\;e^{i\omega t} , $$
(7)

where \( \bar{W} = \bar{W}(\bar{x}_{k} ) \) and \( \bar{\Psi } = \bar{\Psi }\left( {\bar{x}_{k} } \right) \) are the spatial functions of the primary variables and ω is the circular natural frequency. Replacing Eqs. (7) in the energy expressions U and T of Eq. (6) and then integrating by parts, the governing element equations are obtained:

$$ \left[ {\left( {EI\bar{\Psi }^{{\prime }} } \right)^{{\prime }} + \kappa AG\left( {\bar{W}^{{\prime }} - \bar{\Psi }} \right) - \rho I\omega^{2} \bar{\Psi }} \right]_{k} = 0, $$
(8)
$$ \left\{ {\kappa \left[ {AG\left( {\bar{W}^{{\prime }} - \bar{\Psi }} \right)} \right]^{{\prime }} + \rho A\omega^{2} \bar{W}} \right\}_{k} = 0\,;\quad {\text{for}}\quad k = 1,{ 2}, \ldots N_{e} , $$
(9)

where \( \kappa AG\left( {\bar{W}^{{\prime }} - \bar{\Psi }} \right) = \bar{Q} \) the transverse shear force and \( EI\bar{\Psi }^{{\prime }} = \bar{M} \) the bending moment are the secondary variables.

The external boundary conditions at beam’s ends are:

$$ \kappa A_{j} G_{j} \left( {\bar{W}^{'}_{j} - \bar{\Psi }_{j} } \right) \pm k_{{W_{j} }} \bar{W}_{j} = 0;\quad E_{j} I_{j} \,\bar{\Psi }_{j}^{'} \, \pm k_{{\Psi_{j} }} \bar{\Psi }_{j} = 0 $$
(10)

for j = 1 and j = N e at \( \bar{x}_{1} = 0 \) and \( \bar{x}_{Ne} = L_{Ne} \), respectively. Different combinations of classical boundary conditions can be obtained from Eqs. (10).

Geometrical compatibility conditions between two adjacent beam elements are:

$$ \bar{W}_{k} \left( {L_{k} } \right) - \bar{W}_{k + 1} (0) = 0;\quad \bar{\Psi }_{k} \left( {L_{k} } \right) - \bar{\Psi }_{k + 1} (0) = 0;\quad {\text{for}}\quad k = 1,{ 2}, \ldots N_{e} - 1 , $$
(11)

and internal compatibility conditions of shear forces and bending moments are:

$$ \begin{gathered} \kappa A_{k} G_{k} \left( {\bar{W}_{k}^{{\prime }} \left( {L_{k} } \right) - \bar{\Psi }_{k} \left( {L_{k} } \right)} \right) - \kappa A_{k + 1} G_{k + 1} \left( {\bar{W}_{k + 1}^{{\prime }} \left( 0 \right) - \bar{\Psi }_{k + 1} (0)} \right) = 0; \hfill \\ E_{k} I_{k} \bar{\Psi }_{k}^{{\prime }} \left( {L_{k} } \right) - E_{k + 1} I_{k + 1} \bar{\Psi }_{k + 1}^{{\prime }} (0) = 0;\quad {\text{ for}}\quad k = 1,{ 2}, \ldots N_{e} - 1. \hfill \\ \end{gathered} $$
(12)

Notation of non-dimensional expressions is introduced as follows:

$$ \begin{aligned} x & = \frac{{\overline{x}_{k} }}{{L_{\,k} }};\quad l_{k} = \frac{{L_{k} }}{L};\quad s_{k} = L\sqrt {\frac{{\left( {A_{k} } \right)_{x = 0} }}{{\left( {I_{k} } \right)_{x = 0} }}} ;\quad W_{k} = \frac{{\overline{W}_{k} }}{{L_{\,k} }};\quad \Psi_{k} = \bar{\Psi }_{k} ; \\ \alpha_{k} & = \frac{{\left( {A_{k} } \right)_{x = 0} }}{{A_{0} }};\quad \beta_{k} = \frac{{\left( {I_{k} } \right)_{x = 0} }}{{I_{0} }};\quad \delta_{k} = \frac{{\left( {E_{k} } \right)_{x = 0} }}{{E_{0} }};\quad \eta_{k} = \frac{{\left( {\rho_{k} } \right)_{x = 0} }}{{\rho_{0} }}; \\ Q_{k} & = \frac{{\bar{Q}_{k} }}{{\left( {E_{k} A_{k} } \right)_{x = 0} }};\quad M_{k} = \frac{{\bar{M}_{k} \;L_{k} }}{{\left( {E_{k} I_{k} } \right)_{x = 0} }}, \\ \end{aligned} $$
(13)

and the natural non dimensional frequency coefficient is expressed as:

$$ \Omega = \sqrt {{{\rho_{0} A_{0} } \mathord{\left/ {\vphantom {{\rho_{0} A_{0} } {\left( {E_{0} I_{0} } \right)}}} \right. \kern-0pt} {\left( {E_{0} I_{0} } \right)}}} \;L^{2} \omega ; $$
(14)

where ρ 0 = ρ 1(0); A 0 = A 1(0); E 0 = E 1(0); I 0 = I 1(0).

Finally, the governing differential element equations become:

$$ \frac{{\kappa_{k} s_{1}^{2} \, s_{k}^{2} }}{2(1 + \nu )}\,E_{k} A_{k} \left( {\Psi_{k} - W_{k}^{'} } \right) - \frac{{s_{1}^{2} }}{{l_{k}^{2} }}\left( {E_{k}^{'} I_{k} \Psi_{k}^{'} + E_{k} I_{k} \Psi_{k}^{''} } \right) - \Omega^{2} \rho_{k} I_{k} \Psi_{k} = 0; $$
(15)
$$ \frac{{\kappa_{k} s_{1}^{2}}}{{2(1 + \nu_{k} )l_{k}^{2} }}\left[ {E_{k}^{'} A_{k} \left( {W_{k}^{'} - \Psi_{k} } \right) + E_{k} A_{k} \left( {W_{k}^{''} - \Psi_{k}^{'} } \right)} \right] + \Omega^{2} \rho_{k} A_{k} W_{k} = 0; $$
(16)

for k = 1, 2,…N e .

3 The DQM

In order to obtain the DQM analog equations of the governing equations of the AFG stepped Timoshenko beam, each beam subdomain k is discretized in a grid of N points using the Chebyshev–Gauss–Lobato expression [20–22]

$$ x_{i} = \left\{ {1 - \cos \left[ {(i - 1)\,\pi /\,(N - 1)} \right]} \right\}/2\,,\quad i = 1, 2, \ldots , N, $$

where x i is the coordinate of point i. Based on the quadrature rules [21], the qth order derivatives of flexural displacement W and section rotation Ψ at a point i of the grid are expressed as:

$$ \left. {\frac{{d^{(q)} W_{k} }}{{dx^{q} }}} \right|_{{\,x_{i} }} = \sum\limits_{j = 1}^{N} {C_{i\,j}^{(q)} \,} W_{k\,j} ;\,\left. {\frac{{d^{(q)} \Psi_{k} }}{{dx^{q} }}} \right|_{{\,x_{i} }} = \sum\limits_{j = 1}^{N} {C_{i\,j}^{(q)} } \,\Psi_{k\,j} , $$
(17)

where W kj and Ψ kj correspond to point j of subdomain k, and C (q) ij are the weighting coefficients associated with the qth order derivative. They were obtained using Lagrange interpolating functions:

$$ \Pi \left( {x_{i} } \right) = \prod _{j = 1j \ne i}^{N} \left( {x_{i} - x_{j} } \right)\quad {\text{for}}\quad i, j = 1, 2, \ldots ,N. $$

The off-diagonal terms of the weighting coefficient matrix of the first-order derivative are:

$$ C_{\,ij\,}^{(1)} = \frac{{\prod {\left( {x_{\,i\,} } \right)} }}{{(x_{i} - x_{j} )\,\,\prod {\left( {x_{j\,} } \right)} }}\quad {\text{for}}\quad i, j = 1, 2, \ldots , N\;{\text{and}}\;i \ne j. $$
(18)

The off-diagonal terms of the weighting coefficient matrix of the second-order and higher-order derivatives are obtained through the recurrence expression:

$$ C_{ij}^{\left( q \right)} = q\left[ {C_{{i\,i}}^{{\left( {q - 1} \right)}} C_{ij}^{\left( 1 \right)} - \frac{{C_{ij}^{{\left( {q - 1} \right)}} }}{{\left( {x_{i} - x_{j} } \right)}}} \right]\quad {\text{for}}\quad i, j = 1, 2, \ldots , N\;{\text{and}}\;i \ne j;\;2 \le q \le \left( {N - 1} \right). $$
(19)

And the diagonal terms of the weighting coefficient matrix are given by:

$$ C_{ii}^{\left( q \right)} = - \sum _{j = 1j \ne i}^{N} C_{ij}^{(r)} ;\quad {\text{for}}\quad i = 1, 2, \ldots , N;{ 1} \le q \le \left( {N - 1} \right). $$
(20)

Using the quadrature rules, Eq. (18), the differential quadrature analogs of the governing Eqs. (16) and (17) of a node i are:

$$ \frac{{s_{1}^{2} s_{k}^{2} \kappa_{k} }}{{2(1 + \nu_{ki} )}}A_{ki} E_{ki} \left( {\Psi_{{k\, i}} - \sum\limits_{j = 1}^{N} {C_{{ij}}^{(1)} \; W_{{k\,j}} } } \right) - \frac{{s_{1}^{2} }}{{l_{k}^{2} }}I_{ki} E_{ki}^{'} \sum\limits_{j = 1}^{N} {C_{ij}^{(1)} \;\Psi_{k\;j} } - \frac{{s_{1}^{2} }}{{l_{k}^{2} }}I_{ki} E_{ki} \left( {\sum\limits_{j = 1}^{N} {C_{ij}^{(2)}\;\Psi_{{k\, j}} } } \right) - \Omega^{2} \, \rho_{ki} I_{ki} \Psi_{{k\,i}} = 0, $$
(21)
$$\frac{{\kappa_{k} }}{{2(1 + \nu_{k} )}}\frac{{s_{1}^{2} }}{{l_{k}^{2} }}E_{ki}^{'} A_{ki}^{{}} \left[ {\left( {\sum\limits_{j = 1}^{N} {\left( {C_{{{\kern 1pt} ij}}^{(1)} } \right){\kern 1pt} \,W_{{k{\kern 1pt} j}} } - \Psi_{{k{\kern 1pt} j}} } \right)} + E_{ki}^{{}} A_{ki}^{{}} {\left( {\sum\limits_{j = 1}^{N} {\left( {C_{{{\kern 1pt} ij}}^{(2)} } \right){\kern 1pt} \,W_{{k{\kern 1pt} j}} - \sum\limits_{j = 1}^{N} {\left( {C_{{{\kern 1pt} ij}}^{(1)} } \right){\kern 1pt} \,\Psi_{{k{\kern 1pt} j}} } } } \right)} \right] + \Omega^{2} \rho_{ki} A_{ki} {\kern 1pt} {\kern 1pt} W_{k\,i} \; = 0. $$
(22)

The analog equations of internal forces at node i:

$$ Q_{ki} = \frac{{\kappa_{ki} }}{{2(1 + \nu_{ki} )}}E_{ki} A_{ki} \left[ {\left( {\sum\limits_{j = 1}^{N} {C_{ij}^{(1)} \,W_{kj} } } \right) - \Psi_{ki} } \right];\quad M_{ki} = E_{ki} I_{ki} \left( {\sum\limits_{j = 1}^{N} {C_{ij}^{(1)} \,\Psi_{kj} } } \right); $$
(23)

the outer boundary conditions are given by:

$$ Q_{1\;1} = k_{{W_{1} }} l_{1}^{3} W_{1\;1} ;M_{1\;1} = k_{{\Psi_{1} }} l_{1} \Psi_{1\;1} ;\quad Q_{Ne\;N} = - k_{{W_{Ne} }} \;l_{Ne}^{\;3} \;W_{Ne\;N} \,;\quad M_{Ne\;N} = - k_{{\Psi_{Ne} }} l_{Ne} \Psi_{Ne\;N} . $$
(24)

the analog continuity equations at adjacent beam elements become, for the geometrical compatibility conditions:

$$ l_{k} W_{kN} - l_{k + 1} W_{{\left( {k + 1} \right) 1}} = 0;\quad \Psi_{kN} - \Psi_{{\left( {k + 1} \right) 1}} = 0, $$
(25)

and for the internal compatibility conditions of shear forces and bending moment using secondary variables Eqs. (23):

$$ \alpha_{k} \delta_{k} Q_{kN} - \alpha_{(k + 1)} \delta_{(k + 1)} Q_{{\left( {k + 1} \right) 1}} = 0;\quad \frac{{\beta_{k} \delta_{k} }}{{l_{k} }}M_{kN} - \frac{{\beta_{{\left( {k + 1} \right)}} \delta_{{\left( {k + 1} \right)}} }}{{l_{k + 1} }}M_{{\left( {k + 1} \right)1}} = 0, $$
(26)

where the constants α k , β k , δ k , defined in Eqs. (13), take into account the discontinuities in material properties and in geometry. The set of analog Eqs. (21–26) constitute the linear system of equations that allows determining the natural frequencies of the stepped AFG Timoshenko beam.

4 Numerical results

The natural frequency coefficients, Eq. (14), are obtained for a range of illustrative examples. Timoshenko beams with different material properties and different locations of the abrupt discontinuities are studied. The cross-section is of rectangular form and the geometrical relation between height and length can be expressed as:

$$ \frac{h}{L} = \frac{{\sqrt {12} }}{{s_{1} }}\;;{\text{ with}}\quad h = h_{ 1} \left( 0 \right). $$

In all the numerical examples the shear correction factor is assumed as: κ = 5/6.

Table 1 contains a convergence analysis. The DQM results for the first six frequency coefficients of a uniform homogeneous Timoshenko beam under various classical boundary conditions are listed. The rate of convergence and accuracy of the proposed differential quadrature procedure can be observed as the number of grid points, N, increases. The obtained values are compared with results available in the literature. The agreement between those results is excellent, and it can be concluded that the proposed procedure has adequate accuracy with N = 41 grid points.

Table 1 Convergence analysis: first six natural frequency coefficients of uniform homogeneous Timoshenko beams: h/L = 0.35; κ = 5/6; ν = 0.30
Full size table

Table 2 presents the first six frequency coefficients of a tapered AFG Timoshenko beam under three different combinations of boundary conditions. The grid is obtained taking N = 41 points. To make a comparison with published results, material properties are assumed to vary according to Eq. (1), with n = 1, 2, 3 and 4.

Table 2 First six natural frequency coefficients of AFG Timoshenko beams, with a small taper in height: h(x) = h 0(1 − 0.1x); h 0/L = 0.35; κ = 5/6; ν = 0.30; χ E  = 0.35; χ ρ  = 0.47; N = 41
Full size table
$$ E_{k} = E_{k} (x) = E_{a} \left[ {1 + \left( {\chi_{{E_{k} }} - 1} \right)x^{n} } \right];\quad \rho_{k} = \rho_{k} (x) = \rho_{a} \left[ {1 + \left( {\chi_{{\rho_{k} }} - 1} \right)x^{n} } \right], $$
(27)

with \( \chi_{{E_{k} }} = {{E_{b} } \mathord{\left/ {\vphantom {{E_{b} } {E_{a} }}} \right. \kern-0pt} {E_{a} }} \) and \( \chi_{{\rho_{k} }} = {{\rho_{b} } \mathord{\left/ {\vphantom {{\rho_{b} } {\rho_{a} }}} \right. \kern-0pt} {\rho_{a} }}. \)

The beam cross section has variable height h(x) and constant wide b(x) = b.

In the calculations, the constituents of the inhomogeneous material are assumed to be aluminum Al and zirconia ZrO2. Their Young modulus and density are:

$$ E_{\text{Al}} = 70\,{\text{GPa}};\quad \rho_{\text{Al}} = 2{,}700\,{\text{kg/m}}^{ 3} ;\quad E_{{{\text{ZrO}}_{2} }} = 200\,{\text{GPa;}}\quad \rho_{{{\text{ZrO}}_{2} }} = 5{,}700\,{\text{kg/m}}^{3} ;\quad \nu_{\text{Al}} = \nu_{{{\text{ZrO}}_{2} }} = 0.30 $$
(28)

It can be seen that the agreement with previous published results is excellent.

Tables 1 and 2 demonstrate the rate of convergence and accuracy of the approach proposed.

The results on Table 3 show the effect of an AFG material on the frequency coefficients of a uniform Timoshenko beam. s 1 = 12.5, is equivalent to h 0/L ≅ 0.28; L 1 = L. Eight different combinations of classical boundary conditions are adopted. The material properties vary according to Eqs. (27), with n = 1, 2 and 3. The domain is discretized in a grid of N = 41 points.

Table 3 First six natural frequency coefficients of uniform cross-section AFG Timoshenko beams with various boundary conditions
Full size table

Next, free vibrations of stepped AFG Timoshenko beams are studied. Different boundary conditions, step locations and material properties are considered. Cases A–C described the geometric variation as follows:

Case A

L = L 1 + L 2

h 2 = h 1;

b 2 = ξ b b 1;

A 2 = ξ b A 1;

I 2 = ξ b I 1.

Case B

L = L 1 + L 2

h 2 = ξ h h 1;

b 2 = b 1;

A 2 = ξ h A 1;

I 2 = ξ 3 h A 1.

Case C

L = L 1 + L 2

h 2 = ξ h h 1;

b 2 = ξ b b 1;

A 2 = ξ h ξ b A 1;

I 2 = ξ b ξ 3 h A 1.

with ξ b and ξ h constants. The three geometrical cases, Fig. 3, are assumed introducing stepped variations of the area and the second moment of area, [10]. One of the elements of the stepped beam has constant material properties while the other has AFG properties.

Fig. 3
figure 3

Stepped AFG Timoshenko beams

Full size image

The material properties of the portion of the beam of length L 1 are supposed to have AFG characteristics, Eqs. (27–28): n 1 = 1, 2 and 3; \( \chi_{{E_{1} }} = 70/ 200 = 0. 3 5 \); \( \chi_{{\rho_{1} }} = 2{,}700/5{,}700 = 0. 4 7 4 \) with constant cross-section A 1.While the other part of the stepped beam of length L 2, has homogeneous material: \( \chi_{{E_{2} }} = 200/200 = 1 \); \( \chi_{{\rho_{2} }} = 5{,}700/5{,}700 = 1 \) = 1, and the cross-sectional area being constant and equal to A 2.

Tables 4, 5 and 6 present the first six natural frequency coefficients of cantilever beams of Fig. 3 with a step located at l 1 = L 1/L = 0.250, 0.370, 0.620 and 0.750.

Table 4 First six natural frequency coefficients of clamped-free AFG beams with a step
Full size table
Table 5 First six natural frequency coefficients of clamped-free AFG beams with a step
Full size table
Table 6 First six natural frequency coefficients of clamped-free AFG beams with a step
Full size table

In Tables 4 and 5 a comparison is made with Mao et al. [10] when the material properties are assumed to be constant in both beam elements. Mao et al. [10] have based their results on Euler–Bernoulli beam theory. In the present paper, h 0/L = 0.0017 is used to propose a limiting situation. The mentioned value is small enough to neglect the effects of shear force and rotary inertia in the application of the Timoshenko beam theory. For that reason, results calculated with 0.0017, become comparable to Euler–Bernoulli theory’s results (as shown in Tables 4, 5). It can be seen that the agreement with [10] is excellent.

Figure 4 shows the fundamental frequency coefficients for cantilever beams, with different locations of the step. l 1 is equal to 0.25, 0.375, 0.625, 0.75 and AFG material properties for the part of the beam of length L 1 are \( \chi_{{E_{1} }} = 70/ 200 = 0. 3 5 \); \( \chi_{{\rho_{1} }} = 2{,}700/5{,}700 = 0. 4 7 4 \); and for the element of length L 2: \( \chi_{{E_{2} }} = 200/200 = 1 \); \( \chi_{{\rho_{2} }} = 5{,}700/5{,}700 = 1. \) h 0/L = 0.0017 (Beam A, color solid line; Beam B, color dotted line; Beam C, color dashed line). The frequency coefficients of the stepped beams can be compared with the coefficients of the uniform beam of similar material properties, which is indicated by a solid black line. It can be seen that it is possible to have lighter structures with higher coefficients of fundamental frequency when the beams are of AFG materials. [1].

Fig. 4
figure 4

Fundamental natural frequency coefficient for cantilever AFG stepped beams (N = 41)

Full size image

Hereafter there are several numerical examples of frequency coefficients of stepped Timoshenko beams with different AFG materials and combinations of classical or elastic boundary conditions.

Table 6 is similar to 4, with h 0/L = 0.28. Table 7 presents natural frequency coefficients of stepped AFG Timoshenko beams. For element k = 1: l 1 = 0.625; \( \chi_{{E_{1} }} = 70/ 200 = 0. 3 5 \); \( \chi_{{\rho_{1} }} = 2{,}700/ 5{,}700 = 0. 4 7 4 \); and for element k = 2: l 2 = 0.375; \( \chi_{{E_{2} }} = 200/200 \); \( \chi_{{\rho_{2} }} = 5{,}700/5{,}700 \) (Case C).

Table 7 First six natural frequency coefficients of beams of AFG materials with a step
Full size table

Figure 5 shows the fundamental mode shapes of cantilever Timoshenko beams. Figure 5a corresponds to a uniform beam of homogeneous material. Figure 5b–d correspond to stepped beams, (case Beam C; b 2 = 0.5b 1; h 2 = 0.5h 1), with the step located at l 1 = 0.375, 0.625 and 0.750, respectively. Again the portion of the beam of length L 1 is made of AFG material with n = 3 Eqs. (27–28). The span of length L 2 has homogeneous material. In general, the effect of the step on the dynamic behavior of the beam can be observed in the magnitude of the fundamental frequency coefficient and in the shape associated to this mode.

Fig. 5
figure 5

Fundamental mode shapes of cantilever Timoshenko beams. Beam C; κ = 0.833333; h 0/L = 0.28; h 0 = h 1; h 2 = 0.5h 1; b 2 = 0.5b 1. N = 41. a Uniform beam l 1 = 1, homogeneous material. b Stepped beam l 1 = 0.375, AFG material, n = 3. c Stepped beam l 1 = 0.625, AFG material, n = 3. d Stepped beam l 1 = 0.750, AFG material, n = 3

Full size image

Tables 8 and 9 present frequency coefficients for stepped Timoshenko beams with elastic restrains at external ends. Both Tables are related with the case of stepped Beam C with b 2 = 0.5b 1; h 2 = 0.5h 1. The beam element of length L 1 = 0.625L is made of AFG material with cubic variation, n = 3: \( \chi_{{E_{1} }} = 70/ 200 = 0. 3 5 \); \( \chi_{{\rho_{1} }} = 2{,}700/5{,}700 = 0. 4 7 4 \); the beam element of length L 2 is of homogeneous material: \( \chi_{{E_{2} }} = 200/200 \) = 1; \( \chi_{{\rho_{2} }} = 5{,}700/5{,}700 = 1 \). Boundary conditions are assumed elastic. The translational restrain conditions indicated by \( K_{{W_{j} }} \) with j = 1 and j = N e and the rotational restrains by \( K_{{\Psi_{j} }} \) with j = 1 and j = N e . are varied.

Table 8 First six natural frequency coefficients of beams of AFG material with a step and elastic boundary conditions
Full size table
Table 9 First six natural frequency coefficients of beams of AFG materials with a step and elastic boundary conditions
Full size table

In Table 8 variable boundary conditions are presented, while in Table 9 constant boundary conditions for translational displacements are assumed: \( k_{{W_{1} }} = k_{{W_{Ne} }} = 0.10. \)

In both tables it can be observed that frequency coefficients increase as the boundary conditions stiffen.

5 Conclusions

This paper examines the case of vibrations of stepped inhomogeneous beams on the basis of the Timoshenko beam theory. Different combinations of classical and elastic boundary conditions are considered. The equations of motion for the AFG stepped beams are obtained applying Hamilton’s principle.

The DQM directly solves the ordinary differential equations and it is applied for any type of inhomogeneity in the axial direction (stepped change in geometry and/or material properties).

The variation of the material properties and stepped changes play an important role on the variations of the natural frequency coefficients. It is possible to have lighter structures with higher coefficients of fundamental frequency when the beams are of AFG materials and have stepped variations of the cross-sectional area, second moment of area and material properties.

Additionally, since to the authors’ knowledge this technological situation has not been previously studied in the literature, the present results may be used as a means of comparison for future studies.