1 Introduction

Seeking the analytical solutions is very important in properly understanding features of many phenomena in different fields of natural science. These solutions can be found by using computer symbolic systems like MAPLE or Mathematica. Therefore, studying of various structures of analytical solutions is imperative for mathematics and physics to the complexity and variety of nonlinear dynamics determined by the nonlinear evolution equations (NLEEs) [1,2,3,4,5,6,7,8,9,10].

Many methods have been used to derive the analytical solutions for NLEEs such as the Darboux transformation, bilinear method, homogeneous balance method, and Jacobian elliptic method [11,12,13,14,15,16,17,18].

Here, we introduce the unified method (UM) which is a simple algorithm to construct and study various single traveling wave solutions (TWS) [19,20,21], while to get multi-soliton solutions, the generalized unified method (GUM) is used [22,23,24]. These two methods give us the waveguide (which is a structure that guides waves, such as electromagnetic waves or sound waves) to visualize the propagation of single TWS and multi-soliton solutions under linear refractive index and transmission by considering the dispersion and nonlinearity parameters as the functions of time. We mention that there are other types of the waveguide that can be used in different branches of science such as optical fibers [25, 26], electrodynamics [27], dust plasma [28], and surface water wave in finite water depth [29].

In this paper, we study the single TWS and the double-soliton rational solutions of the KdV–Sawada–Kotera–Ramani equation with variable coefficients which is given by:

$$\begin{aligned}&u_{t}+\,\lambda (t)\,\left( 3\,u^{2}+u_{xx}\right) _{x}+\,\mu (t) \nonumber \\&\quad \left( 15\,u^{3}+15\,u\,u_{x}+u_{xxxx}\right) _{x}=0, \end{aligned}$$
(1)

where \(u=u(x,t)\) is a real-valued function, x is the propagation coordinate and t is the retarded time, and \(\lambda (t),\,\mu (t)\) are arbitrary time-dependent functions. The KdV–Sawada–Kotera–Ramani equation with variable coefficients was widely used when \(\lambda (t)\,\text {and}\,\mu (t)\) are constants [30,31,32]. When \(\lambda (t)=0\) and \(\mu (t)\) is a constant value, Eq. (1) is reduced to the Sawada–Kotera equation which belongs to the completely integrable hierarchy of higher-order KdV equations and has many sets of conservation laws. Also, Eq. (1) is reduced to the KdV equation when \(\mu (t)=0\) and \(\lambda (t)\) is a constant value. Thus it is a linear combination of the KdV equation and the Sawada–Kotera equation.

This paper is organized as follows: In Sect. 2, a brief description of the unified method (UM) and the generalized unified method (GUM) is presented. The application of these methods to the KdV–Sawada–Kotera–Ramani equation with variable coefficients and the waveguide of the obtained solutions is given in Sects. 3 and 4. Finally, conclusions are addressed in Sect. 5.

2 The description of the unified method (UM) and its generalized form (GUM)

In this section, we present the outline of the unified method (UM) and the generalized unified method (GUM).

Consider the NLEEs equations of the type (q + 1)-dimension

$$\begin{aligned}&F_{i}(u_{j},\,(u_{j})_{t},\,(u_{j})_{x_{1}},\ldots ,\,(u_{j})_{x_{q}},\,(u_{j})_{x_{1}\,x_{2}} ,\,(u_{j})_{x_{1}\,x_{3}},\ldots )\,=\,0, \nonumber \\&\quad i,\,j=1,\,2, \ldots \,m, \end{aligned}$$
(2)

where \(u_{j}=u_{j}(t,x_{1},\ldots ,x_{q})\).

2.1 The unified method (UM)

This method is used to find single traveling wave solutions of Eq. (2). The obtained solutions by UM are classified to be the polynomial function solutions or the rational function solutions. Here, we confine ourselves to find only the rational function solutions.

The rational function solution

To get the rational function solutions of Eq. (2), the unified method suggests that

$$\begin{aligned}&u_{j}=u_{j}(z,t)=\displaystyle \sum ^{n}_{i=0}p_{i_{j}}(t)\,\phi ^{i}(z)/ \nonumber \\&\qquad \sum ^{r}_{i=0}q_{i_{j}}(t)\,\phi ^{i}(z),\,n\ge r, \nonumber \\&(\phi '(z))^{p}=\displaystyle \sum ^{p\,k}_{i=0}c_{i}(t)\,\phi ^{i}(z), \nonumber \\&\qquad z=\int \alpha _{0}(t)\,{\hbox {d}}t+\,\sum ^{q}_{s=1}\alpha _{s}\,x_{s}, \nonumber \\&\qquad j=1,2,\ldots ,m,\,p=1,2, \end{aligned}$$
(3)

where \(p_{i_{j}}(t),\, q_{i_{j}}(t)\) and \(c_{i}(t)\) are arbitrary functions to be determined later. It is worth noticing that \(n,\,r\) and k are determined from the balance equation by the criteria given in [19,20,21]. Also, a second condition (the consistency condition), which asserts that the arbitrary functions in Eq. (3) could be consistently determined, is used.

When \(p=1\), (3) solves to elementary solutions (explicit or implicit), while when \(p=2\), it solves to elliptic solutions.

2.2 The generalized unified method (GUM)

Here, we use GUM to find only the solutions in the form of multi-wave rational function solutions [22,23,24].

The multi-wave rational function solutions

Each physical observable \(u_{j}\) in (2) possesses \((q+1)\) basic traveling wave solutions that satisfy the equation

$$\begin{aligned}&H_{i}(U_{j},\,(U_{j})_{z_{1}},\ldots ,\,(U_{j})_{z_{q}},\,(U_{j})_{z_{1}\,z_{2}},\,(U_{j})_{z_{1}\,z_{3}},\ldots )\,=\,0, \nonumber \\&\quad z_{j}\,=\,\int \alpha _{j}(t)\,{\hbox {d}}t+\,\sum ^{q}_{s=1}\alpha _{j,s}\,x_{s}, \end{aligned}$$
(4)

where \(U_{j}=U_{j}(z_{1},\ldots ,z_{q+1})\), \(\alpha _{j}(t)\) are arbitrary functions in t and \(\alpha _{j,s}\) are arbitrary constants. To get the multi-wave rational function solution of Eq. (4), which is a bilinear transform in a linear or a nonlinear combinations of the auxiliary functions \(\phi _{l}(z_{l}),\,l=1,2,\ldots ,N+q-1\), we introduce the steps of computations as follows:

  • Step 1 The GUM asserts the N-wave rational function solutions of Eq. (4)

    $$\begin{aligned}&U_{j}(z_{1},z_{2},\ldots ,z_{N+q-1}) \nonumber \\&\quad \,=\,\dfrac{P_{n}(\phi _{1}(z_{1}),\,\phi _{2}(z_{2}),\ldots ,\phi _{N+q-1}(z_{N+q-1}))}{Q_{r}(\phi _{1}(z_{1}),\,\phi _{2}(z_{2}),\ldots ,\phi _{N+q-1}(z_{N+q-1}))}, \nonumber \\&\quad n\ge r,\,j=1,2,\ldots ,m, \end{aligned}$$
    (5)

    where \(P_{n}\) and \(Q_{r}\) are polynomials in the auxiliary functions \(\phi _{l}(z_{l})\), \(l=1,2,\ldots ,N+q-1\) which satisfy the auxiliary equations

    $$\begin{aligned} (\phi '_{l_{j}}(z_{l_{j}}))^{p}\,= & {} \,\displaystyle \sum _{r=0}^{p\,k}b_{j,r}(t)\,\phi _{l_{j}}^{r}(z_{l_{j}}),\,\,z_{l_{j}} \nonumber \\= & {} \,\int \alpha _{j,0}(t)\,{\hbox {d}}t+\,\displaystyle \sum ^{q}_{s=1} \alpha _{j,s}\,x_{s}, \nonumber \\ p= & {} \,1, 2, \,k\ge 1. \end{aligned}$$
    (6)

    It is worth noticing that \(n,\,r\) and k are determined from the balance equation by the criteria given in [22,23,24]. Also, a second condition (the consistency condition) is used.

    Also, when \(p=1\), (6) solves to elementary solutions (explicit or implicit), while when \(p=2\), it solves to elliptic solutions.

    When \(p=1\) and \(n=r\), then \(k=1\) and the solutions of the auxiliary Eq. (6) are called “jet streams.”

    The polynomial in the numerator of the rational function solutions when \(n=r,\,k=1\) takes the form

    $$\begin{aligned}&P_{n}(\phi _{1}(z_{1}),\,\phi _{2}(z_{2}),\ldots ,\phi _{N+q-1}(z_{N+q-1}))\,=\,a_{0}(t) \nonumber \\&\quad +\,\displaystyle \sum ^{n}_{i_{1}=1}a_{i_{1}}(t) \,\phi _{i_{1}}(z_{i_{1}})+\displaystyle \sum ^{n}_{i_{1},\,i_{2}=1}a_{i_{1},i_{2}}(t)\,\phi _{i_{1}}(z_{i_{1}})\,\phi _{i_{2}}(z_{i_{2}})\nonumber \\&\quad +\,\cdots +\,\displaystyle \sum ^{n}_{i_{1},\,i_{2},\ldots ,i_{N+q-1}=1}a_{i_{1},i_{2},\ldots ,i_{N+q-1}}(t)\, \nonumber \\&\quad \phi _{i_{1}} (z_{i_{1}})\,\phi _{i_{2}}(z_{i_{2}})\ldots \phi _{i_{N+q}}(z_{i_{N+q-1}})+b_{N}(t)\,\displaystyle \nonumber \\&\quad \prod ^{N}_{k=1}\,\phi _{k}(z_{k}),\,n=N+q-1,\nonumber \\ \end{aligned}$$
    (7)

    where \(i_{1}<i_{2}<\cdots <i_{N+q-1}\), \(N\ge 2\) and \(a_{0}(t),\,a_{i_{1}}(t),\,a_{i_{1},i_{2}}(t),\ldots ,a_{i_{1},i_{2},\ldots ,i_{N+q-1}}(t),\,b_{N}(t)\) are arbitrary functions to be determined latter. The polynomial \(Q_{r}(\phi _{1}(z_{1}),\,\phi _{2}(z_{2}),\ldots ,\phi _{N+q-1}(z_{N+q-1}))\) takes a similar form as in (7).

  • Step 2 By inserting (5) together the auxiliary Eq. (6) into (4), we get an equation which is splitting to a set of nonlinear algebraic equations, namely “the principle equations.” They are solved by any computer algebra system. Step 3 Solving the auxiliary equations. Step 4 Finding the formal exact solutions which is given in (5).

For convenience and simplicity, we confine ourselves to find the solutions for one and double-soliton solutions in the form of rational functions.

3 Single rational solutions by using UM

In this section, we apply UM described in Sect. 2 to find single rational solutions of the KdV–Sawada–Kotera–Ramani equation with variable coefficients given by Eq. (1).

Let \(u(x,t)=v(z),\,z=\alpha \,x+\,\int \beta (t)\,{\hbox {d}}t\), where \(\alpha \) and \(\beta (t)\) are the characteristic wave length and frequency, respectively. Substituting about \(u(x,t)=v(z)\) into Eq. (1) yields

$$\begin{aligned}&\mu (t)\,\alpha ^{5}\,v^{(5)}(z) \nonumber \\&\quad +\,(15\,\alpha ^{3}\,\mu (t)\,v(z)+\,\lambda (t)\,\alpha ^{3})\,v^{(3)}(z) \nonumber \\&\quad + \,15\,\alpha ^{3}\,\mu (t)\,\,v'(z)\,v''(z) \nonumber \\&\quad +\,(\beta (t)+6\,\alpha \,\lambda (t)\,v(z)+45\,\alpha \,\mu (t)\,v^{2}(z))\,v'(z), \nonumber \\&\quad z=\,\alpha \,x+\,\int \beta (t)\,{\hbox {d}}t. \end{aligned}$$
(8)

3.1 Soliton solutions

To obtain these solutions, we put \(p=2\) in the auxiliary equation given by (3). From Eq. (3) when \(k=1\) and \(n=r\), we have

$$\begin{aligned}&v(z)=v_{1}(z,t)=\,\dfrac{p_{0}(t)+p_{1}(t)\,\phi (z)}{q_{0}(t) +q_{1}(t)\,\phi (z)}, \nonumber \\&\phi '(z)=\sqrt{c_{0}(t)+c_{1}(t)\,\phi (z)+c_{2}(t)\phi (z)^{2}}. \end{aligned}$$
(9)

By substituting from (9) into (8) and by equating the coefficients of \(\sqrt{c_{0}(t)+c_{1}(t)\,\phi (z)+c_{2}(t)\phi (z)^{2}}\) and \(\phi (z)\) to be zero, we get a set of algebraic equations. By using any package in symbolic computations (such as the elimination method or other suitable solvable method with the aid of Mathematica or MAPLE), we get

$$\begin{aligned}&p_{0}(t)=-\dfrac{q_{1}(t)\,(5\,\alpha ^{2}\,\mu (t)\,c_{2}(t)\,(c_{1}(t)-5\,R(t))+\lambda (t)\,(c_{1}(t)+R(t)))}{30\,\mu (t)\,c_{2}(t)}, \nonumber \\&q_{0}(t)=\dfrac{q_{1}(t)\,(c_{1}(t)+R(t))}{2\,c_{2}(t)}, \nonumber \\&p_{1}(t)=-\dfrac{q_{1}(t)\,(\lambda (t)+5\,\alpha ^{2}\,\mu (t)\,c_{2}(t))}{15\,\mu (t)}, \nonumber \\&\beta (t)=-\alpha ^{5}\,\mu (t)\,c_{2}^{2}(t)+\,\dfrac{\alpha \,\lambda ^{2}(t)}{5\,\mu (t))}, \end{aligned}$$
(10)

where \(R^{2}(t)=\,c_{1}^{2}(t)-4\,c_{0}(t)\,c_{2}(t)\), \(\alpha \) is an arbitrary constant, \(c_{2}(t), c_{1}(t), c_{0}(t)\) and \(q_{1}(t)\) are arbitrary functions.

By solving the auxiliary equations \(\phi '(z)=\,\sqrt{c_{0}(t)+c_{1}(t)\,\phi (z)+c_{2}(t)\phi (z)^{2}}\) and substituting together with (10) into (8), we get the solution of Eq. (1), namely

$$\begin{aligned} u(x,t)= & {} \,-\dfrac{\lambda (t)\,(R(t)+e^{\sqrt{c_{2}(t)}\,(\alpha \,x+\,\int \beta (t)\,{\hbox {d}}t)})^{2} + 5\,\alpha ^{2}\,\mu (t)\,c_{2}(t)\,e^{2\,\sqrt{c_{2}(t)}\,(\alpha \,x+\,\int \beta (t)\,{\hbox {d}}t)}}{15\,\mu (t)\,(e^{\sqrt{c_{2}(t)}\,(\alpha \,x+\,\int \beta (t)\,{\hbox {d}}t)}+R(t))^{2}} \nonumber \\&+\,\dfrac{50\,\alpha ^{2}\,\mu (t)\,c_{2}(t)\,R(t)\,e^{\sqrt{c_{2}(t)}\,(\alpha \,x+\,\int \beta (t)\,{\hbox {d}}t)}+R^{2}(t)}{15\,\mu (t)\,(e^{\sqrt{c_{2}(t)}\,(\alpha \,x+\,\int \beta (t)\,{\hbox {d}}t)}+R(t))^{2}}, \end{aligned}$$
(11)

where \(\beta (t)=\,-\alpha ^{5}\,\mu (t)\,c_{2}^{2}(t)+\,\dfrac{\alpha \,\lambda ^{2}(t)}{5\,\mu (t))}\) and \(c_{2}(t)>0\).

3.2 Periodic solutions

By using the auxiliary equation \(\phi '(z)=\sqrt{c^{2}_{0}(t)-c^{2}_{2}(t)\phi (z)^{2}}\) and by substituting about v(z) given by (9) into (8), we get the rational periodic solutions of (1) as

$$\begin{aligned} u(x,t)= & {} \,-\dfrac{\lambda (t)}{15\,\mu (t)} \nonumber \\&+\,\dfrac{\alpha ^{2}\,c^{2}_{2}(t)\,(-2+\,\sin (c_{2}(t)\,(\alpha \,x+\,\int \beta (t)\,{\hbox {d}}t)))}{3\,(1+\,\sin (c_{2}(t)\,(\alpha \,x+\,\int \beta (t)\,{\hbox {d}}t)))},\nonumber \\ \end{aligned}$$
(12)

where \(\beta (t)=\,-\alpha ^{5}\,\mu (t)\,c_{2}^{4}(t)+\,\dfrac{\alpha \,\lambda ^{2}(t)}{5\,\mu (t))}\), \(\alpha \) is an arbitrary constant and \(c_{2}(t),\,\lambda (t),\,\mu (t)\) are arbitrary functions.

3.3 Elliptic solutions

To obtain rational elliptic solutions, we put \(p=k=2\) in Eq. (3). In this case, the auxiliary equation is given by \(\phi '(z)=\,\sqrt{c_{0}(t)+c_{2}(t)\,\phi ^{2}(z)+c_{4}(t)\,\phi ^{4}(z)}\). By substituting about v(z) given by (9) with the last auxiliary equation into (8) and by using the same steps as we did in the last two cases above, we find that \(c_{i}(t),\,i=0,2,4\) are arbitrary functions and \(c_{4}(t)\,>\,0,\, c_{2}(t)\,c_{0}(t)<0\). For particular values of \(c_{i}(t)\) we get different solutions in Jacobi elliptic functions. So we can take \(c_{i}(t)=\,c_{i}=\text {constant}\).

According to the classification in [33], namely

$$\begin{aligned} c_{4}= & {} \,\frac{4}{m},\,c_{2}=-(m^{2}+6\,m+1),\,c_{0} \nonumber \\= & {} \,m^{4}+2\,m^{3}+m^{2}, \end{aligned}$$
(13)

the auxiliary function takes the form \(\phi (z)=\,\dfrac{m\,\text {dn}(z,m)\,\text {cn}(z,m)}{m\,(\text {sn}^{2}(z,m)-1)}\) and the solution of Eq. (1) will be in the form

$$\begin{aligned} u(x,t)= & {} \,-\dfrac{(4\,\text {cn}(z,m)\,\text {dn}(z,m)+2(m+1)\,\sqrt{m}\,(-1+\,\text {sn}^{2}(z,m)))\,\lambda (t)}{15\,(4\,\text {cn}(z,m)+2\,(1+m)\,\sqrt{m}\,(-1+\,\text {sn}^{2}(z,m)))\,\mu (t)} \nonumber \\&-\dfrac{5\,\alpha ^{2}\,(4\,(5+6\,m+5\,m^{2})\,\text {cn}(z,m)\,\text {dn}(z,m)-2\sqrt{m}(1+m)\,(m^{2}-18\,m+1)((-1+\text {sn}^{2}(z,m))))\mu (t)}{15\,(4\,\text {cn}(z,m)+2\,(1+m)\,\sqrt{m}\,(-1+\,\text {sn}^{2}(z,m)))\,\mu (t)},\nonumber \\ \end{aligned}$$
(14)

where \(z=\,\alpha \,x+\,\int \beta (t)\,{\hbox {d}}t\), \(\beta (t)=\,-\tfrac{\alpha \,(5(1+60\,m+134\,m^{2}+60\,m^{3}+m^{4})\,\alpha ^{4}\,\mu ^{2}(t)-\lambda ^{2}(t))}{5\,\mu (t)}\) and \(0<m<1\) is called the modulus of the Jacobi elliptic functions. When \(m\rightarrow 0\), \(\text {sn}(z)\), \(\text {cn}(z)\) and \(\text {dn}(z)\) degenerate to \(\sin (z)\), \(\cos (z)\) and 1 respectively. While when \(m\rightarrow 1\), \(\text {sn}(z)\), \(\text {cn}(z)\) and \(\text {dn}(z)\) degenerate to \(\tanh (z)\), \(\text {sech}(z)\) and \(\text {sech}(z)\), respectively.

Fig. 1
figure 1

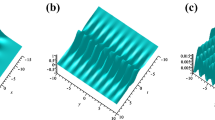
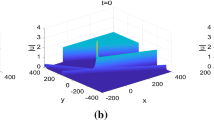
a, b 3D plot and the contour plot for u(x, t) when \(\lambda (t)=\,\tanh (t),\,\mu (t)=\,2+\,\text {sn}(t,0.5)\). c, d 3D plot and the contour plot for u(x, t) when \(\lambda (t)=\,5\,e^{-(t-1)^{2}}+3\,e^{-(t+1)^{2}},\,\mu (t)=2+\,\sin (3\,t)\). \(\alpha _{1}=\,0.4\), \(\beta _{1}=0.35\), and \(c_{1}(t)=2.4,\,c_{2}(t)=2\), \(q_{2}(t)=q_{3}(t)=q_{0}(t)=p_{0}(t)=1\)

Full size image

4 Double-soliton rational solutions by using GUM

Here, we use GUM to find two-soliton rational solutions of Eq. (1). To this end, we use a simple transformation \(u(x,t)=\,u_{1x}(x,t)\) in Eq. (1), and integrating both sides with respect to x, Eq. (1)) can be written as

$$\begin{aligned}&u_{1t}+\,\lambda (t)\,\left( 3\,u_{1x}^{2}+u_{1xxx}\right) +\,\mu (t) \nonumber \\&\quad \left( 15\,u_{1x}^{3}+15\,u_{1x}\,u_{1xx}+u_{1xxxxx}\right) =0, \end{aligned}$$
(15)

where the constant of integration is considered to be zero.

From Eqs. (5) and (6) when \(N=2\), we have

$$\begin{aligned} u_{1}(x,y,t)= & {} \,U(z_{1},z_{2}) \nonumber \\= & {} \,\dfrac{p_{0}(t)+p_{1}(t)\,\phi _{1}(z_{1})+p_{2}(t)\,\phi _{2}(z_{2})+p_{12}(t)\,\phi _{1}(z_{1})\,\phi _{2}(z_{2})}{q_{0}(t)+q_{1}(t)\,\phi _{1}(z_{1})+q_{2}(t)\,\phi _{2}(z_{2})+q_{11}(t)\,\phi _{1}(z_{1})\,\phi _{2}(z_{2})}, \end{aligned}$$
(16)

where \(z_{1}=\,\alpha _{1}\,x+\,\int \alpha _{2}(t)\,{\hbox {d}}t\), \(z_{2}=\,\beta _{1}\,x+\,\int \beta _{2}(t)\,{\hbox {d}}t\), \(\alpha _{1}\), \(\beta _{1}\) are arbitrary constants and \(\alpha _{2}(t)\), \(\beta _{2}(t)\), \(p_{i}(t)\), \(q_{i}(t)\), \(r_{i}(t),\,i=0,1,2,3\) are arbitrary functions. The auxiliary functions \(\phi _{j}(z_{j})\) satisfy the auxiliary equations \(\phi '_{j}(z_{j})=c_{j}(t)\,\phi _{j}(z_{j})\), where \(c_{j}(t)\) are arbitrary analytic functions, \(j=1,2\).

By substituting from (16) into (15) and by equating the coefficients of \(\phi _{j}(z_{j})\) to be zero, we get a set of algebraic equations. By using the same steps as we did in the last two sections, we obtain two-soliton rational solutions of Eq. (1), namely

$$\begin{aligned} u(x,t)= & {} \,u_{1x}(x,t),\,\,u_{1}(x,t)=U(z_{1},z_{2})\nonumber \\= & {} \,\dfrac{R_{-}(t)\,p_{0}(t)\,q_{0}(t)\,q_{2}(t)+R^{2}(t)\,R_{+}(t)\,q_{0}(t)\,q_{3}(t)\, (p_{0}(t)+2\,\alpha _{1}\,c_{1}(t)\,q_{0}(t))\,e^{c_{1}(t)\,z_{1}}}{{R_{-}(t)\,q_{2}(t)\,q_{0}(t)(q_{0}(t)+ q_{2}(t)\,e^{c_{2}(t)\,z_{2}}+q_{3}(t)\,e^{c_{1}(t)\,z_{1}+c_{2}(t)\,z_{2}})+ q^{2}_{0}(t)\,q_{3}(t)\,R_{+}(t)\,e^{c_{1}(t)\,z_{1}}}} \nonumber \\&+\,\dfrac{R_{-}(t)\,q_{2}(t)\,(q_{2}(t)\,(p_{0}(t)+2\,\beta _{1}\,c_{2}(t)\,q_{0}(t))\,e^{c_{2}(t)\,z_{2}}+q_{3}(t)\,(p_{0}(t)+ 2\,R(t)\,q_{0}(t))\,e^{c_{1}(t)\,z_{1}+c_{2}(t)\,z_{2}})}{{R_{-}(t)\,q_{2}(t)\,q_{0}(t)(q_{0}(t)+ q_{2}(t)\,e^{c_{2}(t)\,z_{2}}+q_{3}(t)\,e^{c_{1}(t)\,z_{1}+c_{2}(t)\,z_{2}})+ q^{2}_{0}(t)\,q_{3}(t)\,R_{+}(t)\,e^{c_{1}(t)\,z_{1}}}},\nonumber \\ \end{aligned}$$
(17)

where \(R(t)=\,\alpha _{1}\,c_{1}(t)+\,\beta _{1}\,c_{2}(t)\), \(R_{\pm }(t)=\,(3\,\lambda (t)+5\,\mu (t)\,(\alpha _{1}^{2}\,c_{1}^{2}(t)\pm \alpha _{1}\,\beta _{1}\,c_{1}(t)\,c_{2}(t) +\,\beta _{1}^{2}\,c_{2}^{2}(t)))\,(\alpha _{1}\,c_{1}(t)\pm \beta _{1}\,c_{2}(t))^{2}\), \(z_{1}=\,\alpha _{1}\,x+\,\int \alpha _{2}(t){\hbox {d}}t\), \(z_{2}=\,\beta _{1}\,x+\,\int \beta _{2}(t){\hbox {d}}t\) and \(\alpha _{2}(t)=\,-c_{1}^{2}(t)\,\alpha _{1}^{3}\,(\lambda (t)+\,\mu (t)\,c_{1}^{2}(t)\,\alpha _{1}^{2})\), \(\beta _{2}(t)=\,-c_{2}^{2}(t)\,\beta _{1}^{3}\,(\lambda (t)+\,\mu (t)\,c_{2}^{2}(t)\,\beta _{1}^{2})\).

The solution in (17) of Eq. (1) is shown in Fig. 1 for different values of \(\lambda (t)\) and \(\mu (t)\).

Next, we will investigate the interaction between two-soliton waves based on the solution in (17).

In such inhomogeneous medium as the shallow water and lattice, there are always multiple soliton waves that interact with each other. Figure 1 displays the interactions between the two-soliton waves. The two-soliton waves coincide into one wave and gradually separate into two waves when t tends to positive or negative infinity, which exhibits the typical properties of solitons. It can be seen that when \(\lambda (t)\) and \(\beta (t)\) are being variable the soliton wave with the larger velocity overtakes the one with the lower velocity, and both of them propagate to the opposite direction after the interaction.

We bear in mind that the solutions in this later case (when \(\lambda (t)\) and \(\beta (t)\) are chosen to be periodic or elliptic functions) lead to the formation of rogue waves. Thus, a mechanism or the construction of these waves is due to the interaction between solitons and periodic waves. Also, the position or widths of the solitonic waves change periodically.

5 Conclusion

Here, we have analytically investigated single TWS and multi-soliton rational solutions of the KdV–Sawada–Kotera–Ramani equation with variable coefficients by using the unified method and the generalized unified method, respectively. The methods which we have proposed in this work are standard, direct and computerized methods, which allow us to do complicated and tedious algebraic calculation. Various solutions such as soliton rational solutions, periodic rational solutions, elliptic rational solutions, and two-soliton rational solutions have been obtained. Moreover, the waveguide properties of the characterizing two-soliton waves are shown to be a graded index with reflection component and transmission with periodic distributions in long-distance communication.