1 Introduction

The nonlinear Schrödinger equation (NLSE) is a foundational model to describe numerous nonlinear physical phenomena in the field of nonlinear science such as optical solitons in optical fibers [1]. Optical fiber solitons are considered to be the most important milestone on the road of communication technology. This is because optical solitons are formed as a result of perfect balance between the group velocity dispersion (GVD) and the nonlinear effect, which are considered to be the major problems in optical fibers. The GVD causes the temporal broadening of the optical pulse, due to the frequency dependence on the index of refraction. When an intense optical pulse propagates in silica fiber, the medium tends to behave nonlinearly. Kerr nonlinearity is defined as the intensity dependent index of refraction also called as self-phase modulation (SPM) [2]. As is well known, generalized inhomogeneous nonlinear Schrödinger equation (GINLSE) model is one of the most important and universal models of modern nonlinear science.

However, in a real fiber, the core medium is not homogeneous [3]. There are always some nonuniformities due to many factors and important factors among them are: (i) that which arises from a variation in the lattice parameters of the fiber medium, so that the distance between two neighboring atoms is not constant throughout the fiber and (ii) that due to the variation of the fiber geometry (diameter fluctuations, etc.). These nonuniformities influence various effects such as loss (or gain), dispersion, phase modulation. In recent years, the problem of nonlinear wave propagation in inhomogeneous media is of great interest and has a wide range of applications. When the inhomogeneities in the medium is considered, the dynamics of the optical pulse propagation is governed by the variable coefficient (vc) NLSE [4]. Moreover, the problem of soliton control and the applications of dispersion and nonlinearity management soliton in the nonlinear systems have been also designated by NLSE with variable coefficients and have been extensively studied because of their potential applications and interesting features [5]. Nonautonomous soliton for generalized Hirota equation has been reported [6]. Currently, many effects have been attempted toward the propagation dynamics of optical solitons in inhomogeneous optical fiber media. For instance, with the periodic amplification and dispersion compensation, the propagation of optical pulses in a transmission system is governed by the vc NLSE model [7].

In a general situation, a system receives some form of external time-dependent or space-dependent force, namely a nonautonomous system. These systems support temporal or spatial solitons, soliton lasers and ultrafast soliton switches for experiments. One of the important exact solutions is the so-called nonautonomous soliton solutions, which are potentially useful for various applications in optical soliton telecommunications due to their special properties. These nonautonomous soliton solutions can maintain their overall shapes but allow their widths, amplitudes and the pulse center to change according to the management of the system’s parameters, such as the dispersion, nonlinearity and gain [8]. Up to now, the generalized nonautonomous NLSE with variable coefficients (including dispersion, nonlinearity and gain (loss) terms) and an external potential have been investigated by several authors and also their very interesting properties are reported [9, 10]. He and Li [11] have studied the generalized nonautonomous cubic–quintic NLSE with time- and space-dependent distributed coefficients and external potentials and given the analytical solitary wave solutions to it. You et al. [12] have dealt with snakelike solitons of cubic–quintic NLSE with combined spatiotemporal modulation of nonlinearities and time-dependent linear-lattice potential. More generally, nonautonomous systems with time- and space-dependent distributed coefficients also have very interesting properties but have been the subject of relatively fewer studies. Very recently, Akhmediev breather (AB) of the (3 + 1)-dimensional generalized NLSE with external potentials has been investigated [13] and effect of parity time (PT) symmetric potential has been discussed [14]. Mani Rajan et al. [15] have investigated the generalized NLS–MB equation with external potentials.

However, there are a number of factors, which affect the dynamics of optical solitons and the conditions for the generation of optical solitons in real fibers. In this paper, we aim to provide exact bright multi-soliton solutions of a nonautonomous NLS equation with different form of external potentials, which are important in the realization of real fiber system.

1.1 Nonautonomous nonlinear Schrödinger equation with external potentials

The solution of the NLSE in an inhomogeneous medium is of great importance for investigating wave propagation in various types of physical situations such as plasma physics, nonlinear optics and condensed matter. Serkin et al. [16] have introduced the GINLS equation with external potentials and obtained the one-soliton solution through Lax pair technique. Nonautonomous system with generalized external potentials has some very interesting properties, but relatively there are few studies. They generally move with varying amplitudes, speeds and spectra adapted both to the external potentials and to the dispersion and nonlinearity variations. Due to this novel characteristic, colored nonautonomous solitons in nonlinear and dispersive nonautonomous physical systems have attracted much attention in many different fields. A natural and important issue is how to control the nonautonomous soliton under the influence of external potentials. Therefore it is desired to obtain the stable soliton transmission in fibers, but it is difficult to properly manage the dispersion and nonlinearity in fibers with external potentials even in the presence of dissipation and/or gain? The answer for this question highly depends on our investigation on dynamical behavior of the optical solitons, which is to be taken in this paper. Based on the above motivations, in this paper, we consider GINLS equation with external potentials and gain or loss of the following form:

$$ iQ_{z} + \frac{D(z)}{2}Q_{tt} + \sigma R(z)\left| Q \right|^{2} Q - 2\alpha (z)tQ - \frac{{\varOmega^{2} (z)}}{2}t^{2} Q + iG(z)Q = 0 $$
(1)

with

$$ - \frac{{\varOmega^{2} (z)}}{2}D(z) = \frac{{\partial^{2} }}{{\partial z^{2} }}\ln D(z) + R(z)\frac{{\partial^{2} }}{{\partial z^{2} }}\frac{1}{R(z)} - \frac{\partial }{\partial z}\ln D(z)\frac{\partial }{\partial z}\ln R(z) $$

where Q(z, t) is the complex envelope of the field, D(z) represents the group velocity dispersion (GVD) function and R(z) is the nonlinearity management function. We modify phase modulation term in the Lax pair given in [16] to include gain or loss term, which is to be investigated in this paper. This means that phase modulation and gain parameters are interrelated. Thus one can control the gain through manipulating the phase modulation. The study of Eq. (1) is of great interest and has wide range of applications, which could be used to manage soliton in nonlinear optics. However, the nonlinear equation cannot be solved analytically without any integrable condition. Wu et al. [17] have obtained the rogue wave solution for Eq. (1). Some authors [18] have explained effect of external potential on nonautonomous single soliton via Darboux transformation. However, they did not generate two-soliton solutions, where soliton interaction is possible. In the present work, a generalized nonautonomous NLSE with an external potential describing soliton management in nonlinear optics has been studied.

2 Lax pair

As we know, Lax pair plays an important role in studying the integrable properties of NLS equations. Here we construct the Lax pair of a given system represented by Eq. (1) through AKNS scheme [19] and provide a means for obtaining soliton solutions. The Lax pair of a given system confirms its integrability and provides a means for obtaining soliton solutions. By applying the AKNS formalism, we can construct the linear eigenvalue problem for Eq. (1) as follows:

$$ \psi_{t} = U\psi ,\quad \psi_{z} = V\psi $$
(2)
$$ {\text{where}}\;U\;{\text{and}}\;V\;{\text{are}}\quad U = \left( {\begin{array}{*{20}c} { - i\lambda } & {\sqrt{\sigma} q} \\ { - \sqrt{\sigma} q^{ * } } & {i\lambda } \\ \end{array} } \right)$$
(3)
$$ \begin{aligned} V & = i\left( {\begin{array}{*{20}c} {\frac{\sigma }{2}Dqq^{*} - \alpha t} & {\sqrt{\sigma} D\left( {\frac{1}{2}q_{t} - i\theta tq} \right)} \\ {\sqrt{\sigma} D\left( {\frac{1}{2}q_{t}^{ * } + i\theta tq^{*} } \right)} & { - \frac{\sigma }{2}Dqq^{*} + \alpha t} \\ \end{array} } \right) - i\lambda D\left( {\begin{array}{*{20}c} {\theta t} & {i\sqrt{\sigma} q} \\ { - i\sqrt{\sigma} q^{ * } } & { - \theta t} \\ \end{array} } \right) \\ & \quad - i\lambda^{2} D\left( {\begin{array}{*{20}c} 1 & 0 \\ 0 & 1 \\ \end{array} } \right) \\ \end{aligned} $$

where

$$ \theta (z) = \frac{{D(z)\frac{\partial R(z)}{\partial z} - R(z)\frac{\partial D(z)}{\partial z}}}{{D(z)^{2} R(z)}} - \frac{G(z)}{D(z)} $$

with the transformation

$$ q(z,t) = \sqrt{\frac{R}{D}} Q(z,t)\exp \frac{1}{2}(it^{2} \theta ) $$
(4)

Equation (1) can be obtained from the compatibility condition U z  − V t  + [U, V] = 0 and this condition is satisfied by considering the flow to be nonisospectral:

$$ \lambda = {\text{e}}^{{\int {D(z)\,\theta (z){\text{d}}z} }} (\lambda (0) + \int\limits_{0}^{z} {{\text{e}}^{{ - \int {D(z)\theta (z){\text{d}}z} }} \alpha (z){\text{d}}z)} $$
(5)

The Lax pair confirms the complete integrability of Eq. (1). From this Lax pair, soliton solutions can be obtained by using Darboux transformation as shown below.

3 Darboux transformation

In the present work, with the aid of symbolic computation [20, 21], multi-soliton solutions are generated via Darboux transformation (DT) [22]. The large numbers of effective methods are available to construct soliton solutions for nonlinear Schrödinger equation. Among various methods, the Darboux transformation has been proved to be an efficient technique to find the soliton solution for integrable equations. Moreover, in practice, due to the multi-soliton propagation, the interaction between solitons is inevitable. So we have employed this method to arrive the multi-soliton solution based on the obtained Lax pair as described below

$$ \psi_{t} = U\psi ,\quad \psi_{z} = V\psi $$
(6)

where U and V are given by

$$ U = - i\lambda J + P Z $$
(7)
$$ V = \lambda^{2} D(z)J + \lambda (z)D(z)P + iR $$
(8)

where

$$ J = - i\left( {\begin{array}{*{20}c} 1 & 0 \\ 0 & { - 1} \\ \end{array} } \right),\quad P = \left( {\begin{array}{*{20}c} 0 & q \\ {q^{ * } } & 0 \\ \end{array} } \right) $$
$$ R = i\left( {\begin{array}{*{20}c} {\frac{1}{2}Dqq^{*} - \alpha (z)t} & {D\left( {\frac{1}{2}q_{t} - i\theta tq} \right)} \\ {D\left( {\frac{1}{2}q_{t}^{*} + i\theta tq^{*} } \right)} & { - \frac{1}{2}Dqq^{*} + \alpha (z)t} \\ \end{array} } \right) $$
$$ \theta (z) = \frac{{D(z)\frac{\partial R(z)}{\partial z} - R(z)\frac{\partial D(z)}{\partial z}}}{{D(z)^{2} R(z)}} - \frac{G(z)}{D(z)} $$

with the transformation

$$ q(z,t) = \sqrt{\frac{R}{D}} Q(z,t)\exp \frac{1}{2}(it^{2} \theta ) $$

Equation (1) can be obtained from the compatibility condition U z  + V t  − [U, V] = 0 and this condition is satisfied only if

$$ \frac{\partial \lambda }{\partial z} = \alpha (z) + D(z)\theta (z)\lambda (z) $$

We obtain the two-soliton solutions in clear form by using DT [11]. In the Lax pair, θ(z) is the phase modulation parameter. We stress that phase modulation is related with gain G(z), dispersion D(z) and nonlinearity R(z). This method has been widely used in soliton theory to get exact solution for integrable nonlinear systems. To obtain the multi-soliton solution in explicit form for Eq. (1), based on the Lax pair Eq. (5) and (6), we present N-soliton solution by deriving simple DT as described below.

$$ \psi [1] = (\lambda I - S)\psi $$
(9)
$$ S = H\varLambda H{}^{ - 1} $$
(10)
$$ \varLambda = {\text{diag}}(\varLambda_{1} ,\varLambda_{2} ) $$
(11)

here H is the nonsingular matrix, requiring

$$ H = \left( {\begin{array}{*{20}c} {\phi_{1} } & { - \phi_{2}^{*} } \\ {\phi_{2} } & {\phi_{1}^{*} } \\ \end{array} } \right),\quad \varLambda = \left( {\begin{array}{*{20}c} {\lambda_{1} } & 0 \\ 0 & { - \lambda_{1}^{*} } \\ \end{array} } \right) $$
$$ \varPsi_{t} [1] = U_{1} \varPsi [1] $$

where U 1 = λJ + P 1 with

$$ P_{1} = \left( {\begin{array}{*{20}c} 0 & {q_{1} } \\ {q_{1}^{*} } & 0 \\ \end{array} } \right) $$
(12)

We can get DT for Eq. (1) in the following form,

$$ P_{1} = P + JS - SJ $$
(13)

It is easy to verify that if (φ 1, φ 2)T is a solution of Eq. (4) which corresponds to the eigenvalue λ 1, then (−φ 2*, φ 1*)T(φ 1, φ 2)T is also a solution of Eq. (4), which corresponds to the eigenvalue −λ 1*. Now we take

$$ J = \left( {\begin{array}{*{20}c} 1 & 0 \\ 0 & { - 1} \\ \end{array} } \right) $$

Hence the basic format of S ij is represented through Eq. (9) as

$$ S_{ij} = - i\lambda_{1}^{*} \delta_{ij} - \frac{{i\left( {\lambda_{1} + \lambda_{1}^{*} } \right)\varphi_{i} \varphi_{j}^{*} }}{\Delta } $$
(14)
$$ \Delta = \left| {\varphi_{1} } \right|^{2} + \left| {\varphi_{2} } \right|^{2} $$

Comparing Eqs. (12) and (13), we can get the relation between q 1 and q *1 as

$$ q_{1} = q - 2\sqrt{\frac{D}{R}} S_{12} $$
(15)
$$ q_{1}^{*} = q^{*} - 2\sqrt{\frac{D}{R}} S_{21} $$

Hence the basic form of Darboux transformation for N-soliton solution is,

$$ q_{n} = q + 2\sqrt{\frac{D}{R}} \, \sum {\frac{{\left( {\lambda_{m} + \lambda_{m}^{*} } \right)\phi_{1,m} (\lambda_{m} )\phi^{*}_{2,m} (\lambda_{m} )}}{{A_{m} }}} $$
(16)

where

$$ \phi_{k,m + 1} (\lambda_{m + 1} ) = \left( {\lambda_{m + 1} + \lambda_{m}^{*} } \right)\phi_{k,m} (\lambda_{m + 1} ) - \frac{{B_{m} }}{{A_{m} }}\left( {\lambda_{m} + \lambda_{m}^{*} } \right)\phi_{k,m} (\lambda_{m} ) $$
(17)
$$ A_{m} = \left| {\phi_{1,m} (\lambda_{m} )} \right|^{2} + \left| {\phi_{2,m} (\lambda_{m} )} \right|^{2} $$
$$ B_{m} = \phi_{1,m} (\lambda_{m + 1} )\phi_{1,m}^{*} (\lambda_{m} ) + \phi_{2,m} (\lambda_{m + 1} )\phi_{2,m}^{*} (\lambda_{m} ) $$

where k = 1, 2…n, m = 1, 2…n and ((ϕ 1,1(λ 1), ϕ 2,1(λ 1))T is the eigenfunction of Eq. (4) corresponding to λ 1. Substituting q = 0 in Eq. (17), one can get one-soliton solution for Eq. (1). Using the one-soliton solution as the seed solution in Eq. (17), we can derive the two-soliton solution. Thus in recursion, one can generate up to N-soliton solution. Here we present the one- and two-soliton solutions in explicit forms.

3.1 One-soliton solution

In this way, we present a simple DT for the nonautonomous system and derive some neat analytical expressions for single soliton and two-soliton for the GNLSE, which corresponds to nonisospectral problem. Using DT, the one-soliton solution of the GINLSE is obtained by putting q = 0, k = 1, m = 1 in Eq. (16), with spectral parameter

$$ \lambda (0) = \alpha_{1} + i\beta_{1} $$
(18)

Finally we can get the one-soliton solution of Eq. (1) in the form,

$$ Q_{1} = 2\alpha_{1} \sqrt{\frac{D}{R}} \sec h(2A_{1} )\exp (iB_{1} ) $$
(19)

where

$$ A_{1} = \int {\beta_{1} } D(z)\theta (z)t\;{\text{d}}z - \int {2\alpha_{1} } \beta_{1} \;D(z)\;{\text{d}}z - \beta_{1} t $$
$$ B_{1} = \left( {\int {\alpha_{1}^{2} } D(z){\text{d}}z - \int {\beta_{1}^{2} } D(z){\text{d}}z - \int {\alpha_{1} } D(z)\theta (z)t\;{\text{d}}z - \alpha (z)t} \right) + \frac{1}{2}\theta (z)\;t^{2} $$

Here δ 1 and δ 2 are independent of both z and t. The velocity and the amplitude parameter of the soliton pulses are represented by α 1 and β 1, respectively. D(z) and R(z) correspond to the dispersion and nonlinear parameters, which depend on the propagation distance. If one-soliton solution is calculated, then it is possible to generate the multi-soliton solution in the systematic way.

$$ Q_{n} = Q + 2\sqrt{\frac{D}{R}} \, \sum {\frac{{\left( {\lambda_{m} + \lambda_{m}^{*} } \right)\phi_{1,m} (\lambda_{m} )\phi_{2,m}^{*} (\lambda_{m} )}}{{A_{m} }}} $$
$$ \phi_{k,m + 1} (\lambda_{m + 1} ) = \left( {\lambda_{m + 1} + \lambda_{m}^{*} } \right)\phi_{k,m} (\lambda_{m + 1} ) - \frac{{B_{m} }}{{A_{m} }}\left( {\lambda_{m} + \lambda_{m}^{*} } \right)\phi_{k,m} (\lambda_{m} ) $$
(20)
$$ A_{m} = \left| {\phi_{1,m} (\lambda_{m} )} \right|^{2} + \left| {\phi_{2,m} (\lambda_{m} )} \right|^{2} $$
$$ B_{m} = \phi_{1,m} (\lambda_{m + 1} )\phi_{1,m}^{*} (\lambda_{m} ) + \phi_{2,m} (\lambda_{m + 1} )\phi_{2,m}^{*} (\lambda_{m} ) $$

3.2 Two-soliton solution

The existence of exact soliton pair solutions helps us to understand the collisions between solitons of opposite velocities better. If we take k = 1, 2 and m = 1, 2 in Eq. (20), then we can get the two-soliton solution in the explicit form as follows,

$$ Q(z,t) = Q_{1} + 2\sqrt{\frac{D}{R}} \, \left( {\alpha_{1} \exp (i\beta_{1} )\sec h(2A_{1} ) + 2\alpha_{2} \frac{G}{F}} \right) $$
(21)

where

$$ \begin{aligned} G & = - {\text{e}}^{{ - 2(i\,B_{2} \, + A_{1} \, + A_{2} )}} (({\text{e}}^{{(2i\,B_{2} \, + 2A_{1} \,)}} - ({\text{e}}^{{2i\,B_{2} \,}} + {\text{e}}^{{2(i\,B_{1} \, + A_{1} + A_{2} \,)}} )\sec h(2A_{1} ))\alpha_{1} \\ & \quad + {\text{e}}^{{2i\,B_{2} + \,2A_{1} \,}} (\alpha_{2} + i(\beta_{1} - \beta_{2} )))({\text{e}}^{{2i\,B_{1} }} \sec h(2A_{1} )\alpha_{1} \\ & \quad + {\text{e}}^{{2i\,B_{2} + \,2A_{{_{2} }} \,}} ( - \alpha_{2} + i(\beta_{1} - \beta_{2} ) + \alpha_{1} \tan h(2A_{1} ))) \\ \end{aligned} $$
$$ \begin{aligned} F & = 2(\cos h(2A_{2} )\alpha_{1}^{2} + ( - 2\cos (2(\beta_{1} - \beta_{2} )) + \cos h(2(A_{1} - A_{2} )) - \\ & \quad \cos h(2(A_{1} + A_{2} )))\sec h(2A_{1} )\alpha_{1} \alpha_{2} + \cos h(2A_{2} )(\alpha_{2}^{2} + (\beta_{1} - \beta_{2} )^{2} )) \\ \end{aligned} $$

and

$$ A_{2} = \int {\beta_{2} } D(z)\theta (z)t\,{\text{d}}z - \int {2\alpha_{2} } \beta_{2} D(z)\;{\text{d}}z - \beta_{2} t $$
$$ B_{2} = \left( {\int {\alpha_{2}^{2} } D(z){\text{d}}z - \int {\beta_{2}^{2} } D(z){\text{d}}z - \int {\alpha_{2} } D(z)\theta (z)t\,{\text{d}}z - \alpha (z)t} \right) + \frac{1}{2}\theta (z)t^{2} $$

Having obtained the soliton solution of Eq. (1), our next aim is to analyze the impact of various forms of external potentials by considering various profiles for GVD, nonlinearity and gain parameters as functions of z. Thus this nonautonomous soliton solution can be controlled under dispersion and nonlinearity management. Such an approach may find fruitful applications in Dispersion–Nonlinearity Managed (DNM) soliton systems.

4 Results and discussion

With the entry of dispersion management, the GVD coefficient is no longer a constant, but a function of propagation distance (z). It is a well-known fact that when the group velocity dispersion is varied even slightly, the behavior of the pulse changes drastically from its regular one. The underlying principle of soliton dispersion management is the robustness of optical solitons. In our system represented by Eq. (1), gain parameter is directly related with phase modulation term. Hence, we control phase modulation through gain and vice versa. This is the main feature of our system. This means that whenever we select a specific form for gain, phase modulation gets a new form. As few examples, we have investigated periodic distributed amplification system, dispersion decreasing fiber system and boomerang soliton.

Here, we have considered some important systems that are currently being discussed in the literature and also some new systems for which, we get some exotic solitons like boomerang solitons, phase-shifting solitons, reported for the first time for bright solitons.

4.1 Periodic distributed amplification system

Periodic distributed systems are very important in optical fiber communication system. Because of its potential applications in long distance DMS communication systems. Equation (1) includes mainly two arbitrary distributed functions D(z) and R(z). Thus by selecting the specific form for them, we can analyze this system. To investigate periodic distributed amplification system, varying group velocity dispersion parameter D(z) and nonlinearity parameter R(z) are taken as below [23–26]:

$$ D(z) = \frac{1}{{d_{0} }}\, \exp (kz)R(z) $$
(22)
$$ R(z) = R_{0} + R_{1} \sin (gz) $$

where R 0, R 1 and g are the parameters describing Kerr nonlinearity and d 0 is the parameter related to the initial peak power in the system, respectively. Here, for the sake of simplicity, we take R 0 = 0, d 0 = 1 and g = 1. In this article, we apply the profile (22) in Eqs. (19) and (21) with k > 0.

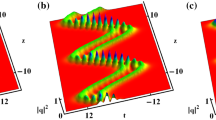
For the choice of k > 0, amplitude of the soliton gradually increases while width oscillates periodically as depicted in Fig. 1(a) and 1(b). This behavior is different from breathing soliton in which, amplitude also varying periodically. It is well known that the classical soliton arises due to the balance between dispersion and nonlinear effects. Then, we can conclude that this oscillating feature that comes from this balance is destroyed periodically. Many different soliton shapes can be achieved through manipulation of dispersion and gain terms. This result has not been reported in the literature and is important for an optimal control of the transmission of optical soliton. If we ignore the gain term, the soliton behavior is different from previous one as shown in Fig. 1(c). With the ignoring of gain term, soliton width is gradually decreased while amplitude is gradually increased which can be clearly observed in Fig. 1(d).

Fig. 1
figure 1

(a) The evolution of the bright one-soliton solution in periodic amplification system with the parameters μ 1 = 1.5, γ 1 = 0.1, and k = 0.07 with G(z) = sin(z). (b) Contour plot of (a). c G(z) = 0. (d) Corresponding to contour plot. (e) The evolution of the bright two-soliton solution in periodic amplification system with parameters are μ 1 = −0.18, μ 2 = −0.15, γ 1 = 2.5, γ 2 = −2.5, k = 0.07 with G(z) = sin(z). (f) Contour plot of (e). (g) The evolution of the bright two-soliton solution in periodic amplification system with parameters are μ 1 = −0.18, μ 2 = −0.15, γ 1 = 2.5, γ 2 = −2.5, k = 0.07 with G(z) = 0. (h) Contour plot of (g)

Full size image

Figure 1(e) and 1(g) denotes the two-soliton behavior under the periodic amplification system without and with gain, respectively. From Fig. 1(e) and 1(g), we can conclude that the interaction between the solitons can be manipulated through gain term. Due to the choice of Eq. (22), solitons are collided periodically as shown in Fig. 1(e). On the other hand, period of oscillation for one of the soliton is gradually decreased while no change in the period of another soliton. If we include the gain term, period of oscillation for both solitons gradually increases with propagation distance. From the analysis, we would like to stress that soliton can be controlled through gain, which is essential for soliton control and soliton management. And this analysis tells that dynamical behaviors of nonautonomous solitons be controlled through gain parameter. Moreover, the soliton under periodic dispersion management can evolve as an oscillating soliton, or breathing soliton, or oscillating breathing soliton. This investigation is constructive to control the soliton.

4.2 Pulse compression

Let us consider the pulse compression of an optical pulse in a dispersion decreasing optical fiber. For this purpose, we assume that the GVD and the nonlinearity functions are distributed in the form given as follows [27–30]:

$$ D(z) = d\,\exp ( - g\;z) $$
(23)
$$ R(z) = r\,\exp ( - k\;z) $$

where d and g are related to GVD parameter and r and k describe the nonlinearity. For g < 0, solitons are compressed exponentially during the propagation. For g > 0, solitons get broadened. For k = −g, width of the pulse remains unchanged.

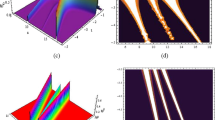
In the absence of gain coefficient, the compression behavior of soliton abruptly disappears with phase shift as shown in Fig. 2(a). From Fig. 2(b), we can infer that the soliton gets compressed during its propagation due to k ≠ 0 with the presence of gain term. This property implies that we can control the soliton width by controlling the gain parameter, which is needful to increase the channel capacity of optical communication system. Figure 2(a) and 2(b) exemplify the soliton pulse management regime under the exponentially distributed dispersion coefficient. In the presence of gain parameter, which is related with phase modulation, the pulse width gradually becomes narrower and narrower. Furthermore, the compressed soliton is completely free from the pedestals, which make the compressed soliton extraordinarily stable during the propagation along the fiber. We hope that obtained results might be useful for soliton compression to achieve the ultrashort pulse. Recently, in dispersion decreasing fiber (DDF), bright and dark soliton solution of NLSE with variable coefficients for various profiles of power law nonlinearity has been studied [31]. In the aspect of soliton application, it is desirable to know how to design related management parameters for certain properties of solitons. Here, as an example, we have studied the nonautonomous soliton propagation in exponentially (DDF).

Fig. 2
figure 2

The evolution of the bright two-soliton solution in dispersion decreasing fiber system with parameters are μ 1 = 0.06, μ 2 = 0.09, γ 1 = 0.8, γ 2 = −0.8 (a) when G(z) = exp (−g z) and (b) when G(z) = 0 with d = r = 1, g = −0.03, and k = −0.04

Full size image

4.3 Boomerang solitons

For soliton application, it is desirable to know how to design related management parameters to understand certain properties of solitons. When we need a certain property of solitons, the explicit functions can give us some hints to design the modulations. This has a significant potential in the application of solitons. For example, to achieve stable peak with varying phase shift along the propagation distance, GVD and nonlinear parameters are considered as follows [32]

$$ D(z) = R(z) = a - bz $$
(24)

In the above expression (24), both the dispersion and nonlinearity parameters are varying linearly with the distance z. For this choice of GVD, nonlinearity and gain parameter, we have obtained boomerang-like solitons as illustrated in the figures of this section. Initially, the parameter G(z), which represents the gain of the medium, has not been kept as a constant. For the simplicity, the gain parameter also considers same as D(z) and R(z). For this choice of gain parameter, we observed two solitons with constant amplitudes as shown in Fig. 3(a). When the gain parameter is made to be zero, one can obtain same behavior except phase shift as depicted in Fig. 3(b). An important point that in the absence of gain parameter, point of collision is not affected. This is one of the peculiar property of soliton.

Fig. 3
figure 3

The evolution of the bright two boomerang soliton with parameters are μ 1 = −0.18, μ 2 = −0.15, γ 1 = 2.5, γ 2 = −2.5, a = 1, b = 0.14: (a) for G(z) = 1, (b) contour plot of (a), (c) for G(z) = 0. (d) contour plot of (c)

Full size image

Based on these graphical illustrations, which describe properties of soliton, including its motion and shape, we can conclude that when the parameters are selected as specific form as given in Eq. (24), the soliton’s shape keeps unchanged even after the collision, which is very desirable for soliton-based communication system. This provides a good way to get stable optical soliton by managing parameters. We believe that it is meaningful in the study of nonautonomous soliton in external potentials. Li and Chen [33] have obtained a particular type of dark solitons, which they have called as boomerang solitons. In the anomalous dispersion regime, one would get bright solitons and we have found that such bright boomerang solitons can exist in nonautonomous NLS systems as depicted in Fig. 3(a)–3(d). Recently, this kind of solitons is observed without interaction in Hirota–Maxwell–Bloch system [34]. Interaction of boomerang solitons of generalized inhomogeneous NLS-MB system has been investigated earlier [35]. It is worth pointing out that the nonautonomous soliton in the present case keeps its shape but its trajectory changes gradually. It provides a possible application in the designing of specific gadgets in the field of optical communication system. We conclude that the law of a soliton adaptation to the external potential offers many opportunities for future scientific studies.

In the optical fiber communications and nonlinear optics, nonlinear Schrödinger systems with variable coefficients such as Eq. (1) have been investigated with the effect of external potential because, it has potential applications in the optical fiber transmission system, ultrafast optical switches, pulse compression, logic gate devices etc. Some previous studies reveal that nonautonomous soliton control is also possible in Bose–Einstein condensate [18, 36, 37]. Furthermore, in this paper, Lax pair with nonisospectral is considered for investigation [38, 39].

5 Conclusions

In this paper, we have analytically investigated the nonautonomous NLS equation with variable coefficients. With symbolic computation, we have applied Darboux transformation to generalized nonautonomous NLS equation with external potentials. By means of obtained one- and two-soliton solutions, propagation characteristics of nonautonomous soliton have been analyzed. With different choices of variable coefficients and through graphical illustrations, the nonautonomous characteristics of the solitons have been studied. A certain way to manage dispersion, nonlinearity and the gain term is found to keep the amplitude of the nonautonomous soliton unchanged, which can be used to improve the quality of soliton transmission.

With the consideration of varying dispersion, nonlinearity and gain, Eq. (1) describes the propagation of optical pulse in an inhomogeneous fiber. In practical case, the model is of primary interest not only for the compression and amplification of optical solutions in an inhomogeneous system, but also for the stable transmission of soliton control. We have found that the gain coefficient function G(z) is only included in the phase modulation function θ(z), therefore, gain can be controlled through phase modulation and vice versa, which is very distinctive from that reported earlier [36].

Up to now, no attempts had been made by relating phase modulation and gain parameters in the literature. The properties are meaningful for the investigation on the stability of soliton propagation in optical soliton communications. Moreover, the characteristic contributions of different control parameters to the soliton dynamics have been clearly identified, which is of significance to guide experiment to control the soliton dynamics. In this paper, main impacts of various types of external potentials on multi-soliton solutions, which are having potential applications in optical communication systems are studied. Obtained result reveals that soliton management can be realized by adjusting the related control parameters. Our results also indicate that a new soliton control technique might be developed. This may make the soliton control technique more realistic and provide prospects for applications in soliton communication system. We hope our outcomes is useful for the further study in optical communications and relative subjects and stimulate novel experiments in the field.