A new design method for adaptive IIR system identification using hybrid CPSO and DE

Abstract

Adaptive infinite impulse response filters have received much attention due to its utilization in a wide range of real-world applications. The design of the IIR filters poses a typically nonlinear, non-differentiable and multimodal problem in the estimation of the coefficient parameters. The aim of the current study is the application of a novel hybrid optimization technique based on the combination of cellular particle swarm optimization and differential evolution called CPSO–DE for the optimal parameter estimation of IIR filters. DE is used as the evolution rule of the cellular part in CPSO to improve the performance of the original CPSO. Benchmark IIR systems commonly used in the specialized literature have been selected for tuning the parameters and demonstrating the effectiveness of the CPSO–DE method. The proposed CPSO–DE method is experimentally compared with two new design methods: the tissue-like membrane system (TMS), the hybrid particle swarm optimization and gravitational search algorithm (HPSO–GSA), the original CPSO-outer and CPSO-inner, and classical implementations of PSO, GSA and DE. Computational results and comparison of CPSO–DE with the other evolutionary and hybrid methods show satisfactory results. The hybridization of CPSO and DE demonstrates powerful estimation ability. In particular, to our knowledge, this hybridization has not yet been investigated for the IIR system identification.

1 Introduction

Adaptive infinite impulse response (IIR) filters have received much attention in recent years due to its current utilization in a wide range of real-world applications such as signal processing, control, communications, parameter identification, image processing and dynamical system modeling [37]. In general, IIR filters are able to model plants more accurately than finite impulse response (FIR) filters [23]. Besides, the IIR filter needs a lesser number of parameters to approximate the dynamical behavior of an unknown plant.

IIR filters are those where the poles and zeros of the transfer function can be adjusted by the coefficient change in the polynomials defining the numerator and denominator [4]. In contrast to the FIR filter, the IIR filter has the advantage that its output is a function of the previous input and output values.

The design of the adaptive IIR filter poses an interesting challenge involving the estimation of the coefficient parameters by a search algorithm [12, 44].

Nevertheless, this design commonly employs a mean square error function (MSE) between the desired response and the output estimated by the filter. MSE is typically nonlinear, non-differentiable and multimodal [24]. Algorithms based on gradient-step methods have been employed in the design of adaptive IIR filters and are able to determine efficiently the optimal solution for unimodal objective functions. However, these can easily fall into local minima and do not converge into the global minimum for multimodal cases [3, 32].

One alternative in the design of adaptive IIR filters are evolutionary and metaheuristic algorithms. These methods have been successfully applied in the mathematical optimization of non-differentiable, nonlinear and multimodal functions. Therefore, there is a significant increase of research in the utilization of these algorithms for the design of adaptive IIR filters.

A number of methods have been proposed for the optimization of adaptive IIR filter design using bio-inspired techniques. For instance, genetic algorithms [13, 21, 26, 42, 43], cat swarm optimization [27], ant colony optimization [14], modified firefly algorithm [33], particle swarm optimization (PSO) [2, 8, 11, 17, 19] and differential evolution (DE) [20]. From these works, PSO and DE show better performance. In order to avoid a premature convergence into local minima and improve the variety of solutions, some hybrid algorithms have been presented combining different techniques [1, 12, 28, 44].

Cellular particle swarm optimization (CPSO) is a recent proposal combining the features of PSO with the neighborhood behavior of cellular automata (CA) [35]. CPSO has been tested on a variety of optimization problems, for instance in milling process [6], the layout of truss structures [10], and the job shop scheduling problem [7], among others. The obtained results have indicated that compared to the existing evolutionary algorithms, the method shows three advantages: better convergence, stronger robustness and a better balance between exploration and exploitation.

The hybridization study of PSO and CA has shown powerful optimization ability for solving complex problems. In particular, to our knowledge, CPSO has not yet been investigated for the problem of IIR system identification.

Based on the above consideration, the motivation of the current study is the application of a novel hybrid optimization technique based on the combination of PSO, CA and DE (CPSO–DE) in the optimal parameter estimation for adaptive IIR system identification. In particular, DE is used as the evolution rule of the cellular part of CPSO to execute a local search in order to improve each particle of the swarm. This hybridization improves the performance of the original CPSO in the parameter estimation.

The paper is organized as follows: Sect. 2 describes the preliminaries of adaptive IIR filters. Section 3 explains the basics of PSO, DE and the two variants of CPSO. Section 4 presents the hybrid algorithm CPSO–DE proposed in this paper for the optimal design of adaptive IIR filter. Section 5 shows the computational results and comparison of CPSO–DE with other evolutionary and hybrid methods, obtaining satisfactory results. The last section gives the concluding remarks of the paper.

2 Adaptive IIR filter

The transfer function in Z of a IIR filter is defined by:

$$\begin{aligned} \frac{Y(z)}{U(z)} = \frac{b_0 + b_1z^{-1}+ \cdots + b_Nz^{-N}}{1+a_1z^{-1}+ \cdots + a_Mz^{-M}} \end{aligned}$$

(1)

where Y(z) and U(z) are the output and the input, respectively, of the IIR filter, $a_1 \; a_2\; \ldots \; a_M$ and $b_0 \; b_1\; \ldots \; b_N$ are the real coefficients of the polynomials, and N and M express the corresponding order of the numerator and the denominator. The difference equation for Eq. 1 is defined by:

$$\begin{aligned} y(k) +\cdots +a_My(k-M)=b_0u(k)+ \cdots + b_N u(k-N) \end{aligned}$$

(2)

If Eq. 2 is represented using a summation notation:

$$\begin{aligned} y(k) = -\sum _{j=1}^{M}a_j y(k-j)+\sum _{i=0}^{N}b_i u(k-i) \end{aligned}$$

(3)

the difference equation is rewritten as:

$$\begin{aligned} y(k) = \varTheta \phi ^T(k) \end{aligned}$$

(4)

where $\varTheta = [-a_1, -a_2, \ldots , -a_M, b_0, b_1, \ldots , b_N]$ and $\phi = [y(k-1), \ldots , y(k-M),u(k), u(k-1), \ldots , u(k-N)]$.

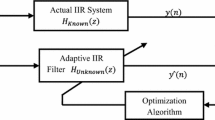
For an adaptive IIR filter, $\varTheta$ is a vector whose elements must be adjusted in order to obtain a desired output y(k). Thus, the output of the IIR filter is a function of $\varTheta$. Figure 1 presents the block diagram for an adaptive IIR filter, which is a classic scheme to identify unknown dynamical systems.

Fig. 1

Identification of a unknown IIR system by means of an adaptive filter

u(k) is the input signal for the unknown system and the adaptive IIR filter, and d(k) is the output signal of the unknown system. v(k) is a noise signal added to d(k); then, y(k) is an output signal of the unknown system with noise. $\hat{y}(k)$ is the estimate output signal from the adaptive IIR filter; e(k) is the deviation between the outputs of both systems; and $\varDelta \varTheta (k)$ is a rate change in the coefficients of the adaptive IIR filter introduced by the evolutionary algorithm to minimize e(k).

Therefore, the identification of the coefficients in $\varTheta$ can be handled as an optimization problem:

$$\begin{aligned} \mathrm{min} E(\varTheta ) = \mathrm{min}\frac{1}{L}\sum _{k=1}^{N}(d(k)-y(k))^2 \end{aligned}$$

(5)

where $E(\varTheta )$ is the MSE produced by the proposed coefficients for the IIR filter, and L is the number of input samples.

3 Particle swarm optimization and differential evolution

Particle swarm optimization (PSO) is a population-based random search method originally developed from studies of social behavior of birds flocks [16]. Since its inception in 1995 by Eberhart and Kennedy [15, 34], it has become one of the most important swarm intelligence-based algorithms. PSO is easy to implement, requires little computational resources and few control parameters [5, 9].

PSO starts with an initial population of randomly generated particles. Each particle is represented as a candidate solution to a problem in a D-dimensional space. We denote the ith particle as $X_{i}=(x_{i1},x_{i2},$ $\ldots ,x_{iD})$, and its velocity as $V_{i}=(v_{i1},v_{i2},\ldots ,v_{iD})$. During the search process, each particle is attracted by its own previous personal best position ($P_{i}$) and the global best position discovered by the swarm ($P_g$). At each time step t, the velocity $V_{i}$ and the position $X_{i}$ of particle i are updated as follows:

$$\begin{aligned} V_{i}^{t+1}= & {} w^tV_i^t+c_1r_1(P_i^t-X_i^t)+c_2r_2(P_g^t-X_i^t) \end{aligned}$$

(6)

$$\begin{aligned} X_i^{t+1}= & {} X_i^t+V_i^{t+1} \end{aligned}$$

(7)

where $i=1,2,\ldots ,Q$ is the particle index and Q is the population size, $c_1$ and $c_2$ are the cognitive and social acceleration parameters, respectively, and $r_1$ and $r_2$ are two uniform distributed random numbers within[0, 1]. Each velocity $V_i$ is bounded between $V_\mathrm{min}$ and $V_\mathrm{max}$. Parameter w is the inertial weight used to balance the global and local search [34]. The inertial weight decreases linearly as:

$$\begin{aligned} w^t=w_\mathrm{max}-t \left( \frac{w_\mathrm{max}-w_\mathrm{min}}{T} \right) \end{aligned}$$

(8)

where $w_\mathrm{max}$ and $w_\mathrm{min}$ define the range of the inertial weight, $t=1,2,\ldots ,T$ is the iteration number and T is a predefined maximum number of iterations.

3.1 Differential evolution

Differential evolution (DE) is a population-based stochastic method for global optimization introduced by Ken Price and Rainer Storn [29, 38,39,40,41].

Similar to PSO, DE starts with an initial population X randomly generated with Q members searching in a D-dimensional space. The basic operators of DE are: mutation, crossover and selection.

The most common scheme “DE/rand/1” creates a new solution $O_{i}=(o_{i1},o_{i2},\ldots ,o_{iD})$ from original solutions in the population as below :

$$\begin{aligned} O_{i}=X_{r_1}+c_3(X_{r_2}-X_{r_3}) \end{aligned}$$

(9)

where $r_1, r_2, r_3 \in \{1,2,\ldots ,Q\}$ are randomly chosen integers, distinct from each other and also different from i. Factor $c_3$ is a real value between [0, 2] used to scale the differential variation $(X_{r_2}-X_{r_3})$.

The crossover is introduced to increment the population’s diversity by creating a trial vector $H_i=(h_{i1},h_{i2},$ $\ldots ,h_{iD})$:

$$\begin{aligned} h_{ij}=\left\{ \begin{array}{ccl} o_{ij},&{} \;&{} \quad \text{ if } r_{ij} \le C_r \; or \; j=j_\mathrm{rand}, \\ \\ x_{ij},&{} \;&{} \quad \mathrm{otherwise}, \end{array} \right. \end{aligned}$$

(10)

where $r_{ij}$ is an uniformly distributed random number within [0, 1], $C_r \in [0,1]$ is the crossover probability factor and $j_{rand}\in \{ 1,2,\ldots ,D\}$ is a randomly chosen index, which ensures that $H_i$ copies at least one component from $O_i$. The selection operation is employed to decide which element ($o_{ij}$ or $x_{ij}$) should be a member of the next generation by

$$\begin{aligned} X'_i=\left\{ \begin{array}{ccl} O_{i},&{} \;&{}\quad if\; f(O_i)\le f(X_i), \\ \\ X_{i},&{} \;&{}\quad \mathrm{otherwise}, \end{array} \right. \end{aligned}$$

(11)

where $X'_i$ is the ith new population individual and f() is the objective function used to compute the fitness values.

3.2 Cellular particle swarm optimization

Cellular particle swarm optimization (CPSO) is a variant of PSO proposed by Shi, Liu, Gao and Zhang [35]. CPSO explores how a particle swarm works similar to cellular automata (CA) [22]. Cellular automata ideas lead to two versions of CPSO, namely, CPSO-inner and CPSO-outer. In the CPSO-inner, each particle is updated by using the information inside the swarm. Meanwhile CPSO-outer exploits the information outside the swarm during the updating process. Particles in the swarm (smart-cells) communicate with cells outside the swarm in order to improve their fitness value. The cellular automata elements used in the PSO algorithm are:

• (a) configuration: (Q particles or smart-cells);

• (b) cell space: the set of all cells;

• (c) cell state: the particle’s information at time t, $S_i^t=[P_i^t,P_g^t,V_i^t,X_i^t]$;

• (d) neighborhood: $\varPhi (i)=\{i+\delta _j\}, 1 \le j \le l$ (l is the neighborhood size).

• (e) transition rule: $S_i^{t+1}=\varphi (S_i^t\cup S^t_{\varPhi (i)})$

3.3 CPSO-inner

In CPSO-inner, all information is derived from the cells inside the swarm. The communication between cells is limited locally to neighborhoods according to three typical lattice structures (cubic, trigonal and hexagonal). The lattice contains the same number of grids that the swarm size.

In CPSO-inner, the transition rule defines a new state $S_i(P_\varPhi )$ for every cell i as:

$$\begin{aligned} S_i^{t+1}(P_\varPhi )= & {} \varphi \left( f \left( S_i^t \left( P_i \right) \right) ,f \left( S_{i+\delta _1}^t \left( P_{i+\delta _1} \right) \right) ,\ldots ,\right. \nonumber \\&\left. f \left( S_{i+\delta _l}^t \left( P_{i+\delta _l} \right) \right) \right) \end{aligned}$$

(12)

where in this case $\varphi$ returns the neighbor with best fitness value.

In order to integrate CA with PSO, the velocity $V_i$, position $X_i$ and personal best state $S_i(P_i)$ of the ith particle are combinated as below:

$$\begin{aligned} V_i^{t+1}= & {} w^tV_i^t+c_1r_1(S_i^t(P_i)-X_i^t)\nonumber \\&+c_2r_2(S_i^{t+1}(P_\varPhi )-X_i^t) \end{aligned}$$

(13)

$$\begin{aligned} X_i^{t+1}= & {} X_i^t+V_i^{t+1} \end{aligned}$$

(14)

3.4 CPSO-outer

In CPSO-outer, the generalized CA strategy is extended by two types of particles: “ smart-cell ” and “ cell .” A smart-cell represents a particle of PSO; on the other hand, a cell represents a candidate solution not sampled yet in the search space. The ith particle’s position $X_i^t$ defines the cell state $S_i^t=X_i^t$. Every smart-cell constructs its neighborhood by the next function:

$$\begin{aligned} \varPhi (j)=\left\{ \begin{array}{lcccc} X_i^t+{f(P_g^t) \over f(X_i^t)}R_j \circ V_i^t \qquad \qquad f(X_i^t)\ne 0,\quad f(P_g^t) \ge 0\\ X_i^t+\left|{f(X_i^t) \over f(P_g^t)} \right|R_j \circ V_i^t \qquad \quad f(X_i^t)\ne 0,\quad f(P_g^t)< 0\\ X_i^t+\left( \frac{e^{f(P_g^t)}}{e^{f(X_i^t)}}\right) ^2 R_j \circ V_i^t \quad f(X_i^t) = 0,\quad f(P_g^t) \ge 0\\ X_i^t+\left( \frac{e^{f(X_i^t)}}{e^{f(P_g^t)}}\right) ^2 R_j \circ V_i^t \quad f(X_i^t) = 0,\quad f(P_g^t) < 0\\ \end{array} \right. \end{aligned}$$

(15)

where $R_j$ is the $1\times D$ vector of direction coefficients composed of D uniform random numbers in $[-1,1]$ for $1 \le j \le l$ and “ $\circ$ ” is the Hadamard product.

At the early iterations, Eq. 15 produces small changes, when the difference between the fitness value of particles with that of the $P_g$ is relatively large. Then, when the particles converge at a point, Eq. 15 provokes larger changes to improve the search. The transition rule in CPSO-outer is similar that the defined in Eq. 12. In this case, the ith particle is replaced by its neighbor with the best fitness values. CPSO-outer gives to particles the ability to make a wise jump, to improve the exploring of the search space in a local competition and enhance the diversity of the swarm.

4 Hybrid cellular particle swarm optimization and differential evolution

In this work, a type of hybridization is presented between CPSO and DE. To achieve this, we are using the key concepts of CPSO-inner and CPSO-outer as base structure, and the idea is to improve the generation of new local information applying DE over the swarm.

CPSO-inner is a kind of local search model, and take the information inside the swarm according to a type of CA lattice structure. For this reason, its optimization capability varies sharply. On the other hand, CPSO-outer has better performance because every particle is able to generate new information from outside the swarm in order to jump from local optima to better positions.

Our proposal (called CPSO–DE) consists of taking the best of both versions, where every particle generates locally new and better information from inside the swarm by an improved transition rule based on DE.

In CPSO–DE, the ith particle’s position $X_i^t$ is the cell state $S_i^t$. We define “smart-cells” and “cells” as well. First, only smart-cells participate in the updating process using the PSO algorithm as follows:

$$\begin{aligned} V_i^{t+1}= & {} w^tV_i^t+c_1r_1(P_i^t-S_i^t)+c_2r_2(Pg^t-S_i^t) \end{aligned}$$

(16)

$$\begin{aligned} S_i^{t+1}= & {} S_i^t+V_i^{t+1} \end{aligned}$$

(17)

In CPSO-outer, the transition rule generates random cells within an arbitrary radius from a smart-cell. In CPSO–DE, however, the inception of new cells is more complex because each smart-cell uses the stochastic optimization method DE in order to produce its neighborhood.

The operators used for determining the neighborhood of each smart-cell are mutation and crossover. Mutation is achieved by the basic schema according to Eq. 9 that calculates a mutated vector $O_i$ for each particle’s neighbor as follows:

$$\begin{aligned} O_{i,k}^t=S_{r_1}^t+c_3(S_{r_2}^t-S_{r_3}^t) \end{aligned}$$

(18)

where $k=1,2,\ldots ,l$ enumerates every neighbor and l is the neighborhood size. $S^t_{r_1}$, $S^t_{r_3}$ and $S^t_{r_3}$ are updated for each neighbor. The crossover follows Eq. 10 in order to create l trial vectors $H_{i,k}$ combining the information of the current smart-cell with each one of the l mutated vector. The advantage of applying differential evolution is to improve the diversity of neighbors instead of a simple l random variations of the smart-cell, obtaining a better jumping ability provided by the swarm. Finally, Eq. 12 is applied over the trial vectors to update the state of the current smart-cell:

$$\begin{aligned} S_i^{t+1}(P_\varPhi )= & {} \varphi (f(S_i^{t+1}),f(H_{i,1}),\nonumber \\&f(H_{i,2}),\ldots ,f(H_{i,l})) \end{aligned}$$

(19)

The transition rule in Eq. 19 means that the cell in the neighborhood (include the same smart-cell) with best fitness value is chosen for updating the smart-cell state.

Figure 2 illustrates the CPSO–DE mechanism. A two-dimensional space is considered and divided by infinite virtual grids. Every grid contains only one solution. Among these grids, smart-cells are marked by gray circles and available neighbors by circles with gray dots. The smart-cell $S_i^t$ is updated to $S_i^{t+1}$ by the PSO algorithm according to Eqs. 16 and 17. Then, three random smart-cells ($S^t_{r_1}$, $S^t_{r_2}$, $S^t_{r_3}$) are selected to generate the mutated vector $O_{i,k}^t$ with Ec. 18. Finally, the possible neighbor is determined by crossover process; thus, the neighbor can be: $H_{i,k}(\alpha _2,\beta _1)$, $H_{i,k}(\alpha _1,\beta _2)$, $O_{i,k}^t$ and even $S_i^{t+1}$. The process is repeated l times for each smart-cell.

The proposed CPSO–DE method is described in Algorithm 1. First, the algorithm sets the control parameters; $x^\mathrm{min}$, $x^\mathrm{max}$, $v_\mathrm{max}$, Q, l, D, $w_\mathrm{min}$, $w_\mathrm{max}$, $c_1$, $c_2$, $c_3$, $C_r$ and T. Next, the velocity, best local position and state (S) are randomly initialized for each cell as in the PSO method. Then, each particle is evaluated and the best global position is identified. In line 11, the process halts according to the stopping criteria of iteration and convergence. Otherwise, the velocity and state of ith cell is updated in lines 13 and 14, respectively. Later, following the DE method, the neighborhood of size l is generated for each cell. Each neighbor is defined by a mutation vector calculated from 3 random cell states ($S_{r_1}$,$S_{r_2}$ and $S_{r_3}$) in line 18. The crossover process in line 19 determines the final neighbor. The transition rule inspired in CA behavior is applied in line 27 to determined the new cell state. Finally, the best local and global position are updated in lines 31 and 34, respectively. The process is repeated by each cell and neighbor. This method will be tuned and tested with the identification of IIR filters in the next section.

Fig. 2

Schematic drawing for CPSO–DE

4.1 Computational complexity analysis

We briefly analyze the time complexity of the proposed method. The identification method consists of four main steps: initialization, local search with differential evolution, swarm evolution with PSO and halting judgment. Note that the CPSO–DE has Q “ smart-cells ” and each one generates l new particles by differential evolution. Let T be the maximum iteration number. Initialization step contains a single loop (Q times), so its time complexity is O(Q). For local search, there are triple loop (Q, l and T times); therefore, its time complexity is O(QlT). The swarm evolution step contains double loop (Q and T times), so its time complexity is O(QT). For halting step, its time complexity is O(1). Therefore, the time complexity of the proposed method is O(QlT).

5 Simulation results and comparison

5.1 Sensitivity analysis of population and neighborhood size

The performance of CPSO–DE depends mainly on the population and neighborhood sizes. Thus, five different benchmark examples with the actual order and reduced order of the plants have been used for tuning these parameters. For the sake of simplicity, the possibles values of the population size Q and the number of neighbors l are selected from the set $\{20,30,40,50,60,70,80,90$, $100\}$ and $\{5,10,15,20,25\}$, respectively. Results are obtained taking the average over 50 independent runs. To overcome the problem caused by the differences of the MSE values for different plants, a normalized function is implemented as follows:

$$\begin{aligned} \varPsi _\kappa (\tau )=\frac{fit_\kappa (\tau )-fit_\mathrm{min}(\tau )}{fit_\mathrm{max}(\tau )-fit_\mathrm{min}(\tau )}, \quad \quad \in [0,1] \end{aligned}$$

(20)

where $\tau$ denotes different benchmark plants $(\tau =$ Example 1: Case 1,$\ldots$,Example 5: Case 1, Example 1: Case 2,$\ldots$, Example 5: Case 2).

$\kappa$ represents the combination between population and neighborhood; in this way, $\kappa = 2ij+m(1-i)-j$, where i and j represents the group index of different parameters Q and l (seemingly, $i=1,2,\ldots ,9$ and $j=1,2,\ldots ,5)$, respectively. m is the neighborhood group size $(m=5)$. $fit_\kappa (\tau )$ is average MSE fitness under the $\kappa$th combinations (ith, jth). $fit_\mathrm{min}(\tau )$ and $fit_\mathrm{max}(\tau )$ denote the minimum and maximum MSE fitness under all $\kappa$th combination for plant $\tau$, respectively. It is evident from the results that the performance of the CPSO–DE is severely affected in two ways. First, all the populations smaller than 30 individuals $(\kappa \le 10)$ have bad performance, as shown in Figs. 3 and  4 (examples with full order and reduced order, respectively). Second, neighborhood sizes greater than 5 individuals have good performance, as shown in Fig. 4.

In conclusion, the CPSO–DE has better performance with population greater than 30 individuals and more than 5 neighbors. It is clear in Fig. 4 that the best results are obtained when population and neighborhood size are fixed at 100 and 25, respectively. Run time, however, is an important issue; therefore, the first point of convergence in the full-order cases $(\kappa =12)$ is chosen for our computational simulations. Hence, a population size of $Q=40$ particles and a neighborhood size $l=10$ are a reasonable choice for the proposed algorithm in the following comparative analysis.

Fig. 3

Normalized average MSE values with different sizes of population and neighborhood for full-order IIR filters

Fig. 4

Normalized average MSE values with different sizes of population and neighborhood for reduced-order IIR filters

5.2 Parameters settings

In the next experiments, five benchmark IIR systems reported in [18, 25, 27, 36] and [31] have been selected to demonstrate the applicability and effectiveness of the CPSO–DE method. For all the cases, the input signal x(k) is a white noise with zero mean, unit variance and uniform distribution, the noise v(k) is absent and the data samples length $L=200$. For maintaining stability, the search space of adaptive IIR filter coefficient used for each case is restricted in the range $(-2,2)$ and 50 independent runs are carried out for all algorithms.

To evaluate the effectiveness and efficiency of the proposed CPSO–DE method, it is experimentally compared with two new design methods: the TMS [44], and the HPSO–GSA [12]. The CPSO-outer and CPSO-inner presented in [35] are also applied. The original PSO [34], GSA [30] and DE [40] have been used as well. Population size $Q=40$ was chosen for the seven algorithms and a maximum number of iterations $T=500$ was taken for all the experimental simulations. The parameters of CPSO, TMS and HPSO–GSA were obtained from [35, 44] and [12], respectively. For PSO, standard velocity model was used, with learning factors $c_1=c_2=1.49491$ and the inertial weight was linearity decreased from 1.4 to 0.6. DE used the original crossover and selection operations reported in [40] and the mutation “DE/rand/1.” The parameters for GSA were configured as recommended by [12] and [30]. Input parameters of CPSO–DE were defines as: $l=10$, $c_1=c_3=0.5$, $c_2=2$, $C_r=0.9$, $w_\mathrm{max}=0.75$, $w_\mathrm{min}=0.15$.

All optimization programs were executed on a Mac OS environment using Intel Core Xeon, 3.5 GHz, 32G RAM memory, and the codes were developed using MATLAB 7.14.

5.3 Description of IIR system identification problems and parameter settings

In order to prove our proposal, we have taken five classical benchmark identification problems reported in [18, 25, 27, 36] and [31]. Each unknown plant is estimated by an IIR filter in two modes, with the same order and with reduced order.

Example 1

The transfer function of a second-order plant is defined by Eq. 21. This has been considered in the works, [25, 36] and [27].

$$\begin{aligned} G_p(z) = \frac{0.05-0.4z^{-1}}{1-1.1314z^{-1}+0.25z^{-2}} \end{aligned}$$

(21)

Case 1 The transfer function of a second-order IIR filter to model the second-order plant is defined by Eq. 22

$$\begin{aligned} G_p(z) = \frac{b_0-b_1z^{-1}}{1-a_1z^{-1}-a_2z^{-2}} \end{aligned}$$

(22)

Case 2 Equation 23 is a reduced-order filter used for identify the dynamics of the second-order plant in Eq. 21.

$$\begin{aligned} G_p(z) = \frac{b_0}{1-a_1z^{-1}} \end{aligned}$$

(23)

Example 2

The transfer function of a third-order plant is defined by Eq. 24. This has been considered in [27].

$$\begin{aligned} G_p(z) = \frac{-0.2-0.4z^{-1}+0.5z^{-2}}{1-0.6z^{-1}+0.25z^{-2}-0.2z^{-3}} \end{aligned}$$

(24)

Case 1 The transfer function of a third-order IIR filter to model the third-order plant is defined by Eq. 25.

$$\begin{aligned} G_p(z) = \frac{b_0+b_1z^{-1}+b_2z^{-2}}{1-a_1z^{-1}-a_2z^{-2}-a_3z^{-3}} \end{aligned}$$

(25)

Case 2 Equation 26 defines a reduced-order filter used to identify the dynamics of the third-order plant in Eq. 24.

$$\begin{aligned} G_p(z) = \frac{b_0+b_1z^{-1}}{1-a_1z^{-1}-a_2z^{-2}} \end{aligned}$$

(26)

Example 3

The transfer function of a fourth-order plant is defined by Eq. 27. This has been considered in [27].

$$\begin{aligned} G_p(z) = \frac{1-0.9z^{-1}+0.81z^{-2}-0.729z^{-3}}{1+0.04z^{-1}+0.2775z^{-2}-0.2101z^{-3}+0.14z^{-4}} \end{aligned}$$

(27)

Case 1 The transfer function of a fourth-order IIR filter to model the fourth-order plant is defined by Eq. 28.

$$\begin{aligned} G_p(z) = \frac{b_0+b_1z^{-1}+b_2z^{-2}+b_3z^{-3}}{1-a_1z^{-1}-a_2z^{-2}-a_3z^{-3}-a_4z^{-4}} \end{aligned}$$

(28)

Case 2 Equation 29 describes a third-order IIR filter used to identify the dynamics of the fourth-order plant in Eq. 27.

$$\begin{aligned} G_p(z) = \frac{b_0+b_1z^{-1}+b_2z^{-2}}{1-a_1z^{-1}-a_2z^{-2}-a_3z^{-3}} \end{aligned}$$

(29)

Table 1 Parameter estimation for Example 1, Case 1

Table 2 Statistical results of MSE values for Example 1, Case 1

Example 4

The transfer function of a fifth-order plant is defined by Eq. 30. This has been considered in [27] and [18].

$$\begin{aligned} G_p(z) = \frac{0.1084+0.5419z^{-1}+1.0837z^{-2}+1.0837z^{-3}+0.5419z^{-4}+0.1084z^{-5}}{1+0.9853z^{-1}+0.9738z^{-2}-0.3854z^{-3}+0.1112z^{-4}+0.0113z^{-5}} \end{aligned}$$

(30)

Case 1 The transfer function of a fifth-order IIR filter to model the fifth-order plant is defined in Eq. 31.

$$\begin{aligned} G_p(z) = \frac{b_0+b_1z^{-1}+b_2z^{-2}+b_3z^{-3}+b_4z^{-4}+b_5z^{-5}}{1-a_1z^{-1}-a_2z^{-2}-a_3z^{-3}-a_4z^{-4}-a_5z^{-5}} \end{aligned}$$

(31)

Case 2 Equation 32 describes a reduced-order filter used to identify the dynamics of the fifth-order plant in Eq. 30.

$$\begin{aligned} G_p(z) = \frac{b_0+b_1z^{-1}+b_2z^{-2}+b_3z^{-3}+b_4z^{-4}}{1-a_1z^{-1}-a_2z^{-2}-a_3z^{-3}-a_4z^{-4}} \end{aligned}$$

(32)

Example 5

The transfer function of a sixth-order plant is defined by Eq. 33. This has been considered in [27] and [18].

$$\begin{aligned} G_p(z) = \frac{1-0.4z^{-2}-0.65z^{-4}+0.26z^{-6}}{1-0.77z^{-2}-0.8498z^{-4}+0.6486z^{-6}} \end{aligned}$$

(33)

Case 1 The transfer function of a sixth-order IIR filter to model the sixth-order plant is defined by Eq. 34.

$$\begin{aligned} G_p(z) = \frac{b_0+b_2z^{-2}+b_4z^{-4}+b_6z^{-6}}{1-a_2z^{-2}-a_4z^{-4}-a_6z^{-6}} \end{aligned}$$

(34)

Case 2 Equation 35 describes a reduced-order filter used to identify the dynamics of the sixth-order plant in Eq. 33.

$$\begin{aligned} G_p(z) = \frac{b_0+b_1z^{-1}+b_2z^{-2}+b_3z^{-3}+b_4z^{-4}+b_5z^{-5}}{1-a_1z^{-1}-a_2z^{-2}-a_3z^{-3}-a_4z^{-4}-a_5z^{-5}} \end{aligned}$$

(35)

Table 3 Statistical results of elapsed time (sec) for Example 1, Case 1

Table 4 Statistical results of MSE values for Example 1, Case 2

Table 5 Statistical results of elapsed time (sec) for Example 1, Case 2

5.4 Simulation results and comparison

The results obtained in all the simulations are shown in the next tables and figures in terms of the convergence characteristics, mean square error (MSE) and elapsed times for both full and reduced order of the IIR plants. The actual and estimated parameters are also provided for full-order plants. The best results obtained by the algorithms are bold-faced in the respective tables. Each run stops when an error zero is reached or the maximum number of iterations is computed.

Example 1: A second-order plant. Two cases with the same-order and reduced-order IIR filters are implemented to validate the performance of CPSO–DE. The estimated parameters values of different algorithms for Case 1 are listed in Table 1. From the table, CPSO-inner (CPSO-I), CPSO-outer (CPSO-O), PSO, DE, HPSO–GSA, TMS and CPSO–DE are capable to estimate the coefficients better than GSA. Tables 2 and 3 provide a quantitative assessment of the performance of all the algorithms considered in terms of MSE values and elapsed times. It is clear that DE and CPSO–DE provide the best results with respect to MSE values. However, CPSO–DE requires higher elapsed times in comparison with PSO, and less run times than CPSO-O, CPSO-I, GSA, DE, HPSO–GSA and TMS in terms of average times. This is because that the CPSO–DE requires more steps than the PSO to update solutions.

In Case 2, a first-order IIR filter is used to model the second-order plant. The statistical results of MSE values and elapsed times are shown in Tables 4 and 5. Table 4 shows that the CPSO–DE obtains the best average results in terms of the MSE values, and the best elapsed times are obtained by PSO.

The convergence behaviors of the best MSE values of two cases using different algorithms are shown in Fig. 5. For Case 1, it is observed that CPSO–DE, DE and TMS obtain the best MSE fitness zero with different number of iterations without any abrupt oscillations. HPSO–GSA shows similar convergence properties; however, they present different solution quality. CPSO-O shows a final convergence value similar to HPSO–GSA but with a slower convergence. The other algorithms are trapped in local minima. Moreover, CPSO–DE rapidly converges to the minimum fitness compared with other algorithms. For Case 2, it can be seen that algorithms fall into local optimum, but CPSO–DE, TMS, DE and HPSO–GSA are able to improve their optima with very similar convergence curves. CPSO-O reaches as well a similar final convergence value but with a slower convergence. Generally, CPSO–DE is successful in finding the minimum MSE solution among the reported methods and can obtain higher-quality estimated coefficients with better convergence property.

Fig. 5

Convergence behaviors for Example 1: a Case 1, b Case 2

Fig. 6

Convergence behaviors for Example 2: a Case 1, b Case 2

Table 6 Parameter estimation for Example 2, Case 1

Example 2: A third-order plant. In the first case, the full-order IIR filters is considered. The convergence behaviors in Fig. 6a indicate that CPSO–DE and DE obtain the best MSE fitness zero with different number of iterations without any abrupt oscillations. TMS shows similar convergence properties; nevertheless, with minor quality. Moreover, CPSO–DE rapidly converges to the minimum fitness compared with other algorithms. Table 6 shows that CPSO-O, PSO, GSA, DE, HPSO–GSA, TMS and CPSO–DE are capable to estimate the coefficients better than CPSO-I. Tables 7 and 8 indicate that DE and CPSO–DE give the best results with respect to MSE values. CPSO–DE demands higher elapsed times in comparison with PSO and GSA and less run times than CPSO-O, CPSO-I, DE, HPSO–GSA and TMS, in terms of average times.

Table 7 Statistical results of MSE values for Example 2, Case 1

Table 8 Statistical results of elapsed time (sec) for Example 2, Case 1

Table 9 Statistical results of MSE values for Example 2, Case 2

Table 10 Statistical results of elapsed time (sec) for Example 2, Case 2

Fig. 7

Convergence behaviors for Example 3: a Case 1, b Case 2

Table 11 Parameter estimation for Example 3, Case 1

In Case 2, a second-order IIR filter is used to model the plant. The convergence behaviors in Fig. 6b show that TMS and CPSO–DE have very similar convergence curves. The other algorithms obtain almost identical values but with a slower convergence. Table 9 shows that the TMS obtains the best average results in terms of the MSE values, but CPSO–DE is very close to it; besides of having the best MSE value. The best elapsed time in average is obtained by PSO from Table 10. In conclusion, CPSO–DE is successful in finding the minimum or close to minimum MSE values with better convergence property.

Example 3: A fourth-order plant. The first case evaluates the full-order IIR filter. The convergence behaviors in Fig. 7a show that CPSO–DE rapidly converges to the minimum MSE fitness zero with the least number of iterations without any abrupt oscillations. DE, GSA and TMS have similar convergence properties; however, they present minor solution quality. CPSO-O improves its convergence in the last iterations. The other algorithms are trapped in local minima. Table 11 shows that CPSO-O, GSA, DE, TMS and CPSO–DE are capable to estimate the coefficients better than the other algorithms. Tables 12 and 13 show that CPSO–DE gives the best results with respect to MSE values requiring higher elapsed times in comparison with PSO, GSA and DE; and less run times than CPSO-O, CPSO-I, HPSO–GSA and TMS in terms of average times.

In Case 2, a third-order IIR filter is used to model the fourth-order plant. The convergence behaviors in Fig. 7b show that algorithms fall into local optimum, but DE, CPSO–DE, TMS and HPSO are able to improve their optima with similar convergence curves. CPSO-O reaches as well a similar final convergence value but with slower convergence. Tables 14 and 15 show that the CPSO–DE obtains the best average MSE value, and the best elapsed time is obtained by PSO.

Table 12 Statistical results of MSE values for Example 3, Case 1

Table 13 Statistical results of elapsed time (sec) for Example 3, Case 1

Table 14 Statistical results of MSE values for Example 3, Case 2

Table 15 Statistical results of elapsed time (sec) for Example 3, Case 2

Fig. 8

Convergence behaviors for Example 4: a Case 1, b Case 2

Table 16 Parameter estimation for Example 4, Case 1

Example 4: A fifth-order plant. The first case evaluates the full-order IIR filter. The convergence behaviors in Fig. 8a show that CPSO–DE falls into a local minimum, but rapidly improves and obtains the best MSE fitness zero without abrupt oscillations. The other algorithms are trapped in local minima. Table 16 shows that CPSO–DE is able to estimate the coefficients better than all the other algorithms. Tables 17 and 18 show that CPSO–DE provides the best results with respect to MSE values requiring higher elapsed times in comparison with all the other algorithms, except for TMS, because of its complexity.

In Case 2, a fourth-order IIR filter is used to model the fifth-order plant. The convergence behaviors in Fig. 8b show that CPSO–DE rapidly converges to the best MSE fitness value without abrupt oscillations. The other algorithms fall into local optimum, but DE, TMS and CPSO-O are able to improve their optima with a convergence slower than CPSO–DE. Tables 19 and 20 show that the CPSO–DE obtains the best average MSE value, and the best elapsed time is obtained by PSO.

Example 5: A sixth-order plant. The first case evaluates the full-order IIR filter. The convergence behaviors in Fig. 9a show that CPSO–DE rapidly converges to best MSE fitness value, with least number of iterations, without any abrupt oscillations. The other algorithms are trapped in local minima. Table 21 shows that CPSO–DE is able to estimate the coefficients better than all the other algorithms. Tables 22 and 23 show that CPSO–DE provides the best results with respect to MSE values requiring higher elapsed times, except for TMS.

In Case 2, a fifth-order IIR filter is used to model the sixth-order plant. The convergence behaviors in Fig. 9b show that CPSO–DE falls into local optimum, but is able to improve and converge to the best MSE fitness value. The other algorithms reach final convergence values with different quality. Tables 24 and 25 show that the CPSO–DE obtains the best average results in terms of the MSE values, and the best elapsed times are obtained by PSO.

Table 17 Statistical results of MSE values for Example 4, Case 1

Table 18 Statistical results of elapsed time (sec) for Example 4, Case 1

Table 19 Statistical results of MSE values for Example 4, Case 2

Table 20 Statistical results of elapsed time (sec) for Example 4, Case 2

Fig. 9

Convergence behaviors for Example 5: a Case 1, b Case 2

Table 21 Parameter estimation for Example 5, Case 1

Table 22 Statistical results of MSE values for Example 5, Case 1

Table 23 Statistical results of elapsed time (sec) for Example 5, Case 1

Table 24 Statistical results of MSE values for Example 5, Case 2

Table 25 Statistical results of elapsed time (sec) for Example 5, Case 2

Generally, CPSO–DE is successful in finding the minimum MSE solution among the reported methods and can obtain higher-quality estimated coefficients with better convergence property.

6 Conclusion

This paper has introduced the use of CPSO–DE hybrid algorithm to develop a novel method for identifying the optimal set of system coefficients with both full-order and reduced-order adaptive IIR filter design.

The proposed method has been compared with seven state-of-the-art evolutionary algorithms. Simulation results show that the proposed method has advantages over PSO, GSA, DE, HPSO–GSA, TMS and both versions of CPSO in terms of the convergence speed and the MSE levels.

Incorporation of CPSO optimization with DE local search brings a remarkable improvement in finding the optimal set of coefficients. The two mechanism can enhance the diversity of solutions and balance exploitation and exploration during the process design.

However, the complexity of the CPSO–DE is higher than that of PSO, GSA, DE and near to that of CPSO-inner, CPSO-outer, HPSO–GSA and TMS. Nevertheless, in all full-order cases, the proposed approach shows convergence in a fewer number of iterations than the other algorithms.

The IIR filters considered in this paper are general, further work should imply the modification of the proposed method to design optimal special filters to solve special image/signal processing problems. Other alternative is to extend the application of the CPSO–DE and explore other optimization problems.