1 Introduction

System identification based on infinite impulse response (IIR) models are preferably utilized in real world applications because they model physical plants more accurately than equivalent FIR (finite impulse response) models. In addition, they are typically capable of meeting performance specifications using fewer filter parameters. However, IIR structures tend to produce multimodal error surfaces for which their cost functions are significantly difficult to minimize. Therefore many conventional methods, especially stochastic gradient optimization strategies, may become trapped in local minima.

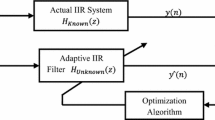
In a system identification configuration, which is generally shown in Fig. 1, the adaptive algorithm attempts to iteratively determine the adaptive filter parameters to get an optimal model for the unknown plant based on minimizing some error function between the output of the adaptive filter and the output of the plant. The optimal model or solution is attained when this error function is minimized. The adequacy of the estimated model depends on the adaptive filter structure, the adaptive algorithm, and also the characteristic and quality of the input-output data (Krusienski 2004). In many cases, however especially when an IIR filter model is applied, this error function becomes multimodal. Hence, in order to use IIR modeling, a practical, efficient, and robust global optimization algorithm is necessary to minimize the multimodal error function. In this regard, two important sets of algorithms are utilized for estimating parameters of IIR model structures: classical algorithms such as gradient based techniques (specially least mean square (LMS)) and the family of least squares, and population based evolutionary algorithms. Krusienski and Jenkins (2005) have shown that LMS may become trapped in local minima and may not find the optimal solution. On the other hand, evolutionary algorithms are robust search and optimization techniques, which have found applications in numerous practical problems. Their robustness are due to their capacity to locate the global optimum in a multimodal landscape (Hegde et al. 2000). Thus several researchers have proposed various methods in order to use EAs, specially genetic algorithm and particle swarm optimization in IIR system identification (Nambiar et al. 1992; Ng et al. 1996; Krusienski 2004; Krusienski and Jenkins 2005). Genetic algorithm is also applied by Yao and Sethares (1994) for identifying IIR and nonlinear models. This issue is explored in more detail by Ng et al. (1996), in which estimated parameters of each IIR model are embedded in one chromosome as real values. Then GA searches the optimal solution (the optimal model) based on mean squared error (MSE) between the unknown plant and the estimated model in the iterative circled process including: selection, reproduction and mutation. Meanwhile, they also have introduced a new search algorithm by combining GA and LMS. Breeder genetic algorithm that has partly changed in selection process is applied to identify adaptive filter model parameters by Montiel et al. (2003 and 2004).

Fig. 1
figure 1

System identification configuration using output error

Full size image

Genetic algorithm and particle swarm optimization (PSO) are applied as an adaptive algorithm for system identification by Krusienski and Jenkins (2005), in which some benchmark IIR and nonlinear filters are used as unknown plants. For IIR plants, the considered models are IIR filters with matched order and reduced order structures. Modified algorithms based on PSO are also applied for IIR model identification (Krusienski and Jenkins 2005; Fang et al. 2009; Majhi and Panda 2009; Luitel and Venayagamoorthy 2010). The enhancements of the most modified PSO algorithms address the two main weaknesses of conventional PSO: outlying particles and stagnation.

Another population based algorithm that has been used for estimating parameters of IIR models is ant colony optimization (ACO) (Karaboga et al. 2004). ACO tends to local minima in complex problems. Meanwhile, its convergence speed is rather low. Karaboga (2009) have applied artificial bee colony algorithm (ABC) for various benchmark IIR model structures in order to show that ABC, similar to PSO, can be useful for system identification. Another evolutionary algorithm named seeker optimization algorithm (SOA) is utilized by Dai et al. (2010) for five benchmark IIR models, and is compared with GA and PSO. The simulation results in this paper show that SOA can compete with PSO in convergence speed and reaching lower MSE surface. Panda et al. (2011) have employed cat swarm optimization algorithm for IIR model identification, and its convergence speed is shown to be not as good as that of PSO.

In this paper three popular algorithms from both classical methods (recursive least square (RLS)) and new population-based algorithms (GA and PSO) are compared for IIR model identification. This comparative study illustrates that these new adaptive algorithms can perform better than the classical one in many complex situations.

This paper is organized as follows. System identification using IIR filter modeling and RLS algorithm as a classical adaptive algorithm are described in Sect. 2. In Sects. 3 and 4, genetic algorithm and particle swarm optimization for IIR modeling are given. Simulations and comparative study come in Sect. 5. Finally, the conclusions and discussions are presented in Sect. 6.

2 Problem statement and RLS algorithm

Consider an IIR filter, that is characterized in direct form by the following recursive expression (Shynk 1989)

$$\begin{aligned} y(n)=\sum _{i=0}^{N} {b_i u(n-i)} -\sum _{j=1}^{M} {a_j y(n-j)} \end{aligned}$$
(1)

where \(u(n)\) and \(y(n)\) represent \(n\)th input and output of the system, \(M\) and \(N\) are the number of numerator and denominator, \(a_{j}\)’s and \(b_{i}\)’s are filter coefficients that define its poles and zeroes respectively. This expression can also be written as the transfer function:

$$\begin{aligned} G(z)=\frac{b_0 +b_1 z^{-1}+{\cdots }+b_M z^{-M}}{1+a_1 z^{-1}+{\cdots }+a_N z^{-N}} \end{aligned}$$
(2)

In IIR model identification based on output error method (see Fig. 1) \(a_{j}\)’s and \(b_{i}\)’s are the unknown constant parameters that can be separated from the known signals \((u(n-i), y(n-j))\) by considering the following static parametric model (Ioannou and Fidan 2006):

$$\begin{aligned} y(n)=\theta ^{*T}(n)\Phi (n) \end{aligned}$$
(3)

where

$$\begin{aligned} \theta ^{*}&= [a_1^*{\ldots }a_N^*b_0^*{\ldots }b_M^*]\end{aligned}$$
(4)
$$\begin{aligned} \Phi (n)&= [-y(n-1){\ldots }-y(n-N)u(n)u(n-1){\ldots }u(n-M)] \end{aligned}$$
(5)

where \(\theta ^{*}\) is the unknown constant vector that should be adjusted by an adaptive algorithm. The estimated output of the process in step n is computed on base of the previous process inputs \(u\) and outputs \(y\) according to Eq. (6):

$$\begin{aligned} \hat{{y}}(n)=\hat{{\theta }}^{T}(n-1)\Phi (n) \end{aligned}$$
(6)

where

$$\begin{aligned} \hat{\theta }=\left[ {\hat{\mathrm{a}}_{1} ,{\ldots },\hat{\mathrm{a}}_N ,\hat{\mathrm{b}}_0 , \hat{\mathrm{b}}_1 ,{\ldots },\hat{\mathrm{b}}_M} \right] \end{aligned}$$
(7)

is the current estimation of unknown model parameters.

One of the conventional classical methods for estimating parameters of \(\theta ^{*}\) is recursive least square, which is developed by solving the minimization problem (Bobal et al. 2005)

$$\begin{aligned} J=\sum _{j=1}^n {\mathop \lambda \nolimits ^{2(n-j)} \varepsilon ^{2}} (j) \end{aligned}$$
(8)

where

$$\begin{aligned} \varepsilon (j)=y(j)-\hat{{\theta }}^{T}(n)\Phi (j) \end{aligned}$$
(9)

and \(0<\lambda \le 1\) is the forgetting factor, and The vector of parameter estimates is updated according to the recursive relation

$$\begin{aligned} \hat{{\theta }}(n)=\hat{{\theta }}(n-1)+g(n)\hat{{e}}(n) \end{aligned}$$
(10)

where

$$\begin{aligned} \hat{{e}}(n)=y(n)-\theta ^{T}(n-1)\Phi (n) \end{aligned}$$
(11)

is the prediction error, and

$$\begin{aligned} g(n)=\frac{p(n-1)\Phi (n)}{\lambda +\Phi ^{T}(n)p(n-1)\Phi (n)} \end{aligned}$$
(12)

is the gain estimation. The square covariance matrix \(p\) is updated by relation

$$\begin{aligned} p(n)=\frac{1}{\lambda }[I-g(n)\Phi ^{T}(n)]p(n-1) \end{aligned}$$
(13)

3 Genetic algorithm for IIR modeling

The genetic algorithm (GA) is an optimization and search technique based on the principles of genetics and natural selection, which is developed by John Holland in the 1960s AD. The usefulness of the GA for function optimization, has attracted increasing attention of researchers in signal processing applications. The GA begins, like any other optimization algorithm, by defining the optimization variables, the cost function, and the cost. It ends also, by testing for convergence.

For IIR model identification, the goal is to optimize the mean squared error between the output plant and output estimated model where we search for an optimal solution in terms of the variables of the vector \(\theta ^{*}\) . Therefore we begin the process of fitting it to a GA by defining a chromosome as an array of variable values to be optimized.

$$\begin{aligned} chromosome=\left[ {\hat{\mathrm{a}}_{1} ,{\ldots },\hat{\mathrm{a}}_N ,\hat{\mathrm{b}}_0 ,\hat{\mathrm{b}}_1 ,{\ldots },\hat{\mathrm{b}}_M } \right] \end{aligned}$$
(14)

The GA starts with a group of chromosomes known as the population. GA allows a population composed of many individuals to evolve under specified selection rules to a state that minimizes the MSE cost function

$$\begin{aligned} \min f=\frac{1}{N_t }\sum _{n=1}^{N_t } {[y(n)-\hat{{y}}_i (n)]^{2}} \end{aligned}$$
(15)

in which \(N_{t}\) is sampling number and \(f\) is the mean squared error between the output plant \((y)\) and output estimated IIR model by \(i\)th chromosome \((\hat{{y}})\). However it is calculated based on decibel (dB) in many practical applications

$$\begin{aligned} \min f=20\log _{10} \left( \frac{1}{N_t }\sum _{n=1}^{N_t } {[y(n)-\hat{{y}}_i (n)]^{2}} \right) \end{aligned}$$
(16)

Survival of the fittest translates into discarding the chromosomes with the highest cost. First, the population costs and associated chromosomes are ranked from lowest cost to highest cost. Then, only the best are selected to continue, while the rest are deleted.

Natural selection occurs in each generation of the algorithm. Of the group of chromosomes in a generation, only the tops survive for mating, and the bottoms are discarded to make room for the new offspring. In this stage, two chromosomes are selected from the mating pool of top chromosomes to produce two new offspring. Pairing takes place in the mating population until the number of offspring are born to replace the discarded chromosomes.

Random mutations alter a certain percentage of the bits in the list of chromosomes. If we manage without mutation term, the GA can converge too quickly into one region of the cost surface. If this area is in the region of the global minimum, that is good. However, MSE cost function for IIR model identification, often, have many local minima. Consequently, If we do nothing to solve this tendency to converge quickly, we could end up in a local rather than a global minimum. To avoid this problem of overly fast convergence, we force the routine to explore other areas of the cost surface by random mutations.

After the mutations take place, the costs associated with the offspring and mutated chromosomes are calculated. The described process is iterated while an acceptable solution is reached or a set number of iterations is exceeded (Haupt and Haupt 2004).

4 Particle swarm optimization for IIR modeling

PSO is a relatively new approach to problem solving that mimics the foraging movement of a flock of birds. The behavior of each bird in the flock to confront to nutrient places is influenced by its own perspective, and also by the reaction of other birds in the flock. PSO exploits a similar mechanism for solving optimization problems.

From the 1995 when the conventional PSO was proposed, PSO attracted the attention of increasing numbers of researchers in signal processing applications. Recall that, for IIR model identification, a global optimization algorithm with fast convergence is required to optimize the MSE cost function, in order to find an optimal solution in terms of the variables of the vector \(\theta ^{*}\). Therefore we embed it to a PSO by defining a position of each particle as an array of variable values to be optimized

$$\begin{aligned} x_{iD} =\left[ {{\hat{\mathrm{a}}}_{1} ,{\ldots },\hat{\mathrm{a}}_N ,\hat{\mathrm{b}}_0 ,\hat{\mathrm{b}}_1 ,{\ldots },\hat{\mathrm{b}}_M } \right] \end{aligned}$$
(17)

The \(D (D=M+N+1)\) dimensional domain of the search space is formed by MSE cost function for the particles

$$\begin{aligned} P_{iD}= f(x_{iD}) \end{aligned}$$
(18)

where f is MSE cost function (Eq. (15) or (16)). Each particle moves through the search space according to its own velocity vector

$$\begin{aligned} \text{ v }_\mathrm{i} =\left( {\text{ v }_{\mathrm{i1}} ,\text{ v }_{\mathrm{i2}},{\ldots },\text{ v }_{\mathrm{iD}} } \right) \end{aligned}$$
(19)

In a PSO algorithm, position and velocity vectors of the particles are adjusted at each iteration of the algorithm

$$\begin{aligned}&\text{ x }_{\mathrm{iD}} \left( {\text{ k }+\text{1 }} \right) = \text{ x }_{\mathrm{iD}} \left( \text{ k } \right) +\text{ v }_{\mathrm{iD}} \left( {\text{ k }+{1}} \right) \end{aligned}$$
(20)
$$\begin{aligned} \text{ v }_{\mathrm{iD}}&\left( {\text{ k }+\text{1 }} \right) =\omega *\text{ v }_{\mathrm{iD}} \left( \text{ k } \right) +\text{ c }_{1} *\text{ rand }_{1} ()*\left( {\text{ P }^{best}_{\mathrm{iD}} -\text{ x }_{\mathrm{iD}} } \right) +\text{ c }_{2} *\text{ rand }_{2} ()*\left( {\text{ P }^{best}_{\mathrm{gD}} -\text{ x }_{\text{ iD }} } \right) \nonumber \\ \end{aligned}$$
(21)

where \(P^{best}_{iD}\) is the priori personal best position found by particle \(i\), the position where the particle found the smallest MSE cost function value, and \(P^{best}_{gD}\) is the global best position found in a whole swarm. Weight \(w\) controls the influence of the previous velocity vector. Parameter \(c_{1}\) controls the impact of the personal best position. Parameter \(c_{2}\) determines the impact of the best position that has been found so far by any of the particles in the swarm. \(rand_{1}\) and \(rand_{2}\) generate random values with uniform probability from the interval \([0, 1]\) for each particle at every iteration (Merkle and Middendorf 2008; Krusienski and Jenkins 2005).

5 Simulation results

In this section, performance of RLS algorithm as a popular classical method is compared with two successful evolutionary algorithms: GA and PSO, for IIR system identification. For this issue, three benchmark IIR filters are considered as unknown plants and optimal reduced order models are searched. In simulations, \(\lambda =1\) is applied for RLS, and \(30\) chromosomes and particles are considered for GA and PSO, with a maximum iteration of \(300\). In addition, input (test) signal is white noise with \(50\) samples \((N_{t}=50)\).

case 1

The first example is a second order benchmark (Netto et al. 1995) with the following transfer function:

$$\begin{aligned} H_{PLANT} (z^{-1})=\frac{0.05-0.4z^{-1}}{1-1.1314z^{-1}+0.25z^{-2}} \end{aligned}$$
(22)

and the model to be identified is a reduced order IIR filter considered as:

$$\begin{aligned} H_{MODEL} (z^{-1})=\frac{b}{1+az^{-1}} \end{aligned}$$
(23)

In this case, The error function is multimodal and finding the optimal solution, \([b,a]=[-0.311,-0.906]\) (Fang et al. 2009) is challenging. Table 1 shows simulation results for 100 independent trials for each algorithm comparatively. Despite the fact that RLS is a proper method for linear identification, it was hardly able here to find the optimal solution. In addition, genetic algorithm has been challenged for finding the optimal model and has succeeded only in 26 % of trials. However, PSO has reached the optimal solution in 93 trials. The values of best estimated results (model parameters) between 100 trials for each algorithm are listed in Table 2. In Fig. 2 MSE fitness curves for three algorithms are plotted for the best trial. It shows that speed convergence of all three algorithms are suitable, while PSO has the fastest convergence. However, only evolutionary algorithms could reach the lower MSE surface and find the global minimum.

Table 1 Case 1 in 100 trials with randomly chosen initial positions
Full size table
Table 2 Best estimated values between 100 trials for case 1
Full size table
Fig. 2
figure 2

Fitness curves for case 1

Full size image

case 2

Consider the second benchmark IIR filter which is selected for this issue (Dai et al. 2010)

$$\begin{aligned} H_{PLANT} (z^{-1})=\frac{-0.3z^{-1}+0.4z^{-2}-0.5z^{-3}}{1-1.2z^{-1}+0.5z^{-2}-0.1z^{-3}} \end{aligned}$$
(24)

and the following reduced order model is meant to be identified:

$$\begin{aligned} H_{MODEL} (z^{-1})=\frac{b_0 +b_1 z^{-1}}{1+a_1 z^{-1}+a_2 z^{-2}} \end{aligned}$$
(25)

In this case, The error function is again multimodal and finding the optimal solution is challenging. Table 3 shows simulation results for 100 independent trials for each algorithm comparatively. As in case 1, again RLS could never find the optimal solution. Genetic algorithm found the optimal model in only 2 trials, and PSO in 16 trials. Table 4 is a list of values of best estimated model parameters between 100 trials for each algorithm. Figure 3 depicts MSE fitness curves for three employed methods. This figure again indicates better convergence speed and also lower MSE surface for evolutionary algorithms.

Table 3 Case 2 in 100 trials with randomly chosen initial positions
Full size table
Table 4 Best estimated values between 100 trials for case 2
Full size table
Fig. 3
figure 3

Fitness curves for case 2

Full size image

In order to more clearly illustrate the better quality of estimated models by evolutionary algorithms compared to RLS for this case, step responses, impulse responses and bode diagrams of best estimated model by each algorithm between 100 independent trials are depicted in Figs. 4, 5, and 6 comparatively. These diagrams illustrate valuable information about system structure that is necessary for other applications such as in controller designing. Therefore it is important that the estimated model behave as similar as possible to the real plant in such responses.

Fig. 4
figure 4

Comparative step responses for case 2

Full size image
Fig. 5
figure 5

Comparative impulse responses for case 2

Full size image
Fig. 6
figure 6

Comparative bode diagrams for case 2

Full size image

Figures 4 and 5 show that how estimated models by evolutionary algorithms have better estimates of step and impulse responses, compared to that of RLS, with respect to the real plant. In addition, they indicate that estimated models by evolutionary algorithms can be acceptable whereas estimated model by RLS is hardly similar to the real plant. Similar results can be seen in bode diagrams in Fig. 6.

case 3

Another benchmark IIR filter which is considered for this issue, is the fifth order IIR plant (Krusienski and Jenkins 2005) with the following transfer function and the reduced order model:

$$\begin{aligned} H_{PLANT} (z^{-1})&= \frac{0.1084\!+\!0.5419z^{-1}\!+\!1.0837z^{-2}\!+\!1.0837z^{-3} \!+\!0.5419z^{-4}\!+\!0.1084z^{-5}}{1\!+\!0.9853z^{-1}\!+\!0.9738z^{-2}\!+\!0.3864z^{-3} \!+\!01112z^{-4}\!+\!0.0113z^{-5}}\qquad \qquad \end{aligned}$$
(26)
$$\begin{aligned} H_{MODEL} (z^{-1})&= \frac{b_0 +b_1 z^{-1}+b_2 z^{-2}+b_3 z^{-3}+b_4 z^{-4}}{1+a_1 z^{-1}+a_2 z^{-2}+a_3 z^{-3}+a_4 z^{-4}} \end{aligned}$$
(27)

This is an example of cases in which RLS algorithm can be successful to estimate parameters of a reduced order model. Simulation results for 100 independent trials for each algorithm are listed in Table 5, where RLS algorithm succeeded to find the optimal solution in whole 100 trials with lowest MSE surfaces. However GA and PSO can find the optimal solution and rarely entrapped to local minima, They are not as capable as RLS to reach the lowest MSE surface on average. Figure 7 has depicted fitness curves for three algorithms in best recorded trial in which all three algorithms could reach proper MSE surface but RLS has faster convergence than the others. Figures 8, 9, and 10 illustrate the acceptable estimates of step and impulse responses and also bode diagrams of all three algorithms. However, it tacks place for evolutionary algorithms when at least, they reach the MSE surfaces under -60 dB. Consequently, RLS outperforms evolutionary algorithms. Therefore, if RLS can escape from local minima, it can quickly tend to the global solution with only a few variables (Table 5).

Table 5 Case 3 in 100 trials with randomly chosen initial positions
Full size table
Fig. 7
figure 7

Fitness curves for case 3

Full size image
Fig. 8
figure 8

Step responses of best estimated models of case 3

Full size image
Fig. 9
figure 9

Impulse responses of best estimated models of case 3

Full size image
Fig. 10
figure 10

Bode diagrams of best estimated models of case 3

Full size image

6 Conclusion

In this study, RLS algorithm as a popular method in classical category was compared with that of two well-known population-based optimization techniques, genetic algorithm and particle swarm optimization, in IIR model identification. From the simulation results, it was observed that evolutionary algorithms are more successful in finding the optimal solution in multimodal landscapes. However in such cases, where RLS escapes from local minima, it can quickly converge to the optimal model, while evolutionary algorithms are still analyzing the costs of the initial population. For these problems the optimizer should use the experience of the past, and employ RLS.

Therefore in practice, where there is no priori information about system order, and multimodality, it is probable that the selected IIR model is reduced order and doesn’t have a same structure of real system. Thus, for such cases it is probable that in system identification process, the error function be multimodal and challenging. Hence evolutionary algorithms have more chance to find the optimal model. Moreover, for such cases with no priori information, that RLS might be more successful, evolutionary algorithms eventually can find an acceptable estimate model. Whereas, if we employ RLS, it may never find an optimal model.