1 Introduction

It is well known that to investigate the integrable properties and construct exact solutions for the nonlinear evolutions equations (NLEEs) play a pivotal role in many nonlinear science fields such as nonlinear optics, fluid dynamics, plasma physical, biology and many other fields. There exist lots of ways to look for special solutions of NLEEs, such as inverse scattering transformation (IST) [1], Lie group method [2], Hirota bilinear method [3], Darboux transformation (DT) [4] and the tanh-coth method [5, 6]. The bilinear method is a canonical and effective way to consider the integrability and exact solutions of NLEEs. However, the method is depended on a appropriate variable transformations, while it is difficult to find such transformations for different equations. Up to now, there is no a effective and convenient method to get such transformations for different equations. Based on above methods, there are plenty of works to be consider for studying integrable properties and exact solutions of NLEEs [7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28].

In the early 1980s, with help of Hirota’s bilinear method and the Riemann theta functions, a successful and effective way [29] is proposed by Nakamura to derive a kind of quasiperiodic solutions of NLEEs. Based on the Bell polynomials [30], a lucid and systematic way [31, 32] is presented by Lambert to investigate bilinear BTs and Lax pairs of integrable equations. More recently, there are a number of works to investigate quasiperiodic solutions of NLEEs [33,34,35,36,37,38,39,40,41,42,43,44,45,46,47].

In recent years, as a part of the KP-type equations, the (3 + 1)-dimensional B-type Kadomtsev–Petviashvili (BKP) equations have attracted intensive attention since they can exactly describe the propagation of nonlinear waves in fluid mechanics and other fields. In the present paper, we would like to investigate a generalized (3 + 1)-dimensional variable-coefficient B-type Kadomtsev–Petviashvili (VC-BKP) equation

$$\begin{aligned}&\left( u_{x}+u_{y}+u_{z}\right) _{t}+\alpha u_{xxxy}+\beta \left( u_{x}u_{y}\right) _{x}\nonumber \\&\qquad +\,\gamma \left( u_{xx}+u_{zz}\right) =0, \end{aligned}$$
(1)

where \(u=u(x,y,z,t)\), \(\alpha =\alpha (t)\), \(\beta =\beta (t)\) and \(\gamma =\gamma (t)\) are all the real differentiable functions, and \(\alpha \), \(\beta \) satisfy the relation \(\alpha /\beta ={\text {constant}}\). If taking \(\alpha =1\), \(\beta =\chi \), \(\gamma =-1\), Eq. (1) can be reduced to the following (3 + 1)-dimensional BKP equation

$$\begin{aligned}&\left( u_{x}+u_{y}+u_{z}\right) _{t}+u_{xxxy} +\chi \left( u_{x}u_{y}\right) _{x}\nonumber \\&\qquad -\left( u_{xx}+u_{zz}\right) =0, \end{aligned}$$
(2)

which can be widely used to describe the propagation of nonlinear waves in fluid dynamics. Its multiple-soliton solutions and conservation laws have been discussed with some specific parameters in [48, 49].

To the best of authors’ knowledge, much research has been studied for the special cases of Eq. (1)., but the multi-periodic wave solutions of Eq. (1) with general form have not been considered before. The main purpose of the present paper is to construct the soliton solutions, periodic wave solutions, traveling wave solutions of Eq. (1), respectively. Furthermore, three crucial theorems are presented to succinctly show a relationship between periodic wave solutions and soliton solutions.

The structure of this paper is given as below. In Sect. 2, the bilinear representations and N-soliton solutions of Eq. (1) will be derived. In Sect. 3, we will construct the multi-periodic wave solutions of Eq. (1). In Sect. 4, more traveling wave solutions of Eq. (1) will be presented. In Sect. 5, the relationship between soliton solutions and periodic wave solutions is strictly established . Some conclusions and appendix are presented in the last section.

2 The bilinear representation and soliton solution

To begin with, let us introduce the following transformation

$$\begin{aligned} u=dq_{x}, \end{aligned}$$
(3)

in which d is a constant. Substituting (3) into Eq. (1) and integrating the obtained equation with respect to x, we obtain

$$\begin{aligned} E(q)= & {} q_{xt}+q_{yt}+q_{zt}+ \alpha \left( q_{xxxy}+3q_{xx}q_{xy}\right) \nonumber \\&+\,\gamma \left( q_{xx}+q_{zz}\right) =0, \end{aligned}$$
(4)

under the following constraint

$$\begin{aligned} {d=3\alpha /\beta ={\text {constant}}.} \end{aligned}$$
(5)

With the use of the results presented in [43,44,45,46,47], we obtain

$$\begin{aligned} E(q)= & {} P_{xt}+P_{yt}+P_{zt}+\alpha P_{xxxy}\nonumber \\&+\,\gamma \left( P_{xx}+P_{zz}\right) =0. \end{aligned}$$
(6)

The expression (6) leads to the following bilinear form

$$\begin{aligned}&\left( \left( D_{x}+D_{y}+D_{z}\right) D_{t}+\alpha D_{x}^{3}D_{y}\right. \nonumber \\&\quad \left. +\,\gamma \left( D_{x}^{2}+D_{z}^{2}\right) \right) F\cdot F=0, \end{aligned}$$
(7)

with the aid of the following transformation

$$\begin{aligned} q=2\ln \left( F\right) \Leftrightarrow u=d(t)q_{x}=\frac{6\alpha }{\beta }\left[ \ln \left( F\right) \right] _{x}. \end{aligned}$$
(8)

Summing up the above detailed analysis, the following Theorem is easily established.

Theorem 2.1

Substituting the following transformation

$$\begin{aligned} u=\frac{6\alpha }{\beta }\left[ \ln (F)\right] _{x} \end{aligned}$$
(9)

into Eq. (1), the VC-BKP equation (1) can be linearized into

$$\begin{aligned}&\left( \left( D_{x}+D_{y}+D_{z}\right) D_{t}+\alpha D_{x}^{3}D_{y}+\gamma \left( D_{x}^{2}+D_{z}^{2}\right) \right) \nonumber \\&\quad F \times \, F=0, \end{aligned}$$
(10)

if and only if \(3\alpha /\beta \) is a constant.

Once the bilinear representation in hand, the N-soliton solutions of Eq. (1) can be easily derived by

$$\begin{aligned}&u=\frac{6\alpha }{\beta }\left[ \ln (F)\right] _{x},\nonumber \\&F=\sum _{\rho =0,1}\exp \left( \sum _{j=1}^{N}\rho _{i}\eta _{i}+\sum _{1\le i<j\le N}\rho _{i}\rho _{j}A_{ij}\right) ,\nonumber \\&\eta _{i}=\mu _{i}x_{i}+\nu _{i}y_{i}+\varrho _{i}z+\omega _{i} t+\delta _{i},\nonumber \\&\omega _{i}=-\frac{\alpha \mu _{i}^{3}\nu _{i}+\gamma \left( \mu _{i}^{2} +\varrho _{i}^{2}\right) }{\mu _{i}+\nu _{i}+\varrho _{i}}, \end{aligned}$$
(11)

with

$$\begin{aligned}&\exp (A_{ij})\nonumber \\&\quad =\frac{\left[ \left( \mu _{i}-\mu _{j}\right) +\left( \nu _{i}-\nu _{j}\right) +\left( \varrho _{i}-\varrho _{j}\right) \right] \left( \omega _{i}-\omega _{j}\right) +\alpha \left( \mu _{i}-\mu _{j}\right) ^{3}\left( \nu _{i}-\nu _{j}\right) +\gamma \left[ \left( \mu _{i}-\mu _{j}\right) ^{2}+\left( \varrho _{i}-\varrho _{j}\right) ^{2}\right] }{\left[ \left( \mu _{i}+\mu _{j}\right) +\left( \nu _{i}+\nu _{j}\right) +\left( \varrho _{i}+\varrho _{j}\right) \right] \left( \omega _{i}+\omega _{j}\right) +\alpha \left( \mu _{i}+\mu _{j}\right) ^{3}\left( \nu _{i}+\nu _{j}\right) +\gamma \left[ \left( \mu _{i}+\mu _{j}\right) ^{2}+\left( \varrho _{i}+\varrho _{j}\right) ^{2}\right] }, \end{aligned}$$
(12)

where \(\mu _{i},\nu _{i},\varrho _{i},\delta _{i}(i=1,2,\ldots ,N)\) are arbitrary real constants, \(\sum _{\rho =0,1}\) is the summation that takes over all possible combinations of \(\rho _{i},\rho _{j}=0,1(i,j=1,2,\ldots ,N)\).

In view of the above expression (12), the VC-BKP equation (1) satisfies the following one-soliton solution

$$\begin{aligned} u=\frac{6\alpha }{\beta }\left[ \ln (1+e^{\eta })\right] _{x}, \end{aligned}$$
(13)

in which \(\eta =\mu x+\nu y+\varrho z -\frac{\alpha \mu ^{3}\nu +\gamma \left( \mu ^{2}+\varrho ^{2}\right) }{\mu +\nu +\varrho } t+\delta \), and \(\mu ,\nu ,\varrho ,\delta \) are arbitrary constants.

In the same process, the two-soliton solution of Eq. (1) admits the following explicit form

$$\begin{aligned}&u=\frac{6\alpha }{\beta }\left[ \ln \left( 1+e^{\eta _{1}}+e^{\eta _{2}}+e^{\eta _{1} +\eta _{2}+A_{12}}\right) \right] _{x},\nonumber \\&\exp (A_{12})\nonumber \\&\quad =\frac{\left[ \left( \mu _{1}-\mu _{2}\right) +\left( \nu _{1}-\nu _{2}\right) +\left( \varrho _{1}-\varrho _{2}\right) \right] \left( \omega _{1}-\omega _{2}\right) +\alpha \left( \mu _{1}-\mu _{2}\right) ^{3}\left( \nu _{1}-\nu _{2}\right) +\gamma \left[ \left( \mu _{1}-\mu _{2}\right) ^{2}+\left( \varrho _{1}-\varrho _{2}\right) ^{2}\right] }{\left[ \left( \mu _{1}+\mu _{2}\right) +\left( \nu _{1}+\nu _{2}\right) +\left( \varrho _{1}+\varrho _{2}\right) \right] \left( \omega _{1}+\omega _{2}\right) +\alpha \left( \mu _{1}+\mu _{2}\right) ^{3}\left( \nu _{1}+\nu _{2}\right) +\gamma \left[ \left( \mu _{1}+\mu _{2}\right) ^{2}+\left( \varrho _{1}+\varrho _{2}\right) ^{2}\right] },\nonumber \\ \end{aligned}$$
(14)

where \(\eta _{i}=\mu _{i}x+\nu _{i}y+\varrho _{i}z -\frac{\alpha \mu _{i}^{3}\nu _{i}+\gamma \left( \mu _{i}^{2}+\varrho _{i}^{2}\right) }{\mu _{i}+\nu _{i}+\varrho _{i}} t+\delta _{i} (i=1,2)\).

In a similar way, three-soliton solution of Eq. (1) admits the following explicit form

$$\begin{aligned}&u=\frac{6\alpha }{\beta }\left[ \ln \left( 1+e^{\eta _{1}}+e^{\eta _{2}}+e^{\eta _{3}}+e^{\eta _{1} +\eta _{2}+A_{12}}+e^{\eta _{1} +\eta _{3}+A_{13}} +e^{\eta _{2}+\eta _{3}+A_{23}}+e^{\eta _{1}+\eta _{2}+\eta _{3}+A_{12}+A_{13}+A_{23}}\right) \right] _{x},\nonumber \\&\exp (A_{ij})\nonumber \\&\quad =\frac{\left[ \left( \mu _{i}-\mu _{j}\right) +\left( \nu _{i}-\nu _{j}\right) +\left( \varrho _{i}-\varrho _{j}\right) \right] \left( \omega _{i}-\omega _{j}\right) +\alpha \left( \mu _{i}-\mu _{j}\right) ^{3}\left( \nu _{i}-\nu _{j}\right) +\gamma \left[ \left( \mu _{i}-\mu _{j}\right) ^{2}+\left( \varrho _{i}-\varrho _{j}\right) ^{2}\right] }{\left[ \left( \mu _{i}+\mu _{j}\right) +\left( \nu _{i}+\nu _{j}\right) +\left( \varrho _{i}+\varrho _{j}\right) \right] \left( \omega _{i}+\omega _{j}\right) +\alpha \left( \mu _{i}+\mu _{j}\right) ^{3}\left( \nu _{i}+\nu _{j}\right) +\gamma \left[ \left( \mu _{i}+\mu _{j}\right) ^{2}+\left( \varrho _{i}+\varrho _{j}\right) ^{2}\right] }, \end{aligned}$$
(15)

where \(\eta _{i}=\mu _{i}x+\nu _{i}y+\varrho _{i}z -\frac{\alpha \mu _{i}^{3}\nu _{i}+\gamma \left( \mu _{i}^{2}+\varrho _{i}^{2}\right) }{\mu _{i}+\nu _{i}+\varrho _{i}} t+\delta _{i} (i,j=1,2,3,i<j)\).

3 Multi-periodic wave solutions

In order to find multi-periodic wave solution of Eq. (1), to begin with, let us consider the following multi-dimensional Riemann theta function

$$\begin{aligned} \vartheta (\xi )=\vartheta (\xi ,\tau )=\sum _{n\in Z^{N}}\exp \left( \pi i\langle n\tau ,n\rangle +2\pi i\langle \xi ,n\rangle \right) ,\nonumber \\ \end{aligned}$$
(16)

in which the vector \(n=(n_{1},n_{2},\dots ,n_{N})^{T}\in Z^{N}\) and variables \(\xi =(\xi _{1},\ldots ,\xi _{N})^{T}\in {\mathbb {C}}^{N}\) and \(-i\tau \) is a real-valued and positive-definite symmetric \(N\times N\) matrix.

If the VC-BKP equation (i.e., Eq. 1) holds the nonzero asymptotic condition \(u\rightarrow u_{0}\) as \(|\xi |\rightarrow 0\), the solution of Eq. (1) has the following form

$$\begin{aligned} u=u_{0}y+\frac{6\alpha }{\beta }\left( \ln \vartheta (\xi )\right) _{x}, \end{aligned}$$
(17)

where \(u_{0}y\) is a solution of Eq. (1), and \(\xi =(\xi _{1},\xi _{2},\ldots ,\xi _{n})^{T},\xi _{i}=k_{i}x+l_{i}y+r_{i}z +{\mathcal {M}}_{i}t+\varepsilon _{i},i=1,\ldots ,n\).

By inserting (17) into Eq. (1), and by integrating with respect to x, Eq. (10) is obtained as follows

$$\begin{aligned}&{\mathscr {Q}}(D_{t},D_{x},D_{y},D_{z})\vartheta (\xi )\cdot \vartheta (\xi )\nonumber \\&\quad = \left( \left( D_{x}+D_{y}+D_{z}\right) D_{t}+\alpha D_{x}^{3}D_{y}+3\alpha u_{0}D_{x}^{2}\right. \nonumber \\&\qquad \left. +\,\gamma \left( D_{x}^{2}+D_{z}^{2}\right) +{\mathcal {C}}\right) F\cdot F=0, \end{aligned}$$
(18)

in which \({\mathcal {C}}={\mathcal {C}}(y,z,t)\) is an integral constant.

In the following, one-periodic wave solutions, two-periodic wave solutions and three-periodic wave solutions will be strictly derived by using Ref. [43].

3.1 One-periodic waves

If we take \(N=1\), the Riemann theta function (16) reduces to the following Fourier series

$$\begin{aligned} \vartheta (\xi )=\vartheta (\xi ,\tau )=\sum _{n\in Z^{N}}\exp ({\pi in^{2}\tau +2\pi in\xi }){,} \end{aligned}$$
(19)

with the phase variable \(\xi =k x+ly+rz+{\mathcal {M}} t+\varepsilon \), and the parameter \({\text {Im}}(\tau )>0\). With the help of Theorem 1 in [43], the following expressions should be satisfied

$$\begin{aligned}&\sum _{n=-\infty }^{+\infty }\varGamma [4n\pi i(k,l,r,{\mathcal {M}})]e^{2n^{2}\pi i\tau }=0,\nonumber \\&\sum _{n=-\infty }^{+\infty }\varGamma [2n\pi i(2n-1)(k,l,r,{\mathcal {M}})]e^{(2n^{2}-2n+1)\pi i\tau }=0. \end{aligned}$$
(20)

The expressions (20) can be rewritten as a linear system by using (18)

$$\begin{aligned}&\sum _{n=-\infty }^{+\infty }\left[ -\left( 16n^{2}\pi ^{2}k +16n^{2}\pi ^{2}l+16n^{2}\pi ^{2}r\right) {\mathcal {M}}\right. \nonumber \\&\qquad +\,256 \alpha n^{4}\pi ^{4}k^{3}l\nonumber \\&\left. \qquad -\gamma \left( 16n^{2}\pi ^{2}k^{2}+16n^{2}\pi ^{2}r^{2}\right) +{\mathcal {C}}\right] e^{2n^{2}\pi i\tau }=0,\nonumber \\&\sum _{n=-\infty }^{+\infty }\left[ -\left( 4\pi ^{2}(2n-1)^{2}k+4\pi ^{2}(2n-1)^{2}l\right. \right. \nonumber \\&\qquad \left. +\,4\pi ^{2}(2n-1)^{2}r\right) {\mathcal {M}} \nonumber \\&\qquad +\,16 \alpha \pi ^{4}(2n-1)^{4}k^{3}l{-}\gamma \left( 4n^{2}\pi ^{2}k^{2} {+}4n^{2}\pi ^{2}r^{2}\right) \nonumber \\&\left. \qquad +\,{\mathcal {C}}\right] e^{(2n^{2}-2n+1)\pi i\tau }=0,~u_{0}=0. \end{aligned}$$
(21)

It is not hard to know that system (21) is equivalent to the following matrix equation

$$\begin{aligned} \left( \begin{array}{cc} a_{11} &{} \quad a_{12} \\ a_{21}&{} \quad a_{22} \\ \end{array} \right) \left( \begin{array}{c} {\mathcal {M}} \\ {\mathcal {C}}\\ \end{array} \right) = \left( \begin{array}{c} b_{1} \\ b_{2} \\ \end{array} \right) , \end{aligned}$$
(22)

where

$$\begin{aligned}&a_{11}=-\sum _{n=-\infty }^{+\infty }\left( 16n^{2}\pi ^{2}k+16n^{2}\pi ^{2}l +16n^{2}\pi ^{2}r\right) {\mathscr {A}}^{2n^{2}},\nonumber \\&a_{12}=\sum _{n=-\infty }^{+\infty }{\mathscr {A}}^{2n^{2}},\nonumber \\&a_{21}=-\sum _{n=-\infty }^{+\infty }\left( 4\pi ^{2}(2n-1)^{2}k\right. \nonumber \\&\left. \qquad +\,4\pi ^{2}(2n-1)^{2}l+4\pi ^{2}(2n-1)^{2}r\right) {\mathscr {A}}^{2n^{2}-2n+1},\nonumber \\&b_{1}=\sum _{n=-\infty }^{+\infty }\left[ -256 \alpha n^{4}\pi ^{4}k^{3}l \right. \nonumber \\&\left. \qquad +\,\gamma \left( 16n^{2}\pi ^{2}k^{2} +16n^{2}\pi ^{2}r^{2}\right) \right] {\mathscr {A}}^{2n^{2}},\nonumber \\&a_{22}=\sum _{n=-\infty }^{+\infty }{\mathscr {A}}^{2n^{2}-2n+1},\nonumber \\&b_{2}=\sum _{n=-\infty }^{+\infty }\left[ -16 \alpha \pi ^{4}(2n-1)^{4}k^{3}l\right. \nonumber \\&\left. \qquad +\,\gamma \left( 4(2n-1)^{2}\pi ^{2}k^{2}+4(2n-1)^{2}\pi ^{2}r^{2}\right) \right] {\mathscr {A}}^{2n^{2}-2n+1},\nonumber \\&{\mathscr {A}}=e^{\pi i\tau }. \end{aligned}$$
(23)

By taking the above system, one-periodic wave of Eq. (1) can be determined by

$$\begin{aligned} u=u_{0}y+\frac{6\alpha }{\beta }\left( \ln \vartheta (\xi )\right) _{x}, \end{aligned}$$
(24)

where the vector \(({\mathcal {M}},{\mathcal {C}})^{T}\) is obtained by using the Cramer’s rule

$$\begin{aligned} {\mathcal {M}}=\frac{\left| \begin{array}{ccc} b_{1} &{} \quad a_{12} \\ b_{2} &{} \quad a_{22} \end{array}\right| }{\left| \begin{array}{ccc} a_{11} &{}\quad a_{12} \\ a_{21} &{}\quad a_{22} \end{array}\right| },~~~~~~ {\mathcal {C}}=\frac{\left| \begin{array}{ccc} a_{11} &{}\quad b_{1} \\ a_{21} &{}\quad b_{2} \end{array}\right| }{\left| \begin{array}{ccc} a_{11} &{}\quad a_{12} \\ a_{21} &{}\quad a_{22} \end{array}\right| }, \end{aligned}$$
(25)

and the other parameters \(k,l,r,\tau ,u_{0}\) are free.

Summing up the above analysis in detail, the following Theorem is easily hold.

Theorem 3.1

Supposing that \(\vartheta (\xi ,\tau )\) is one Riemann theta function with \(N=1\) and \(\xi =k x+ly+rz+{\mathcal {M}} t+\varepsilon ,\) the VC-BKP equation (1) admits the following one-periodic wave solution

$$\begin{aligned} u=u_{0}y+\frac{6\alpha }{\beta }\partial _{x}\ln \vartheta (\xi ), \end{aligned}$$
(26)

where the expression satisfies conditions (23) and (25).

3.2 Two-periodic waves

In order to seek two-periodic wave solutions of Eq. (1). If we take \(N=2\), the Riemann theta function (16) reduces to the following from

$$\begin{aligned} \vartheta (\xi _{1},\xi _{2},\tau )=\sum _{n\in Z^{2}}\exp (\pi i\langle \tau n,n\rangle +2\pi i\langle \xi ,n\rangle ), \end{aligned}$$
(27)

in which \(n=(n_{1},n_{2})\in Z^{2},(\xi _{1},\xi _{2})\in C^{2},\xi _{i}=k_{i} x+l_{i}y+r_{i}z+{\mathcal {M}}_{i} t +\varepsilon _{i},(i=1,2)\). \(-i\tau \) is a positive-define and real-valued symmetric \(2\times 2\) matrix, which is of a explicit form

$$\begin{aligned} \tau =\left( \begin{array}{cc} \tau _{11} &{}\quad \tau _{12} \\ \tau _{21} &{} \quad \tau _{22} \\ \end{array} \right) , \end{aligned}$$
(28)

where \({\text {Im}}(\tau _{11})>0,~{\text {Im}}(\tau _{22})>0,~\tau _{11}\tau _{22}-\tau _{12}^{2}<0\).

Based on Theorem 2 in Ref. [43], the parameters \(k_{i},l_{i},r_{i},{\mathcal {M}}_{i}\) should hold the following expressions

$$\begin{aligned}&\sum _{n\in Z^{2}}\varGamma \left[ 2\pi i(\langle 2n-\theta _{j},k_{i}\rangle , \langle 2n-\theta _{j},l_{i}\rangle \right. ,\nonumber \\&\quad \left. \langle 2n -\theta _{j},r_{i}\rangle ,\langle 2n-\theta _{j},{\mathcal {M}}_{i}\rangle )\right] \nonumber \\&\quad \exp \left[ \pi i(\langle (n-\theta _{j}),n-\theta _{j}\rangle +\langle \pi n,\tau \rangle \right] =0, \end{aligned}$$
(29)

where \(\theta _{j}= \left( \begin{array}{c} \theta _{j}^{1} \\ \theta _{j}^{2}\\ \end{array} \right) , \theta _{1}= \left( \begin{array}{c} 0 \\ 0\\ \end{array} \right) , \theta _{2}= \left( \begin{array}{c} 1\\ 0\\ \end{array} \right) , \theta _{3}= \left( \begin{array}{c} 0 \\ 1\\ \end{array} \right) , \theta _{4}= \left( \begin{array}{c} 1 \\ 1\\ \end{array} \right) ,~~j=1,2,3,4.\) Linking expressions (18) and (29) arrive at the following expressions

$$\begin{aligned}&\sum _{n\in Z^{2}}\left[ -4\pi ^{2}\langle 2n-\theta _{j},{\mathcal {M}}\rangle \left( \langle 2n-\theta _{j},k\rangle +\langle 2n-\theta _{j},l\rangle \right. \right. \nonumber \\&\left. \left. \qquad +\,\langle 2n-\theta _{j},r\rangle \right) +16 \alpha \pi ^{4}\langle 2n-\theta _{j},k\rangle ^{3}\langle 2n-\theta _{j},l\rangle \right. \nonumber \\&\left. \qquad -\,12\alpha u_{0} \pi ^{2}\langle 2n-\theta _{j},k\rangle ^{2}-4\pi ^{2}\gamma \left( \langle 2n-\theta _{j},k\rangle ^{2} \right. \right. \nonumber \\&\left. \left. \qquad +\,\langle 2n-\theta _{j},r\rangle ^{2}\right) +{\mathcal {C}}\right] \exp \left[ \pi i(\langle (n-\theta _{j}),n-\theta _{j})\right. \nonumber \\&\left. \qquad +\,\langle \pi n,\tau \rangle \right] =0, \quad j=1,2,3,4. \end{aligned}$$
(30)

The above equation can be reduced to a new form of matrix equation

$$\begin{aligned} \left( \begin{array}{cccc} h_{11} &{}\quad h_{12} &{}\quad h_{13} &{}\quad h_{14} \\ h_{21}&{}\quad h_{22} &{}\quad h_{23} &{}\quad h_{24} \\ h_{31} &{}\quad h_{32} &{}\quad h_{33} &{}\quad h_{34} \\ h_{41} &{}\quad h_{42} &{}\quad h_{43} &{}\quad h_{44} \\ \end{array} \right) \left( \begin{array}{c} {\mathcal {M}}_{1} \\ {\mathcal {M}}_{2} \\ u_{0} \\ {\mathcal {C}} \\ \end{array} \right) =\left( \begin{array}{c} b_{1} \\ b_{2}\\ b_{3} \\ b_{4} \\ \end{array} \right) , \end{aligned}$$
(31)

where

$$\begin{aligned}&H=(h_{ij})_{4\times 4}, \quad b=(b_{1},b_{2},b_{3},b_{4})^{T},\nonumber \\&h_{i1}=-4\pi ^{2}\sum _{(n_{1},n_{2})\in Z^{2}}\left( \langle 2n-\theta _{j},k\rangle +\langle 2n-\theta _{j},l\rangle \right. \nonumber \\&\left. \qquad +\,\langle 2n-\theta _{j},r\rangle \right) \left( 2n_{1}-\theta _{1}\right) {\mathscr {N}}_{i}(n), \nonumber \\&h_{i2}=-4\pi ^{2}\sum _{(n_{1},n_{2})\in Z^{2}}\left( \langle 2n-\theta _{j},k\rangle +\langle 2n-\theta _{j},l\rangle \right. \nonumber \\&\left. \qquad +\,\langle 2n-\theta _{j},r\rangle \rangle \right) (2n_{2}-\theta _{i}^{2}){\mathscr {N}}_{i}(n),\nonumber \\&h_{i3}=-12\alpha \pi ^{2}\sum _{(n_{1},n_{2})\in Z^{2}}\langle 2n-\theta _{i},k\rangle ^{2}{\mathscr {N}}_{i}(n),\nonumber \\&h_{i4}=\sum _{(n_{1},n_{2})\in Z^{2}}{\mathscr {N}}_{i}(n),\nonumber \\&b_{i}=\sum _{(n_{1},n_{2})\in Z^{2}}\left[ -16 \alpha \pi ^{4}\langle 2n-\theta _{i},k\rangle ^{3}\langle 2n-\theta _{i},l\rangle \right. \nonumber \\&\left. \qquad +\,4\pi ^{2}\gamma \left( \langle 2n-\theta _{j},k\rangle ^{2}+\langle 2n-\theta _{j},r\rangle ^{2}\right) \right] {\mathscr {N}}_{i}(n),\nonumber \\&{\mathscr {N}}_{i}(n)={\mathscr {A}}_{1}^{n_{1}^{2}+(n_{1}-\theta _{i}^{1})^{2}}{\mathscr {A}}_{2}^{n_{2}^{2}+(n_{2}-\theta _{i}^{2})^{2}} {\mathscr {A}}_{3}^{n_{1}n_{2}+(n_{1}-\theta _{i}^{1})(n_{2}-\theta _{i}^{2})},\nonumber \\&{\mathscr {A}}_{1}=e^{\pi i\tau _{11}},\quad {\mathscr {A}}_{2}=e^{\pi i\tau _{22}},\quad {\mathscr {A}}_{3}=e^{\pi i\tau _{12}},\quad i=1,2,3,4. \end{aligned}$$
(32)

By taking the above system, two-periodic wave solution is also given by

$$\begin{aligned} u=u_{0}y+\frac{6\alpha }{\beta }\left( \ln \vartheta \left( \xi _{1},\xi _{2},\tau \right) \right) _{x}, \end{aligned}$$
(33)

from which the vector \(({\mathcal {M}}_{1},{\mathcal {M}}_{2},u_{0},{\mathcal {C}})^{T}\) and theta function \(\vartheta (\xi _{1},\xi _{2},\tau )\) are obtained by Eq. (27), the other parameters \(k_{i},l_{i},r_{i},\varepsilon _{i}\) are free.

According to the above analysis for the two-periodic wave solution, the following Theorem is easily constructed.

Theorem 3.2

Supposing that \(\vartheta (\xi _{1},\xi _{2},\tau )\) is a Riemann theta function with \(N=2\) and \(\xi _{i}=k_{i}x+l_{i}y+r_{i}z+{\mathcal {M}}_{i}t+\varepsilon _{i}(i=1,2)\). The VC-BKP equation (1) admits a two-periodic wave solution as follows

$$\begin{aligned} u=u_{0}y+\frac{6\alpha }{\beta }\partial _{x}\ln \vartheta (\xi _{1},\xi _{2},\tau ), \end{aligned}$$
(34)

where \(u_{0}\) and \(\vartheta (\xi _{1},\xi _{2},\tau )\) fulfill the expression (31) and (32). Additionally, \(\theta _{j}= \left( \begin{array}{c} \theta _{j}^{1} \\ \theta _{j}^{2}\\ \end{array} \right) , \theta _{1}= \left( \begin{array}{c} 0 \\ 0\\ \end{array} \right) , \theta _{2}= \left( \begin{array}{c} 1\\ 0\\ \end{array} \right) , \theta _{3}= \left( \begin{array}{c} 0 \\ 1\\ \end{array} \right) , \theta _{4}= \left( \begin{array}{c} 1 \\ 1\\ \end{array} \right) (j=1,2,3,4).\) The other parameters \(k_{i},l_{i},r_{i},\tau _{ij},\varepsilon _{i}(i,j=1,2)\) are free.

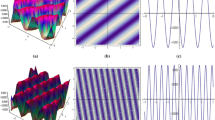
The figures of the one-periodic wave solution (26) and two-periodic wave solution (33) are plotted by choosing the suitable parameters in Figs. 1, 2 and 3, respectively, which are useful for understanding the dynamical behaviors of the periodic wave solutions.

In what follows, the characteristics of the one-periodic wave solution (26) and two-periodic wave solution (33) will be graphically discussed and simulated by selecting the appropriate parameters.

Figure 1 shows the 3D space plots and the propagation of the wave along some axes of the one-periodic wave (26) by selecting some appropriate parameters. Figure 1a–c describes the 3D plots of the one-periodic wave whose widths, amplitudes, velocity, shapes and density remain unchanged during the propagation. Figure 1e–g shows the propagation of the wave along x-axis, y-axis and t-axis with the same amplitude, respectively. Additionally, it is necessary to point out that one-periodic wave has only one wave pattern and it can be seen as a parallel superposition of overlapping one-solitary waves, placed one period apart separately. Particularly, in the phase variable \(\xi \), it has two fundamental periods 1 and \(\tau \), and its speed parameter \({\mathcal {M}}\) is determined by

$$\begin{aligned} {\mathcal {M}}=\frac{\left| \begin{array}{ccc} b_{1} &{}\quad a_{12} \\ b_{2} &{}\quad a_{22} \end{array}\right| }{\left| \begin{array}{ccc} a_{11} &{}\quad a_{12} \\ a_{21} &{}\quad a_{22} \end{array}\right| }. \end{aligned}$$
(35)

Figures 2 and 3 show the 3D space plots and the propagation of the wave along some axes of the two-periodic wave (33) by selecting some parameters. From the 3D space plots, it is easy to find that the spread of the wave is periodic in all directions; however, the cycle is not the same (see Figs. 2, 3). The velocity, shapes, density are not same in different spaces but remain unchanged during the propagation in each space. From Figs. 2 and 3d–f, we find that two-periodic possess different spreading shapes in x, y, t-axis, but they have same amplitude. Furthermore, there are two phase variables \(\xi _{1}\) and \(\xi _{2}\) (i.e., its surface pattern is two-dimensional), and it has 2N fundamental periods \((\zeta _{i},i=1,2,\ldots ,N)\) and \((\tau _{i},i=1,2,\ldots ,N)\) in \((\xi _{1},\xi _{2})\). Besides, a novel phenomenon is demonstrated in Figs. 2 and 3, it is easy to find that every two-periodic wave is spatially periodic in two direction, but it do not need be periodic in t directions. There are varying degrees of oscillation in the propagation of the wave along the axes. In general, the wave is not smooth in the spread process, but the whole periodic wave is periodic along the different axes.

Fig. 1
figure 1

(Color online) One-periodic wave via solutions (26) with parameters: \(k=1\), \(l=1,r=1\), \(\tau =I\), \(u_{0}=0\), \(\alpha =1,\beta =1,\gamma =1\) and \(\varepsilon =0\). This figure shows that every one-periodic wave is one-dimensional, and it can be seen as a superposition of overlapping solitary waves, placed one period apart. Perspective view of the real part of the periodic wave \(\mathrm {Re}(u)\) with: \(\mathbf{a } \,\,z=t=0\). \(\mathbf{b } \,\, t=y=0\). \(\mathbf{c } \,\, y=z=0\). Wave propagation pattern of the wave along with: \(\mathbf{d }\) the x axis. \(\mathbf{e }\) the y axis. \(\mathbf{f }\) the t axis

Full size image
Fig. 2
figure 2

(Color online) Two-periodic wave via solutions (33) with parameters: \(k_{1}=0.5,k_{2}=-1\), \(l_{1}=0.1,l_{2}=-2\), \(r_{1}=-0.1,r_{2}=-0.3\), \(\tau _{11}=I, \tau _{12}=0.5I, \tau _{22}=2I\), \(\alpha =1,\beta =1,\gamma =1\) and \(\varepsilon _{1}=\varepsilon _{2}=0\). This figure shows that every two-periodic wave is almost one-dimensional. Perspective view of the real part of the periodic wave \(\mathrm {Re}(u)\) with: \(\mathbf{a } \,\, y=z=0\). \(\mathbf{b } \,\, t=y=0\). \(\mathbf{c } \,\, y=x=0\). Wave propagation pattern of the wave along with: \(\mathbf{d }\) the x axis. \(\mathbf{e }\) the z axis. \(\mathbf{f }\) the t axis

Full size image
Fig. 3
figure 3

(Color online) Two-periodic wave via solutions (33) with parameters: \(k_{1}=0.5,k_{2}=1\), \(l_{1}=0.5,l_{2}=1\), \(r_{1}=0.5,r_{2}=1\), \(\tau _{11}=I, \tau _{12}=0.5I, \tau _{22}=2I\), \(\alpha =1,\beta =1,\gamma =1\) and \(\varepsilon _{1}=\varepsilon _{2}=0\). This figure reveals that every two-periodic wave is almost one-dimensional. Perspective view of the real part of the periodic wave \(\mathrm {Re}(u)\) with: \(\mathbf{a } \,\, y=z=0\). \(\mathbf{b } \,\, t=y=0\). \(\mathbf{c } \,\, y=x=0\). Wave propagation pattern of the wave along with: \(\mathbf{d }\) the x axis. \(\mathbf{e }\) the z axis. \(\mathbf{f }\) the t axis

Full size image

4 Using the tanh method and tan method

In this section, based on the hyperbolic functions, we will apply other approaches in order to determine more traveling wave solutions of Eq. (1).

4.1 The tanh method

The tanh method satisfies the use of the tanh equation

$$\begin{aligned} u(x,y,z,t)=a_{0}+a_{1}\tanh \left( kx+ly+mz-\omega t\right) ,\nonumber \\ \end{aligned}$$
(36)

as another solution of Eq. (1). In order to determine \(a_{0},a_{1}\) and wave speed \(\omega \). Substitution of Eq. (36) into Eq. (1) yields the following relation

$$\begin{aligned} \omega =-\frac{\gamma \left( k^{2}+m^{2}\right) +4k^{3}l}{k+l+m},\quad a_{1}=k, \end{aligned}$$
(37)

in which \(a_{0}\) is left as a free parameter. Based on the above analysis, one obtains the following solitary wave solution Eq. (1)

$$\begin{aligned}&u(x,y,z,t)=a_{0}\nonumber \\&\quad +\,\,k\tanh \left[ kx+ly+mz+\frac{\gamma \left( k^{2}+m^{2}\right) +4k^{3}l}{k+l+m} t\right] .\nonumber \\ \end{aligned}$$
(38)

Replacing tanh by coth in Eq. (37), in a similar way, we obtain the singular solutions

$$\begin{aligned}&u(x,y,z,t)=a_{0}\nonumber \\&\quad +\,k\coth \left[ kx+ly+mz+\frac{\gamma \left( k^{2}+m^{2}\right) +4k^{3}l}{k+l+m} t\right] .\nonumber \\ \end{aligned}$$
(39)

4.2 The tan method

The tan method satisfies the use of the tan equation

$$\begin{aligned} u(x,y,z,t)=a_{0}+a_{1}\tan (kx+ly+mz-\omega t), \end{aligned}$$
(40)

as another solution of Eq. (1). In order to determine \(a_{0},a_{1}\) and wave speed \(\omega \). Substitution of Eq. (36) into Eq. (1) yields the following relation

$$\begin{aligned} \omega =-\frac{\gamma \left( k^{2}+m^{2}\right) -4k^{3}l}{k+l+m},\quad a_{1}=-k, \end{aligned}$$
(41)

in which \(a_{0}\) is left as a free parameter. Based on the above analysis, one obtains the following solitary wave solution of Eq. (1)

$$\begin{aligned}&u(x,y,z,t)=a_{0}\nonumber \\&\quad -k\tan \left[ kx+ly+mz+ \frac{\gamma \left( k^{2}+m^{2}\right) -4k^{3}l}{k+l+m} t\right] .\nonumber \\ \end{aligned}$$
(42)

Replacing tanh by cot in Eq. (37), in a similar way, we obtain the singular solutions

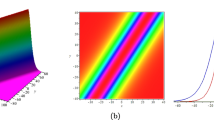
$$\begin{aligned}&u(x,y,z,t)=a_{0}\nonumber \\&\quad +\,k\cot \left[ kx+ly+mz+\frac{\gamma \left( k^{2}+m^{2}\right) -4k^{3}l}{k+l+m} t\right] .\nonumber \\ \end{aligned}$$
(43)

In what follows, the figures of the solitary waves solutions (38 and 42) and the singular solutions (39 and 43) are plotted by choosing the suitable parameters in Figs. 4 and 5, respectively, which are useful for understanding the dynamical behaviors and physical structure of the solutions.

Fig. 4
figure 4

(Color online) The solitary waves solution (38) and the singular solution (39) with parameters: \(\alpha =1,\beta =1,\gamma =1\), \(k=1,l=1\), \(m=1\), \(a_{0}=3\). Perspective view of the real part of the solitary waves solution (38): \(\mathrm {Re}(u)\) with: \(\mathbf{a } \,\, y=z=0\). \(\mathbf{b } \,\, y=z=2\). \(\mathbf{c } \,\, y=z=-2\). Perspective view of the real part of the singular solution (39): \(\mathrm {Re}(u)\) with: \(\mathbf{e } \,\, y=z=0\). \(\mathbf{f } \,\, y=z=2\). \(\mathbf{g } \,\, y=z=-2\)

Full size image
Fig. 5
figure 5

(Color online) The solitary waves solution (42) and the singular solution (43) with parameters: \(\alpha =1,\beta =1,\gamma =1\), \(k=1,l=1\), \(m=1\), \(a_{0}=3\). Perspective view of the real part of the solitary waves solution (42): \(\mathrm {Re}(u)\) with: \(\mathbf{a } \,\, y=z=0\). \(\mathbf{b } \,\, y=z=2\). \(\mathbf{c } \,\, y=z=-2\). Perspective view of the real part of the singular solution (43): \(\mathrm {Re}(u)\) with: \(\mathbf{e } \,\, y=z=0\). \(\mathbf{f } \,\, y=z=2\). \(\mathbf{g } \,\, y=z=-2\)

Full size image

5 Asymptotic properties

In this section, the relationship between the periodic wave solutions and soliton solutions will be established via three crucial Theorems.

Theorem 5.1

If the vector \(({\mathcal {M}},{\mathcal {C}})^{T}\) is a solution of the system (22) and for one-periodic wave solution (26), we take

$$\begin{aligned} u_{0}= & {} 0,\quad k=\frac{\mu }{2\pi i},\quad l=\frac{\nu }{2\pi i},\nonumber \\ m= & {} \frac{\varrho }{2\pi i},\quad \varepsilon =\frac{\delta +\pi i\tau }{2\pi i}, \end{aligned}$$
(44)

in which \(\mu ,\nu ,\varrho \) and \(\delta \) are given by (13). Then we have the following asymptotic properties

$$\begin{aligned}&{\mathcal {C}}\rightarrow 0,\quad \xi \rightarrow \frac{\eta +\pi i \tau }{2\pi i},\nonumber \\&\quad \vartheta (\xi ,\tau )\rightarrow 1+\exp (\eta ) \quad {\text { when}} \quad {\mathscr {A}}\rightarrow 0. \end{aligned}$$
(45)

It shows that the one-periodic wave solution tends to the one-soliton solution under a amplitude limit \((u,{\mathscr {A}}_{1})\rightarrow (u_{0},0)\).

Theorem 5.2

If the vector \(({\mathcal {M}}_{1},{\mathcal {M}}_{2},u_{0},{\mathcal {C}})^{T}\) is a solution of the system (31) and for two-periodic wave solution (33), we set

$$\begin{aligned} k_{i}= & {} \frac{\mu _{i}}{2\pi i},\quad l_{i}=\frac{\nu _{i}}{2\pi i},\quad m_{i}=\frac{\varrho _{i}}{2\pi i},\nonumber \\ \varepsilon _{i}= & {} \frac{\delta _{i}+\pi i\tau }{2\pi i},\quad i,j=1,2,i<j, \end{aligned}$$
(46)

in which \(\mu _{i},\nu _{i},\varrho _{i}\) and \(\delta _{i}\) are given by (14). Then we have the following asymptotic properties

$$\begin{aligned}&u_{0}\rightarrow 0,\quad {\mathcal {C}}\rightarrow 0,\quad \xi _{i}\rightarrow \frac{\eta _{i}+\pi i \tau _{ij}}{2\pi i},\quad \vartheta (\xi _{1},\xi _{2},\tau )\nonumber \\&\quad \rightarrow 1+\exp (\eta _{1})+\exp (\eta _{2})+ \exp (\eta _{1}+\eta _{2}+A_{12})\nonumber \\&{\text { when}} \quad {\mathscr {A}}_{1},{\mathscr {A}}_{2}\rightarrow 0. \end{aligned}$$
(47)

It indicates that the two-periodic wave solution tends to the two-soliton solution under a amplitude limit \((u,{\mathscr {A}}_{1},{\mathscr {A}}_{2})\rightarrow (u_{0},0,0)\).

Theorem 5.3

If the vector \(({\mathcal {M}}_{1},{\mathcal {M}}_{2},{\mathcal {M}}_{3},u_{0},{\mathcal {C}})^{T}\) is a solution of the system (63) and for three-periodic wave solution (see Appendix (66)), we take

$$\begin{aligned} k_{i}= & {} \frac{\mu _{i}}{2\pi i},\quad l_{i}=\frac{\nu _{i}}{2\pi i},\quad m_{i}=\frac{\varrho _{i}}{2\pi i},\nonumber \\ \varepsilon _{i}= & {} \frac{\delta _{i}+\pi i\tau }{2\pi i},\quad i,j=1,2,3,i<j, \end{aligned}$$
(48)

in which \(\mu _{i},\nu _{i},\varrho _{i}\) and \(\delta _{i}\) are given by (15). Then we have the following asymptotic properties

$$\begin{aligned}&u_{0}\rightarrow 0,\quad {\mathcal {C}}\rightarrow 0,\quad \xi _{i}\rightarrow \frac{\eta _{i}+\pi i \tau _{ij}}{2\pi i},\nonumber \\&\quad \vartheta (\xi _{1},\xi _{2},\tau )\rightarrow 1+\exp (\eta _{1})+\exp (\eta _{2})+\exp (\eta _{2})\nonumber \\&\qquad +\,\exp (\eta _{1}+\eta _{2}+\eta _{3}) +\exp (\eta _{1}+\eta _{3}+A_{13})\nonumber \\&\qquad +\exp (\eta _{2}+\eta _{3}+A_{23})\nonumber \\&\qquad +\exp (\eta _{1}+\eta _{2}+\eta _{3}+A_{12}+A_{13}+A_{23}) \nonumber \\&\quad {\text { when}} \quad {\mathscr {A}}_{1},{\mathscr {A}}_{2},{\mathscr {A}}_{3}\rightarrow 0. \end{aligned}$$
(49)

It implies that the three-periodic wave solution (see Appendix (66)) tends to the three-soliton solution under a amplitude limit \((u,{\mathscr {A}}_{1},{\mathscr {A}}_{2},{\mathscr {A}}_{3})\rightarrow (u_{0},0,0,0)\).

According to Ref. [43], we find that the proofs of Theorems 5.1, 5.2 and 5.3 are similar. In what follows, as a example, the proof of Theorem 5.2 will be presented with a detailed derivation.

Proof

To begin with, we can expand the periodic wave function \(\vartheta (\xi _{1},\xi _{2},\tau )\) in a new form

$$\begin{aligned}&\vartheta (\xi _{1},\xi _{2},\tau )=1+\left( e^{2\pi i\xi _{1}}+e^{-2\pi i\xi _{1}}\right) e^{\pi \tau _{11}}\nonumber \\&\quad +\left( e^{2\pi i\xi _{2}}+e^{-2\pi i\xi _{2}}\right) e^{\pi \tau _{22}}\nonumber \\&\quad +\,\left( e^{2\pi i(\xi _{1}+\xi _{2})}+e^{-2\pi i(\xi _{1}+\xi _{2})}\right) e^{\pi (\tau _{11}+2\tau _{12}+\tau _{22})}+\cdots . \end{aligned}$$
(50)

In view of Eq. (48), we have

$$\begin{aligned}&\vartheta (\xi _{1},\xi _{2},\tau )=1+e^{\widehat{\xi _{1}}}+e^{\widehat{\xi _{2}}} +e^{\widehat{\xi _{1}}+\widehat{\xi _{2}}-2\pi i\tau _{12}}\nonumber \\&\quad +\,{\mathscr {A}}_{1}^{2}e^{-\widehat{\xi _{1}}}+{\mathscr {A}}_{2}^{2}e^{-\widehat{\xi _{2}}}+ +{\mathscr {A}}_{1}^{2}{\mathscr {A}}_{2}^{2}e^{-\widehat{\xi _{1}}^{2}-\widehat{\xi _{2}}-2\pi \tau _{12}}\nonumber \\&\quad +\,\cdots \rightarrow 1+e^{\widehat{\xi _{1}}}+e^{\widehat{\xi _{2}}} +e^{\widehat{\xi _{1}}+\widehat{\xi _{2}}+A_{12}}, \nonumber \\&\quad {\text { when}} \quad {\mathscr {A}}_{1},{\mathscr {A}}_{2}\rightarrow 0, \end{aligned}$$
(51)

in which \(\widehat{\xi _{i}}=\mu _{i}x+\nu _{i}y+\varrho _{i}z+\omega _{i}t+\delta _{i}, \omega _{i}=2\pi i{\mathcal {M}}_{i}~(i=1,2)\). In the follows, it is easy to find that

$$\begin{aligned} {\mathcal {C}}\rightarrow & {} 0,\quad \omega _{i}\rightarrow -\frac{\alpha \mu _{i}^{3}\nu _{i} +\gamma \left( \mu _{i}^{2}+\varrho _{i}^{2}\right) }{\mu _{i}+\nu _{i}+\varrho _{i}}, \nonumber \\ \widehat{\xi _{i}}\rightarrow & {} \eta _{i},\quad i=1,2, ~~~{\text { when}} ~~~~{\mathscr {A}}_{1},{\mathscr {A}}_{2}\rightarrow 0. \end{aligned}$$
(52)

The functions \(H,(b_{1},b_{2},b_{3},b_{4})\) and \(({\mathcal {M}}_{1},{\mathcal {M}}_{2},u_{0},{\mathcal {C}})^{T}\) can be transformed into a series form with \({\mathscr {A}}_{1}, {\mathscr {A}}_{2}\) as follow

$$\begin{aligned} H=&\left( \begin{array}{ccccc} 0 &{} \quad 0 &{}\quad 0 &{} \quad 1\\ 0 &{} \quad 0 &{}\quad 0 &{}\quad 0\\ 0 &{} \quad 0 &{}\quad 0 &{}\quad 0\\ 0 &{} \quad 0 &{}\quad 0 &{}\quad 0\\ \end{array} \right) \nonumber \\&+\left( \begin{array}{ccccc} 0 &{} \quad 0 &{}\quad 0 &{}\quad 0\\ -8\pi ^{2}\left( k_{1}+l_{1}+r_{1}\right) &{}\quad 0 &{}\quad -24\alpha \pi ^{2}k_{1}^{2} &{} \quad 2 \\ 0 &{}\quad 0 &{} \quad 0 &{} \quad 0\\ 0 &{} \quad 0 &{} \quad 0 &{}\quad 0\\ \end{array} \right) {\mathscr {A}}_{1}\nonumber \\&+\left( \begin{array}{ccccc} 0 &{}\quad 0 &{}\quad 0 &{}\quad 0\\ 0 &{}\quad 0 &{} \quad 0 &{}\quad 0\\ 0 &{}\quad -8\pi ^{2}\left( k_{2}+l_{2}+r_{2}\right) &{}\quad -24\alpha \pi ^{2}k_{2}^{2} &{} \quad 2 \\ 0 &{}\quad 0 &{} \quad 0 &{}\quad 0\\ \end{array} \right) {\mathscr {A}}_{2}\nonumber \\&+\left( \begin{array}{ccccc} -32\pi ^{2}\left( k_{1}+l_{1}+r_{1}\right) &{} \quad 0&{}\quad 384\alpha \pi ^{2}k_{1}^{2}&{}\quad 2 \\ 0 &{} \quad 0&{}\quad 0 &{}\quad 0 \\ 0 &{} \quad 0&{} \quad 0 &{}\quad 0 \\ 0 &{} \quad 0&{} \quad 0 &{}\quad 0 \\ \end{array} \right) {\mathscr {A}}_{1}^{2}\nonumber \\&+\left( \begin{array}{ccccc} 0 &{} \quad -32\pi ^{2}\left( k_{2}+l_{2}+r_{2}\right) &{}\quad 384\alpha \pi ^{2}k_{2}^{2} &{}\quad 2 \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 \\ 0 &{} \quad 0 &{}\quad 0 &{}\quad 0 \\ \end{array} \right) {\mathscr {A}}_{2}^{2} \nonumber \\&+\left( \begin{array}{ccccc} 0 &{}\quad 0 &{}\quad 0 &{} \quad 0 \\ 0 &{}\quad 0 &{} \quad 0 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 \\ \varTheta _{1} &{} \quad -\varTheta _{1} &{}\quad \varTheta _{2} &{}\quad 2\\ \end{array} \right) {\mathscr {A}}_{1}{\mathscr {A}}_{2}\nonumber \\&+\left( \begin{array}{ccccc} 0 &{}\quad 0 &{} \quad 0 &{} \quad 0 \\ 0 &{}\quad 0 &{} \quad 0 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 \\ \varTheta _{3} &{}\quad \varTheta _{3} &{}\quad \varTheta _{4} &{}\quad 2 \\ \end{array} \right) {\mathscr {A}}_{1}{\mathscr {A}}_{2}{\mathscr {A}}_{3}+o\left( {\mathscr {A}}_{1}^{i}{\mathscr {A}}_{2}^{j}{\mathscr {A}}_{3}^{k}\right) ,\nonumber \\&\quad i+j+k\ge 3, \end{aligned}$$
(53)
$$\begin{aligned} b=&\left( \begin{array}{c} 0 \\ \varOmega _{1} \\ 0 \\ 0 \\ \end{array} \right) {\mathscr {A}}_{1} +\left( \begin{array}{c} 0 \\ 0 \\ \varOmega _{2} \\ 0 \\ \end{array} \right) {\mathscr {A}}_{2} +\left( \begin{array}{c} \varOmega _{3} \\ 0 \\ 0 \\ 0 \\ \end{array} \right) {\mathscr {A}}_{1}^{2} \nonumber \\&+\left( \begin{array}{c} \varOmega _{4} \\ 0 \\ 0 \\ 0 \\ \end{array} \right) {\mathscr {A}}_{2}^{2} +\left( \begin{array}{c} 0 \\ 0 \\ 0 \\ \varOmega _{5} \\ \end{array} \right) {\mathscr {A}}_{1}{\mathscr {A}}_{2} \nonumber \\&+\left( \begin{array}{c} 0 \\ 0 \\ 0 \\ \varOmega _{6} \\ \end{array} \right) {\mathscr {A}}_{1}{\mathscr {A}}_{2}{\mathscr {A}}_{3}\nonumber \\&+o\left( {\mathscr {A}}_{1}^{i}{\mathscr {A}}_{2}^{j}{\mathscr {A}}_{3}^{k}\right) ,\quad i+j+k\ge 3, \end{aligned}$$
(54)
$$\begin{aligned}&\left( \begin{array}{c} {\mathcal {M}}_{1} \\ {\mathcal {M}}_{2} \\ u_{0} \\ {\mathcal {C}} \\ \end{array} \right) = \left( \begin{array}{c} ({\mathcal {M}}_{1})^{00} \\ ({\mathcal {M}}_{2})^{00} \\ (u_{0})^{00} \\ ({\mathcal {C}})^{00} \\ \end{array} \right) +\left( \begin{array}{c} ({\mathcal {M}}_{1})^{11} \\ ({\mathcal {M}}_{2})^{11} \\ (u_{0})^{11} \\ ({\mathcal {C}})^{11} \\ \end{array} \right) {\mathscr {A}}_{1} \nonumber \\&\qquad +\,\left( \begin{array}{c} ({\mathcal {M}}_{1})^{21} \\ ({\mathcal {M}}_{2})^{21} \\ (u_{0})^{21} \\ ({\mathcal {C}})^{21} \\ \end{array} \right) {\mathscr {A}}_{2} +\left( \begin{array}{c} ({\mathcal {M}}_{1})^{12} \\ ({\mathcal {M}}_{2})^{12} \\ (u_{0})^{12} \\ ({\mathcal {C}})^{12} \\ \end{array} \right) {\mathscr {A}}_{1}^{2} \nonumber \\&\qquad +\,\left( \begin{array}{c} ({\mathcal {M}}_{1})^{22} \\ ({\mathcal {M}}_{2})^{22} \\ (u_{0})^{22} \\ ({\mathcal {C}})^{22} \\ \end{array} \right) {\mathscr {A}}_{2}^{2}\nonumber \\&\qquad +\,\left( \begin{array}{c} ({\mathcal {M}}_{1})^{2} \\ ({\mathcal {M}}_{2})^{2} \\ (u_{0})^{2} \\ ({\mathcal {C}})^{2} \\ \end{array} \right) {\mathscr {A}}_{1}{\mathscr {A}}_{2} +\left( \begin{array}{c} ({\mathcal {M}}_{1})^{3} \\ ({\mathcal {M}}_{2})^{3} \\ (u_{0})^{3} \\ ({\mathcal {C}})^{3} \\ \end{array} \right) {\mathscr {A}}_{1}{\mathscr {A}}_{2}{\mathscr {A}}_{3}\nonumber \\&\qquad +\,o\left( {\mathscr {A}}_{1}^{i}{\mathscr {A}}_{2}^{j}{\mathscr {A}}_{3}^{k}\right) ,\quad i+j+k\ge 3, \end{aligned}$$
(55)

\(\square \)

in which \(\varLambda ,\varOmega \) are presented as below

$$\begin{aligned} \varTheta _{1}&=-8\pi ^{2}\left[ \left( k_{1}-k_{2}\right) ^{2}+\left( l_{1}-l_{2}\right) ^{2} +\left( r_{1}-r_{2}\right) ^{2}\right] , \nonumber \\ \varTheta _{3}&=-8\pi ^{2}\left[ \left( k_{1}+k_{2}\right) ^{2}+\left( l_{1}+l_{2}\right) ^{2}+\left( r_{1}+r_{2}\right) ^{2}\right] , \nonumber \\ \varTheta _{2}&=32\alpha \pi ^{4}(k_{1}-k_{2})^{3}(l_{1}-l_{2}), \nonumber \\ \varTheta _{4}&=32\alpha \pi ^{4}(k_{1}+k_{2})^{3}(l_{1}+l_{2}), \nonumber \\ \varOmega _{1}&=8\pi ^{2}\left[ -4\alpha \pi ^{2}k_{1}^{3}l_{1}+\gamma \left( k_{1}^{2}+r_{1}^{2}\right) \right] ,\nonumber \\ \varOmega _{2}&=8\pi ^{2}\left[ -4\alpha \pi ^{2}k_{2}^{3}l_{2}+\gamma \left( k_{2}^{2}+r_{2}^{2}\right) \right] ,\nonumber \\ \varOmega _{3}&=32\pi ^{2}\left[ -16\alpha \pi ^{2}k_{1}^{3}l_{1}+\gamma \left( k_{1}^{2}+r_{1}^{2}\right) \right] ,\nonumber \\ \varOmega _{4}&=32\pi ^{2}\left[ -16\alpha \pi ^{2}k_{2}^{3}l_{2}+\gamma \left( k_{2}^{2}+r_{2}^{2}\right) \right] ,\nonumber \\ \varOmega _{5}&=8\pi ^{2}\left[ -4\alpha \pi ^{2}(k_{1}-k_{2})^{3}(l_{1}-l_{2})\right. \nonumber \\&\left. \quad +\,\gamma \left[ (k_{1}-k_{2})^{2}+(r_{1}-r_{2})^{2}\right] \right] ,\nonumber \\ \varOmega _{6}&=8\pi ^{2}\left[ -4\alpha \pi ^{2}(k_{1}+k_{2})^{3}(l_{1}+l_{2})\right. \nonumber \\&\left. \quad +\,\gamma \left[ (k_{1}+k_{2})^{2}+(r_{1}+r_{2})^{2}\right] \right] . \end{aligned}$$
(56)

By combining above systems and expression (31) and by applying for \(A*X=B\), the following relations are easily obtained

$$\begin{aligned}&{\mathcal {C}}^{(00)}={\mathcal {C}}^{(11)}={\mathcal {C}}^{(21)}={\mathcal {C}}^{(2)}={\mathcal {C}}^{(3)}=0,\nonumber \\&\varOmega _{1}=-8\pi ^{2}\left( k_{1}+l_{1}+r_{1}\right) {\mathcal {M}}_{1}^{00}-24\alpha \pi ^{2}k_{1}^{2}u_{0}^{00},\nonumber \\&\varOmega _{2}=-8\pi ^{2}\left( k_{2}+l_{3}+r_{3}\right) {\mathcal {M}}_{2}^{00}-24\alpha \pi ^{2}k_{3}^{2}u_{0}^{00},\nonumber \\&\varOmega _{3}=-32\pi ^{2}\left( k_{1}+l_{1}+r_{1}\right) ){\mathcal {M}}_{1}^{00}+348\alpha \pi ^{2}k_{1}^{2}u_{0}^{00},\nonumber \\&\varOmega _{4}=-32\pi ^{2}\left( k_{2}+l_{2}+r_{2}\right) ){\mathcal {M}}_{1}^{00}+348\alpha \pi ^{2}k_{2}^{2}u_{0}^{00},\nonumber \\&\varOmega _{5}=\varTheta _{1}{\mathcal {M}}_{1}^{00}-\varTheta _{1}{\mathcal {M}}_{2}^{00}+\varTheta _{2}u_{0}^{00},\nonumber \\&\varOmega _{6}=\varTheta _{3}{\mathcal {M}}_{1}^{00}+\varTheta _{3}{\mathcal {M}}_{2}^{00}+\varTheta _{3}u_{0}^{00},\ldots . \end{aligned}$$
(57)

By considering \(u_{0}^{(00)}=0\), we have the following results

$$\begin{aligned}&u_{0}=o({\mathscr {A}}_{1},{\mathscr {A}}_{2})\rightarrow 0,\quad {\mathcal {C}}\rightarrow 0,\nonumber \\&2\pi i{\mathcal {M}}_{1}=-2\pi i\frac{-4\alpha \pi ^{2}k_{1}^{3}l_{1}+\gamma (k_{1}^{2}+r_{1}^{2})}{k_{1}+l_{1}+r_{1}} +o({\mathscr {A}}_{1},{\mathscr {A}}_{2})\nonumber \\&\quad \rightarrow -\frac{-4\alpha \mu _{1}^{3}\nu _{1}+\gamma (\mu _{1}^{2}+\varrho _{1}^{2})}{\mu _{1}+\nu _{1}+\varrho _{1}},\nonumber \\&2\pi i{\mathcal {M}}_{2}=--2\pi i\frac{-4\alpha \pi ^{2}k_{2}^{3}l_{2}+\gamma (k_{2}^{2}+r_{2}^{2})}{k_{2}+l_{2}+r_{2}} +o({\mathscr {A}}_{1},{\mathscr {A}}_{2})\nonumber \\&\quad \rightarrow -\frac{-4\alpha \mu _{2}^{3}\nu _{2}+\gamma (\mu _{2}^{2}+\varrho _{2}^{2})}{\mu _{2}+\nu _{2}+\varrho _{2}}, \quad {\text {as}}\quad ({\mathscr {A}}_{1},{\mathscr {A}}_{2})\rightarrow (0,0){,} \end{aligned}$$
(58)

which shows Eq. (52). Summing up the above analysis, we can obtain the relationship that the two-periodic solution tends to two-soliton solution under limited condition \(({\mathscr {A}}_{1},{\mathscr {A}}_{2})\rightarrow (0,0)\).

6 Conclusions

In this work, a generalized (3 + 1)-dimensional variable-coefficient BKP equation has been systematically investigated. The Hirota method is applied to construct the bilinear form and exact solution of Eq. (1). Based on the bilinear formalism and Riemann theta function, the Riemann theta function periodic wave solutions of Eq. (1) are derived with a detailed derivation. Besides, the tanh method and the tan method are applied to construct the traveling wave solutions of Eq. (1), The figures of the solutions are presented (see Figs. 1, 2, 3, 4, 5). At last, the relation between the soliton solutions and periodic wave solutions is strictly established in detailed. According to Theorems 5.1, 5.2 and 5.3, one can see that the N-periodic wave solution tends to N-soliton solution (11) under the certain condition.

The paper shows that the effective method provides a direct and powerful mathematical tool to seek exact solution of other NLEEs, which should be suitable to study other models in mathematical physics and engineering. We hope that our results can be used to enrich the dynamical behavior of higher-dimensional nonlinear wave field.