Solitons, breath-wave transitions, quasi-periodic waves and asymptotic behaviors for a (2+1)-dimensional Boussinesq-type equation

Abstract

In this paper, the N-soliton solutions of a (2+1)-dimensional Boussinesq-type equation are obtained by the Hirota’s bilinear method, and one-, two-, three-soliton solutions and their clear images are given in detail. Then, one breath-wave solution and two breath-wave solution are obtained by taking the complex conjugate of soliton solutions. The transformation mechanism of the breath-waves is analyzed systematically. Through the multi-dimensional Riemann theta function and bilinear method, the quasi-periodic wave solutions are obtained. Among these periodic waves, the high-dimensional complex three-periodic waves are firstly presented, the one-periodic waves are often applied to one-dimensional models of periodic waves in shallow water, the two-periodic waves and three-periodic waves are the generalization of one-periodic waves. The asymptotic behaviors of one-, two-, three-periodic waves and the relations between periodic wave solutions and soliton wave solutions are strictly established and proved by a limiting procedure. The characteristic line method is developed to analyze the dynamical characteristics of the quasi-periodic waves.

1 Introduction

Nonlinear science is a basic subject to study the commonness of nonlinear phenomena. As we all know, the research subjects of nonlinear science are chaos, solitons and fractals. Among them, solitons represent unpredictable organized behaviors in nonlinear science, which is the result of the balance between dispersion and nonlinearity in nonlinear dynamic systems. As a typical nonlinear phenomenon, it frequently appears in nonlinear optics [1,2,3,4], electromagnetism [5,6,7,8], plasma physics, condensed matter physics and biophysics [9,10,11,12,13].

The nonlinear Boussinesq equation plays an important role in marine research. The classical Boussinesq equation describes the propagation of long waves in shallow water. In addition, the Boussinesq equation also simulates the large-scale atmospheric and ocean currents leading to cold fronts and jets. The Boussinesq equation of surface gravity wave has been proved to be an effective tool for simulating wave propagation in coastal and marine areas [14]. In the past decades, researchers have given the exact analytical solutions [15], bright and dark soliton solutions [16], rogue wave solutions [17] and degenerate breather solutions [18] of the Boussinesq equation.

Quasi-periodic wave solutions have always been a hot topic of research in the field of integrable systems [19,20,21,22]. Some scholars have given the existence of quasi-periodic wave solutions of coupled Duffing-type equation [23], Vanderpol-Mathieu equation [24], etc. [25, 26]. The quasi-periodic wave solutions of algebraic geometry are constructed in a unified way on the basis of finite gap theory [27]. The quasi-periodic wave solutions of Kadomtsev-Petviashvili (KP) equation are obtained by Baker-Akhiezer functions when seeking compatible solution [28]. The quasi-periodic wave solutions of Saweda-Kotera-Kadomtsev-Petviashvili equation (SKKP) are gained by asymptotic analysis [29]. The quasi-periodic wave solutions have been also obtained via bilinear Bäcklund transformation [30], the Riemann-Bäcklund method [31] and the Riemann theta function [32]. In addition, the quasi-periodic wave solutions appear in many fields of science and technology [33, 34], including optics, electromagnetism, etc.

The Boussinesq equation is usually written in the form of ${u_{tt}} + {u_{xx}} - {({u^2})_{xx}} + \frac{1}{3}{u_{xxxx}} = 0,$ where the index x and t present partial derivatives. By the transformation $u \rightarrow u+1,$ ${(u + 1)_{tt}} + {(u + 1)_{xx}} - {({(u + 1)^2})_{xx}} + \frac{1}{3}{(u + 1)_{xxxx}} = 0,$ ${u_{tt}} + {u_{xx}} - {({u^2} + 2u + 1)_{xx}} + \frac{1}{3}{u_{xxxx}} = 0,$ we have got another widely used Boussinesq equation ${u_{tt}} - {u_{xx}} - {({u^2})_{xx}} + \frac{1}{3}{u_{xxxx}} = 0,$ this equation was introduced by Boussinesq in 1871 [35, 36] to study the propagation of long waves in shallow water. In this paper, we devote to considering the following (2+1)-dimensional Boussinesq-type equation

$$\begin{aligned} {u_{tt}} + {c_1}{u_{xx}} + {c_2}{u_{xy}} + {c_3}\left( {6u_x^2 + 6u{u_{xx}} + {u_{xxxx}}} \right) = 0, \end{aligned}$$

(1)

where $u = u(x,y,t).$ Eq. (1) is integrable nonlinear partial differential equations in the sense of the theory of bilinear, the N-soliton solutions of Eq. (1) are obtained in the following statement, and it is a generalization of classical (2+1)-dimensional Boussinesq equation [37,38,39]. When $c_3=1,$ Eq. (1) can be written into the form of another (2+1)-dimensional Boussinesq-type equation [40]. When $c_2 = 0,$ the above equation reduces to a generalized two dimensional Boussinesq equation [41, 42]. The lump and rogue wave solutions of this generalized Boussinesq equation have been discussed in [40, 41]. However, there was no discussion about the breath-wave transitions and quasi-periodic wave solutions, especially the high-dimensional Riemann theta function quasi-periodic wave solutions. In this work, we shall investigate solitons, transformation mechanism of the breath-waves and quasi-periodic wave solutions in detail.

The organization of this paper is as follows. In Sect. 2, we briefly introduce the Hirota’s bilinear method and derive the bilinear form and N-soliton solutions of Eq. (1) and present the Riemann theta function and its properties. In Sect. 3, we obtain one and two breath-wave solutions via taking the complex conjugate of soliton solutions and briefly introduce the breath-wave transitions. In Sections 4,5,6, we apply the Hirota’s bilinear method and Riemann theta function to construct one-, two- and three-periodic wave solutions of Eq. (1). We further apply the limiting method and characteristic line method to analyze the characteristics and asymptotic behaviors of one-, two- and three-periodic wave solutions in detail. It is strictly proved that under a “small-amplitude” limit, the periodic wave solutions tend to the known soliton solutions. Finally, some conclusions are given in the last section.

2 Bilinear form and the Riemann theta function

In this section, we briefly introduce the bilinear form of Eq. (1) and some brief conclusions of the Riemann theta function.

2.1 Bilinear form of Eq. (1)

The Hirota’s bilinear method [43,44,45,46,47,48] is an important tool for constructing exact solutions of many nonlinear equations. If a nonlinear equation is transformed into a bilinear form by a dependent variable transformation, the multi-soliton solutions are often obtained.

By the dependent variable transformation

$$\begin{aligned}u = 2\left( {\ln f(x,y,t)} \right) _{xx},\end{aligned}$$

Eq. (1) can be transformed into a bilinear form

$$\begin{aligned} \left( {D_t^2 + {c_1}D_x^2 + {c_2}{D_x}{D_y} + {c_3}D_x^4} \right) f(x,y,t)f(x,y,t) = 0, \end{aligned}$$

(2)

where the bilinear differential operators $D_x,$ $D_y$ and $D_t$ are defined by

$$\begin{aligned}D_x^mD_y^nD_t^pf(x,y,t)g(x,y,t) = {(\partial x - \partial x')^m}{(\partial y - \partial y')^n}{(\partial t - \partial t')^p}f(x,y,t)g(x',y',t'){|_{x' = x,y' = y,t' = t}}.\end{aligned}$$

These operators have a great property when applying to exponential function, that is

$$\begin{aligned}D_x^mD_y^nD_t^p\mathrm{{e}}^{{\tau_1}}\mathrm{{e}}^{{\tau _2}} = {({\varepsilon _1} - {\varepsilon _2})^m}{({\eta _1} - {\eta _2})^n}{({\omega _1} - {\omega _2})^p}\mathrm{{e}}^{{\tau _1} + {\tau _2}},\end{aligned}$$

where ${\tau _j} = {\varepsilon _j}x + {\eta _j}y + {\omega _j}t + {\upsilon _j}~(j = 1,2).$ Furthermore, we have

$$\begin{aligned} B({D_x},{D_y},{D_t})\mathrm{{e}}^{{\tau _1}}\mathrm{{e}}^{{\tau _2}} = B({\varepsilon _1} - {\varepsilon _2},{\eta _1} - {\eta _2},{\omega _1} - {\omega _2})\mathrm{{e}}^{{\tau _1} + {\tau _2}}, \end{aligned}$$

(3)

where $B({D_x},{D_y},{D_t})$ is a polynomial about $D_x,$ $D_y$ and $D_t.$ This property plays an important role in the subsequent construction of periodic wave solutions.

The N-soliton solutions of Eq. (1) can be found by applying Hirota’s bilinear theory. It can be written in the form of

$$\begin{aligned}f = {f_N} = \sum \limits _{\mu = 0,1} {\exp \left( {\sum \limits _{j = 1}^N {{\mu _j}{\sigma _j} + } \sum \limits _{j < s}^N {{\mu _j}{\mu _s}{A_{js}}} } \right) } ,\end{aligned}$$

with phase variable ${\sigma _j} = {k_j}x + {l_j}y + \sqrt{ - {c_2}{} {k_j}{l_j} - {c_3}{k_j}^4 - {c_1}{} {k_j}^2} t + {\delta _j},$ ${k_j},{l_j}$ and ${\delta _j}$ are free constants,

$$\begin{aligned} e^{{A_{{js}} }} = & \left( {c_{2} k_{s} l_{j} + c_{2} k_{j} l_{s} + 4c_{3} k_{s} ^{3} k_{j} + 4c_{3} k_{j} ^{3} k_{s} - 6c_{3} k_{s} ^{2} k_{j} ^{2} + 2c_{1} k_{s} k_{j} } \right. \\ & {{\left. { + 2\sqrt { - c_{3} k_{s} ^{4} - c_{1} k_{s} ^{2} - c_{2} k_{s} l_{s} } \times \sqrt { - c_{2} k_{j} l_{j} - c_{3} k_{j} ^{4} - c_{1} k_{j} ^{2} } } \right)} \mathord{\left/ {\vphantom {{\left. { + 2\sqrt { - c_{3} k_{s} ^{4} - c_{1} k_{s} ^{2} - c_{2} k_{s} l_{s} } \times \sqrt { - c_{2} k_{j} l_{j} - c_{3} k_{j} ^{4} - c_{1} k_{j} ^{2} } } \right)} {\left( {c_{2} k_{j} l_{s} + c_{2} k_{s} l_{j} + 4c_{3} k_{s} ^{3} k_{j} } \right.}}} \right. \kern-\nulldelimiterspace} {\left( {c_{2} k_{j} l_{s} + c_{2} k_{s} l_{j} + 4c_{3} k_{s} ^{3} k_{j} } \right.}} \\ & \left. { + 6c_{3} k_{s} ^{2} k_{j} ^{2} + 4c_{3} k_{j} ^{3} k_{s} + 2c_{1} k_{s} k_{j} + 2\sqrt { - c_{3} k_{s} ^{4} - c_{1} k_{s} ^{2} - c_{2} k_{s} l_{s} } \sqrt { - c_{2} k_{j} l_{j} - c_{3} k_{j} ^{4} - c_{1} k_{j} ^{2} } } \right). \\ \end{aligned}$$

The mark $\sum \nolimits _{\mu = 0,1}$ means summation over all possible combinations of ${\mu _j} = 0,1~(j=1...N ),$ the $\sum \nolimits _{j < s}^N$ summation is over all possible combinations of N elements in the specific condition $\ j<s.$

Therefore, the one-soliton solution of Eq. (1) has the form of

$$\begin{aligned} {u_1} = 2{\left( {\ln (1 + \mathrm{{e}}^\sigma }) \right) _{xx}},\end{aligned}$$

(4)

where phase variable ${\sigma } = {k}x + {l}y + \sqrt{ - {c_2}{} {k}{l} - {c_3}{k}^4 - {c_1}{} {k}^2} t + {\delta },$ k, l and ${\delta }$ are free constants (Fig. 1).

Fig. 1

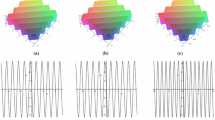
(Color online) One-soliton wave Eq. (4) with parameters $c_1=-10, c_2=10, c_3=-20, k=0.15, l=-0.1, \delta =-0.1.$ a Three-dimensional stereogram of one-soliton wave when $t=0.$ b Vertical view of (a). c The wave moves along the x-axis($-65 \le x \le 65$)(red) when $y=0,t=0,$ y-axis($-65 \le y \le 65$)(blue) when $x=0,t=0,$ t-axis($-65 \le t \le 65$)(green) when $x=0,y=0$

While the two-soliton solution has the form of

$$\begin{aligned} {u_2}= 2{\left( {\ln (1 + \mathrm{{e}^{{\sigma _1}}} + \mathrm{{e}^{{\sigma _2}}} + \mathrm{{e}}^{{\sigma _1} + {\sigma _2} + {A_{12}}})} \right) _{xx}}, \end{aligned}$$

(5)

(Fig. 2) with phase variable ${\sigma _j} = {k_j}x + {l_j}y + \sqrt{ - {c_2}{} {k_j}{l_j} - {c_3}{k_j}^4 - {c_1}{} {k_j}^2} t + {\delta _j}~(j=1,2),$ $\mathrm{{e}}^{{A_{12}}}=\mathrm{{e}}^{{A_{js}}}(j=1,s=2).$

Fig. 2

(Color online) Two-soliton wave Eq. (5) with parameters $c_1=-10, c_2=1, c_3=-20, k_1=-0.8, l_1=0.5, k_2=0.8, l_2=0.5, \delta _1=0, \delta _2=0.$ a Three-dimensional stereogram of two-soliton wave when $t=0.$ b Vertical view of (a). c The wave moves along the x-axis($-35 \le x \le 35$)(red) when $y=0,t=0,$ y-axis($-35 \le y \le 35$)(blue) when $x=0,t=0,$ t-axis($-35 \le t \le 35$)(green) when $x=0,y=0$

Based on the above analysis, the three-soliton solution has the form of

$$u_{3} = 2\left( {\ln \left( {1 + {\text{e}}^{{\sigma _{{\text{1}}} }} + {\text{e}}^{{\sigma _{{\text{2}}} }} + {\text{e}}^{{\sigma _{{\text{3}}} }} + {\text{e}}^{{\sigma _{{\text{1}}} {\text{ + }}\sigma _{{\text{2}}} {\text{ + A}}_{{{\text{12}}}} }} + {\text{e}}^{{\sigma _{{\text{2}}} {\text{ + }}\sigma _{{\text{3}}} {\text{ + A}}_{{{\text{23}}}} }} + {\text{e}}^{{\sigma _{{\text{1}}} {\text{ + }}\sigma _{{\text{3}}} {\text{ + A}}_{{{\text{13}}}} }} + {\text{e}}^{{\sigma _{{\text{1}}} {\text{ + }}\sigma _{{\text{2}}} {\text{ + }}\sigma _{{\text{3}}} {\text{ + A}}_{{{\text{12}}}} {\text{ + A}}_{{{\text{23}}}} {\text{ + A}}_{{{\text{13}}}} }} } \right)} \right)_{{xx}} ,$$

(6)

(Fig. 3) with phase variable ${\sigma _j}~(j=1,2,3),$ $\mathrm{{e}}^{{A_{12}}}=\mathrm{{e}}^{{A_{js}}}(j=1,s=2),$ $\mathrm{{e}}^{{A_{23}}}=\mathrm{{e}}^{{A_{js}}}(j=2,s=3),$ $\mathrm{{e}}^{{A_{13}}}=\mathrm{{e}}^{{A_{js}}}(j=1,s=3).$

Fig. 3

(Color online) Three-soliton wave Eq. (6) with parameters $c_1=-10, c_2=1, c_3=-20, k_1=-0.8, l_1=0.5, k_2=0.8, l_2=0.5, k_3=0.6, l_3=0.9,\delta _1=0, \delta _2=0, \delta _3=0.$ a Three-dimensional stereogram of three-soliton wave when $t=0.$ b Vertical view of (a). c The wave moves along the x-axis($-40 \le x \le 15$)(red) when $y=0,t=0,$ y-axis($-40 \le y \le 15$)(blue) when $x=0,t=0,$ t-axis($-40 \le t \le 15$)(green) when $x=0,y=0$

In order to construct the multi-periodic wave solutions, we consider

$$\begin{aligned} u = {u_0} + 2{\left( {\ln \varphi (\tau )} \right) _{xx}}, \end{aligned}$$

(7)

where $u_0$ is a constant solution of Eq. (1), and phase variable $\tau$ has the form of $\tau = {({\tau _1},{\tau _2},...,{\tau _N})^T},$ ${\tau _j} = {\varepsilon _j}x + {\eta _j}y + {\omega _j}t + {\upsilon _j}~(j = 1,2,...,N).$ By substituting Eq. (7) into Eq. (1) and integrating about variable x, we obtain the following bilinear form

$$\begin{aligned} B({D_x},{D_y},{D_t})\varphi (\tau )\varphi (\tau ) = \left( {D_t^2 + {c_1}D_x^2 + {c_2}{D_x}{D_y} + {c_3}D_x^4 + 6{u_0}D_x^2 + c} \right) \varphi (\tau )\varphi (\tau ) = 0, \end{aligned}$$

(8)

where c is an integration constant.

2.2 Riemann theta function and its periodicity

Definition 1.

The multi-dimensional Riemann theta function of genus N is defined as the form of

$$\begin{aligned} \varphi (\tau ) = \varphi (\tau ,a) = \sum \limits _{n \in {Z^N}}{\mathrm{{e}}^{ - \pi \left\langle {an,n} \right\rangle + 2\pi \mathrm{{i}}\left\langle {\tau ,n} \right\rangle }}, \end{aligned}$$

(9)

where the integer value vector $n = {({n_1},{n_2},...,{n_N})^T} \in {Z^N},$ and complex phase variable $\tau = ({\tau _1},{\tau _2},...,$ ${\tau _N})^T \in {C^N}.$ Furthermore, for two vectors $h = {({h_1},{h_2},...,{h_N})^T}$ and $p = {({p_1},{p_2},...,{p_N})^T},$ their inner product is defined by $< h,p > = {h_1}{p_1} + {h_2}{p_2} + \cdots+ {h_N}{p_N}.$ The $a = ({a_{ij}})$ is a positive definite and real-valued symmetric $N \times N$ matrix.

Proposition 1

Let ${\mathrm{{e}}_j}$ be the jth column of $N \times N$ identity matrix ${I_N},$ ${a_j}$ be the jth column of positive matrix a,  ${a_{jj}}$ be the element in row j,  column j. Then the theta function $\varphi (\tau )$ has the following periodic properties:

$$\begin{aligned}\begin{array}{l} (1)\;\varphi (\tau + {\mathrm{{e}}_j},a) = \varphi (\tau ,a),\\ (2)\;\varphi (\tau + \mathrm{{i}}{a_j},a) = {\mathrm{{e}}^{ - 2\pi \mathrm{{i}}{\tau _j} + \pi {a_{jj}}}}\varphi (\tau ,a),\\ (3)\;{\left( {\ln \varphi (\tau + {\mathrm{{e}}_j},a)} \right) _{{\tau _j}{\tau _j}}} = {(\ln \varphi (\tau ,a))_{{\tau _j}{\tau _j}}},j = 1,...,N,\\ (4)\;{(\mathrm{{ln}}\varphi (\tau + \mathrm{{i}}{a_j},a))_{{\tau _j}{\tau _j}}} = {(\ln \varphi (\tau ,a))_{{\tau _j}{\tau _j}}},j = 1,...,N. \end{array}\end{aligned}$$

3 Breath-wave solutions and their transitions

3.1 The one-breath-wave solution of Eq. (1)

In this section, we obtain the one breath-wave solution of Eq. (1) by taking complex conjugate about real parameters of two-soliton solution(5), that is, letting

$$\begin{aligned} {k_1} = {a_1} + {b_1}\mathrm{{i}},~{k_2} = {a_1} - {b_1}\mathrm{{i}},~{l_1} = {p_1} + {q_1}\mathrm{{i}},~{l_2} = {p_1} - {q_1}\mathrm{{i}},~{\delta _1} = \ln \frac{{{\alpha _1}}}{2} + {\beta _1} + {\gamma _1}\mathrm{{i}},~{\delta _2} = \ln \frac{{{\alpha _1}}}{2} + {\beta _1} - {\gamma _1}\mathrm{{i}}, \end{aligned}$$

(10)

where ${a_1},{b_1},{p_1},{q_1} \ne 0,{\alpha _1} > 0,{\beta _1}$ and ${\gamma _1}$ are arbitrary real constants. By letting ${f_2} = (1 + \mathrm{{e}^{{\sigma _1}}} + \mathrm{{e}^{{\sigma _2}}} + \mathrm{{e}^{{\sigma _1} + {\sigma _2} + {A_{12}}}})$ in Eq. (5), and substituting Eq. (10) into $f_2$, we obtain the following expression of the one breath-wave solution

$$\begin{aligned} {f_2} \sim 2\sqrt{{\alpha _2}}\cosh ({\theta _1} + \frac{1}{2}\ln {\alpha _2}) + {\alpha _1}\cos ({\Lambda _1}), \end{aligned}$$

(11)

where

$$\begin{aligned} \theta _{1} = & a_{1} x + p_{1} y + h_{1} t + \beta _{1} ,~\Lambda _{1} = b_{1} x + q_{1} y + d_{1} t + \gamma _{1} ,~\alpha _{2} = \frac{{\alpha _{1} ^{2} G_{1} }}{4}, \\ G_{1} = & \frac{{ - 2c_{1} (a_{1} ^{2} + b_{1} ^{2} ) + 2c_{2} (a_{1} p_{1} + b_{1} q_{1} ) + 2c_{3} (a_{1} ^{4} - 7b_{1} ^{4} - 6a_{1} ^{2} b_{1} ^{2} ) + 2\sqrt {\Lambda _{3} ^{2} + \Lambda _{4} ^{2} } }}{{ - 2c_{1} (a_{1} ^{2} + b_{1} ^{2} ) + 2c_{2} (a_{1} p_{1} + b_{1} q_{1} ) + 2c_{3} (7a_{1} ^{4} - b_{1} ^{4} + 6a_{1} ^{2} b_{1} ^{2} ) + 2\sqrt {\Lambda _{3} ^{2} + \Lambda _{4} ^{2} } }}, \\ \Lambda _{3} = & - c_{1} (a_{1} ^{2} - b_{1} ^{2} ) - c_{2} (a_{1} p_{1} - b_{1} q_{1} ) - c_{3} (a_{1} ^{4} - 6a_{1} ^{2} b_{1} ^{2} + b_{1} ^{4} ), \\ \Lambda _{4} = & - c_{1} (2a_{1} b_{1} ) - c_{2} (b_{1} p_{1} + a_{1} q_{1} ) - c_{3} (4a_{1} ^{3} b_{1} - 4a_{1} b_{1} ^{3} ), \\ \sqrt {\Lambda _{3} + \Lambda _{4} {\text{i}}} = & h_{1} + d_{1} {\text{i}},~\sqrt {\Lambda _{3} - \Lambda _{4} {\text{i}}} = h_{1} - d_{1} {\text{i}}. \\ \end{aligned}$$

Then, by substituting Eq. (11) into Eq. (5), we obtain the one breath-wave solution of Eq. (1) as follows,

$$\begin{aligned} {u_2} = \frac{{2(2\sqrt{{\alpha _2}}\cosh ({\theta _1} + \frac{1}{2}\ln {\alpha _2}){a_1}^2 - {\alpha _1}\cos ({\Lambda _1}){b_1}^2)}}{{2\sqrt{{\alpha _2}}\cosh ({\theta _1} + \frac{1}{2}\ln {\alpha _2}) + {\alpha _1}\cos ({\Lambda _1})}} - \frac{{2{{(2\sqrt{{\alpha _2}}\sinh ({\theta _1} + \frac{1}{2}\ln {\alpha _2}){a_1} - {\alpha _1}sin({\Lambda _1}){b_1})}^2}}}{{{{(2\sqrt{{\alpha _2}}\cosh ({\theta _1} + \frac{1}{2}\ln {\alpha _2}) - {\alpha _1}\cos ({\Lambda _1}))}^2}}}. \end{aligned}$$

(12)

Based on the work of the transitions of the breath-waves for the (2+1)-dimensional Ito equation [49], one breath-wave solution (12) of Eq. (1) has the following characteristics.

• (1) It can be seen from expression (12) that the one breath-wave solution includes a hyperbolic function $(\mathrm {cosh,sinh})$ and a trigonometric function $(\mathrm {sin,cos})$, in which the hyperbolic function controls the local properties of one breath-wave, and the periodic properties are dominated by trigonometric function, so one breath-wave can be regarded as the combination of soliton and periodic wave.

• (2) It is obviously noticed that the wave velocity of soliton along x-axis is $v_x^s = -\frac{{{a_1}{h_1}}}{{{a_1}^2 + {p_1}^2}},$ and the wave velocity of soliton along y-axis is $v_y^s = -\frac{{{p_1}{h_1}}}{{{a_1}^2 + {p_1}^2}},$ the velocity of periodic wave along x-axis is $v_x^p = -\frac{{{b_1}{d_1}}}{{{b_1}^2 + {q_1}^2}},$ the velocity of periodic wave along y-axis is $v_y^p = -\frac{{{q_1}{d_1}}}{{{b_1}^2 + {q_1}^2}},$

• (3) From Eq. (12), the one breath-wave has two characteristic lines: ${\theta _1} + \frac{1}{2}\ln {\alpha _2} = {a_1}x + {p_1}y + {h_1}t + {\beta _1} + \frac{1}{2}\ln {\alpha _2} = 0,~{\Lambda _1} = {b_1}x + {q_1}y + {d_1}t + {\gamma _1} = 0.$

  • (i) If one has the following relation of $\left| {\begin{array}{*{20}{c}} {{a _1}}&{}{{p _1}}\\ {{b _1}}&{}{{q _1}} \end{array}} \right| \ne 0,$ the two characteristic lines are not parallel, as shown in Fig. (4).

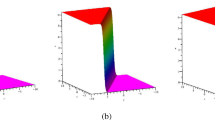
    Fig. 4

    

    (Color online) a One breath-wave of Eq. (1) with parameters $c_1=c_2=c_3=1,a_1= 0.3,b_1=1.5,p_1=0.5,q_1=-2,\alpha _1=2,\beta _1=0,\gamma _1=0.$ This figure is three-dimensional stereogram of one breath-wave when $t=0.$ b the corresponding contour figure of (a), the red line ($1.5x-2y=0$) and the green line ($0.3x+0.5y+1.153310513=0$) are two characteristic lines of one breath wave

  • (ii) If one has the following relation of $\left| {\begin{array}{*{20}{c}} {{a _1}}&{}{{p _1}}\\ {{b _1}}&{}{{q _1}} \end{array}} \right| = 0,$ that is the two characteristic lines are parallel, as shown in Fig. (5). Based on this special condition, the one breath-wave can be transformed into a series of nonlinear waves including quasi-anti-dark soliton, M-shaped soliton, oscillation M-shaped soliton, multi-peak soliton, quasi-sine wave, quasi-periodic W-shaped wave, quasi-periodic anti-dark soliton wave and quasi-periodic wave. In Fig. 5a and b, quasi-anti-dark soliton $({\frac{{{b_1}}}{{{a_1}}} < 0.4})$ has only one characteristic line and is symmetrical about extreme line. In Fig. 5c and d, M-shaped soliton $({0.4 \le \frac{{{b_1}}}{{{a_1}}} \le 1})$ has two peaks, one valley, three characteristic lines and is asymmetrical about extreme line. With the value of $\frac{{{b_1}}}{{{a_1}}}$ increasing, the one breath-wave becomes a asymmetrical oscillation M-shaped soliton $\left({1 < \frac{{{b_1}}}{{{a_1}}} \le 2.5}\right)$, and the number of characteristic lines also increases, if the value of $\frac{{{b_1}}}{{{a_1}}}$ increases continuously, the oscillation becomes acute, and the one breath-wave becomes a asymmetrical multi-peak soliton $\left( {\left\{ {2.5 < \frac{{b_{1} }}{{a_{1} }} < 50} \right\}} \right)$, as shown in Fig. 5e–h. When the value of $\frac{{{b_1}}}{{{a_1}}}$ becomes very large, the one breath-wave transforms quasi-sine wave $({\frac{{{b_1}}}{{{a_1}}} \ge 50})$, quasi-periodic W-shaped wave $\left(\frac{{{b_1}}}{{{a_1}}} {\approx } 1000\right)$, quasi-periodic anti-dark soliton wave $\left(\frac{{{b_1}}}{{{a_1}}} {\approx } 1000\right)$ and quasi-periodic wave $\left({\frac{{{b_1}}}{{{a_1}}} \ge 1500}\right)$. Their locality almost disappears and the periodicity becomes more and more obvious, as shown in Fig. 6. Finally, the distribution of diverse transformed nonlinear waves is given in Fig. 7(a).

  Fig. 5

  

  (Color online) One breath-wave transformation of Eq. (1) with parameters $c_1=c_2=c_3=1.$ a $a_1=1, b_1=0.01, p_1=2, q_1=0.02, \alpha _1=2, \beta _1=0, \gamma _1=0.$ This figure is three-dimensional stereogram of one breath-wave transformation when $t=0.$ b The wave moves along the x-axis when $y=0,t=0.$ c $a_1=0.2, b_1=0.2, p_1=0.2, q_1=0.2, \alpha _1=2, \beta _1=0, \gamma _1=0.$ d The wave moves along the x-axis when $y=0,t=0.$ e $a_1=0.2, b_1=0.5, p_1=0.4, q_1=1, \alpha _1=2, \beta _1=0, \gamma _1=0.$ f The wave moves along the x-axis when $y=0,t=0.$ g $a_1=0.2, b_1=2, p_1=0.4, q_1=4, \alpha _1=2, \beta _1=0, \gamma _1=0.$ h The wave moves along the x-axis when $y=0,t=0$

  Fig. 6

  

  (Color online) One breath-wave transformation of Eq. (1) with parameters $c_1=c_2=c_3=1.$ a $a_1=0.04, b_1=2, p_1=0.05, q_1=2.5, \alpha _1=2, \beta _1=0, \gamma _1=0.$ This figure is three-dimensional stereogram of one breath-wave transformation when $t=0.$ b The wave moves along the x-axis when $y=0,t=0.$ c $a_1=0.001, b_1=1, p_1=0.002, q_1=2, \alpha _1=0.6, \beta _1=0, \gamma _1=0.$ d The wave moves along the x-axis when $y=0,t=0.$ e $a_1=0.001, b_1=1, p_1=0.0015, q_1=1.5, \alpha _1=0.6, \beta _1=0, \gamma _1=0.$ f The wave moves along the x-axis when $y=0,t=0.$ g $a_1=0.0015, b_1=1.5, p_1=0.002, q_1=3, \alpha _1=0.6, \beta _1=0, \gamma _1=0.$ h The wave moves along the x-axis when $y=0,t=0$

  Fig. 7

  

  (Color online) a The distributions of diverse transformed nonlinear waves, in which ”QAN” represents quasi-anti-dark soliton, ”MS”(M-shaped soliton), ”OM”(oscillation M-shaped soliton), ”QPW”(quasi-periodic W-shaped soliton”, ”QPAN”(quasi-periodic anti-dark soliton), ”QP”(quasi-periodic wave), ”MP”(multi-peak soliton) and ”QSW”(quasi-sine wave). b Two breath-wave of Eq. (1) with parameters $c_1=c_2=c_3=1,a_1= 0.3,b_1=1.5,p_1=0.5,q_1=-2,a_2= 0.5,b_2=2,p_2=0.5,q_2=-3,\alpha _1=2,\beta _1=0,\gamma _1=0,\alpha _3=2,\beta _2=0,\gamma _2=0.$ This figure is three-dimensional stereogram of two breath-wave when $t=0.$ c the corresponding contour figure of (b), the red lines ($1.5x-2y=0, 0.3x+0.5y=0$) and the green lines ($0.5x+0.5y=0, 2x-3y=0$) are two sets of characteristic lines of two breath-wave

3.2 The two breath-wave solution of Eq. (1)

In this section, the two breath-wave solution of Eq. (1) is obtained by a similar method as one. The four-soliton solution has the form of

$$\begin{aligned} f_{4} = & 1 + {\text{e}}^{{\sigma _{{\text{1}}} }} + {\text{e}}^{{\sigma _{{\text{2}}} }} + {\text{e}}^{{\sigma _{{\text{3}}} }} + {\text{e}}^{{\sigma _{{\text{4}}} }} + {\text{e}}^{{\sigma _{{\text{1}}} {\text{ + }}\sigma _{{\text{2}}} {\text{ + A}}_{{{\text{12}}}} }} + {\text{e}}^{{\sigma _{{\text{1}}} {\text{ + }}\sigma _{{\text{3}}} {\text{ + A}}_{{{\text{13}}}} }} \\ & + {\text{e}}^{{\sigma _{{\text{1}}} {\text{ + }}\sigma _{{\text{4}}} {\text{ + A}}_{{{\text{14}}}} }} + {\text{e}}^{{\sigma _{{\text{2}}} {\text{ + }}\sigma _{{\text{3}}} {\text{ + A}}_{{{\text{23}}}} }} + {\text{e}}^{{\sigma _{{\text{2}}} {\text{ + }}\sigma _{{\text{4}}} {\text{ + A}}_{{{\text{24}}}} }} + {\text{e}}^{{\sigma _{{\text{3}}} {\text{ + }}\sigma _{{\text{4}}} {\text{ + A}}_{{{\text{34}}}} }} \\ & + {\text{e}}^{{\sigma _{{\text{1}}} {\text{ + }}\sigma _{{\text{2}}} {\text{ + }}\sigma _{{\text{3}}} {\text{ + A}}_{{{\text{12}}}} {\text{ + A}}_{{{\text{23}}}} {\text{ + A}}_{{{\text{13}}}} }} + {\text{e}}^{{\sigma _{{\text{1}}} {\text{ + }}\sigma _{{\text{2}}} {\text{ + }}\sigma _{{\text{4}}} {\text{ + A}}_{{{\text{12}}}} {\text{ + A}}_{{{\text{24}}}} {\text{ + A}}_{{{\text{14}}}} }} \\ & + {\text{e}}^{{\sigma _{{\text{1}}} {\text{ + }}\sigma _{{\text{3}}} {\text{ + }}\sigma _{{\text{4}}} {\text{ + A}}_{{{\text{13}}}} {\text{ + A}}_{{{\text{34}}}} {\text{ + A}}_{{{\text{14}}}} }} + {\text{e}}^{{\sigma _{{\text{2}}} {\text{ + }}\sigma _{{\text{3}}} {\text{ + }}\sigma _{{\text{4}}} {\text{ + A}}_{{{\text{23}}}} {\text{ + A}}_{{{\text{34}}}} {\text{ + A}}_{{{\text{24}}}} }} \\ & + {\text{e}}^{{\sigma _{{\text{1}}} {\text{ + }}\sigma _{{\text{2}}} {\text{ + }}\sigma _{{\text{3}}} {\text{ + }}\sigma _{{\text{3}}} {\text{ + A}}_{{{\text{12}}}} {\text{ + A}}_{{{\text{23}}}} {\text{ + A}}_{{{\text{13}}}} {\text{ + A}}_{{{\text{23}}}} {\text{ + A}}_{{{\text{34}}}} {\text{ + A}}_{{{\text{24}}}} }} . \\ \end{aligned}$$

(13)

By letting

$$\begin{aligned} {k_3} = {a_2} + {b_2}\mathrm{{i}},~{k_4} = {a_2} - {b_2}\mathrm{{i}},~{l_3} = {p_2} + {q_2}\mathrm{{i}},~{l_4} = {p_2} - {q_2}\mathrm{{i}},~{\delta _3} = \ln \frac{{{\alpha _3}}}{2} + {\beta _2} + {\gamma _2}\mathrm{{i}},~{\delta _4} = \ln \frac{{{\alpha _3}}}{2} + {\beta _2} - {\gamma _2}\mathrm{{i}}, \end{aligned}$$

(14)

where ${a_2},{b_2},{p_2},{q_2} \ne 0,{\alpha _3} > 0,{\beta _2}$ and ${\gamma _2}$ are arbitrary real constants and substituting (14) into $f_4,$ we obtain the another expression of

$$\begin{aligned} f_{4} = & 1 + \alpha _{1} e^{{\theta _{1} }} \cos \left( {\Lambda _{1} } \right) + \frac{{\alpha _{1} ^{2} G_{1} e^{{2\theta _{1} }} }}{4} + \alpha _{3} e^{{\theta _{2} }} \cos \left( {\Lambda _{2} } \right) + \frac{{\alpha _{3} ^{2} G_{2} e^{{2\theta _{2} }} }}{4} \\ & + \frac{{\alpha _{1} ^{2} \alpha _{3} ^{2} G_{1} G_{2} }}{{16}}e^{{2\theta _{1} + 2\theta _{2} }} \left( {H_{{3R}}^{2} + H_{{3I}}^{2} } \right)\left( {H_{{4R}}^{2} + H_{{4I}}^{2} } \right) \\ & + \frac{{\alpha _{1} \alpha _{3} }}{2}e^{{\theta _{1} + \theta _{2} }} \left( {H_{{3R}} \cos \left( {\Lambda _{1} + \Lambda _{2} } \right) - H_{{3I}} \sin \left( {\Lambda _{1} + \Lambda _{2} } \right)} \right) \\ & + \frac{{\alpha _{1} \alpha _{3} }}{2}e^{{\theta _{1} + \theta _{2} }} (H_{{4R}} \cos (\Lambda _{1} - \Lambda _{2} ) - H_{{4I}} \sin (\Lambda _{1} - \Lambda _{2} )) \\ & + \frac{{\alpha _{1} ^{2} \alpha _{3} G_{1} }}{4}e^{{2\theta _{1} + \theta _{2} }} \left( {\left( {H_{{3R}} H_{{4R}} + H_{{3I}} H_{{4I}} } \right)\cos \left( {\Lambda _{2} } \right) - \left( {H_{{3I}} H_{{4R}} - H_{{3R}} H_{{4I}} } \right)\sin (\left( {\Lambda _{2} } \right)} \right) \\ & + \frac{{\alpha _{1} \alpha _{3} ^{2} G_{2} }}{4}e^{{\theta _{1} + 2\theta _{2} }} \left( {\left( {H_{{3R}} H_{{4R}} - H_{{3I}} H_{{4I}} } \right)\cos \left( {\Lambda _{1} } \right) - \left( {H_{{3I}} H_{{4R}} + H_{{3R}} H_{{4I}} } \right)\sin \left( {\Lambda _{1} } \right)} \right), \\ \end{aligned}$$

(15)

where

$$\begin{aligned} \theta _{2} & = a_{2} x + p_{2} y + h_{2} t + \beta _{2} ,\;\Lambda _{2} = b_{2} x + q_{2} y + d_{2} t + \gamma _{2} , \\ G_{2} & = \frac{{ - 2c_{1} (a_{2}^{2} + b_{2}^{2} ) + 2c_{2} (a_{2} p_{2} + b_{2} q_{2} ) + 2c_{3} (a_{2}^{4} - 7b_{2}^{4} - 6a_{2}^{2} b_{2}^{2} ) + 2\sqrt {\Lambda _{5}^{2} + \Lambda _{6}^{2} } }}{{ - 2c_{1} (a_{2}^{2} + b_{2}^{2} ) + 2c_{2} (a_{2} p_{2} + b_{2} q_{2} ) + 2c_{3} (7a_{2}^{4} - b_{2}^{4} + 6a_{2}^{2} b_{2}^{2} ) + 2\sqrt {\Lambda _{5}^{2} + \Lambda _{6}^{2} } }}, \\ H_{{3R}} & = \text{Re} (e^{{A_{{13}} }} ),H_{{3I}} = \text{Im} (e^{{A_{{13}} }} ),H_{{4R}} = \text{Re} (e^{{A_{{14}} }} ),H_{{4I}} = \text{Im} (e^{{A_{{14}} }} ), \\ \Lambda _{5} & = - c_{1} (a_{2}^{2} - b_{2}^{2} ) - c_{2} (a_{2} p_{2} - b_{2} q_{2} ) - c_{3} (a_{2}^{4} - 6a_{2}^{2} b_{2}^{2} + b_{2}^{4} ), \\ \Lambda _{6} & = - c_{1} (2a_{2} b_{2} ) - c_{2} (b_{2} p_{2} + a_{2} q_{2} ) - c_{3} (4a_{2}^{3} b_{2} - 4a_{2} b_{2}^{3} ),\sqrt {\Lambda _{5} + \Lambda _{6} i} \\ & = h_{2} + d_{2} i,\,\sqrt {\Lambda _{5} - \Lambda _{6} i} = h_{2} - d_{2} i. \\ \end{aligned}$$

It is different from the one breath-wave solution, in Figs. 7, 8, the two breath-wave solution has two sets of characteristic lines: ${\theta _1} = {a_1}x + {p_1}y + {h_1}t + {\beta _1} = 0,~{\Lambda _1} = {b_1}x + {q_1}y + {d_1}t + {\gamma _1} = 0$ and ${\theta _2} = {a_2}x + {p_2}y + {h_2}t + {\beta _2} = 0,~{\Lambda _2} = {b_2}x + {q_2}y + {d_2}t + {\gamma _2} = 0.$

• (1) If two breather waves have

  $$\begin{aligned}\left| {\begin{array}{*{20}{c}} {{a_1}}&{}{{p_1}}\\ {{a_2}}&{}{{p_2}} \end{array}} \right| = 0,~\left| {\begin{array}{*{20}{c}} {{b_1}}&{}{{q_1}}\\ {{b_2}}&{}{{q_2}} \end{array}} \right| = 0,~\left| {\begin{array}{*{20}{c}} {{a_1}}&{}{{p_1}}\\ {{b_1}}&{}{{q_1}} \end{array}} \right| \ne 0,~\left| {\begin{array}{*{20}{c}} {{a_2}}&{}{{p_2}}\\ {{b_2}}&{}{{q_2}} \end{array}} \right| \ne 0,\end{aligned}$$

  the two breather waves are parallel, as shown in Fig. 8.

  Fig. 8

  

  (Color online) a Two breath-wave of Eq. (1) with parameters $c_1=c_2=c_3=1,a_1= 0.3,b_1=1.5,p_1=0.5,q_1=-2,a_2= 0.4,b_2=2,p_2=\frac{2}{3},q_2=-\frac{8}{3},\alpha _1=0.7,\beta _1=5,\gamma _1=-5,\alpha _3=2,\beta _2=0,\gamma _2=0.$ This figure is three-dimensional stereogram of two breath-wave when $t=0.$ b the corresponding contour figure of (a), the red lines ($0.3x+0.5y+5=0, 1.5x-2y-5=0$) and the green lines ($0.4x+0.6666666667y=0, 2x-\frac{8}{3}y=0$) are two sets of characteristic lines of two-breath wave

• (2) If two breather waves have

  $$\begin{aligned}\left| {\begin{array}{*{20}{c}} {{a_1}}&{}{{p_1}}\\ {{a_2}}&{}{{p_2}} \end{array}} \right| \ne 0,~~\left| {\begin{array}{*{20}{c}} {{b_1}}&{}{{q_1}}\\ {{b_2}}&{}{{q_2}} \end{array}} \right| \ne 0, \end{aligned}$$

  the waves are not parallel.

• (i) If

  $$\begin{aligned}\left| {\begin{array}{*{20}{c}} {{a_1}}&{}{{p_1}}\\ {{b_1}}&{}{{q_1}} \end{array}} \right| \ne 0,~~\left| {\begin{array}{*{20}{c}} {{a_2}}&{}{{p_2}}\\ {{b_2}}&{}{{q_2}} \end{array}} \right| \ne 0,\end{aligned}$$

  the two breather waves collide, as shown in Fig. 7. Then, in Figs. 9, 10, 11, 12, 13, 14, and 15, the transformation mechanism of two breath-wave is discussed in detail as follows.

  Fig. 9

  

  (Color online) a Two breath-wave transformation of Eq. (1) with parameters $c_1=c_2=c_3=1,a_1= 2.3,b_1=0.23,p_1=2.3,q_1=0.23,a_2=0.3,b_2=1.5,p_2=0.5,q_2=-2,\alpha _1=2,\beta _1=0,\gamma _1=0,\alpha _3=2,\beta _2=0,\gamma _2=0.$ This figure is three-dimensional stereogram of two breath-wave transformation when $t=0$. b Vertical view of (a). c The corresponding contour figure of (a), the red line ($2.3x+2.3y=0$) is characteristic line of quasi-anti-dark soliton, the green lines ($0.3x+0.5y=0, 1.5x-2y=0$) are two characteristic lines of one breath wave

  Fig. 10

  

  (Color online) a Two breath-wave transformation of Eq. (1) with parameters $c_1=c_2=c_3=1,a_1= 0.2,b_1=0.3,p_1=-0.2,q_1=-0.3,a_2= 0.3,b_2=1.5,p_2=0.5,q_2=-2,\alpha _1=2,\beta _1=0,\gamma _1=0,\alpha _3=2,\beta _2=0,\gamma _2=0.$ This figure is three-dimensional stereogram of two breath-wave transformation when $t=0$. b Vertical view of (a). c The wave moves along the x-axis when $y=-20,t=0$(green), x-axis when $y=20,t=0$(red)

  Fig. 11

  

  (Color online) a Two breath-wave transformation of Eq. (1) with parameters $c_1=c_2=c_3=1,a_1= 0.01,b_1=1,p_1=-0.01,q_1=-1,a_2= 0.3,b_2=1.5,p_2=0.5,q_2=-2,\alpha _1=2,\beta _1=0,\gamma _1=0,\alpha _3=2,\beta _2=0,\gamma _2=0.$ This figure is three-dimensional stereogram of two breath-wave transformation when $t=0$. b Vertical view of (a). c Two breath-wave transformation of Eq. (1) with parameters $c_1=c_2=c_3=1,a_1= 0.01,b_1=1,p_1=-0.01,q_1=-1,a_2= 0.01,b_2=1.5,p_2=-0.01,q_2=1.5,\alpha _1=2,\beta _1=0,\gamma _1=0,\alpha _3=2,\beta _2=0,\gamma _2=0.$ This figure is three-dimensional stereogram of two breath-wave transformation when $t=0$

  Fig. 12

  

  (Color online) a Two breath-wave transformation of Eq. (1) with parameters $c_1=c_2=c_3=1,a_1= 2.3,b_1=0.23,p_1=2.3,q_1=0.23,a_2=2.3,b_2=0.23,p_2=-2.3,q_2=-0.23,\alpha _1=2,\beta _1=0,\gamma _1=0,\alpha _3=0.6,\beta _2=0,\gamma _2=0.$ This figure is three-dimensional stereogram of two breath-wave transformation when $t=0$. b Vertical view of (a). c The corresponding contour figure of (a), the red line ($2.3x+2.3y=0$) and the green line ($2.3x-2.3y=0$) are characteristic lines of two quasi-anti-dark solitons

  Fig. 13

  

  (Color online) a Two breath-wave transformation of Eq. (1) with parameters $c_1=c_2=c_3=1,a_1= 1.2,b_1=0.1,p_1=1.2,q_1=0.1,a_2=0.2,b_2=0.2,p_2=-0.2,q_2=-0.2,\alpha _1=2,\beta _1=0,\gamma _1=0,\alpha _3=2,\beta _2=0,\gamma _2=0.$ This figure is three-dimensional stereogram of two breath-wave transformation when $t=0$. b Vertical view of (a). c The wave moves along the x-axis when $y=-20,t=0$ (green), x-axis when $y=20,t=0$(red)

  Fig. 14

  

  (Color online) a Two breath-wave transformation of Eq. (1) with parameters $c_1=c_2=c_3=1,a_1= 0.2,b_1=0.2,p_1=0.2,q_1=0.2,a_2=0.2,b_2=0.2,p_2=-0.2,q_2=-0.2,\alpha _1=0.9,\beta _1=0,\gamma _1=0,\alpha _3=2,\beta _2=0,\gamma _2=0.$ This figure is three-dimensional stereogram of two breath-wave transformation when $t=0$. b Vertical view of (a). c The wave moves along the x-axis when $y=-30,t=0$(green), x-axis when $y=30,t=0$(red)

  Fig. 15

  

  (Color online) a Two breath-wave transformation of Eq. (1) with parameters $c_1=c_2=c_3=1,a_1= 0.01,b_1=-1.01,p_1=0.01,q_1=-1.01,a_2=0.2,b_2=0.2,p_2=-0.2,q_2=-0.2,\alpha _1=2,\beta _1=0,\gamma _1=0,\alpha _3=2,\beta _2=0,\gamma _2=0.$ This figure is three-dimensional stereogram of two breath-wave transformation when $t=0$. b Vertical view of (a)

• (ii) If

  $$\begin{aligned}\left| {\begin{array}{*{20}{c}} {{a_1}}&{}{{p_1}}\\ {{b_1}}&{}{{q_1}} \end{array}} \right| = 0,~~\left| {\begin{array}{*{20}{c}} {{a_2}}&{}{{p_2}}\\ {{b_2}}&{}{{q_2}} \end{array}} \right| \ne 0,\end{aligned}$$

  one of the breather waves can be transformed into a series of nonlinear waves including quasi-anti-dark soliton, M-shaped soliton and quasi-periodic wave. In Fig. 9, the two breather waves are transformed into one breather wave and quasi-anti-dark soliton $\left(\left| {\frac{{{a_1}}}{{{b_1}}}} \right| = \left| {\frac{{{p_1}}}{{{q_1}}}} \right| = 10\right)$. In Fig. 10, the two breather waves are transformed into one breather wave and M-shaped soliton $\left(\left| {\frac{{{a_1}}}{{{b_1}}}} \right| = \left| {\frac{{{p_1}}}{{{q_1}}}} \right| \approx 1\right)$. In Fig. 11a and b, the two breather waves are transformed into one breather wave and quasi-periodic wave$\left(\left| {\frac{{{a_1}}}{{{b_1}}}} \right| = \left| {\frac{{{p_1}}}{{{q_1}}}} \right| \le 0.01\right)$.

• (iii) If

  $$\begin{aligned}\left| {\begin{array}{*{20}{c}} {{a_1}}&{}{{p_1}}\\ {{b_1}}&{}{{q_1}} \end{array}} \right| = 0,~~\left| {\begin{array}{*{20}{c}} {{a_2}}&{}{{p_2}}\\ {{b_2}}&{}{{q_2}} \end{array}} \right| = 0,\end{aligned}$$

  the two breather waves can be transformed into a series of nonlinear waves. In Fig. 12, the two breather waves are transformed into two nonparallel quasi-anti-dark solitons $\left(\left| {\frac{{{a_1}}}{{{b_1}}}} \right| = \left| {\frac{{{p_1}}}{{{q_1}}}} \right| = \left| {\frac{{{a_2}}}{{{b_2}}}} \right| = \left| {\frac{{{p_2}}}{{{q_2}}}} \right| = 10\right)$. In Fig. 13, the two breather waves are transformed into quasi-anti-dark soliton $\left(\left| {\frac{{{a_2}}}{{{b_2}}}} \right| = \left| {\frac{{{p_2}}}{{{q_2}}}} \right| \approx 10\right)$ and M-shaped soliton $\left(\left| {\frac{{{a_1}}}{{{b_1}}}} \right| = \left| {\frac{{{p_1}}}{{{q_1}}}} \right| = 1\right)$. In Fig. 14, the two breather waves are transformed into two nonparallel M-shaped solitons $\left(\left| {\frac{{{a_1}}}{{{b_1}}}} \right| = \left| {\frac{{{p_1}}}{{{q_1}}}} \right| = \left| {\frac{{{a_2}}}{{{b_2}}}} \right| = \left| {\frac{{{p_2}}}{{{q_2}}}} \right| = 1\right)$. In Fig. 15, the two breather waves are transformed into quasi-periodic wave $\left(\left| {\frac{{{a_2}}}{{{b_2}}}} \right| = \left| {\frac{{{p_2}}}{{{q_2}}}} \right| \le 0.01\right)$ and M-shaped soliton $\left(\left| {\frac{{{a_1}}}{{{b_1}}}} \right| = \left| {\frac{{{p_1}}}{{{q_1}}}} \right| = 1\right)$. In Fig. 11c, the two breather waves are transformed into bright and dark solitons $\left(\left| {\frac{{{a_1}}}{{{b_1}}}} \right| = \left| {\frac{{{p_1}}}{{{q_1}}}} \right| \le 0.01\right)$, $\left(\left| {\frac{{{a_2}}}{{{b_2}}}} \right| = \left| {\frac{{{p_2}}}{{{q_2}}}} \right| \le 0.01\right)$. Based on the above analysis, as the radio of ${{a_j}}$ and ${b_j}$, ${{p_j}}$ and ${q_j}$ decreases, the periodicity of the two breather waves becomes obvious, the locality almost disappears.

4 One-periodic waves and asymptotic properties

In this section, one-periodic wave solution of Eq. (1) is obtained via bilinear method and Riemann theta function. When ${N=1,}$ the theta function degenerates the following Fourier series

$$\begin{aligned} \varphi (\tau ,a) = \sum \limits _{n = - \infty }^{ + \infty } {{\mathrm{{e}}^{2\pi \mathrm{{i}}n\tau - \pi {n^2}a}}}, \end{aligned}$$

(16)

with phase variable ${\tau } = {\varepsilon }x + {\eta }y + {\omega }t + {\upsilon },$ and the first-order matrix ${a>0.}$

4.1 Construction of one-periodic waves

In order to obtain one-periodic wave solution, we take Eq. (16) into Eq. (8), and gain the following relation through Eq. (3):

$$\begin{aligned} B(D_{x} ,D_{y} ,D_{t} )\varphi (\tau ,a)\varphi (\tau ,a) = & \sum\limits_{{n = - \infty }}^{{ + \infty }} {\sum\limits_{{m = - \infty }}^{{ + \infty }} {B(D_{x} ,D_{y} ,D_{t} )} } e^{{2\pi in\tau - \pi n^{2} a}} e^{{2\pi im\tau - \pi m^{2} a}} \\ &= \sum\limits_{{n = - \infty }}^{{ + \infty }} {\sum\limits_{{m = - \infty }}^{{ + \infty }} {B(2\pi i(n - m)\varepsilon ,2\pi i(n - m)\eta ,2\pi i(n - m)\omega )} } e^{{2\pi i(n + m)\tau - \pi (n^{2} + m^{2} )a}} \\ & \mathop = \limits^{{m = m^{\prime} - n}} \sum\limits_{{m^{\prime} = - \infty }}^{{ + \infty }} {\left\{ {\sum\limits_{{n = - \infty }}^{{ + \infty }} {B(2\pi i(2n - m^{\prime})\varepsilon ,2\pi i(2n - m^{\prime})\eta ,2\pi i(2n - m^{\prime})\omega )e^{{ - \pi [n^{2} + (n - m^{\prime})^{2} ]a}} } } \right\}} \\ & \times e^{{2\pi im^{\prime}\tau }} = \sum\limits_{{m^{\prime} = - \infty }}^{{ + \infty }} {\mathop {{\text{ }}B}\limits^{{\_\_}} (} m^{\prime})e^{{2\pi im^{\prime}\tau }} , \\ \end{aligned}$$

(17)

where

$$\begin{aligned} \mathop B\limits ^{\_\_} (m^{\prime}) = \sum \limits _{n = - \infty }^{ + \infty } {B(2\pi \mathrm{{i}}(2n - m^{\prime}) \varepsilon ,2\pi \mathrm{{i}}(2n - m^{\prime})\eta ,2\pi \mathrm{{i}}(2n - m^{\prime})\omega )} {\mathrm{{e}}^{ - \pi [{n^2} + {{(n - m^{\prime})}^2}]a}}. \end{aligned}$$

(18)

Letting the summation index ${n=n'+1,}$ Eq. (18) have the following form of

$$\begin{aligned}\mathop B\limits ^{\_\_} (m^{\prime}) &= \sum \limits _{n^{\prime} = - \infty }^{ + \infty } {B(2\pi \mathrm{{i}}(2n^{\prime} - (m^{\prime} - 2))\varepsilon ,2\pi \mathrm{{i}}(2n^{\prime} - (m^{\prime} - 2))\eta ,2\pi \mathrm{{i}}(2n^{\prime} - (m^{\prime} - 2))\omega )}\\&\quad\times {\mathrm{{e}}^{ - \pi a[n{^{\prime 2}} + {{(n^{\prime} - (m^{\prime} - 2))}^2}]}} \times {\mathrm{{e}}^{ - 2\pi (m^{\prime} - 1)a}} = \mathop B\limits ^{\_\_} (m^{\prime} - 2) {\mathrm{{e}}^{ - 2\pi (m^{\prime} - 1)a}} = ...\\&= \left\{ \begin{array}{l} \mathop B\limits ^{\_\_} (0) {\mathrm{{e}}^{ - \frac{{\pi am{^{\prime 2}}}}{2}}},\;\;\;\;\;\;\;\;m^{\prime}\;\;\mathrm {is}\;\;\mathrm {even},\\ \mathop B\limits ^{\_\_} (1){\mathrm{{e}}^{ - \frac{{\pi a(m{^{\prime 2}} - 1)}}{2}}},\;\;\;m^{\prime}\;\;\mathrm {is}\;\; \mathrm {odd}, \end{array} \right. \end{aligned}$$

which shows that $\mathop B\limits ^{\_\_} (m'), m' \in Z$ is entirely determined by two formulas $\mathop B\limits ^{\_\_} (0)$ and $\mathop B\limits ^{\_\_} (1),$ that is, if the following two equations are satisfied

$$\begin{aligned} \mathop B\limits ^{\_\_} (0) = \mathop B\limits ^{\_\_} (1) = 0, \end{aligned}$$

(19)

then $\mathop B\limits ^{\_\_} (m') = 0, (m'\in Z),$ so $B({D_x},{D_y},{D_t})\varphi (\tau ,a)\varphi (\tau ,a) = 0.$ According to Eq. (18), Eq. (19) has the following form of

$$\begin{aligned} \mathop B\limits ^{\_\_} (0) &= \sum \limits _{n = - \infty }^{ + \infty } {B(2\pi \mathrm{{i}}(2n - 0)\varepsilon ,2\pi \mathrm{{i}}(2n - 0)\eta ,2\pi \mathrm{{i}}(2n - 0)\omega )} {\mathrm{{e}}^{ - 2{n^2}\pi a}}\nonumber \\ &= \sum \limits _{n = - \infty }^{ + \infty } {( - 16{\pi ^2}{n^2}{\omega ^2} - } 16{\pi ^2}{n^2}{\varepsilon ^2}{c_1} - 16{\pi ^2}{n^2}\varepsilon \eta {c_2} + 256{\pi ^4}{n^4}{\varepsilon ^4}{c_3} - 96{\pi ^2}{n^2}{\varepsilon ^2}{u_0} + c){\mathrm{{e}}^{ - 2{n^2}\pi a}} = 0,\nonumber \\ \mathop B\limits ^{\_\_} (1) &= \sum \limits _{n = - \infty }^{ + \infty } {B(2\pi \mathrm{{i}}(2n - 1)\varepsilon ,2\pi \mathrm{{i}}(2n - 1)\eta ,2\pi \mathrm{{i}}(2n - 1)\omega )} {\mathrm{{e}}^{ - (2{n^2}-2n+1) \pi a}}\nonumber \\ &= \sum \limits _{n = - \infty }^{ + \infty } {( - 4{\pi ^2}{{(2n - 1)}^2}{\omega ^2} - } 4{\pi ^2}{(2n - 1)^2}{\varepsilon ^2}{c_1} - 4{\pi ^2}{(2n - 1)^2}\varepsilon \eta {c_2} + 16{\pi ^4}{(2n - 1)^4}{\varepsilon ^4}{c_3}\nonumber \\&\quad- 24{\pi ^2}{(2n - 1)^2}{\varepsilon ^2}{u_0} + c){\mathrm{{e}}^{ - (2{n^2}-2n+1)\pi a}} = 0. \end{aligned}$$

(20)

By introducing the marks as

$$\begin{aligned}&\psi = {\mathrm{{e}}^{ - \pi a}},~{a_{11}} = - \sum \limits _{n = - \infty }^{ + \infty } {16{\pi ^2}{n^2}{\psi ^{2{n^2}}}} ,~{a_{12}} = \sum \limits _{n = - \infty }^{ + \infty } {{\psi ^{2{n^2}}}} ,\nonumber \\&{a_{21}} = - \sum \limits _{n = - \infty }^{ + \infty } {4{\pi ^2}{{(2n - 1)}^2}{\psi ^{2{n^2} - 2n + 1}}}, ~{a_{22}} = \sum \limits _{n = - \infty }^{ + \infty } {{\psi ^{2{n^2} - 2n + 1}}},\nonumber \\&{b_1} = \sum \limits _{n = - \infty }^{ + \infty } ( 16{\pi ^2}{n^2}{\varepsilon ^2}{c_1} + 16{\pi ^2}{n^2}\varepsilon \eta {c_2} - 256{\pi ^4}{n^4}{\varepsilon ^4}{c_3} + 96{\pi ^2}{n^2}{\varepsilon ^2}{u_0}){\psi ^{2{n^2}}},\nonumber \\&{b_2} = \sum \limits _{n = - \infty }^{ + \infty } ( 4{\pi ^2}{(2n - 1)^2}{\varepsilon ^2}{c_1} + 4{\pi ^2}{(2n - 1)^2}\varepsilon \eta {c_2}- 16{\pi ^4}{(2n - 1)^4}{\varepsilon ^4}{c_3} + 24{\pi ^2}{(2n - 1)^2}{\varepsilon ^2}{u_0}){\psi ^{2{n^2} - 2n + 1}}, \end{aligned}$$

(21)

Eq. (19) can be written as the form of a system of linear equations about frequency $\omega$ and integration constant c,  that is

$$\begin{aligned} \left( {\begin{array}{*{20}{c}} {{a_{11}}}&{}{{a_{12}}}\\ {{a_{21}}}&{}{{a_{22}}} \end{array}} \right) \left( \begin{array}{l} {\omega ^2}\\ c \end{array} \right) = \left( \begin{array}{l} {b_1}\\ {b_2} \end{array} \right) . \end{aligned}$$

(22)

Then solve Eq. (22), we get the frequency and integration constant, that is

$$\begin{aligned}{\omega ^2} = \frac{{{b_1}{a_{22}} - {b_2}{a_{12}}}}{{{a_{11}}{a_{22}} - {a_{12}}{a_{21}}}},~~~~~c = \frac{{{b_2}{a_{11}} - {b_1}{a_{21}}}}{{{a_{11}}{a_{22}} - {a_{12}}{a_{21}}}}, \end{aligned}$$

so we obtain the one-periodic wave solution of Eq. (1)

$$\begin{aligned} u = {u_0} + 2{\left( {\ln \varphi (\tau ,a)} \right) _{xx}}, \end{aligned}$$

(23)

where the theta function $\varphi (\tau ,a)$ is given by Eq. (16), the other parameters ${c_1},{c_2},{c_{3,}}a,\varepsilon ,\eta ,{{u_0}}$ and $\upsilon$ are free, the three parameters $a,\varepsilon$ and $\eta$ play a major role in one-periodic waves.

4.2 Characteristics of one-periodic waves

• (1) It is bounded for all complex variables (x, y, t).

• (2) It has two fundamental periods 1 and $\mathrm{{i}}a$ about the phase variable $\tau .$

• (3) Equation (17) can be written as the following form of

  $$\begin{aligned}B({D_x},{D_y},{D_t})\varphi (\tau ,a)\varphi (\tau ,a) &= \sum \limits _{n = - \infty }^{ + \infty } {\sum \limits _{m = - \infty }^{ + \infty } {B({D_x},{D_y},{D_t})} } {\mathrm{{e}}^{2\pi \mathrm{{i}}n\tau - \pi {n^2}a}}{\mathrm{{e}}^{2\pi \mathrm{{i}}m\tau - \pi {m^2}a}}\\&= \sum \limits _{m' = - \infty }^{ + \infty } {\mathop B\limits ^{\_\_} (} m'){\mathrm{{e}}^{2\pi \mathrm{{i}}m'\tau }} = \sum \limits _{m' = - \infty }^{ + \infty } {\mathop B\limits ^{\_\_} (} m')cos(m'\tau ). \end{aligned}$$

  (24)

  It can be seen from expression (24) that the one-periodic wave solution has one characteristic line: ${\tau } = {\varepsilon }x + {\eta }y + {\omega }t + {\upsilon }=0,$ the propagation direction of wave is completely determined by $\tau ,$ and $\frac{{{v_x}}}{{{v_y}}} = \frac{\varepsilon }{\eta },$ where $v_x$ and $v_y$ are the propagation velocity along the x-axis and y-axis, respectively. In Fig. 16a, the points (x, y) ($\varepsilon x + \eta y = 2k\pi , k=0,1,2,...$) are the peak points of one-periodic waves, and the points (x, y) ($\varepsilon x + \eta y = 2k\pi +\pi , k=0,1,2,...$) are the trough points of one-periodic waves.

Fig. 16

(Color online) A one-periodic wave of Eq. (1) with parameters $c_1=1,~c_2=2,~c_3=3,~a = 2,\varepsilon = 0.5,\eta = 2.$ This figure can be regarded as a superposition of a series of soliton waves. a Three-dimensional stereogram of one-periodic wave when $t=0.$ b Vertical view of plot (a). c The wave moves along the x-axis when $y=0,t=0.$ d The wave moves along the y-axis when $x=0,t=0.$ e The wave moves along t-axis when $x=0,y=0$

4.3 Asymptotic properties of one-periodic waves

In what follows, we further analyze asymptotic properties of the one-periodic wave solution by solving Eq. (22) and taking a limit condition. In order to solve Eq. (22), one makes

$$\begin{aligned}\left( {\begin{array}{*{20}{c}} {{a_{11}}}&{}{{a_{12}}}\\ {{a_{21}}}&{}{{a_{22}}} \end{array}} \right) = {M_0} + {M_1}\psi + {M_2}{\psi ^2} + \cdots,~~~\left( \begin{array}{l} {b_1}\\ {b_2} \end{array} \right) = {N_0} + {N_1}\psi + {N_2}{\psi ^2} + \cdots,~~~\left( \begin{array}{l} {\omega ^2}\\ c \end{array} \right) = {X_0} + {X_1}\psi + {X_2}{\psi ^2} + \cdots, \end{aligned}$$

then taking $u_0=0$ and expanding ${a_{ij}},{b_j}~(i,j = 1,2)$ into the sum of $\psi$

$$\begin{aligned} {a_{11}} &= - 32{\pi ^2}({\psi ^2} + 4{\psi ^8} + 9{\psi ^{18}} + \cdots),~~{a_{12}} = 1 + 2{\psi ^2} + 2{\psi ^8} + 2{\psi ^{18}} + \cdots,\\{a_{21}} &= - 8{\pi ^2}(\psi + 9{\psi ^5} + 25{\psi ^{13}} + \cdots),~~{a_{22}} = 2\psi + 2{\psi ^5} + 2{\psi ^{13}} + 2{\psi ^{25}} + \cdots,\\{b_1} &= (32{\pi ^2}{\varepsilon ^2}{c_1} + 32{\pi ^2}\varepsilon \eta {c_2} - 512{\pi ^4}{\varepsilon ^4}{c_3}){\psi ^2} + (32{\pi ^2}{\varepsilon ^2}{c_1} + 32{\pi ^2}\varepsilon \eta {c_2} - 2048{\pi ^4}{\varepsilon ^4}{c_3})4{\psi ^8} + \cdots,\\{b_2} &= (8{\pi ^2}{\varepsilon ^2}{c_1} + 8{\pi ^2}\varepsilon \eta {c_2} - 32{\pi ^4}{\varepsilon ^4}{c_3}){\psi } + (8{\pi ^2}{\varepsilon ^2}{c_1} + 8{\pi ^2}\varepsilon \eta {c_2} - 288{\pi ^4}{\varepsilon ^4}{c_3})9{\psi ^5} + \cdots, \end{aligned}$$

we have

$$\begin{aligned} M_{0} & = \left( {\begin{array}{*{20}c} 0 & 1 \\ 0 & 0 \\ \end{array} } \right),~~M_{1} = \left( {\begin{array}{*{20}c} 0 & 0 \\ { - 8\pi ^{2} } & 2 \\ \end{array} } \right),~~M_{2} = \left( {\begin{array}{*{20}c} { - 32\pi ^{2} } & 2 \\ 0 & 0 \\ \end{array} } \right),~~M_{3} = M_{4} = 0,~~M_{5} = \left( {\begin{array}{*{20}c} 0 & 0 \\ { - 72\pi ^{2} } & 2 \\ \end{array} } \right), \cdots ,\\{N_0} &= 0,~~{N_1} = \left( \begin{array}{l} ~~~~~~~~~~~~~~~~~0\\ 8{\pi ^2}{\varepsilon ^2}{c_1} + 8{\pi ^2}\varepsilon \eta {c_2} - 32{\pi ^4}{\varepsilon ^4}{c_3} \end{array} \right) ,~~ {N_2} = \left( \begin{array}{l} 32{\pi ^2}{\varepsilon ^2}{c_1} + 32{\pi ^2}\varepsilon \eta {c_2} - 512{\pi ^4}{\varepsilon ^4}{c_3}\\ ~~~~~~~~~~~~~~~~~~~~~0 \end{array} \right) ,\\{N_3} &= {N_4} = 0,~~{N_5} = \left( \begin{array}{l} ~~~~~~~~~~~~~~~~~~~~~0\\ 72{\pi ^2}{\varepsilon ^2}{c_1} + 72{\pi ^2}\varepsilon \eta {c_2} - 2592{\pi ^4}{\varepsilon ^4}{c_3} \end{array} \right) ,\ldots . \end{aligned}$$

Therefore, one has

$$\begin{aligned} {X_0} = \left( \begin{array}{l} - {\varepsilon ^2}{c_1} - \varepsilon \eta {c_2} + 4{\pi ^2}{\varepsilon ^4}{c_3}\\ ~~~~~~~~~~~~~0 \end{array} \right) ,~~{X_1} = {X_3} = 0,~~ {X_2} = \left( \begin{array}{l} -96{\pi ^2}{\varepsilon ^4}{c_3}\\ -384{\pi ^4}{\varepsilon ^4}{c_3} \end{array} \right) ,~~ {X_4} = \left( \begin{array}{l} -288{\pi ^2}{\varepsilon ^4}{c_3}\\ -2304{\pi ^4}{\varepsilon ^4}{c_3} \end{array} \right) . \end{aligned}$$

(25)

Interestingly, the relation of the one-soliton wave solution and one-periodic wave solution is given as follows.

Theorem 1

If one-periodic wave solution Eq. (23) satisfies the condition of

$$\begin{aligned} {u_0} = 0,\;\;\varepsilon = \frac{k}{{2\pi \mathrm {i}}},\;\;\eta = \frac{l}{{2\pi \mathrm {i}}},\;\;\upsilon = \frac{{\delta + \pi a}}{{2\pi \mathrm {i}}}, \end{aligned}$$

(26)

where k, l and $\delta$ are given by Eq. (4), we have the following asymptotic properties:

$$\begin{aligned} c \rightarrow 0,\;\;\tau \rightarrow \frac{{\sigma + \pi a}}{{2\pi \mathrm {i}}},\;\;\varphi (\tau ,a) \rightarrow 1 + \mathrm{{e}^\sigma },\;\;\psi \rightarrow 0.\end{aligned}$$

Proof

By applying Eq. (25), we obtain

$$\begin{aligned}{\omega ^2} &= ( - {\varepsilon ^2}{c_1} - \varepsilon \eta {c_2} + 4{\pi ^2}{\varepsilon ^4}{c_3}) - 96{\pi ^2}{\varepsilon ^4}{c_3}{\psi ^2} -288{\pi ^2}{\varepsilon ^4}{c_3}{\psi ^4} + o({\psi ^4}),\\c &= -384{\pi ^4}{\varepsilon ^4}{c_3}{\psi ^2} -2304{\pi ^4}{\varepsilon ^4}{c_3}){\psi ^4} + o({\psi ^4}), \end{aligned}$$

and by using condition (26), we have

$$\begin{aligned} c \rightarrow 0,~2\pi \mathrm{{i}}\omega \rightarrow \sqrt{ - 4{\pi ^2}( - {\varepsilon ^2}{c_1} - \varepsilon \eta {c_2} + 4{\pi ^2}{\varepsilon ^4}{c_3})} = \sqrt{ - {c_2}{} kl - {c_3}{k^4} - {c_1}{} {k^2}} ,~\psi \rightarrow 0. \end{aligned}$$

Then expanding the theta function

$$\begin{aligned}\varphi (\tau ,a) = 1 + \psi (\mathrm{{e}}^{2\pi \mathrm {i}\tau } + \mathrm{{e}}^{ - 2\pi \mathrm {i}\tau }) + {\psi ^4}(\mathrm{{e}}^{4\pi \mathrm {i}\tau } + \mathrm{{e}}^{ - 4\pi \mathrm {i}\tau }) + \cdots , \end{aligned}$$

by applying condition (26), we have

$$\begin{aligned} \varphi (\tau ,a) = 1 + \mathrm{{e}}^{\tau '} + {\psi ^2}(\mathrm{{e}}^{ - \tau '} + \mathrm{{e}}^{2\tau '}) + {\psi ^6}(\mathrm{{e}}^{ - 2\tau '} + \mathrm{{e}}^{3\tau '}) + ... \rightarrow 1 + \mathrm{{e}}^{\tau '},~\psi \rightarrow 0. \end{aligned}$$

(27)

where

$$\begin{aligned} \tau ' = 2\pi \mathrm{{i}}\tau - \pi a \rightarrow kx + ly + \sqrt{ - {c_2}{} kl - {c_3}{k^4} - {c_1}{} {k^2}} t + \delta = \sigma ,~\psi \rightarrow 0. \end{aligned}$$

(28)

What is more, $\tau \rightarrow \frac{{\sigma + \pi a}}{{2\pi \mathrm {i}}},$ finally, combining Eq. (27) and Eq. (28), we obtain

$$\begin{aligned}\varphi (\tau ,a) \rightarrow 1 + \mathrm{{e}}^\sigma ,~\psi \rightarrow 0. \end{aligned}$$

Therefore, one-periodic wave solution tends to one-soliton solution under the condition of $\psi \rightarrow 0.$ $\hfill\square$

5 Two-periodic waves and asymptotic properties

In this section, two-periodic wave solution of Eq. (1) is similar to the one-periodic wave solution. When ${N=2,}$ the theta function degenerates the following Fourier series

$$\begin{aligned} \varphi (\tau ,a) = \varphi (\tau _1,\tau _2 ,a) = \sum \limits _{n = - \infty }^{ + \infty } {{\mathrm{{e}}^{2\pi \mathrm{{i}}< \tau ,n> - \pi < an,n > }}}, \end{aligned}$$

(29)

with phase variable ${\tau _1} = {\varepsilon _1}x + {\eta _1}y + {\omega _1}t + {\upsilon _1},~{\tau _2} = {\varepsilon _2}x + {\eta _2}y + {\omega _2}t + {\upsilon _2},$ where $n = {({n_1},{n_2})^T} \in {Z^2},\tau = {({\tau _1},{\tau _2})^T} \in {C^2},$ and a is a positive definite and real-valued symmetric $2 \times 2$ matrix, that is $a = \left( {\begin{array}{*{20}{c}} {{a_{11}}}&{}{{a_{12}}}\\ {{a_{21}}}&{}{{a_{22}}} \end{array}} \right) ,$ where ${a_{11}}> 0,{a_{22}} > 0$ and ${a_{11}}{a_{22}} - {a_{12}}^2 > 0.$

5.1 Construction of two-periodic waves

In order to obtain two-periodic wave solution, we take Eq. (29) into Eq. (8) and finally gain the following relation through Eq. (3):

$$\begin{aligned} &B(D_{x} ,D_{y} ,D_{t} )\varphi (\tau _{1} ,\tau _{2} ,a)\varphi (\tau _{1} ,\tau _{2} ,a) = \sum\limits_{{n = - \infty }}^{{ + \infty }} {\sum\limits_{{m = - \infty }}^{{ + \infty }} {B(D_{x} ,D_{y} ,D_{t} )} } {\text{e}}^{{2\pi {\text{i}} < \tau ,n > - \pi < an,n >}} {\text{e}}^{{2\pi {\text{i}} < \tau ,m > - \pi < am,m >}} \\ &\quad = \sum\limits_{{n = - \infty }}^{{ + \infty }} {\sum\limits_{{m = - \infty }}^{{ + \infty }} {B(2\pi {\text{i}} < n - m,\varepsilon > ,2\pi {\text{i}} < n - m,\eta >,2\pi {\text{i}} < n - m,\omega > )} } {\text{e}}^{{2\pi {\text{i}} < \tau ,n + m > - \pi ( < an,n > + < am,m > )}} \\ &\quad \mathop = \limits^{{m = m^{\prime} - n}} \sum\limits_{{m^{\prime} = - \infty }}^{{ + \infty }} {\Bigg\{ \sum\limits_{{n = - \infty }}^{{ + \infty }} {B(2\pi {\text{i}} < 2n - m^{\prime},\varepsilon > ,2\pi {\text{i}} < 2n - m^{\prime},\eta >,2\pi {\text{i}} < 2n - m^{\prime},\omega >)} } \\ &\quad\quad \times {\text{e}}^{{ - \pi [ < a(n - m^{\prime}),n - m^{\prime} > + < an,n >]}} \Bigg\} \times {\text{e}}^{{2\pi {\text{i}} < \tau ,m^{\prime} >}} = \sum\limits_{{m^{\prime} = - \infty }}^{{ + \infty }} {\mathop {{\text{ }}B}\limits^{{\_\_}} (} m_{1} ^{\prime } ,m_{2} ^{\prime } ){\text{e}}^{{2\pi {\text{i}} < \tau ,m^{\prime} >}} ~(m,n \in Z^{2} ), \\ \end{aligned}$$

(30)

where

$$\begin{aligned} {\mathop B\limits ^{\_\_} (} {m_1}',{m_2}') = \sum \limits _{n = - \infty }^{ + \infty } B(2\pi \mathrm{{i}}< 2n - m',\varepsilon> ,2\pi \mathrm{{i}}< 2n - m',\eta> ,2\pi \mathrm{{i}}< 2n - m',\omega> ){\mathrm{{e}}^{ - \pi [< a(n - m'),n - m'> + < an,n > ]}}. \end{aligned}$$

(31)

Letting the summation index ${n_j={n_j}'+\delta _{jl},}$ where ${\delta _{jl}} = \left\{ \begin{array}{l} 0,~l \ne j\\ 1,~l = j \end{array}, \right.$ Eq. (31) has the form of

$$\begin{aligned} {\mathop B\limits ^{\_\_} (} {m_1}',{m_2}') &= \sum \limits _{n = - \infty }^{ + \infty } {B(} 2\pi \mathrm{{i}}\sum \limits _{j = 1}^2 {[2{n_j}' - ({m_j}' - 2{\delta _{jl}})]{\varepsilon _j}} ,2\pi \mathrm{{i}}\sum \limits _{j = 1}^2 {[2{n_j}' - ({m_j}' - 2{\delta _{jl}})]{\eta _j}} ,2\pi \mathrm{{i}}\sum \limits _{j = 1}^2 {[2{n_j}' - ({m_j}' - 2{\delta _{jl}})]{\omega _j})}\\&\quad \times {\mathrm{{e}}^{ - \pi \sum \limits _{j, k = 1}^2 {({n_j}' + {\delta _{jl}}){a_{jk}}({n_k}' + {\delta _{kl}})}- \pi \sum \limits _{j,k = 1}^2 {[({m_j}' - 2{\delta _{jl}} - {n_j}') + {\delta _{jl}}]{a_{jk}}[({m_k}' - 2{\delta _{kl}} - {n_k}') + {\delta _{kl}}]}}} \\&= \left\{ \begin{array}{l} {\mathop B\limits ^{\_\_} (} {m_1}'-2,{m_2}'){\mathrm{{e}}^{2\pi {a_{11}} - 2\pi ({a_{11}}{m_1}' + {a_{12}}{m_2}')}},~l = 1,\\ {\mathop B\limits ^{\_\_} (} {m_1}',{m_2}'-2){\mathrm{{e}}^{2\pi {a_{22}} - 2\pi ({a_{12}}{m_1}' + {a_{22}}{m_2}')}},~l = 2, \end{array} \right. \end{aligned}$$

which shows that $\mathop B\limits ^{\_\_} ({m_1}',{m_2}')~({m_1}' \in Z^2,{m_2}' \in Z^2)$ is entirely determined by four formulas $\mathop B\limits ^{\_\_} (0,0),$ $\mathop B\limits ^{\_\_} (0,1),$ $\mathop B\limits ^{\_\_} (1,0),$ $\mathop B\limits ^{\_\_} (1,1).$ That is, if the following four equations are satisfied

$$\begin{aligned} \mathop B\limits ^{\_\_} (0,0) = \mathop B\limits ^{\_\_} (0,1) = \mathop B\limits ^{\_\_} (1,0)=\mathop B\limits ^{\_\_} (1,1)=0, \end{aligned}$$

(32)

then $\mathop B\limits ^{\_\_} ({m_1}',{m_2}') = 0~({m_1}' \in Z^2,{m_2}' \in Z^2),$ so $B({D_x},{D_y},{D_t})\varphi (\tau _1,\tau _2, a)\varphi (\tau _1,\tau _2 ,a) = 0.$ Then introducing the marks as

$$\begin{aligned}M &= {({a_{jl}})_{4 \times 5}},~b = {({b_1},{b_2},{b_3},{b_4})^T},~{a_{j1}} = \sum \limits _{{n_1},{n_2} \in {Z^2}} { - 4{\pi ^2}{{(2{n_1} - s_1^j)}^2}{v_j}(n)} ,~{a_{j2}} = \sum \limits _{{n_1},{n_2} \in {Z^2}} { - 4{\pi ^2}{{(2{n_2} - s_2^j)}^2}{v_j}(n)} ,\\{a_{j3}} &= \sum \limits _{{n_1},{n_2} \in {Z^2}} { - 24{\pi ^2} < 2n - {s^j},\varepsilon { > ^2}{v_j}(n)} ,~{a_{j4}} = \sum \limits _{{n_1},{n_2} \in {Z^2}} {{v_j}(n)} ,~{a_{j5}} = \sum \limits _{{n_1},{n_2} \in {Z^2}} { - 8{\pi ^2}(2{n_1} - s_1^j)(2{n_2} - s_2^j){v_j}(n)} ,\\{b_j} &= \sum \limits _{{n_1},{n_2} \in {Z^2}} (4{\pi ^2}{c_1} < 2n - {s^j},\varepsilon { > ^2} + 4{\pi ^2}{c_2} < 2n - {s^j},\varepsilon > < 2n - {s^j},\eta > - 16{\pi ^4}{c_3} < 2n - {s^j},\varepsilon { > ^4}){v_j}(n) ,\\{v_j}(n) &= {\psi _1}^{{n_1}^2 + {{({n_1} - s_1^j)}^2}}{\psi _2}^{{n_2}^2 + {{({n_2} - s_2^j)}^2}}{\psi _3}^{{n_1}{n_2} + ({n_1} - s_1^j)({n_2} - s_2^j)},~~{\psi _1} = {\mathrm{{e}}^{ - \pi {a_{11}}}},~~{\psi _2} = {\mathrm{{e}}^{ - \pi {a_{22}}}},~~{\psi _3} = {\mathrm{{e}}^{ - 2\pi {a_{12}}}},\\{s^1} &= (0,0),~{s^2} = (0,1),~{s^3} = (1,0),~{s^4} = (1,1),~{s^j} = (s_1^j,s_2^j), \end{aligned}$$

Eq. (32) can be written as the form of a system of linear equations about frequency $\omega _1,$ $\omega _2,$ constant $u_0$ and integration constant c,  that is

$$\begin{aligned} M({\omega _1}^2,{\omega _2}^2,{u_0},c,{\omega _1}{\omega _2}) = b, \end{aligned}$$

(33)

so we obtain the two-periodic wave solution of Eq. (1)

$$\begin{aligned} u = {u_0} + 2{\left( {\ln \varphi ({\tau _1},{\tau _2},a)} \right) _{xx}}, \end{aligned}$$

(34)

where the theta function $\varphi (\tau _1 ,\tau _2,a)$ is given by Eq. (29), ${u_0}$ is determined by formula (33), the other parameters ${c_1},{c_2},{c_3,} a_{11},a_{12},a_{22},\varepsilon _1 ,\eta _1 ,$ $\varepsilon _2 ,\eta _2 ,\upsilon _1$ and $\upsilon _2$ are free, the seven parameters $a_{11},a_{22},a_{12},\varepsilon _1,\eta _1,\varepsilon _2$ and $\eta _2$ play a major role in two-periodic waves. Figures 17, 18, 19, and 20 systematically show the dynamic characteristics of two-periodic waves.

Fig. 17

(Color online) A two-periodic wave of Eq. (1) with parameters $c_1=c_2=c_3=1,\varepsilon _1 = 0.5,\eta _1 = 1,\varepsilon _2 = 0.3,\eta _2 = -0.25,a_{11}=1,a_{12}=0.3,a_{22}=1.$ a Three-dimensional stereogram of two-periodic wave when $t=0.$ b Vertical view of plot a. c The wave moves along the x-axis when $y=0,t=0.$ d The wave moves along the y-axis when $x=0,t=0.$ e The wave moves along t-axis when $x=0,y=0$

Fig. 18

(Color online) A two-periodic wave of Eq. (1) with parameters $c_1=1,c_2=2,c_3=3,\varepsilon _1 = 0.5,\eta _1 = 0.3,\varepsilon _2 = 0.5,\eta _2 = 0.3,a_{11}=1,a_{12}=0.3,a_{22}=1.$ a Three-dimensional stereogram of two-periodic wave when $t=0.$ b Vertical view of plot (a). c The wave moves along the x-axis when $y=0,t=0.$ d The wave moves along the y-axis when $x=0,t=0.$ e The wave moves along t-axis when $x=0,y=0$

Fig. 19

(Color online) A two-periodic wave of Eq. (1) with parameters $c_1=c_2=c_3=1,\varepsilon _1 = 0.5,\eta _1 = 0.5,\varepsilon _2 = 0.3,\eta _2 = 0.3,a_{11}=1,a_{12}=0.3,a_{22}=1.$ a Three-dimensional stereogram of two-periodic wave when $t=0.$ b Vertical view of plot (a). c The wave moves along the x-axis when $y=0,t=0.$ d The wave moves along the y-axis when $x=0,t=0.$ e The wave moves along t-axis when $x=0,y=0$

Fig. 20

(Color online) A two-periodic wave of Eq. (1) with parameters $c_1=c_2=c_3=1,\varepsilon _1 = 0.5,\eta _1 = 0.5,\varepsilon _2 = 0.5,\eta _2 = -0.5,a_{11}=1,a_{12}=0.3,a_{22}=1.$ a Three-dimensional stereogram of two-periodic wave when $t=0.$ b Vertical view of plot (a). c The wave moves along the x-axis when $y=0,t=0.$ d The wave moves along the y-axis when $x=0,t=0.$ e The wave moves along t-axis when $x=0,y=0$

5.2 Characteristics of two-periodic waves

• (1) It is bounded for all complex variables (x, y, t).

• (2) It is obvious that two-periodic waves are the generalization of the one-periodic waves, but there are two phase variables $\tau _1$ and $\tau _2,$ it has two independent periods in two independent horizontal directions, respectively, and it can be regarded as the superposition of a periodic wave propagating along the x-axis and y-axis, respectively.

• (3) It has 2N fundamental periods $\{ {e_j},j = 1,2,...,N\}$ and $\{ \mathrm{{i}}{a_j},j = 1,2,...,N\}$ in $({\tau _1},{\tau _2}).$ Its velocity of the propagation has the form of

  $$\begin{aligned} \dfrac{{{\mathrm{{d}}x}}}{{{\mathrm{{d}}t}}} = \dfrac{{{\omega _2}{\varepsilon _1} - {\omega _1}{\varepsilon _2}}}{{{\varepsilon _1}{\eta _2} - {\varepsilon _2}{\eta _1}}},\;\;\;\;\dfrac{{{\mathrm{{d}}y}}}{{{\mathrm{{d}}t}}} = \dfrac{{{\omega _1}{\eta _2} - {\omega _2}{\eta _1}}}{{{\varepsilon _1}{\eta _2} - {\varepsilon _2}{\eta _1}}}. \end{aligned}$$

• (4) Eq. (30) can be written as the form of

  $$\begin{aligned} B({D_x},{D_y},{D_t})\varphi ({\tau _1},{\tau _2},a)\varphi ({\tau _1},{\tau _2},a) = \sum \limits _{m' = - \infty }^{ + \infty } {\mathop B\limits ^{\_\_} (} {m_1}',{m_2}'){\mathrm{{e}}^{2\pi \mathrm{{i}} < \tau ,m' > }} = \sum \limits _{m' = - \infty }^{ + \infty } {\mathop B\limits ^{\_\_} (} {m_1}',{m_2}')\cos ({\tau _1}{m_1}')\cos ({\tau _2}{m_2}'). \end{aligned}$$

  According to the above formula, two-periodic wave has two characteristic lines: ${\tau _1} = {\varepsilon _1}x + {\eta _1}y + {\omega _1}t + {\upsilon _1}=0$ and ${\tau _2} = {\varepsilon _2}x + {\eta _2}y + {\omega _2}t + {\upsilon _2}=0.$

• (i) If we give the following relations of $\left| {\begin{array}{*{20}{c}} {{\varepsilon _1}}&{}{{\eta _1}}\\ {{\varepsilon _2}}&{}{{\eta _2}} \end{array}} \right| \ne 0,$ that is the two characteristic lines are not parallel. In one case, the included angle of the characteristic line is a general angle, that is $\frac{{{\varepsilon _1}}}{{{\eta _1}}} \ne \frac{{{\varepsilon _2}}}{{{\eta _2}}},$ as shown in Fig. 17, and in the other case, the included angle is a right angle, that is $\frac{{{\varepsilon _1}}}{{{\eta _1}}} = -\frac{{{\eta _2}}}{{{\varepsilon _2}}},$ as shown in Fig. 20. What they have in common is the collision of phase variables $\tau _1$ and $\tau _2$ makes the two-periodic waves appear honeycomb, and these hill-shaped bulges propagate periodically along the x-axis and y-axis, the points (x, y) (${\varepsilon _1} x + {\eta _1} y = 2k\pi , {\varepsilon _2} x + {\eta _2} y = 2k\pi , k=0,1,2,...$) are the peak points of two-periodic waves, the points (x, y) (${\varepsilon _1} x + {\eta _1} y = 2k\pi +\pi , {\varepsilon _2} x + {\eta _2} y = 2k\pi +\pi , k=0,1,2,...$) are the trough points of two-periodic waves. The different is that Fig. 17 has two strict periods along x-axis and y-axis, whereas Fig. 20 has one period along x-axis and y-axis.

• (ii) If we give the following relations of $\left| {\begin{array}{*{20}{c}} {{\varepsilon _1}}&{}{{\eta _1}}\\ {{\varepsilon _2}}&{}{{\eta _2}} \end{array}} \right| = 0,$ that is the two characteristic lines are parallel. In one case $\frac{{{\varepsilon _1}}}{{{\eta _1}}} = \frac{{{\varepsilon _2}}}{{{\eta _2}}}=k,$ where k is a constant, $k \ne 1,$ as shown in Fig. 18, and in the other case $\frac{{{\varepsilon _1}}}{{{\eta _1}}} = \frac{{{\varepsilon _2}}}{{{\eta _2}}}=1,$ as shown in Fig. 19. What they have in common is the parallel of phase variables $\tau _1,\tau _2$ makes the periodic wave fluctuate in parallel and propagate periodically along the x-axis and y-axis. The different is that Fig. 19 has two strict periods along x-axis and y-axis, whereas Fig. 18 has one period along x-axis and y-axis.

5.3 Asymptotic properties of two-periodic waves

In what follows, we further analyze asymptotic properties of the two-periodic wave solution by solving Eq. (33) and taking a limit condition. The expansion of matrix M has the following form of

$$\begin{aligned} M &= \left( {\begin{array}{*{20}{c}} 0&{}0&{}0&{}1&{}0\\ 0&{}0&{}0&{}0&{}0\\ 0&{}0&{}0&{}0&{}0\\ 0&{}0&{}0&{}0&{}0 \end{array}} \right) + \left( {\begin{array}{*{20}{c}} 0&{}0&{}0&{}0&{}0\\ 0&{}0&{}0&{}0&{}0\\ { - 8{\pi ^2}}&{}0&{}{ - 48{\pi ^2}{\varepsilon _1}^2}&{}2&{}0\\ 0&{}0&{}0&{}0&{}0 \end{array}} \right) {\psi _1} + \left( {\begin{array}{*{20}{c}} 0&{}0&{}0&{}0&{}0\\ 0&{}{ - 8{\pi ^2}}&{}{ - 48{\pi ^2}{\varepsilon _2}^2}&{}2&{}0\\ 0&{}0&{}0&{}0&{}0\\ 0&{}0&{}0&{}0&{}0 \end{array}} \right) {\psi _2}\nonumber \\ &\quad + \left( {\begin{array}{*{20}{c}} { - 32{\pi ^2}}&{}0&{}{ - 192{\pi ^2}{\varepsilon _1}^2}&{}2&{}0\\ 0&{}0&{}0&{}0&{}0\\ 0&{}0&{}0&{}0&{}0\\ 0&{}0&{}0&{}0&{}0 \end{array}} \right) {\psi _1}^2 + \left( {\begin{array}{*{20}{c}} 0&{}{ - 32{\pi ^2}}&{}{ - 192{\pi ^2}{\varepsilon _2}^2}&{}2&{}0\\ 0&{}0&{}0&{}0&{}0\\ 0&{}0&{}0&{}0&{}0\\ 0&{}0&{}0&{}0&{}0 \end{array}} \right) {\psi _2}^2\nonumber \\ &\quad + \left( {\begin{array}{*{20}{c}} 0&{}0&{}0&{}0&{}0\\ 0&{}0&{}0&{}0&{}0\\ 0&{}0&{}0&{}0&{}0\\ { - 8{\pi ^2}}&{}{ - 8{\pi ^2}}&{}{ - 48{\pi ^2}[{{({\varepsilon _1} - {\varepsilon _2})}^2} + {{({\varepsilon _1} + {\varepsilon _2})}^2}{\psi _3}]}&{}2(1+{\psi _3})&{}{ - 16{\pi ^2}({\psi _3} - 1)} \end{array}} \right) {\psi _1}{\psi _2} + o({\psi _1}^i{\psi _2}^j), \end{aligned}$$

(35)

where $i + j \ge 2.$ and

$$\begin{aligned} b &= \left( {\begin{array}{*{20}{c}} 0\\ 0\\ {{\Delta _1}}\\ 0 \end{array}} \right) {\psi _1} + \left( {\begin{array}{*{20}{c}} 0\\ {{\Delta _2}}\\ 0\\ 0 \end{array}} \right) {\psi _2} + \left( {\begin{array}{*{20}{c}} {{\Delta _3}}\\ 0\\ 0\\ 0 \end{array}} \right) {\psi _1}^2 + \left( {\begin{array}{*{20}{c}} {{\Delta _4}}\\ 0\\ 0\\ 0 \end{array}} \right) {\psi _2}^2 + \left( {\begin{array}{*{20}{c}} 0\\ 0\\ 0\\ {{\Delta _5}} \end{array}} \right) {\psi _1}{\psi _2}, \nonumber \\ {\Delta _1} &= 8{\pi ^2}{\varepsilon _1}^2{c_1} + 8{\pi ^2}{\varepsilon _1}{\eta _1}{c_2} - 32{\pi ^4}{\varepsilon _1}^4{c_3},~~{\Delta _2} = 8{\pi ^2}{\varepsilon _2}^2{c_1} + 8{\pi ^2}{\varepsilon _2}{\eta _2}{c_2} - 32{\pi ^4}{\varepsilon _2}^4{c_3},\nonumber \\ {\Delta _3} &= 32{\pi ^2}{\varepsilon _1}^2{c_1} + 32{\pi ^2}{\varepsilon _1}{\eta _1}{c_2} - 512{\pi ^4}{\varepsilon _1}^4{c_3},~~{\Delta _4} = 8{\pi ^2}{\varepsilon _2}^2{c_1} + 8{\pi ^2}{\varepsilon _2}{\eta _2}{c_2} - 32{\pi ^4}{\varepsilon _2}^4{c_3},\nonumber \\ {\Delta _5} &= 8{\pi ^2}{c_1}[{({\varepsilon _1} - {\varepsilon _2})^2} + {({\varepsilon _1} + {\varepsilon _2})^2}{\psi _3}] + 8{\pi ^2}{c_2}[({\varepsilon _1} - {\varepsilon _2})({\eta _1} - {\eta _2}) + ({\varepsilon _1} + {\varepsilon _2})({\eta _1} + {\eta _2}){\psi _3}\nonumber \\ &\quad - 32{\pi ^4}{c_3}[{({\varepsilon _1} - {\varepsilon _2})^4} + {({\varepsilon _1} + {\varepsilon _2})^4}{\psi _3}]. \end{aligned}$$

(36)

Then, we assume that the solution of $M({\omega _1}^2,{\omega _2}^2,{u_0},c,{\omega _1}{\omega _2}) = b$ has the following form of

$$\begin{aligned} \left( {\begin{array}{*{20}{c}} {{\omega _1}^2}\\ {{\omega _2}^2}\\ {{u_0}}\\ c\\ {{\omega _1}{\omega _2}} \end{array}} \right) = \left( {\begin{array}{*{20}{c}} {{\omega _1}^{2(0)}}\\ {{\omega _2}^{2(0)}}\\ {u_0^{(0)}}\\ {{c^{(0)}}}\\ {{\omega _1}{\omega _2}^{(0)}} \end{array}} \right) + \left( {\begin{array}{*{20}{c}} {{\omega _1}^{2(1)}}\\ {{\omega _2}^{2(1)}}\\ {u_0^{(1)}}\\ {{c^{(1)}}}\\ {{\omega _1}{\omega _2}^{(1)}} \end{array}} \right) {\psi _1} + \left( {\begin{array}{*{20}{c}} {{\omega _1}^{2(2)}}\\ {{\omega _2}^{2(2)}}\\ {u_0^{(2)}}\\ {{c^{(2)}}}\\ {{\omega _1}{\omega _2}^{(2)}} \end{array}} \right) {\psi _2} + \left( {\begin{array}{*{20}{c}} {{\omega _1}^{2(11)}}\\ {{\omega _2}^{2(11)}}\\ {u_0^{(11)}}\\ {{c^{(11)}}}\\ {{\omega _1}{\omega _2}^{(11)}} \end{array}} \right) {\psi _1}^2\nonumber \\ + \left( {\begin{array}{*{20}{c}} {{\omega _1}^{2(22)}}\\ {{\omega _2}^{2(22)}}\\ {u_0^{(22)}}\\ {{c^{(22)}}}\\ {{\omega _1}{\omega _2}^{(22)}} \end{array}} \right) {\psi _2}^2 + \left( {\begin{array}{*{20}{c}} {{\omega _1}^{2(12)}}\\ {{\omega _2}^{2(12)}}\\ {u_0^{(12)}}\\ {{c^{(12)}}}\\ {{\omega _1}{\omega _2}^{(12)}} \end{array}} \right) {\psi _1}{\psi _2} + o({\psi _1}^i{\psi _2}^j),i + j \ge 2. \end{aligned}$$

(37)

Interestingly, the relation of the two-soliton wave solution and two-periodic wave solution is given as follows.

Theorem 2

If two-periodic wave solution Eq. (34) satisfies the following condition of

$$\begin{aligned} \varepsilon _j = \frac{k_j}{{2\pi \mathrm {i}}},\;\;\;\eta _j = \frac{l_j}{{2\pi \mathrm {i}}},\;\;\;\upsilon _j = \frac{{\delta _j + \pi a_{jj}}}{{2\pi \mathrm {i}}},\;\;\;a_{12} = \frac{{A_{12}}}{{-2\pi }},\;\;(j=1,2) \end{aligned}$$

(38)

where $k_j, l_j$ and $\delta _j~(j=1,2)$ are given by Eq. (5), we have the following asymptotic properties:

$$\begin{aligned}u_0 \rightarrow 0, ~c \rightarrow 0,~\tau _j \rightarrow \frac{{\sigma _j + \pi a_{jj}}}{{2\pi \mathrm {i}}}\;(j=1,2),~\varphi (\tau _1,\tau _2 ,a) \rightarrow 1 + \mathrm{{e}}^{\sigma _1}+{\mathrm {e}}^{\sigma _2}+{\mathrm {e}}^{\sigma _1+\sigma _2+A_{12}} ,\;\;\;\psi _1,\psi _2 \rightarrow 0. \end{aligned}$$

Proof

By substituting Eq. (35-37) into Eq. (33), we obtain the following relations of

$$\begin{aligned} c^{{(0)}} & = c^{{(1)}} = c^{{(2)}} = c^{{(12)}} = 0,~~\omega _{1} ^{{2(0)}} + 6\varepsilon _{1} u_{0}^{{(0)}} = - \varepsilon _{1} ^{2} c_{1} - \varepsilon _{1} \eta _{1} c_{2} + 4\pi ^{2} \varepsilon _{1} ^{2} c_{3} , \\ \omega _{2} ^{{2(0)}} + 6\varepsilon _{2} u_{0}^{{(0)}} &= - \varepsilon _{2} ^{2} c_{1} - \varepsilon _{2} \eta _{2} c_{2} + 4\pi ^{2} \varepsilon _{2} ^{2} c_{3} ,~\omega _{1} ^{{2(1)}} + 6\varepsilon _{1} u_{0}^{{(1)}} = 0,~\,\omega _{2} ^{{2(1)}} + 6\varepsilon _{2} u_{0}^{{(1)}} = 0, \\ & \quad c^{{(11)}} - 32\pi ^{2} \omega _{1} ^{{2(0)}} - 192\pi ^{2} \varepsilon _{1} ^{2} u_{0}^{{(0)}} = 32\pi ^{2} \varepsilon _{1} ^{2} c_{1} + 32\pi ^{2} \varepsilon _{1} \eta _{1} c_{2} - 512\pi ^{4} \varepsilon _{1} ^{4} c_{3} , \\ &\quad c^{{(22)}} - 32\pi ^{2} \omega _{2} ^{{2(0)}} - 192\pi ^{2} \varepsilon _{2} ^{2} u_{0}^{{(0)}} = 32\pi ^{2} \varepsilon _{2} ^{2} c_{1} + 32\pi ^{2} \varepsilon _{2} \eta _{2} c_{2} - 512\pi ^{4} \varepsilon _{2} ^{4} c_{3} . \\ \end{aligned}$$

(39)

$\hfill\square$

By using condition(38), and taking $u_0^{(0)}=0,$ Eq. (39) has the following form of

$$\begin{aligned}c &= - 384{\pi ^4}{\varepsilon _1}^4{c_3}{\psi _1}^2 - 384{\pi ^4}{\varepsilon _2}^4{c_3}{\psi _2}^2 + o({\psi _1}^2{\psi _2}^2),\\2\pi \mathrm{{i}}{\omega _1} &= \sqrt{ - 4{\pi ^2}{\omega _1}} = \sqrt{ - 4{\pi ^2}( - {\varepsilon _1}^2{c_1} - {\varepsilon _1}{\eta _1}{c_2} + 4{\pi ^2}{\varepsilon _1}^2{c_3})} ,\\2\pi \mathrm{{i}}{\omega _2} &= \sqrt{ - 4{\pi ^2}{\omega _2}} = \sqrt{ - 4{\pi ^2}( - {\varepsilon _2}^2{c_1} - {\varepsilon _2}{\eta _2}{c_2} + 4{\pi ^2}{\varepsilon _2}^2{c_3})} , \end{aligned}$$

and using condition(38), we have

$$\begin{aligned}u_0 \rightarrow 0, ~c \rightarrow 0,~~2\pi \mathrm{{i}}{\omega _1} \rightarrow \sqrt{ - {k_1}^2{c_1} - {k_1}{l_1}{c_2} - {k_1}^2{c_3}} ,~~2\pi \mathrm{{i}}{\omega _2} \rightarrow \sqrt{ - {k_2}^2{c_1} - {k_2}{l_2}{c_2} - {k_2}^2{c_3}} ,~~{\psi _1},{\psi _2} \rightarrow 0. \end{aligned}$$

By expanding the theta function

$$\begin{aligned} \varphi ({\tau _1},{\tau _2},a) = 1 + ({\mathrm{{e}}^{2\pi \mathrm{{i}}{\tau _1}}} + {\mathrm{{e}}^{ - 2\pi \mathrm{{i}}{\tau _1}}}){\mathrm{{e}}^{ - \pi {a_{11}}}} + ({\mathrm{{e}}^{2\pi \mathrm{{i}}{\tau _2}}} + {\mathrm{{e}}^{ - 2\pi \mathrm{{i}}{\tau _2}}}){\mathrm{{e}}^{ - \pi {a_{22}}}} + \left( {{\mathrm{{e}}^{2\pi \mathrm{{i}}({\tau _1} + {\tau _2})}} + {\mathrm{{e}}^{ - 2\pi \mathrm{{i}}({\tau _1} + {\tau _2})}}} \right) {\mathrm{{e}}^{ - \pi ({a_{11}} + 2{a_{12}} + {a_{22}})}} + \cdots , \end{aligned}$$

and applying condition(38), one has

$$\begin{aligned} \varphi ({\tau _1},{\tau _2},a) &= 1 + {\mathrm{{e}}^{{\tau _1}'}} + {\mathrm{{e}}^{{\tau _2}'}} + {\mathrm{{e}}^{{\tau _1}' + {\tau _2}' - 2\pi {a_{12}}}} + {\psi _1}^2{\mathrm{{e}}^{ - {\tau _1}'}} + {\psi _2}^2{\mathrm{{e}}^{ - {\tau _2}'}} + {\psi _1}^2{\psi _2}^2{\mathrm{{e}}^{ - {\tau _1}' - {\tau _2}' - 2\pi {a_{12}}}} + \cdots \nonumber \\ \rightarrow& 1 + {\mathrm{{e}}^{{\tau _1}'}} + {\mathrm{{e}}^{{\tau _2}'}} + {\mathrm{{e}}^{{\tau _1}' + {\tau _2}' + {A_{12}}}},~~{\psi _1},{\psi _2} \rightarrow 0, \end{aligned}$$

(40)

where

$$\begin{aligned} {\tau _1}' &= 2\pi \mathrm{{i}}{\tau _1} - \pi {a_{11}} \rightarrow {k_1}x + {l_1}y + \sqrt{ - {c_2}{} {k_1}{l_1} - {c_3}{k_1}^4 - {c_1}{} {k_1}^2} t + {\delta _1} = {\sigma _1},\nonumber \\ {\tau _2}' &= 2\pi \mathrm{{i}}{\tau _2} - \pi {a_{22}} \rightarrow {k_2}x + {l_2}y + \sqrt{ - {c_2}{} {k_2}{l_2} - {c_3}{k_2}^4 - {c_1}{} {k_2}^2} t + {\delta _2} = {\sigma _2},~~{\psi _1},{\psi _2} \rightarrow 0. \end{aligned}$$

(41)

Combining Eqs. (40) and (41), we obtain

$$\begin{aligned} \varphi ({\tau _1},{\tau _2},a) \rightarrow 1 + {\mathrm{{e}}^{{\sigma _1}}} + {\mathrm{{e}}^{{\sigma _2}}} + {\mathrm{{e}}^{{\sigma _1} + {\sigma _2} + {A_{12}}}},~{\psi _1},{\psi _2} \rightarrow 0. \end{aligned}$$

Therefore, two-periodic wave solution tends to two-soliton solution under the condition of $\psi _1,\psi _2 \rightarrow 0.$

6 Three-periodic waves and asymptotic properties

In this section, three-periodic wave solution of Eq. (1) is more complex than the two-periodic wave solution. When ${N=3,}$ the theta function degenerates the following Fourier series

$$\begin{aligned} \varphi (\tau ,a) = \varphi (\tau _1,\tau _2,\tau _3 ,a) = \sum \limits _{n = - \infty }^{ + \infty } {{\mathrm{{e}}^{2\pi \mathrm{{i}}< \tau ,n> - \pi < an,n > }}}, \end{aligned}$$

(42)

with phase variable ${\tau _1} = {\varepsilon _1}x + {\eta _1}y + {\omega _1}t + {\upsilon _1},~{\tau _2} = {\varepsilon _2}x + {\eta _2}y + {\omega _2}t + {\upsilon _2}~\mathrm{{and}}~{\tau _3} = {\varepsilon _3}x + {\eta _3}y + {\omega _3}t + {\upsilon _3},$ where $n = {({n_1},{n_2},{n_3})^T} \in {Z^3},\tau = {({\tau _1},{\tau _2},{\tau _3})^T} \in {C^3},$ and a is a positive definite and real-valued symmetric $3 \times 3$ matrix, that is, $a = \left( {\begin{array}{*{20}{c}} {{a_{11}}}&{}{{a_{12}}}&{}{{a_{13}}}\\ {{a_{21}}}&{}{{a_{22}}}&{}{{a_{23}}}\\ {{a_{31}}}&{}{{a_{32}}}&{}{{a_{33}}} \end{array}} \right) .$

6.1 Construction of three-periodic waves

The structure of three-periodic waves is similar to that of two-periodic waves, where

$$\begin{aligned}B({m_1}',{m_2}',{m_3}') = \left\{ \begin{array}{l} B({m_1}' - 2,{m_2}',{m_3}'){\mathrm{{e}}^{2\pi (1 - {m_1}'){a_{11}} - 2\pi ({a_{12}}{m_2}' + {a_{13}}{m_3}')}},~~l = 1,\\ B({m_1}',{m_2}' - 2,{m_3}'){\mathrm{{e}}^{2\pi (1 - {m_2}'){a_{22}} - 2\pi ({a_{21}}{m_1}' + {a_{23}}{m_3}')}},~~l = 2,\\ B({m_1}',{m_2}',{m_3}' - 2){\mathrm{{e}}^{2\pi (1 - {m_3}'){a_{33}} - 2\pi ({a_{31}}{m_1}' + {a_{32}}{m_2}')}},~~l = 3, \end{array} \right. \end{aligned}$$

which shows that $\mathop B\limits ^{\_\_} ({m_1}',{m_2}',{m_3}') ~({m_1}' \in Z^3,{m_2}' \in Z^3,{m_3}' \in Z^3)$ is entirely determined by eight formulas $\mathop B\limits ^{\_\_} (0,0,0),$ $\mathop B\limits ^{\_\_} (1,0,0),$ $\mathop B\limits ^{\_\_} (0,1,0),$ $\mathop B\limits ^{\_\_} (0,0,1),$ $\mathop B\limits ^{\_\_} (1,1,0),$ $\mathop B\limits ^{\_\_} (1,0,1),$ $\mathop B\limits ^{\_\_} (0,1,1),$ $\mathop B\limits ^{\_\_} (1,1,1),$ that is, if the following eight equations are satisfied

$$\begin{aligned} \mathop B\limits ^{\_\_} (0,0,0) = \mathop B\limits ^{\_\_} (1,0,0) = \mathop B\limits ^{\_\_} (0,1,0)=\mathop B\limits ^{\_\_} (0,0,1)=\mathop B\limits ^{\_\_} (1,1,0)=\mathop B\limits ^{\_\_} (1,0,1) =\mathop B\limits ^{\_\_} (0,1,1) =\mathop B\limits ^{\_\_} (1,1,1)=0 \end{aligned}$$

(43)

then

$$\begin{aligned} \mathop B\limits ^{\_\_} ({m_1}',{m_2}',{m_3}') = 0~ ({m_1}' \in Z^3,~{m_2}' \in Z^3,~{m_3}' \in Z^3),~~B({D_x},{D_y},{D_t})\varphi (\tau _1,\tau _2,\tau _3, a)\varphi (\tau _1,\tau _2 ,\tau _3,a) = 0. \end{aligned}$$

Then introducing the marks as

$$\begin{aligned}M &= {({a_{jl}})_{8 \times 11}},~b = {({b_1},{b_2},{b_3},{b_4},{b_5},{b_6},{b_7},{b_8})^T},\\{a_{j1}} &= \sum \limits _{{n_1},{n_2},{n_3} \in {Z^3}} { - 4{\pi ^2}{{(2{n_1} - s_1^j)}^2}{v_j}(n)} , \\{a_{j2}} &= \sum \limits _{{n_1},{n_2},{n_3} \in {Z^3}} { - 4{\pi ^2}{{(2{n_2} - s_2^j)}^2}{v_j}(n)} ,\\{a_{j3}} &= \sum \limits _{{n_1},{n_2},{n_3} \in {Z^3}} { - 4{\pi ^2}{{(2{n_3} - s_3^j)}^2}{v_j}(n)} ,\\{a_{j4}} &= \sum \limits _{{n_1},{n_2},{n_3} \in {Z^3}} { - 4{\pi ^2}{c_2}< 2n - {s^j},\varepsilon> (2{n_1} - s_1^j){v_j}(n)} ,\\{a_{j5}} &= \sum \limits _{{n_1},{n_2},{n_3} \in {Z^3}} { - 4{\pi ^2}{c_2}< 2n - {s^j},\varepsilon> (2{n_2} - s_2^j){v_j}(n)} , \\{a_{j6}} &= \sum \limits _{{n_1},{n_2},{n_3} \in {Z^3}} { - 4{\pi ^2}{c_2}< 2n - {s^j},\varepsilon> (2{n_3} - s_3^j){v_j}(n)} ,\\{a_{j7}} &= \sum \limits _{{n_1},{n_2},{n_3} \in {Z^3}} { - 24{\pi ^2}< 2n - {s^j},\varepsilon {> ^2}{v_j}(n)} ,\\ {a_{j8}} &= \sum \limits _{{n_1},{n_2},{n_3} \in {Z^3}} {{v_j}(n)} ,\\{a_{j9}} &= \sum \limits _{{n_1},{n_2},{n_3} \in {Z^3}} { - 8{\pi ^2}(2{n_1} - s_1^j)(2{n_2} - s_2^j){v_j}(n)} , \\{a_{j10}} &= \sum \limits _{{n_1},{n_2},{n_3} \in {Z^3}} { - 8{\pi ^2}(2{n_1} - s_1^j)(2{n_3} - s_3^j){v_j}(n)} ,\\{a_{j11}} &= \sum \limits _{{n_1},{n_2},{n_3} \in {Z^3}} { - 8{\pi ^2}(2{n_2} - s_2^j)(2{n_3} - s_3^j){v_j}(n)} , \\{b_j} &= \sum \limits _{{n_1},{n_2},{n_3} \in {Z^3}} {(4{\pi ^2}{c_1}< 2n - {s^j},\varepsilon {> ^2} - 16{\pi ^4}{c_3} < 2n - {s^j},\varepsilon { > ^4}){v_j}(n)} ,\\{v_j}(n) &= {\psi _1}^{{n_1}^2 + {{({n_1} - s_1^j)}^2}} \times {\psi _2}^{{n_2}^2 + {{({n_2} - s_2^j)}^2}} \times {\psi _3}^{{n_3}^2 + {{({n_3} - s_3^j)}^2}} \times {\psi _{12}}^{{n_1}{n_2} + ({n_1} - s_1^j)({n_2} - s_2^j)}\\&\quad\times {\psi _{13}}^{{n_1}{n_3} + ({n_1} - s_1^j)({n_3} - s_3^j)} \times {\psi _{12}}^{{n_2}{n_3} + ({n_2} - s_2^j)({n_3} - s_3^j)},\\{\psi _1} &= {\mathrm{{e}}^{ - \pi {a_{11}}}},~{\psi _2} = {\mathrm{{e}}^{ - \pi {a_{22}}}}, {\psi _3} = {\mathrm{{e}}^{ - \pi {a_{33}}}},~{\psi _{12}} = {\mathrm{{e}}^{ - 2\pi {a_{12}}}},~{\psi _{13}} = {\mathrm{{e}}^{ - 2\pi {a_{13}}}},~{\psi _{23}} = {\mathrm{{e}}^{ - 2\pi {a_{23}}}},\\{s^1} &= (0,0,0),~{s^2} = (1,0,0),~{s^3} = (0,1,0),~{s^4} = (0,0,1),~{s^5} = (1,1,0),\\{s^6} &= (1,0,1),~{s^7} = (0,1,1),{s^8} = (1,1,1),~{s^j} = (s_1^j,s_2^j,s_3^j), \end{aligned}$$

Eq. (43) can be written as the form of a system of linear equations about $\eta _1,$ $\eta _2,$ $\eta _3,$ frequency $\omega _1,$ $\omega _2,$ $\omega _3,$ constant $u_0$ and integration constant c,  that is

$$\begin{aligned} M({\omega _1}^2,{\omega _2}^2,{\omega _3}^2,{\eta _1},{\eta _2},{\eta _3},{u_0},c,{\omega _1}{\omega _2},{\omega _1}{\omega _3},{\omega _2}{\omega _3}) = b, \end{aligned}$$

(44)

then we obtain the three-periodic wave solution of Eq. (1)

$$\begin{aligned} u = {u_0} + 2{\left( {\ln \varphi ({\tau _1},{\tau _2},{\tau _3},a)} \right) _{xx}}, \end{aligned}$$

(45)

where the theta function $\varphi (\tau _1 ,\tau _2,\tau _3,a)$ is given by Eq. (42), ${u_0}$ is determined by formula (44), the other parameters ${c_1},{c_2},{c_3,} a_{11},a_{12},a_{13},$ $a_{23}, a_{22}, a_{33},\varepsilon _1 ,\varepsilon _2 ,\varepsilon _3 ,\upsilon _1,\upsilon _2$ and $\upsilon _3$ are free, the nine parameters $a_{11},a_{12},a_{13},a_{23},a_{22},a_{33},\varepsilon _1, \varepsilon _2$ and $\varepsilon _3$ play a major role in three-periodic waves.

6.2 Characteristics of three-periodic waves

• (1) It is bounded for all complex variables (x, y, t).

• (2) It is obvious that three-periodic waves are the direct generalization of the one- and two-periodic waves, but there are three phase variables $\tau _1,\tau _2$ and $\tau _3,$ it has three independent periods in two independent horizontal directions, respectively.

• (3) $B({D_x},{D_y},{D_t})\varphi ({\tau _1},{\tau _2},{\tau _3},a)\varphi ({\tau _1},{\tau _2},{\tau _3},a)$ can be written as the form of

  $$\begin{aligned} \sum \limits _{m' = - \infty }^{ + \infty } {\mathop B\limits ^{\_\_} (} {m_1}',{m_2}',{m_3}')\cos ({\tau _1}{m_1}')\cos ({\tau _2}{m_2}')\cos ({\tau _3}{m_3}'). \end{aligned}$$

  According to the above formula, three-periodic wave has three characteristic lines: ${\tau _1} = {\varepsilon _1}x + {\eta _1}y + {\omega _1}t + {\upsilon _1}=0,$ ${\tau _2} = {\varepsilon _2}x + {\eta _2}y + {\omega _2}t + {\upsilon _2}=0$ and ${\tau _3} = {\varepsilon _3}x + {\eta _3}y + {\omega _3}t + {\upsilon _3}=0.$

If giving the relations $\varepsilon _1> 0(<0),\varepsilon _2>0(<0),\varepsilon _3> 0(<0),$ we obtain $\frac{{{\varepsilon _1}}}{{{\eta _1}}} \approx \frac{{{\varepsilon _2}}}{{{\eta _2}}} \approx \frac{{{\varepsilon _3}}}{{{\eta _3}}},$ that is the three characteristic lines are parallel, as shown in Figs. 21, 22, 23 and 24. In Fig. 21, ${\varepsilon _1} \ne {\varepsilon _2} \ne {\varepsilon _3}$, it presents three strict periods along the x-axis, y-axis and t-axis. Then we consider the special relations of $\varepsilon _1=-\varepsilon _2,$ and $\varepsilon _3 \ne \varepsilon _1,\varepsilon _2,$ it presents two periods along the x-axis, y-axis and t-axis, and appears interesting Hill-shaped protrusions, as shown in Fig. 24. In Fig. 22, ${\varepsilon _1} = {\varepsilon _2} \ne {\varepsilon _3}$, it presents two periods along the x-axis, y-axis and t-axis. In Fig. 23, ${\varepsilon _1} = {\varepsilon _2} = {\varepsilon _3}$, three-periodic wave degenerates into one-periodic wave in the x-axis, y-axis and t-axis, and they are superimposed in three directions.

Fig. 21

(Color online) A three-periodic wave of Eq. (1) with parameters $c_1=c_2=c_3=1,\varepsilon _1 = 0.5,\varepsilon _2 = 0.45,\varepsilon _3 = 0.4,a_{11}=1,a_{12}=0.3,a_{13}=0.3,a_{23}=0.3,a_{22}=1,a_{33}=1.$ a Three-dimensional stereogram of three-periodic wave when $t=0.$ b Vertical view of plot (a). c The wave moves along the x-axis when $y=0,t=0.$ d The wave moves along the y-axis when $x=0,t=0.$ e The wave moves along t-axis when $x=0,y=0$

Fig. 22

(Color online) A three-periodic wave of Eq. (1) with parameters $c_1=c_2=c_3=1,\varepsilon _1 = 0.5,\varepsilon _2 = 0.5,\varepsilon _3 = 0.3,a_{11}=1,a_{12}=0.3,a_{13}=0.3,a_{23}=0.3,a_{22}=1,a_{33}=1.$ a Three-dimensional stereogram of three-periodic wave when $t=0.$ b Vertical view of plot (a). c The wave moves along the x-axis when $y=0,t=0.$ d The wave moves along the y-axis when $x=0,t=0.$ e The wave moves along t-axis when $x=0,y=0$

Fig. 23

(Color online) A three-periodic wave of Eq. (1) with parameters $c_1=c_2=c_3=1,\varepsilon _1 = 0.5,\varepsilon _2 = 0.5,\varepsilon _3 = 0.5,a_{11}=1,a_{12}=0.3,a_{13}=0.3,a_{23}=0.3,a_{22}=1,a_{33}=1.$ a Three-dimensional stereogram of three-periodic wave when $t=0.$ b Vertical view of plot (a). c The wave moves along the x-axis when $y=0,t=0.$ d The wave moves along the y-axis when $x=0,t=0.$ e The wave moves along t-axis when $x=0,y=0$

Fig. 24

(Color online) A three-periodic wave of Eq. (1) with parameters $c_1=c_2=c_3=1,\varepsilon _1 = 0.5,\varepsilon _2 = -0.5,\varepsilon _3 = 0.3,a_{11}=1,a_{12}=0.3,a_{13}=0.3,a_{23}=0.3,a_{22}=1,a_{33}=1.$ a Three-dimensional stereogram of three-periodic wave when $t=0.$ b Vertical view of plot (a). c The wave moves along the x-axis when $y=0,t=0.$ d The wave moves along the y-axis when $x=0,t=0.$ e The wave moves along t-axis when $x=0,y=0$

6.3 Asymptotic properties of three-periodic waves

In what follows, we further analyze asymptotic properties of the three-periodic wave solution by solving Eq. (44) and taking a limit condition. The expansion of matrix M has the following form of

$$\begin{aligned}M &= \left( {\begin{array}{*{20}{c}} {\overbrace{\begin{array}{*{20}{c}} 0\cdots01 \end{array}}^{1 \times 8}\begin{array}{*{20}{c}} 0{}0{}0 \end{array}}\nonumber \\ {}{} {\underbrace{\begin{array}{*{20}{c}} \cdots {}0{} \cdots \end{array}}_{7 \times 11}} \end{array}} \right) +\left( {\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} \cdots {}0{} \cdots \end{array}}\nonumber \\ {}{} {\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} { - 8{\pi ^2}}{}0{}0{}{ - 8{\pi ^2}{\varepsilon _1}{c_2}}{}0{}0{}{ - 48{\pi ^2}{\varepsilon _1}^2} \end{array}}20{\begin{array}{*{20}{c}} 0{}0 \end{array}} \end{array}}\nonumber \\ {}{} {\underbrace{\begin{array}{*{20}{c}} \cdots {}0{} \cdots \end{array}}_{6 \times 11}} \end{array}} \right) {\psi _1}\nonumber \\&\quad+ \left( {\begin{array}{*{20}{c}} {\overbrace{\begin{array}{*{20}{c}} \cdots {}0{} \cdots \end{array}}^{2 \times 11}}\nonumber \\ {}{} {\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} 0{}{ - 8{\pi ^2}}{}0{}0{}{ - 8{\pi ^2}{\varepsilon _2}{c_2}}{}0{}{ - 48{\pi ^2}{\varepsilon _2}^2} \end{array}}20{\begin{array}{*{20}{c}} 0{}0 \end{array}} \end{array}}\nonumber \\ {}{} {\underbrace{\begin{array}{*{20}{c}} \cdots {}0{} \cdots \end{array}}_{5 \times 11}} \end{array}} \right) {\psi _2} \\&\quad+ \left( {\begin{array}{*{20}{c}} {\overbrace{\begin{array}{*{20}{c}} \cdots {}0{} \cdots \end{array}}^{3 \times 11}}\nonumber \\ {}{} {\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} 0{}0{}{ - 8{\pi ^2}}{}0{}0{}{ - 8{\pi ^2}{\varepsilon _3}{c_2}}{}{ - 48{\pi ^2}{\varepsilon _3}^2} \end{array}}20{\begin{array}{*{20}{c}} 0{}0 \end{array}} \end{array}}\nonumber \\ {}{} {\underbrace{\begin{array}{*{20}{c}} \cdots {}0{} \cdots \end{array}}_{4 \times 11}} \end{array}} \right) {\psi _3} \nonumber \\&\quad+ \left( {\begin{array}{*{20}{c}} {\overbrace{\begin{array}{*{20}{c}} \cdots {}0{} \cdots \end{array}}^{4 \times 11}}\nonumber \\ {}{} {\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} { - 8{\pi ^2}}{}{ - 8{\pi ^2}}{}0{}{{\Gamma _1}}{}{{\Gamma _2}}{}0{}{{\Gamma _3}} \end{array}}2(1+\psi _{12}){ - 16{\pi ^2}({\psi _{12}} - 1)}{\begin{array}{*{20}{c}} 0{}0 \end{array}} \end{array}}\nonumber \\ {}{} {\underbrace{\begin{array}{*{20}{c}} \cdots {}0{} \cdots \end{array}}_{3 \times 11}} \end{array}} \right) {\psi _1}{\psi _2}\nonumber \\&\quad+ \left( {\begin{array}{*{20}{c}} {\overbrace{\begin{array}{*{20}{c}} \cdots {}0{} \cdots \end{array}}^{5 \times 11}}\nonumber \\ {}{} {\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} { - 8{\pi ^2}}{}0{}{ - 8{\pi ^2}}{}{{\Gamma _4}}{}0{}{{\Gamma _5}}{}{{\Gamma _6}} \end{array}}2(1+\psi _{13})0{\begin{array}{*{20}{c}} { - 16{\pi ^2}({\psi _{13}} - 1)}{}0 \end{array}} \end{array}}\nonumber \\ {}{} {\underbrace{\begin{array}{*{20}{c}} \cdots {}0{} \cdots \end{array}}_{2 \times 11}} \end{array}} \right) {\psi _1}{\psi _3}\nonumber \\&\quad+ \left( {\begin{array}{*{20}{c}} {\overbrace{\begin{array}{*{20}{c}} \cdots {}0{} \cdots \end{array}}^{6 \times 11}}\nonumber \\ {}{} {\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} 0{}{ - 8{\pi ^2}}{}{ - 8{\pi ^2}}{}0{}{{\Gamma _7}}{}{{\Gamma _8}}{}{{\Gamma _9}} \end{array}}2(1+\psi _{23})0{\begin{array}{*{20}{c}} 0{}{ - 16{\pi ^2}({\psi _{23}} - 1)} \end{array}} \end{array}}\nonumber \\ {}{} {\underbrace{\begin{array}{*{20}{c}} \cdots {}0{} \cdots \end{array}}_{1 \times 11}} \end{array}} \right) {\psi _2}{\psi _3}\nonumber \\&\quad+ \left( {\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} { - 32{\pi ^2}}00{ - 32{\pi ^2}{\varepsilon _1}{c_2}}00{ - 192{\pi ^2}{\varepsilon _1}^2}{\begin{array}{*{20}{c}} 2{}0{}0{}0 \end{array}} \end{array}}\nonumber \\ {}{} {\underbrace{\begin{array}{*{20}{c}} \cdots {}0{} \cdots \end{array}}_{7 \times 11}} \end{array}} \right) {\psi _1}^2\nonumber \\&\quad+ \left( {\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} 0{ - 32{\pi ^2}}00{ - 32{\pi ^2}{\varepsilon _2}{c_2}}0{ - 192{\pi ^2}{\varepsilon _2}^2}{\begin{array}{*{20}{c}} 2{}0{}0{}0 \end{array}} \end{array}}\nonumber \\ {}{} {\underbrace{\begin{array}{*{20}{c}} \cdots {}0{} \cdots \end{array}}_{7 \times 11}} \end{array}} \right) {\psi _2}^2\nonumber \\&\quad+ \left( {\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} 00{ - 32{\pi ^2}}00{ - 32{\pi ^2}{\varepsilon _3}{c_2}}{ - 192{\pi ^2}{\varepsilon _3}^2}{\begin{array}{*{20}{c}} 2{}0{}0{}0 \end{array}} \end{array}}\nonumber \\ {}{} {\underbrace{\begin{array}{*{20}{c}} \cdots {}0{} \cdots \end{array}}_{7 \times 11}} \end{array}} \right) {\psi _3}^2\nonumber \\&\quad+ \left( {\begin{array}{*{20}{c}} {\overbrace{\begin{array}{*{20}{c}} \cdots {}0{} \cdots \end{array}}^{7 \times 11}}\nonumber \\ {}{} {\begin{array}{*{20}{c}} { - 8{\pi ^2}}{}{ - 8{\pi ^2}}{}{ - 8{\pi ^2}}{}{{\Gamma _{10}}}{}{{\Gamma _{11}}}{}{{\Gamma _{12}}}{}{{\Gamma _{13}}}{}{{\Gamma _{14}}}{}{{\Gamma _{15}}}{}{{\Gamma _{16}}}{}{{\Gamma _{16}}} \end{array}} \end{array}} \right) {\psi _1}{\psi _2}{\psi _3}+ o({\psi _1}^i{\psi _2}^j{\psi _3}^k),i+j+k \ge 3, \nonumber \\{\Gamma _1} &= {\Gamma _2} = - 8{\pi ^2}{c_2}[({\varepsilon _1} + {\varepsilon _2}){\psi _{12}} + ({\varepsilon _1} - {\varepsilon _2})],~{\Gamma _3} = - 48{\pi ^2}[{({\varepsilon _1} + {\varepsilon _2})^2}{\psi _{12}} + {({\varepsilon _1} - {\varepsilon _2})^2}],\nonumber \\{\Gamma _4} &= {\Gamma _5} = - 8{\pi ^2}{c_2}[({\varepsilon _1} + {\varepsilon _3}){\psi _{13}} + ({\varepsilon _1} - {\varepsilon _3})],~{\Gamma _6} = - 48{\pi ^2}[{({\varepsilon _1} + {\varepsilon _3})^2}{\psi _{13}} + {({\varepsilon _1} - {\varepsilon _3})^2}],\nonumber \\{\Gamma _7} &= {\Gamma _8} = - 8{\pi ^2}{c_2}[({\varepsilon _2} + {\varepsilon _3}){\psi _{23}} + ({\varepsilon _2} - {\varepsilon _3})],~{\Gamma _9} = - 48{\pi ^2}[{({\varepsilon _2} + {\varepsilon _3})^2}{\psi _{23}} + {({\varepsilon _2} - {\varepsilon _3})^2}],\nonumber \\{\Gamma _{10}} &= - 48{\pi ^2}{c_2}[({\varepsilon _1} + {\varepsilon _2} + {\varepsilon _3}){\psi _{12}}{\psi _{13}}{\psi _{23}} + ({\varepsilon _1} - {\varepsilon _2} - {\varepsilon _3}){\psi _{23}} + ({\varepsilon _1} - {\varepsilon _2} + {\varepsilon _3}){\psi _{13}} + ({\varepsilon _1} + {\varepsilon _2} - {\varepsilon _3}){\psi _{12}}],\nonumber \\{\Gamma _{11}} &= - 48{\pi ^2}{c_2}[({\varepsilon _1} + {\varepsilon _2} + {\varepsilon _3}){\psi _{12}}{\psi _{13}}{\psi _{23}} + ( - {\varepsilon _1} + {\varepsilon _2} + {\varepsilon _3}){\psi _{23}} +( - {\varepsilon _1} + {\varepsilon _2} - {\varepsilon _3}){\psi _{13}} + ({\varepsilon _1} + {\varepsilon _2} - {\varepsilon _3}){\psi _{12}}],\nonumber \\{\Gamma _{12}} &= - 48{\pi ^2}{c_2}[({\varepsilon _1} + {\varepsilon _2} + {\varepsilon _3}){\psi _{12}}{\psi _{13}}{\psi _{23}} + ( - {\varepsilon _1} + {\varepsilon _2} + {\varepsilon _3}){\psi _{23}} +({\varepsilon _1} - {\varepsilon _2} + {\varepsilon _3}){\psi _{13}} + ( - {\varepsilon _1} - {\varepsilon _2} + {\varepsilon _3}){\psi _{12}}],\nonumber \\{\Gamma _{13}} &= - 48{\pi ^2}[{({\varepsilon _1} + {\varepsilon _2} + {\varepsilon _3})^2}{\psi _{12}}{\psi _{13}}{\psi _{23}} + {( - {\varepsilon _1} + {\varepsilon _2} + {\varepsilon _3})^2}{\psi _{23}} + {({\varepsilon _1} - {\varepsilon _2} + {\varepsilon _3})^2}{\psi _{13}} + {({\varepsilon _1} + {\varepsilon _2} - {\varepsilon _3})^2}{\psi _{12}}],\nonumber \\{\Gamma _{14}}&= 2(\psi _{12}+\psi _{13}+\psi _{23}+\psi _{12}\psi _{13}\psi _{23}),~~{\Gamma _{15}} = - 16{\pi ^2}({\psi _{12}}{\psi _{13}}{\psi _{23}} + {\psi _{12}} - {\psi _{13}} - {\psi _{23}}), \nonumber \\{\Gamma _{16}} &= - 16{\pi ^2}({\psi _{12}}{\psi _{13}}{\psi _{23}} + {\psi _{13}} - {\psi _{12}} - {\psi _{23}}),~~{\Gamma _{17}} = - 16{\pi ^2}({\psi _{12}}{\psi _{13}}{\psi _{23}} + {\psi _{23}} - {\psi _{12}} - {\psi _{13}}), \end{aligned}$$

(46)

and

$$\begin{aligned}b &= \left( {\begin{array}{*{20}{c}} 0\\ {{\mathrm{H}_1}}\\ 0\\ 0\\ 0\\ 0\\ 0\\ 0 \end{array}} \right) {\psi _1} + \left( {\begin{array}{*{20}{c}} 0\\ 0\\ {{\mathrm{H}_2}}\\ 0\\ 0\\ 0\\ 0\\ 0 \end{array}} \right) {\psi _2} + \left( {\begin{array}{*{20}{c}} 0\\ 0\\ 0\\ {{\mathrm{H}_3}}\\ 0\\ 0\\ 0\\ 0 \end{array}} \right) {\psi _3} + \left( {\begin{array}{*{20}{c}} {{\mathrm{H}_4}}\\ 0\\ 0\\ 0\\ 0\\ 0\\ 0\\ 0 \end{array}} \right) {\psi _1}^2 + \left( {\begin{array}{*{20}{c}} {{\mathrm{H}_5}}\\ 0\\ 0\\ 0\\ 0\\ 0\\ 0\\ 0 \end{array}} \right) {\psi _2}^2 + \left( {\begin{array}{*{20}{c}} {{\mathrm{H}_6}}\\ 0\\ 0\\ 0\\ 0\\ 0\\ 0\\ 0 \end{array}} \right) {\psi _3}^2 \nonumber \\&\quad+ \left( {\begin{array}{*{20}{c}} 0\\ 0\\ 0\\ 0\\ {{\mathrm{H}_7}}\\ 0\\ 0\\ 0 \end{array}} \right) {\psi _1}{\psi _2} + \left( {\begin{array}{*{20}{c}} 0\\ 0\\ 0\\ 0\\ 0\\ {{\mathrm{H}_8}}\\ 0\\ 0 \end{array}} \right) {\psi _1}{\psi _3} + \left( {\begin{array}{*{20}{c}} 0\\ 0\\ 0\\ 0\\ 0\\ 0\\ {{\mathrm{H}_9}}\\ 0 \end{array}} \right) {\psi _2}{\psi _3} + \left( {\begin{array}{*{20}{c}} 0\\ 0\\ 0\\ 0\\ 0\\ 0\\ 0\\ {{\mathrm{H}_{10}}} \end{array}} \right) {\psi _1}{\psi _2}{\psi _3}, \end{aligned}$$

(47)

where

$$\begin{aligned}{\mathrm{H}_1} &= 8{\pi ^2}{\varepsilon _1}^2{c_1} - 32{\pi ^4}{\varepsilon _1}^4{c_3},~{\mathrm{H}_2} = 8{\pi ^2}{\varepsilon _2}^2{c_1} - 32{\pi ^4}{\varepsilon _2}^4{c_3},~{\mathrm{H}_3} = 8{\pi ^2}{\varepsilon _3}^2{c_1} - 32{\pi ^4}{\varepsilon _3}^4{c_3},\\{\mathrm{H}_4} &= 32{\pi ^2}{\varepsilon _1}^2{c_1} - 512{\pi ^4}{\varepsilon _1}^4{c_3},~{\mathrm{H}_5} = 32{\pi ^2}{\varepsilon _2}^2{c_1} - 512{\pi ^4}{\varepsilon _2}^4{c_3},~{\mathrm{H}_6} = 32{\pi ^2}{\varepsilon _3}^2{c_1} - 512{\pi ^4}{\varepsilon _3}^4{c_3},\\{\mathrm{H}_7} &= 8{\pi ^2}{c_1}[{({\varepsilon _1} + {\varepsilon _2})^2}{\psi _{12}} + {({\varepsilon _1} - {\varepsilon _2})^2}] - 32{\pi ^4}{c_3}[{({\varepsilon _1} + {\varepsilon _2})^4}{\psi _{12}} + {({\varepsilon _1} - {\varepsilon _2})^4}],\\{\mathrm{H}_8} &= 8{\pi ^2}{c_1}[{({\varepsilon _1} + {\varepsilon _3})^2}{\psi _{13}} + {({\varepsilon _1} - {\varepsilon _3})^2}] - 32{\pi ^4}{c_3}[{({\varepsilon _1} + {\varepsilon _3})^4}{\psi _{13}} + {({\varepsilon _1} - {\varepsilon _3})^4}],\\{\mathrm{H}_9} &= 8{\pi ^2}{c_1}[{({\varepsilon _2} + {\varepsilon _3})^2}{\psi _{23}} + {({\varepsilon _2} - {\varepsilon _3})^2}] - 32{\pi ^4}{c_3}[{({\varepsilon _2} + {\varepsilon _3})^4}{\psi _{23}} + {({\varepsilon _2} - {\varepsilon _3})^4}],\\{\mathrm{H}_{10}} &= 8{\pi ^2}{c_1}[{({\varepsilon _1} + {\varepsilon _2} + {\varepsilon _3})^2}{\psi _{12}}{\psi _{13}}{\psi _{23}} + {( - {\varepsilon _1} + {\varepsilon _2} + {\varepsilon _3})^2}{\psi _{23}}\\ &\quad+ {({\varepsilon _1} - {\varepsilon _2} + {\varepsilon _3})^2}{\psi _{13}} + {({\varepsilon _1} + {\varepsilon _2} - {\varepsilon _3})^2}{\psi _{12}}]- 32{\pi ^4}{c_3}[{({\varepsilon _1} + {\varepsilon _2} + {\varepsilon _3})^4}{\psi _{12}}{\psi _{13}}{\psi _{23}} \\ &\quad+ {( - {\varepsilon _1} + {\varepsilon _2} + {\varepsilon _3})^4}{\psi _{23}} + {({\varepsilon _1} - {\varepsilon _2} + {\varepsilon _3})^4}{\psi _{13}} + {({\varepsilon _1} + {\varepsilon _2} - {\varepsilon _3})^4}{\psi _{12}}]. \end{aligned}$$

Then, we assume the solution of $M({\omega _1}^2,{\omega _2}^2,{\omega _3}^2,\eta _1,\eta _2,\eta _3,{u_0},c,{\omega _1}{\omega _2},{\omega _1}{\omega _3},{\omega _2}{\omega _3}) = b$ has the following form of

$$\begin{aligned}&{({\omega _1}^2,{\omega _2}^2,{\omega _3}^2,{\eta _1},{\eta _2},{\eta _3},{u_0},c,{\omega _1}{\omega _2},{\omega _1}{\omega _3},{\omega _2}{\omega _3},)^T}\nonumber \\&= {({\omega _1}^{2(0)},{\omega _2}^{2(0)},{\omega _3}^{2(0)},{\eta _1}^{(0)},{\eta _2}^{(0)},{\eta _3}^{(0)},{u_0}^{(0)},{c^{(0)}},{\omega _1}{\omega _2}^{(0)},{\omega _1}{\omega _3}^{(0)},{\omega _2}{\omega _3}^{(0)})^T}\nonumber \\&\quad+ {({\omega _1}^{2(1)},{\omega _2}^{2(1)},{\omega _3}^{2(1)},{\eta _1}^{(1)},{\eta _2}^{(1)},{\eta _3}^{(1)},{u_0}^{(1)},{c^{(1)}},{\omega _1}{\omega _2}^{(1)},{\omega _1}{\omega _3}^{(1)},{\omega _2}{\omega _3}^{(1)})^T}{\psi _1}\nonumber \\&\quad+ {({\omega _1}^{2(2)},{\omega _2}^{2(2)},{\omega _3}^{2(2)},{\eta _1}^{(2)},{\eta _2}^{(2)},{\eta _3}^{(2)},{u_0}^{(2)},{c^{(2)}},{\omega _1}{\omega _2}^{(2)},{\omega _1}{\omega _3}^{(2)},{\omega _2}{\omega _3}^{(2)})^T}{\psi _2}\nonumber \\&\quad+ {({\omega _1}^{2(3)},{\omega _2}^{2(3)},{\omega _3}^{2(3)},{\eta _1}^{(3)},{\eta _2}^{(3)},{\eta _3}^{(3)},{u_0}^{(3)},{c^{(3)}},{\omega _1}{\omega _2}^{(3)},{\omega _1}{\omega _3}^{(3)},{\omega _2}{\omega _3}^{(3)})^T}{\psi _3}\nonumber \\&\quad+ {({\omega _1}^{2(11)},{\omega _2}^{2(11)},{\omega _3}^{2(11)},{\eta _1}^{(11)},{\eta _2}^{(11)},{\eta _3}^{(11)},{u_0}^{(11)},{c^{(11)}},{\omega _1}{\omega _2}^{(11)},{\omega _1}{\omega _3}^{(11)},{\omega _2}{\omega _3}^{(11)})^T}{\psi _1}^2\nonumber \\&\quad+ {({\omega _1}^{2(22)},{\omega _2}^{2(22)},{\omega _3}^{2(22)},{\eta _1}^{(22)},{\eta _2}^{(22)},{\eta _3}^{(22)},{u_0}^{(22)},{c^{(22)}},{\omega _1}{\omega _2}^{(22)},{\omega _1}{\omega _3}^{(22)},{\omega _2}{\omega _3}^{(22)})^T}{\psi _2}^2\nonumber \\&\quad+ {({\omega _1}^{2(33)},{\omega _2}^{2(33)},{\omega _3}^{2(33)},{\eta _1}^{(33)},{\eta _2}^{(33)},{\eta _3}^{(33)},{u_0}^{(33)},{c^{(33)}},{\omega _1}{\omega _2}^{(33)},{\omega _1}{\omega _3}^{(33)},{\omega _2}{\omega _3}^{(33)})^T}{\psi _3}^2\nonumber \\&\quad+ {({\omega _1}^{2(12)},{\omega _2}^{2(12)},{\omega _3}^{2(12)},{\eta _1}^{(12)},{\eta _2}^{(12)},{\eta _3}^{(12)},{u_0}^{(12)},{c^{(12)}},{\omega _1}{\omega _2}^{(12)},{\omega _1}{\omega _3}^{(12)},{\omega _2}{\omega _3}^{(12)})^T}{\psi _1}{\psi _2}\nonumber \\&\quad+ {({\omega _1}^{2(13)},{\omega _2}^{2(13)},{\omega _3}^{2(13)},{\eta _1}^{(13)},{\eta _2}^{(13)},{\eta _3}^{(13)},{u_0}^{(13)},{c^{(13)}},{\omega _1}{\omega _2}^{(13)},{\omega _1}{\omega _3}^{(13)},{\omega _2}{\omega _3}^{(13)})^T}{\psi _1}{\psi _3}\nonumber \\&\quad+ {({\omega _1}^{2(23)},{\omega _2}^{2(23)},{\omega _3}^{2(23)},{\eta _1}^{(23)},{\eta _2}^{(23)},{\eta _3}^{(23)},{u_0}^{(23)},{c^{(23)}},{\omega _1}{\omega _2}^{(23)},{\omega _1}{\omega _3}^{(23)},{\omega _2}{\omega _3}^{(23)})^T}{\psi _2}{\psi _3}\nonumber \\&\quad+ {({\omega _1}^{2(123)},{\omega _2}^{2(123)},{\omega _3}^{2(123)},{\eta _1}^{(123)},{\eta _2}^{(123)},{\eta _3}^{(123)},{u_0}^{(123)},{c^{(123)}},{\omega _1}{\omega _2}^{(123)},{\omega _1}{\omega _3}^{(123)},{\omega _2}{\omega _3}^{(123)})^T} \nonumber \\&\quad\times {\psi _1}{\psi _2}{\psi _3}+o({\psi _1}^i{\psi _2}^j{\psi _3}^k), i+j+k \ge 3. \end{aligned}$$

(48)

Finally, the relation of the three-soliton wave solution and three-periodic wave solution is given as follows.

Theorem 3

If three-periodic wave solution Eq. (45) satisfies the condition of

$$\begin{aligned} \varepsilon _j = \frac{k_j}{{2\pi \mathrm {i}}},\;\;\;\eta _j = \frac{l_j}{{2\pi \mathrm {i}}},\;\;\;\upsilon _j = \frac{{\delta _j + \pi a_{jj}}}{{2\pi \mathrm {i}}},\;\;\;a_{js} = \frac{{A_{js}}}{{-2\pi }},\;\;(j=1,2,3) \end{aligned}$$

(49)

where $k_j, l_j$ and $\delta _j(j=1,2,3)$ are given by Eq. (5), we have the following asymptotic properties:

$$\begin{aligned}u_0 \rightarrow 0, ~c \rightarrow& 0,~~\tau _j \rightarrow \frac{{\sigma _j + \pi a_{jj}}}{{2\pi \mathrm{{i}}}}~(j=1,2,3),\\\varphi (\tau _1,\tau _2,\tau _3 ,a) \rightarrow& 1 + \mathrm{{e}}^{\sigma _1}+\mathrm{{e}}^{\sigma _2}+\mathrm{{e}}^{\sigma _3}+\mathrm{{e}}^{\sigma _1+\sigma _2+A_{12}} +\mathrm{{e}}^{\sigma _1+\sigma _3+A_{13}}+\mathrm{{e}}^{\sigma _2+\sigma _3+A_{23}}\\ &\quad+\mathrm{{e}}^{\sigma _1+\sigma _2+\sigma _3+A_{12}+A_{13}+A_{23}}, ~~\psi _1,\psi _2,\psi _3 \rightarrow 0. \end{aligned}$$

Proof

By substituting Eq. (46-48) into Eq. (44), we obtain the following relations of

$$\begin{aligned}{c^{(0)}} &= {c^{(1)}} = {c^{(2)}} = {c^{(3)}} = {c^{(12)}} = {c^{(13)}} = {c^{(23)}} = {c^{(123)}} = 0, \nonumber \\&{\omega _1}^{2(0)} + 6{\varepsilon _1}u_0^{(0)} = - {\varepsilon _1}^2{c_1} - {\varepsilon _1}{\eta _1}^{(0)}{c_2} + 4{\pi ^2}{\varepsilon _1}^2{c_3},\nonumber \\&{\omega _2}^{2(0)} + 6{\varepsilon _2}u_0^{(0)} = - {\varepsilon _2}^2{c_1} - {\varepsilon _2}{\eta _2}^{(0)}{c_2} + 4{\pi ^2}{\varepsilon _2}^2{c_3}, \nonumber \\&{\omega _3}^{2(0)} + 6{\varepsilon _3}u_0^{(0)} = - {\varepsilon _3}^2{c_1} - {\varepsilon _3}{\eta _3}^{(0)}{c_2} + 4{\pi ^2}{\varepsilon _3}^2{c_3},\nonumber \\&{\omega _1}^{2(1)} + {\varepsilon _1}{\eta _1}^{(1)}{c_2} + 6{\varepsilon _1}u_0^{(1)} = 0,~{\omega _2}^{2(1)} + {\varepsilon _2}{\eta _2}^{(1)}{c_2} + 6{\varepsilon _2}u_0^{(1)} = 0,~{\omega _3}^{2(1)} + {\varepsilon _3}{\eta _3}^{(1)}{c_2} + 6{\varepsilon _3}u_0^{(1)} = 0,\nonumber \\&{c^{(11)}} - 32{\pi ^2}{\omega _1}^{2(0)} - 32{\pi ^2}{\varepsilon _1}{\eta _1}^{(0)}{c_2} - 192{\pi ^2}{\varepsilon _2}^2u_0^{(0)} = 32{\pi ^2}{\varepsilon _1}^2{c_1} - 512{\pi ^4}{\varepsilon _1}^4{c_3},\nonumber \\&{c^{(22)}} - 32{\pi ^2}{\omega _2}^{2(0)} - 32{\pi ^2}{\varepsilon _2}{\eta _2}^{(0)}{c_2} - 192{\pi ^2}{\varepsilon _2}^2u_0^{(0)} = 32{\pi ^2}{\varepsilon _2}^2{c_1} - 512{\pi ^4}{\varepsilon _2}^4{c_3}, \nonumber \\&{c^{(33)}} - 32{\pi ^2}{\omega _3}^{2(0)} - 32{\pi ^2}{\varepsilon _3}{\eta _3}^{(0)}{c_2} - 192{\pi ^2}{\varepsilon _3}^2u_0^{(0)} = 32{\pi ^2}{\varepsilon _3}^2{c_1} - 512{\pi ^4}{\varepsilon _3}^4{c_3}. \end{aligned}$$

(50)

$\hfill\square$

Then by using condition (49), taking $u_0^{(0)}=0,~\eta _j^{(0)}=\eta _j,(j=1,2,3)$ and letting the remaining components of $\eta$ are zero, Eq. (50) has the following form of

$$\begin{aligned} c &= - 384{\pi ^4}{\varepsilon _1}^4{c_3}{\psi _1}^2 - 384{\pi ^4}{\varepsilon _2}^4{c_3}{\psi _2}^2 - 384{\pi ^4}{\varepsilon _3}^4{c_3}{\psi _3}^2+ o({\psi _1}^2{\psi _2}^2{\psi _3}^2),\\ 2\pi \mathrm{{i}}{\omega _1} &= \sqrt{ - 4{\pi ^2}{\omega _1}} = \sqrt{ - 4{\pi ^2}( - {\varepsilon _1}^2{c_1} - {\varepsilon _1}{\eta _1}{c_2} + 4{\pi ^2}{\varepsilon _1}^2{c_3})} ,\\ 2\pi \mathrm{{i}}{\omega _2} &= \sqrt{ - 4{\pi ^2}{\omega _2}} = \sqrt{ - 4{\pi ^2}( - {\varepsilon _2}^2{c_1} - {\varepsilon _2}{\eta _2}{c_2} + 4{\pi ^2}{\varepsilon _2}^2{c_3})} ,\\ 2\pi \mathrm{{i}}{\omega _3} &= \sqrt{ - 4{\pi ^2}{\omega _3}} = \sqrt{ - 4{\pi ^2}( - {\varepsilon _3}^2{c_1} - {\varepsilon _3}{\eta _3}{c_2} + 4{\pi ^2}{\varepsilon _3}^2{c_3})} . \end{aligned}$$

By using condition (49), we have

$$\begin{aligned}u_0 \rightarrow 0, ~c \rightarrow& 0,~2\pi \mathrm{{i}}{\omega _1} \rightarrow \sqrt{ - {k_1}^2{c_1} - {k_1}{l_1}{c_2} - {k_1}^2{c_3}} ,\\ 2\pi \mathrm{{i}}{\omega _2} \rightarrow& \sqrt{ - {k_2}^2{c_1} - {k_2}{l_2}{c_2} - {k_2}^2{c_3}} , \\ 2\pi \mathrm{{i}}{\omega _3} \rightarrow& \sqrt{ - {k_3}^2{c_1} - {k_3}{l_3}{c_2} - {k_3}^2{c_3}} , ~~{\psi _1},{\psi _2},{\psi _3} \rightarrow 0. \end{aligned}$$

By expanding the theta function

$$\begin{aligned}\varphi ({\tau _1},{\tau _2},{\tau _3},a) &= 1 + ({\mathrm{{e}}^{2\pi \mathrm{{i}}{\tau _1}}} + {\mathrm{{e}}^{ - 2\pi \mathrm{{i}}{\tau _1}}}){\mathrm{{e}}^{ - \pi {a_{11}}}} +({\mathrm{{e}}^{2\pi \mathrm{{i}}{\tau _2}}} + {\mathrm{{e}}^{ - 2\pi \mathrm{{i}}{\tau _2}}}){\mathrm{{e}}^{ - \pi {a_{22}}}} \\ &\quad+({\mathrm{{e}}^{2\pi \mathrm{{i}}{\tau _3}}} + {\mathrm{{e}}^{ - 2\pi \mathrm{{i}}{\tau _3}}}){\mathrm{{e}}^{ - \pi {a_{33}}}} + \left( {{\mathrm{{e}}^{2\pi \mathrm{{i}}({\tau _1} + {\tau _2})}} + {\mathrm{{e}}^{ - 2\pi \mathrm{{i}}({\tau _1} + {\tau _2})}}} \right) {\mathrm{{e}}^{ - \pi ({a_{11}} + 2{a_{12}} + {a_{22}})}}\\&\quad+\left( {{\mathrm{{e}}^{2\pi \mathrm{{i}}({\tau _1} + {\tau _3})}} + {\mathrm{{e}}^{ - 2\pi \mathrm{{i}}({\tau _1} + {\tau _3})}}} \right) {\mathrm{{e}}^{ - \pi ({a_{11}} + 2{a_{13}} + {a_{33}})}}+\left( {{\mathrm{{e}}^{2\pi \mathrm{{i}}({\tau _2} + {\tau _3})}} + {\mathrm{{e}}^{ - 2\pi \mathrm{{i}}({\tau _2} + {\tau _3})}}} \right) {\mathrm{{e}}^{ - \pi ({a_{22}} + 2{a_{23}} + {a_{33}})}}\\&\quad+\left( {{\mathrm{{e}}^{2\pi \mathrm{{i}}({\tau _1} + {\tau _2}+{\tau _3})}} + {\mathrm{{e}}^{ - 2\pi \mathrm{{i}}({\tau _1} + {\tau _2}+{\tau _3})}}} \right) {\mathrm{{e}}^{ - \pi ({a_{11}} + 2{a_{12}}+ 2{a_{13}}+ 2{a_{23}} + {a_{22}}+ {a_{33}})}} +\cdots , \end{aligned}$$

and applying condition(49), one yields

$$\begin{aligned}\varphi ({\tau _1},{\tau _2},{\tau _3},a) &= 1 + {\mathrm{{e}}^{{\tau _1}'}} + {\mathrm{{e}}^{{\tau _2}'}} + {\mathrm{{e}}^{{\tau _3}'}} + {\mathrm{{e}}^{{\tau _1}' + {\tau _2}' - 2\pi {a_{12}}}} + {\mathrm{{e}}^{{\tau _1}' + {\tau _3}' - 2\pi {a_{13}}}} + {\mathrm{{e}}^{{\tau _2}' + {\tau _3}' - 2\pi {a_{23}}}} \nonumber \\&\quad+{\mathrm{{e}}^{{\tau _1}'+{\tau _2}' + {\tau _3}' - 2\pi ( {a_{12}}+{a_{13}}+{a_{23}})}}+{\psi _1}^2{\mathrm{{e}}^{ - {\tau _1}'}} + {\psi _2}^2{\mathrm{{e}}^{ - {\tau _2}'}} + {\psi _3}^2{\mathrm{{e}}^{ - {\tau _3}'}}\nonumber\\ &\quad+\cdots \rightarrow 1 + {\mathrm{{e}}^{{\tau _1}'}} + {\mathrm{{e}}^{{\tau _2}'}} + {\mathrm{{e}}^{{\tau _3}'}} + \mathrm{{e}}^{{\tau _1}' + {\tau _2}' + {A_{12}}}+\mathrm{{e}}^{{\tau _1}' + {\tau _3}' + {A_{13}}}\nonumber\\&\quad+\mathrm{{e}}^{{\tau _2}' + {\tau _3}' + {A_{23}}} + \mathrm{{e}}^{{\tau _1}' + {\tau _2}'+{\tau _3}' + {A_{12}}+ {A_{13}}+ {A_{23}}},~~{\psi _1},{\psi _2},{\psi _3} \rightarrow 0, \end{aligned}$$

(51)

where

$$\begin{aligned}&{\tau _1}' = 2\pi \mathrm{{i}}{\tau _1} - \pi {a_{11}} \rightarrow {k_1}x + {l_1}y + \sqrt{ - {c_2}{} {k_1}{l_1} - {c_3}{k_1}^4 - {c_1}{} {k_1}^2} t + {\delta _1} = {\sigma _1},\nonumber \\&{\tau _2}' = 2\pi \mathrm{{i}}{\tau _2} - \pi {a_{22}} \rightarrow {k_2}x + {l_2}y + \sqrt{ - {c_2}{} {k_2}{l_2} - {c_3}{k_2}^4 - {c_1}{} {k_2}^2} t + {\delta _2} = {\sigma _2}, \nonumber \\&{\tau _3}' = 2\pi \mathrm{{i}}{\tau _3} - \pi {a_{33}} \rightarrow {k_3}x + {l_3}y + \sqrt{ - {c_2}{} {k_3}{l_3} - {c_3}{k_3}^4 - {c_1}{} {k_3}^2} t + {\delta _3} = {\sigma _3},~~{\psi _1},{\psi _2},{\psi _3} \rightarrow 0. \end{aligned}$$

(52)

Finally, combining Eqs. (51) and (52), we obtain

$$\begin{aligned} \varphi ({\tau _1},{\tau _2},{\tau _3},a) \rightarrow& 1 + {\mathrm{{e}}^{{\sigma _1}}} + {\mathrm{{e}}^{{\sigma _2}}} +{\mathrm{{e}}^{{\sigma _3}}} + {\mathrm{{e}}^{{\sigma _1} + {\sigma _2} + {A_{12}}}}+ {\mathrm{{e}}^{{\sigma _1} + {\sigma _3} + {A_{13}}}}+ {\mathrm{{e}}^{{\sigma _2} + {\sigma _3} + {A_{23}}}} \\ &\quad+{\mathrm{{e}}^{{\sigma _1} + {\sigma _2}+{\sigma _3} + {A_{12}}+ {A_{13}}+ {A_{23}}}},~~{\psi _1},{\psi _2},{\psi _3} \rightarrow 0. \end{aligned}$$

Therefore, three-periodic wave solution tends to three-soliton solution under the condition of $\psi _1,\psi _2,\psi _3$ $\rightarrow 0.$

7 Conclusion

In this paper, we have investigated the soliton solutions, breath-wave solutions and their transformations, and one-, two-, and three-periodic waves for a (2+1)-dimensional Boussinesq-type equation. Based on the Hirota’s bilinear method, the soliton solutions have been derived. By taking the complex conjugate condition to the soliton solutions, the breather solutions are further obtained. And transformation mechanism of the one breather wave is systematically studied by considering the case which two characteristic lines are parallel, that is $\left| {\begin{array}{*{20}{c}} {{a _1}}&{}{{p _1}}\\ {{a _2}}&{}{{p _2}} \end{array}} \right| = 0$, under this condition, a large number of types of nonlinear waves are obtained, including quasi-anti-dark soliton, M-shaped soliton, oscillation M-shaped soliton, multi-peak soliton, quasi-sine wave, quasi-periodic W-shaped wave, quasi-periodic anti-dark soliton wave and quasi-periodic wave. The transformation of two breather waves is further studied.

According to the Riemann theta function, we have got one- and two-period wave solutions. At the same time, we firstly extend the study of periodic wave to three-periodic wave solution. In addition, when studying the dynamic characteristics of periodic waves, the characteristic line method is also firstly introduced. It is obvious that the one-periodic wave solution has one characteristic line of ${\tau } = {\varepsilon }x + {\eta }y + {\omega }t + {\upsilon }=0,$ the propagation direction of wave is completely determined by $\tau ,$ and $\frac{{{v_x}}}{{{v_y}}} = \frac{\varepsilon }{\eta },$ as shown in Fig. 16. And the two-periodic wave has two characteristic lines of ${\tau _1} = {\varepsilon _1}x + {\eta _1}y + {\omega _1}t + {\upsilon _1}=0$ and ${\tau _2} = {\varepsilon _2}x + {\eta _2}y + {\omega _2}t + {\upsilon _2}=0.$ By considering whether the two characteristic lines are parallel or not, the different forms of two-periodic wave are obtained, as shown in Figs. 17, 18, 19 and 20. The three-periodic wave has three characteristic lines of ${\tau _1} = {\varepsilon _1}x + {\eta _1}y + {\omega _1}t + {\upsilon _1}=0,$ ${\tau _2} = {\varepsilon _2}x + {\eta _2}y + {\omega _2}t + {\upsilon _2}=0$ and ${\tau _3} = {\varepsilon _3}x + {\eta _3}y + {\omega _3}t + {\upsilon _3}=0.$ By considering the relationship between the values of $\varepsilon _1 ,\varepsilon _2$ and $\varepsilon _3,$ the different forms of three-periodic wave are gained, as shown in Figs. 21, 22, 23 and 24.

The generalized Boussinesq equation can be reduced into some integrable equations including rich algebraic and geometric structures, and it appears in many disciplines and research fields, such as fluid mechanics, ocean waves, nonlinear optics and atmospheric science. The obtained results about the transformation mechanism of the breather waves and high-dimensional Riemann theta function quasi-periodic waves, in particular the three-periodic waves, will play an important role in explaining the nonlinear phenomena existing in Eq. (1). Furthermore, the characteristic line method has been well extended to analyze the dynamical behaviors of the quasi-periodic waves, which gives a new perspective to consider the Riemann theta function periodic waves. The analytic method presented in this paper can be applied to other integrable systems to explore rich integrable properties.