1 Introduction

Nonlinear phenomena can be observed in many areas such as physics, chemistry, biology, ocean engineering, and communication engineering. In physics precisely, nonlinearity is present in fluid dynamics, nonlinear optics, plasma physics, communication technology and so on [1–16]. In order to understand the mechanisms of those physical phenomena which can be described by nonlinear evolution equations (NLEEs), it is necessary to explore their solutions and properties. At the present time, there are many powerful methods for seeking the exact and approximated solutions of these NLEEs, such as inverse scattering method [17, 18], Hirota bilinear transformation [19], the modified simple equation method [20, 21], the \((G^{\prime }/G)\)—expansion method [22], the trial equation method [23] and many more.

Fig. 1
figure 1

A nonlinear transmission line

Full size image

In communication engineering, a transmission line is a specialized medium or other structure designed to carry alternating current of radio frequency, that is, currents with a frequency high enough that their wave nature must be taken into account. Transmission lines are used for purposes such as connecting radio transmitters and receivers with their antennas, distributing cable television signals, trunklines routing calls between telephone switching centers, computer network connections and high speed computer data buses.

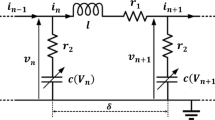
In this paper, we apply the improved extended tanh-function method to seek the soliton wave solutions in a NLTL. The NLTLs are very convenient tools to study the propagation of electrical solitons which can propagate in the form of voltage waves in nonlinear dispersive media. The NLTL model used in this work is shown in Fig. 1 using inductors \(\ell \), and voltage dependent (and hence nonlinear) capacitors, \(c\left( V \right) \). By applying Kirchhoff current law at node n, whose voltage with respect to ground is \({V_n}\), and applying Kirchhoff voltage law across the two inductors connected to this node, the voltages of adjacent nodes on this NLTL are related via:

$$\begin{aligned} \ell \frac{d}{{\hbox {d}t}}\left[ {c({{V_n}})\frac{{\hbox {d}{V_n}}}{{\hbox {d}t}}} \right] = \left( {{V_{n + 1}} + {V_{n - 1}} - 2{V_n}} \right) . \end{aligned}$$
(1.1)

The right-hand side of (1.1) can be approximated with partial derivatives with respect to distance x, from the beginning of the line, assuming that the spacing between two adjacent sections is \(\delta \) (i.e., \({x_n} = n\delta \)). An approximate continuous partial differential equation can be obtained by using the Taylor expansions of \(V(x-\delta )\), V(x), and \(V(x+\delta )\) to evaluate the right-hand side of (1.1). Assuming a small \(\delta \), and ignoring the high order terms, we obtain:

$$\begin{aligned} L\frac{\partial }{{\partial t}}\left[ {C(V)\frac{{\partial V}}{{\partial t}}} \right] = \frac{{{\partial ^2}V}}{{\partial {x^2}}} + \frac{{{\delta ^2}}}{{12}}\frac{{{\partial ^4}V}}{{\partial {x^4}}}, \end{aligned}$$
(1.2)

where C and L are the capacitance and inductance per unit length, respectively. For more detail see also [10].

2 Description of the method

In this section, we outline the main steps of the improved extended tanh-equation method as following:

Suppose that we have a nonlinear evolution equation in the form:

$$\begin{aligned} F\left( {u,{u_t},{u_x},{u_{xx}},{u_{xt}},\ldots } \right) = 0, \end{aligned}$$
(2.1)

where \(u = u(x,t)\) is an unknown function, F is a polynomial in u and its various partial derivatives \({u_t},{u_x}\) with respect to t, x, respectively, in which the highest order derivatives and nonlinear terms are involved.

Step 1. Using the traveling wave transformation

$$\begin{aligned} u(x,t) = U(\xi ),\quad \xi = k(x - vt), \end{aligned}$$
(2.2)

where k, c are constant to be determined later. Then, Eq. (2.1) is reduced to a nonlinear ordinary differential equation of the form

$$\begin{aligned} P\left( {U,-kvU^{\prime },kU^{\prime },k^2U^{\prime \prime },\ldots } \right) = 0, \end{aligned}$$
(2.3)

Step 2. We assume that the solution of Eq. (2.3) can be expressed in the form

$$\begin{aligned} U(\xi ) = \sum \limits _{i = 0}^N {{\alpha _i}{\omega ^i}} + \sum \limits _{i = 1}^N {{\beta _i}{\omega ^{-i}}}, \end{aligned}$$
(2.4)

where \(\omega \) satisfies

$$\begin{aligned} \omega ^{\prime } = \varepsilon \sqrt{{a_0} + {a_1}\omega + {a_2}{\omega ^2} + {a_3}{\omega ^3} + {a_4}{\omega ^4}}, \end{aligned}$$
(2.5)

where \(\varepsilon =\pm 1\). This equation gives various kinds of fundamental solutions [15]. From these solutions, more new exact solutions for (2.1) can be obtained.

Step 3. Determine the positive integer number N in Eq. (2.4) by balancing the highest order derivatives and the nonlinear terms in Eq. (2.3).

Step 4. Substitute (2.4) into (2.3) along with (2.5). As a result of this substitution, we get a polynomial of \(\omega \). In this polynomial, we gather all terms of same powers and equating them to be zero, we get an over-determined system of algebraic equations which can be solved by the maple or mathematica to get the unknown parameters \(k,v,\alpha _0,\alpha _i\) and \(\beta _i (i=1,2,\ldots )\). Consequently, we obtain the exact solutions of (2.1).

3 Exact and soliton solutions

In this section, the improved extended tanh-function method is applied to our NLTL model. To this end, we approximate the capacitor’s voltage dependence using the following first-order linear relationship

$$\begin{aligned} C(V)=C_0(1-bV), \end{aligned}$$
(3.1)

where \(C_0\) and b are arbitrary constants. In this case, Eq. (1.2) reduces to

$$\begin{aligned} \frac{{{\partial ^2}V}}{{\partial {t^2}}} - \frac{b}{2}\frac{{{\partial ^2}{V^2}}}{{\partial {t^2}}} = \frac{1}{{L{C_0}}}\frac{{{\partial ^2}V}}{{\partial {x^2}}} + \frac{{{\delta ^2}}}{{12L{C_0}}}\frac{{{\partial ^4}V}}{{\partial {x^4}}}. \end{aligned}$$
(3.2)

Introduce the voltage in the form of the traveling wave

$$\begin{aligned} V(x,t)=V(\xi ), \quad \xi =x-v t \end{aligned}$$
(3.3)

where v represent the velocity of propagation. Then, Eq. (3.2) reduces to the following ODE:

$$\begin{aligned} \frac{{{\delta ^2}}}{{12 L {C_0}}}V^{\prime \prime \prime \prime } + \left( \frac{1}{L {C_0}} - {v^2}\right) V^{\prime \prime } + \frac{{b{v^2}}}{2}{\left( V^2\right) }^{\prime \prime } = 0.\nonumber \\ \end{aligned}$$
(3.4)

Integrating Eq. (3.4) twice with zero constants of integration, we obtain

$$\begin{aligned} \frac{{{\delta ^2}v_0^2}}{{12}}V^{\prime \prime } + \left( v_0^2 - {v^2}\right) V + \frac{{b{v^2}}}{2}{V^2} = 0, \end{aligned}$$
(3.5)

where \({v_0} = \frac{1}{{\sqrt{L{C_0}}}}\).

Balancing \(V^{\prime \prime }\) with \(V^2\) in Eq. (3.5), then we get \(N=2\). Then, the solution of Eq. (3.5) has the form

$$\begin{aligned} V(\xi )=\alpha _0+\alpha _1 \omega +\alpha _2\omega ^2+\beta _1\omega ^{-1}+\beta _2\omega ^{-2}. \end{aligned}$$
(3.6)

Substituting \(V(\xi )\) and its derivatives with (2.5) into (3.5) and equating all the coefficients of \(\omega ^j, j\in [{-}4,4]\) to be zero, then we obtain a system of algebraic equations. Solving this system via mathematica and consider the various kinds of fundamental solutions [15], we obtain the following cases which leads to different types of wave propagation of our model (Eq. 3.2)

Case 1: \({a_0} = {a_1} = {a_3} =0\). We have the following results

$$\begin{aligned} {\alpha _0}= & {} {\alpha _1} = {\beta _1} = {\beta _2} = 0,\nonumber \\ {a_2}= & {} \frac{{3\left( {{v^2} - v_0^2} \right) }}{{{\delta ^2}v_0^2}},\quad {\alpha _2} = - \frac{{{a_4}{\delta ^2}v_0^2}}{{{v^2}b}}. \end{aligned}$$
(3.7)

and

$$\begin{aligned} {\alpha _0}= & {} \frac{{2\left( {{v^2} - v_0^2} \right) }}{{{v^2}b}},\quad {\alpha _1} = {\beta _1} = {\beta _2} = 0,\nonumber \\ {a_2}= & {} - \frac{{3\left( {{v^2} - v_0^2} \right) }}{{{\delta ^2}v_0^2}},\quad {\alpha _2} = - \frac{{{a_4}{\delta ^2}v_0^2}}{{{v^2}b}}. \end{aligned}$$
(3.8)

We obtain, solitary wave solutions, singular periodic solutions and rational solution

$$\begin{aligned} V(\xi )= & {} \frac{{3\left( {{v^2} - v_0^2} \right) }}{{{v^2}b}} \sec {\mathrm{h}^2}\left[ {\frac{{\sqrt{3\left( {{v^2} - v_0^2} \right) } }}{{\delta {v_0}}}(x - vt)} \right] ,\nonumber \\ {v^2}> & {} v_0^2, \end{aligned}$$
(3.9)
$$\begin{aligned} V(\xi )= & {} \frac{{3\left( {{v^2} - v_0^2} \right) }}{{{v^2}b}}{\sec ^2}\left[ {\frac{{\sqrt{3\left( {v_0^2 - {v^2}} \right) } }}{{\delta {v_0}}}(x - vt)} \right] ,\nonumber \\ {v^2}< & {} v_0^2, \end{aligned}$$
(3.10)
$$\begin{aligned} V(\xi )= & {} \frac{{ - {\delta ^2}}}{b}\frac{1}{{{{(x - vt)}^2}}},\nonumber \\ {v^2}= & {} v_0^2 \end{aligned}$$
(3.11)

and

$$\begin{aligned} V(\xi )= & {} \frac{{{v^2} - v_0^2}}{{{v^2}b}}\left( {2 - 3\sec {\mathrm{h}^2}\left[ {\frac{{\sqrt{3\left( {v_0^2 - {v^2}} \right) } }}{{\delta {v_0}}}(x - vt)} \right] } \right) ,\nonumber \\ {v^2}< & {} v_0^2, \end{aligned}$$
(3.12)
$$\begin{aligned} V(\xi )= & {} \frac{{{v^2} - v_0^2}}{{{v^2}b}}\left( {2 - 3{{\sec }^2}\left[ {\frac{{\sqrt{3\left( {{v^2} - v_0^2} \right) } }}{{\delta {v_0}}}(x - vt)} \right] } \right) ,\nonumber \\ {v^2}> & {} v_0^2, \end{aligned}$$
(3.13)
$$\begin{aligned} V(\xi )= & {} \frac{{3\left( {{v^2} - v_0^2} \right) }}{{{v^2}b}} - \frac{{{\delta ^2}v_0^2}}{{{v^2}b}}\frac{1}{{{{(x - vt)}^2}}},\nonumber \\ {v^2}= & {} v_0^2. \end{aligned}$$
(3.14)

Case 2:

  1. (i)

    \({a_1} = {a_3} =0, a_0=\frac{a_2^2}{4 a_4}\). We have

    $$\begin{aligned}&{\alpha _1} = {\alpha _2} = {\beta _1} = 0,{a_0} = \frac{{{a_2}^2}}{{4{a_4}}},\quad {\alpha _0} = \frac{{3\left( {{v^2} - v_0^2} \right) }}{{{v^2}b}},\nonumber \\&{\beta _2} = - \frac{{9{{\left( {{v^2} - v_0^2} \right) }^2}}}{{{v^2}{\delta ^2}{a_4}bv_0^2}},\quad {a_2} = \frac{{6\left( { - {v^2} + v_0^2} \right) }}{{{\delta ^2}v_0^2}}. \end{aligned}$$
    (3.15)

    We obtain, singular soliton solution and singular periodic solution

    $$\begin{aligned}&V(\xi )= \frac{{3\left( {v_0^2 - {v^2}} \right) }}{{{v^2}b}}\mathrm{csch}^2\left[ {\frac{{\sqrt{3\left( {{v^2} - v_0^2} \right) } }}{{\delta {v_0}}}(x - vt)} \right] ,\nonumber \\&{v^2} > v_0^2, \end{aligned}$$
    (3.16)
    $$\begin{aligned}&V(\xi ) = \frac{{3\left( {{v^2} - v_0^2} \right) }}{{{v^2}b}}\mathrm{csc}^2\left[ {\frac{{\sqrt{3\left( {v_0^2 - {v^2}} \right) } }}{{\delta {v_0}}}(x - vt)} \right] ,\nonumber \\&{v^2} < v_0^2. \end{aligned}$$
    (3.17)
  2. (ii)

    \({a_1} = {a_3} =0,{a_0} = \frac{{{a_2}^2{m^2}\left( {1 - {m^2}} \right) }}{{{a_4}{{\left( {2{m^2} - 1} \right) }^2}}}\). We have

    $$\begin{aligned} {\alpha _1}= & {} {\alpha _2} = {\beta _1} = 0,\quad {\alpha _0} = \frac{{3\left( {{v^2} - v_0^2} \right) - {a_2}{\delta ^2}v_0^2}}{{3{v^2}b}},\nonumber \\ {\beta _2}= & {} \frac{{9{m^2}\left( { - 1 + {m^2}} \right) {{\left( {{v^2} - v_0^2} \right) }^2}}}{{\left( {1 - 7{m^2} + 7{m^4}} \right) {v^2}{\delta ^2}{a_4}bv_0^2}},\nonumber \\ {a_2}= & {} - \frac{{3\left( {1 - 2{m^2}} \right) \left( {{v^2} - v_0^2} \right) }}{{\sqrt{\left( {1 - 7{m^2} + 7{m^4}} \right) } {\delta ^2}v_0^2}}, \end{aligned}$$
    (3.18)

    and

    $$\begin{aligned} {\alpha _0}= & {} \frac{{3\left( {{v^2} - v_0^2} \right) - {a_2}{\delta ^2}v_0^2}}{{3{v^2}b}},\quad {\alpha _1} = {\beta _1} = {\beta _2} = 0,\nonumber \\ {\alpha _2}= & {} - \frac{{{\delta ^2}{a_4}v_0^2}}{{{v^2}b}},\nonumber \\ {a_2}= & {} - \frac{{3\left( {1 - 2{m^2}} \right) \left( {{v^2} - v_0^2} \right) }}{{\sqrt{\left( {1 - 7{m^2} + 7{m^4}} \right) } {\delta ^2}v_0^2}}. \end{aligned}$$
    (3.19)

    We obtain, Jacobi elliptic doubly periodic type solutions

    $$\begin{aligned} V(\xi )= & {} \frac{{\left( {{v^2} - v_0^2} \right) }}{{{v^2}b}}\left( 1 + \frac{{1 - 2{m^2}}}{{\sqrt{1 - 7{m^2} + 7{m^4}} }}\right. \nonumber \\&+\, \frac{{3(1 - {m^2})}}{{\sqrt{1 - 7{m^2} + 7{m^4}} }}\mathrm{nc}^2\nonumber \\&\left. \times \,\left[ {\xi \sqrt{\frac{{3\left( {{v^2} - v_0^2} \right) }}{{\sqrt{1 - 7{m^2} + 7{m^4}} {\delta ^2}v_0^2}}} } \right] \right) \nonumber \\ \end{aligned}$$
    (3.20)

    and

    $$\begin{aligned} V(\xi )= & {} \frac{{\left( {{v^2} - v_0^2} \right) }}{{{v^2}b}}\left( 1 + \frac{{1 - 2{m^2}}}{{\sqrt{1 - 7{m^2} + 7{m^4}} }}\right. \nonumber \\&+\, \frac{{3{m^2}}}{{\sqrt{1 - 7{m^2} + 7{m^4}} }}\mathrm{cn}^2\nonumber \\&\left. \times \,\left[ {\xi \sqrt{\frac{{3\left( {{v^2} - v_0^2} \right) }}{{\sqrt{1 - 7{m^2} + 7{m^4}} {\delta ^2}v_0^2}}} } \right] \right) ,\nonumber \\ \end{aligned}$$
    (3.21)
  3. (iii)

    \({a_1} = {a_3} =0, {a_0} = \frac{{{{{a_2}^2}}\left( {1 - {m^2}} \right) }}{{{a_4}{{\left( {2 - {m^2}} \right) }^2}}}\). We have

    $$\begin{aligned} {\alpha _1}= & {} {\beta _1} = {\beta _2} = 0,\quad {\alpha _0} = \frac{{3\left( {{v^2} - v_0^2} \right) - {a_2}{\delta ^2}v_0^2}}{{3{v^2}b}},\nonumber \\ {\alpha _2}= & {} - \frac{{{\delta ^2}{a_4}v_0^2}}{{{v^2}b}},\nonumber \\ {\alpha _2}= & {} \frac{{3\left( { - 2 + {m^2}} \right) \left( {{v^2} - v_0^2} \right) }}{{\sqrt{1 - {m^2} + {m^4}} {\delta ^2}v_0^2}} \end{aligned}$$
    (3.22)

    and

    $$\begin{aligned} {\alpha _0}= & {} \frac{{3\left( {{v^2} - v_0^2} \right) - {a_2}{\delta ^2}v_0^2}}{{3{v^2}b}},\quad {\alpha _1} = {\alpha _2} = {\beta _1} = 0,\nonumber \\ {\beta _2}= & {} \frac{{9\left( { - 1 + {m^2}} \right) {{\left( {{v^2} - v_0^2} \right) }^2}}}{{\left( {1 - {m^2} + {m^4}} \right) {v^2}{\delta ^2}{a_4}bv_0^2}},\nonumber \\ {a_2}= & {} \frac{{3\left( { - 2 + {m^2}} \right) \left( {{v^2} - v_0^2} \right) }}{{\sqrt{1 - {m^2} + {m^4}} {\delta ^2}v_0^2}}. \end{aligned}$$
    (3.23)

    We obtain

    $$\begin{aligned} V(\xi )= & {} 2 - {m^2}\left( 1 + \frac{{{m^2}}}{{2 - {m^2}}}{\delta ^2}\mathrm{dn}^2\right. \nonumber \\&\times \,\left[ {\xi \sqrt{\frac{{3\left( {v_0^2 - {v^2}} \right) }}{{\sqrt{1 - {m^2} + {m^4}} {\delta ^2}v_0^2}}} } \right] v_0^2 \nonumber \\&-\, \left. \frac{{\left( { - 2 + {m^2}} \right) }}{{\sqrt{1 - {m^2} + {m^4}} }} \right) \end{aligned}$$
    (3.24)

    and

    $$\begin{aligned} V(\xi )= & {} \frac{{\left( {{v^2} - v_0^2} \right) }}{{{v^2}b}}\left( 1 + \frac{{2 - {m^2}}}{{\sqrt{1 - {m^2} + {m^4}} }}\right. \nonumber \\&+\, \frac{{9\left( {{m^2} - 2} \right) \left( {{m^2} - 1} \right) \left( {{v^2} - v_0^2} \right) }}{{{m^2}\left( {1 - {m^2} + {m^4}} \right) {\delta ^2}v_0^2}}\mathrm{nd}^2\nonumber \\&\left. \times \,\left[ {\sqrt{3} \xi \sqrt{\frac{{ - {v^2} + v_0^2}}{{\sqrt{1 - {m^2} + {m^4}} {\delta ^2}v_0^2}}} } \right] \right) .\nonumber \\ \end{aligned}$$
    (3.25)
  4. (iv)

    \({a_1} = {a_3} =0, {a_0} = \frac{{{a_2}^2{m^2}}}{{{a_4}{{\left( {{m^2} + 1} \right) }^2}}}\). We have

    $$\begin{aligned} {\alpha _1}= & {} {\beta _1} = {\beta _2} = 0,\quad {\alpha _0} = \frac{{\left( {{v^2} - v_0^2} \right) }}{{{v^2}{b_1}}} - \frac{{{\delta ^2}v_0^2{a_2}}}{{3{v^2}b}},\nonumber \\ {\alpha _2}= & {} - \frac{{{\delta ^2}{a_4}v_0^2}}{{{v^2}b}},\nonumber \\ {a_2}= & {} \frac{{3\left( {1 + {m^2}} \right) \left( {{v^2} - v_0^2} \right) }}{{\sqrt{1 - {m^2} + {m^4}} {\delta ^2}v_0^2}} \end{aligned}$$
    (3.26)

    and

    $$\begin{aligned} {\alpha _0}= & {} \frac{{\left( {{v^2} - v_0^2} \right) }}{{{v^2}b}} - \frac{{{\delta ^2}v_0^2{a_2}}}{{3{v^2}b}},\quad {\alpha _1} = 0,\quad {\alpha _2} = 0,\quad {\beta _1} = 0,\nonumber \\ {\beta _2}= & {} - \frac{{9{m^2}{{\left( {{v^2} - v_0^2} \right) }^2}}}{{\left( {1 - {m^2} + {m^4}} \right) {v^2}{\delta ^2}{a_4}bv_0^2}},\nonumber \\ {a_2}= & {} \frac{{3\left( {{v^2} - v_0^2} \right) \left( {1 + {m^2}} \right) }}{{\sqrt{1 - {m^2} + {m^4}} {\delta ^2}v_0^2}}. \end{aligned}$$
    (3.27)

    We obtain

    $$\begin{aligned} V(\xi )= & {} \frac{{\left( {{v^2} - v_0^2} \right) }}{{{v^2}b}}\left( 1 - \frac{{1 + {m^2}}}{{\sqrt{1 - {m^2} + {m^4}} }}\right. \nonumber \\&+\, \frac{{3{m^2}}}{{\sqrt{1 - {m^2} + {m^4}} }}\mathrm{sn}^2\nonumber \\&\left. \times \,\left[ {\xi \sqrt{\frac{{3\left( {v_0^2 - {v^2}} \right) }}{{\sqrt{1 - {m^2} + {m^4}} {\delta ^2}v_0^2}}} } \right] \right) \end{aligned}$$
    (3.28)

    and

    $$\begin{aligned} V(\xi )= & {} \frac{{\left( {{v^2} - v_0^2} \right) }}{{{v^2}b}}\left( 1 - \frac{{1 + {m^2}}}{{\sqrt{1 - {m^2} + {m^4}} }} \right. \nonumber \\&+\, \frac{3}{{\sqrt{1 - {m^2} + {m^4}} }}\mathrm{ns}^2\nonumber \\&\left. \times \,\left[ {\xi \sqrt{\frac{{3\left( {v_0^2 - {v^2}} \right) }}{{\sqrt{1 - {m^2} + {m^4}} {\delta ^2}v_0^2}}} } \right] \right) . \end{aligned}$$
    (3.29)

Case 3: \(a_2=a_4=0, a_0,a_1\ne 0\). We have

$$\begin{aligned} {\alpha _0}= & {} \frac{{\left( {{v^2} - v_0^2} \right) \left( {7 + \sqrt{21} } \right) }}{{7{v^2}b}},\quad {\alpha _1} = {\alpha _2} = 0,\nonumber \\ {\beta _2}= & {} - \sqrt{\frac{7}{{48}}} \frac{{{v^2}b\beta _1^2}}{{\left( {{v^2} - v_0^2} \right) }},\nonumber \\ {a_0}= & {} \sqrt{\frac{7}{{48}}} \frac{{{v^4}{b^2}\beta _1^2}}{{{\delta ^2}v_0^2\left( {{v^2} - v_0^2} \right) }},\quad {a_1} = - \frac{{2{v^2}b{\beta _1}}}{{{\delta ^2}v_0^2}},\nonumber \\ {a_3}= & {} \frac{{48{{\left( {{v^2} - v_0^2} \right) }^2}}}{{7{v^2}{\delta ^2}bv_0^2{\beta _1}}}. \end{aligned}$$
(3.30)

We obtain Weierstrass elliptic doubly periodic type solution

$$\begin{aligned} V(\xi )= & {} \frac{{\left( {7 + \sqrt{21} } \right) \left( {{v^2} - v_0^2} \right) }}{{7{v^2}b}}\nonumber \\&+\, {\beta _1}{\left( {\wp \left( {\frac{{\sqrt{{a_3}} }}{2}\xi ;{g_2},{g_3}} \right) } \right) ^{ - 1}}\nonumber \\&-\, \frac{{\sqrt{\frac{7}{3}} {v^2}b\beta _1^2}}{{4\left( {{v^2} - v_0^2} \right) }}{\left( {\wp \left( {\frac{{\sqrt{{a_3}} }}{2}\xi ;{g_2},{g_3}} \right) } \right) ^{ - 2}},\nonumber \\ \end{aligned}$$
(3.31)

where

$$\begin{aligned} {g_2} = \frac{{7{v^4}{b^2}\beta _1^2}}{{6{{\left( {{v^2} - v_0^2} \right) }^2}}},\quad {g_3} = - \frac{{7\sqrt{\frac{7}{3}} {v^6}{b^3}\beta _1^3}}{{48{{\left( {{v^2} - v_0^2} \right) }^3}}}. \end{aligned}$$
(3.32)

Case 4: \(a_3 = a_4 = 0, a_0=\frac{{a_1}^2}{4a_2}\). We have

$$\begin{aligned} {\alpha _0}= & {} 0,\quad {\alpha _1} = 0,\quad {\alpha _2} = 0,{\beta _1} = - \frac{{{\delta ^2}{a_1}v_0^2}}{{2{v^2}b}},\nonumber \\ {\beta _2}= & {} \frac{{{\delta ^4}a_1^2v_0^4}}{{48{v^2}b\left( { - {v^2} + v_0^2} \right) }},\nonumber \\ {a_2}= & {} - \frac{{12\left( { - {v^2} + v_0^2} \right) }}{{{\delta ^2}v_0^2}} \end{aligned}$$
(3.33)

and

$$\begin{aligned} {\alpha _0}= & {} \frac{{2\left( {{v^2} - v_0^2} \right) }}{{{v^2}b}},\quad {\alpha _1} = 0,\quad {\alpha _2} = 0,\quad {\beta _1} = - \frac{{{\delta ^2}{a_1}v_0^2}}{{2{v^2}b}},\nonumber \\ {\beta _2}= & {} - \frac{{{\delta ^4}a_1^2v_0^4}}{{48{v^2}b\left( { - {v^2} + v_0^2} \right) }},\quad {a_2} = \frac{{12\left( { - {v^2} + v_0^2} \right) }}{{{\delta ^2}v_0^2}}.\nonumber \\ \end{aligned}$$
(3.34)

We obtain two exponential type solutions

$$\begin{aligned} V(\xi )= - \frac{{288{\hbox {e}^{\left( {\frac{{2\varepsilon \sqrt{3\left( {{v^2} - v_0^2} \right) } }}{{{v_0}\delta }}} \right) \xi }}{\delta ^2}v_0^2{a_1}{{\left( {{v^2} - v_0^2} \right) }^2}}}{{{v^2}b{{\left( {24{\hbox {e}^{\left( {\frac{{2\varepsilon \sqrt{3\left( {{v^2} - v_0^2} \right) } }}{{{v_0}\delta }}} \right) \xi }}\left( {v_0^2 - {v^2}} \right) + {\delta ^2}v_0^2{a_1}} \right) }^2}}}\nonumber \\ \end{aligned}$$
(3.35)

and

$$\begin{aligned} V(\xi )= & {} \frac{{96\left( {{v^2} - v_0^2} \right) }}{{48{v^2}b}}\nonumber \\&+\, \frac{{{\delta ^4}a_1^2v_0^4}}{{48{v^2}b\left( {{v^2} - v_0^2} \right) {{\left( {{\hbox {e}^{\left( {\frac{{2\varepsilon \sqrt{3\left( {v_0^2 - {v^2}} \right) } }}{{{v_0}\delta }}} \right) \xi }} + \frac{{{\delta ^2}v_0^2{a_1}}}{{24\left( {{v^2} - v_0^2} \right) }}} \right) }^2}}} \nonumber \\&-\,\frac{{{\delta ^2}v_0^2{a_1}}}{{2{v^2}b\left( {{\hbox {e}^{\left( {\frac{{2\varepsilon \sqrt{3\left( {v_0^2 - {v^2}} \right) } }}{{{v_0}\delta }}} \right) \xi }} + \frac{{{\delta ^2}v_0^2{a_1}}}{{24\left( {{v^2} - v_0^2} \right) }}} \right) }}. \end{aligned}$$
(3.36)

Case 5: (i) \(a_0=a_1=0.\) We have

$$\begin{aligned} {\alpha _0}= & {} \frac{{2\left( {{v^2} - v_0^2} \right) }}{{{v^2}b}},\quad {\alpha _1} = 0,\,{\beta _1} = 0,\quad {\beta _2} = 0,\nonumber \\ {a_2}= & {} \frac{{3\left( {1 - \frac{{{v^2}}}{{v_0^2}}} \right) }}{{{\delta ^2}}},\quad {a_3} = 0,{a_4} = - \frac{{{v^2}b{\alpha _2}}}{{{\delta ^2}v_0^2}} \end{aligned}$$
(3.37)

and

$$\begin{aligned} {\alpha _0}= & {} \frac{{2\left( {{v^2} - v_0^2} \right) }}{{{v^2}b}},\quad {\alpha _2} = \frac{{{v^2}b\alpha _1^2}}{{12\left( {{v^2} - v_0^2} \right) }}, \nonumber \\ {\beta _1}= & {} 0,\quad {\beta _2} = 0,\nonumber \\ {a_2}= & {} - \frac{{12\left( {{v^2} - v_0^2} \right) }}{{{\delta ^2}v_0^2}},\nonumber \\ {\alpha _1}= & {} - \frac{{{\delta ^2}v_0^2{a_3}}}{{2{v^2}b}},\quad {a_4} = - \frac{{{v^4}{b^2}\alpha _1^2}}{{12{\delta ^2}v_0^2\left( {{v^2} - v_0^2} \right) }}. \end{aligned}$$
(3.38)

We obtain singular periodic and soliton type solutions

$$\begin{aligned} V(\xi )= & {} \frac{{{v^2} - v_0^2}}{{{v^2}b}}\left( {2 - 3{{\mathrm{csc}}^2}\left[ {\frac{{\sqrt{3\left( {{v^2} - v_0^2} \right) } }}{{\delta {v_0}}}(x - vt)} \right] } \right) ,\nonumber \\ {v^2}> & {} v_0^2, \end{aligned}$$
(3.39)
$$\begin{aligned} V(\xi )= & {} \frac{{{v^2} - v_0^2}}{{{v^2}b}}\left( {2 + 3{{{\mathrm{csch}} }^2}\left[ {\frac{{\sqrt{3\left( {v_0^2 - {v^2}} \right) } }}{{\delta {v_0}}}(x - vt)} \right] } \right) ,\nonumber \\ v_0^2> & {} {v^2} \end{aligned}$$
(3.40)

and

$$\begin{aligned} V(\xi )= & {} \frac{{\left( {{v^2} - v_0^2} \right) }}{{{v^2}b}}\left( 2 + \frac{{3\hbox {sech}{{\left[ {\frac{{\sqrt{3\left( {v_0^2 - {v^2}} \right) } }}{{\delta {v_0}}}\xi } \right] }^4}}}{{{{\left( {1 - \varepsilon \tanh \left[ {\frac{{\sqrt{3\left( {v_0^2 - {v^2}} \right) } }}{{\delta {v_0}}}\xi } \right] } \right) }^2}}}\right. \nonumber \\&\left. -\, \frac{{6\hbox {sech}{{\left[ {\frac{{\sqrt{3\left( {v_0^2 - {v^2}} \right) } }}{{\delta {v_0}}}\xi } \right] }^2}}}{{1 - \varepsilon \tanh \left[ {\frac{{\sqrt{3\left( {v_0^2 - {v^2}} \right) } }}{{\delta {v_0}}}\xi } \right] }} \right) \end{aligned}$$
(3.41)

(ii) \(a_0=a_1=0, a_3=2\varepsilon \sqrt{a_2 a_4}\). We have

$$\begin{aligned} {\alpha _0}= & {} \frac{{2\left( {{v^2} - v_0^2} \right) }}{{{v^2}b}},\quad {\alpha _1} = - \frac{{{\delta ^2}{v_0}^2{a_3}}}{{2{v^2}b}},\nonumber \\ {\alpha _2}= & {} - \frac{{{\delta ^2}{a_4}v_0^2}}{{{v^2}b}},\quad {\beta _1} = 0,{\beta _2} = 0,\nonumber \\ {a_2}= & {} - \frac{{12\left( {{v^2} - v_0^2} \right) }}{{{\delta ^2}v_0^2}},\quad {a_3} = - \frac{{4\sqrt{3{a_4}\left( {v_0^2 - {v^2}} \right) } }}{{\delta {v_0}}}\nonumber \\ \end{aligned}$$
(3.42)

and

$$\begin{aligned} {\alpha _0}= & {} 0,\quad {\alpha _1} = - \frac{{{\delta ^2}{v_0}^2{a_3}}}{{2{v^2}b}},\quad {\alpha _2} = - \frac{{{\delta ^2}{a_4}v_0^2}}{{{v^2}b}},\nonumber \\ {\beta _1}= & {} 0,\quad {\beta _2} = 0,\quad {a_2} = \frac{{12\left( {{v^2} - v_0^2} \right) }}{{{\delta ^2}v_0^2}},\nonumber \\ {a_3}= & {} - \frac{{4\sqrt{3{a_4}\left( {{v^2} - v_0^2} \right) } }}{{\delta {v_0}}}. \end{aligned}$$
(3.43)

We obtain

$$\begin{aligned} V(\xi )= & {} \frac{{\left( {{v^2} - v_0^2} \right) }}{{{v^2}b}}\left( 2 - 6\varepsilon \left( {1 + \tanh \left[ {\frac{{\sqrt{3\left( {v_0^2 - {v^2}} \right) } }}{{{v_0}\delta }}\xi } \right] } \right) \right. \nonumber \\&\left. +\, 3{{\left( {1 + \tanh \left[ {\frac{{\sqrt{3\left( {v_0^2 - {v^2}} \right) } }}{{{v_0}\delta }}\xi } \right] } \right) }^2} \right) \nonumber \\ \end{aligned}$$
(3.44)

and

$$\begin{aligned} V(\xi )= & {} \frac{{3\varepsilon \left( {{v^2} - v_0^2} \right) }}{{{v^2}b}}\left( {1 + \tanh \left[ {\frac{{\sqrt{3\left( {{v^2} - v_0^2} \right) } }}{{{v_0}\delta }}\xi } \right] } \right) \nonumber \\&\times \,\left( {2 - \varepsilon \left( {1 + \tanh \left[ {\frac{{\sqrt{3\left( {{v^2} - v_0^2} \right) } }}{{{v_0}\delta }}\xi } \right] } \right) } \right) .\nonumber \\ \end{aligned}$$
(3.45)

4 Conclusions

In communication engineering, a transmission line is a specialized medium to carry the signals in wave form. It is a very convenient tool to study the propagation of electrical solitons which propagate in the form of voltage waves in nonlinear dispersive media. So, it is important to study the NLTL model analytically and discuss the type of solutions. Thus, the improved extended tanh-function method has been applied successfully to construct the solitary wave solutions, singular periodic solutions, singular soliton solutions, Jacobi elliptic doubly periodic type solutions and Weierstrass elliptic doubly periodic type solutions.