Exact solutions of the Drinfel’d–Sokolov–Wilson equation using Bäcklund transformation of Riccati equation and trial function approach

Abstract

In this paper, two integration schemes are employed to obtain solitons, singular periodic waves and other types of solutions of the Drinfel’d–Sokolov–Wilson equation. The two schemes studied in this paper are the Bäcklund transformation of Riccati equation and the trial function approach. The corresponding constraint conditions of the solutions are also given.

1 Introduction

It is well known that nonlinear evolution equations (NLEEs) are widely used to describe physical phenomena in various scientific and engineering fields, such as fluid mechanics, plasma physics, optical fibres, biology, solid-state physics, etc. In order to understand the mechanisms of those physical phenomena, it is necessary to explore their solutions and properties. Considerable efforts have been made by many mathematicians and physical scientists to obtain exact solutions of such nonlinear evolution equations and a number of powerful and efficient methods, such as trial equation method [1,2], multiple exp-function method [3], extended tanh method [4], $(G^{\prime }/G)$-expansion method [5], transformed rational function method [6,7] etc. have been developed by those scientists. The Drinfel’d–Sokolov–Wilson equation (DSWE) that is to be studied in this paper is given by

$$ \left\{ \begin{array}{l} {u_{t}} + pv{v_{x}} = 0,\\ {v_{t}} + ru{v_{x}} + s{u_{x}}v + q{v_{xxx}} = 0, \end{array} \right. $$

(1)

where p,q,r,s are some nonzero parameters. Equation (1) is originally introduced by Drinfel’d and Sokolov [8] and Wilson [9] as a model of dispersive water waves, and it plays an important role in fluid dynamics [10,11]. Recently, eq. (1) has been studied by several researchers [12–14].

Lu [15] has introduced a reliable and effective method called the Bäcklund transformation method of Riccati equation to look for new exact solutions of nonlinear fractional PDEs. The Bäcklund transformation method of Riccati equation [15] is based on the assumption that exact solutions of NLEEs can be expressed by a polynomial in ψ, such that ψ = ψ(ξ) satisfies the Bäcklund transformation of Riccati equation. In this paper, we employ two integration schemes, the Bäcklund transformation of Riccati equation [15] and the trial function approach [1,2], to obtain explicit expression of solutions of eq. (1).

2 Integration schemes

In this section, we outline the description of the Bäcklund transformation of Riccati equation method and the trial function approach.

2.1 The Bäcklund transformation of Riccati equation

Recall that the Riccati equation

$$ \phi '(\xi ) = \sigma + {\phi^{2}}(\xi ), $$

(2)

has the following exact solutions:

$$ \phi = \left\{ \begin{array}{ll} - \sqrt { - \sigma } \,\tanh\!\left( {\sqrt { - \sigma } \,\xi } \right),&\quad\sigma < 0,\\ - \sqrt { - \sigma } \,\coth\!\left( {\sqrt { - \sigma } \,\xi } \right),&\quad\sigma < 0,\\ \sqrt \sigma \,\tan\!\left( {\sqrt \sigma \,\xi } \right),&\quad\sigma > 0,\\ - \sqrt \sigma \,\cot\!\left( {\sqrt \sigma \,\xi } \right),&\quad\sigma > 0,\\ - \displaystyle\frac{1}{{\xi + \pi }},\,\pi = \text{const}.,&\quad\sigma = 0. \end{array} \right. $$

(3)

Next, let us consider the nonlinear evolution equation (NLEE):

$$ F {\kern-2.25pt} \left( {u,{u_{t}},{u_{x}},{u_{xx}},{u_{xt}},...} \right) = 0, $$

(4)

where u = u(x, t) is an unknown function, F is a polynomial in u and its various partial derivatives u _t ,u _x with respect to t,x respectively, in which the highest-order derivatives and nonlinear terms are involved.

By using the travelling wave transformation

$$ u(x,t) = U(\xi ),\qquad\xi = k(x - c t) , $$

(5)

where k,c are constants to be determined later, we can reduce eq. (4) to a nonlinear ordinary differential equation (NLODE) of the form

$$ P\!\left( {U,U^{\prime},U^{\prime\prime},...} \right) = 0. $$

(6)

Step 1. Suppose that eq. (6) has the following solution:

$$ u(\xi ) = \sum\limits_{l = 0}^{N} {{a_{l}}{\psi^{l}}(\xi ),} $$

(7)

where a _l (l=0,...,N) are constants to be determined and ψ(ξ) comes from the following Bäcklund transformation for the Riccati equation:

$$ \psi (\xi ) = \frac{{ - \sigma B + D\,\phi (\xi )}}{{D + B\,\phi (\xi )}}, $$

(8)

that is ψ(ξ) satisfies the Riccati equation

$$ \psi^{\prime} (\xi )=\sigma +\psi^{2} (\xi ), $$

(9)

where B,D are arbitrary parameters, σ is a constant to be determined and B ≠ 0, ϕ(ξ) are the well-known solutions (3).

Step 2. Balancing the highest-order derivatives and nonlinear term in (6) to determine the positive integer N in (7). Step 3. Substituting the explicit formal solution (7) with (8) into eq. (6) and setting the coefficients of the powers of ϕ(ξ) to be zero, we obtain a system of algebraic equations which can be solved by Maple or Mathematica to get the unknown constants a _l (l=0,...,N), σ, k and c. Consequently, we obtain the exact solutions of eq. (4).

2.2 Trial equation approach

In this subsection we outline the main steps of the trial equation method as follows:

Step 1. Take the trial equation

$$ {\left( {u^{\prime}} \right)^{2}} = F(u) = \sum\limits_{l = 0}^{s} {{a_{l}}{u^{l}},} $$

(10)

where a _l (l=0,1,...,s) are constants to be determined. Substituting eq. (10) and other derivative terms such as $u^{\prime \prime }$ or $u^{\prime \prime \prime }$ and so on into eq. (6) yields a polynomial G(u) of u. According to the balance principle we can determine the value of s. Setting the coefficients of G(u) to zero, we get a system of algebraic equations. Solving this system, we shall determine c,k and values of a ₀,a ₁,...,a _s .

Step 2. Rewrite eq. (10) by the integral form

$$ \pm (\xi - {\xi_{0}}) = \int {\frac{1}{{\sqrt {F(u)} }}\mathrm{d}u.} $$

(11)

According to the complete discrimination system of the polynomial, we classify the roots of F(u), and solve the integral equation (11). Thus, we obtain the exact solutions to eq. (4).

3 The Drinfel’d–Sokolov–Wilson equation

Hirota and Satsuma [16] have proposed a system of coupled KdV equations, describing the interaction of two long waves with different dispersion relations:

$$ \left\{ \begin{array}{l} u_{t}-\frac{1}{2}\!\left( u_{xxx}+6uu_{x}\right)-2bvv_{x}=0,\\ v_{t}+v_{xxx}+3uv_{x}=0, \end{array} \right. $$

(12)

where it was shown that this equation is a special case of the four-reduced Kadomtsev–Petviashvili (KP) hierarchy. Moreover, as has been shown by Wilson, eq. (12) can be obtained within a general construction due to Drinfel’d and Sokolov. In fact, Wilson [9] has shown how this equation can be related to the affine Lie algebra $C^{(1)}_{2}$. Starting from this general Drinfel’d–Sokolov construction, Wilson has also identified another interesting equation that reads as

$$ \left\{ \begin{array}{l} {u_{t}} + 3v{v_{x}} = 0,\\ {v_{t}} + 2u{v_{x}} + {u_{x}}v + 2{v_{xxx}} = 0, \end{array} \right. $$

(13)

and is referred to as the Drinfel’d–Sokolov–Wilson (DSW) equation.

In this section, we employ the Bäcklund transformation of Riccati equation method and the trial function approach to eq. (1). To this end, we use the wave transformation

$$ u(x,t) = U(\xi ),\qquad v(x,t)=V(\xi),\qquad\xi = k(x - ct), $$

(14)

to convert eq. (1) to the following ODEs:

$$ \left\{ \begin{array}{l} - kcU^{\prime} + pkVV^{\prime} = 0,\\ - kcV^{\prime} + rkUV^{\prime} + skU^{\prime}V + q{k^{3}}V^{\prime\prime\prime} = 0. \end{array} \right. $$

(15)

By integrating the first equation in eq. (15), we obtain

$$ U = \frac{p}{{2c}}{V^{2}}. $$

(16)

Substituting (16) into the second equation in eq. (15), we can obtain

$$ - kcV^{\prime} + \frac{{pk}}{{2c}}(r + 2s){V^{2}}V^{\prime} + q{k^{3}}V^{\prime\prime\prime} = 0, $$

(17)

which can be reduced to

$$ - 6{c^{2}}V + p(r + 2s){V^{3}} + 6qc{k^{2}}V^{\prime\prime} = 0, $$

(18)

with zero constant of integration.

3.1 The Bäcklund transformation of Riccati equation method applied to DSW equation

In this subsection, the Bäcklund transformation of the Riccati equation is applied to obtain the exact solutions of the DSW equation.

Balancing $V^{\prime \prime }$ with V ³ in eq. (18), we obtain N=1. Then the solution has the form

$$ V(\xi)=a_{0}+a_{1}\!\!\left( \frac{{ - \sigma\! B + D\!\phi (\xi )}}{{D + B\!\phi (\xi )}} \right). $$

(19)

Substituting (19) along with (2) into (18) and then setting the coefficients of ϕ(ξ) to be zero, we can obtain a set of algebraic equations which can be solved by Mathematica to get the following solution:

$$ {a_{0}} = 0,\qquad\sigma = \frac{c}{{2{k^{2}}q}},\qquad{a_{1}} = \pm k\sqrt {-\frac{{ 12cq}}{{p(r + 2s)}}} \,, $$

(20)

where c,k are arbitrary real constants. The solution of eq. (1) corresponding to eq. (20) has the following cases:

If c q < 0, we obtain

$$ {u_{1}}(x,t ) = \frac{{6c}}{{r + 2s}}{\left( {\frac{{\sqrt {\frac{{ - c}}{{2q{k^{2}}}}} \,B - D\,\tanh\! \left( {\sqrt {\frac{{ - c}}{{2q{k^{2}}}}} \,\left( k(x - ct)\right) } \right)}}{{D - \sqrt {\frac{{ - c}}{{2q{k^{2}}}}} \,B\,\tanh\! \left( {\sqrt {\frac{{ - c}}{{2q{k^{2}}}}} \,\left( k(x - ct)\right) } \right)\,}}} \right)^{2}}, $$

(21)

$$ {v_{1}}(x,t ) = \pm \sqrt {\frac{{12{c^{2}}}}{{p(r + 2s)}}} \left( {\frac{{\sqrt {\frac{{ - c}}{{2q{k^{2}}}}} \,B - D\,\tanh \!\left( {\sqrt {\frac{{ - c}}{{2q{k^{2}}}}} \,\left( k(x - ct)\right) } \right)}}{{D - \sqrt {\frac{{ - c}}{{2q{k^{2}}}}} \,B\,\tanh \!\left( {\sqrt {\frac{{ - c}}{{2q{k^{2}}}}} \,\left( k(x - ct)\right) } \right)\,}}} \right) $$

(22)

or

$$ {u_{2}}(x,t ) = \frac{{6c}}{{r + 2s}}{\left( {\frac{{\sqrt {\frac{{ - c}}{{2q{k^{2}}}}} \,B - D\,\coth \!\left( {\sqrt {\frac{{ - c}}{{2q{k^{2}}}}} \,\left( k(x - ct)\right) } \right)}}{{D - \sqrt {\frac{{ - c}}{{2q{k^{2}}}}} \,B\,\coth\! \left( {\sqrt {\frac{{ - c}}{{2q{k^{2}}}}} \,\left( k(x - ct)\right) } \right)\,}}} \right)^{2}}, $$

(23)

$$ {v_{2}}(x,t ) = \pm \sqrt {\frac{{12{c^{2}}}}{{p(r + 2s)}}} \left( {\frac{{\sqrt {\frac{{ - c}}{{2q{k^{2}}}}} \,B - D\,\coth \!\left( {\sqrt {\frac{{ - c}}{{2q{k^{2}}}}} \,\left( k(x - ct)\right) } \right)}}{{D - \sqrt {\frac{{ - c}}{{2q{k^{2}}}}} \,B\,\coth \!\left( {\sqrt {\frac{{ - c}}{{2q{k^{2}}}}} \,\left( k(x - ct)\right) } \right)\,}}} \right). $$

(24)

If c q > 0, we obtain

$$ {u_{3}}(x,t ) = \frac{{ - 6c}}{{r + 2s}}{\left( {\frac{{ - \sqrt {\frac{c}{{2q{k^{2}}}}} \,B + D\,\tan \!\left( {\sqrt {\frac{c}{{2q{k^{2}}}}} \,\left( k(x - ct)\right) } \right)}}{{D + \sqrt {\frac{c}{{2q{k^{2}}}}} \,B\,\tan \!\left( {\sqrt {\frac{c}{{2q{k^{2}}}}} \,\left( k(x - ct)\right) } \right)\,}}} \right)^{2}}, $$

(25)

$$ {v_{3}}(x,t ) = \pm \sqrt {\frac{{ - 12{c^{2}}}}{{p(r + 2s)}}} \left( {\frac{{ - \sqrt {\frac{c}{{2q{k^{2}}}}} \,B + D\,\tan \!\left( {\sqrt {\frac{c}{{2q{k^{2}}}}} \,\left( k(x - ct)\right) } \right)}}{{D + \sqrt {\frac{c}{{2q{k^{2}}}}} \,B\,\tan\! \left( {\sqrt {\frac{c}{{2q{k^{2}}}}} \,\left( k(x - ct)\right) } \right)\,}}} \right)\, $$

(26)

or

$$ {u_{4}}(x,t ) = \frac{{ - 6c}}{{r + 2s}}{\left( {\frac{{\sqrt {\frac{c}{{2q{k^{2}}}}} \,B + D\,\cot \!\left( {\sqrt {\frac{c}{{2q{k^{2}}}}} \,\left( k(x - ct)\right) } \right)}}{{ - D + \sqrt {\frac{c}{{2q{k^{2}}}}} \,B\,\cot\! \left( {\sqrt {\frac{c}{{2q{k^{2}}}}} \,\left( k(x - ct)\right) } \right)\,}}} \right)^{2}}, $$

(27)

$$ {v_{4}}(x,t ) = \pm \sqrt {\frac{{ - 12{c^{2}}}}{{p(r + 2s)}}} \left( {\frac{{\sqrt {\frac{c}{{2q{k^{2}}}}} \,B + D\,\cot\! \left( {\sqrt {\frac{c}{{2q{k^{2}}}}} \,\left( k(x - ct)\right) } \right)}}{{ - D + \sqrt {\frac{c}{{2q{k^{2}}}}} \,B\,\cot \!\left( {\sqrt {\frac{c}{{2q{k^{2}}}}} \,\left( k(x - ct)\right) } \right)\,}}} \right). $$

(28)

These solutions are being reported here for the first time because B ≠ 0.

3.2 The trial equation method applied to the DSW equation

The trial equation method is applied to obtain exact solutions of the DSW equation. Balancing $V^{\prime \prime }$ with V ³ in eq. (18), we get s=4. Using the solution procedure of the trial equation method, we obtain the system of algebraic equations as follows:

$$ 3cqk^{2}a_{1}=0, $$

(29)

$$ 6c(qk^{2}a_{2}-c) =0, $$

(30)

$$ 9cqk^{2}a_{3}=0, $$

(31)

$$ 12cqk^{2}a_{4}+p(r+2s)=0. $$

(32)

Solving the above system of algebraic equations, we obtain the following results:

$$ a_{1}= 0, \qquad a_{2}=\frac{c}{qk^{2}}, \qquad a_{3}= 0, \qquad a_{4}= -\frac{p(r+2s)}{12cqk^{2}}. $$

(33)

Substituting these results into eqs (10) and (11), we get

$$ \pm (\xi - {\xi_{0}}) = \int {\frac{1}{{\sqrt {a_{0}+\frac{c}{qk^{2}} V^{2}-\frac{p(r+2s)}{12cqk^{2}} V^{4}} }}\mathrm{d} V}, $$

(34)

where a ₀ is an arbitrary real constant. Now, we discuss two cases as follows:

Case 1. If we set a ₀=0 in eq. (34) and integrating with respect to V, we get the following exact solution of eq. (1):

If c q > 0, we obtain

$$ {u_{1}}(x,t ) = \frac{6c}{r + 2s} {\text{sech}^{2}}\!\! \left( {\sqrt {\frac{c}{{q{k^{2}}}}} \,(k(x - ct) - {\xi_{0}})} \right), $$

(35)

$$ {v_{1}}(x,t ) = \pm \sqrt {\frac{{12{c^{2}}}}{{p(r + 2s)}}} \, {\text{sech}}\!\!\left( {\sqrt {\frac{c}{{q{k^{2}}}}} \,(k(x - ct)- {\xi_{0}})} \right) $$

(36)

or

$$ {u_{2}}(x,t ) = \frac{{-6c}}{{r + 2s}} {\text{csch}^{2}}\!\!\left( {\sqrt {\frac{c}{{q{k^{2}}}}} \,(k(x - ct) - {\xi_{0}})} \right), $$

(37)

$$ {v_{2}}(x,t ) = \pm \sqrt {\frac{{-12{c^{2}}}}{{p(r + 2s)}}} \, {\text{csch}}\!\!\left( {\sqrt {\frac{c}{{q{k^{2}}}}} \,(k(x - ct) - {\xi_{0}})} \right). $$

(38)

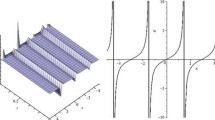
Solutions (35) and (36) are solitary wave solutions and solutions (37) and (38) are singular solitary wave solutions.

If c q < 0, we obtain

$$ {u_{3}}(x,t ) = \frac{{6c}}{{r + 2s}}\sec^{2}{}\left( {\sqrt {\frac{-c}{{q{k^{2}}}}} \,(k(x - ct) - {\xi_{0}})} \right), $$

(39)

$$ {v_{3}}(x,t ) = \pm \sqrt {\frac{{12{c^{2}}}}{{p(r + 2s)}}} \,\sec{}\left( {\sqrt {\frac{-c}{{q{k^{2}}}}} \,(k(x - ct) - {\xi_{0}})} \right) $$

(40)

or

$$ {u_{4}}(x,t ) = \frac{{-6c}}{{r + 2s}}\csc^{2}{}\left( {\sqrt {\frac{-c}{{q{k^{2}}}}} \,(k(x - ct) - {\xi_{0}})} \right), $$

(41)

$$ {v_{4}}(x,t ) = \mp \sqrt {\frac{{12{c^{2}}}}{{p(r + 2s)}}} \,\csc{}\left( {\sqrt {\frac{-c}{{q{k^{2}}}}} \,(k(x - ct) - {\xi_{0}})} \right). $$

(42)

These solutions are singular periodic wave solutions.

Case 2. If we set a ₀=−3c ³/(p q k ²(r+2s)) in eq. (34) and integrating with respect to V, we get the following exact solution of eq. (1):

If c q < 0, we obtain

$$ {u_{5}}(x,t ) = \frac{{6c}}{{r + 2s}}\tanh^{2}{}\left( {\sqrt {\frac{{ - c}}{{2q{k^{2}}}}} \,(k(x - ct) - {\xi_{0}})} \right), $$

(43)

$$ {v_{5}}(x,t ) = \pm \sqrt {\frac{{12{c^{2}}}}{{p(r + 2s)}}} \,\tanh{}\left( {\sqrt {\frac{{ - c}}{{2q{k^{2}}}}} \,(k(x - ct) - {\xi_{0}})} \right) $$

(44)

or

$$ {u_{6}}(x,t ) = \frac{{6c}}{{r + 2s}}\coth^{2}\left( {\sqrt {\frac{{ - c}}{{2q{k^{2}}}}} \,(k(x - ct) - {\xi_{0}})} \right), $$

(45)

$$ {v_{6}}(x,t ) = \pm \sqrt {\frac{{12{c^{2}}}}{{p(r + 2s)}}} \,\coth\left( {\sqrt {\frac{{ - c}}{{2q{k^{2}}}}} \,(k(x - ct) - {\xi_{0}})} \right). $$

(46)

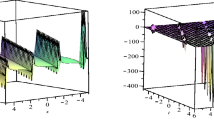
Solutions (43) and (44) are shock wave solutions and (45) and (46) are singular soliton solutions.

If c q > 0, we obtain

$$ {u_{7}}(x,t ) = \frac{{-6c}}{{r + 2s}}\tan^{2}{}\left( {\sqrt {\frac{{ - c}}{{2q{k^{2}}}}} \,(k(x - ct) - {\xi_{0}})} \right), $$

(47)

$$ {v_{7}}(x,t ) = \pm \sqrt {\frac{{-12{c^{2}}}}{{p(r + 2s)}}} \,\tan{}\left( {\sqrt {\frac{{ - c}}{{2q{k^{2}}}}} \,(k(x - ct) - {\xi_{0}})} \right) $$

(48)

or

$$ {u_{8}}(x,t ) = \frac{{-6c}}{{r + 2s}}\cot^{2}{}\left( {\sqrt {\frac{{ - c}}{{2q{k^{2}}}}} \,(k(x - ct) - {\xi_{0}})} \right), $$

(49)

$$ {v_{8}}(x,t ) = \mp \sqrt {\frac{{-12{c^{2}}}}{{p(r + 2s)}}} \,\cot{}\left( {\sqrt {\frac{{ - c}}{{2q{k^{2}}}}} \,(k(x - ct) - {\xi_{0}})} \right). $$

(50)

These solutions are singular periodic wave solutions.

The solutions (37), (38), (41) and (42) obtained by using the trial solution approach are not reported in [12–14] using the direct algebraic method and the exp-function method.

4 Conclusions

Many powerful methods are used in solitary wave theory to examine exact soliton solutions for NLEEs [1–16]. In this paper, we studied the new application of the Bäcklund transformation of Riccati equation [15] and the trial function approach [1,2] to derive new solitary wave solutions, singular periodic solutions and other types of solutions of the Drinfel’d–Sokolov–Wilson equation. These methods are not only efficient, but also have the merit of being widely applicable. The results show that the proposed methods are direct, effective and can be applied to many other NLEEs in mathematical physics.