1 Introduction

It is well known that ecosystems are characterized by interactions between different species, and between species and natural environment. And predator–prey model is one of the important models in ecosystems. Since the pioneering works of Lotka [1] and Volterra [2], predator–prey model describing the dynamical interaction between two species have long been and will continue to be one of the dominant themes in both ecology and mathematics. We know that functional response function that reflects predator–prey interaction relationships is a crucial component of predator–prey model. In order to describe the features of the predator–prey interaction, many types of usual functional response functions, such as Holling I–IV types, ratio-dependent type, Hassell–Varley type, Beddington–DeAngelis type, Crowley–Martin type and the ones with Allee effect [3–6], have been proposed and investigated widely.

In natural ecosystems, many living beings live forming herds and all members of a group do not interact at a time. There are many reasons for this herd behavior, such as searching for food resources, defending the predators. As for modelling group defense mathematically, the first being Freedman and Wolkowicz [7]. Different functional responses as a result of prey–predator forming groups have been considered. The most common and among the simplest method of incorporating group defense in a predator–prey model is by using Holling type IV functional responses [8]. However, Holling type IV functional response will become negatively sloped when the prey densities are large, which is a consequence of group defense. And we note that Holling type IV functional responses usually result in an upper threshold of prey density, beyond which the predator cannot survive. This implies that choosing Holling type IV functional responses to model group defense is a strong group defense. Of course, there are other ways of modelling group defense. More recently, in [9], a new predator–prey interaction has been studied for a more elaborated social model, in which the individuals of one population in the large herbivores populating the savannas gather together in huge herds, with generally the strongest individuals on the border and the weakest being concentrated in the middle of the bunch, while the other one shows a more individualistic behavior. This leads to the consequence that the capture of a prey by a successful predator attack occurs mainly on the boundary, involving therefore mostly the individuals that occupy the outermost positions in the herd. Let u be the density of a population that gathers in herds, and suppose that herd occupies an area A. The number of individuals staying at outermost positions in the herd is proportional to the length of the perimeter of the patch, where the herd is located. Obviously, its length is proportional to \(\sqrt{A}\). Since u is distributed over a two-dimensional domain, \(\sqrt{u}\) would therefore count the individuals at the edge of the patch. Thus, when attack of a predator on this population is to be modelled, the functional response should be in terms of square root of prey population. So, based on the above facts, the authors in [9] have proposed a new predator–prey model described by the following ordinary differential equations

$$\begin{aligned} \left\{ \begin{array}{lll} \frac{\mathrm{d}u}{\mathrm{d}t}=u(1-u)-\sqrt{u}v,\\ \frac{\mathrm{d}v}{\mathrm{d}t}=\gamma v(-\beta +\sqrt{u}), \end{array}\right. \end{aligned}$$
(1)

where u(t) and v(t) stand for the prey and predator densities, respectively, at time t. \(\beta \gamma \) is the death rate of the predator in the absence of prey; \(\gamma \) is the conversion or consumption rate of prey to predator. This model is also known as the predator–prey model with herb behavior and has been shown that the sustained limit cycles are possible and the solution behavior near the origin is more subtle and interesting than the classical predator–prey models [9, 10].

In the real world, the predator and the prey may move for many reasons, such as currents and turbulent diffusion. So, we should consider the spatial disperse associated with model (1). In [11], the authors mainly focused on the delay effect on the reaction–diffusion system corresponding to model (1) and investigated the stability/instability of the coexistence equilibrium and associated Hopf bifurcation, the instability of the Hopf bifurcation induced by diffusion and delay, respectively, which can lead to the emergence of spatial patterns.

Apart from the instability of Hopf bifurcation, we know the diffusion-driven instability. In 1952, Turing [12] derived the conditions under which the spatially uniform equilibrium solution is stable in the absence of diffusion but becomes unstable in the presence of diffusion. The diffusion-driven instability of the equilibrium leads to a spatially inhomogeneous distribution of species concentration, which is the so-called Turing instability. Although Turing instability was first investigated in a morphogenesis, it has quickly spread to ecological systems [3, 4, 6, 13–24], chemical reaction system [25–30] and other reaction–diffusion system [31–38]. From [39], we know that the phenomenon of spatial pattern formation in (1) with diffusion can not occur under all possible diffusion rates. So, the authors in [39, 40] change linear mortality sv into quadratic mortality \({ sv}^{2}\) in (1) with diffusion and have investigated Turing patterns, stability, Turing instability and Hopf bifurcations; for the same reason, authors of [4, 19] investigated the Turing instability of a predator–prey model with hyperbolic mortality rate.

Self-organized patterning in reaction–diffusion system driven by self-diffusion has been extensively studied since the seminal paper of Turing [12]. Nevertheless, in many experimental cases, the gradient of the density of one species induces a flux of another species or of the species itself, and therefore, cross-diffusion effects should be taken into account [41–43]. Recently, cross-diffusion terms have appeared to model different physical phenomena in diverse contexts like population dynamics and ecology [44–49] and chemical reactions [29, 30, 50–52]. But, as far as we know, the work on the rich dynamics deduced by the Turing–Hopf bifurcation in predator–prey type reaction–diffusion systems [53–55] near the bifurcation point was all reported numerically, except paper [56, 57]. In [56, 57], the authors have discussed the classification of the spatiotemporal dynamics in a neighborhood of the bifurcation point in detail, which can be figured out in the framework of the normal forms.

However, to the best of our knowledge, there are no results on spatiotemporal dynamics near Turing–Hopf bifurcation point of reaction–diffusion systems with cross-diffusion. So, motivated by the above works, we can now focus on the following predator–prey model with herd behavior and cross-diffusion:

$$\begin{aligned} \left\{ \begin{array}{ll} \frac{\partial u}{\partial t}{=}u(1{-}u){-}\sqrt{u}v{+}d_{11}\Delta u{+}d_{12}\Delta v,&{}\quad x\in \Omega ,\,t{>}0,\\ \frac{\partial v}{\partial t}{=}\gamma v({-}\beta {+}\sqrt{u}){+}d_{21}\Delta u+d_{22}\Delta v,&{}\quad x\in \Omega ,\,t{>}0,\\ \frac{\partial u}{\partial \mathbf n }{=}\frac{\partial v}{\partial \mathbf n }{=}0,&{}\quad x\in \partial \Omega ,\,t{>}0,\\ u(x,0){=}\phi (x)\ge 0,\,\,v(x,0){=}\psi (x)\ge 0,&{}\quad x\in \Omega , \end{array}\right. \nonumber \\ \end{aligned}$$
(2)

where \(\Delta u\) is a m-dimensional Laplace operator: \(\Delta u=u_{x_{1}x_{1}}+u_{x_{2}x_{2}}+\cdots +u_{x_{m}x_{m}}, {\Omega }\) is a bounded domain in \(\mathbb {R}^{m}, m\ge 1, \mathbf n \) is the outward unit normal vector of the boundary of \(\partial \Omega \) which we will assume is smooth. The nonnegative constants \(d_{11}\) and \(d_{22}\) are the diffusion coefficients of prey and predator, respectively, and \(d_{12}\) and \(d_{21}\), called cross-diffusion coefficients, describe the respective population fluxes of preys and predators resulting from the presence of the other species, respectively. In [58], we have investigated the cross-diffusion-induced spatiotemporal patterns of model (2) in the Turing region only. Based on the paper [58], we shall continue to explore the other dynamics of model (2) such as the existence and priori bound of a solution for the model without cross-diffusion, and complex spatiotemporal dynamics near the Turing–Hopf bifurcation point of the model with cross-diffusion in the framework of normal form, which are different from the results in [58]; for instance, the stable spatially inhomogeneous periodic solutions are found. Here, we have to point out the fact that, although the method of computing the normal form in this paper is motivated by the one in [56, 57], because of the existence of cross-diffusion, the procedure of computing normal form in this paper need be deduced again. This implies that our results generalize the application scope of references [56, 57].

The rest of the paper is organized as follows. In Sect. 2, we show the existence and priori bound of a solution for the model (2) without cross-diffusion. In Sect. 3, we investigate the existence of Turing–Hopf bifurcation firstly. Then, by computing and analyzing normal form on the center manifold-associated Turing–Hopf bifurcation, we study the complex spatiotemporal dynamics near the Turing–Hopf bifurcation point of the model (2), which are presented by numerical simulations. Finally, conclusions and discussions are presented in Sect. 4.

2 The existence and priori bound of solution for model (2) without cross-diffusion

In this section, we give out a sufficient condition for the existence of a positive solution of system (2) without cross-diffusion. Meanwhile, we derive a priori bound of the solution.

When \(d_{12}=d_{21}=0\), system (2) becomes

$$\begin{aligned} \left\{ \begin{array}{ll} \frac{\partial u}{\partial t}=u(1-u)-\sqrt{u}v+d_{11}\Delta u,&{}\quad x\in \Omega ,\; t>0,\\ \frac{\partial v}{\partial t}=\gamma v(-\beta +\sqrt{u})+d_{22}\Delta v,&{}\quad x\in \Omega ,\; t>0,\\ \frac{\partial u}{\partial \mathbf n }{=}\frac{\partial v}{\partial \mathbf n }{=}0,&{}\quad x\in \partial \Omega ,\; t>0,\\ u(x,0){=}\phi (x)\ge 0,\,v(x,0){=}\psi (x)\ge 0,&{}\quad x\in \Omega , \end{array}\right. \nonumber \\ \end{aligned}$$
(3)

It is easy to check that systems (1), (2) and (3) have all the same uniform equilibria: two boundary equilibria (0, 0) and (1, 0) and a unique positive equilibrium \((u^{*},v^{*})\) (\(0<\beta <1\)), where

$$\begin{aligned} u^{*}=\beta ^{2},\quad v^{*}=\beta (1-\beta ^{2}). \end{aligned}$$

Theorem 1

Suppose that \(0<\beta <1,\gamma >0\) and \(\Omega \subset \mathbb {R}^{m}\) is a bounded domain with smooth boundary. Then

  1. (i)

    for \(\phi (x)\ge 0, \psi (x)\ge 0\) and \(\phi (x)\not \equiv 0, \psi (x)\not \equiv 0\), system (3) has a unique solution (u(x, t), v(x, t)) satisfying

    $$\begin{aligned}&0<u(x, t)\le u^{*}(t),\quad 0<v(x, t)\le v^{*}(t)\\&\quad \mathrm{for}\;\;t>0\quad \mathrm{and}\;\;x\in \Omega , \end{aligned}$$

    where \((u^{*}(t), v^{*}(t))\) is the unique solution of

    $$\begin{aligned} \left\{ \begin{array}{ll} \frac{\mathrm{d}u}{\mathrm{d}t}=u(1-u),&{}\\ \frac{\mathrm{d}v}{\mathrm{d}t}=\gamma v(-\beta +\sqrt{u}),&{}\\ u(0){=}\phi ^{*}{=}\sup \nolimits _{x\in \overline{\Omega }}\phi (x),&{} v(0){=}\psi ^{*}{=}\sup \nolimits _{x\in \overline{\Omega }}\psi (x); \end{array}\right. \nonumber \\ \end{aligned}$$
    (4)
  2. (ii)

    for any solution (u(x, t), v(x, t)) of system (3), we have

    $$\begin{aligned}&\limsup \limits _{t\rightarrow \infty }u(x,t)=1,\quad \limsup \limits _{t\rightarrow \infty }\frac{1}{|\Omega |}\\&\times \int _{\Omega }v(x, t)\mathrm{d}x\le \frac{1+\beta \gamma }{\beta }. \end{aligned}$$

Moreover, when \(d_{11}=d_{22}\), one can obtain \( \limsup \nolimits _{t\rightarrow \infty }v(x,t)\le \frac{1+\beta \gamma }{\beta }, \forall x\in \overline{\Omega }\).

Proof

Let

$$\begin{aligned} f(u, v)=u(1-u)-\sqrt{u}v,\quad g(u, v)=\gamma v(-\beta +\sqrt{u}). \end{aligned}$$

Then we have \(f_{v}\le 0\) and \(g_{u}\ge 0\) for \((u, v)\in \mathbb {R}^{2}_{+}=\{(u, v)|u\ge 0,~v\ge 0\}\) and from [59, 60] system (3) is a mixed quasi-monotone system. Let

$$\begin{aligned} (u_{1}(x, t), v_{1}(x, t))= & {} (0, 0)\quad \hbox { and }\;\;(u_{2}(x, t), v_{2}(x, t))\\= & {} (u^{*}(t), v^{*}(t)). \end{aligned}$$

Since

$$\begin{aligned}&\frac{\partial u_{2}}{\partial t}-d_{11}\Delta u_{2}-f(u_{2}, v_{1})=0\ge 0\\&\quad =\frac{\partial u_{1}}{\partial t}-d_{11}\Delta u_{1}-f(u_{1}, v_{2}),\\&\frac{\partial v_{2}}{\partial t}-d_{22}\Delta v_{2}-g(u_{2}, v_{2})=0\ge 0\\&\quad =\frac{\partial v_{1}}{\partial t}-d_{11}\Delta v_{1}-g(u_{1}, v_{1}) \end{aligned}$$

and \( 0\le \phi (x)\le \phi ^{*},\,0\le \psi (x)\le \psi ^{*}, (u_{1}(x, t), v_{1}(x, t))\) and \((u_{2}(x, t), v_{2}(x, t))\) are the lower and upper solutions of system (3), respectively. From Theorem 8.3.3 in [59] or Theorem 5.3.3 in [60], we know that (3) has a unique globally defined solution (u(x, t), v(x, t)) which satisfies

$$\begin{aligned} 0\le u(x, t)\le u^{*}(t),\quad 0\le v(x, t)\le v^{*}(t),\quad t>0. \end{aligned}$$

The strong maximum principle implies that \(u(x, t)>0, v(x, t)>0\) when \(t>0,\) for \(x\in \Omega .\) This completes the proof of (i).

From the above discussion, we know that \(u(x, t)\le u^{*}(t), v(x, t)\le v^{*}(t)\) for all \(t>0\), and \(u^{*}(t)\) is the unique solution of

$$\begin{aligned} \frac{\mathrm{d}u}{\mathrm{d}t}=u(1-u),\quad u(0)=\phi ^{*}>0. \end{aligned}$$

One can see that \(u^{*}(t)\rightarrow 1\) as \(t\rightarrow \infty \). Thus for any \(\varepsilon >0\), there exists \(T_{0}>0\) such that

$$\begin{aligned} u(x, t)\le 1+\varepsilon ,\quad \mathrm{for}\quad t>T_{0},~x\in \overline{\Omega }, \end{aligned}$$

which implies that

$$\begin{aligned} \limsup \limits _{t\rightarrow \infty }u(x, t)=1. \end{aligned}$$

Let

$$\begin{aligned}&r(t)=\int _{\Omega }u(x, t)\mathrm{d}x,\quad s(t)=\int _{\Omega }v(x, t)\mathrm{d}x,\\&w(t)=\gamma r(t)+s(t). \end{aligned}$$

Then

$$\begin{aligned} \frac{\mathrm{d}r}{\mathrm{d}t}= & {} \int _{\Omega }d_{11}\Delta u\mathrm{d}x+\int _{\Omega } \left[ u(1-u)-\sqrt{u}v\right] \mathrm{d}x, \\ \frac{\mathrm{d}s}{\mathrm{d}t}= & {} \int _{\Omega }d_{22}\Delta v\mathrm{d}x+\int _{\Omega }\left[ \gamma v(-\beta +\sqrt{u})\right] \mathrm{d}x. \end{aligned}$$

By virtue of the Neumann boundary condition, we can get

$$\begin{aligned} \frac{\mathrm{d}w}{\mathrm{d}t}= & {} \gamma \frac{\mathrm{d}r}{\mathrm{d}t}+\frac{\mathrm{d}s}{\mathrm{d}t}\\= & {} -\beta \gamma s+\gamma \int _{\Omega }u(1-u)\mathrm{d}x\\= & {} -\beta \gamma (\gamma r+s)+\beta \gamma ^{2}r+\gamma \int _{\Omega }u(1-u)\mathrm{d}x\\\le & {} -\beta \gamma w+\gamma (\beta \gamma +1)r. \end{aligned}$$

From

$$\begin{aligned} \limsup \limits _{t\rightarrow \infty }u(x, t)\le 1, \end{aligned}$$

we have

$$\begin{aligned} \limsup \limits _{t\rightarrow \infty }r(t)\le |\Omega |. \end{aligned}$$

Thus for small \(\varepsilon >0,\) there exists \(T_{1}>0\) such that

$$\begin{aligned} \frac{\mathrm{d}w}{\mathrm{d}t}\le -\beta \gamma w+\gamma (\beta \gamma +1)|\Omega |,\quad t>T_{1}. \end{aligned}$$
(5)

It is well known that the solution w(t) of

$$\begin{aligned} \frac{\mathrm{d}w}{\mathrm{d}t}=-\beta \gamma w+\gamma (\beta \gamma +1)(1+\varepsilon )|\Omega | \end{aligned}$$

satisfies

$$\begin{aligned} \lim \limits _{t\rightarrow \infty }w(t)=\frac{\beta \gamma +1}{\beta } (1+\varepsilon )|\Omega |. \end{aligned}$$

In terms of comparison principle and using (5), we obtain that, for \(T_{2}>T_{1}\),

$$\begin{aligned} \int _{\Omega }v(x,t)\mathrm{d}x= & {} s(t)<w(t)\\&\le \frac{\beta \gamma +1}{\beta }(1+\varepsilon )|\Omega |+\varepsilon ,\;\; t>T_{2}, \end{aligned}$$

which implies that

$$\begin{aligned} \limsup \limits _{t\rightarrow \infty }\int _{\Omega }v(x, t)\mathrm{d}x\le \frac{1+\beta \gamma }{\beta }|\Omega |. \end{aligned}$$

Let

$$\begin{aligned} W(x, t)=\gamma u(x, t)+v(x, t). \end{aligned}$$

If \(d_{11}=d_{22}=d\), from system (3) it follows that

$$\begin{aligned} \left\{ \begin{array}{ll} \frac{\mathrm{d}W}{\mathrm{d}t}=\mathrm{d}\Delta W+\gamma u(1-u)-\beta \gamma v,&{}\quad x\in \Omega ,\, t>T_{0},\\ \frac{\partial W}{\partial \mathbf n }=0,&{}\quad x\in \partial \Omega ,\; t>T_{0},\\ W(x, T_{0})=u(x, T_{0})+v(x, T_{0}),&{}\quad x\in \Omega . \end{array}\right. \nonumber \\ \end{aligned}$$
(6)

From the previous proof, we also have \(u(x, t)\le 1+\varepsilon \), for \(t>T_{0}\). Then, using similar to the above methods and (6), we can obtain that

$$\begin{aligned} \limsup \limits _{t\rightarrow \infty }v(x, t)\le \frac{1+\beta \gamma }{\beta }. \end{aligned}$$

This completes the proof.

3 The dynamics induced by Turing–Hopf bifurcation and numerical simulations

In this section, we shall analyze the dynamics near the Turing–Hopf bifurcation point of the model (2) by computing the normal form on the center manifold. In the rest of this paper, we will assume, unless we state explicitly otherwise, that \(\Omega =(0, \pi ), \Delta u\) is a one-dimensional Laplace operator: \(\Delta u=u_{xx}.\) And for the Newmann boundary condition, define the real-valued Sobolev space

$$\begin{aligned} X= & {} \left\{ (u, v)^\mathrm{T}\in \left( W^{2,2}(0, \pi )\right) ^2,\right. \\&\left. \frac{\partial u}{\partial x}=\frac{\partial v}{\partial x}=0\,~\text{ at }\,x=0, \pi \right\} , \end{aligned}$$

and for \(U_1=(u_1, v_1)^\mathrm{T}, U_2=(u_2, v_2)^\mathrm{T}\in X,\) define the inner product

$$\begin{aligned} \left[ U_1, U_2\right] =\int _0^\pi \left( u_1u_2+v_1v_2\right) \mathrm{d}x \end{aligned}$$

such that X becomes a Hilbert space.

3.1 Existence of Turing–Hopf bifurcation

In this subsection, we show the existence of Turing–Hopf bifurcation. From Sect. 2, we know that the only positive equilibrium of system (2) is \((u^{*}, v^{*})=(\beta ^{2}, \beta (1-\beta ^{2}))(0<\beta <1)\). Thus, the linearization of system (2) at positive equilibrium \((u^{*}, v^{*})\) is as follows:

$$\begin{aligned} \begin{array}{lll} \left( \begin{array}{ccc} \frac{\partial u}{\partial t} \\ \frac{\partial v}{\partial t} \end{array}\right) =\mathrm{d}\Delta \left( \begin{array}{ccc} u \\ v \end{array}\right) +A\left( \begin{array}{ccc} u \\ v \end{array}\right) , \end{array} \end{aligned}$$
(7)

with

$$\begin{aligned} \mathrm{d}\Delta= & {} \left( \begin{array}{ccc} d_{11}\frac{\partial ^{2}}{\partial x^{2}}&{}d_{12}\frac{\partial ^{2}}{\partial x^{2}} \\ d_{21}\frac{\partial ^{2}}{\partial x^{2}}&{}d_{22}\frac{\partial ^{2}}{\partial x^{2}} \end{array}\right) ,\\ A= & {} \left( \begin{array}{ccc} a_{11}&{}a_{12} \\ a_{21}&{}a_{22} \end{array}\right) =\left( \begin{array}{ccc} \frac{1}{2}(1-3\beta ^{2})&{}-\beta \\ \frac{1}{2}\gamma (1-\beta ^{2})&{}0 \end{array}\right) . \end{aligned}$$

It is well known that the eigenvalue problem

$$\begin{aligned} -\eta ''=\mu \eta ,\quad x\in (0, \pi );\quad \eta '(0)=\eta '(\pi )=0 \end{aligned}$$

has eigenvalues \(\mu _{k}=k^{2} (k=0, 1,\ldots )\), with corresponding normalized eigenfunctions \(\eta _{k}(x)=\frac{\cos kx}{||\cos kx||_{2, 2}}\). Let

$$\begin{aligned} \left( \begin{array}{ccc} \phi \\ \psi \end{array}\right) =\sum \limits _{k=0}^\infty \left( \begin{array}{ccc} a_{_{k}} \\ b_{k} \end{array} \right) \eta _{k}(x) \end{aligned}$$

be an eigenfunction of \(\mathrm{d}\Delta +A\) corresponding to an eigenvalue \(\sigma \), that is

$$\begin{aligned} (\mathrm{d}\Delta +A)(\phi , \psi )^{\mathrm{T}}=\sigma (\phi , \psi )^{\mathrm{T}}. \end{aligned}$$

Then, we have

$$\begin{aligned} \mathscr {Q}_{k}\left( \begin{array}{ccc} a_{_{k}} \\ b_{k} \end{array} \right) =\sigma \left( \begin{array}{ccc} a_{_{k}} \\ b_{k} \end{array} \right) ,\quad k=0, 1, \ldots , \end{aligned}$$

where

$$\begin{aligned} \mathscr {Q}_{k}=\left( \begin{array}{ccc} a_{11}-d_{11}k^{2}&{}a_{12}-d_{12}k^{2} \\ a_{21}-d_{21}k^{2}&{}a_{22}-d_{22}k^{2} \end{array}\right) , \end{aligned}$$

which follows that the eigenvalues of \(\mathrm{d}\Delta +A\) are given by the eigenvalues of \(\mathscr {Q}_{k},~k=0, 1, \ldots .\) We know that the linear stability of the positive equilibrium \((u^{*}, v^{*})\) can be analyzed by introducing a small inhomogeneous perturbation to the system (7) at the zero equilibrium. So, we introduce the perturbation solution of system (7), which can be written as a spectral decomposition given by

$$\begin{aligned} \left( \begin{array}{ccc} u \\ v \end{array}\right) =\sum \limits _{k=0}^\infty q_k^\mathrm{T}\left( \begin{array}{ccc} \xi _k^1 \\ \xi _k^2 \end{array} \right) \mathrm{e}^{\lambda t}, \quad q_k=\left( \begin{array}{ccc} q_{k1} \\ q_{k2} \end{array} \right) \in \mathbb {C}^2, \end{aligned}$$
(8)

where

$$\begin{aligned} \xi _k^1(x)=\left( \begin{array}{ccc} \eta _k(x) \\ 0 \end{array} \right) ,\quad \xi _k^2(x)=\left( \begin{array}{ccc} 0\\ \eta _k(x) \end{array} \right) ,\quad k=0, 1, 2, \ldots . \end{aligned}$$

Substituting (8) in (7) yields to the following sequence of quadratic equations

$$\begin{aligned} \Delta _{k}\triangleq \lambda ^{2}-T_{k}\lambda +D_{k}=0, \end{aligned}$$
(9)

where

$$\begin{aligned}&T_{k}=\frac{1}{2}(1-3\beta ^{2})-(d_{11}+d_{22})k^{2}, \nonumber \\&D_{k}=(d_{11}d_{22}-d_{12}d_{21})k^{4}-\left( \frac{1}{2}d_{22}(1-3\beta ^{2})\right. \nonumber \\&\left. +\,d_{21}\beta - \frac{1}{2}d_{12}\gamma (1-\beta ^{2})\right) k^{2}+\frac{1}{2}\beta \gamma (1-\beta ^{2}).\nonumber \\ \end{aligned}$$
(10)

From the necessary conditions for yielding Turing patterns and together with (9) and (10), we can get that \(d_{11}d_{22}-d_{12}d_{21}>0\) and

$$\begin{aligned}&(1-3\beta ^{2})d_{22}+2\beta d_{21} -(1-\beta ^{2})\gamma d_{12}\\&\quad -\,2\sqrt{2(d_{11}d_{22}-d_{12}d_{21})\beta \gamma (1-\beta ^{2})}=0, \end{aligned}$$

which is denoted by L in the \(\gamma -\beta \) plane.

So, in the following, we shall show the existence of Turing–Hopf bifurcation under the condition of \(d_{11}d_{22}-d_{12}d_{21}>0\). For this aim, we give out the definition of Turing–Hopf bifurcation firstly. If there exist a nonnegative integer \(k_{1}\) and a positive integer \(k_{2}\ne k_{1}\) such that \(\Delta _{k_{1}}=0\) has a pair of purely imaginary roots and \(\Delta _{k_{2}}=0\) a simple zero root, and no other roots of (9) has a zero real part, and the transversality condition holds, then we call the bifurcation as a Turing–Hopf bifurcation. It is easy to see that the positive equilibrium \((u^{*}, v^{*})\) is asymptotically stale as \(\frac{\sqrt{3}}{3}<\beta <1\) and unstable as \(0<\beta <\frac{\sqrt{3}}{3}\) when system (2) has no diffusion. And we can get that \(\Delta _{0}=0\) has a pair of purely imaginary roots \(\pm i\sqrt{D_{0}}\) iff \(\beta =\frac{\sqrt{3}}{3}\), which implies that system (2) undergoes a Hopf bifurcation at \(\beta =\frac{\sqrt{3}}{3}\) near the positive equilibrium \((u^{*}, v^{*})\). Further, we consider the case that system (2) has diffusion. Then, in the \(\gamma -\beta \) plane, we denote this Hopf bifurcation curve \(\beta =\frac{\sqrt{3}}{3}\) by \(H_{0}\). Meanwhile, we let \(D_{k}=0,\) that is

$$\begin{aligned}&(d_{11}d_{22}-d_{12}d_{21})k^{4}-\left( \frac{1}{2}d_{22}(1-3\beta ^{2}) \right. \nonumber \\&\left. \quad +d_{21}\beta - \frac{1}{2}d_{12}\gamma (1-\beta ^{2})\right) k^{2} +\frac{1}{2}\beta \gamma (1-\beta ^{2})=0,\nonumber \\ \end{aligned}$$
(11)

which is called Turing bifurcation curve denoted by \(L_{k}\) in the \(\gamma -\beta \) plane.

Obviously, if \(d_{11}d_{22}>d_{12}d_{21}+\frac{\sqrt{3}}{3}d_{21}\), then the Turing bifurcation curve \(L_{k}\) doesn’t interact with the Hopf bifurcation curve \(H_{0}\). That is, system (2) is always stable over the Hopf bifurcation curve \(H_{0}\). On the other hand, if \(d_{12}d_{21}<d_{11}d_{22}<d_{12}d_{21}+\frac{\sqrt{3}}{3}d_{21}\), substituting \(\beta =\frac{\sqrt{3}}{3}\) into (11) and solving (11) for \(\gamma \), we have that

$$\begin{aligned} \gamma (k)=\frac{3d_{21} k^{2}-3\sqrt{3}(d_{11}d_{22}-d_{12}d_{21})k^{4}}{\sqrt{3}d_{12}k^{2}+1},\,k\in [1, k^{*}], \end{aligned}$$

where \(k^{*}=\left[ \sqrt{\frac{\sqrt{3}d_{21}}{3(d11d22-d_{12}d_{21})}} \right] \) and \([\cdot ]\) stands for the integer part function.

Let

$$\begin{aligned} f(x)=\frac{3d_{21} x-3\sqrt{3}(d_{11}d_{22}-d_{12}d_{21})x^{2}}{\sqrt{3}d_{12}x+1},\quad x\in [1, k^{*}]. \end{aligned}$$

It is easy to verify that \(f^{'}(x)\ge 0\) for \(x\le x^{*}\) and \(f^{'}(x)<0\) for \(x>x^{*}\), where

$$\begin{aligned} x^{*}=\frac{-(d_{11}d_{22}-d_{12}d_{21})+\sqrt{(d_{11}d_{22}-d_{12}d_{21})^{2}+d_{12}d_{21}(d_{11}d_{22}-d_{12}d_{21})}}{\sqrt{3}d_{12}(d_{11}d_{22}-d_{12}d_{21})}. \end{aligned}$$

Setting

$$\begin{aligned} k_{*}=\left\{ \begin{array}{ll} 1,&{}\quad { if}\,\;x^{*}\le 1,\\ {[\sqrt{x^{*}}]},&{}\quad { if}\,\,\gamma ([\sqrt{x^{*}}]{+}1)\le \gamma ([\sqrt{x^{*}}]),\,1{<}x^{*}<k^{*},\\ {[\sqrt{x^{*}}]}{+}1,&{}\quad { if}\,\,\gamma ([\sqrt{x^{*}}])<\gamma ([\sqrt{x^{*}}]+1),\,1{<}x^{*}{<}k^{*},\\ k^{*},&{}\quad { if}\,\,x^{*}{\ge } k^{*}, \end{array}\right. \nonumber \\ \end{aligned}$$
(12)

we can conclude that there exists a \(k_{*}\in [1, k^{*}]\) such that \(\gamma ^{*}=\gamma (k_{*})=\max \nolimits _{1\le k\le k^{*}}\gamma (k)\). Thus, the Hopf bifurcation curve \(H_{0}\) intersects with the Turing bifurcation curve \(L_{k_{*}}\) at \((\gamma ^{*}, \beta ^{*})=\left( \frac{3d_{21}k^{2}_{*}-3\sqrt{3}(d_{11}d_{22}-d_{12}d_{21})k^{4}_{*}}{\sqrt{3}d_{12}k^{2}_{*}+1}, \frac{\sqrt{3}}{3}\right) \), which is Turing–Hopf bifurcation point. And we shall discuss the dynamics of system (2) near the Turing–Hopf bifurcation point \((\gamma ^{*}, \beta ^{*})\) in the next subsection.

Next, we continue to verify the transversality condition. For fixed \(\gamma \), taking \(\beta \) as parameter and then denoting the root of (9) by \(\lambda (\beta )\), we have

$$\begin{aligned} \frac{\mathrm{d} Re\{\lambda (\beta )\}}{\mathrm{d}\beta }\Big |_{H_{0}}=-\frac{\sqrt{3}}{2}<0, \end{aligned}$$

and

$$\begin{aligned}&\frac{\mathrm{d} Re\{\lambda (\beta )\}}{\mathrm{d}\beta }\Big |_{L_{k_{*}}}\\&\quad =\frac{2(3d_{22} \beta -d_{21}-d_{12}\beta \gamma )k^{2}+\gamma (1-3\beta ^{2})}{2T_{k}}<0, \end{aligned}$$

which are derived by direct computation together with (11) and (12).

Based on the above discussion and the qualitative theory of the dynamical systems, we have the following results.

Theorem 2

Assume that \(0<\beta <1, H_{0}\) is defined by \(\beta =\frac{\sqrt{3}}{3}\) and \(L_{k_{*}}\) is defined (11) with \(k_{*}\) given in (12). Then we conclude

  1. (1)

    if \(d_{12}d_{21}+\frac{\sqrt{3}}{3}d_{21}<d_{11}d_{22}\), then system (2) is always stable over the Hopf bifurcation curve \(H_{0}\), that is, system (2) doesn’t undergo Turing–Hopf bifurcation;

  2. (2)

    if \(d_{12}d_{21}<d_{11}d_{22}<d_{12}d_{21}+\frac{\sqrt{3}}{3}d_{21}\), then we can obtain that

    1. (i)

      the Hopf bifurcation curve \(H_{0}\) intersects with the Turing bifurcation curve \(L_{k_{*}}\) and a codimension-2 Turing–Hopf bifurcation occurs at the intersect point \((\gamma ^{*}, \beta ^{*}),\) where

      $$\begin{aligned}&\gamma ^{*}=\frac{3d_{21}k^{2}_{*}-3\sqrt{3}(d_{11}d_{22}-d_{12}d_{21})k^{4}_{*}}{\sqrt{3}d_{12}k^{2}_{*}+1},\\&\beta ^{*}=\frac{\sqrt{3}}{3}; \end{aligned}$$
    2. (ii)

      for \((\gamma , \beta )=(\gamma ^{*}, \beta ^{*}),\) the equation \(\Delta _{0}=0\) has a pair of purely imaginary roots \(\pm i\omega _c\) and \(\Delta _{k}=0\) has a simple zero root, and for (9), there are no other roots with zero real parts, where

      $$\begin{aligned} \omega _c=\frac{1}{2}\sqrt{2\beta ^{*}\gamma ^{*}(1-\beta ^{*2})}. \end{aligned}$$

Remark 1

Taking \(d_{11}=d_{12}=1, d_{21}=11, d_{22}=15\), together with the results in Sect. 3.1, we can conclude that \(k^{*}=k_{*}=1\) and

$$\begin{aligned}&H_{0}:~\beta =\frac{\sqrt{3}}{3};\,L_{1}:~8-15(1-3\beta ^{2})-22\beta \\&\qquad +\,\gamma (1+\beta )(1-\beta ^{2})=0;\\&L:~15(1-3\beta ^{2})+22\beta -(1-\beta ^{2})\gamma \\&\quad -4\sqrt{2\beta \gamma (1-\beta ^{2})}=0. \end{aligned}$$

Furthermore, the Hopf bifurcation curve \(H_{0}\) intersects with Turing bifurcation curve \(L_{1}\) at the point \((\gamma ^{*}, \beta ^{*})=(4.4711, \frac{\sqrt{3}}{3})\) and system (2) undergoes Turing–Hopf bifurcation near the positive equilibrium \((\frac{1}{3}, \frac{2\sqrt{3}}{9})\); see Fig. 1.

Fig. 1
figure 1

Bifurcation diagram for system (2) in \(\gamma -\beta \) plane with \(k_{*}=1\). \(H_{0}\) denotes the Hopf bifurcation curve, \(L_{1}\) denotes the Turing bifurcation curve

Full size image

3.2 Normal form on the center manifold for the Turing–Hopf bifurcation

In this subsection, we compute the normal form on the center manifold associated with codimension-2 Turing–Hopf bifurcation such that the spatiotemporal dynamics of system (2) can be determined in the neighborhood of Turing–Hopf bifurcation point \((\gamma ^{*}, \beta ^{*})\). Since the methods used are standard, we omit the detailed calculations and only give the main results here. For researchers who are interested in these calculations, we refer them to references [57], where the calculation of normal form for Turing–Hopf bifurcation is developed for the reaction–diffusion system without cross-diffusion. Although the procedure in [57] is developed for the case without cross-diffusion, it is still applicable for the case with cross-diffusion.

Firstly, introduce a new parameter \(\mu =(\mu _1,\mu _2)\in \mathbb {R}^{2}\) by setting \( \mu _{1}=\gamma -\gamma ^{*}, \mu _{2}=\beta -\beta ^{*}\) such that \(\mu =0\) is the value of Turing–Hopf bifurcation, and rewrite the positive equilibrium as a parameter-dependent form \((u^{*}(\mu ), v^{*}(\mu ))\) with

$$\begin{aligned} u^*(\mu )= & {} \left( \frac{\sqrt{3}}{3}+\mu _{2}\right) ^{2},\\ v^*(\mu )= & {} \left( \frac{\sqrt{3}}{3}+\mu _{2}\right) \left( 1-\left( \frac{\sqrt{3}}{3}+\mu _{2}\right) ^{2}\right) . \end{aligned}$$

Secondly, set \(\tilde{u}(\cdot ,t)=u(\cdot , t)-u^*(\mu ),~\tilde{v}(\cdot ,t)=v(\cdot , t)-v^*(\mu ),~\tilde{U}(t)=(\tilde{u}(\cdot ,t),\tilde{v}(\cdot ,t))\) and then drop the tildes for simplification of notations. One can obtain that system (2) can be written as the equation

$$\begin{aligned} \frac{\mathrm{d}U(t)}{\mathrm{d}t}=\mathrm{d}\Delta U+L_{0}(U)+f(U, \mu ), \end{aligned}$$
(13)

where

$$\begin{aligned}&\mathrm{d}\Delta =\left( \begin{array}{ccc} d_{11}\frac{\partial ^{2}}{\partial x^{2}}&{} d_{12}\frac{\partial ^{2}}{\partial x^{2}}\\ d_{21}\frac{\partial ^{2}}{\partial x^{2}}&{} d_{22}\frac{\partial ^{2}}{\partial x^{2}} \end{array}\right) ,\nonumber \\&L_0(U)=\left( \begin{array}{l} \frac{1}{2}(1-3\beta ^{*2})u-\beta ^{*}v \frac{1}{2}\gamma ^{*}(1-\beta ^{*2})u \end{array}\right) ,\nonumber \\&f(U,\mu )=\sum \limits _{i+j+l_{1}+l_{2}\ge 2}\frac{1}{i!j!l_{1}!l_{2}!}f_{ijl_{1}l_{2}}u^{i}v^{j}\mu _{1}^{l_{1}}\mu _{2}^{l_{2}},\nonumber \\&f_{ijl_{1}l_{2}}=\left( f_{ijl_{1}l_{2}}^{(1)}, f_{ijl_{1}l_{2}}^{(2)}\right) ^\mathrm{T}, \end{aligned}$$
(14)

with \(f^{(k)}_{ijl_{1}l_{2}}=\frac{\partial ^{i+j+l_{1}+l_{2}} \widetilde{f}^{(k)}(0,0,0,0)}{\partial u^{i} \partial v^{j} \partial \mu _{1}^{l_{1}}\partial \mu _{2}^{l_{2}}}, ~k=1,2,\) and

$$\begin{aligned} \widetilde{f}^{(1)}(u,v,\mu _{1},\mu _{2})= & {} (u+u^{*}(\mu ))(1-(u+u^{*}(\mu )))\\&-\,\sqrt{u+u^{*}(\mu )}(v+v^{*}(\mu )),\\ \widetilde{f}^{(2)}(u,v,\mu _{1},\mu _{2})= & {} (\gamma ^{*}+\mu _{1})(v+v^{*})(-(\beta ^{*}+\mu _{2})\\&+\,\sqrt{u+u^{*}(\mu )}). \end{aligned}$$

For the linearized system of (13) at the origin

$$\begin{aligned} \frac{\mathrm{d}U}{\mathrm{d}t}=\mathscr {L}(U), \end{aligned}$$
(15)

where \(\mathscr {L}(U)=\mathrm{d}\Delta U+L_{0}(U).\) Denote by \(\Lambda =\{i \omega _{c}, -i \omega _{c}, 0\}\) the finite set of all its eigenvalues having zero real parts, with which a stable invariant manifold is associated. Set \(\mathscr {B}_{k}=\text{ span }\left\{ \left[ \varphi (\cdot ), \xi _k^{i}\right] \xi _{k}^{i}|~\varphi \in X, i=1, 2\right\} \). Then it is easy to verify that

$$\begin{aligned} L_{0}(\mathscr {B}_{k})\subset \text{ span }\left\{ \xi _k^{1}, \xi _k^{2}\right\} ,\quad k\in \mathbb {N}_0. \end{aligned}$$

Assume that \(y(t)\in \mathbb {R}^{2}\) and

$$\begin{aligned} y^\mathrm{T}(t)\left( \begin{array}{c} \xi _{k}^{1} \\ \xi _{k}^{2} \end{array} \right) \in \mathscr {B}_{k}. \end{aligned}$$

Then, on \(\mathscr {B}_{k}\), the linear partial differential equation (15) is equivalent to the ODE on \(\mathbb {R}^{2}\)

$$\begin{aligned} \dot{y}(t)=\left( \begin{array}{cc} -d_{11}k^{2} &{} -d_{12}k^{2} \\ -d_{21}k^{2} &{} -d_{22}k^{2} \end{array} \right) y(t)+L_{0}(y(t)), \end{aligned}$$
(16)

where for \(y(t)\in \mathbb {R}^{2}\), we use the same formal expression \(L_0(y(t))\) as in (14). Clearly, the linear ordinary differential equation (16) has the same characteristic equation (9) as the linear partial differential equation (15).

Notice

$$\begin{aligned} \mathscr {M}_{k}= \left( \begin{array}{cc} -d_{11} k^{2}+\frac{1}{2}(1-3\beta ^{*2})&{} -d_{12}k^{2}-\beta ^{*} \\ -d_{21}k^{2}+\frac{1}{2}\gamma ^{*}(1-\beta ^{*2}) &{} -d_{22}k^{2} \end{array}\right) ,\nonumber \\ \end{aligned}$$
(17)

is the characteristic matrix of (16). Then \(\Lambda _{k}\) is the finite set of all eigenvalues of the matrix (17) having zero real parts. The standard adjoint theory for ODEs can be used to decompose \(\mathbb {C}^{2}\) by \(\Lambda _{k}\) as

$$\begin{aligned} \mathbb {C}^{2}=P_{k} \oplus Q_{k}, \end{aligned}$$

where \(P_{k}\) is the generalized eigenspace associated with the eigenvalues in \(\Lambda _{k}\) and \(Q_{k}=\left\{ \varphi \in \mathbb {C}^2:\langle \psi , \varphi \rangle =0 ~\text{ for } \text{ all } \psi \in P_{k}^{*}\right\} ,\) where \(P_{k}^{*}\) is the dual space of \(P_{k}\) and \(\langle \cdot , \cdot \rangle \) is the scalar product of two complex vectors defined by

$$\begin{aligned} \left\langle \psi ^\mathrm{T}, \varphi \right\rangle =\psi ^\mathrm{T}\varphi , \quad \text{ for }\quad \varphi , \psi \in \mathbb {C}^{2} \end{aligned}$$

such that for dual bases \(\Phi _{k}\) and \(\Psi _{k}\) of \(P_{k}\) and \(P_{k}^{*},\) respectively, \(\langle \Psi _{k}, \Phi _{k}\rangle =I_{m_{k}},\) where \(m_{k}=\dim P_{k}\) and \(I_{m_{k}}\) is a \(m_{k}\times m_{k}\) identity matrix.

Notice that \(k=0, k_{*}>0\) in the Turing–Hopf bifurcation. By a straightforward calculation, we obtain \(\Phi _{0}=\left( p_{0}, \bar{p}_{0}\right) , \Phi _{k_{*}}=p_{k_{*}}, \Psi _{0}=\text{ col }\left( q_{0}^\mathrm{T}, \bar{q}_{0}^\mathrm{T}\right) , \Psi _{k_{*}}=q_{k_{*}}^\mathrm{T}\), where

$$\begin{aligned}&p_{0}=\left( \begin{array}{c} 1 \\ \frac{\frac{1}{2}(1-3\beta ^{*2})-i\omega _{c}}{\beta ^{*}} \end{array} \right) , \quad q_{0}=\left( \begin{array}{c} \frac{1}{2} \\ -\frac{\beta ^{*}}{2i\omega _{c}} \end{array} \right) ,\\&p_{k_{*}}=\left( \begin{array}{c} 1 \\ -\frac{d_{11}k^{2}_{*}-\frac{1}{2}(1-3\beta ^{*2})}{d_{12}k^{2}_{*}+\beta ^{*}} \end{array} \right) , \quad q_{k_{*}}=\left( \begin{array}{c} -\frac{d_{22}k^{2}_{*}}{T_{k_{*}}} \\ \frac{d_{12}k^{2}_{*}+\beta ^{*}}{T_{k_{*}}} \end{array} \right) . \end{aligned}$$

Then, by the procedure developed in [57], the normal form for Turing–Hopf bifurcation point \((\gamma ^{*}, \beta ^{*})\) can be obtained as follows

$$\begin{aligned} \dot{\rho }= & {} \alpha _{1}(\mu )\rho +\kappa _{11}\rho ^{3}+\kappa _{12}\rho r^{2},\nonumber \\ \dot{r}= & {} \alpha _{2}(\mu )r+\kappa _{21}\rho ^{2} r+\kappa _{22}r^{3}, \end{aligned}$$
(18)

with

$$\begin{aligned}&\alpha _{1}(\mu )=Re\left( B_{11}\right) \mu _{1}+Re\left( B_{21}\right) \mu _2,\\&\alpha _{2}(\mu )=B_{13}\mu _{1}+B_{23}\mu _{2},\\&\kappa _{11}=Re(B_{210}), \kappa _{12}=Re(B_{102}),\\&\kappa _{21}=B_{111}, \kappa _{22}=B_{003}, \end{aligned}$$

where

$$\begin{aligned}&B_{11}=p_{01}\left( q^\mathrm{T}_{0} f_{1010}\right) + p_{02}\left( q^\mathrm{T}_{0} f_{0110}\right) ,\\&B_{21}=p_{01}\left( q^\mathrm{T}_{0} f_{1001}\right) +p_{02}\left( q^\mathrm{T}_{0} f_{0101}\right) ,\\&B_{13}=p_{k_{*}1}\left( q^\mathrm{T}_{k_{*}} f_{1010}\right) +p_{k_{*}2}\left( q^\mathrm{T}_{k_{*}} f_{0110}\right) ,\\&B_{23}=p_{k_{*}1}\left( q^\mathrm{T}_{k_{*}} f_{1001}\right) +p_{k_{*}2}\left( q^\mathrm{T}_{k_{*}} f_{0101}\right) , \end{aligned}$$

and the calculation of \(B_{210}, B_{102}, B_{111}\) and \(B_{003}\) are very complicated and we leave them in “Appendix.”

3.3 Numerical simulations

In this subsection, we present some numerical simulations to illustrate our analytical results. Choosing \(d_{11}=d_{12}=1, d_{21}=11, d_{22}=15\), together with the results in Sect. 3.1, we can conclude that \(k^{*}=k_{*}=1\) and

Fig. 2
figure 2

Bifurcation and phase portraits of system (19) near point \((\gamma ^{*}, \beta ^{*})=(4.4711, \frac{\sqrt{3}}{3})\). Here, the origin of the \(\mu _{1}-\mu _{2}\) plane corresponds to point \((\gamma ^{*}, \beta ^{*})=(4.4711, \frac{\sqrt{3}}{3})\) in \(\gamma -\beta \) plane

Full size image
Fig. 3
figure 3

When \((\mu _{1}, \mu _{2})=(0.08, 0.01)\) lies in region \(\textcircled {1}\), the positive constant equilibrium \((u^{*}, v^{*})=(0.3333, 0.3849)\) is asymptotically stable. The initial condition \(u(x, 0)=0.3333-0.2\cos x, v(x, 0)=0.3849-0.1\cos x\)

Full size image
$$\begin{aligned} H_{0}:~\beta= & {} \frac{\sqrt{3}}{3};\,L_{1}:~8-15(1-3\beta ^{2})-22\beta \\&+\,\gamma (1+\beta )(1-\beta ^{2})=0. \end{aligned}$$

Furthermore, the Hopf bifurcation curve \(H_{0}\) intersects with Turing bifurcation curve \(L_{1}\) at the point \((\gamma ^{*}, \beta ^{*})=(4.4711, \frac{\sqrt{3}}{3})\) and system (2) undergoes Turing–Hopf bifurcation near the positive equilibrium \((\frac{1}{3}, \frac{2\sqrt{3}}{9})\); see Fig. 1.

Following the procedure in Sect. 3.2 with \(k_{*}=1\), we can obtain the following normal form truncating to the third-order terms

Fig. 4
figure 4

When \((\mu _{1}, \mu _{2})=(0.5, -0.01)\) lies in region \(\textcircled {2}\), the positive equilibrium \((u^{*}, v^{*})=(0.3219, 0.3847)\) becomes unstable and there exists a stable spatially homogeneous periodic solution. The initial condition \(u(x, 0)=0.3219+0.30\cos x, v(x, 0)=0.3847+0.30\cos x\)

Full size image
Fig. 5
figure 5

When \((\mu _{1}, \mu _{2})=(-0.5, -0.03)\) lies in region \(\textcircled {3}\), the positive equilibrium \((u^{*}, v^{*})=(0.2996, 0.3834)\) is unstable. There are unstable spatially inhomogeneous steady states and a stable homogeneous periodic solution, and there exists an orbit connecting these two states. The initial condition \(u(x, 0)=0.2996+0.25\cos x, v(x, 0)=0.3834+0.25\cos x\)

Full size image
$$\begin{aligned} \left\{ \begin{array}{l} \dot{\rho }{=}-0.8660\mu _{2}\rho -0.1790\rho ^{3}+0.5245\rho r^{2},\\ \dot{r}{=}({-}0.0329\mu _{1}{-}0.7750\mu _{2})r{-}0.3293\rho ^{2}r{-}0.6954r^{3}. \end{array}\right. \nonumber \\ \end{aligned}$$
(19)

Noticing that \(\rho >0\) and r is an arbitrary real number gives that system (19) has a zero equilibrium \(A_{0}=(0, 0)\) for all \(\mu _{1}, \mu _{2}\), three trivial equilibria \(A_{1}=(\sqrt{-4.8380\mu _{2}}, 0)\) for \(\mu _{2}<0, A^{\pm }_{2}=(0, \pm \sqrt{-0.0473\mu _{1}-1.1145\mu _{2}})\) for \(0.0473\mu _{1}+1.1145\mu _{2}<0\), and two nontrivial equilibria

$$\begin{aligned}&A^{\pm }_{3}=(\sqrt{-0.0582\mu _{1}-3.3940\mu _{2}},\\&\quad \pm \sqrt{-0.0199\mu _{1}+0.4926\mu _{2}}) \end{aligned}$$

for \(0.0580\mu _{1}+3.3993\mu _{2}<0\) and \(-0.0198\mu _{1}+0.4908\mu _{2}>0\). Define the critical bifurcation lines as follows:

$$\begin{aligned} \left\{ \begin{array}{l} H_{0}:~\mu _{2}=0;\,T:~\mu _{2}=-0.0424\mu _{1}; \\ T_{1}:~\mu _{2}=-0.0171\mu _{1},~\mu _{1}<0;\,T_{2}:~\\ \mu _{2}=0.0404\mu _{1},~\mu _{1}<0. \end{array}\right. \end{aligned}$$
Fig. 6
figure 6

When \((\mu _{1}, \mu _{2})=(-4.30, -0.02)\) lies in region \(\textcircled {4}\), the positive equilibrium \((u^{*}, v^{*})=(0.3107, 0.3842)\) is unstable and there are stable spatially inhomogeneous periodic solutions. The initial condition is \(u(x, 0)=0.3107-0.015, v(x, 0)=0.3842+0.01\cos x\). a, c are transient behaviors for u and v, respectively. b, d are long-term behaviors for u and v, respectively

Full size image
Fig. 7
figure 7

When \((\mu _{1}, \mu _{2})=(-0.02, -4.30)\) lies in region \(\textcircled {4}\), the positive equilibrium \((u^{*}, v^{*})=(0.3107, 0.3842)\) is unstable and there are stable spatially inhomogeneous periodic solutions. The initial condition is \(u(x, 0)=0.3140-0.25\cos x, v(x, 0)=0.3844+0.25\cos x\). a, c are transient behaviors for u and v, respectively. b, d are long-term behaviors for u and v, respectively

Full size image
Fig. 8
figure 8

When \((\mu _{1}, \mu _{2})=(-3.0000, 0.0005)\) lies in region \(\textcircled {5}\), the positive equilibrium \((u^{*}, v^{*})=(0.3340, 0.3849)\) is unstable and there are stable spatially inhomogeneous periodic solutions. The initial condition is \(u(x, 0)=0.3340-0.25\cos x, v(x, 0)=0.3849+0.25\cos x\). a, c are transient behaviors for u and v, respectively. b, d are long-term behaviors for u and v, respectively

Full size image

Then, according to the results in [61], the bifurcation diagram in the \(\mu _{1}-\mu _{2}\) parameter plane and the corresponding phase portraits of system (19) in the \(\rho -r\) plane is shown in Fig. 2. The \((\mu _{1}, \mu _{2})\) parameter plane is divided into six regions characterized by the phase portraits; see Fig. 2. And we know that the zero equilibrium \(A_{0}\) of system (19) corresponds to the positive equilibrium \((u^{*}, v^{*})\) of the original system (2). The equilibrium \(A_{1}\) in the \(\rho \)-axis of (19) corresponds to the spatially homogeneous periodic solution of the original system (2). The equilibria \(A^{\pm }_{2}\) in the r-axis of (19) correspond to the nonconstant steady-state solutions of the original system (2) like a shape of \(\cos x\)-shape. But the nontrivial equilibria \(A^{\pm }_{3}\) generate solutions of the original system (2) with spatial structure like \(\cos x\)-shape and periodic temporal structure, which is called as spatially inhomogeneous periodic solutions. So, for system (2), the spatiotemporal dynamics near the Turing–Hopf bifurcation point \((\gamma ^{*}, \beta ^{*})\) can be identified in terms of the dynamics of the normal form system (19).

In what follows, we shall analyze the stability and existence of six equilibrium and carry out some numerical simulations in six regions, respectively. In region \(\textcircled {1}\), system (19) has only one equilibrium \(A_{0}\) and it is asymptotically stable. Correspondingly, there is only one positive constant equilibrium \((u^{*}, v^{*})\) of the original system (2), which is asymptotically stable, as shown in Fig. 3 for \((\mu _{1}, \mu _{2})=(0.08, 0.01)\) and the initial condition \(u(x, 0)=0.3333-0.2\cos x, v(x, 0)=0.3849-0.1\cos x\).

In region \(\textcircled {2}\), system (19) has two equilibria: \(A_{0}\) and \(A_{1}\), and \(A_{0}\) is unstable, \(A_{1}\) is asymptotically stable. Taking \((\mu _{1}, \mu _{2})=(0.5, -0.01)\) and and the initial condition \(u(x, 0)=0.3219+0.30\cos x, v(x, 0)=0.3847+0.30\cos x\), the positive constant equilibrium becomes unstable and only the Hopf bifurcation occurs. The emerging state of system (2) is homogeneously periodic oscillation as shown in Fig. 4.

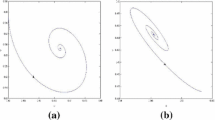
In region \(\textcircled {3}\), system (19) has four equilibria: \(A_{0}, A_{1}, A^{+}_{2}\) and \(A^{-}_{2}\), and \(A_{0}\) and \(A_{1}\) are unstable, and \(A^{+}_{2}\) and \(A^{-}_{2}\) are still asymptotically stable. Therefore, the original system (2) has an unstable positive constant equilibrium \((u^{*}, v^{*})\), and there are two spatially inhomogeneous steady states and a homogeneous periodic solution. Taking \((\mu _{1}, \mu _{2})=(-0.5, -0.03)\) and the initial condition \(u(x, 0)=0.2996+0.25\cos x, v(x, 0)=0.3834+0.25\cos x\), the dynamics of system (2) is that the spatially inhomogeneous steady states are unstable and the homogeneous periodic solution is asymptotically stable, and there exists an orbit connecting the unstable steady state to the stable spatially homogeneous periodic solution, as shown in Fig. 5.

In region \(\textcircled {4}\), system (19) has six equilibria: \(A_{0}, A_{1}, A^{\pm }_{2}\) and \(A^{\pm }_{3}\), and \(A_{0}, A_{1}, A^{\pm }_{2}\) are unstable, and \(A^{+}_{3}\) and \(A^{-}_{3}\) are asymptotically stable. This implies that system (2) has two stable spatially inhomogeneous periodic solution. For the fixed the parameter \((\mu _{1}, \mu _{2})=(-4.30, -0.02)\) and different initial conditions, system (2) converges to the stable spatially inhomogeneous periodic solution. For the initial condition \(u(x, 0)=0.3140-0.015, v(x, 0)=0.3844+0.01\cos x\) close to the unstable periodic solution, the dynamics of system (2) evolves from unstable spatially homogeneous periodic solution to stable spatially inhomogeneous periodic solution, as shown in Fig. 6. However, for the initial condition \(u(x, 0)=0.3140-0.25\cos x, v(x, 0)=0.3844+0.25\cos x\) close to the unstable nonconstant steady state, the dynamics of system (2) evolves from unstable nonconstant steady state like \(\cos x\)-shape to the stable spatially inhomogeneous periodic solution, as shown in Fig. 7.

In region \(\textcircled {5}\), system (19) has five equilibria: \(A_{0}, A^{\pm }_{2}\) and \(A^{\pm }_{3}\), and \(A_{0}, A^{+}_{2}\) and \(A^{-}_{2}\) are unstable, and \(A^{+}_{3}\) and \(A^{-}_{3}\) are asymptotically stable. Choosing \((\mu _{1}, \mu _{2})=(-3.0000, 0.0005)\) and the initial condition \(u(x, 0)=0.3340-0.25\cos x, v(x, 0)=0.3849+0.25\cos x\) close to the unstable nonconstant steady state, the dynamics of system (2) evolves from unstable nonconstant steady state like \(\cos x\)-shape to the stable spatially inhomogeneous periodic solution as shown in Fig. 8.

Fig. 9
figure 9

When \((\mu _{1}, \mu _{2})=(-3.850, 0.0675)\) lies in region \(\textcircled {6}\), the positive constant equilibrium \((u^{*}, v^{*})=(0.4159, 0.3767)\) is unstable and there are two stable spatially inhomogeneous steady states like \(\cos x\). a, b The initial condition is \(u(x, 0)=0.4159+0.25\cos x, v(x, 0)=0.3767+0.25\cos x\). c, d The initial condition is \(u(x, 0)=0.4159-0.25\cos x, v(x, 0)=0.3767-0.25\cos x\)

Full size image

In region \(\textcircled {6}\), system (19) has three equilibria: \(A_{0}, A^{+}_{2}\) and \(A^{-}_{2}\), and \(A_{0}\) is unstable, and \(A^{+}_{2}\) and \(A^{-}_{2}\) are asymptotically stable. That is, the original system (2) has an unstable positive constant equilibrium \((u^{*}, v^{*})\) and two stable nonconstant steady states like \(\cos x\)-shape, for the fixed \((\mu _{1}, \mu _{2})=(-3.850, 0.0675)\), which are shown in Fig. 9a, b for the initial condition \(u(x, 0)=0.4159+0.25\cos x, v(x, 0)=0.3767+0.25\cos x\) and Fig. 9c, d for the initial condition \(u(x, 0)=0.4159-0.25\cos x, v(x, 0)=0.3767-0.25\cos x\).

4 Conclusion

In this paper, the dynamical behavior of a predator–prey model (2) with herd behavior and cross-diffusion subject to homogeneous Neumann boundary condition are investigated. Firstly, we showed the existence and priori bound of a solution for the model (2) without cross-diffusion. Then, we discussed complex spatiotemporal dynamics near the Turing–Hopf bifurcation point of the model (2) with cross-diffusion in the framework of normal form. Since the Turing–Hopf bifurcation is codimension-2 bifurcation, we choose \(\beta \), which is proportional to the death rate of the predator, and the conversion or consumption rate \(\gamma \) of prey to predator as bifurcation parameters. Following the method of computing the normal form in [56, 57], we have obtained the normal form of model (2). Based on the obtained normal form, we then classified the spatiotemporal patterns and their stability, which have been well verified quantitatively by numerical simulations; see Figs. 3, 4, 5, 6, 7, 8 and 9. Particularly, the stable spatially inhomogeneous periodic solutions is found in regions \(\textcircled {4}\) and \(\textcircled {5}\), respectively; see Figs. 6, 7 and 8. From the analysis above, we can see that the conversion or consumption rate of prey to predator and death rate of the predator are two important factors for predator–prey system or other ecosystems and can affect the stability of predator–prey system. So, we can make the predator and prey coexist through controlling the conversion or consumption rate of prey to predator and death rate of the predator. Of course, the methods and the results in the present paper generalized the ones in [56, 57] and can also be applied to other reaction–diffusion systems with and without cross-diffusion. We hope that our work could be instructive to study in population dynamics.