New results on positive pseudo-almost periodic solutions for a delayed Nicholson’s blowflies model

Abstract

This paper is concerned with a non-autonomous Nicholson’s blowflies model with an oscillating death rate. Under proper conditions, we employ a novel argument to establish a criterion on the global exponential stability of positive pseudo-almost periodic solution, which improves and extends some known relevant results. Moreover, an example along with its numerical simulations is presented to demonstrate the validity of the proposed result.

1 Introduction

In a classic study of population dynamics, the delayed Nicholson’s blowflies model can be described as follows:

$$\begin{aligned} x' (t)= -\delta x(t)+P x (t-\tau )e^{-a x(t-\tau )}, \end{aligned}$$

(1.1)

which has agreed with the experimental data on the population of the Australian sheep blowfly in [1, 2]. Here x(t) is the size of the population at time t, P is the maximum per capita daily egg production, $\frac{1}{a}$ is the size at which the population reproduces at its maximum rate, $\delta$ is the per capita daily adult death rate, and $\tau$ is the generation time. Since the coefficients and delays in differential equations of population and ecology problems are usually time-varying in the real world, the model (1.1) has been naturally generalized to the following Nicholson’s blowflies model with time-varying coefficients and delays:

$$\begin{aligned} x' (t)= & {} - a(t)x(t)\nonumber \\&+\,\sum \limits _{j=1}^{m}\beta _{j}(t) x (t-\tau _{j} (t) )e^{-\gamma _{j}(t) x(t-\tau _{j}(t))}.\nonumber \\ \end{aligned}$$

(1.2)

In particular, there have been extensive results on the problem of the convergence and persistence of model (1.2) in the literature. We refer the reader to [3–5] and the references cited therein. Recently, the attractivity of periodic or almost periodic solutions and other dynamical aspects have been studied by [6–10], where some criteria were established to guarantee the global exponential stability of positive periodic solutions and positive almost periodic solutions, respectively. Moreover, in these known results in [1–10], we find the following conditions:

$(A_{0})$ :

the coefficient function a(t) in the death rate is not oscillating, i. e.,

$$\begin{aligned} \inf \limits _{t\in \mathbb {R}}a(t)> 0, \end{aligned}$$

has been adopted as fundamental for the considered dynamic behaviors of (1.1) and (1.2).

On the other hand, as pointed out in [11], equations with oscillating coefficients appear in linearizations of population dynamics models with seasonal fluctuations, where during some seasons the death or harvesting rates may be greater or lesser than the birth rate. As we known, the existence of pseudo-almost periodic solutions is among the most attractive topics in qualitative theory of differential equations due to their applications, especially in biology, economics, physics and engineering [12–15]. Now, a question naturally arises: How to find the new criteria to guarantee the existence and exponential stability of the positive pseudo-almost periodic solutions of (1.2) with an oscillating coefficient in death rate.

Motivated by the above discussions, avoiding the condition $(A_{0})$, the main purpose of this paper is to give some sufficient conditions for the existence and global exponential stability of the positive pseudo-almost periodic solutions of (1.2), and the exponential convergence rate can be unveiled. The proof is based on the exponential dichotomy theory and fixed point theorem. Particularly, our result not only generalizes the results in the literature [6–10], but also improves them. In fact, one can see the following Remarks 3.1 and 4.1 for details.

For the sake of simplicity of notations, given a bounded and continuous function g defined on $\mathbb {R}$, we denote

$$\begin{aligned} g^{+}\,=\,\sup \limits _{t\in \mathbb {R}}g(t)\qquad \hbox {and} \qquad g^{-}\,=\,\inf \limits _{t\in \mathbb {R}}g(t). \end{aligned}$$

It will be assumed that $a :\mathbb {R}\rightarrow \mathbb {R}$ is an almost periodic function, $\beta _{j}, \tau _{j }, \gamma _{j }:\mathbb {R}\rightarrow [0, \ +\infty )$ are pseudo-almost periodic functions, and

$$\begin{aligned} M[a]= & {} \lim \limits _{T\rightarrow +\infty }\frac{1}{T}\int _{t}^{t+T}a(s)\mathrm{d}s>0,r\nonumber \\= & {} \max _{1\le j \le m}{\tau _{j}^{+}}, \min _{1\le j \le m}\gamma ^{-}_{j} \ge 1. \end{aligned}$$

(1.3)

As usual, $C= C([-r, \ 0], \mathbb {R})$ is the Banach space of the set of all continuous functions from $[-r, \ 0]$ to $\mathbb {R}$ equipped with supremum norm $||\cdot ||$ and $C_{+}=\{\varphi \in C| \varphi (\theta )\ge 0$ for $\theta \in [-r, \ 0]\}$. Furthermore, for a continuous function x defined on $[t_0-r, \ \sigma )$ with $t_0<\sigma$ and $t\in [t_0, \ \sigma )$, we define $x_t\in C$ by $x_t(\theta )=x(t+\theta )$ for $\theta \in [-r, \ 0]$.

We write by $x_{t}(t_{0}, \varphi )(x(t; t_{0}, \varphi ))$ an admissible solution of (1.2) with admissible initial conditions

$$\begin{aligned} x_{t_0}=\varphi , \ \ \ \varphi \in C_+ \hbox { and } \varphi (0)>0. \end{aligned}$$

(1.4)

Also, let $[t_{0},\eta (\varphi ))$ be the maximal right interval of the existence of $x_t(t_{0}, \varphi )$.

Two positive numbers will be crucial in stating our results. Since the function $\frac{ 1-x}{e^x}$ is decreasing with the range $[0, \ 1]$, it follows easily that there exists a unique $\kappa \in (0, \ 1)$ such that

$$\begin{aligned} \frac{1-\kappa }{e^{\kappa }}=\frac{1}{e^{2}}. \end{aligned}$$

(1.5)

Obviously,

$$\begin{aligned} \sup \limits _{x\ge \kappa }\left| \frac{1-x}{e^{x}}\right| =\frac{1}{e^{2}}. \end{aligned}$$

(1.6)

Moreover, since $xe^{-x}$ increases on $[0, \ 1]$ and decreases on $[1, {+}\infty )$, let $\widetilde{\kappa }$ be the unique number in $(1, \ +\infty )$ such that

$$\begin{aligned} \kappa e^{-\kappa }=\widetilde{\kappa } e^{-\tilde{\kappa }}. \end{aligned}$$

We let $BC(\mathbb {R},\mathbb {R})$ be the set of bounded and continuous functions from $\mathbb {R}$ to $\mathbb {R}$. Clearly, $(BC(\mathbb {R},\mathbb {R}), \Vert \cdot \Vert _{\infty })$ is a Banach space where $\Vert \cdot \Vert _{\infty }$ denotes the supremum $\Vert f\Vert _{\infty } := \sup \limits _{ t\in \mathbb {R}} |f (t)|$. We denote by $AP(\mathbb {R},\mathbb {R})$ the set of the almost periodic functions from $\mathbb {R}$ to $\mathbb {R}$, which can be found in [12, 13]. Define the class of functions $PAP_{0}(\mathbb {R},\mathbb {R})$ as follows:

$$\begin{aligned} \big \{f\in BC(\mathbb {R},\mathbb {R})|\lim \limits _{T\rightarrow +\infty }\frac{1}{2T}\int _{-T}^{T}|f(t)|\mathrm{d}t=0\big \}. \end{aligned}$$

A function $f\,\in \,{BC(\mathbb {R},\mathbb {R})}$ is called pseudo-almost periodic if it can be expressed as

$$\begin{aligned} f=h+\varphi , \end{aligned}$$

where $h\in {AP(\mathbb {R},\mathbb {R})}$ and $\varphi \in {PAP_{0}(\mathbb {R},\mathbb {R})}.$ The collection of such functions will be denoted by $PAP(\mathbb {R},\mathbb {R}).$ In particular, $(PAP(\mathbb {R},\mathbb {R}),\Vert .\Vert _{\infty })$ is a Banach space [12].

2 Preliminary results

In this section, we give some results which will be of importance in the discussion of Sect. 3.

Lemma 2.1

Let $a^{*} :\mathbb {R}\rightarrow (0, \ +\infty )$ be an almost periodic function, $F^{S}$, $F^{i}$, $\eta ^{S}$, $\eta ^{i}$ and M be positive constants such that

$$\begin{aligned}&F^{i} e ^{ -\int _{s}^{t}a^{*}(u)\mathrm{d}u}\le e ^{ -\int _{s}^{t}a(u)\mathrm{d}u}\nonumber \\&\quad \le F^{S} e ^{ -\int _{s}^{t}a^{*}(u)\mathrm{d}u}, \ \quad \hbox {for all} t,s\in \mathbb {R} \hbox { and }t-s\ge 0, \nonumber \\ \end{aligned}$$

(2.1)

$$\begin{aligned}&\left\{ \begin{array}{lll} -\eta ^{S}&{}=&{}\sup \limits _{t\in \mathbb {R}} \left\{ - a^{*}(t)M + F^{S}\frac{1}{e}\sum \limits _{j=1}^m \frac{\beta _{j} (t)}{\gamma _{j} (t)} \right\} , \\ \eta ^{i}&{}= &{}\inf \limits _{t\in \mathbb {R} } \left\{ - a^{*}(t) +F^{i}\sum \limits _{j=1}^{m}\frac{\beta _{j} (t)}{\gamma _{j} (t)} e^{-\kappa } \right\} ,\end{array} \right. \end{aligned}$$

(2.2)

$$\begin{aligned}&\quad M>\kappa , \ \max \limits _{1\le j\le m} \gamma _j ^{+} \le \frac{\widetilde{\kappa }}{M}. \end{aligned}$$

(2.3)

Then, the set of $\{x_t(t_{0},\varphi ): t\in [t_{0}, \ \eta (\varphi ))\}$ is bounded, and $\eta (\varphi )=+\infty$. Moreover, there exists $t _{\varphi }>t_{0}$ such that

$$\begin{aligned} \kappa < x (t; t_{0}, \varphi ) < M \quad \hbox {for all } t \ge t _{\varphi }. \end{aligned}$$

(2.4)

Proof

Since $\varphi \in C_+$, using Theorem 5.2.1 in [16, p. 81], we have $x_t(t_{0},\varphi )\in C_+$    for all $t \in [t_{0}, \ \eta (\varphi ))$. Let $x (t )= x (t; t_{0},\varphi )$. Multiplying both sides of (1.2) by $e ^{ \int _{t_{0}}^{t}a(v)\mathrm{d}v}$, and integrating it on $[t_{0}, \ t]$, in view of $x (t_{0})=\varphi (0)>0$, we have

$$\begin{aligned} x (t)= & {} e^{-\int _{t_{0}}^{t} a(v) \mathrm{d}v}x (t_{0})\nonumber \\&+\,\int _{t_{0}}^{t} e^{ -\int _{s}^{t} a(v) \mathrm{d}v}\sum \limits _{j=1}^{m} \beta _{j} (s) x (s-\tau _{j} (s))\nonumber \\&\times \, e^{- \gamma _{j} (s) x (s-\tau _{j} (s))}\mathrm{d}s\nonumber \\> & {} 0, \quad \hbox {for all } \ t\in [t_{0}, \ \eta (\varphi )). \end{aligned}$$

(2.5)

According to (2.1), (2.2), (2.5) and the fact that $\sup \limits _{u\ge 0} ue^{- u}=\frac{1}{ e}$, we get

$$\begin{aligned} x (t)= & {} e^{-\int _{t_{0}}^{t} a(v) \mathrm{d}v}x (t_{0})\\&+\,\int _{t_{0}}^{t} e^{ -\int _{s}^{t} a(v) \mathrm{d}v}\sum \limits _{j=1}^{m} \frac{\beta _{j} (s)}{\gamma _{j} (s)} \gamma _{j} (s)x (s-\tau _{j} (s))\\&\times \, e^{- \gamma _{j} (s) x (s-\tau _{j} (s))}\mathrm{d}s\\\le & {} F^{S} e^{-\int _{t_{0}}^{t} a^{*}(v) \mathrm{d}v}x (t_{0}) + \int _{t_{0}}^{t} e^{ -\int _{s}^{t} a^{*}(v) \mathrm{d}v}\nonumber \\&\times \, F^{S}\sum \limits _{j=1}^{m} \frac{\beta _{j} (s)}{\gamma _{j} (s)} \frac{1}{e}\mathrm{d}s \\\le & {} F^{S} e^{-\int _{t_{0}}^{t} a^{*}(v) \mathrm{d}v}x (t_{0}) \\&+\,\int _{t_{0}}^{t} e^{ -\int _{s}^{t} a^{*}(v) \mathrm{d}v}[-\eta ^{S}+a^{*}(s)M]\mathrm{d}s\\\le & {} F^{S} e^{-\int _{t_{0}}^{t} a^{*}(v) \mathrm{d}v}x (t_{0}) \\&+\,\sup \limits _{t\in \mathbb {R}}\frac{-\eta ^{S}}{a^{*}(t)}\left[ 1-e^{-\int _{t_{0}}^{t} a^{*}(v) \mathrm{d}v}\right] \\&+\,M\left[ 1-e^{-\int _{t_{0}}^{t} a^{*}(v) \mathrm{d}v}\right] \\:= & {} A(t), \quad \hbox {for all} \ t\in [t_{0}, \ \eta (\varphi )). \end{aligned}$$

From Theorem 2.3.1 in [17] and the boundedness of A(t), we can obtain $\eta (\varphi )=+\infty$. Furthermore, we have

$$\begin{aligned} \lim \limits _{t\rightarrow +\infty }A(t)=\sup \limits _{t\in \mathbb {R}}\frac{-\eta ^{S}}{a^{*}(t)}+M< M, \end{aligned}$$

which implies that there exists $t_{1}\in [t_{0}, \ +\infty )$ such that

$$\begin{aligned} 0<x(t )<M, \quad \hbox {for all } \ t\in [t_{1}, \ +\infty ). \end{aligned}$$

(2.6)

We now show that $l:=\liminf \limits _{t\rightarrow +\infty } x(t)>0$. By way of contradiction, we assume that $l=0$. For each $t\ge t_{0}$, we define

$$\begin{aligned} m(t)=\max \left\{ \varrho |\varrho \le t, x (\varrho )=\min \limits _{t_{0} \le s\le t} x (s)\right\} . \end{aligned}$$

It follows from $l=0$ that $m(t) \rightarrow +\infty$ as $t\rightarrow +\infty$ and that

$$\begin{aligned} \lim \limits _{t\rightarrow +\infty }x (m(t))=0. \end{aligned}$$

From the definition of m(t), we know that there exists $t_{2}>t_{1}+r$ such that

$$\begin{aligned}&0<x(m(t))<\kappa , \ \ m(t)>t_{1}+r, \nonumber \\&\quad \hbox {for all } \ t\in [t_{2}, \ +\infty ), \end{aligned}$$

(2.7)

and

$$\begin{aligned} x(m(t)) \le \gamma _{ j}(s )x (s -\tau _{ j}(s )) \le \gamma _j^+M\le \widetilde{\kappa }, \end{aligned}$$

(2.8)

where $s\in [t_{1}+r, \ m(t)], \ t\in [t_{2}, \ +\infty ), \ j=1, 2, \ldots , m.$ Note that $xe^{-x}$ increases on $[0, \ 1]$ and decreases on $[1, \ +\infty )$. In view of (2.1), (2.2), (2.7), (2.8) and the fact that $\kappa e^{-\kappa }=\widetilde{\kappa } e^{-\tilde{\kappa }}$, we have

$$\begin{aligned} x (m(t))= & {} e^{-\int _{t_{1}+r}^{m(t)} a(v) \mathrm{d}v}x (t_{1}+r)\\&+\,\int _{t_{1}+r}^{m(t)} e^{ -\int _{s}^{m(t)} a(v) \mathrm{d}v}\sum \limits _{j=1}^{m} \frac{\beta _{j} (s)}{\gamma _{j} (s)} \gamma _{j} (s)x \nonumber \\&\times \, (s-\tau _{j} (s))e^{- \gamma _{j} (s) x (s-\tau _{j} (s))}\mathrm{d}s\\\ge & {} F^{i} e^{-\int _{t_{1}+r}^{m(t)} a^{*}(v) \mathrm{d}v} x (m(t)) \nonumber \\&+\,\int _{t_{1}+r}^{m(t)} e^{ -\int _{s}^{m(t)} a^{*}(v) \mathrm{d}v}\\&\times \,F^{i}\sum \limits _{j=1}^{m} \frac{\beta _{j} (s)}{\gamma _{j} (s)} x (m(t))e^{-x (m(t)) }\mathrm{d}s, \nonumber \\&\quad \hbox {for all } \ t\in [t_{2}, \ +\infty ), \end{aligned}$$

and

$$\begin{aligned} 1\ge & {} F^{i} e^{-\int _{t_{1}+r}^{m(t)} a^{*}(v) \mathrm{d}v} + \int _{t_{1}+r}^{m(t)} e^{ -\int _{s}^{m(t)} a^{*}(v) \mathrm{d}v}F^{i}\nonumber \\&\times \, \sum \limits _{j=1}^{m} \frac{\beta _{j} (s)}{\gamma _{j} (s)} e^{-x (m(t)) }\mathrm{d}s \nonumber \\\ge & {} F^{i} e^{-\int _{t_{1}+r}^{m(t)} a^{*}(v) \mathrm{d}v} + \int _{t_{1}+r}^{m(t)} e^{ -\int _{s}^{m(t)} a^{*}(v) \mathrm{d}v}F^{i}\nonumber \\&\times \, \sum \limits _{j=1}^{m} \frac{\beta _{j} (s)}{\gamma _{j} (s)} e^{-\kappa }\mathrm{d}s \nonumber \\\ge & {} F^{i} e^{-\int _{t_{1}+r}^{m(t)} a^{*}(v) \mathrm{d}v} \nonumber \\&+\,\int _{t_{1}+r}^{m(t)} e^{ -\int _{s}^{m(t)} a^{*}(v) \mathrm{d}v}\left[ \eta ^{i}+a^{*}(s)\right] \mathrm{d}s \nonumber \\\ge & {} F^{i} e^{-\int _{t_{1}+r}^{m(t)} a^{*}(v) \mathrm{d}v} \nonumber \\&+\,\inf \limits _{t\in \mathbb {R}}\frac{ \eta ^{i}}{a^{*}(t)} \left[ 1-e^{-\int _{t_{1}+r}^{m(t)} a^{*}(v) \mathrm{d}v}\right] \nonumber \\&+\,\left[ 1-e^{-\int _{t_{1}+r}^{m(t)} a^{*}(v) \mathrm{d}v}\right] , \quad \nonumber \\&\quad \hbox {for all } \ t \in [t_{2}, \ +\infty ). \end{aligned}$$

(2.9)

Letting $t\rightarrow +\infty$, (2.9) yields

$$\begin{aligned} \inf \limits _{t\in \mathbb {R}}\frac{ \eta ^{i}}{a^{*}(t)}<0, \end{aligned}$$

which contradicts (2.2). Thus, $\liminf \limits _{t\rightarrow +\infty } x(t)\,=\,l>0.$

We next prove that $\liminf \limits _{t\rightarrow +\infty } x(t)\,=\,l>\kappa$. Again, by way of contradiction, we assume that $l\le \kappa$. Then, for any positive constant $\varLambda <l$, there exists $t_{3}>t_{1}+r$ such that

$$\begin{aligned} l-\varLambda\le & {} x (s -\tau _{ j}(s )) \nonumber \\\le & {} \gamma _{ j}(s )x (s -\tau _{ j}(s )) \le \gamma _j^+M\le \widetilde{\kappa }, \nonumber \\&\quad \hbox {for all } s\in [t_{3}, \ +\infty ), \end{aligned}$$

where $j=1, 2, \ldots , m.$ Again from the facts that $\kappa e^{-\kappa }=\widetilde{\kappa } e^{-\tilde{\kappa }}$, $xe^{-x}$ increases on $[0, \ 1]$ and decreases on $[1, \ +\infty )$, we obtain

$$\begin{aligned} x (t)= & {} e^{-\int _{t_{3} }^{t} a(v) \mathrm{d}v}x (t_{3} )\\&+\,\int _{t_{3} }^{t} e^{ -\int _{s}^{t} a(v) \mathrm{d}v}\sum \limits _{j=1}^{m} \frac{\beta _{j} (s)}{\gamma _{j} (s)} \gamma _{j} (s)x (s-\tau _{j} (s))\\&\times \, e^{- \gamma _{j} (s) x (s-\tau _{j} (s))}\mathrm{d}s \\\ge & {} e^{-\int _{t_{3} }^{t} a(v) \mathrm{d}v}x (t_{3} ) + \int _{t_{3} }^{t} e^{ -\int _{s}^{t} a(v) \mathrm{d}v}\\&\times \, \sum \limits _{j=1}^{m} \frac{\beta _{j} (s)}{\gamma _{j} (s)} (l-\varLambda )e^{- (l-\varLambda )}\mathrm{d}s\\\ge & {} e^{-\int _{t_{3} }^{t} a(v) \mathrm{d}v}x (t_{3} ) + \int _{t_{3} }^{t} e^{ -\int _{s}^{t} a(v) \mathrm{d}v}\\&\times \, \sum \limits _{j=1}^{m} \frac{\beta _{j} (s)}{\gamma _{j} (s)} (l-\varLambda )e^{- \kappa }\mathrm{d}s\\\ge & {} F^{i} e^{-\int _{t_{3} }^{t} a^{*}(v) \mathrm{d}v}x (t_{3} ) + F^{i} \int _{t_{3} }^{t} e^{ -\int _{s}^{t} a^{*}(v) \mathrm{d}v}\\&\times \, \sum \limits _{j=1}^{m} \frac{\beta _{j} (s)}{\gamma _{j} (s)} (l-\varLambda )e^{- \kappa }\mathrm{d}s\\\ge & {} F^{i} e^{-\int _{t_{3} }^{t} a^{*}(v) \mathrm{d}v}x (t_{3} ) + \int _{t_{3} }^{t} e^{ -\int _{s}^{t} a^{*}(v) \mathrm{d}v}\\&\times \, (\eta ^{i}+a^{*}(s))(l-\varLambda )\mathrm{d}s\\\ge & {} F^{i} e^{-\int _{t_{3} }^{t} a^{*}(v) \mathrm{d}v}x (t_{3} ) +\,\inf \limits _{t\in \mathbb {R}}\frac{ \eta ^{i}}{a^{*}(t)}(l-\varLambda )\\&\times \, \left[ 1-e^{-\int _{t_{3} }^{t} a^{*}(v) \mathrm{d}v}\right] \\&+\,(l-\varLambda )\left[ 1-e^{-\int _{t_{3} }^{t} a^{*}(v) \mathrm{d}v}\right] \\:= & {} B(t), \quad \hbox {for all } \ t \in [t_{3}, \ +\infty ), \end{aligned}$$

and

$$\begin{aligned} \lim \limits _{t\rightarrow +\infty }B(t)=\inf \limits _{t\in \mathbb {R}}\frac{ \eta ^{i}}{a^{*}(t)}(l-\varLambda )+(l-\varLambda ), \end{aligned}$$

which, together with the arbitrariness of $\varLambda$, entail that

$$\begin{aligned} l= & {} \liminf \limits _{t\rightarrow +\infty }x(t)\\\ge & {} \lim \limits _{t\rightarrow +\infty }B(t)\ \hbox {and } \ l \ge \inf \limits _{t\in \mathbb {R}}\frac{ \eta ^{i}}{a^{*}(t)}l+l>l. \end{aligned}$$

This is a contradiction. Hence, $l>\kappa$ and there exists $t_{4}\in [t_{1}+r, \ +\infty )$ such that

$$\begin{aligned} \kappa <x(t ), \quad \hbox {for all } \ t\in [t_{4}, \ +\infty ). \end{aligned}$$

(2.10)

In view of (2.6) and (2.10), there exists $t _{\varphi }>t_{4}$ such that

$$\begin{aligned} \kappa < x (t; t_{0}, \varphi ) < M \quad \hbox {for all} t \ge t _{\varphi }. \end{aligned}$$

The proof is complete. $\square$

Lemma 2.2

(see [18, Lemma 2.8]) Set

$$\begin{aligned} B^{*}= & {} \bigg \{\varphi |\varphi \in PAP(\mathbb {R},\mathbb {R}) \quad \hbox {is uniformly continuous on }\\&\mathbb {R}, K_{1}\le \varphi (t) \le K_{2}, \quad \hbox {for all } \ t\in \mathbb {R} \bigg \}. \end{aligned}$$

Then, $B^*$ is a closed subset of $PAP(\mathbb {R},\mathbb {R})$.

3 Main results

In this section, we establish sufficient conditions on the existence and global exponential stability of positive pseudo-almost periodic solutions of (1.2).

Theorem 3.1

Let

$$\begin{aligned} \sup \limits _{t\in \mathbb { R} }\bigg \{- a^{*}(t) +\,F^{^{S}}\sum _{j=1}^{m} \beta _{ j} (t)\frac{1}{e^{2}} \bigg \} <0, \end{aligned}$$

(3.1)

and the assumptions of Lemma 2.1 hold. Then, Eq. (1.2) has at least one positive pseudo-almost periodic solution.

Proof

By (3.1), we can choose a constant $\varsigma \in (0, 1]$ such that

$$\begin{aligned} \sup \limits _{t\in R} \bigg \{- a^{*} (t ) + F^{^{S}}\sum \limits _{j=1}^{m}\beta _{ j} (t)\frac{1}{e^{2}} e^{\varsigma }\bigg \} <0. \end{aligned}$$

(3.2)

Set

$$\begin{aligned} B= & {} \bigg \{\varphi |\varphi \in PAP(\mathbb {R},\mathbb {R}) \ \hbox { is uniformly continuous on }\\&\mathbb {R}, \kappa \le \varphi (t) \le M, \quad \hbox {for all } \ t\in \mathbb {R}\bigg \}. \end{aligned}$$

It follows from Lemma 2.2 that B is a closed subset of $PAP(\mathbb {R},\mathbb {R})$. Let $\phi \in B$ and $f(t,z)= \phi (t-z).$ In view of Theorem 5.3 in [12, p. 58] and Definition 5.7 in [12, p. 59], the uniform continuity of $\phi$ implies that $f \in PAP(\mathbb {R}\times \varOmega )$ and f is continuous in $z\in L$ and uniformly in $t\in \mathbb {R}$ for all compact subset L of $\varOmega \subset \mathbb {R}$. This, together with $\tau _{j} \in PAP(\mathbb {R},\mathbb {R})$ and Theorem 5.11 in [12, p. 60], yields

$$\begin{aligned} \phi (t-\tau _{j} (t)) \in PAP(\mathbb {R},\mathbb {R}), \ \ j =1, 2, \ldots , m. \end{aligned}$$

According to Corollary 5.4 in [12, p. 58] and the composition theorem of pseudo-almost periodic functions, we have

$$\begin{aligned} \sum \limits _{j=1}^{m}\beta _{j}(t) \phi (t-\tau _{j} (t) )e^{-\gamma _{j}(t) \phi (t-\tau _{j}(t))} \in PAP(\mathbb {R},\mathbb {R}). \end{aligned}$$

We next consider an auxiliary equation

$$\begin{aligned} x '(t)= & {} -a(t)x(t)+\sum \limits _{j=1}^{m}\beta _{j}(t) \phi (t-\tau _{j} (t) )\nonumber \\&\times \, e^{-\gamma _{j}(t) \phi (t-\tau _{j}(t))}. \end{aligned}$$

(3.3)

In view of the fact that $M[a]>0,$ it follows from Theorem 2.3 in [19] that the system (3.3) has exactly one pseudo-almost periodic solution

$$\begin{aligned} x^{\phi }(t)= & {} \int _{-\infty }^{t}e^{-\int _{s}^{t}a(u)\mathrm{d}u}\Biggl [\sum \limits _{j=1}^{m}\beta _{j}(s) \phi (s-\tau _{j} (s) )\nonumber \\&\times \, e^{-\gamma _{j}(s) \phi (s-\tau _{j}(s))}\Biggr ]\mathrm{d}s, \end{aligned}$$

(3.4)

for any $\phi \in B.$ Define a mapping $T:B\longrightarrow PAP(\mathbb {R},\mathbb {R})$ by setting

$$\begin{aligned} T(\phi (t))=x^{\phi }(t), \ \forall \ \phi \in B. \end{aligned}$$

For any $\phi \in B$, from (2.1) to (2.2), together with the fact that $\sup \limits _{u\ge 0} ue^{- u}=\frac{1}{ e}$, we have

$$\begin{aligned} x^{\phi }(t)= & {} \int _{-\infty }^{t}e^{-\int _{s}^{t}a(u)\mathrm{d}u} \Biggl [\sum \limits _{j=1}^{m}\frac{\beta _{j}(s)}{\gamma _{j}(s)} \gamma _{j}(s)\phi (s\!-\!\tau _{j} (s) )\nonumber \\&\times \, e^{-\gamma _{j}(s) \phi (s-\tau _{j}(s))}\Biggr ]\mathrm{d}s \nonumber \\\le & {} \int _{-\infty }^{t}e^{-\int _{s}^{t}a^{*}(u)\mathrm{d}u} \left[ F^{S}\sum \limits _{j=1}^{m}\frac{\beta _{j}(s)}{\gamma _{j}(s)}\frac{1}{ e}\right] \mathrm{d}s \nonumber \\\le & {} \int _{-\infty }^{t}e^{-\int _{s}^{t}a^{*}(u)\mathrm{d}u}[-\eta ^{S}+a^{*}(s) M] \mathrm{d}s \!\le \! M, \nonumber \\&\hbox {for all } \ t\in \mathbb {R}. \end{aligned}$$

(3.5)

Note that $xe^{-x}$ increases on $[0, \ 1]$ and decreases on $[1, \ +\,\infty )$. In view of (2.1–2.3) and the facts that

$$\begin{aligned} \kappa e^{-\kappa }= & {} \widetilde{\kappa } e^{-\tilde{\kappa }}, \ \ \kappa \le \gamma _{ j}(t )\phi (t -\tau _{ j}(t )) \le \gamma _j^+M\le \widetilde{\kappa }, \\&\hbox {for all } \ t\in \mathbb {R}, ~j=1, 2, \ldots , m, \end{aligned}$$

we obtain

$$\begin{aligned} x^{\phi }(t)= & {} \int _{-\infty }^{t}e^{-\int _{s}^{t}a(u)\mathrm{d}u} \Biggl [\sum \limits _{j=1}^{m}\frac{\beta _{j}(s)}{\gamma _{j}(s)} \gamma _{j}(s)\phi (s\!-\!\tau _{j} (s) )\nonumber \\&\times \, e^{-\gamma _{j}(s) \phi (s-\tau _{j}(s))}\Biggr ]\mathrm{d}s \nonumber \\\ge & {} \int _{-\infty }^{t}e^{-\int _{s}^{t}a^{*}(u)\mathrm{d}u} F^{i}\sum \limits _{j=1}^{m}\frac{\beta _{j}(s)}{\gamma _{j}(s)}\kappa e^{-\kappa }\mathrm{d}s \nonumber \\\ge & {} \int _{-\infty }^{t}e^{-\int _{s}^{t}a^{*}(u)\mathrm{d}u}[\eta ^{i}+a^{*}(s)] \kappa \mathrm{d}s\ge \kappa , \nonumber \\&\hbox {for all } \ t\in \mathbb {R}, \end{aligned}$$

(3.6)

which, together with (3.5), leads to

$$\begin{aligned} \kappa \le x^{\phi }(t) \le M, \quad \hbox {for all } \ t\in \mathbb {R} . \end{aligned}$$

(3.7)

Subsequently, from (3.3), we get that $(x ^{\phi }(t))'$ is bounded $\hbox {for all } \ t\in \mathbb {R}$, and

$$\begin{aligned} x ^{\phi } \in PAP(\mathbb {R},\mathbb {R} ) \ \hbox { is uniformly continuous on } \mathbb {R}. \end{aligned}$$

Thus, $x ^{\phi } \in B$, and the mapping T is a self-mapping from B to B .

Now, we prove that the mapping T is a contraction mapping on B .

In fact, for $\varphi , \psi \in B$, we get

$$\begin{aligned}&\Vert T(\varphi )-T(\psi )\Vert _{\infty } \nonumber \\&\quad = \sup _{t \in R}\Biggl |\int _{-\infty }^{t}e^{-\int _{s}^{t}a(u)\mathrm{d}u}\nonumber \\&\qquad \times \, \sum \limits _{j=1}^{m}\Biggl [\frac{\beta _{j} (s)}{\gamma _{j} (s)}(\gamma _{j} (s)\varphi (s-\tau _{j} (s))e^{-\gamma _{j} (s)\varphi (s-\tau _{j}(s))}\nonumber \\&\qquad -\gamma _{j} (s)\psi (s-\tau _{j} (s))e^{-\gamma _{j} (s)\psi (s-\tau _{j}(s))}) \Biggr ]\mathrm{d}s\Biggr | \nonumber \\&\quad \le \sup _{t \in R}\int _{-\infty }^{t}e^{-\int _{s}^{t}a(u)\mathrm{d}u} \sum \limits _{j=1}^{m}\Biggl [\frac{\beta _{j} (s)}{\gamma _{j} (s)}|\gamma _{j} (s)\varphi \nonumber \\&\qquad \times \, (s-\tau _{j} (s)) e^{-\gamma _{j} (s)\varphi (s-\tau _{j}(s))} \nonumber \\&\qquad -\gamma _{j} (s)\psi (s-\tau _{j} (s))e^{-\gamma _{j} (s)\psi (s-\tau _{j}(s))} | \Biggr ]\mathrm{d}s. \end{aligned}$$

(3.8)

In view of $\sup \limits _{\kappa \le u \le \widetilde{\kappa }}|\frac{1-u}{e^{u}}|=\frac{1}{e^{2}}$ and the inequality

$$\begin{aligned} |xe^{-x}-ye^{-y}|= & {} \left| \frac{1-(x+\theta (y-x))}{e^{x+\theta (y-x)}}\right| \,| x -y |\nonumber \\\le & {} \frac{1}{e^{2}}| x -y | \ \hbox { where } \nonumber \\&x,y\in [\kappa , \ +\infty ), \ 0< \theta <1, \end{aligned}$$

(3.9)

then, (2.1) and (2.6) give us that

$$\begin{aligned}&\Vert T(\varphi )-T(\psi )\Vert _{\infty } \\&\quad \le \sup _{t \in R}\int _{-\infty }^{t}e^{-\int _{s}^{t}a^{*}(u)\mathrm{d}u}F^{S} \sum \limits _{j=1}^{m}\beta _{j} (s)\\&\qquad \times \,\frac{1}{e^{2}} |\varphi (s-\tau _{j}(s)) - \psi (s-\tau _{j}(s))| \mathrm{d}s\\&\quad \le \Vert \varphi -\psi \Vert _{\infty }\sup _{t \in R}\int _{-\infty }^{t}e^{-\int _{s}^{t}a^{*}(u)\mathrm{d}u}F^{S}\\&\qquad \times \,\sum \limits _{j=1}^{m}\beta _{j} (s)\frac{1}{e^{2}} \mathrm{d}s \\&\quad \le \Vert \varphi -\psi \Vert _{\infty }\sup _{t \in R}\int _{-\infty }^{t}e^{-\int _{s}^{t}a^{*}(u)\mathrm{d}u}a^{*}(s)\frac{1}{e ^{\varsigma }} \mathrm{d}s\\&\quad \le \frac{1}{e ^{\varsigma }}\Vert \varphi -\psi \Vert _{\infty }, \end{aligned}$$

It follows from $e^{-\varsigma }<1$ that the mapping T is a contraction on B . Using Theorem 0.3.1 of [20], we obtain that the mapping T possesses a unique fixed point $\varphi ^{*}\in B$, $T\varphi ^{*}=\varphi ^{*}$. By (3.2), $\varphi ^{*}$ satisfies (1.2). So $\varphi ^{*}$ is a positive pseudo-almost periodic solution of (1.2) in B . This completes the proof.

Theorem 3.2

Suppose that all conditions in Theorem 3.1 are satisfied. Let $x^{*}(t)$ be the positive pseudo-almost periodic solution of Eq. (1.2) in Theorem 3.1. Then, $x^{*}(t)$ is globally exponentially stable, i.e., the solution $x(t; t_{0}, \varphi )$ of (1.2) with admissible initial conditions (1.4) converges exponentially to $x ^{* }(t )$ as $t\rightarrow +\infty$.

Proof

By (3.1), we can choose a constant $\lambda \in (0, \ \inf \limits _{t\in \mathbb {R}}a^{* }(t )]$ such that

$$\begin{aligned} \sup \limits _{t\in R} \bigg \{- a^{*} (t )+\lambda + F^{^{S}}\sum \limits _{j=1}^{m}\beta _{ j} (t)\frac{1}{e^{2}}e^{ \lambda \tau _{j} ^{+}} \bigg \} <0. \nonumber \\ \end{aligned}$$

(3.10)

Assume that $x^{*}(t)$ is the positive pseudo-almost periodic solution of Eq. (1.2)  in Theorem 3.1. To prove Theorem 3.2, we should show the global exponential stability for $x^{*}(t)$. Let $x (t )= x (t; t_{0},\varphi )$. In view of Lemma 2.1, we have that there exists $t _{\varphi }\in [t_{0}, \ +\infty )$ such that

$$\begin{aligned} \kappa <x(t)<M \quad \hbox {for all } t\in [t _{\varphi }, \ +\infty ). \end{aligned}$$

(3.11)

Set $y(t)=x (t )-x^{*}(t).$ Then

$$\begin{aligned} y' (t)= & {} -a(t)y(t) \\&+\,\sum \limits _{j=1}^{m}\beta _{j}(t) [x (t-\tau _{j} (t) )e^{-\gamma _{j}(t) x(t-\tau _{j}(t))}\\&-\,x^{*} (t-\tau _{j} (t) )e^{-\gamma _{j}(t) x^{*}(t-\tau _{j}(t))}], \end{aligned}$$

and

$$\begin{aligned} y (t)= & {} e^{-\int _{t_{0}}^{t} a(v) \mathrm{d}v}y (t_{0}) \nonumber \\&+\,\int _{t_{0}}^{t} e^{ -\int _{s}^{t} a(v) \mathrm{d}v}\sum \limits _{j=1}^{m} \frac{\beta _{j} (s)}{\gamma _{j} (s)}\nonumber \\&\times \,[\gamma _{j} (s)x (s-\tau _{j} (s))e^{- \gamma _{j} (s) x (s-\tau _{j} (s))}\nonumber \\&-\gamma _{j} (s)x ^{*}(s-\tau _{j} (s))e^{- \gamma _{j} (s) x^{*} (s-\tau _{j} (s))}]\mathrm{d}s, \nonumber \\ \end{aligned}$$

(3.12)

$\hbox { where } \ t\in [t_{0}, \ +\infty ).$

Let

$$\begin{aligned} t_{\xi }= & {} t _{\varphi }+r, \ K_{\varphi }=F^{S}+1, \ \ \Vert y\Vert _{\xi }\nonumber \\= & {} \max \limits _{t\in [t_{0}-r, \ t_{\xi } ]}|x(t)-x^{*} (t)|. \end{aligned}$$

(3.13)

Consequently, for any $\varepsilon >0$, it is obvious that

$$\begin{aligned} |y(t_{\xi })|< & {} \Vert y\Vert _{\xi }+\varepsilon , \\ |y(t) |< & {} K_{\varphi }(\Vert y\Vert _{\xi }+\varepsilon )e^{ \lambda t_{\xi }}e^{-\lambda t},\\&\hbox {for all } t \in [t_{0}-r, \ t_{\xi } ]. \end{aligned}$$

In the following, we will show

$$\begin{aligned} \Vert y(t)\Vert< & {} K_{\varphi }(\Vert y\Vert _{\xi }+\varepsilon )e^{ \lambda t_{\xi }}e^{-\lambda t} \nonumber \\&\hbox {for all } t > t_{\xi }. \end{aligned}$$

(3.14)

Otherwise, there must exist $\theta >t_{\xi }$ such that

$$\begin{aligned} \left\{ \begin{array}{lll} |y(\theta ) |&{}=&{} K_{\varphi }(\Vert y\Vert _{\xi }+\varepsilon )e^{ \lambda t_{\xi }} e^{-\lambda \theta },\\ |y(t) | &{}<&{}K_{\varphi }(\Vert y\Vert _{\xi }+\varepsilon )e^{ \lambda t_{\xi }}e^{-\lambda t}, \quad \hbox {for all } t \in [t_{0}-r, \ \theta ). \end{array} \right. \nonumber \\ \end{aligned}$$

(3.15)

With the help of (3.9), (3.11), (3.12), (3.13) and (3.15), we have

$$\begin{aligned} | y (\theta )|= & {} e^{-\int _{t_{\xi }}^{\theta } a(v) \mathrm{d}v}|y (t_{\xi })| \\&+\,\int _{t_{\xi }}^{\theta } e^{ -\int _{s}^{\theta } a(v) \mathrm{d}v}\sum \limits _{j=1}^{m} \frac{\beta _{j} (s)}{\gamma _{j} (s)}\nonumber \\&\times \,|\gamma _{j} (s)x (s-\tau _{j} (s))e^{- \gamma _{j} (s) x (s-\tau _{j} (s))}\\&-\gamma _{j} (s)x ^{*}(s-\tau _{j} (s))e^{- \gamma _{j} (s) x^{*} (s-\tau _{j} (s))}|\mathrm{d}s\\\le & {} F^{S} e^{-\int _{t_{\xi }}^{\theta } a^{*}(v) \mathrm{d}v}|y (t_{\xi })| + \int _{t_{\xi }}^{\theta } e^{ -\int _{s}^{\theta } a^{*}(v) \mathrm{d}v} F^{S}\\&\times \,\sum \limits _{j=1}^{m}\beta _{j} (s)\frac{1}{e^{2}} |y (s-\tau _{j}(s))|\mathrm{d}s \\\le & {} F^{S} e^{-\int _{t_{\xi }}^{\theta } a^{*}(v) \mathrm{d}v}(\Vert y\Vert _{\xi }+\varepsilon )\\&+\,\int _{t_{\xi }}^{\theta } e^{ -\int _{s}^{\theta } a^{*}(v) \mathrm{d}v} F^{S}\\&\times \,\sum \limits _{j=1}^{m}\beta _{j} (s)\frac{1}{e^{2}} K_{\varphi }(\Vert y\Vert _{\xi }+\varepsilon )e^{ \lambda t_{\xi }}e^{-\lambda (s-\tau _{j}(s))} \mathrm{d}s \\ \end{aligned}$$

$$\begin{aligned}\le & {} K_{\varphi }(\Vert y\Vert _{\xi }+\varepsilon )e^{ \lambda t_{\xi }}e^{ -\lambda \theta }\\&\times \,\Biggl [\frac{F^{S}}{K_{\varphi }} e^{-\int _{t_{\xi }}^{\theta } a^{*}(v) \mathrm{d}v}e^{ \lambda (\theta - t_{\xi })}\\&+\,e^{ \lambda \theta }\int _{t_{\xi }}^{\theta } e^{ -\int _{s}^{\theta } a^{*}(v) \mathrm{d}v} F^{S}\\&\times \,\sum \limits _{j=1}^{m}\beta _{j} (s)\frac{1}{e^{2}}e^{ \lambda \tau _{j} ^{+}} e^{-\lambda s } \mathrm{d}s \Biggr ]\\= & {} K_{\varphi }(\Vert y\Vert _{\xi }+\varepsilon )e^{ \lambda t_{\xi }}e^{ -\lambda \theta }\Biggl [\frac{F^{S}}{K_{\varphi }} e^{-\int _{t_{\xi }}^{\theta } (a^{*}(v)-\lambda ) \mathrm{d}v}\\&+\,\int _{t_{\xi }}^{\theta } e^{ -\int _{s}^{\theta } (a^{*}(v)-\lambda ) \mathrm{d}v} F^{S}\sum \limits _{j=1}^{m}\beta _{j} (s)\frac{1}{e^{2}}e^{ \lambda \tau _{j} ^{+}} \mathrm{d}s \Biggr ]\\\le & {} K_{\varphi }(\Vert y\Vert _{\xi }+\varepsilon )e^{ \lambda t_{\xi }}e^{ -\lambda \theta }\Biggl [\frac{F^{S}}{K_{\varphi }} e^{-\int _{t_{\xi }}^{\theta } (a^{*}(v)-\lambda ) \mathrm{d}v}\\&+\,\int _{t_{\xi }}^{\theta } e^{ -\int _{s}^{\theta } (a^{*}(v)-\lambda ) \mathrm{d}v} (a^{*}(s)-\lambda ) \mathrm{d}s \Biggr ]\\\le & {} K_{\varphi }(\Vert y\Vert _{\xi }+\varepsilon )e^{ \lambda t_{\xi }}e^{ -\lambda \theta }\\&\times \,\Biggl [1-\Biggl (1-\frac{F^{S}}{K_{\varphi }}\Biggr ) e^{-\int _{t_{\xi }}^{\theta } (a^{*}(v)-\lambda ) \mathrm{d}v}\Biggr ]\\< & {} K_{\varphi }(\Vert y\Vert _{\xi }+\varepsilon )e^{ \lambda t_{\xi }}e^{ -\lambda \theta }, \end{aligned}$$

which contradicts the first Eq. in (3.15). Hence, (3.14) holds. Letting $\varepsilon \longrightarrow 0^{+}$, we have from (3.14) that

$$\begin{aligned} |y(t) | \le K_{\varphi } \Vert y\Vert _{\xi } e^{ \lambda t_{\xi }}e^{-\lambda t} \quad \hbox { for all } t > t_{\xi }, \end{aligned}$$

which ends the proof. $\square$

Remark 3.1

Most recently, Liu [6, 10] considered the periodic solution and almost periodic solution problem of (1.2) with almost periodic coefficients and delays under the following assumption:

$$\begin{aligned} a(t)\equiv a^{*}(t) ~\hbox {satisfies}~ (2.1), (2.2), (2.3)~ \hbox {and }~ (3.1). \end{aligned}$$

Noting that the pseudo-almost periodic functions is a natural generalization of the concept of almost periodicity and the fact that $AP(\mathbb {R},\mathbb {R})$ is a proper subspace of $PAP(\mathbb {R},\mathbb {R})$ (see [12]), it is obvious that all the results in [6, 10] are special cases of our results.

4 Example and remark

Example 4.1

Consider the following Nicholson’s blowflies model with an oscillating death rate:

$$\begin{aligned} x' (t)= & {} - (0.4040326+\sin 200 t)x(t)\nonumber \\&+\,\frac{1}{2}\frac{100+ \cos \sqrt{2} t}{100+ \sin t} x(t- \sin ^{2}t-e^{ -t^{2}\sin ^{4 }t })\nonumber \\&\times \,e^{ -x(t-\sin ^{2}t-e^{ -t^{2}\sin ^{4 }t })}\nonumber \\&+\,\frac{1}{2}\frac{100+ \cos \sqrt{3} t}{100+ \sin t} x(t- \cos ^{2}t-e^{ -t^{2}\sin ^{4 }t }) \nonumber \\&\times \,e^{ -x(t-\cos ^{2}t-e^{ -t^{2}\sin ^{4 }t })}. \end{aligned}$$

(4.1)

Fig. 1

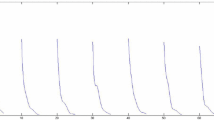
Numerical solutions x(t) of system (3.1) for initial value $x_{0}\equiv 0.93, 0.96, 1$

Obviously,

$$\begin{aligned}&a (t)= 0.4040326 +\sin 200 t, a^{*}(t) = 0.4040326,\\&\quad F^{S}= e^{ \frac{1}{100}}, \ F^{i}= e^{-\frac{1}{100}},\\&\quad F^{i} e ^{ -\int _{s}^{t}a^{*}( u)\mathrm{d}u}\le e ^{ -\int _{s}^{t}a ( u)\mathrm{d}u}\le F^{S} e ^{ -\int _{s}^{t}a^{*}( u)\mathrm{d}u}, \\&\qquad \hbox {for all }\quad t,s\in \mathbb {R}\quad \hbox {and}\quad t-s\ge 0,\\&M[a]=\lim \limits _{T\rightarrow +\infty }\frac{1}{T}\int _{t}^{t+T}a(s)\mathrm{d}s\\&\quad =0.4040326+\lim \limits _{T\rightarrow +\infty } \frac{1}{200T}\\&\qquad \times \,[\cos 200 t -\cos 200(t+T) ]=0.4040326, \\&\qquad r=2, \quad \beta _{i}^-=\frac{1}{2}\frac{99}{101}, \quad \beta _{j}^+= \frac{1}{2}\frac{101}{99}, \quad \\&\qquad \gamma _{1}^-=\gamma _{1}^+=1. \end{aligned}$$

Note $\kappa \approx 0.7215355$ and $\tilde{\kappa }\approx 1.342276$. Let $M=1.203432$. Then

$$\begin{aligned} a^{*} M= & {} 0.4040326 \times 1.203432 \\\approx & {} 0.4862258, \end{aligned}$$

$$\begin{aligned} F^{S}\left( \frac{\beta ^{+}_{1}}{\gamma ^{-}_{1}} \frac{1}{e}+\frac{\beta ^{+}_{2}}{\gamma ^{-}_{2}}\right) \frac{1}{e}= & {} e^{ \frac{1}{100}}\frac{101}{99}\frac{1}{e}\approx 0.37,\\ F^{i}\left( \frac{\beta _{1}^{-}}{\gamma _{1}^{+}}+\frac{\beta _{2}^{-}}{\gamma _{2}^{+}}\right) e^{-\kappa }= & {} e^{ -\frac{1}{100}} \frac{99}{101}e^{-\kappa }\\\approx & {} \frac{99}{101}e^{-0.7215355}\approx 0.47, \end{aligned}$$

$$\begin{aligned} F^{S}(\beta _{ 1} ^{+}+\beta _{ 2} ^{+})\frac{1}{e^{2}}= & {} e^{ \frac{1}{100}}\frac{101}{99}\frac{1}{e^{2}}\approx 0.13, \end{aligned}$$

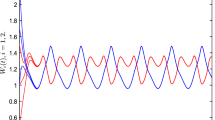
which implies that the Nicholson’s blowflies model (4.1) satisfies all the conditions in Theorem 3.2. Hence, from Theorem 3.2, Eq. (4.1) has exactly one positive pseudo-almost periodic solution $x^{*}(t)$. Moreover, $x^{*}(t)$ is globally exponentially stable. This fact is verified by the numerical simulations in Figs. 1 and 2. In this case, $x^{*}(t)\in [0.7215355, \ 1.203432]$, and the solution $x(t; t_{0}, \varphi )$ of (4.1) with $x_{0}\equiv 0.93, 0.96, 1, 0.1, 0.20.5, 0.8$ converges exponentially to $x ^{* }(t )$ as $t\rightarrow +\infty$, where the exponential convergent rate $\lambda$ is approximately equal to 0.01.

Fig. 2

Numerical solutions x(t) of system (3.1) for initial value $x_{0}\equiv 0.1, 0.20.5, 0.8$

Remark 4.1

It is worth mentioning that computing the upper right derivative of Lyapunov function is the key method to prove the stability of biological dynamics model in [3–5, 7–9, 21, 22], which is invalid for the Nicholson’s blowflies model with oscillating death rate coefficients. In (4.1), the time-varying oscillating death rate

$$\begin{aligned} a (t)= 0.4040326 +\sin 200 t \end{aligned}$$

is oscillating, and doesn’t satisfy $(A_{0})$. For all we know, there is no research on the global exponential stability of positive pseudo-almost periodic solutions of Nicholson’s blowflies model with oscillating death rate. Thus, all the results in the Refs. [3–5, 7–9] and [21, 22] cannot be applicable to prove that all the solutions of (4.1) converge exponentially to the positive pseudo-almost periodic solution.

5 Conclusions

In this paper, the global exponential stability of positive pseudo-almost periodic solution for a Nicholson’s blowflies model has been analyzed. Without assuming that the death rate is not oscillating, based on the pseudo-almost periodic function theory and differential inequality techniques, we employ a novel proof to establish some criteria to guarantee the existence and global exponential stability of positive pseudo-almost periodic solution for the model. Finally, two numerical simulation figures are given to demonstrate the effectiveness and feasibility of the theoretical results. Moreover, the method used in this paper provides a possible approach to study the pseudo-almost periodic problem of the higher dimension Nicholson’s blowflies systems with oscillating death rates. This is the aim of our future work.