1 Introduction

Sliding mode control (SMC) technique has attractive properties such as strong robustness in contrast to the variations of the parameters, fast response, remarkable transient performance, satisfactory computational simplicity, guaranteed stability, precise control, easy implementation, and insensitivity to the matched parametric uncertainties and external disturbances [1–4]. Generally, the design of SMC consists of two main steps: (a) the definition of a switching surface and (b) the design of a control law to derive the states to the sliding mode [5, 6]. The most significant trait of SMC is that after reaching the sliding surface, the controlled system is completely robust against the parameter variations and external disturbances [7, 8]. Nevertheless, during the reaching phase of SMC, the system can be destabilized by matched uncertainties and disturbances [9]. In SMC, the control signal is changed from one value to an infinite value with fast rate, and the mentioned action is undesirable in the practical dynamical systems [10, 11]. This undesired switching effect is called chattering phenomenon [12]. In the recent years, the concept of global sliding mode control (GSMC) method is proposed to offer a general structure to eliminate the reaching phase and to overcome the chattering problem which is undesirable for most systems [13–15]. In GSMC, by using an extra term in the switching curve, the reaching interval of SMC is removed and the states move on the switching curve exactly from the beginning [16, 17]. Actually, GSMC has been widely employed into practice since it can guarantee the robustness and acceleration of the system and remove the reaching phase [18, 19].

Recently, more attentions are paid for the application of GSMC technique [20]. In [13], an LMI-based GSMC is suggested for asymptotic stabilization and improving the stability of the uncertain nonlinear systems. In [20], the stability problem of nonlinear systems using the GSMC approach is established to force the state trajectories to be stable and improve the stability and robustness performances. In [21], an output-feedback SMC technique is suggested for SISO uncertain nonlinear time-varying systems using variable gain observer which attains global tracking performance with respect to a small residual set. In [22], a GSMC tracking control scheme is proposed for a helicopter with the effects of input delays and external disturbances. In [23], an adaptive backstepping GSMC technique is presented for tracking control problem of flight simulator servo-systems with parametric uncertainties and nonlinear friction compensations. In [24], a GSMC method is offered for the missile actuator servo-system with high uncertainties where using a new optimal integral switching function based on the linear quadratic regulator (LQR) concept, the initial states of the controlled system are set on the sliding curve, and the optimal switching motion is satisfied. In [25], a backstepping-based global fuzzy SMC method for tracking controller design of multi-joint robotic manipulators is presented which is focused on the chattering phenomenon of SMC. In [26], a GSMC based on the disturbance observer and LQR is proposed for the tracking control of motor servo-systems which their performance is assailable to the parameter variations and external disturbances. All mentioned works were proposed under the assumption that the upper bounds of the system uncertainties and external disturbances are known. To the best of our knowledge, a very little consideration has been paid to the same problem when the upper bounds of the uncertain terms are unknown; therefore, it is still open in the literature. Also, no GSMC procedure based on the damping ratio improvement is employed to modify the steady-state and transient performances of disturbed nonlinear systems. These goals motivate the presentation of our research.

In this paper, an adaptive GSMC approach is developed to eliminate the reaching interval and overcome the chattering problem. Using a nonlinear function in the global nonlinear switching surface, the damping ratio of the disturbed nonlinear system is improved to a high value and finally the performance of the system is improved. Moreover, an adaptive gain tuning control procedure is adapted in the offered GSMC which estimates the unknown upper bound of the external disturbances and guarantees the finite-time convergence to the switching surface. Finally, some numerical simulations on Genesio chaotic system are presented to validate the effectiveness and applicability of the recommended technique. The objective of this paper is to present GSMC to stabilize the nonlinear systems in the existence of system uncertainties and external disturbances. The main contributions of this research can be listed as follows:

  • An adaptive GSMC with finite-time convergence is suggested for the transient performance improvement of disturbed nonlinear systems.

  • An adaptation law is proposed, and by using it, the information for the upper bounds of the disturbances is not required.

  • By elimination of the reaching mode, the robustness performance against nonlinearity and disturbances is satisfied right from the beginning.

  • The suggested control law removes the chattering problem, and hence, it is suitable for the practical applications.

This paper is organized as follows: Sect. 2 depicts the problem description. The stability analysis and the planned control scheme are presented in Sect. 3. In Sect. 4, the suggested technique is employed to control the Genesio chaotic systems and the simulation results are presented. Finally, the conclusions are addressed in Sect. 5.

2 Problem description

Consider the disturbed nonlinear dynamical system described by:

$$\begin{aligned} \dot{x}(t)= & {} Ax(t)+B\left( {u(t)+f(x)} \right) , \nonumber \\ y(t)= & {} Cx(t), \end{aligned}$$
(1)

where \(x(t)\in R^{n},\, y(t)\in R^{p}\) and \(u(t)\in R^{m}\) represent the state vector, the system output and the control input, respectively. The function f(x) is the external disturbance, and \(A,\, B,\, C\) are matrices of appropriate dimensions. Without loss of generality, we assume \(x(t)=\left[ x_1^T (t) x_2^T (t)\right] ^{T},\, A=\left[ {{\begin{array}{ll} {A_{11}} &{} {A_{12}} \\ {A_{21}} &{} {A_{22}} \\ \end{array} }} \right] \), and \(B=[0 B_2^T ]^{T}\), where \(B_2 \) with \(m\times m\) dimensions is a nonsingular matrix. Hence, from (1), the following dynamics is obtained:

$$\begin{aligned} \begin{aligned}&\dot{x}_1 (t)=A_{11} x_1 (t)+A_{12} x_2 (t), \\&\dot{x}_2 (t)=A_{21} x_1 (t)\\&\quad \qquad +A_{22} x_2 (t)+B_2 u(t)+B_2 f(x), \\&y(t)=Cx(t). \end{aligned} \end{aligned}$$
(2)

Assumption 1

Pair (A, B) is completely controllable; then, one can conclude that using the dynamics (2), the controllability of (A, B) results that of \((A_{11} ,A_{12} )\). For any given symmetric and positive-definite matrix W, there exists an unique symmetric positive-definite matrix P as the solution of the subsequent Lyapunov criterion:

$$\begin{aligned} \left( {A_{11} -A_{12} F} \right) ^{T}P+P\left( {A_{11} -A_{12} F} \right) =-W. \end{aligned}$$
(3)

3 Adaptive GSMC design for disturbed nonlinear system

The global nonlinear sliding surface for system (2) is specified as:

$$\begin{aligned} s(t)=G(t)\left( {x(t)-H_n (t)x(0)} \right) , \end{aligned}$$
(4)

with

$$\begin{aligned} G(t)=\left[ F-\psi (x_1 )A_{12}^T P \,\, I_{m}\right] , \end{aligned}$$
(5)

where \(I_m\) is \(m\times m\) identity matrix, P is an \((n-m)\times (n-m)\) positive-definite matrix, F is an \(m\times (n-m)\) constant gain matrix, \(\psi (x_1 )\) is a diagonal \(m\times m\) matrix with nonpositive nonlinear functions of \(x_1 (t)\), and \(H_n (t)=\hbox {diag}[e^{-\beta _1 t}, \ldots , e^{-\beta _n t}]\), where \(\beta _i >0 (i=1, 2, \ldots , n)\) are appropriate constants. Furthermore, the following inequality can be satisfied for some constants \(\rho , q>0\):

$$\begin{aligned} \left\| {H_n (t)} \right\| \le qe^{-\rho t}. \end{aligned}$$
(6)

The nonlinear function \(\psi (x_1)\) is chosen in the form of an exponential function as:

$$\begin{aligned} \psi (x_1 )= & {} \hbox {diag}[\psi _1 (x_1 ), \ldots , \psi _m (x_1 )], \end{aligned}$$
(7)
$$\begin{aligned} \psi _i (x_1 )= & {} -\frac{\mu _i }{1-e^{-1}}\left( {e^{-\left( {\frac{x_1 (t)}{x_1 (0)}} \right) ^{2}}-e^{-1}} \right) , \end{aligned}$$
(8)

where \(x_1 (0)\) is the initial value of \(x_1 (t)\) and \(\mu _i \) is a positive constant. The function \(\psi _i (x_1 )\) changes its value from 0 to \(-\mu _i \) as the state value \(x_1 (t)\) approaches to the origin from the initial value. During the sliding mode \(s(t)=0\), from (4), we obtain:

$$\begin{aligned} x_2 (t)=\left( {\psi (x_1 )A_{12}^T P-F} \right) x_1 (t)+G(t)H_n (t)x(0),\nonumber \\ \end{aligned}$$
(9)

where substituting (9) in (2) yields:

$$\begin{aligned} \dot{x}_1 (t)= & {} \left( {A_{11} -A_{12} F+A_{12} \psi (x_1 )A_{12}^T P} \right) x_1 (t) \nonumber \\&+\,A_{12} G(t)H_n (t)x(0). \end{aligned}$$
(10)

Theorem 1

Consider the closed-loop system (10). Suppose that the Assumption 1 is satisfied. Then, the sliding dynamics (10) converges exponentially to the origin.

Proof

Let the Lyapunov function candidate be described by:

$$\begin{aligned} V_1 (t)=x_1^T (t)Px_1 (t), \end{aligned}$$
(11)

where P is the positive-definite matrix. Differentiating (11) along the trajectory of the dynamics (10) gives:

$$\begin{aligned} \dot{V}_1 (t)= & {} x_1^T (t)P\dot{x}_1 (t)+\dot{x}_1^T (t)Px_1 (t) \nonumber \\= & {} x_1^T (t)\left\{ P\left( {A_{11} -A_{12} F+A_{12} \psi (x_1 )A_{12}^T P} \right) \right. \nonumber \\&+\left. \left( {A_{11} -A_{12} F+A_{12} \psi (x_1 )A_{12}^T P} \right) ^{T}P \right\} x_1 (t) \nonumber \\&+\,x_1^T (t)PA_{12} G(t)H_n (t)x(0) \nonumber \\&+\,\left( {A_{12} G(t)H_n (t)x(0)} \right) ^{T}Px_1 (t). \end{aligned}$$
(12)

Taking the limit of \(H_n (t)\) as t goes to infinity follows that:

$$\begin{aligned} \mathop {\lim }\limits _{t\rightarrow \infty } H_n (t)=0, \end{aligned}$$
(13)

and then using (3) and (13), (12) is simplified as:

$$\begin{aligned} \dot{V}_1 (t)=x_1^T (t)\left\{ {-W+2PA_{12} \psi (x_1 )A_{12}^T P} \right\} x_1 (t).\nonumber \\ \end{aligned}$$
(14)

Since \(\psi (x_1 )<0\) and \(W>0\), then (14) is obtained as:

$$\begin{aligned} \dot{V}_1 (t)\le & {} -x_1^T (t)Wx_1 (t) \nonumber \\\le & {} -\lambda _{\min } (W)\left\| {x_1 (t)} \right\| ^{2}<0, \end{aligned}$$
(15)

where \(\lambda _{\min } (W)\) signifies the lowest eigenvalue of W. Hence, it is simply demonstrated that (15) is represented as:

$$\begin{aligned} \dot{V}_1 (t) \le -\alpha _1 V_1 (t), \end{aligned}$$
(16)

with:

$$\begin{aligned} \alpha _1 ={\lambda _{\min } (W)}/{\lambda _{\max } (P)}, \end{aligned}$$
(17)

where it is obvious that \(\alpha _1 >0\). \(\square \)

Theorem 2

The disturbed nonlinear dynamics (2) is considered. Applying the control signal as:

$$\begin{aligned} u(t)= & {} -\left( {G(t)B} \right) ^{-1}\left\{ \dot{G}(t)\left[ {x(t)-H_n (t)x(0)} \right] \right. \nonumber \\&+\,G(t)Ax(t)-G(t)\dot{H}_n (t)x(0)+k_1 s(t) \nonumber \\&\left. +\,k_2 \,\mathrm{sgn}(s(t)) \right\} , \end{aligned}$$
(18)

with \(k_1 >0\) and \(k_2 >\left| {G(t)Bf(x)} \right| \), then the state trajectories of the system (2) are moved from initial conditions to the switching surface (4) in the finite time and remained on it.

Proof

The Lyapunov function candidate is defined as:

$$\begin{aligned} V_2 (t)=\frac{1}{2}s^{T}(t)s(t). \end{aligned}$$
(19)

Calculating the time derivative of \(V_2 (t)\) along the trajectories of (1) and (4) gives:

$$\begin{aligned} \dot{V}_2 (t)= & {} s^{T}(t)\dot{s}(t) \nonumber \\= & {} s^{T}(t)\left\{ \dot{G}(t)\left( {x(t)-H_n (t)x(0)} \right) \right. \nonumber \\&\left. +\,G(t)\left( {\dot{x}(t)-\dot{H}_n (t)x(0)} \right) \right\} \nonumber \\= & {} s^{T}(t)\left\{ \dot{G}(t)\left( {x(t)-H_n (t)x(0)} \right) \right. \nonumber \\&+\,G(t)Ax(t) -\,G(t)\dot{H}_n (t)x(0)\nonumber \\&+\left. \Delta f(x)+G(t)Bu(t) \right\} , \end{aligned}$$
(20)

where \(\Delta f(x)=G(t)Bf(x)\). Substituting (18) in (20), one can obtain:

$$\begin{aligned} \dot{V}_2 (t)= & {} s^{T}(t)\left\{ {\Delta f(x)-k_1 s(t)-k_2 \,\mathrm{sgn}(s(t))} \right\} \nonumber \\< & {} \left| {s(t)} \right| \left| {\Delta f(x)} \right| -k_2 \left| {s(t)} \right| \nonumber \\= & {} \left| {s(t)} \right| \left( {\left| {\Delta f(x)} \right| -k_2 } \right) <0. \end{aligned}$$
(21)

Thus, the state trajectories are convergent to the switching curve \(s=0\) in the finite time and remain on the curve thereafter. \(\square \)

In practice, the upper bound of the disturbances is unknown; therefore, the term \(\left| {\Delta f(x)} \right| \) is hard to determine. In the following theorem, an adaptive law is adapted to estimate the unknown upper bound of the system disturbance.

Theorem 3

Let the switching surface be in the form of (4) and assume that the external disturbance is unknown but bounded, i.e., \(L>\left| {\Delta f(x)} \right| \), where L is an unknown positive constant. Besides, suppose that \(\hat{{L}}\) is the estimation value of L which is introduced via the following adaptive tuning law:

$$\begin{aligned} \dot{\hat{{L}}}=\kappa \left| {s(t)} \right| , \end{aligned}$$
(22)

where \(\kappa \) is a positive constant. Using the adaptive control law specified by:

$$\begin{aligned} u(t)= & {} -\left( {G(t)B} \right) ^{-1}\left\{ \dot{G}(t)\left[ {x(t)-H_n (t)x(0)} \right] \right. \nonumber \\&+\,G(t)Ax(t)-G(t)\dot{H}_n (t)x(0)+k_1 s(t) \nonumber \\&\left. +\,\hat{{L}} \,\mathrm{sgn}(s(t)) \right\} , \end{aligned}$$
(23)

then the finite-time convergence to the sliding surface \(s(t)=0\) is guaranteed from any initial condition.

Proof

The Lyapunov function candidate is defined as:

$$\begin{aligned} V_3 (t)=\frac{1}{2}s^{T}(t)s(t)+\frac{1}{2}\gamma \tilde{L}^{T}\tilde{L}, \end{aligned}$$
(24)

where \(\tilde{L}=\hat{{L}}-L\). Calculating the time derivative of \(V_3 (t)\) yields:

$$\begin{aligned} \dot{V}_3 (t)= & {} s^{T}(t)\dot{s}(t)+\gamma \tilde{L}\dot{\tilde{L}} \nonumber \\= & {} s^{T}(t)\left\{ \dot{G}(t)\left( {x(t)-H_n (t)x(0)} \right) \right. \nonumber \\&+\,G(t)Ax(t) -G(t)\dot{H}_n (t)x(0)+\Delta f(x) \nonumber \\&+\left. G(t)Bu(t)+\gamma \left( {\hat{{L}}-L} \right) \dot{\hat{{L}}} \right\} , \end{aligned}$$
(25)

where substituting (22) and (23) in (25), one can obtain:

$$\begin{aligned} \dot{V}_3 (t)= & {} s^{T}(t)\left\{ \Delta f(x)-k_1 s(t)-\hat{{L}}\hbox { sgn}(s(t)) \right. \nonumber \\&\left. +\,\gamma \kappa \left( {\hat{{L}}-L} \right) \left| {s(t)} \right| \right\} \nonumber \\\le & {} \left| {s(t)} \right| \left| {\Delta f(x)} \right| -\hat{{L}}\left| {s(t)} \right| +L\left| {s(t)} \right| \nonumber \\&-\,L\left| {s(t)} \right| +\gamma \kappa \left( {\hat{{L}}-L} \right) \left| {s(t)} \right| \nonumber \\= & {} -\left( {L-\left| {\Delta f(x)} \right| } \right) \left| {s(t)} \right| \nonumber \\&-\,\tilde{L}\left( {1-\gamma \kappa } \right) \left| {s(t)} \right| . \end{aligned}$$
(26)

Since \(L>\left| {\Delta f(x)} \right| \) and \(\gamma \kappa <1\), then (26) is expressed as:

$$\begin{aligned} \dot{V}_3 (t)\le & {} -\sqrt{2}\left( {L-\left| {\Delta f(x)} \right| } \right) \frac{\left| {s(t)} \right| }{\sqrt{2}} \nonumber \\&-\,\sqrt{\frac{2}{\gamma }}\left( {1-\gamma \kappa } \right) \left| {s(t)} \right| \frac{\tilde{L}}{\sqrt{\frac{2}{\gamma }}} \nonumber \\\le & {} -\min \left\{ \sqrt{2}\left( {L-\left| {\Delta f(x)} \right| } \right) , \right. \nonumber \\&\left. \sqrt{\frac{2}{\gamma }}\left( {1-\gamma \kappa } \right) \left| {s(t)} \right| \right\} \left( {\frac{\left| {s(t)} \right| }{\sqrt{2}}+\frac{\tilde{L}}{\sqrt{\frac{2}{\gamma }}}} \right) \nonumber \\= & {} -\chi V_3 (t)^{\frac{1}{2}}, \end{aligned}$$
(27)

where \(\chi =\min \left\{ \sqrt{2}\left( L-\left| {\Delta f(x)} \right| \right) , \sqrt{\frac{2}{\gamma }}\left( {1-\gamma \kappa } \right) \left| {s(t)} \right| \right\} >0\). Hence, the convergence to the switching surface \(s=0\) in the finite time is guaranteed from any initial condition. \(\square \)

Since the discontinuous switching function sgn(.) illustrated in (23) creates the chattering phenomenon, inappropriate responses are occurred in the practical systems. To eschew the mentioned phenomenon, the function sgn(.) is replaced by the saturation function as:

$$\begin{aligned} \hbox {sat}(s(t))=\left\{ \begin{array}{ll} \hbox {sgn}(s(\hbox {t})), &{} \quad \left| {s(t)} \right| >\Phi \\ \frac{s(t)}{\Phi }, &{} \quad \left| {s(t)} \right| \le \Phi \\ \end{array} \right. \end{aligned}$$
(28)

where \(\Phi \) is the boundary layer thickness. Furthermore, although the existence of the proposed technique can be guaranteed outside the \(\Phi \), it cannot be satisfied inside the \(\Phi \). In the worst situation, the state trajectories of the system would just reach \(\Phi \). This will obtain a considerable influence on the steady-state characteristics of the system. To reduce the chattering behavior, the control law (23) is modified to the following form:

$$\begin{aligned} u(t)= & {} -\left( {G(t)B} \right) ^{-1}\left\{ \dot{G}(t)\left[ {x(t)-H_n (t)x(0)} \right] \right. \nonumber \\&+\,G(t)Ax(t)-G(t)\dot{H}_n (t)x(0)+k_1 s(t) \nonumber \\&\left. +\,\hat{{L}}\hbox {sat}(s(t)) \right\} . \end{aligned}$$
(29)

4 Simulation results

In this section, the proposed control scheme is employed on a class of chaotic systems to indicate the efficiency of the technique offered in this work. Consider the Genesio chaotic system as [27]:

$$\begin{aligned} \dot{x}_1= & {} x_2 , \nonumber \\ \dot{x}_2= & {} x_3 , \nonumber \\ \dot{x}_3= & {} -cx_1 -bx_2 -ax_3 +x_1^2 , \end{aligned}$$
(30)

where \((x_1 , x_2 , x_3 )\) are the system states, and the coefficients (a, b, c) are the positive constant values with the condition \(ab<c\). The Genesio system has a chaotic behavior with values \(a=1.2,\, b=2.92\) and \(c=6\).

Now, the system (30) is considered to be perturbed by \(\Delta b(x)\) and d(t). Then, the Genesio chaotic system is signified by:

$$\begin{aligned} \dot{x}_1= & {} x_2 , \nonumber \\ \dot{x}_2= & {} x_3 , \nonumber \\ \dot{x}_3= & {} -cx_1 -bx_2 -ax_3 +x_1^2 \nonumber \\&+\,\Delta b(x)+d(t)+u, \end{aligned}$$
(31)

where u denotes the control input, \(\Delta b(x)=0.1\sin (4\pi x_1)\sin (2\pi x_2 )\sin (\pi x_3 )\) and \(d(t)=0.2\cos (4t)\). If the system (31) is expressed in the form of (2), one can obtain:

$$\begin{aligned}&A_{11} = \left[ \begin{array}{ll} 0&{}\quad 1 \\ 0&{}\quad 0 \\ \end{array} \right] , A_{12} =\left[ \begin{array}{l} 0 \\ 1 \\ \end{array}\right] , A_{21} =\left[ \begin{array}{ll} {-6} &{} {-2.92} \\ \end{array}\right] , \\&A_{22} = -1.2, B_2 =1, \\&f(x)= x_1^2 +0.2\cos (4t)+0.1\sin (4\pi x_1 )\\&\quad \quad \quad \quad \sin (2\pi x_2 )\sin (\pi x_3 ). \end{aligned}$$

The simulations are carried out using \(\hbox {Matlab}^{\circledR }\) software. The initial conditions are selected as: \(x(0)=\left[ {{\begin{array}{lll} {-1}&{} 1&{} 0 \\ \end{array} }} \right] ^{T}\). The constant parameters are taken as: \(k_1 =2,\, \kappa =0.1,\, \beta _1 =1,\, \beta _2 =2,\, \beta _3 =3,\, \gamma =1,\, \mu _1 =16,\, \Phi =0.1\), and \(F=\left[ {{\begin{array}{ll} {8.1633}&{} {2.2858} \\ \end{array}}} \right] \). By solving the Lyapunov function (3) for \(W=\left[ {{\begin{array}{ll} {0.1} &{} \quad 0 \\ 0 &{} \quad {0.1} \\ \end{array} }} \right] \), the positive-definite matrix P is obtained as: \(P=\left[ {{\begin{array}{ll} {0.0386} &{} \quad {-0.05} \\ {-0.05} &{} \quad {0.2004} \\ \end{array}}} \right] \).

Fig. 1
figure 1

The chaotic trajectories of the uncertain Genesio system

Full size image
Fig. 2
figure 2

State trajectories of the Genesio chaotic system

Full size image

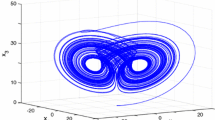
The simulation results of the proposed control method are shown in comparison with the results of the controller of [1]. The chaotic trajectories of uncontrolled uncertain Genesio system are demonstrated in Fig. 1. Figure 2 shows the time responses of the system states. It is noticed that the state trajectories converge fast to the origin in comparison with the linear sliding surface and the method of [1]. Besides, it is evidently observed from Fig. 2 that the overshoot and settling time both decrease considerably in the case of the suggested control technique. A comprehensive comparison of the transient responses is proposed in Table 1. It is obvious from Table 1 that the suggested control method produces zero overshoot and small settling time over those achieved by using the other techniques. As a result, the nonlinear function \(\psi (x_1 )\) in the proposed controller improves the value of the damping ratio. The time responses of the control inputs and sliding surfaces are plotted in Fig. 3. It is evident from Fig. 3 that the proposed control input produces faster and better settling time and low overshoot. Moreover, it is concluded from this figure that the proposed surface approaches to the origin faster than the surface offered in [1]. Time responses of the nonlinear function \(\psi (x_1 )\), the eigenvalues \((\lambda _1 , \lambda _2 )\), and the adaptive gain \(\hat{{L}}\) are demonstrated in Fig. 4. It is obvious from this figure that the nonlinear function value reduces from zero to a negative magnitude as the state \(x_1 (t)\) converges to the origin. These simulations illustrate the efficiency and usefulness of the suggested approach compared to the controller without the nonlinear function \(\psi (x_1 )\) and the control method of [1].

Table 1 Comparison of the performance indices between three methods
Full size table

In the following, the robustness of the designed control method is verified in a different situation. In this scenario, the new values of the initial conditions and external disturbances are set as: \(x(0)=\left[ {{\begin{array}{lll} 1&{} {-1}&{} 2 \\ \end{array} }} \right] ^{T}\), \(f(x)=2x_1^2 +0.5\sin (5\pi t)+0.3\cos (3\pi ^{2}x_1 )\sin (2\pi x_2 t)\cos (3\pi x_3 )\). The trajectories of the system states, control input and sliding surface are shown in Figs. 5 and 6. These figures show the fast transient responses of the suggested controller over the other technique. The results prove the reasonable performance and robustness of the recommended control method in the new situation compared to the controller of [1].

Fig. 3
figure 3

Control input u(t) and sliding surface s(t)

Full size image
Fig. 4
figure 4

Nonlinear function \(\psi (x_1 )\), eigenvalues \((\lambda _1 , \lambda _2 )\), adaptive gain \(\hat{{L}}\)

Full size image
Fig. 5
figure 5

Trajectories of the system states

Full size image
Fig. 6
figure 6

Trajectories of the control input and sliding surface

Full size image

For further robustness analysis, the impacts of the initial condition \(x(0)=\left[ {{\begin{array}{lll} {-2}&{} 4&{} {-3} \\ \end{array} }} \right] ^{T}\) and Gaussian noise on the states of the Genesio chaotic system are studied. A zero-mean Gaussian noise with standard deviation 0.01 is applied which is shown in Fig. 7. Figure 8 displays the time trajectories of the states in the new situation, with different values of the initial conditions and in the presence of the Gaussian noise. The time responses of the control inputs and sliding surfaces are shown in Fig. 9. It is observed that the offered control signal in this paper is free of the chattering. In contrast, the control input attained by the method of [1] suffers from the chattering. These results are similar to the previous simulation, which illustrate that the suggested approach has better robust performance compared to the controller of [1] in the face of measurement noise, too.

Fig. 7
figure 7

Measurement noise

Full size image
Fig. 8
figure 8

Time responses of the system states

Full size image
Fig. 9
figure 9

Time responses of the control signal and sliding surface

Full size image

The effects of changing the design parameters on the convergence speed, control signal and sliding surface are concluded as follows:

  1. (I)

    If the parameter \(k_1\) is increased, the overshoot of the sliding surface is decreased, the amplitude of the control input is increased, and the convergence speed is improved.

  2. (II)

    If the parameter \(\kappa \) is increased, a somewhat fast convergence is achieved, but the amplitude of the control signal is increased and chattering is observed in the sliding surface and control signal.

  3. (III)

    By increasing the parameters \(\beta _{1} , \beta _2 ,\beta _3\), the overshoot of the state trajectories is increased, the amplitudes of the control signal and sliding surface are augmented, but the convergence rate is improved.

  4. (IV)

    If one increases the parameter \(\mu _1\), the convergence rate is improved and the overshoot is removed from the states of the system. However, high overshoot in the control signal and sliding surface is occurred and some chattering in the control input is observed.

  5. (V)

    By decreasing \(\Phi \), some chattering is observed in the control signal, but the convergence speed of the sliding surface slightly goes up.

5 Conclusions

This paper investigates a novel adaptive global nonlinear sliding mode control procedure to improve the steady-state and transient performances of the disturbed nonlinear systems. Using a nonlinear function in the global nonlinear switching surface, the damping ratio of the controlled system is improved from its initial low value to a high value to ensure a quick settling time and a low control action. This scheme not only guarantees robustness against nonlinearity and disturbance, but also avoids chattering problem and eliminates the reaching interval. The offered structure contains two terms: GSMC and adaptive stabilizer. The GSMC is designed to construct a switching surface and an equivalent control law for the elimination of the reaching phase. The adaptive stabilizer is applied to create a tuning law for removing the impacts of the unwanted disturbances and guaranteeing the finite-time convergence of the states to the switching surface. Finally, a Genesio system proves the reliability of the suggested technique. This scheme has the flexibility to be easily applied to the hyper-chaotic systems. It should be noted that the proposed scheme can be extended to a large class of the perturbed nonlinear control problems.