1 Introduction

Decades after the first discovery of chaos phenomenon, OGY method presented by Edward Ott et al. [1] has successfully prospered the chaos control research. The random-like chaotic performance is responsible for many industrial deteriorated manufacturing processes. For example, it has been reported that occurrence of the voltage collapse within power systems is closely related to chaotic oscillation [2]. In many cases, removing chaos is beneficial to avoid operating failure and improve system performance; hence, chaos control usually refers to the stabilization of unstable periodic orbits immersed in a chaotic attractor [3].

In recent years, considerable efforts have been devoted into the control of chaotic systems, and numerous controller design approaches have been proposed, such as adaptive control [4, 5], feedback linearization [6], sliding mode approach [7, 8], back-stepping method [9, 10], noisy synchronization method [11], and fuzzy control [12]. Among these methods, sliding mode control (SMC) is popular for fast dynamic response and robustness to system disturbances.

It is well known that the design of an SMC process consists of two steps. First, establish the proper sliding surface, on which the desired system state performance can be obtained. Second, design the controller that can drive the system state to reach and stick on the sliding surface [13].

The control methods proposed in [14] and [15] stand for one way of the SMC design for chaotic systems. With this approach, the switching function s is designed in a specific form such that when the sliding surface is reached, time derivative of one system state performs in a pre-chosen way and guides other system states asymptotically converging to zero. Design of such sliding surface totally depends on the specific form of each chaotic system, which weakens the applicability of this method. [16] studied the control of Chua’s circuit and the Lorenz chaotic system. By unifying the system model in a generalized form, the proposed sliding surface design is applicable for other chaotic systems with the same kind of system description. Despite that application of the proposed method can be broaden to a general class of chaotic systems, the sliding surface designed in [16] can only guarantee asymptotical stable of the system states, like that of [14] and [15].

In practice, it is usually required that the chaotic states can be stabilized as quickly as possible. Thus, the study of finite time stabilization of the chaotic system is necessary. By combining back-stepping idea with dynamic surface control method, [8] presented a high-order SMC approach to suppress chaotic oscillation in power system and managed to stabilize system states in fixed time. To stabilize a general class of chaotic systems in finite time, [17] proposed a fast terminal sliding surface that contains a signum function. Although the sliding surface possesses an elegant form and is theoretically proved to be reachable in finite time, it can hardly be achieved in practice due to the discontinuous nature of the signum function [18]. Therefore, selecting a proper sliding surface is critical for finite time stabilization of system states.

Once a suitable sliding surface is established, a control law that can drive the system states to the selected sliding surface is needed. Adopting the signum function into SMC design for the chaotic system is a widely accepted approach due to its simplicity in implementation and convenience in stability analysis, despite the fact that existence of signum function leads to the chattering problem. Generally, robustness of SMC can be guaranteed by the selection of large control gains, whereas a large gain leads to the well-known chattering phenomenon.

Some approaches have been proposed to decrease chattering for the SMC design. For instance, a general chattering reduction scheme is recently suggested in [19]. By implementing the low-pass filtered signum function into the control law, together with an integral sliding surface design, the proposed scheme demonstrates a superior performance in terms of chattering attenuation and trajectory tracking. [20] proposed a new dynamical sliding mode surface with integral and differential operators for chaotic systems and managed to divert the discontinuous signum function into the first derivative of the control input. In such manner, the input chattering of chaotic system is eliminated after the integral operation. This work is later extended by [21] to a more general case. Nevertheless, implementing the proposed sliding mode controllers in [20] and [21] requires a relatively high calculating capacity of the actuator, which limits their applications.

Among the existing methods, one interesting approach to realize the SMC chattering reduction task is to design the reaching law for the switching function, since chattering is caused by the non-ideal reaching at the end of the sliding mode reaching phase [22]. Reaching law of the switching function not only affects the chattering level of the controller, but is also responsible for the time that system states take to arrive at the sliding surface. [16] and [23] suggested two new reaching law and deduced the corresponding continuous controllers for chaos systems. With the proposed reaching laws, chattering in the controller is eliminated, yet reaching time of the new method is not proved to outperform the conventional constant rate reaching law.

Motivated by the above discussions, this paper introduces a new sliding mode controller to stabilize a general class of chaotic systems in finite time. The proposed controller contains a new nonlinear adaptive reaching law, which is based on the choice of a negative power term that adapts to the variations of the switching function. Compared to conventional sliding mode reaching law, the proposed one settles the reaching time/chattering dilemma. Parameter tuning principles of the new controller are provided in detail. With proper parameter selection, states of the chaotic system can reach the pre-defined sliding surface in shorter time, and system chattering can be reduced afterward. On the designed sliding surface, system states can be stabilized in finite time. Effectiveness of the proposed control scheme is verified via simulations on two chaotic systems.

The rest of the paper is organized as follows. Section 2 describes the formulation for the chaotic systems and analyzes properties of a commonly used reaching law. Section 3 presents a new reaching law design. Section 4 suggests the control scheme for the chaotic systems. Simulation results of the proposed new controller are illustrated in Sect. 5. Finally, a conclusion closes the paper.

2 Preliminaries

2.1 System description

In this paper, a class of controlled chaotic systems that can be presented in the following form is considered

$$\begin{aligned} \begin{aligned} {{\dot{\mathbf x}}} = A\mathbf {x}+N(\mathbf {x})+B\mathbf {u}(t) \end{aligned} \end{aligned}$$
(1)

where \(\mathbf {x}\in R^n\) is the state vector; \(N(\mathbf {x})=[\mathbf {0}, N_2( \mathbf {x})]^\mathrm{T}\), with the zero vector \(\mathbf{0 } \in R^{(n-m)\times 1}\), and \(N_2(\mathbf {x})\in R^{m \times 1}\) contains the system nonlinear terms that we consider \(n/2\le m<n\) is always satisfied; \(B=[\mathbf {0}, B_2]^\mathrm{T}\) with \(\mathbf {0} \in R^{(n-m)\times m}\), and \(B_2\in R^{m \times m}\) is a full rank matrix; \(\mathbf {u}\in R^m\) is the control input.

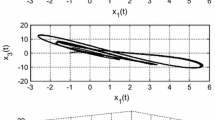
Here, we take the Lü system as example to give readers a clear understand of the formulation. Mathematical model for uncontrolled Lü system can be expressed as [24]

$$\begin{aligned} \left\{ \begin{aligned} {\dot{x}}_1&= \sigma _1(x_2-x_1)\\ {\dot{x}}_2&= -x_1x_3 + \sigma _2 x_2\\ {\dot{x}}_3&= x_1x_2-\sigma _3 x_3 \end{aligned} \right. , \end{aligned}$$
(2)

which is chaotic when \(\sigma _1 = 36\), \(\sigma _2 = 20\), and \(\sigma _3=3\). Chaotic attractor of the system is shown in Fig. 1. For this system, the state vector is \(\mathbf {x} = [x_1,x_2,x_3]^\mathrm{T}\), and nonlinear parts of the system lead to \(N_2(\mathbf {x}) = [-\,x_1x_3,~x_1x_2]^\mathrm{T} \in R^{2\times 1}\) . According to the formulation in (1), a control input with dimension \(m=2\) is designed for (2) as \(\mathbf {u}(t) = [u_1(t),~u_2(t)]^\mathrm{T}\).

Fig. 1
figure 1

Uncontrolled Lü chaotic attractor

Full size image

Objective of this paper is to design proper sliding mode controller \(\mathbf {u}(t)\) in (1) such that the states of the controlled chaotic system can be stabilized in finite time for any given initial condition, i.e., \(\lim \limits _{t\rightarrow T_s}||\mathbf {x}(t)||=0\), and \(||\mathbf {x}(t)||\equiv 0\), if \(t\ge T_s\).

Remark 1

Formulation (1) depicts characteristics of considerable amounts of chaotic systems, such as dynamics of the smooth-air-gap in permanent magnet synchronous motor [25], Chen’s attractor, hyper-Lorenz systems. Nevertheless, it is inappropriate to be applied to Genesio system, Rössler attractor, etc., due to the dimension requirement for system nonlinear terms (\(n/2\le m<n\)).

2.2 Reaching law method for SMC design

In general, an SMC process usually consists of two phases: the reaching phase and the sliding phase. During the reaching phase, trajectories of system states are controlled to reach the pre-chosen sliding surface \(s=0\), where s is the switching function [13]. After that, the system states enter the sliding mode and slide toward the origin. The sliding phase reaching condition is usually expressed as \(s\cdot {\dot{s}}<0\).

The reaching law method proposed by [26] is an efficient way to ensure the arrival of system states to the sliding surface. Here we take a simple second-order system as example to briefly explain its design principle. Consider the following system

$$\begin{aligned} \left\{ \begin{aligned} {\dot{x}}_1&= x_2\\ {\dot{x}}_2&= f(x)+bu \end{aligned} \right. \end{aligned}$$
(3)

where \(x = [x_1,x_2]^\mathrm{T}\) is the system state vector, b is not zero, and u is the control input. A typical switching function s can be selected as

$$\begin{aligned} s = cx_1+x_2 \end{aligned}$$
(4)

where c is a nonzero constant. To drive the system state vector to reach the sliding phase, controller u in (3) should be designed in a way such that the sliding mode reaching condition \(s\cdot {\dot{s}}<0\) can be met.

A reaching law is the differential description that specifies the dynamics of s. Here, we analyze the properties of a popularly adopted reaching law

$$\begin{aligned} {\dot{s}} = -k\cdot \mathrm{sgn}(s),~ k>0~~ \end{aligned}$$
(5)

where \(\mathrm{sgn}(\cdot )\) denotes the signum function. Substitute (3) and (4) in (5) yields

$$\begin{aligned} cx_2+ f(x)+bu= -k\cdot \mathrm{sgn}(s)~. \end{aligned}$$
(6)

Therefore, controller for the system can be chosen as

$$\begin{aligned} u = -b^{-1}\left( cx_2+f(x)+k\cdot \mathrm{sgn}(s)\right) . \end{aligned}$$
(7)

Such design of the controller ensures the occurrence of the sliding phase and guarantees that dynamics of the switching function can be kept in the form of (5).

It can be computed that switching function with reaching law (5) will move toward its sliding surface \(\{x|s=0\}\) at a constant speed. The time \(t_0\) it takes for s to reach sliding surface for the first time is

$$\begin{aligned} t_0 = \frac{|s(0)|}{k} \end{aligned}$$
(8)

where s(0) is the initial value of the switching function.

In digital environment, the discrete form of (5) is calculated as

$$\begin{aligned} s(n+1)-s(n) = -\,kT\mathrm{sgn}\left( s(n)\right) \end{aligned}$$
(9)

where T is the device sampling period. When the switching function reaches \(s=0\) and slides back and forth on sliding surface due to the discrete nature of digital processors, we have

$$\begin{aligned} \left\{ \begin{aligned} s(n+1)&= -k T, ~~\mathrm{if}~ s(n) = 0^+\\ s(n+1)&= k T, ~~ \mathrm{if}~ s(n) = 0^- \end{aligned} \right. . \end{aligned}$$
(10)

It can be estimated that width of the sliding mode band in digital environment is

$$\begin{aligned} \Delta _0 = 2kT ~~ . \end{aligned}$$
(11)

Merit of reaching law (5) is its simplicity in structure. Nevertheless, the contradiction between fast reaching time \(t_0\) and small sliding mode band \(\Delta _0\) can be observed from (8) and (11). The value of k should be increased if a fast reaching time is required, which in turn widens the chattering band of the system. To solve this dilemma, a new reaching law for the sliding mode controller design is introduced in the next section.

3 A new reaching law design

The reaching law proposed in this paper is as follows:

$$\begin{aligned} \begin{aligned}&{\dot{s}} = -\frac{k}{\Omega (s)}\cdot \mathrm{sgn}(s)\\&\Omega (s) = \eta + \gamma \left( 1+|s|/\mu \right) ^{-1} \end{aligned} \end{aligned}$$
(12)

where s is the switching function, \(\gamma > 0\), \(0<\eta <1\), \(|\cdot |\) denotes the absolute value, and \(\mu = \alpha |s(0)|,~ \alpha > 0\), s(0) is the initial value of the switching function. Parameter selection principle for this reaching law is stated in proposition 2.

Proposition 1

With the proposed reaching law (12), switching function s will reach the sliding surface in finite time \(t_1\):

$$\begin{aligned} t_1 = \frac{|s(0)|}{k}\left[ \eta +\gamma \cdot \alpha \cdot \mathrm{ln}(1+\frac{1}{\alpha }) \right] ~~. \end{aligned}$$

Proof

From simple calculation of (12), it can be obtained that

$$\begin{aligned} -k ~\mathrm{d}t = \eta + \gamma (1+|s|/\mu )^{-1}\mathrm{sgn}(s)~\mathrm{d}s~~. \end{aligned}$$
(13)

Assume that \(t_1\) is the time for the switching function s to reach the sliding surface, and thus \(s(t_1) = 0\). Integrating (13) from 0 to \(t_1\), the result is presented below.

Case 1 \(s(0)>0\)

$$\begin{aligned} \begin{aligned} t_1&=-\frac{1}{k}\int _{s(0)}^{s(t_t)}\eta +\gamma (1+s/\mu )^{-1} ~\mathrm{d}s\\&=-\frac{1}{k}\left[ \eta s+\gamma \mu ~\mathrm{ln}(1+s/\mu )\right] \Big |_{s(0)}^{s(t_1)}\\&=\frac{1}{k}\left[ \eta s(0) + \gamma \mu ~\mathrm{ln}\left( 1+s(0)/\mu \right) \right] ~~; \end{aligned} \end{aligned}$$
(14)

Case 2 \(s(0)<0\)

$$\begin{aligned} \begin{aligned} t_1&=\frac{1}{k}\int _{s(0)}^{s(t_t)}\eta +\gamma (1-s/\mu )^{-1} ~\mathrm{d}s\\&=\frac{1}{k}\left[ \eta s-\gamma \mu ~\mathrm{ln}(1-s/\mu )\right] \Big |_{s(0)}^{s(t_1)}\\&=\frac{1}{k}\left[ -\eta s(0) + \gamma \mu ~\mathrm{ln}\left( 1-s(0)/\mu \right) \right] ~~. \end{aligned} \end{aligned}$$
(15)

Combining the above cases, expression of \(t_1\) can be rewritten as

$$\begin{aligned} t_1 = \frac{1}{k} \left[ \eta |s(0)|+\gamma \mu ~\mathrm{ln}(1+\frac{|s(0)|}{\mu }) \right] ~~. \end{aligned}$$
(16)

Substituting \(\mu = \alpha |s(0)|\) into (16) yields

$$\begin{aligned} t_1 = \frac{|s(0)|}{k}\left[ \eta +\gamma \cdot \alpha \cdot \mathrm{ln}(1+\frac{1}{\alpha }) \right] ~~, \end{aligned}$$
(17)

which completes the proof. \(\square \)

Proposition 2

Compared to adopting reaching law (5), if dynamics of the switching function s is designed according to reaching law (12) and \(\eta \), \(\gamma \) are chosen to satisfy \(\eta +\gamma >1\), the controlled system can acquire faster reaching time and lower chattering level simultaneously.

Proof

Intuitively, when the switching function reaches around the sliding surface, \({\dot{s}}\) in (12) approximates to \(-\,k\cdot \mathrm{sgn}(s)/(\eta +\gamma )\), of which the digital form can be evaluated as

$$\begin{aligned} s(n+1)- s(n) \approx -\frac{kT}{\eta +\gamma }~\mathrm{sgn}\left( s(n)\right) ~~. \end{aligned}$$
(18)

By the same manner presented in (10), width of the sliding mode band regarding to new reaching law (12) is

$$\begin{aligned} \Delta _1 = \frac{2kT}{\eta +\gamma }~~. \end{aligned}$$
(19)

Compared with the chattering level in (11), with the same gain k, when \(\eta +\gamma >1\) is satisfied, \(\Delta _1\) can be reduced on the basis of \(\Delta _0\).

Comparing \(t_1\) in (17) with \(t_0\) in (8), it is known that reaching time derived from the new reaching law can be smaller than the conventional one if the following inequality is satisfied:

$$\begin{aligned} \eta + \gamma \cdot \alpha \cdot \mathrm{ln}(1+\frac{1}{\alpha })<1~~. \end{aligned}$$
(20)

To achieve fast reaching time and decrease chattering level at the same time, (20) and \(\eta +\gamma >1\) should hold simultaneously, which leads to:

$$\begin{aligned} 1-\eta<\gamma <\frac{1}{\alpha \cdot \mathrm{ln}(1+1/\alpha )}\cdot (1-\eta )~~. \end{aligned}$$
(21)

Let \(f(\alpha ) =\alpha \cdot \mathrm{ln}(1+\frac{1}{\alpha })\). Via calculation of \(f'(\alpha )\), it can be easily known that \(f(\alpha )\) is a monotonically increasing function. According to the L’Hôpital’s Rule, it can be obtained that \(\lim \limits _{\alpha \rightarrow \infty } \alpha \cdot \mathrm{ln}(1+\frac{1}{\alpha }) = 1\). Hence, the following inequality holds

$$\begin{aligned} \alpha \cdot \mathrm{ln}(1+\frac{1}{\alpha })<1~~, \end{aligned}$$
(22)

which leads to the fact that (21) is always guaranteed. This completes the proof. \(\square \)

By introducing the negative power term of s and its initial value s(0), the proposed reaching law (12) manages to solve the reaching time/chattering-level dilemma of constant rate reaching law (5). It should be noted that such dilemma can be addressed by implementing other reaching laws as well. In the following contents, two other reaching laws are presented and briefly compared with (12).

In their paradigmatic work [26], Gao and Huang introduced two other types of reaching law besides (5), which are also popular and extensively applied. One is the constant plus proportional rate reaching law

$$\begin{aligned} {\dot{s}} = -\,k\mathrm{sgn}(s) - q s, \end{aligned}$$
(23)

and the other is the power rate reaching law

$$\begin{aligned} {\dot{s}} = -\,k|s|^\beta \mathrm{sgn}(s), ~~0<\beta <1. \end{aligned}$$
(24)

Compared with the constant rate reaching law (5), merit of (23) is that it obtains fast reaching speed without increasing the chattering level. The existence of extra term \(-qs\) leads to fast reaching rate toward the sliding surface when s is large; At the end of the reaching phase, \(-\,qs\) disappears as \(s\rightarrow 0\), and chattering level of (23) is the same as (5). However, with the constant plus proportional rate reaching law, magnitude of the corresponding controller depends on the value of s. As a result, big initial value of s can lead to overly large control input u. If the system is subjected to input signal, then k should be adjusted small enough to avoid possible input saturation, which in turn extends reaching time when s becomes smaller. With the proposed reaching law (12), influence of s on the derived controller u is bounded in certain range, since value of \(\frac{k}{\Omega (s)}\) decreases from \(\frac{k}{\eta +\gamma (1+1/\alpha )^{-1}}\) to \(\frac{k}{\eta +\gamma }\) when s decreases from s(0) to 0. Therefore, controller derived from (12) tends to be more “stable” compared to (23).

Same as (23), the power rate reaching law (24) accelerates reaching phase when states are far away from the sliding surface. Due to the existence of \(|s|^\beta \), reaching speed decreases when s is relatively small, and chattering is eliminated on the sliding surface. Nevertheless, controller derived by adopting (24) cannot ensure insensitivity of the system in the presence of disturbances and model uncertainties, even if they satisfy matching conditions. This is resulted from the fact that dynamics of s becomes zero on the sliding surface, and hence the controller loses its discontinuous term to counteract disturbances and uncertainties. For the proposed reaching law (12), when s arrives on the sliding surface, \({\dot{s}}\) becomes \(-k\cdot \mathrm{sgn}(s)/(\eta +\gamma )\). Nonzero derivative of s provides robustness to the corresponding controller to deal with system disturbances and model uncertainties.

4 Main results

4.1 Design of the sliding surface

Dividing system state vector \(\mathbf {x}\) into two subvectors such that \(\mathbf {x} = [\mathbf {x_1},~\mathbf {x_2}]^\mathrm{T}\) with \(\mathbf {x_1}\in R^{n-m}\), \(\mathbf {x_2}\in R^{m}\), (1) can be reformulated as

$$\begin{aligned} \left\{ \begin{aligned} {{\dot{\mathbf x}}_1}&= A_{11}\mathbf {x_1}+A_{12}\mathbf {x_2}\\ {{\dot{\mathbf x}}_2}&= A_{21}\mathbf {x_1}+A_{22}\mathbf {x_2}+N_2(\mathbf {x})+B_2\mathbf {u}(t) \end{aligned} \right. \end{aligned}$$
(25)

where \(A_{11}\in R^{(n-m)\times (n-m)}\), \(A_{12} \in R^{(n-m)\times m}\), \(A_{21} \in R^{m\times (n-m)}\), \(A_{22}\in R^{m\times m}\). The sliding variable vector \(\mathbf {s}\) for the system is designed as follows:

$$\begin{aligned} \mathbf {s} = C_1\mathbf {x_1}+C_2\mathbf {x_2} + L\sigma (\mathbf {x_1}) \end{aligned}$$
(26)

where \(\mathbf {s}=\left[ s_1,\ldots ,s_{m}\right] ^\mathrm{T}\in R^m\); \(C_1 \in R^{m\times (n-m)}\), \(C_2 \in R^{m\times m}\) is a full rank matrix; \(L\in R^{m\times (n-m)}\), \(\sigma (\mathbf {x_1})=[|x_1|^{\tau }\mathrm{sgn}(x_1),\ldots ,|x_{n-m}|^{\tau }\mathrm{sgn}(x_{n-m})]^\mathrm{T}\), \(0<\tau <1\). Design principles for parameter matrices \(C_1\), \(C_2\) and L will be shown later.

4.2 Design of the controller

The proposed controller \(\mathbf {u}\) designed for system (1) is as follows:

$$\begin{aligned} \mathbf {u} =\left\{ \begin{aligned}&-(C_2B_2)^{-1}\Big [CA\mathbf {x}+L\Lambda _1(A_{11}\mathbf {x_1}+A_{12}\mathbf {x_2})\\&\quad \quad \quad \quad \quad \quad +C_2N_2(\mathbf {x})+\mathbf {U_s} \Big ],\\&\quad \quad \quad \quad \quad \quad \mathrm{for\;any}~x_i\ne 0~(i=1,\ldots ,n-m);\\&-B_2^{-1}\Big [A_{21}\mathbf {x_1}+A_{22}\mathbf {x_2}+ N_2(\mathbf {x})+\varphi \mathbf {x_2}\Big ],\\&\quad \quad \quad \quad \quad \quad \mathrm{for~any}~x_i = 0~(i=1,\ldots ,n-m). \end{aligned} \right. \nonumber \\ \end{aligned}$$
(27)

where \(C = [C_1, C_2]\), \(A = \begin{bmatrix} A_{11}&A_{12}\\ A_{21}&A_{22} \end{bmatrix} \), \(\mathbf {x} = [\mathbf {x_1},~\mathbf {x_2}]^\mathrm{T}\), \(\Lambda _1=\mathrm{diag}\Big (\tau |x_1|^{\tau -1},\ldots ,\tau |x_{n-m}|^{\tau -1}\Big )\in R^{(n-m) \times (n-m)}\) is the diagonal matrix, \(\varphi >0\) is a constant number, \(\mathbf {U_s} =\left[ u_{s_1},\ldots ,u_{s_m}\right] ^\mathrm{T}\) with each element designed as

$$\begin{aligned} \begin{aligned}&u_{s_i} = \frac{k\cdot \mathrm{sgn}(s_i)}{\eta +\gamma (1+|s_i|/\alpha |s_i(0)|)^{-1}}~, \\&k,\gamma ,\alpha >0,~~0<\eta <1,~~i = 1,\ldots ,m. \end{aligned} \end{aligned}$$

The second controller form in (27) is the strategy handling the situation where the ith term in \(\Lambda _1\) does not exist when any \(x_i=0\) happens during the reaching phase.

Theorem 1

With the proposed control input (27), system (1) starts from any initial state will move toward the designed sliding surface \(\mathbf {s}=\mathbf {0}\) and reach it in finite time.

Proof

Constructing a Lyapunov function \(V_1 = \frac{1}{2}\mathbf {s}^T\mathbf {s}\) and differentiating it with respect to time give

$$\begin{aligned} \begin{aligned} {\dot{V}}_1(t)&=\mathbf {s}^T\left( C_1{{\dot{\mathbf x}}_1}+C_2{{\dot{\mathbf x}}_2}+L{\dot{\sigma }}(\mathbf {x_1})\right) \\&= \mathbf {s}^T\Big (C_1(A_{11}\mathbf {x_1}+A_{12}\mathbf {x_2})\\&\quad +C_2(A_{21}\mathbf {x_1}+A_{22}\mathbf {x_2}+N_2(\mathbf {x})+B_2\mathbf {u})\\&\quad +L\Lambda _1(A_{11}\mathbf {x_1}+A_{12}\mathbf {x_2})\Big ) \end{aligned} \end{aligned}$$
(28)

First we consider the situation that system states \(x_i\ne 0~ (i = 1,\ldots ,n-m)\). Using the first control law in (27), \({\dot{V}}_1\) becomes

$$\begin{aligned} \begin{aligned} {\dot{V}}_1&=-\mathbf {s}^T\mathbf {U_s}\\&= \sum \limits _{i = 1}^{m} \frac{-k~|s_i|}{\eta +\gamma (1+|s_i|/\alpha |s_i(0)|)^{-1}}\\&\le 0 \end{aligned} \end{aligned}$$
(29)

Given \({\dot{V}}_1 \le 0\) and the result obtained in (17), it can be known that with the proposed control input, each element \(s_i\) in \(\mathbf {s}\) will reach \(s_i = 0\) in finite time. Thus, the system state vector \(\mathbf {x}\) will reach \(\mathbf {s}=\mathbf {0}\) in finite time \(T_1\)

$$\begin{aligned} T_1 = \max \limits _{i=1,\ldots ,m} \bigg \{\frac{|s_i(0)|}{k}\Big [\eta +\gamma \cdot \alpha \cdot \mathrm{ln}(1+1/\alpha )\Big ]\bigg \} \end{aligned}$$

and slide on \(\mathbf {s}=\mathbf {0}\).

When any \(x_i=0~(i = 1,\ldots , n-m)\) occurs during the reaching phase, substituting the second control law into (25) yields

$$\begin{aligned} {{\dot{\mathbf x}}_2} = -\varphi \mathbf {x_2}~. \end{aligned}$$
(30)

Thus, it can be obtained that

$$\begin{aligned} \mathbf {x_2} = \Psi e^{-\varphi t} \end{aligned}$$
(31)

where \(\Psi = [\psi _1,\ldots ,\psi _m]\) is a constant vector. Therefore, \(\mathbf {x_1}\) turns into

$$\begin{aligned} {{\dot{\mathbf x}}_1} = A_{11}\mathbf {x_1} + A_{12}\Psi e^{-\varphi t}~. \end{aligned}$$
(32)

Such dynamics of \(\mathbf {x_1}\) will force any of its zero element away from zero; then the first control law in (27) takes effect again and drives the system states to the sliding surface. \(\square \)

To ensure that the system state vector converge to zero after reaching \(\mathbf {s}=\mathbf {0}\), design principles of parameter matrices for (26) are given in the following theorem.

Theorem 2

On the designed sliding surface \(\mathbf {s}=\mathbf {0}\), states of the nonlinear chaotic system can be stabilized in finite time if parameter matrices \(C_1\), \(C_2\) and L in (26) are chosen to satisfy the following conditions:

$$\begin{aligned} \left\{ \begin{aligned}&A_{11}-A_{12}C_2^{-1}C_1+\left( A_{11}-A_{12}C_2^{-1}C_1\right) ^T\le 0 \\&A_{12}C_2^{-1}L=diag\left( \lambda _1,\ldots ,\lambda _{n-m}\right) ,\\&\quad \forall \lambda _i>0,~i=1,\ldots ,n-m. \end{aligned} \right. \end{aligned}$$
(33)

Proof

It has been shown in Theorem 1 that system states can reach \(\mathbf {s}=\mathbf {0}\) in finite time. Within the sliding phase, \(C_1\mathbf {x_1}+C_2\mathbf {x_2}+L\sigma (\mathbf {x_1})=\mathbf {0}\) is satisfied, which leads to

$$\begin{aligned} \mathbf {x_2} = -C_2^{-1}C_1\mathbf {x_1}-C_2^{-1}L\sigma (\mathbf {x_1})~. \end{aligned}$$
(34)

Substituting (34) into system description (25) yields the sliding mode equation for \(\mathbf {x_1}\):

$$\begin{aligned} {{\dot{\mathbf x}}_1} = \left( A_{11}-A_{12}C_2^{-1}C_1\right) \mathbf {x_1} - A_{12}C_2^{-1}L\sigma (\mathbf {x_1})~. \end{aligned}$$
(35)

Constructing a Lyapunov function \(V_2\) as

$$\begin{aligned} V_2 = \frac{1}{2}\mathbf {x_1}^T\mathbf {x_1} = \frac{1}{2}||\mathbf {x_1}||^2. \end{aligned}$$
(36)

Due to the requirement of \(m\ge n/2\) in (1), it can be guaranteed that \(A_{12}C_2^{-1}L=diag\left( \lambda _i\right) \) is a full rank matrix. Differentiating \(V_2\) with respect to time and considering the conditions in (33) yields

$$\begin{aligned} \begin{aligned} {\dot{V}}_2(t)&= \frac{1}{2} \mathbf {x_1}^T\bigg [\left( A_{11}-A_{12}C_2^{-1}C_1\right) +\\&\quad \left( A_{11}-A_{12}C_2^{-1}C_1\right) ^T\bigg ]\mathbf {x_1}\\&\quad \quad \quad -\mathbf {x_1}^T\cdot A_{12}C_2^{-1}L\cdot \sigma (\mathbf {x_1})\\&\le -\mathbf {x_1}^T\cdot A_{12}C_2^{-1}L\cdot \sigma (\mathbf {x_1})\\&=-\Big (\lambda _1|x_1|^{\tau +1}+\cdots +\lambda _{n-m}|x_{n-m}|^{\tau +1}\Big )\\&\le -\lambda \Big (|x_1|^{\tau +1}+\cdots +|x_{n-m}|^{\tau +1}\Big )\\&\le -\lambda \Big (x_1^2+\cdots +x_{n-m}^2\Big )^{\frac{\tau +1}{2}}\\&= -2^{\frac{\tau +1}{2}}\lambda V_2(t)^{\frac{\tau +1}{2}} \end{aligned} \end{aligned}$$
(37)

where \(\lambda = \mathrm{min}\{\lambda _1,\ldots ,\lambda _{n-m}\}\). Since \(\frac{\tau +1}{2}<1\), \({\dot{V}}_2\le -2^{(\tau +1)/2}\lambda V_2^{(\tau +1)/2}\) ensures \(V_2\) to reach zero in finite time. Assume that after \(\mathbf {x}\) reach the sliding surface in \(T_1\), \(\mathbf {x_1}\) will converge to zero in \(T_2\), namely \(V_2(T_2) = 0\). From (37) it can be derived that

$$\begin{aligned} \int ^{T_2}_{T_1}~\mathrm{d}t \le -(2^{\frac{\tau +1}{2}}\lambda )^{-1}\cdot \int ^{V_2(T_2)}_{V_2(T_1)}V_2^{-\frac{(\tau +1)}{2}}~\mathrm{d}V_2 \end{aligned}$$
(38)

which leads to

$$\begin{aligned} T_2\le T_1+2^{\frac{1-\tau }{2}}\cdot \frac{ V_2(T_1)^{\frac{1-\tau }{2}}}{\lambda (1-\tau )}~~. \end{aligned}$$
(39)

Once \(\mathbf {x_1}\) turns to zero, according to (34), \(\mathbf {x_2}\) will converge to zero as well. This completes the proof. \(\square \)

5 Numerical examples

In this section, two chaotic systems are used as examples to verify effectiveness of the proposed new reaching law and the controller design. During simulation processes, the fourth-order Runge–Kutta integration method is utilized to obtain the solutions of differential equations.

5.1 Lü system

Here, the chaotic Lü system presented in Fig. 1 is controlled separately by two sliding mode controllers: the new controller that adopts the proposed reaching law (12), which is shown in (27), and the controller that utilizes the popular conventional reaching law (5). The conventional controller has the similar form as (27); only those elements in term \(\mathbf {U_s}\) are designed as \(u_{s_i} = k\cdot \mathrm{sgn}(s_i),~i = 1,\ldots , m\).

Initial value of the system is chosen as \(x(0) = [1.5,~0.8,~-\,3]^\mathrm{T}\). Parameters of the sliding surface are: \(C_1 = [0.1,~0.1]^\mathrm{T}\), \(C_2 \in R^{2\times 2}\) is an identity matrix, \(L = [0.1, 0.1]^\mathrm{T}\), \(\tau = 0.5\). Other parameters for the controllers are: \(B_2 \in R^{2\times 2}\) is an identity matrix, \(\varphi =5\), gain k for reaching law (5) and (12) are both 4; additionally, \(\eta = 0.2\), \(\alpha = 0.05\), \(\gamma = 3.3\) for (12).

Fig. 2
figure 2

States trajectories with the new controller

Full size image
Fig. 3
figure 3

States trajectories with the conventional controller

Full size image
Fig. 4
figure 4

Switching functions’ trajectories with the new controller

Full size image
Fig. 5
figure 5

Switching functions’ trajectories with the conventional controller

Full size image

Applying the proposed new controller to Lü system, trajectories of system states, trajectories of switching functions and control inputs are presented in Figs. 2, 4 and 6, respectively. Accordingly, system trajectories that adopt the conventional reaching law \({\dot{s}} = -k\cdot \mathrm{sgn}(s)\) are shown in Figs. 3, 5 and 7. Despite the fact that both controllers are able to stabilize system states, it can be easily observed that the proposed new controller outperforms the conventional one, in terms of reaching time and input chattering reduction.

Fig. 6
figure 6

Output values of the new controller

Full size image
Fig. 7
figure 7

Output values of the conventional controller

Full size image

According to (17), reaching time of the new controller should be around \(70\%\) of the conventional controller. From the magnified windows in Fig. 4, the first time that \(s_1\) and \(s_2\) reach the zero surface is around 0.18s and 0.48s, whereas in Fig. 5, the corresponding reaching time is 0.274s and 0.68s. Also, chattering of the new controller should have been reduced to around \(29\%\) of the conventional controller. In Fig. 6, the new controller chatters around \([-\,1.2,~+\,1.2]\); and the chattering level of the conventional controller is \([-\,4,~+\,4]\) in Fig. 7. Simulation results have confirmed the theoretical analysis.

5.2 Hyper-chaotic system

Consider the four-dimensional hyper-chaotic system proposed in [27] with the control input \(u\in R^3\):

$$\begin{aligned} \left\{ \begin{aligned} {\dot{x}}_1&= -10x_1 + 10x_2 \\ {\dot{x}}_2&= 28x_1 + x_2 - x_1x_3 - x_4 + u_1\\ {\dot{x}}_3&= x_1x_2 - \frac{8}{3}x_3 + u_2\\ {\dot{x}}_4&= 0.02x_1x_3 + u_3 \end{aligned} \right. \end{aligned}$$
(40)

Controller (27) is used to stabilize the system states, with parameters designed as: \(C_1 = [0.1,~0.1, ~0.1]^\mathrm{T}\), \(C_2 \in R^{3\times 3}\) is an identity matrix, \(L = [0.1,~0.1, ~0.1]^\mathrm{T}\), \(\tau = 0.5\), \(\varphi = 10\); Elements of \(U_s\) are \(k = 3\), \(\eta = 0.1\), \(\alpha = 0.1\), \(\gamma = 3.5\).

Figure 8 depicts the states trajectories when initial state vector of the system is \(x(0) = [-\,1.1,~0.8,~1.2,~-\,0.9]^\mathrm{T}\). It can be observed that the states converge to zero successfully.

Fig. 8
figure 8

States trajectories of the controlled hyper-chaotic system

Full size image

Figure 9 verifies the second controller form in (27) by selecting \(x(0) = [0,~0.8,~1.2,~-\,0.9]^\mathrm{T}\), namely \(x_1\) is equal to zero at the beginning. At this point, system does not reach the sliding surface, and the second part of the controller is activated. It can be observed that \(x_1\) is driven away from zero and then gradually converges again, which validates the analysis in (30)–(32).

Fig. 9
figure 9

States trajectories of the controlled hyper-chaotic system (initial value contains zero)

Full size image

Despite the fact that system states are considered fully measurable in this paper, measurement noise is inevitable in actual practice. With the same parameter selections as Fig. 9, a uniformly distributed random noise within \(\pm 0.05\) is added to the system state vector. Namely, the controller is calculated with contaminated system state information. With such control input, behavior of actual system states is presented in Fig. 10. Although all system states have the similar convergence trend as in Fig. 9, it can be compared from the magnified window that control accuracy has been impaired. Problems on state observation/estimation in the presence of measurement noise are out of discussion scope of this paper; Readers are referred to [28, 29] for the relevant results and techniques.

Fig. 10
figure 10

States trajectories of the controlled hyper-chaotic system with measurement noise

Full size image

6 Conclusion

This paper has presented a sliding mode control scheme for a class of chaotic system. A terminal sliding surface and a new reaching law are designed to realize the finite time stabilization of the system states. Compared with earlier controllers that employ the widely used reaching law \({\dot{s}} = -k~\mathrm{sgn}(s)\), the new controller has the advantages in terms of system reaching time and input chattering reduction. Simulation results have shown that the proposed controller is capable of stabilizing the chaotic system and improving system control performance.

In this paper, the presence of model uncertainties and measurement noises is not discussed, which can be further improved by implementing parameter estimators and state observers. Applicability of the proposed control scheme depends on the dimension of nonlinear terms in the chaotic system, which can be viewed as a restriction. Future research work based on this paper would like to extend the suggested control method to uncertain chaotic systems and explore new control structure to stabilize a broader class of chaotic systems.