Analytical study of solitons in magneto-electro-elastic circular rod

Abstract

The nonlinear longitudinal wave equation, describing the propagation of optical solitons in magneto-electro-elastic circular rod, is investigated analytically. Two integration tools that are traveling wave hypothesis and G$^{\prime }$/G expansion scheme are recruited to extract explicit soliton solutions. The existence conditions are derived.

1 Introduction

Recently, the study of nonlinear dynamics of optical solitons in magneto-electro-elastic (MEE) media (such as sensors, actuators, controllers) has attracted a lot of interest [1–20]. As we all know, the governing equation that describes the propagation of optical solitons through MEE media is modeled by the nonlinear longitudinal wave equation (NLWE). Many integration algorithms including variation principle, Jacobi elliptic function expansion approach and ansatz scheme were proposed to solve the NLWE, and explicit solitary wave solutions were reported in the past [1–3]. However, this paper will apply two different ways to extract exact soliton solutions to NLWE. They are traveling wave hypothesis and G$^{\prime }$/G expansion scheme [21–42]. Therefore, this work is an extension of the previous studies.

Under investigation in this work is the following NLWE [1, 2]:

$$\begin{aligned} \frac{\partial ^{2}q}{\partial t^{2}}+a\frac{\partial ^{2}q}{\partial z^{2}}+b\frac{\partial ^{2}(q^{2})}{\partial z^{2}}+c\frac{\partial ^{4}q}{\partial z^{2}\partial t^{2}}=0 \end{aligned}$$

(1)

where q(x, t) is the complex wave profile, while t and x are the time and longitudinal coordinates.

In Eq. (1), $a=-c_0^2,\, b=-\frac{1}{2}c_0^2$ and $c=-N$. $c_0$ gives linear longitudinal wave velocity for a MEE circular rod, while N represents dispersion parameter. It should be noted that both the coefficients of $c_0$ and N depend on material properties and geometry of the rod [1, 2].

In order to obtain analytical traveling wave solutions to Eq. (1), the starting hypothesis is given by

$$\begin{aligned} q(x,t)=u(\xi ),\quad \xi =B(x-vt) \end{aligned}$$

(2)

where B is the wave number, and v represents the wave velocity.

Substituting Eq. (2) into Eq. (1) leads to

$$\begin{aligned} cB^{2}v^{2}{{u}''''}+(v^{2}+a){u}''+b(u^{2})''=0 \end{aligned}$$

(3)

where the prime denotes differentiation with respect to the variable $\xi$.

Integrating Eq. (3) twice with respect to $\xi$, and taking the integration constants equal to zero, one obtains

$$\begin{aligned} cB^{2}v^{2}{u}''+(v^{2}+a)u+bu^{2}=0 \end{aligned}$$

(4)

In the following two subsections, we will perform the traveling wave hypothesis and G$^{\prime }$/G expansion scheme on construction of analytical solitary wave solutions to Eq. (4). As a consequence, explicit dark and singular soliton solutions to Eq. (1) are obtained along with the corresponding constraints.

2 Traveling wave hypothesis

Separating variables and integrating once more, Eq. (4) becomes to

$$\begin{aligned} \xi =\int {\frac{\hbox {d}u}{u\sqrt{a_2 +a_3 u}}} \end{aligned}$$

(5)

where $a_2 =-\frac{v^{2}+a}{cB^{2}v^{2}}$ and $a_3 =-\frac{2b}{3cB^{2}v^{2}}$.

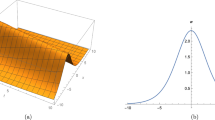
From Eq. (5), exact singular periodic solution, bright and singular soliton solutions can be derived, which are listed as follows:

Case 1: Singular periodic solution

When $(v^{2}+a)c>0$, Eq. (5) admits a solution in the form

$$\begin{aligned} u_1 (\xi )=-\frac{3(v^{2}+a)}{2b}\;\sec ^{2}\left( {\frac{1}{2}\sqrt{\frac{v^{2}+a}{cB^{2}v^{2}}}\xi } \right) \end{aligned}$$

(6)

Finally, explicit singular periodic solution to Eq. (1) is given by

$$\begin{aligned} q_1 (x,t)=-\frac{3(v^{2}+a)}{2b}\;\sec ^{2}\left[ {\frac{1}{2}\sqrt{-\frac{v^{2}+a}{cv^{2}}}(x-vt)} \right] \end{aligned}$$

(7)

Case 2: Soliton solutions

When $(v^{2}+a)c<0$, Eq. (5) admits the following exact solutions:

$$\begin{aligned} u_2 (\xi )=-\frac{3(v^{2}+a)}{2b}\;\hbox {sech}^{2}\left( {\frac{1}{2}\sqrt{-\frac{v^{2}+a}{cB^{2}v^{2}}}\xi } \right) \end{aligned}$$

(8)

and

$$\begin{aligned} u_3 (\xi )=\frac{3(v^{2}+a)}{2b}\;\hbox {csch}^{2}\left( {\frac{1}{2}\sqrt{-\frac{v^{2}+a}{cB^{2}v^{2}}}\xi } \right) \end{aligned}$$

(9)

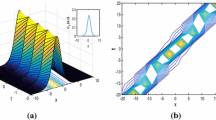
Finally, explicit bright soliton solution to Eq. (1) is given by

$$\begin{aligned} q_2 (x,t)=-\frac{3(v^{2}+a)}{2b}\;\hbox {sech}^{2}\left[ {\frac{1}{2}\sqrt{-\frac{v^{2}+a}{cv^{2}}}(x-vt)} \right] \end{aligned}$$

(10)

and explicit singular soliton solution to Eq. (1) is given by

$$\begin{aligned} q_3 (x,t)=\frac{3(v^{2}+a)}{2b}\;\hbox {csch}^{2}\left[ {\frac{1}{2}\sqrt{-\frac{v^{2}+a}{cv^{2}}}(x-vt)} \right] \end{aligned}$$

(11)

3 G$^{\prime }$/G expansion scheme

According to the balancing principle, Eq. (4) admits the solution in the form

$$\begin{aligned} u(\xi )=a_0 +a_1 \left( {\frac{{G}'(\xi )}{G(\xi )}} \right) +a_2 \left( {\frac{{G}'(\xi )}{G(\xi )}} \right) ^{2} \end{aligned}$$

(12)

where $a_i$ for $i=0,\;1,\;2$ are real constants to be determined later, and $G(\xi )$ satisfies

$$\begin{aligned} {G}''(\xi )+\lambda {G}'(\xi )+\mu G(\xi )=0 \end{aligned}$$

(13)

Putting Eqs. (12) and (13) into Eq. (4), and then taking the coefficients of $\left( {\frac{{G}'(\xi )}{G(\xi )}} \right) ^{m} \,(m=0,\;1,\;2,\;3,\;4)$ to zero yields

$$\begin{aligned}&\left( {\frac{{G}'}{G}} \right) ^{4}:\;6a_2 cB^{2}v^{2}+a_2^2 bB^{2}=0 \end{aligned}$$

(14)

$$\begin{aligned}&\left( {\frac{{G}'}{G}} \right) ^{3}:\;(10a_2 \lambda +2a_1 )cB^{2}v^{2} + 2a_1 a_2 bB^{2}=0 \end{aligned}$$

(15)

$$\begin{aligned}&\left( {\frac{{G}'}{G}} \right) ^{2}:\;(8a_2 \mu +4a_2 \lambda ^{2}+3a_1 \lambda )cB^{2}v^{2} + a_2 (v^{2}+a)\nonumber \\&\quad +\, a_1^2 bB^{2}+2a_0 a_2 bB^{2}=0 \end{aligned}$$

(16)

$$\begin{aligned}&\left( {\frac{{G}'}{G}} \right) ^{1}:\;(6a_2 \lambda \mu +2a_1 \mu \nonumber \\&\quad +\,a_1 \lambda ^{2})cB^{2}v^{2}+a_1 (v^{2}+a)+2a_0 a_1 bB^{2}=0 \end{aligned}$$

(17)

$$\begin{aligned}&\left( {\frac{{G}'}{G}} \right) ^{0}:\;(2a_2 \mu ^{2}+a_1 \lambda \mu )cB^{2}v^{2} \nonumber \\&\quad +\,a_0 (v^{2}+a)+a_0^2 bB^{2}=0 \end{aligned}$$

(18)

Solving the above nonlinear system, one obtains the following results:

Case 1:

$$\begin{aligned} a_0= & {} -\frac{3}{2}\frac{B^{2}c\lambda ^{2}v^{2}+v^{2}+a}{B^{2}b} \end{aligned}$$

(19)

$$\begin{aligned} \mu= & {} \frac{B^{2}c\lambda ^{2}v^{2}+v^{2}+a}{4cB^{2}v^{2}} \end{aligned}$$

(20)

$$\begin{aligned} a_1= & {} -\frac{6cv^{2}\lambda }{b} \end{aligned}$$

(21)

$$\begin{aligned} a_2= & {} -\frac{6cv^{2}}{b} \end{aligned}$$

(22)

where $\lambda ,\, B$ and v are arbitrary constants.

Substituting Eqs. (19)–(22) into Eq. (12), and using the solutions of Eq. (13), one can get analytical solitary wave solutions to Eq. (1), which are listed as follows:

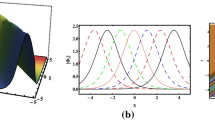
(1) When $(v^{2}+a)c<0$, Eq. (1) admits explicit hyperbolic function solitary wave solution

$$\begin{aligned}&q(x,t)=-\frac{3(v^{2}+a)}{2B^{2}b} \nonumber \\&\qquad +\,\frac{3(v^{2}+a)}{2B^{2}b}\left\{ {\frac{C_1 \;\sinh \left( {\frac{1}{2}\sqrt{-\frac{v^{2}+a}{cv^{2}}}(x-vt)} \right) +C_2 \;\cosh \left( {\frac{1}{2}\sqrt{-\frac{v^{2}+a}{cv^{2}}}(x-vt)} \right) }{C_1 \;\cosh \left( {\frac{1}{2}\sqrt{-\frac{v^{2}+a}{cv^{2}}}(x-vt)} \right) +C_2 \;\sinh \left( {\frac{1}{2}\sqrt{-\frac{v^{2}+a}{cv^{2}}}(x-vt)} \right) }} \right\} ^{2} \end{aligned}$$

(23)

where $C_1$ and $C_2$ are arbitrary constants.

If we take $C_1 =0$ and $C_2 \ne 0$, the solution (23) degenerates to singular soliton

$$\begin{aligned} q(x,t)=\frac{3(v^{2}+a)}{2B^{2}b}\hbox {csch}^{2}\left( {\frac{1}{2}\sqrt{-\frac{v^{2}+a}{cv^{2}}}(x-vt)} \right) \end{aligned}$$

(24)

and if we take $C_2 =0$ and $C_1 \ne 0$, the solution (23) becomes to solitary wave

$$\begin{aligned} q(x,t)=-\frac{3(v^{2}+a)}{2B^{2}b}\;\hbox {sech}^{2}\left( {\frac{1}{2}\sqrt{-\frac{v^{2}+a}{cv^{2}}}(x-vt)} \right) \end{aligned}$$

(25)

(2) When $(v^{2}+a)c>0$, Eq. (1) admits exact trigonometric function solitary wave solution

$$\begin{aligned}&q(x,t)=-\frac{3(v^{2}+a)}{2B^{2}b} -\,\frac{3(v^{2}+a)}{2B^{2}b}\nonumber \\&\qquad \left\{ {\frac{-C_1 \;\sin \left( {\frac{1}{2}\sqrt{\frac{v^{2}+a}{cv^{2}}}(x-vt)} \right) +C_2 \;\cos \left( {\frac{1}{2}\sqrt{\frac{v^{2}+a}{cv^{2}}}(x-vt)} \right) }{C_1 \;\cos \left( {\frac{1}{2}\sqrt{\frac{v^{2}+a}{cv^{2}}}(x-vt)} \right) +C_2 \;\sin \left( {\frac{1}{2}\sqrt{\frac{v^{2}+a}{cv^{2}}}(x-vt)} \right) }} \right\} ^{2}\nonumber \\ \end{aligned}$$

(26)

where $C_1$ and $C_2$ are arbitrary constants.

If we take $C_1 =0$ and $C_2 \ne 0$, the solution (26) degenerates to a singular periodic solution

$$\begin{aligned} q(x,t)= & {} -\frac{3(v^{2}+a)}{2B^{2}b} {csc^2\left( {\frac{1}{2}\sqrt{\frac{v^{2}+a}{cv^{2}}}(x-vt)} \right) } \nonumber \\ \end{aligned}$$

(27)

and if we take $C_2 =0$ and $C_1 \ne 0$, the solution (26) becomes to other singular periodic solution

$$\begin{aligned} q(x,t)=-\frac{3(v^{2}+a)}{2B^{2}b}\left[ {1-\;\tan ^{2}\left( {\frac{1}{2}\sqrt{-\frac{v^{2}+a}{cv^{2}}}(x-vt)} \right) } \right] \end{aligned}$$

(28)

(3) When $a=-v^{2}$, Eq. (1) admits analytical plane-wave solution

$$\begin{aligned} q(x,t)=-\frac{6cv^{2}}{b}\left( {\frac{C_2 }{C_1 +C_2 B(x-vt)}} \right) \end{aligned}$$

(29)

where $C_1$ and $C_2$ are arbitrary constants.

Case 2:

$$\begin{aligned} a_0= & {} -\frac{3B^{2}c\lambda ^{2}v^{2}-v^{2}-a}{2B^{2}b} \end{aligned}$$

(30)

$$\begin{aligned} \mu= & {} \frac{B^{2}c\lambda ^{2}v^{2}-v^{2}-a}{4cB^{2}v^{2}} \end{aligned}$$

(31)

$$\begin{aligned} a_1= & {} -\frac{6cv^{2}\lambda }{b} \end{aligned}$$

(32)

$$\begin{aligned} a_2= & {} -\frac{6cv^{2}}{b} \end{aligned}$$

(33)

where $\lambda ,\, B$ and v are arbitrary constants.

Substituting Eqs. (30)–(33) into Eq. (12), and using the solutions of Eq. (13), one can get analytical solitary wave solutions to Eq. (1), which are listed as follows:

(1) When $(v^{2}+a)c>0$, Eq. (1) admits explicit hyperbolic function solitary wave solution

$$\begin{aligned}&q(x,t)=\frac{v^{2}+a}{2B^{2}b} -\,\frac{3(v^{2}+a)}{2B^{2}b}\nonumber \\&\qquad \times \left\{ {\frac{C_1 \;\sinh \left( {\frac{1}{2}\sqrt{\frac{v^{2}+a}{cv^{2}}}(x-vt)} \right) +C_2 \;\cosh \left( {\frac{1}{2}\sqrt{\frac{v^{2}+a}{cv^{2}}}(x-vt)} \right) }{C_1 \;\cosh \left( {\frac{1}{2}\sqrt{\frac{v^{2}+a}{cv^{2}}}(x-vt)} \right) +C_2 \;\sinh \left( {\frac{1}{2}\sqrt{\frac{v^{2}+a}{cv^{2}}}(x-vt)} \right) }} \right\} ^{2}\nonumber \\ \end{aligned}$$

(34)

where $C_1$ and $C_2$ are arbitrary constants.

If we take $C_1 =0$ and $C_2 \ne 0$, the solution (34) degenerates to singular soliton

$$\begin{aligned} q(x,t)=\frac{v^{2}+a}{2B^{2}b}\left[ {1-3\;\coth ^{2}\left( {\frac{1}{2}\sqrt{\frac{v^{2}+a}{cv^{2}}}(x-vt)} \right) } \right] \end{aligned}$$

(35)

and if we take $C_2 =0$ and $C_1 \ne 0$, the solution (34) becomes to dark soliton

$$\begin{aligned} q(x,t)=\frac{v^{2}+a}{2B^{2}b}\left[ {1-3\tanh ^{2}\left( {\frac{1}{2}\sqrt{\frac{v^{2}+a}{cv^{2}}}(x-vt)} \right) } \right] \end{aligned}$$

(36)

(2) When $(v^{2}+a)c<0$, Eq. (1) admits exact trigonometric function solitary wave solution

$$\begin{aligned}&q(x,t)=\frac{v^{2}+a}{2B^{2}b} +\frac{3(v^{2}+a)}{2B^{2}b}\nonumber \\&\quad \times \left\{ {\frac{-C_1 \;\sin \left( {\frac{1}{2}\sqrt{-\frac{v^{2}+a}{cv^{2}}}(x-vt)} \right) +C_2 \;\cos \left( {\frac{1}{2}\sqrt{-\frac{v^{2}+a}{cv^{2}}}(x-vt)} \right) }{C_1 \;\cos \left( {\frac{1}{2}\sqrt{-\frac{v^{2}+a}{cv^{2}}}(x-vt)} \right) +C_2 \;\sin \left( {\frac{1}{2}\sqrt{-\frac{v^{2}+a}{cv^{2}}}(x-vt)} \right) }} \right\} ^{2}\nonumber \\ \end{aligned}$$

(37)

where $C_1$ and $C_2$ are arbitrary constants.

If we take $C_1 =0$ and $C_2 \ne 0$, the solution (37) degenerates to a singular periodic solution

$$\begin{aligned} q(x,t)= & {} \frac{v^{2}+a}{2B^{2}b}\left[ 1+3\cot ^{2} \right. \nonumber \\&\left. \left( {\frac{1}{2}\sqrt{-\frac{v^{2}+a}{cv^{2}}}(x-vt)} \right) \right] \end{aligned}$$

(38)

and if we take $C_2 =0$ and $C_1 \ne 0$, the solution (26) becomes to other singular periodic solution

$$\begin{aligned}&q(x,t) = \frac{v^{2}+a}{2B^{2}b} \nonumber \\&\quad \left[ {1-3\tan ^{2}\left( {\frac{1}{2}\sqrt{-\frac{v^{2}+a}{cv^{2}}}(x-vt)} \right) } \right] \end{aligned}$$

(39)

(3) When $a=-v^{2}$, Eq. (1) admits analytical plane-wave solution

$$\begin{aligned} q(x,t)=-\frac{6cv^{2}}{b}\left( {\frac{C_2 }{C_1 +C_2 B(x-vt)}} \right) ^{2} \end{aligned}$$

(40)

where $C_1$ and $C_2$ are arbitrary constants.

4 Conclusion

This work studies the nonlinear dynamics of optical solitons in MEE media. The NLWE is solved analytically. Two integration tools are used to construct exact solitons. We first obtain the singular periodic solution, bright and singular soliton solutions by traveling wave hypothesis. Then, we report hyperbolic function solitary wave solutions, trigonometric function solitary wave solutions and plane-wave solutions by the G$^{\prime }$/G expansion scheme. It should be noted that the singular periodic solutions, bright and singular soliton solutions can be derived by choosing appropriate parameter values of $C_1$ and $C_2$.