1 Introduction

Nonlinearity is an enticing aspect of nature, and a number of scientists see nonlinear science as the most critical frontier for gaining a fundamental knowledge of the universe. The exploration of many classes of nonlinear partial differential equations (NLPDE) is crucial for mathematical modeling of complex processes that vary over time. From the mid of the 18th century, different researchers have worked to formulate the complicated physical phenomena into NLPDEs (Iqbal et al. 2018; Lu et al. 2018; Iqbal et al. 2018; Seadawy et al. 2019; Bilal et al. 2021; Younas et al. 2021). Various nonlinear physical phenomena such as fluid mechanics, quantum mechanics, nonlinear optics, epidemiology, neural networks, thermodynamics, plasma wave, solid-state physics, etc., are obtained in different mathematical equations (Younas et al. 2022; Seadawy et al. 2019; Iqbal et al. 2019; Seadawy et al. 2020; Bulut et al. 2018; Younas and Ren 2021). The nonlinear partial differential equations(PDEs) are used to express these phenomena. Looking for the exact solution of nonlinear PDEs has significance in the theory of nonlinear problems. The physical system described by nonlinear PDEs can be understood more clearly if the solution and properties of their corresponding equations are analyzed . There are various types of the solutions such as solitary wave solutions and solitons. The solitary wave phenomena and soliton theory is linked with the above-mentioned fields. So, gaining the soliton solutions of the associated PDEs have become a very important chore to be undertaken (Guo et al. 2018; Iqbal et al. 2020; Seadawy et al. 2020, 2019; Seadawy and Iqbal 2020; Younas et al. 2022). Using symbolic computations such as Mathematica, Matlab, and Maple, a number of potent techniques have been developed for securing the different exact soliton solutions of NLPDEs. Every technique has its own flaws and criteria for application to governing models when discussing precise solutions (Bulut et al. 2017; Khater et al. 2018; Younas and Younis 2020; Younis et al. 2017; Lu et al. 2018; Gao et al. 2020, 2020; Younis et al. 2018; Rizvi and Ahmad 2020)

Furthermore, the study of soliton propagation through MEE media includes as one of its fascinating topics the theory of optical solitons. A soliton is any optical field that does not change during propagation due to a delicate balance of nonlinear and linear effects in the medium. Solitons can be used in a variety of tools, including sensors, actuators, controllers, optical couplers, magneto-optic waveguides, and metamaterials, etc. The theory of optical solitons has drawn the attention of researchers and the scientific community because it is an active research area in the fields of telecommunication engineering and mathematical physics. To put it another way, the shape of solitons is preserved even when they travel over long distances without scattering. It is essential, when studying these equations, to construct soliton solutions in order to comprehend their behaviour and the theory of solitons is an ever-changing field (Nawaz et al. 2019; Eslami and Neirameh 2018).

According to an exhaustive review of the published literature, the MSSEM (Akinyemi et al. 2022) has not been applied to the MEE circular rod. As a result, we are concentrating on utilizing this integrated strategy to identify a variety of solutions. This technique begins by establishing some basic connections between NLPDEs and other simple NLODEs. Using simple solutions and solvable ODEs, it is easy to construct different types of traveling wave solutions for some complex NLPDEs. This is the fundamental principle underlying the method being utilized. This technique enabled us to obtain a large number of new soliton solutions in a single step and also provided a structure for organizing the obtained solutions.

The arrangement of the article is as follows: Description of the proposed method in Sect. 2, and the governing equation in Sect. 3, while the utilization of the methods in Sect. 4, while discussion in Sect. 5, lastly, the conclusion in Sect. 6.

2 Description of the proposed method (Akinyemi et al. 2022)

In this section, we discuss the main steps of the applied method. Assume a NLPDE with the following definition:

$$\begin{aligned} \varpi (\Phi ,\Phi _{t},\Phi _{x},\Phi _{tt},\vartheta \Phi _{xt},\Phi _{xx}, \cdots )=0, \end{aligned}$$
(1)

where \(\Phi =\Phi (x, t)\) is an unknown function. For solving the Eq. (1), we proceed by considering the following hypothesis

$$\begin{aligned} \Phi =\varphi (\xi ), \xi =\rho (x-t \varpi ), \end{aligned}$$
(2)

 where \(\rho \) is the wave number and \(\varpi \) is the velocity. On using Eqs. (1) and (2) together, the following ODE is obtained

$$\begin{aligned} \delta (\varphi , \varphi ',\varphi '', \varphi ''', \cdots )=0, \end{aligned}$$
(3)

where \(\delta \) is a polynomial of \(\varphi \) and its derivatives. While the superscripts indicate ordinary derivatives w.r.t to \(\xi \).

Consider the solution of Eq. (3) is represented as:

$$\begin{aligned} \Phi (\xi )=A_0+\sum _{i=0}^{m} A_{i} R^{i}(\xi ),~~~~~~~~~~~~~~~~~~~~~~~~~~~ \end{aligned}$$
(4)

where \(A_i\) \((0\le i \le m)\) are the constants that are found later, and \(R^{'}(\xi )\) satisfies the following equation

$$\begin{aligned} (R^{'}(\xi ))^2={\gamma _0 +\gamma _2 R (\xi )^2+\gamma _2 R (\xi )^4}, \end{aligned}$$
(5)

where \(\gamma \) are real constants. Furthermore, the general solutions of Eq. (5) with \( \rho \) a constant are outlined as follows: \(\bullet \)  1.   If \(\gamma _0=0, \gamma _1>0, and \gamma _2\ne 0\), then

$$\begin{aligned} R_1(\xi )= & {} \sqrt{-\frac{\gamma _1}{\gamma _2}} \text {sech}(\sqrt{\gamma _1}(\xi +\rho )), \end{aligned}$$
(6)
$$\begin{aligned} R_2(\xi )= & {} \sqrt{\frac{\gamma _1}{\gamma _2}} \text {csch}(\sqrt{\gamma _1}(\xi +\rho )). \end{aligned}$$
(7)

\(\bullet \)  2.  For constants \(\beta _1\) and \(\beta _2\). If \( \gamma _0=0, \gamma _1>0\) and \( \gamma _2=4\beta _1\beta _2\), then

$$\begin{aligned} R_3(\xi )=\frac{4 \beta _1 \sqrt{\gamma _1}}{(4 \beta ^2_1-\gamma _2)\cosh (\sqrt{\gamma _1}(\xi +\xi _0))\pm (4 \beta ^2_1+\gamma _2)\sinh (\sqrt{\gamma _1}(\xi +\xi _0)) }. \end{aligned}$$
(8)

\(\bullet \)  3.  If \( \gamma _0=\frac{\gamma _1^2}{4 \gamma _2}, \gamma _1<0\) and \( \gamma _2>0\), with constants \(A_1\), and \(A_2\), then

$$\begin{aligned} R_4(\xi )=\sqrt{-\frac{\gamma _1}{2\gamma _2}} \tanh \bigg (\sqrt{-\frac{\gamma _1}{2\gamma _2}}(\xi +\rho )\bigg ). \end{aligned}$$
(9)
$$\begin{aligned} R_5(\xi )= & {} \sqrt{-\frac{\gamma _1}{2\gamma _2}} \coth \bigg (\sqrt{-\frac{\gamma _1}{2\gamma _2}}(\xi +\rho )\bigg ). \end{aligned}$$
(10)
$$\begin{aligned} R_6(\xi )= & {} \sqrt{-\frac{\gamma _1}{2\gamma _2}} \bigg (\tanh \sqrt{{-2\gamma _1}}(\xi +\rho )\pm i ~\text {sech}(\sqrt{{-2\gamma _1}}(\xi +\rho )\bigg ). \end{aligned}$$
(11)
$$\begin{aligned} R_7(\xi )= & {} \sqrt{-\frac{\gamma _1}{8\gamma _2}} \bigg (\tanh \sqrt{\frac{-\gamma _1}{8}}(\xi +\rho )+ ~\coth \sqrt{\frac{-\gamma _1}{8}}(\xi +\rho )\bigg ). \end{aligned}$$
(12)
$$\begin{aligned} R_8(\xi )= & {} \sqrt{-\frac{\gamma _1}{2\gamma _2}} \bigg (\frac{\sqrt{A^2_1+A^2_2}-A_1 \cosh (\sqrt{{-2\gamma _1}}(\xi +\rho ))}{A_1 \sinh (\sqrt{{-2\gamma _1}}(\xi +\rho ))+A_2}\bigg ). \end{aligned}$$
(13)
$$\begin{aligned} R_9(\xi )= & {} \sqrt{-\frac{\gamma _1}{2\gamma _2}} \bigg (\frac{\cosh (\sqrt{{-2\gamma _1}}(\xi +\rho ))}{ \sinh (\sqrt{{-2\gamma _1}}(\xi +\rho ))+i}\bigg ). \end{aligned}$$
(14)

\(\bullet \)  4.  If \( \gamma _0=0, \gamma _1<0\) and \( \gamma _2\ne 0\), then

$$\begin{aligned} R_{10}(\xi )= & {} \sqrt{-\frac{\gamma _1}{\gamma _2}} \text {sec}(\sqrt{\gamma _1}(\xi +\rho )), \end{aligned}$$
(15)
$$\begin{aligned} R_{11}(\xi )= & {} \sqrt{\frac{\gamma _1}{\gamma _2}} \text {csc}(\sqrt{\gamma _1}(\xi +\rho )). \end{aligned}$$
(16)

\(\bullet \)  5.  If \( \gamma _0=\frac{\gamma _1^2}{4 \gamma _2}, \gamma _1>0\) and \( \gamma _2>0\), with \(A^2_1-A^2_2>0\), then

$$\begin{aligned} R_{12}(\xi )= & {} \sqrt{\frac{\gamma _1}{2\gamma _2}} \tan \bigg (\sqrt{\frac{\gamma _1}{2\gamma _2}}(\xi +\rho )\bigg ). \end{aligned}$$
(17)
$$\begin{aligned} R_{13}(\xi )= & {} \sqrt{\frac{\gamma _1}{2\gamma _2}} \cot \bigg (\sqrt{\frac{\gamma _1}{2\gamma _2}}(\xi +\rho )\bigg ). \end{aligned}$$
(18)
$$\begin{aligned} R_{14}(\xi )= & {} \sqrt{\frac{\gamma _1}{2\gamma _2}} \bigg (\tan \sqrt{{2\gamma _1}}(\xi +\rho )\pm ~\text {sec}(\sqrt{{2\gamma _1}}(\xi +\rho )\bigg ). \end{aligned}$$
(19)
$$\begin{aligned} R_{14}(\xi )= & {} \sqrt{\frac{\gamma _1}{8\gamma _2}} \bigg (\tan \sqrt{\frac{-\gamma _1}{8}}(\xi +\rho )- ~\cot \sqrt{\frac{\gamma _1}{8}}(\xi +\rho )\bigg ). \end{aligned}$$
(20)
$$\begin{aligned} R_{15}(\xi )= & {} \sqrt{\frac{\gamma _1}{2\gamma _2}} \bigg (\frac{\sqrt{A^2_1-A^2_2}-A_1 \cos (\sqrt{{2\gamma _1}}(\xi +\rho ))}{A_1 \sin (\sqrt{{2\gamma _1}}(\xi +\rho ))+A_2}\bigg ). \end{aligned}$$
(21)
$$\begin{aligned} R_{16}(\xi )= & {} \sqrt{\frac{\gamma _1}{2\gamma _2}} \bigg (\frac{\cos (\sqrt{{2\gamma _1}}(\xi +\rho ))}{ \sin (\sqrt{{2\gamma _1}}(\xi +\rho ))+1}\bigg ). \end{aligned}$$
(22)

For more detail, see the reference (Rizvi and Ahmad 2020).

3 The governing model

Solid mechanics has paid a lot of attention to nonlinear elastic effects on solitary waves over the last two decades. MEE structures (such as sensors, actuators, etc.) are increasingly being used in various engineering fields, which has enticed a large amount of research interested in wave propagation in MEE media. Xue et al. (2011) recently derived a longitudinal wave equation with dispersion caused by the transverse Poisson’s effect in a MEE circular rod, where \(\theta _0\) and \(\Theta \) represent the linear longitudinal wave velocity and dispersion parameter, respectively, both dependent on the material properties and geometry of a MEE circular rod. The circular rod consists of \(BaTiO_3\) and \(C_0Fe_2O_4\) with different values of volume fractions \((v_f) \) of \(BaTiO_3\) with radius \(R= 0.05\) m. Using the simple rule of mixture based on volume fraction, the material characteristics of the composite are estimated.

The NLWE in MEE circular rod reads (Xue et al. 2011)

$$\begin{aligned} \Phi _{tt}-\theta ^2 \Phi _{xx}-\Bigg (\frac{\theta ^2}{2}\Phi ^2+\Theta \Phi _{tt}\Bigg )_{xx}=0, \end{aligned}$$
(23)

where \(\theta \) and \( \Theta \) represent linear longitudinal wave velocity and dispersion parameter for a MEE circular rod which depend on the material property and geometry of the rod.

4 Extraction of solutions

In order to secure different solutions, we’ll apply MSSEM in this section. We proceed with the wave transformation: \(\Phi =\varphi (\xi ), \xi =\rho (x-t \varpi )\), where \(\rho \) is the wave number and \(\varpi \) is the velocity. By using the above relation into Eq. (23), we get the following result from the real part as shown below:

$$\begin{aligned} 2 \Theta \rho ^2 \varpi ^2 \varphi ^{''}-2 \varphi \left( \varpi ^2-\theta ^2\right) +\theta ^2 \varphi ^2=0. \end{aligned}$$
(24)

On applying the balance principle between the terms \( \varphi ^2\) and \(\varphi ''\) in Eq. (24) gives, \(n=1\). Based on \(n=1\), the solutions of (24) is expressed as:

$$\begin{aligned} \varphi (\xi )=A_0+A_1 \chi (\xi )+A_2 \chi ^2(\xi ). \end{aligned}$$
(25)

On solving Eqs. (25) and (24), we get Family-1

$$\begin{aligned} {\left\{ \begin{array}{ll} A_0=\frac{\left( \varpi ^2-\theta ^2\right) \left( \sqrt{\left( \gamma _1^2-3 \gamma _0 \gamma _2\right) \left( -\Theta ^2\right) \varpi ^4}-i \gamma _1 \Theta \varpi ^2\right) }{\theta ^2 \sqrt{\left( \gamma _1^2-3 \gamma _0 \gamma _2\right) \left( -\Theta ^2\right) \varpi ^4}}, A_1=0, \\ A_2=\frac{3 i \gamma _2 \Theta \varpi ^2 (\theta -\varpi ) (\theta +\varpi )}{\theta ^2 \sqrt{\left( \gamma _1^2-3 \gamma _0 \gamma _2\right) \left( -\Theta ^2\right) \varpi ^4}}, \rho =-\frac{(-1)^{3/4} \sqrt{(\theta -\varpi ) (\theta +\varpi )}}{2 \root 4 \of {\left( \gamma _1^2-3 \gamma _0 \gamma _2\right) \left( -\Theta ^2\right) \varpi ^4}}.~~~~~~~~ \end{array}\right. } \end{aligned}$$

For famiy-1, the solutions of Eqs. (24) as well as Eq. (23) are discussed as:

\(\bullet \) For \(\gamma _0=0, \gamma _1>0\) and \( \gamma _2 \ne 0\), we get

The bright soliton solution

$$\begin{aligned} \Phi _{1}(x, t)=\frac{\left( \varpi ^2-\theta ^2\right) \left( \sqrt{\gamma _1^2 \left( -\Theta ^2\right) \varpi ^4}+i \gamma _1 \Theta \varpi ^2 \left( 3 \text {sech}^2\left( \sqrt{\gamma _1} \left( \vartheta -\frac{(-1)^{3/4} \sqrt{(\theta -\varpi ) (\theta +\varpi )} (x-t \varpi )}{2 \root 4 \of {\gamma _1^2 \left( -\Theta ^2\right) \varpi ^4}}\right) \right) -1\right) \right) }{\theta ^2 \sqrt{\gamma _1^2 \left( -\Theta ^2\right) \varpi ^4}}.~~~~~~~~~~~~~~~~~ \end{aligned}$$
(26)

The singular soliton solution

$$\begin{aligned} \Phi _{2}(x, t)=\frac{i (\theta -\varpi ) (\theta +\varpi ) \left( \gamma _1 \Theta \varpi ^2 \left( 3 \text {csch}^2\left( \sqrt{\gamma _1} \left( \vartheta -\frac{(-1)^{3/4} \sqrt{(\theta -\varpi ) (\theta +\varpi )} (x-t \varpi )}{2 \root 4 \of {\gamma _1^2 \left( -\Theta ^2\right) \varpi ^4}}\right) \right) +1\right) +i \sqrt{\gamma _1^2 \left( -\Theta ^2\right) \varpi ^4}\right) }{\theta ^2 \sqrt{\gamma _1^2 \left( -\Theta ^2\right) \varpi ^4}}.~~~~~~~~ \end{aligned}$$
(27)

\(\bullet \) For \( \gamma _0=0, \gamma _1>0\) and \( \gamma _2=4\beta _1\beta _2\), we obtain

The combined bright-singular soliton solution

$$\begin{aligned} \Phi _{3}(x, t)=\frac{\left( \varpi ^2-\theta ^2\right) \left( \sqrt{\gamma _1^2 \left( -\Theta ^2\right) \varpi ^4}-i \gamma _1 \Theta \varpi ^2\right) +\frac{12 i \beta _1 \beta _2 \gamma _1 \Theta \varpi ^2 (\theta -\varpi ) (\theta +\varpi ) \exp \left( 2 \sqrt{\gamma _1} \left( \vartheta -\frac{(-1)^{3/4} \sqrt{(\theta -\varpi ) (\theta +\varpi )} (x-t \varpi )}{2 \root 4 \of {\gamma _1^2 \left( -\Theta ^2\right) \varpi ^4}}\right) \right) }{\left( \beta _2-\beta _1 \exp \left( 2 \sqrt{\gamma _1} \left( \vartheta -\frac{(-1)^{3/4} \sqrt{(\theta -\varpi ) (\theta +\varpi )} (x-t \varpi )}{2 \root 4 \of {\gamma _1^2 \left( -\Theta ^2\right) \varpi ^4}}\right) \right) \right) {}^2}}{\theta ^2 \sqrt{\gamma _1^2 \left( -\Theta ^2\right) \varpi ^4}}.~~~~~ \end{aligned}$$
(28)

\(\bullet \) For \( \gamma _0=\frac{\gamma _1^2}{4 \gamma _2}, \gamma _1<0\) and \( \gamma _2>0\), we obtain

The dark soliton solution

$$\begin{aligned} \Phi _{4}(x, t)=\frac{\left( \varpi ^2-\theta ^2\right) \left( \sqrt{\gamma _1^2 \left( -\Theta ^2\right) \varpi ^4}-i \gamma _1 \Theta \varpi ^2 \left( 3 \tanh ^2\left( \frac{\sqrt{-\gamma _1} \left( \vartheta -\frac{(-1)^{3/4} \sqrt{(\theta -\varpi ) (\theta +\varpi )} (x-t \varpi )}{\sqrt{2} \root 4 \of {\gamma _1^2 \left( -\Theta ^2\right) \varpi ^4}}\right) }{\sqrt{2}}\right) +2\right) \right) }{\theta ^2 \sqrt{\gamma _1^2 \left( -\Theta ^2\right) \varpi ^4}}.~~~~~~~~~~~~~~~ \end{aligned}$$
(29)

The explicit hyperbolic function solution

$$\begin{aligned} \Phi _{5}(x, t)=\frac{\left( \varpi ^2-\theta ^2\right) \left( \sqrt{\gamma _1^2 \left( -\Theta ^2\right) \varpi ^4}-i \gamma _1 \Theta \varpi ^2 \left( 3 \coth ^2\left( \frac{\sqrt{-\gamma _1} \left( \vartheta -\frac{(-1)^{3/4} \sqrt{(\theta -\varpi ) (\theta +\varpi )} (x-t \varpi )}{\sqrt{2} \root 4 \of {\gamma _1^2 \left( -\Theta ^2\right) \varpi ^4}}\right) }{\sqrt{2}}\right) +2\right) \right) }{\theta ^2 \sqrt{\gamma _1^2 \left( -\Theta ^2\right) \varpi ^4}}.~~~~~~~~~~~~~~~ \end{aligned}$$
(30)

The combo bright-dark soliton solution

$$\begin{aligned} \Phi _{6}(x, t)= & {} \frac{i (\theta -\varpi ) (\theta +\varpi )}{\theta ^2 \sqrt{\gamma _1^2 \left( -\Theta ^2\right) \varpi ^4}}\nonumber \\&\times \Bigg (i \sqrt{\gamma _1^2 \Bigg (-\Theta ^2\Bigg ) \varpi ^4}+2 \gamma _1 \Theta \varpi ^2+3 \gamma _1 \Theta \varpi ^2 \bigg (\text {sech} \Bigg (\sqrt{2} \sqrt{-\gamma _1} \Bigg (\vartheta -\frac{(-1)^{3/4} \sqrt{(\theta -\varpi ) (\theta +\varpi )} (x-t \varpi )}{\sqrt{2} \root 4 \of {\gamma _1^2 \Bigg (-\Theta ^2\Bigg ) \varpi ^4}}\Bigg )\Bigg )\nonumber \\&+i \tanh \Bigg (\sqrt{2} \sqrt{-\gamma _1} \Bigg (\vartheta -\frac{(-1)^{3/4} \sqrt{(\theta -\varpi ) (\theta +\varpi )} (x-t \varpi )}{\sqrt{2} \root 4 \of {\gamma _1^2 \Bigg (-\Theta ^2\Bigg ) \varpi ^4}}\Bigg )\Bigg )\Bigg )^2\Bigg ). \end{aligned}$$
(31)

The explicit soliton solution

$$\begin{aligned} \Phi _{7}(x, t)=\frac{\left( \varpi ^2-\theta ^2\right) \left( \sqrt{\gamma _1^2 \left( -\Theta ^2\right) \varpi ^4}+i \gamma _1 \Theta \varpi ^2 \left( 1-3 \text {csch} ^2\left( \frac{\sqrt{-\gamma _1} \left( \vartheta -\frac{(-1)^{3/4} \sqrt{(\theta -\varpi ) (\theta +\varpi )} (x-t \varpi )}{\sqrt{2} \root 4 \of {\gamma _1^2 \left( -\Theta ^2\right) \varpi ^4}}\right) }{\sqrt{2}}\right) \right) \right) }{\theta ^2 \sqrt{\gamma _1^2 \left( -\Theta ^2\right) \varpi ^4}}.~~~~~~~~~~~~~~ \end{aligned}$$
(32)

The hyperbolic function solution

$$\begin{aligned} \Phi _{8}(x, t)=\frac{\left( \varpi ^2-\theta ^2\right) \left( \sqrt{\gamma _1^2 \left( -\Theta ^2\right) \varpi ^4}+\frac{i \gamma _1 \Theta \varpi ^2 \left( \sinh \left( \sqrt{2} \sqrt{-\gamma _1} \left( \vartheta -\frac{(-1)^{3/4} \sqrt{(\theta -\varpi ) (\theta +\varpi )} (x-t \varpi )}{\sqrt{2} \root 4 \of {\gamma _1^2 \left( -\Theta ^2\right) \varpi ^4}}\right) \right) +5 i\right) }{\sinh \left( \sqrt{2} \sqrt{-\gamma _1} \left( \vartheta -\frac{(-1)^{3/4} \sqrt{(\theta -\varpi ) (\theta +\varpi )} (x-t \varpi )}{\sqrt{2} \root 4 \of {\gamma _1^2 \left( -\Theta ^2\right) \varpi ^4}}\right) \right) -i}\right) }{\theta ^2 \sqrt{\gamma _1^2 \left( -\Theta ^2\right) \varpi ^4}}.~~~~~~~~~~~~~~~~~~~~~~ \end{aligned}$$
(33)

\(\bullet \) For \( \gamma _0=0, \gamma _1<0\) and \( \gamma _2\ne 0\), we obtain

The trigonometric function solutions

$$\begin{aligned} \Phi _{9}(x, t)= & {} \frac{\left( \varpi ^2-\theta ^2\right) \left( \sqrt{\gamma _1^2 \left( -\Theta ^2\right) \varpi ^4}+i \gamma _1 \Theta \varpi ^2 \left( 3 \text {sec}^2\left( \sqrt{-\gamma _1} \left( \vartheta -\frac{(-1)^{3/4} \sqrt{(\theta -\varpi ) (\theta +\varpi )} (x-t \varpi )}{2 \root 4 \of {\gamma _1^2 \left( -\Theta ^2\right) \varpi ^4}}\right) \right) -1\right) \right) }{\theta ^2 \sqrt{\gamma _1^2 \left( -\Theta ^2\right) \varpi ^4}}.~~~~~~~~~ \end{aligned}$$
(34)
$$\begin{aligned} \Phi _{10}(x, t)= & {} \frac{i (\theta -\varpi ) (\theta +\varpi )}{\theta ^2 \sqrt{\gamma _1^2 \left( -\Theta ^2\right) \varpi ^4}}\nonumber \\&\times \Bigg (\gamma _1 \Theta \varpi ^2 \left( 3 \text {csc}^2\left( \sqrt{-\gamma _1} \left( \vartheta -\frac{(-1)^{3/4} \sqrt{(\theta -\varpi ) (\theta +\varpi )} (x-t \varpi )}{2 \root 4 \of {\gamma _1^2 \left( -\Theta ^2\right) \varpi ^4}}\right) \right) +1\right) +i \sqrt{\gamma _1^2 \left( -\Theta ^2\right) \varpi ^4}\Bigg ).~~~~~~~~~ \end{aligned}$$
(35)

\(\bullet \) For \( \gamma _0=\frac{\gamma ^2_1}{4\gamma _2}, \gamma _1>0\) and \( \gamma _2> 0\), we obtain periodic wave solutions in different forms as:

$$ \Phi _{{11}} (x,t) = \frac{{\left( {\varpi ^{2} - \theta ^{2} } \right)\left( {\sqrt {\gamma _{1}^{2} \left( { - \Theta ^{2} } \right)\varpi ^{4} } - i\gamma _{1} \Theta \varpi ^{2} \left( {3\tan ^{2} \left( {\frac{{\sqrt {\gamma _{1} } \left( {\vartheta - \frac{{( - 1)^{{3/4}} \sqrt {(\theta - \varpi )(\theta + \varpi )} (x - t\varpi )}}{{\sqrt 2 {\text{ }}\sqrt[4]{{\gamma _{1}^{2} \left( { - \Theta ^{2} } \right)\varpi ^{4} }}}}} \right)}}{{\sqrt 2 }}} \right) + 2} \right)} \right)}}{{\theta ^{2} \sqrt {\gamma _{1}^{2} \left( { - \Theta ^{2} } \right)\varpi ^{4} } }}. $$
(36)
$$ \Phi _{{12}} (x,t) = \,\frac{{\left( {\varpi ^{2} - \theta ^{2} } \right)\left( {\sqrt {\gamma _{1}^{2} \left( { - \Theta ^{2} } \right)\varpi ^{4} } - i\gamma _{1} \Theta \varpi ^{2} \left( {3\cot ^{2} \left( {\frac{{\sqrt {\gamma _{1} } \left( {\vartheta - \frac{{( - 1)^{{3/4}} \sqrt {(\theta - \varpi )(\theta + \varpi )} (x - t\varpi )}}{{\sqrt 2 {\text{ }}\sqrt[4]{{\gamma _{1}^{2} \left( { - \Theta ^{2} } \right)\varpi ^{4} }}}}} \right)}}{{\sqrt 2 }}} \right) + 2} \right)} \right)}}{{\theta ^{2} \sqrt {\gamma _{1}^{2} \left( { - \Theta ^{2} } \right)\varpi ^{4} } }}. $$
(37)
$$ \Phi _{{13}} (x,t) = \frac{{i(\theta - \varpi )(\theta + \varpi )\left( { - \frac{{\gamma _{1} \Theta \varpi ^{2} \left( {\sin \left( {\sqrt 2 \sqrt {\gamma _{1} } \left( {\vartheta - \frac{{( - 1)^{{3/4}} \sqrt {(\theta - \varpi )(\theta + \varpi )} (x - t\varpi )}}{{\sqrt 2 {\text{ }}\sqrt[4]{{\gamma _{1}^{2} \left( { - \Theta ^{2} } \right)\varpi ^{4} }}}}} \right)} \right) + 5} \right)}}{{\sin \left( {\sqrt 2 \sqrt {\gamma _{1} } \left( {\vartheta - \frac{{( - 1)^{{3/4}} \sqrt {(\theta - \varpi )(\theta + \varpi )} (x - t\varpi )}}{{\sqrt 2 {\text{ }}\sqrt[4]{{\gamma _{1}^{2} \left( { - \Theta ^{2} } \right)\varpi ^{4} }}}}} \right)} \right) - 1}} + i\sqrt {\gamma _{1}^{2} \left( { - \Theta ^{2} } \right)\varpi ^{4} } } \right)}}{{\theta ^{2} \sqrt {\gamma _{1}^{2} \left( { - \Theta ^{2} } \right)\varpi ^{4} } }}.~ $$
(38)
$$\begin{aligned} \Phi _{14}(x, t)= & {} \frac{i (\theta -\varpi ) (\theta +\varpi )}{\theta ^2 \sqrt{\gamma _1^2 \left( -\Theta ^2\right) \varpi ^4}}\nonumber \\&\times \Bigg (\frac{3 \gamma _1 \Theta \varpi ^2 \left( \sqrt{a_1^2-a_2^2}-a_1 \cos \left( \sqrt{2} \sqrt{\gamma _1} \left( \vartheta -\frac{(-1)^{3/4} \sqrt{(\theta -\varpi ) (\theta +\varpi )} (x-t \varpi )}{\sqrt{2} \root 4 \of {\gamma _1^2 \left( -\Theta ^2\right) \varpi ^4}}\right) \right) \right) {}^2}{\left( a_1 \sin \left( \sqrt{2} \sqrt{\gamma _1} \left( \vartheta -\frac{(-1)^{3/4} \sqrt{(\theta -\varpi ) (\theta +\varpi )} (x-t \varpi )}{\sqrt{2} \root 4 \of {\gamma _1^2 \left( -\Theta ^2\right) \varpi ^4}}\right) \right) +a_2\right) {}^2}+i \sqrt{\gamma _1^2 \left( -\Theta ^2\right) \varpi ^4}+2 \gamma _1 \Theta \varpi ^2\Bigg ).~~~ \end{aligned}$$
(39)
$$ \Phi _{{15}} (x,t) = \frac{{i(\theta - \varpi )(\theta + \varpi )\left( {\gamma _{1} \Theta \varpi ^{2} \left( {\frac{{3\cos ^{2} \left( {\sqrt 2 \sqrt {\gamma _{1} } \left( {\vartheta - \frac{{( - 1)^{{3/4}} \sqrt {(\theta - \varpi )(\theta + \varpi )} (x - t\varpi )}}{{\sqrt 2 {\text{ }}\sqrt[4]{{\gamma _{1}^{2} \left( { - \Theta ^{2} } \right)\varpi ^{4} }}}}} \right)} \right)}}{{\left( {\sin \left( {\sqrt 2 \sqrt {\gamma _{1} } \left( {\vartheta - \frac{{( - 1)^{{3/4}} \sqrt {(\theta - \varpi )(\theta + \varpi )} (x - t\varpi )}}{{\sqrt 2 {\text{ }}\sqrt[4]{{\gamma _{1}^{2} \left( { - \Theta ^{2} } \right)\varpi ^{4} }}}}} \right)} \right) + 1} \right)^{2} }} + 2} \right) + i\sqrt {\gamma _{1}^{2} \left( { - \Theta ^{2} } \right)\varpi ^{4} } } \right)}}{{\theta ^{2} \sqrt {\gamma _{1}^{2} \left( { - \Theta ^{2} } \right)\varpi ^{4} } }}.~ $$
(40)

\(\bullet \) For \( \gamma _0=0\) and \(\gamma _1>0\), we obtain exponential functional solution

$$ \Phi _{{16}} (x,t) = \frac{{\left( {\varpi ^{2} - \theta ^{2} } \right)\left( {\sqrt {\gamma _{1}^{2} \left( { - \Theta ^{2} } \right)\varpi ^{4} } - i\gamma _{1} \Theta \varpi ^{2} } \right) + \frac{{48i\gamma _{2} \gamma _{1}^{2} \Theta \varpi ^{2} (\theta - \varpi )(\theta + \varpi )\exp \left( {2\sqrt {\gamma _{1} } \left( {\frac{{( - 1)^{{3/4}} \sqrt {(\theta - \varpi )(\theta + \varpi )} (t\varpi - x)}}{{2{\text{ }}\sqrt[4]{{\gamma _{1}^{2} \left( { - \Theta ^{2} } \right)\varpi ^{4} }}}} + \vartheta } \right)} \right)}}{{\left( {\exp \left( {2\sqrt {\gamma _{1} } \left( {\frac{{( - 1)^{{3/4}} \sqrt {(\theta - \varpi )(\theta + \varpi )} (t\varpi - x)}}{{2{\text{ }}\sqrt[4]{{\gamma _{1}^{2} \left( { - \Theta ^{2} } \right)\varpi ^{4} }}}} + \vartheta } \right)} \right) - 4\gamma _{1} \gamma _{2} } \right)^{2} }}}}{{\theta ^{2} \sqrt {\gamma _{1}^{2} \left( { - \Theta ^{2} } \right)\varpi ^{4} } }}. $$
(41)
$$\begin{aligned} \Phi _{17}(x, t)= & {} \frac{\left( \varpi ^2-\theta ^2\right) \left( \sqrt{\gamma _1^2 \left( -\Theta ^2\right) \varpi ^4}-i \gamma _1 \Theta \varpi ^2\right) +\frac{48 i \gamma _2 \gamma _1^2 \Theta \varpi ^2 (\theta -\varpi ) (\theta +\varpi ) \exp \left( 2 \sqrt{\gamma _1} \left( \vartheta -\frac{(-1)^{3/4} \sqrt{(\theta -\varpi ) (\theta +\varpi )} (x-t \varpi )}{2 \root 4 \of {\gamma _1^2 \left( -\Theta ^2\right) \varpi ^4}}\right) \right) }{\left( 1-4 \gamma _1 \gamma _2 \exp \left( 2 \sqrt{\gamma _1} \left( \vartheta -\frac{(-1)^{3/4} \sqrt{(\theta -\varpi ) (\theta +\varpi )} (x-t \varpi )}{2 \root 4 \of {\gamma _1^2 \left( -\Theta ^2\right) \varpi ^4}}\right) \right) \right) {}^2}}{\theta ^2 \sqrt{\gamma _1^2 \left( -\Theta ^2\right) \varpi ^4}}. \end{aligned}$$
(42)

5 Results and discussion

Several scientific and technological disciplines profit from the investigation of optical solitons. In Xue et al. (2011), based on the constitutive relation for transversely isotropic piezoelectric and piezomagnetic materials, combined with the differential equations of motion, the longitudinal wave motion equation in a long circular rod has been derived and solitary wave solutions were extracted by Jacobi elliptic function expansion method, while different solutions were found to the studied model in Ma et al. (2013). The MME circular rod with M-derivative has been discussed and a variety of solutions were recovered by the assistance of Bernoulli sub-equation function method Baskonus and Gomez-Aguilar (2013) and in Hashemi et al. (2016), the soliton solutions were extracted to the MEE circular rod by the assistance of first integral method. A variety of solutions were extracted in different forms by applying expansion function method to the MEE circular rod (Baskonus et al. 2016), while by using semi-inverse variational principle, sine-cosine function method, and rational sine-cosine function method to the studied model different solutions were recovered (Darvishi et al. 2018). Topological, non-topological and singular soliton solutions are extracted by using the extended sinh-Gordon equation expansion method to the governing equation (Bulut et al. 2018), and in Zhou (2016), soliton solutions were recovered by applying \( \frac{G^{'}}{G}\)- expansion method. The solitary wave ansatz has been used to construct the different solution (Younis and Ali 2015). The nonlinear longitudinal wave equation has been discussed by using extended form of two methods, auxiliary equation mapping and direct algebraic method (Iqbal et al. 2019).

We have identified various wave structures in the form of exact solitary wave solutions, including bright, dark, singular and combined forms to the MEE circular rod, using a new computational integration scheme. Additionally, we’ve found solutions to the hyperbolic and periodic functions. Nonlinear dispersive media allow for the propagation of bright and dark solitons.

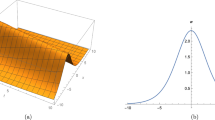
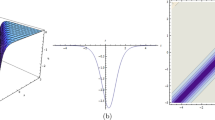
We may further demonstrate the uniqueness of our results by comparing our accomplishments to those that have been studied in the past. For example, some of their solutions are comparable to ours by assigning specific parameter values. We can clearly distinguish our work from previous research because other solutions are so drastically different from ours. Many nonlinear science fields may find this article’s findings useful in clarifying the precise underlying nature of a variety of nonlinear advancement situations. The physical movement of some of the obtained solutions have been depicted 3D, 2D, and contour in Figs. (1, 2, 3, 4, 5, 6, 7, 8 and 9) by allotting different values to parameters.

Fig. 1
figure 1

Plots of solution (26) under parameters \( \theta =0.9, \gamma _1=0.2, \Theta =0.2, \vartheta =0.1, \varpi =1.2\)

Full size image
Fig. 2
figure 2

Plots of solution (27) under parameters \( \theta =0.2, \gamma _1=1.7, \Theta =2, \vartheta =1, \varpi =1\)

Full size image
Fig. 3
figure 3

Plots of solution (29) under parameters \( \theta =0.9, \gamma _1=-1.2, \Theta =0.79, \vartheta =0.1, \varpi =1.\)

Full size image
Fig. 4
figure 4

Plots of solutions (31) under parameters \( \theta =3, \gamma _1=-2, \Theta =1, \vartheta =2, \varpi =1.8\)

Full size image
Fig. 5
figure 5

Plots of solutions (33) under parameters \( \theta =0.05, \gamma _1=-10, \Theta =1.9, \vartheta =0.4, \varpi =0.08\)

Full size image
Fig. 6
figure 6

Plots of solution (34) under parameters \( \theta =0.98, \gamma _1=-0.8, \Theta =0.2, \vartheta =1, \varpi =1.8\)

Full size image
Fig. 7
figure 7

Plots of solution (39) under parameters \( a_2=2, a_1=3, \gamma _1=2, \theta =7.9, \Theta =4, \vartheta =3, \varpi =5 \)

Full size image
Fig. 8
figure 8

Plots of solution (41) under parameters \( \theta =0.7, \gamma _1=2, \gamma _2=0.2, \Theta =1.2, \vartheta =0.4, \varpi =0.1 \)

Full size image
Fig. 9
figure 9

Plots of solution (42) under parameters \( \theta =0.8, \gamma _1=1, \gamma _2=2, \Theta =0.76, \vartheta =0.6, \varpi =0.3 \)

Full size image

6 Concluding remarks

We have discussed propagation of waves in the MEE circular rod which is modeled by nonlinear longitudinal wave equation. A recently developed method called MSSEM has been considered for recovering various forms of solutions. A variety of soliton solutions as well as exponential, hyperbolic and periodic functions are extracted. The results are remarkable and significantly different from those previously reported. Bright soliton solutions will facilitate the regulation of soliton clutter. When the solitons are switched from being attracted to being detached, the clutter is eliminated. Innovative soliton solutions will be required to resolve the current soliton conundrum. This demonstrates that solitons can transition from an attracted to a separated state, which would clean up the mess.

For some nonlinear models, the results show that the proposed strategy is a promising instrument because it can provide a wide range of new wave results. This method’s simplicity and power are demonstrated by the solutions obtained. Nonlinear PDEs can be easily applied to this method, and the majority of the solutions satisfy the PDEs by substituting. To address a wide range of NLPDEs, each of our discoveries provides a different way for different analysts to use this method.

This article’s findings may be useful for clarifying the exact nature of a variety of nonlinear advancement situations that arise in numerous nonlinear science fields. The physical movement of some of the obtained solutions have been depicted 3D, 2D, and contour in figures (1-9) by allotting different values to parameters.

It is anticipated that the solutions will play a crucial role in describing and comprehending the physics of how things change with time.