1 Introduction

Complex networks exist in many fields of sciences and have been intensively studied over the past decades, such as computer networks [1], telephone call graphs [2], the World Wide Web [3], neural networks [4], electrical power grids [5], genetic regulatory networks [6], and metabolic networks [7]. In general, a complex network is made up of a large number of interconnected nodes. Every node of the network is a nonlinear dynamic, which may have some complex dynamic behaviors such as chaotic behavior and bifurcation behavior. But, many complex systems in real world cannot be described by traditional integer-order differential equations, especially some problems about electrochemistry [8], diffusion [9], viscoelastic materials [10], biological systems [11], and so on. Fractional-order systems have attracted increasing attention in recent years by their applications in many fields. Compared with the classical integer-order complex network, there are still many problems in the fractional-order complex network to be solved since the most existing methods for the integer-order dynamic systems cannot be directly extended to the fractional-order dynamic systems.

Synchronization has always been a hot research topic in complex systems. There were some kinds of synchronization have been investigated, such as lag synchronization, which requires the states of response system to synchronize with the past states of the drive system [12]. The situation that the driver and response systems could be synchronized up to a scaling function is named projective synchronization [13]. When a network can be divided into some groups, and coupled nodes in the same cluster can be synchronized, but there is no synchronization among different clusters, the network is said to realize the cluster synchronization [14]. Synchronization of fractional-order systems has been studied in some papers recently. For example, Chen has investigated synchronization of memristor-based fractional-order neural networks in [15]; Bao and Cao [16] have studied projective synchronization of fractional-order memristor-based neural networks. Note that there are some networks that cannot be synchronized by their intrinsic structure. Then, control schemes have been developed to drive networks synchronization. Impulsive control method has been widely used in many areas; the main feature of impulsive control method is that the control action is exerted on a plant only at some discrete instants; then, the controlled network receives signals of control only in discrete times, and the amount of conveyed information is decreased. There were lots of results about impulsive control for integer-order systems [17–19]. Impulsive control of fractional systems just has few results [20–22]. However, in previous studies, all of the nodes should be controlled, when impulsive controllers are added to the dynamical networks with state coupling. Due to the large number of nodes in the real-world complex networks, it is usually difficult to control all nodes of network. Pinning control method is introduced [23–25]. There were just a fraction of nodes would be controlled under pinning control strategy. There were also some results about the pinning scheme for fractional complex networks [26, 27]. It is naturally to ask: Can the impulsive controllers just add for a small number of the whole network? The impulsive pinning method has been developed for the integer-order complex networks, recently [28–32]. To the best of our knowledge, there are no results on the pinning impulsive control for the fractional complex networks. In addition, as a description for the speed of synchronization, exponential synchronization has been attracted lots of attentions for integer-order complex networks, in which the speed of synchronization is in exponential function [33–35]. But, exponential synchronization of fractional systems has not been seen yet.

Motivated by the above, this paper will investigate the exponential synchronization of fractional complex networks. We consider a fractional-order complex network whose node’s dynamic has been described by \(\alpha \) derivative. The fractional complex network will be synchronized by impulsively controlling a small fraction of nodes. At every impulsive moment, nodes with a big deviation from the expected trajectory would be controlled. Then, some criteria are given to judge whether dynamical networks can be globally exponentially forced to a desired orbit by impulsively controlling a small fraction of nodes. Exponential synchronization of the general fractional complex network can be reached under some conditions. The relationship between synchronization region and the order \(\alpha \) has been discussed based on our synchronization criterion. Under some certain parameters, one can result from this paper that there will be a larger synchronization region that can be obtained with increased order \(\alpha \).

The rest of this paper is organized as follows: In Sect. 2, some definitions and some lemmas are introduced. In Sect. 3, the pinning impulsive controllers are designed to make the fractional complex network realize exponential synchronization. Numerical examples are given to demonstrate the effectiveness of the proposed pinning impulsive strategy in Sect. 4. Finally, conclusions are drawn in Sect. 5.

2 Preliminaries

In this section, some definitions, lemmas, and some well-known results about fractional differential equations are recalled. In addition, the mathematic model of fractional complex network will be introduced.

2.1 Caputo fractional operator and Mittag-Leffler function

Caputo fractional operator plays an important role in the fractional systems, since the initial conditions for fractional differential equations with Caputo derivatives take the same form as for integer-order differential, which have well-understood physical meanings [36]. Thus, we use Caputo derivatives as a main tool in this paper. The formula of the Caputo fractional derivative is defined as follows:

Definition 1

[36] The Caputo fractional derivative of function x(t) is defined as

$$\begin{aligned} _{C}D^{\alpha }_{0,t}x(t)=\frac{1}{\varGamma (m-\alpha )} \int _{0}^{t}(t-\tau )^{m-\alpha -1}x^{(m)}(\tau )\mathrm{d}\tau , \end{aligned}$$

where \(m-1<\alpha <m,\ m\in Z^{+}.\)

Let \(m=1\), \(0<\alpha <1,\) then

$$\begin{aligned} _{C}D^{\alpha }_{0,t}x(t)=\frac{1}{\varGamma (1-\alpha )} \int _{0}^{t}(t-\tau )^{-\alpha }x'(\tau )\mathrm{d}\tau . \end{aligned}$$

For simplicity, denote \(D^{\alpha }x(t)\) as the \(_{C}D^{\alpha }_{0,t}x(t)\). The following properties of Caputo operators are specially provided.

Lemma 1

[36] If \(w(t), u(t)\in C^{1}[t_{0},b]\), and \(\alpha >0\), \(\beta >0\), then

$$\begin{aligned} \begin{aligned} (1)&\quad D^{\alpha }D^{-\beta }w(t)=D^{\alpha -\beta }w(t)\\ (2)&\quad D^{\alpha }(w(t)\pm u(t))=D^{\alpha }w(t)\pm D^{\alpha }u(t)\\ \end{aligned} \end{aligned}$$

The Mittag-Leffler function is defined by

$$\begin{aligned} E_{\alpha ,\beta }(z):=\sum _{i=0}^{\infty }\frac{z^{i}}{\varGamma (\alpha i+\beta )}, \end{aligned}$$

where \(\alpha >0, \beta >0\), and \(\varGamma (.)\) is the Gamma function. For short \(E_{\alpha }(z):=E_{\alpha ,1}(z)\). The following properties of Mittag-Leffler function will be used in the later.

Lemma 2

For \(0<\alpha <1\) and \(x\in {\mathbb {R}}\), \(x>0\), \(E_{\alpha }(x)\) is a monotone increasing function [37].

Lemma 3

If \(0<\alpha <1, \mid arg z\mid <\frac{\pi }{2}\), then for any integer \(N^{*}>1\), and \(z\ne 0\), the following asymptotic expansion holds [37, 38]:

$$\begin{aligned} E_{\alpha ,\beta }(z)= \frac{1}{\alpha }z^{\frac{1-\beta }{\alpha }}\mathrm{e}^{z^{\frac{1}{\alpha }}} -\sum _{r=1}^{N^{*}}\frac{z^{-r}}{\varGamma (\beta {-}\alpha r)}+O\left( \frac{1}{Z^{N^{*}+1}}\right) \end{aligned}$$

as \(\mid z\mid \rightarrow +\infty \).

Lemma 4

For \(0<\alpha <1, t\in {\mathbb {R}}, t>0\), we have

$$\begin{aligned} \lim _{t\rightarrow +\infty }E_{\alpha }(t)\leqslant \lim _{t\rightarrow +\infty }\frac{1}{\alpha }\mathrm{e}^{t^{\frac{1}{\alpha }}}. \end{aligned}$$

Proof

From Lemma 3, one has

$$\begin{aligned} \lim _{t\rightarrow \infty }E_{\alpha }(t)\sim \lim _{t\rightarrow + \infty }\left\{ \frac{1}{\alpha }\mathrm{e}^{t^{\frac{1}{\alpha }}} -\sum _{r=1}^{\infty }\frac{t^{-r}}{\varGamma (\beta -\alpha r)}\right\} . \end{aligned}$$

Noting that the second term of the right of above formula is positive for all \(t>0\). Then, Lemma 3 could be obtained.

Remark 1

The Mittag-Leffler function is the generalization of the exponential function. Lemma 4 has established a relationship between Mittag-Leffler function and exponential function as \(t\rightarrow +\infty \), which is an important result in the later analysis about the exponential synchronization of fractional complex network. It is clear that when \(\alpha =1\), Lemma 4 still holds, in which the inequality will be converted into an equation.

Remark 2

Exponential synchronization for fractional systems has not been studied yet, since exponential function is difficult to be applied in fractional calculus. Mittag-Leffler function has been regarded as a generalization of exponential function and has widely been applied for the factional calculus [37–39]. Unfortunately, it is difficult to extend some properties of exponential function to Mittag-Leffler function. But Lemma 4 can establish a connection between exponential function and Mittag-Leffler function; thus, exponential function can be used in some analysis about asymptotic behavior for fractional systems.

Lemma 5

[36] Let V(t) be a continuous function on \([t_0,+\infty )\) and satisfies

$$\begin{aligned} D^{\alpha }V(t)\leqslant \theta V(t), \end{aligned}$$

where \(0<\alpha <1\) and \(\theta \) is a constant, then

$$\begin{aligned} V(t)\leqslant V(t_0)E_{\alpha }(\theta (t-t_0)^{\alpha }). \end{aligned}$$

2.2 Model description

Considering the following fractional-order complex dynamic network:

$$\begin{aligned} D^{\alpha }x_{i}(t)=f(x_{i}(t))+c\sum _{j=1}^{N}a_{ij}\varGamma x_{j}(t), \end{aligned}$$
(1)

where \(0<\alpha <1\), N is the number of nodes, \(x_{i}(t)=(x_{i1}(t),x_{i2}(t),\ldots ,x_{in}(t))^T\in {\mathbb {R}}^{n}(i=1,2,\ldots ,N)\) is the state variables of the ith node, \(f{:}\,{\mathbb {R}}^{n}\rightarrow {\mathbb {R}}^{n}\) is a continuously vector value function, c is the coupling strength, and \(\varGamma \in {\mathbb {R}}^{n\times n}\) is diagonal matrix with positive diagonal elements. \(A=(a_{ij})\in {\mathbb {R}}^{n\times n}\) is the weight configuration matrix. If there is a connection from node i to node j, then \(a_{ij}=a_{ji}>0\); otherwise, \(a_{ij}=a_{ji}=0\), and the diagonal elements of matrix A are defined by

$$\begin{aligned} a_{ii}=-\sum _{j=1,j\ne i}^{N}a_{ij}. \end{aligned}$$
(2)

Under the impulsive control, we can get the controlled model as follows:

$$\begin{aligned} \left\{ \begin{array}{l} D^{\alpha }x_{i}(t)=f(x_{i}(t))+c\sum \nolimits _{j=1}^{N}a_{ij}\varGamma x_{j}(t),\quad t\ne t_{k}\\ x_{i}\left( t_{k}^{+}\right) -x_{i}\left( t_{k}^{-}\right) =\mu (x_{i}\left( t_{k}^{-}\right) -s(t_{k})),\quad k\in {\mathbb {N}},\\ \quad \quad \quad \quad \quad \quad \quad i\in {\mathscr {P}}(t_{k})\\ \end{array} \right. \end{aligned}$$
(3)

where \(\mu \) is impulsive control gain and \({\mathscr {P}}(t_{k})\) is the index set of pinning nodes at impulsive moment \(t_{k}\).

Let s(t) be a solution of the isolated dynamic system: \(D^{\alpha }s(t)=f(s(t))\). Here, s(t) may be an equilibrium point, a periodic orbit, or even a chaotic orbit. In this paper, the objective trajectory that the nonlinear dynamical network (1) will be forced to s(t).

Let \(e_{i}(t)=x_{i}(t)-s(t)\) for \(i=1,2,\ldots ,N\). According to (2), \(c\sum _{j=1}^{N}a_{ij}\varGamma s(t)=0\); then, the following impulsively controlled dynamical network can be obtained:

$$\begin{aligned} \left\{ \begin{array}{l} D^{\alpha }e_{i}(t){=}\tilde{f}(e_{i}(t))+c\sum \nolimits _{j=1}^{N}a_{ij}\varGamma e_{j}(t),\quad t\ne t_{k}\\ e_{i}\left( t_{k}^{+}\right) =(1+\mu )e_{i}\left( t_{k}^{-}\right) ,\quad i\in {\mathscr {P}}(t_{k}) \end{array} \right. \end{aligned}$$
(4)

where \(\tilde{f}(e_{i}(t))=f(x_{i}(t))-f(s(t))\) and the time series \(\{t_1,t_2,\ldots \}\) is a strictly increasing impulsive instant satisfying \(\lim \nolimits _{k\rightarrow \infty }t_k=+\infty \). The selection of pinning nodes would be given later.

Assumption 1

Throughout this paper, we always assume that \(e_{i}\left( t_{k}^{-}\right) =e_{i}(t_{k})\).

Assumption 2

The function f is Lipschitz continuous. That is, there exists a positive constant F such that

$$\begin{aligned} \Vert f(x) -f(y)\Vert \leqslant F\Vert x-y\Vert ,\quad \forall x,y\in R^{n}. \end{aligned}$$
(5)

3 Main results

In this section, a pinning impulsive control scheme is applied for reaching exponential synchronization of fractional complex dynamical network (1).

Theorem 1

When \(\mu \in (-2,0)\), let \(\rho =1+\frac{l}{N}(\mid 1+\mu \mid -1)\in (0,1)\). Suppose that Assumptions 1 and 2 hold, and the average impulsive interval of the impulsive sequence is less than T. Then, the controlled dynamical network (1) can be globally exponentially controlled to the objective trajectory s(t) by using our pinning impulsive strategy, if \((\frac{ln(\rho )}{T}+\delta ^{\frac{1}{\alpha }})<0\), where \(\delta =\max \nolimits _{1\leqslant i \leqslant N}(F+\lambda \sum \nolimits _{j=1}^{N}\mid a_{ji}\mid )\) and \(\lambda \) is the largest eigenvalue of \(\varGamma \).

Proof

Consider the following Lyapunov function:

$$\begin{aligned} V(t)=\sum _{i=1}^{N}\Vert e_{i}(t)\Vert \end{aligned}$$

Let \(\mathrm{sgn}(e_{i}(t))=(\mathrm{sign}(e_{i1}(t)),\mathrm{sign}(e_{i2}(t)),\ldots ,\mathrm{sign}(e_{in}(t)))\), where

$$\begin{aligned} \mathrm{sign}(e_{ij}(t))=\left\{ \begin{aligned}&1, e_{ij}(t)>0\\&0, e_{ij}(t)=0\\&-1, e_{ij}(t)<0 \end{aligned} \right. \end{aligned}$$

For \(t\in (t_{k-1},t_{k}]\), calculating the derivatives of V(t) along the solutions of system (4), one has

$$\begin{aligned} \begin{aligned} D^{\alpha }V(t)&=\sum _{i=1}^{N}D^{\alpha }\Vert e_{i}(t)\Vert =\sum _{i=1}^{N}\sum _{j=1}^{n}D^{\alpha }\mid e_{ij}(t)\mid \\&=\sum _{i=1}^{N}\sum _{j=1}^{n}\mathrm{sign}(e_{ij}(t))D^{\alpha }e_{ij}(t)\\&=\sum _{i=1}^{N}\mathrm{sgn}(e_{i}(t))D^{\alpha }e_{i}(t)\\&=\sum _{i=1}^{N}\mathrm{sgn}(e_{i}(t))\left( \tilde{f}(e_{i}(t)) +c\sum _{j=1}^{N}a_{ij}\varGamma e_{j}(t)\right) \\&\leqslant \sum _{i=1}^{N}\left( \Vert \tilde{f}(e_{i}(t))\Vert +c\sum _{j=1}^{N}\mid a_{ij}\mid \Vert \varGamma e_{j}(t)\Vert \right) \\&\leqslant \sum _{i=1}^{N}\left( F+\lambda \sum _{j=1}^{N}\mid a_{ji}\mid \right) \Vert e_{i}(t)\Vert \\ \end{aligned} \end{aligned}$$

Using the constants \(\delta \) and \(\lambda \) which have been given in Theorem 1, \(D^{\alpha }V(t)\leqslant \delta V(t)\). From Lemma 1, \(V(t)\leqslant E_{\alpha }(\delta (t-t_{k-1})^{\alpha })V(t_{k-1}^{+})\), for \(t\in (t_{k-1},t_{k}]\).

For a coupled dynamical network without controlling, there must be different orbits among nodes, which implies that there exists a different deviation from the expected trajectory s(t). Naturally, the farthest nodes from s(t) should be controlled first. Therefore, those nodes with a big deviation from the expected trajectory s(t) will be pinned in this paper. Apparently, the distance between \(x_{i}(t)\) and s(t) can be described by the norm values of all synchronization errors at impulsive moments \(e_{i}(t_{k})(i=1,2,\ldots ,N)\). Thus, at impulsive moment \(t_{k}\), the index set of pinning nodes \({\mathscr {P}}(t_{k})\) is defined as follows: For the vectors \(e_{1}(t_{k}),e_{2}(t_{k}),\ldots ,e_{N}(t_{k})\), one can reorder the states of the nodes such that \(\Vert e_{p_1}(t_k)\Vert \geqslant \Vert e_{p_2}(t_k)\Vert \geqslant \cdots \Vert e_{p_N}(t_k)\Vert \). Suppose that we choose \(l(l<N)\) nodes of network (1) for controlling; then, the index set of l controlled nodes \({\mathscr {P}}(t_{k})\) is defined as \({\mathscr {P}}(t_{k})=\{p_1,p_2,\ldots ,p_l\}\). Let \(\alpha (t_k)=\mathrm{min}\{\Vert e_{i}(t_{k})\Vert :\ i\in {\mathscr {P}}(t_{k})\}\) and \(\beta (t_k)=\mathrm{max}\{\Vert e_{i}(t_{k})\Vert :\ i\not \in {\mathscr {P}}(t_{k})\}\). It is easy to find that \(\beta (t_k)\leqslant \alpha (t_k)\) from our pinning strategy.

Thus, for any \(k\in {\mathbb {N}}\), we yield

$$\begin{aligned} \begin{aligned} V\left( t_{k}^{+}\right)&=\sum _{i=1}^{n}\left\| e_{i}\left( t_{k}^{+}\right) \right\| \\&=\sum _{i\in {\mathscr {P}}(t_{k})}\left\| e_{i}\left( t_{k}^{+}\right) \right\| +\sum _{i\not \in {\mathscr {P}}(t_{k})}\left\| e_{i}\left( t_{k}^{+}\right) \right\| \\&=\sum _{i\in {\mathscr {P}}(t_{k})}\mid 1+\mu \mid \left\| e_{i}\left( t_{k}^{-}\right) \right\| +\sum _{i\not \in {\mathscr {P}}(t_{k})}\left\| e_{i}\left( t_{k}^{-}\right) \right\| \\&=\,\mid 1+\mu \mid \sum _{i\in {\mathscr {P}}(t_{k})}\left\| e_{i}\left( t_{k}^{-}\right) \right\| +\rho \sum _{i\not \in {\mathscr {P}}(t_{k})}\left\| e_{i}\left( t_{k}^{-}\right) \right\| \\&\quad +\,(1-\rho )\sum _{i\not \in {\mathscr {P}}(t_{k})}\left\| e_{i}\left( t_{k}^{-}\right) \right\| \\&\leqslant \mid 1+\mu \mid \sum _{i\in {\mathscr {P}}(t_{k})}\left\| e_{i}\left( t_{k}^{-}\right) \right\| + \rho \sum _{i\not \in {\mathscr {P}}(t_{k})}\left\| e_{i}\left( t_{k}^{-}\right) \right\| \\&\quad +\,(1-\rho )(N-l)\beta (t_{k})\\&\leqslant \mid 1+\mu \mid \sum _{i\in {\mathscr {P}}(t_{k})}\left\| e_{i}\left( t_{k}^{-}\right) \right\| + \rho \sum _{i\not \in {\mathscr {P}}(t_{k})}\left\| e_{i}\left( t_{k}^{-}\right) \right\| \\&\quad +\,(1-\rho )(N-l)\alpha (t_{k})\\&\leqslant \mid 1+\mu \mid \sum _{i\in {\mathscr {P}}(t_{k})}\left\| e_{i}\left( t_{k}^{-}\right) \right\| + \rho \sum _{i\not \in {\mathscr {P}}(t_{k})}\left\| e_{i}\left( t_{k}^{-}\right) \right\| \\&\quad +\,(\rho -\mid 1+\mu \mid )l\alpha (t_{k})\\&\leqslant \mid 1+\mu \mid \sum _{i\in {\mathscr {P}}(t_{k})}\left\| e_{i}\left( t_{k}^{-}\right) \right\| + \rho \sum _{i\not \in {\mathscr {P}}(t_{k})}\left\| e_{i}\left( t_{k}^{-}\right) \right\| \\&\quad +\,(\rho -\mid 1 +\mu \mid )\sum _{i\in {\mathscr {P}}(t_{k})}\left\| e_{i}\left( t_{k}^{-}\right) \right\| \\&\leqslant \rho \sum _{i=1}^{n}\left\| e_{i}\left( t_{k}^{-}\right) \right\| \\&=\rho V(t_{k}^{-}) \end{aligned} \end{aligned}$$

Then, for \(t\in (t_0,t_1], V(t)\leqslant E_{\alpha }(\delta (t-t_{0})^{\alpha })V\left( t_{0}^{+}\right) \), which leads \(V(t_1)\leqslant E_{\alpha }(\delta (t_1-t_{0})^{\alpha })V\left( t_{0}^{+}\right) \) and \(V(t_1^+)\leqslant \rho V(t_1) \leqslant \rho E_{\alpha }(\delta (t_1-t_{0})^{\alpha })V\left( t_{0}^{+}\right) \).

Similarly, for \(t\in (t_1,t_2]\), \(V(t)\leqslant E_{\alpha }(\delta (t-t_{1})^{\alpha })V(t_{1}^{+})\leqslant \rho E_{\alpha }(\delta (t-t_{1})^{\alpha })E_{\alpha }(\delta (t_1-t_{0})^{\alpha })V\left( t_{0}^{+}\right) \).

In general, for \(t\in (t_k,t_{k+1}]\), \(V(t)\leqslant \prod _{i=1}^{k}E_{\alpha }(\delta (t_i-t_{i-1})^{\alpha })\rho ^{k}E_{\alpha }(\delta (t-t_{k})^{\alpha })V\left( t_{0}^{+}\right) \).

Let \(\xi (t_0,t)\) be the number of impulsive times of the impulsive sequence on the interval \((t_0,t)\). Hence, for any \(t\in {\mathbb {R}}\), we obtain

$$\begin{aligned} V(t)\leqslant & {} \prod _{i=1}^{\xi (t_0,t)}E_{\alpha }(\delta (t_i-t_{i-1})^{\alpha })\rho ^{\xi (t_0,t)}\\&\times \,E_{\alpha }(\delta (t-t_{\xi (t_0,t)})^{\alpha })V\left( t_{0}^{+}\right) . \end{aligned}$$

Since the average impulsive interval of the impulsive sequence is less than T, there exists a positive integer \(N_0\) such that

$$\begin{aligned} \xi (t_0,t)\geqslant \frac{t-t_0}{T}-N_0. \end{aligned}$$

Note that \(\rho \in (0,1)\); thus,

$$\begin{aligned} \begin{aligned} V(t)&\leqslant \prod _{i=1}^{\xi (t_0,t)}E_{\alpha }\left( \delta (t_i-t_{i-1})^{\alpha }\right) \rho ^{\frac{t-t_0}{T}-N_0}\\&\quad \times \, E_{\alpha }\left( \delta (t-t_{\xi (t_0,t)})^{\alpha }\right) V\left( t_{0}^{+}\right) \\&=\prod _{i=1}^{\xi (t_0,t)}E_{\alpha }\left( \delta (t_i-t_{i-1})^{\alpha }\right) \rho ^{-N_0}\mathrm{e}^{\frac{\mathrm{ln}\rho }{T}(t-t_0)}\\&\quad \times \, E_{\alpha }(\delta \left( t -t_{\xi (t_0,t)})^{\alpha }\right) V\left( t_{0}^{+}\right) . \end{aligned} \end{aligned}$$

Due to \((t-t_{0})>t-t_{\xi (t_0,t)}\), then from Lemma 2,

$$\begin{aligned} V(t)\leqslant & {} \prod _{i=1}^{\xi (t_0,t)}E_{\alpha }\left( \delta (t_i-t_{i-1})^{\alpha }\right) \rho ^{-N_0}\mathrm{e}^{\frac{\mathrm{ln}\rho }{T}(t-t_0)}\\&\times E_{\alpha }\left( \delta (t-t_{0})^{\alpha }\right) V\left( t_{0}^{+}\right) . \end{aligned}$$

One can follow from Lemma 4 that \(\lim \nolimits _{t\rightarrow \infty }E_{\alpha }(\delta (t-t_{0})^{\alpha })\leqslant \lim \nolimits _{t\rightarrow \infty }\frac{1}{\alpha }\mathrm{e}^{\delta ^{\frac{1}{\alpha }}(t-t_0)}\). Let

$$\begin{aligned} M_0=\frac{\prod _{i=1}^{\xi (t_0,t)}E_{\alpha }\left( \delta (t_i-t_{i-1})^{\alpha }\right) \rho ^{-N_0}}{\alpha }, \end{aligned}$$

\(\eta =(\frac{\mathrm{ln}(\rho )}{T}+\delta ^{\frac{1}{\alpha }})\), then \(V(t)\leqslant {M_0}\mathrm{e}^{\eta (t-t_0)}V\left( t_{0}^{+}\right) \) as \(t\rightarrow \infty .\) Since \(\eta <0\), we can conclude that the whole dynamical network (4) can be globally exponentially stabilized under the impulsive controller. It means that the network (1) can be exponentially controlled to the objective trajectory s(t). This completes our proof.

Remark 3

Impulsive synchronization for fractional chaotic systems and hyperchaotic systems has been studied in Refs. [17, 18], respectively. But both of them have converted the fractional-order systems into integer-order one by using some approximate approach. Then, the integer-order systems have been investigated actually. This paper has studied the fractional systems, based on some theories of fractional calculus, such as Lemma 5, and the synchronization criterion for the network (1) has been derived.

Remark 4

Under impulsive control, asymptotical synchronization for fractional systems has been researched in Refs. [17–19]. Based on Lemma 4, exponential synchronization for fractional complex network has been guaranteed in this paper by a pinning impulsive controller.

Corollary 1

Suppose that Assumptions 1 and 2 hold, and the average impulsive interval of the impulsive sequence is less than T. When \(\mu \in (-2,0)\), let \(\delta =\max \limits _{1\leqslant j \leqslant N}(F+\lambda \sum _{j=1}^{N}\mid a_{ji}\mid )\), and \(\lambda \) is the largest eigenvalue of \(\varGamma \). Then, the dynamical network (1) can be globally exponential synchronization to the objective trajectory s(t), if one of the following inequations could be satisfied:

$$\begin{aligned} \begin{aligned}&(1)\ \ T<-\frac{\mathrm{ln}\left( 1+\frac{l}{n}(\mid 1+\mu \mid -1)\right) }{\root \alpha \of {\delta }}\\&(2)\ \ -\frac{\mathrm{e}^{-T\root \alpha \of {\delta }}-1}{\frac{l}{n}}-2<\mu <\frac{\mathrm{e}^{-T\root \alpha \of {\delta }}-1}{\frac{l}{n}}\\&(3)\ \ \frac{l}{n}>\frac{\mathrm{e}^{-T\root \alpha \of {\delta }}-1}{\mid 1+\mu \mid -1} \end{aligned} \end{aligned}$$

Remark 5

From Theorem 1, where \(\delta \) and \(\alpha \) are determined by the complex dynamic network itself, \(T, \mu \), and \(\frac{l}{n}\) are depended on the pinning impulsive controllers. The criterion can be easily judged without large computation.

Remark 6

Fractional calculus could be seen as a generation of integer calculus. Based on Remark 1 and the proof of Theorem 1, the synchronization criterion of both Theorem 1 and Corollary 1 are suitable for the case of \(\alpha =1\). Noting that, according to the three inequations of the Corollary 1, every parameter of controllers is influenced by the order \(\alpha \) when others are certain. More discussion will be given in the simulation.

4 Numerical simulations

In this section, a numerical example is given to show the effectiveness of the proposed results, and the connection of synchronization region will be given later. In the end, the connection of controllers’ parameters and order \(\alpha \) will be discussed. The algorithms to simulate the fractional-order complex networks without control can be seen in Ref.  [23].

4.1 Exponential synchronization under pinning impulsive control

Taking the fractional-order Newton–Leipnik’s system as node of network (1), that is

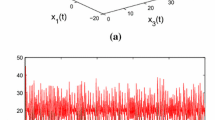
$$\begin{aligned} f(x_{i}(t))=\left( \begin{aligned}&\ \ \ \ -ax_{i1}+x_{i2}+10x_{i2}x_{i3} \\&-x_{i1}-0.4x_{i2}+5x_{i1}x_{i3} \\&\ \ \ \ -5x_{i1}x_{i2}+bx_{i3}\\ \end{aligned} \right) , \end{aligned}$$

where \(\alpha =0.998\). When \(a=0.4, b=0.175\), the system has a double-scrolling chaotic attractor as shown in Fig. 1.

Fig. 1
figure 1

Chaotic behavior of fractional-order Newton–Leipnik’s system

Full size image

A small-world network with \(N=100\) nodes will be considered in this simulation. The small-world network is generated by taking initial neighboring nodes \(k=4\) and the edge adding probability \(p=0.1\). The coupling matrix A is defined as follows: If there is a connection between nodes i and j, then \(a_{ij}=a_{ji}=1\); otherwise, \(a_{ij}=a_{ji}=0\), \(a_{ii}\) are defined in (2). The coupling strength \(c=5\), the inner coupling matrix \(\varGamma =\left( \begin{array}{ccc} 0.1 &{} 0 &{} 0 \\ 0 &{} 0.2 &{} 0 \\ 0 &{} 0 &{} 0.3 \\ \end{array} \right) \), and then \(\lambda =0.3\). Now, we take special values of \(\mu =-0.9, T=0.01, l=20\), and then \(\frac{l}{N}=0.2\). By some simple calculations, we can obtain that \(\rho =0.82 \in (0,1)\), and \(F=11\), then \(\delta =13.8\). One has \((\frac{\mathrm{ln}(\rho )}{T}+\delta ^{\frac{1}{\alpha }})=-4.01<0\). Then, the synchronization region described by the parameters of systems and controllers is shown in Fig. 2.

Fig. 2
figure 2

Synchronization region of the small-world coupled dynamical network (1) under the pinning impulsive controller (4)

Full size image

The trivial point \(s(t)=0\) is taken as the objective trajectory in this example. Figure 3 presents the numerical process for the synchronization control. All initial values of the dynamical network are uniformly randomly selected from \([-10,10]\).

Fig. 3
figure 3

State variables of the small-world coupled dynamical network (1) under the pinning impulsive controller (4)

Full size image

4.2 The connections between controllers’ parameters and the order \(\alpha \)

With different \(\mu \), Fig. 4 displays the synchronization region about T and order \(\alpha \). From Fig. 4, the synchronization region about T is increased as the order \(\alpha \) from 0 to 1, which embodies the memory property of fractional systems.

Fig. 4
figure 4

Estimation of the synchronization region about T and order \(\alpha \)

Full size image

When \(T=0.01, \frac{l}{N}=0.2\), the synchronization region of impulsive gain \(\mu \) and \(\alpha \) is shown in Fig. 5. It is obvious that a bigger \(\alpha \) results in a larger synchronization region.

Fig. 5
figure 5

Estimation of the synchronization region about \(\mu \) and order \(\alpha \)

Full size image

Now, under certain \(\mu \) and \(T=0.01\), Fig. 6 shows the synchronization region about \(\frac{l}{N}\) and order \(\alpha \). In Ref. [23], pinning controllers have been designed for a general fractional complex network, which concluded that the control performance is better with decreasing fractional-order \(\alpha \). Surprisingly, under certain impulsive gain, from Fig. 6, one can easily see that the synchronization region is larger with increasing fractional-order \(\alpha \). Maybe the control performance and the synchronization region are not equivalent [40].

Fig. 6
figure 6

Estimation of the synchronization region about \(\frac{l}{N}\) and order \(\alpha \)

Full size image

Remark 7

From above cases, the order \(\alpha \) has a great influence on the design of our pinning impulsive controllers. From the definition of fractional Caputo operator, the memory property can be expressed by the \((t-\tau )^{(\alpha -1)}\) in the integrand. When \(\alpha \) tends to be 1, the fractional Caputo operator can be degenerated into integer-order systems [36], in which the memory property will disappear. Thus, a larger synchronization region can be obtained with a bigger \(\alpha \).

When we set \(\alpha =0.99\), under some certain values of \(\frac{l}{N}\), the synchronization region about T and \(\mu \) is shown in Fig. 7. From Fig. 7, when we controlled all nodes in the network and set \(\mu =-1\), the T could be infinity, because the error states of the whole network become zero immediately after the impulsive controller. Which can match the statement “If \(x^*\) is an equilibrium of fractional-order system \(D^\alpha x(t)=f(x(t))\) and there exists a time instant \(T>0\) such that \(x(T)=x^*\), then \(x(t)=x^*\) holds for all \(t\geqslant T\)” has been mentioned in some previous papers [41–43].

Fig. 7
figure 7

Estimation of the synchronization region about T and \(\mu \)

Full size image

5 Conclusions and discussion

This paper presents a pinning impulsive control method to synchronize a fractional complex network. By building the a relationship between the asymptotic behavior of exponential function and Mittag-Leffler function, and the appropriate pinning strategy, exponential synchronization for the fractional complex network has been obtained. Those nodes with a big deviation from the expected trajectory will be pinned at some moments in this paper. Based on the conditions in the main results, some discussions of synchronization region about the parameters of controllers have been given in the end of the paper. There is a larger synchronization region for the fractional complex network when the system’s order \(\alpha \) increased to 1, which can show the memory property of fractional-order systems. At last, the effectiveness of the presented results has been illustrated by numerical simulations.