1 Introduction

Since Emelyanov proposed a kind of sliding mode control method (SMC) [1], the theoretical research on the sliding mode control has attracted gradually widespread concern and it becomes a very important branch in the control field because the sliding mode control method takes on many advantages, for example, the system stability only depends on the setting of sliding mode surface and its parameters, the system exhibits the robustness due to the external noise disturbance or the parameters perturbation, and it also shows the characteristics of rapid response and is easy to realize in the physics domain, etc. [2–6]. The attentive object is also enlarged from the original investigation of the linear system with single-input and single-output to the system with multi-input and multi-output in which the errors are taken as state variables [7–9]. Especially in recent years, with the rapid development of the computer, high-power electronic switching devices, and other technologies, the sliding mode control theory and applied research have begun to enter a new phase. The discussion of the tracking control and synchronization on nonlinear continuous systems, discrete systems, and even chaotic systems is involved [10–14]. It is expected that the sliding mode control theory can be widely used in tracking control and synchronization of various complex networks in the near future. The reasons lie in that the synchronization phenomenon of a complex network not only widely exists in nature, but also has wide practicability in many fields, such as laser transmission, information communication, Internet, automation, and so on. Therefore, the investigation of tracking control and synchronization for complex networks using sliding mode control theory is of important practical significance.

The literatures reported previously focused mainly on the traditional first-order sliding mode control method. When the system trajectory reaches the switching surface, the chattering is caused because the speed is limited and the inertia compels the motor points pass through the switching surface, and it superimposes on the ideal sliding mode. Consequently, the first-order sliding mode control method is incomplete, that is, there exists high frequency chattering in the vicinity of the sliding surface. In other words, the formation of the high frequency chattering is owed to the discontinuous control switching operation. So, how to eliminate chattering becomes a key issue for the investigation of sliding mode control. At present, some ways to eliminate high frequency chattering have been proposed and the desired control effect is achieved, such as the filter method [15, 16], the reducing switching gain method [17], the linear matrix inequality (LMI) method [18], the fan-shape zone method [19], the so-called high-order sliding mode control method with second-order and second-order over [20, 21], and so on.

In this paper, projective synchronization of a class of complex network is investigated using second-order sliding mode control. The sliding surface and the control input are designed based on stability theory. The Burgers’ system with spatiotemporal chaotic behavior in physics domain is taken as nodes to constitute the complex network, and the Fisher–Kolmogorov system is taken as the tracking target. The artificial simulation results show that the synchronization technique is effective.

2 Mechanism for network projective synchronization

Consider a complex network consisting of N nodes, with each node being an n-dimensional spatiotemporal chaos system. The state equation of node i can be described by

(1)

where x i (r,t) is the state variable of node i in the network, and x i (r,t)∈R n. ε is the coupling strength between the network nodes, c ij is matrix element of the coupling matrix C, and it represents the topological structure of the network. u i is the sliding mode control input.

Assuming that the tracking target is x d (r,t), and definition of the error between network and tracking target is

$$ e_{i}(r,t) = x_{i}(r,t) - \alpha_{i}x_{d}(r,t) \quad (i = 1,2, \ldots,N) $$
(2)

where α i is scale factor of projective synchronization.

Error evolution equation can be further obtained as follows:

(3)

The design of sliding mode control is usually divided into two processes. First, the appropriate sliding surface is designed to make the controlled system reach the sliding surface and do the expected characteristics movement along the sliding surface. Second, the sliding mode controller or sliding mode control input is designed to ensure that the controlled system can converge to the sliding surface from an arbitrary initial state. Therefore, the sliding surface is defined as s(r,t) and the relation of dynamical evolution satisfies

(4)

where L is configurable gain.

According to second-order sliding mode control theory, it must satisfy s i (r,t)=∂s i (r,t)/∂t=∂ 2 s i (r,t)/∂t 2=0 when the sliding mode surface is moving. Then it can be obtained

$$ \frac{\partial e_{i}(r,t)}{\partial t} = (A + L)e_{i}(r,t) $$
(5)

If A+L is negative definite, it is easy to know that the designed sliding mode surface can stable asymptotically.

In order to determine the form of sliding mode control input, the Lyapunov function is constructed as

$$ V = \frac{1}{2}\sum_{i = 1}^{N} s_{i}^{2}(r,t) + \frac{1}{2\varphi} \sum _{i = 1}^{N} \biggl[\frac{\partial s_{i}(r,t)}{\partial t} \biggr]^{2} $$
(6)

where φ is a positive constant.

Then the derivative form of V can be described as follows:

(7)

Defining the form of sliding mode input as

(8)

then Eq. (7) can be simplified into

(9)

where η is a positive adjustment parameter.

An appropriate value of the adjustment parameter η is selected to satisfy

$$ \bigl \vert s_{i}(r,t) \bigr \vert - \frac{\eta}{\varphi} < 0 $$
(10)

and exist

$$ \frac{\partial V}{\partial t} < 0 $$
(11)

So, the projective synchronization between network and tracking target is realized based on Lyapunov theorem. Namely, each node in complex network can track the tracking target according to the size of the scaling factor.

3 Simulation analysis

The one-dimensional Burgers’ systems with spatiotemporal chaotic behavior in physics domain are taken as nodes to constitute a complex network, and the Fisher–Kolmogorov system is taken as the tracking target. The aim is to check the validity of the above-mentioned theory.

The dynamical equation of one-dimensional Burgers system can be written as [22]

$$ \frac{\partial x(r,t)}{\partial t} = - k\frac{\partial x(r,t)}{\partial r} + \nabla^{2}x(r,t) $$
(12)

where k is a parameter, x(r,t) is state variable of system, and ∇2=∂ 2/∂r 2.

When k is taken as 4, the spatiotemporal evolution and phase diagram of the state variable for the Burgers’ system are shown in Figs. 1 and 2, respectively.

Fig. 1
figure 1

Spatiotemporal evolution of state variable x(r,t)

Full size image
Fig. 2
figure 2

Phase diagram of Burgers system

Full size image

The state equation of Fisher–Kolmogorov can be described as [23]

(13)

where μ and ρ are parameters and x d (r,t) is state variable of system. D is the diffusion coefficient, and ∇2=∂ 2/∂r 2.

The spatiotemporal dynamics behaviors of the Fisher–Kolmogorov system with different parameters are extremely abundant. The spatiotemporal evolution and phase diagram of state variable for the system are shown in Figs. 3 and 4 while the parameters are taken as ρ=1,μ=0.5, and diffusion coefficient D=5.

Fig. 3
figure 3

Spatiotemporal evolution of state variable x d (r,t)

Full size image
Fig. 4
figure 4

Phase diagram of Fisher–Kolmogorov system

Full size image

It can be seen from Figs. 1–4, the bifurcation characteristics and the attraction domain obtained from the Burgers’ system and the Fisher–Kolmogorov system, respectively, are different because two spatiotemporal chaos systems are topological isomerism, leading to a significant difference in the spatiotemporal evolution and phase diagram.

N-Burgers equations (12) are taken as nodes of the network and are constructed according to the state equation (1).

(14)

In simulation, the connections among nodes are arbitrarily taken as the unidirectional star connection, and the coupling matrix C is as follows:

$$ C = \left [ \begin{array}{c@{\quad}c@{\quad}c@{\quad}c@{\quad}c} 0 & 0 & 0 & \cdot\cdot\cdot & 0\\ 1 & - 1 & 0 & \cdot\cdot\cdot & 0\\ 1 & 0 & - 1 & \cdot\cdot\cdot & 0\\ \cdot\cdot\cdot & \cdot\cdot\cdot & \cdot\cdot\cdot & \cdot\cdot\cdot & \cdot \cdot\cdot\\ 1 & 0 & 0 & \cdot\cdot\cdot & - 1\\ \end{array} \right ] $$
(15)

Based on Eq. (8), the structure of sliding mode control input can be determined as

(16)

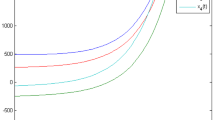
Four nodes are adopted to construct a complex network, and the parameters are taken as λ i =1,φ=1,L=2,η=0.5. The phase diagrams of projective synchronization between the different nodes and tracking target are shown in Figs. 5–8 while the scale factor of projective synchronization are α 1=−1,α 2=2,α 3=0.5,α 4=−3, respectively.

Fig. 5
figure 5

Phase diagram of projective synchronization (α 1=−1)

Full size image

When the projective synchronization between the complex network and tracking target is realized and based on Eq. (2), e i (r,t)=0, namely x i (r,t)=α i x d (r,t). If the scaling factor of projective synchronization is taken as α 1=−1, it means the state variable amplitude of the first node in network is equal to that of the Fisher–Kolmogorov system, which serves as the tracking target and both variable amplitudes are in opposite symbols, corresponding to the case in Fig. 5; α 2=2 means the state variable amplitude of the second node is 2 times as that of the Fisher–Kolmogorov system with the same symbols, shown as in Fig. 6; α 3=0.5 means the state variable amplitude of the third node is half as that of the Fisher–Kolmogorov system with the same symbols, corresponding to the case in Fig. 7; α 4=−3 means the state variable amplitude of the fourth node is 3 times as that of the Fisher–Kolmogorov system with the opposite symbols, corresponding to the case in Fig. 8. All these results indicate that each node in a complex network can track the tracking target according to the value of scale factor.

Fig. 6
figure 6

Phase diagram of projective synchronization (α 2=2)

Full size image
Fig. 7
figure 7

Phase diagram of projective synchronization (α 3=0.5)

Full size image
Fig. 8
figure 8

Phase diagram of projective synchronization (α 4=−3)

Full size image

4 Conclusion

Based on second-order sliding mode control, the projective synchronization of a complex network is investigated in this work. The sliding surface and the control input are designed and their effectiveness is analyzed based on the theory of stability. The Burgers’ system with spatiotemporal chaotic behavior in the physics domain is taken as nodes to constitute a complex network, the Fisher–Kolmogorov system is taken as the tracking target. The artificial simulation results show that no matter what value the scaling factor of projective synchronization takes, each node of complex network can track the tracking target according to the value of the scale factor.