1 Introduction

As a branch of mathematics, fractional calculus deals with derivatives and integrals of order that may be real or complex. The essential difference between models with the fractional-order derivative and the integer-order derivative lies in the following two aspects. First, the integer-order derivative indicates a variation or certain attribute at particular time for a physical or mechanical process, while the fractional-order derivative is concerned with the whole time domain. Second, the integer-order derivative describes the local properties of a certain position for a physical process, while the fractional-order one is related to the whole space. Therefore, compared with traditional integer-order calculus, fractional calculus provides a powerful tool for the description of memory and hereditary effects in various substances, as well as for modeling dynamical processes, for instance, electrochemical processes, flexible structures, biological systems, finance systems, the dielectric polarization, electromagnetic waves, viscoelastic systems, diffusion processes, heat flowing phenomena and so on. For further applications of fractional-order systems to the engineering area, please refer to [1–7].

With more and more physical processes being described by fractional order differential systems, to analyze and synthesize, the fractional-order systems has become a hot research topic. Recent studies have demonstrated the interests in the stability and robust controller design for fractional-order linear systems, especially for fractional-order linear time-invariant (FO-LTI) interval systems [8–14]. It should be pointed out that these results focused on certain systems without consideration of parameter variation uncertainty and external disturbance perturbation. But in practical situations, many systems are inevitably affected by parameter variations and external disturbances. Moreover, some or all of system parameters and external disturbance uncertainties are unknown or vary from time to time. It is clear that these results are not suitable for FO-LTI system with the external disturbances. Thus, to take the external uncertainties and disturbances into account is very necessary and important. Unfortunately, there are few theoretical results on this issue due to lack of theoretical tools to study dynamics of fractional systems. For the special touch, unlike the traditional integral-order system, many advanced control schemes, such as adaptive control [15, 16], sliding-mode control (SMC) [17], fuzzy control [18], neural network control [19], and learning control [20], are still not well established for fractional-order systems, and there are few research reports on it. How to stabilize such fractional-order uncertain systems is a very difficult problem.

On the other hand, SMC theory, originating from the theory of variable structure control [21, 22], has gained much attention for its robustness against uncertainties, disturbances, and unmodeled dynamics, and it has successfully been applied to a wide variety of practical engineering systems [23, 24]. Note that these results all depend on Lyapunov stability theorem, while similar tools have not yet been well developed for fractional systems. In recent years, by using the classical Lyapunov stability direct method for integer-order systems, SMC is introduced to study the synchronization and control problem for fractional-order chaotic systems in the presence of uncertain system parameter variation, external perturbation, and nonlinear control inputs [25–35]. However, it is worth mentioning that the traditional Lyapunov stability theorem showing the convergence of system trajectories to the sliding surface is not appropriate, because the closed-loop system is fractional order. It would be better to explore the stability of the closed-loop system based on the fractional-order stability theory. In addition, most results about SMC for fractional-order systems have been founded for fractional-order systems with Riemann–Liouville derivatives, not for those with Caputo derivatives. In fact, because the Laplace transform of the Caputo derivative allows utilization of initial values of classical integer-order derivatives, which have clear physical interpretations, Caputo derivative is frequently used in engineering.

Motivated by the above discussions, in this paper, the adaptive SMC is designed for a class of FO-LTI system with Caputo derivative and the unknown external uncertainties. The methods to design sliding surface and reaching motion controller for such systems are proposed by using fractional-order system stability theory. Linear matrix inequality (LMI) criteria for the existence of linear sliding surfaces are derived. The solution to conditions can be used to characterize linear sliding surfaces. The reaching motion controller is designed, and the reaching time is also obtained. Further, an adaptation law is given to estimate the upper-bound values of system uncertainties, which can be effectively implemented. Some problems in the existing literature on sliding-mode control and synchronization of fractional-order chaotic systems are pointed out.

The remainder of this paper is organized as follows. In Sect. 2, some necessary definitions, lemmas are presented. Main results are proposed in Sect. 3. In Sect. 4, a numerical example is used to illustrate the validity and feasibility of the proposed method. Finally, conclusions are drawn in Sect. 5.

Notation

Throughout this paper, \(R^n\) and \(R^{n\times m}\), denote, respectively, the \(n\)-dimensional Euclidean space and the set of all \(n\times m\) real matrices; \(\Vert x\Vert =\sqrt{\sum _{i=1}^nx_i^2}\) for \(x=(x_1,x_2,\ldots ,x_n)^T\). \(M^T\) denotes the transpose of matrix \(M\); The notation \(M>0 (M<0)\) means that the matrix \(M\) is positive (negative) definite; \(\otimes \) is the Kronecker product of two matrices and \((A\otimes B)(C\otimes D)=(AC)\otimes (BD)\); Sym\(\{M\}\) is used to denote the expression \(M+M^T\), and \(\star \) is used to denote a block matrix element that is induced by transposition.

2 Model description and preliminaries

There are some definitions for fractional derivatives. The commonly used definitions are Grunwald–Letnikov (GL), Riemann–Liouville (RL), and Caputo (C) definitions. Here and throughout the paper, only the Caputo definition is used, since its Laplace transform allows utilization of initial conditions which have the same forms as for integer-order differential equations with clear physical interpretations. The notation \( D^\alpha \) is chosen as the Caputo fractional derivative operator \(_{C}D_{0,t}^\alpha \).

Definition 1

[1] The fractional integral (Riemann–Liouville integral) \(D_{t_0, t}^{-\alpha }\) with fractional order \(\alpha \in R^+\) of function \(x(t)\) is defined as

$$\begin{aligned} D_{t_0,t}^{-\alpha }x(t)=\frac{1}{{\varGamma }(\alpha )} \int _{t_0}^t(t-\tau )^{\alpha -1}x(\tau )\mathrm{d}\tau , \end{aligned}$$

where \({\varGamma }(\cdot )\) is the gamma function, \({\varGamma }(\tau )\) \({=}\!\int _0^\infty t^{\tau -1}\!\mathrm{e}^{-t}\mathrm{d}t\).

Definition 2

[1] The Riemann–Liouville derivative of fractional order \(\alpha \) of function \(x(t)\) is given as

$$\begin{aligned} _{\mathrm{RL}}D_{t_0,t}^\alpha x(t)&= \frac{\mathrm{d}^n}{\mathrm{d}t^n}D_{t_0,t}^{-(n-\alpha )}x(t)\nonumber \\&= \frac{\mathrm{d}^n}{\mathrm{d}t^n}\frac{1}{{\varGamma }(n-\alpha )}\int _{t_0}^t(t-\tau )^{n-\alpha -1}x(\tau )\mathrm{d}\tau ,\nonumber \\ \end{aligned}$$

where \(n-1\le \alpha <n\in Z^+\).

Definition 3

[1] The Caputo derivative of fractional order \(\alpha \) of function \(x(t)\) is defined as follows

$$\begin{aligned} _{C}D_{t_0,t}^\alpha x(t)&= D_{t_0,t}^{-(n-\alpha )}\frac{\mathrm{d}^n}{\mathrm{d}t^n}x(t)\nonumber \\&= \frac{1}{{\varGamma }(n-\alpha )}\int _{t_0}^t(t-\tau )^{n-\alpha -1}x^{(n)} (\tau )\mathrm{d}\tau , \end{aligned}$$

where \(n-1\le \alpha <n\in Z^+\).

Consider the following fractional-order linear system with nonlinear uncertain disturbances

$$\begin{aligned} D^\alpha x(t)=Ax(t)+Bu(t)+h(x(t),t), \end{aligned}$$
(1)

where \(\alpha \) is the fractional order and belongs to \(0<\alpha <1\), \(x=(x_1, x_2,\ldots , x_n)^T\in R^n\) is the state of system, \(u=(u_1,u_2,\ldots ,u_m)^T\in R^m\) is the control input, \(h(x(t),t)\) denotes the nonlinear external disturbance term. The following assumptions for system (1) need to be made.

Assumption 1

It is also assumed that the pair \((A,B)\) is controllable and the input matrix \(B\in R^{n \times m}\) has full rank \(m<n\).

Assumption 2

The system matrix \(A\) is interval uncertain and belongs to \(A_{\varDelta }\!:=\! \{A_0+{\varDelta } A\!=\!A_0+ DEF , \Vert E\Vert \!\le \! 1\}\) [13], where \(A_0\) is nominal value, \(D\) and \(E\) are known real matrices with appropriate dimensions.

Assumption 3

The nonlinear disturbance \(h(x(t),t)\) satisfies the so-called matched condition, i.e., \(h(x(t),t))=Bf(x(t),t)\).

Under assumptions (1)–(3), system (1) can be transformed into the following equivalent equation:

$$\begin{aligned} D^\alpha x(t)=(A_0+{\varDelta } A)x(t)+B(u(t)+f(x(t),t)). \nonumber \\ \end{aligned}$$
(2)

Obviously, according to Assumption (1), there exists a nonsingular pseudostate transformation \(Tx(t)=z(t)\), where \(T\in R^{n\times n}\) is a nonsingular matrix, such that system (1) has the regular form as follows,

$$\begin{aligned} D^\alpha z(t){=}(\bar{{A_0}}+{\varDelta } \bar{A})z(t){+}\bar{B}[u(t)+f(T^{-1}z(t),t)],\nonumber \\ \end{aligned}$$
(3)

where \(\bar{{A_0}}=TA_0T^{-1}=\left[ \begin{array}{cc} \bar{{A}}_{11} &{} \bar{{A}}_{12}\\ \bar{{A}}_{21} &{} \bar{{A}}_{22} \end{array} \right] ,\, \bar{B}=TB=\left[ \begin{array}{c} 0\\ B_m \end{array} \right] \), \(B_m\in R^{m\times m}\) is nonsingular. \({\varDelta }\bar{{A}}=\) \(\left[ \begin{array}{cc} {\varDelta }\bar{{A}}_{11} &{} {\varDelta }\bar{{A}}_{12}\\ {\varDelta }\bar{{A}}_{21} &{} {\varDelta }\bar{{A}}_{22} \end{array} \right] \)=\(\left[ \begin{array}{cc} D_1\\ D_2 \end{array} \right] F\left[ \begin{array}{cc} E_1&E_2 \end{array} \right] \).

Then system (3) can be rewritten as

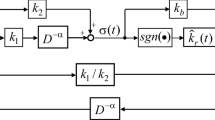
$$\begin{aligned} \left\{ \begin{array}{ll} D^\alpha z_1(t)&{}=(\bar{A}_{11}+{\varDelta }\bar{A}_{11})z_1(t)\\ &{}\quad +(\bar{A}_{12}+{\varDelta }\bar{A}_{12})z_2(t),\\ D^\alpha z_2(t)&{}=(\bar{A}_{21}\\ &{}\quad +{\varDelta }\bar{A}_{21})z_1(t) +(\bar{A}_{22}+{\varDelta }\bar{A}_{22})z_2(t)\\ &{}\quad +\,B_m[u(t)+f(T^{-1}z(t),t)].\end{array} \right. \end{aligned}$$
(4)

It is obvious that the first equation of system (4) denotes the sliding motion dynamics of system (2), here the corresponding surface can be designed as follows:

$$\begin{aligned} S=\{z(t)\in R^n: s(t)=[-N\ \ I_m]z(t)=0\}, \end{aligned}$$
(5)

where \(s(t)\) is the switching function and \( N\in R^{m\times (n-m)}\) is the sliding surface parameter to be determined latter. It follows from (5) that \(z_2(t)=Nz_1(t)\), and substituting it into the first equation of system (4), one obtains the sliding motion

$$\begin{aligned} \displaystyle D^\alpha z_1(t)=\left[ \left( \bar{A}_{11}+{\varDelta }\bar{A}_{11}\right) \!+\!\left( \bar{A}_{12}\!+\!{\varDelta }\bar{A}_{12}\right) N\right] z_1(t).\nonumber \\ \end{aligned}$$
(6)

Thus, our aim is to design constant gains \(N\in R^{m\times (n-m)}\) and a reaching motion control law \(u(t)\) such that

  1. (i)

    the sliding motion (6) is asymptotically stable;

  2. (ii)

    system (4) is asymptotically stable under the reaching motion control law \(u(t)\).

To this end, the following lemmas are presented firstly.

Lemma 1

[36] Let \(x(t)\in R^n\) be a continuous and derivable function. Then, for any time instant \(t\ge t_0\)

$$\begin{aligned} {\frac{1}{2}}{_{C}D_{t_0,t}^\alpha } x^2(t)\le x(t)_{C}D_{t_0,t}^\alpha x(t), \ \ \ \ \ \forall \alpha \in (0,1). \end{aligned}$$

Lemma 2

[36] For the fractional-order system

$$\begin{aligned} D^\alpha x(t)=f(x(t)), \end{aligned}$$
(7)

where \(\alpha \in (0,1), x=0\) is the equilibrium point and \(x(t)\in R^n\), if the following condition is satisfied

$$\begin{aligned} x(t)f(x(t))\le 0, \end{aligned}$$

then the origin of the system (7) is stable. And if

$$\begin{aligned} x(t)f(x(t))< 0,\quad \forall x\ne 0, \end{aligned}$$

then the origin of the system (7) is asymptotically stable.

3 Main results

In the following section, we will first derive a LMI condition for the existence of the sliding surface parameter matrix \(N\) guaranteeing the asymptotic stability of sliding-mode dynamics (6).

Theorem 1

When fractional-order \(\alpha : 0<\alpha <1\), the sliding-mode dynamics (6) is robustly asymptotically stable if there exist a symmetric positive definite matrices \(P\), a matrix \(Q\) with appropriate dimensions, and scalar constants \(\varepsilon _{i1}>0, \eta _{i1}>0\;(i=1,2)\) such that

$$\begin{aligned} {\varPhi }=\left[ \begin{array}{ll} {\varPhi }_{11}&{} {\varPhi }_{12} \\ \star &{} {\varPhi }_{22}\\ \end{array} \right] <0, \end{aligned}$$
(8)

where

$$\begin{aligned} {\varPhi }_{11}&= \sum _{i=1}^2 \left\{ \text {Sym}\{{\varTheta }_{i1}\otimes (\bar{A}_{11}P +\bar{A}_{12}Q)\}\right. \nonumber \\&\left. +\,\varepsilon _{i1}\left( I_2\otimes D_{1}D_{1}^{T}\right) +\eta _{i1}\left( I_2\otimes D_1D_1^T\right) \right\} ,\nonumber \\ {\varPhi }_{12}&= \left[ I_2\otimes (E_1P)^T \ I_2\otimes (E_1P)^T \right. \\&\left. \quad I_2\otimes (E_2Q)^T \ I_2\otimes (E_2Q)^T\right] ,\nonumber \\ {\varPhi }_{22}&= -{\text {diag}}\left[ \varepsilon _{11}I \ \varepsilon _{21}I \ \eta _{11}I \ \eta _{21}I\right] \otimes I_2. \end{aligned}$$

Moreover, sliding surface parameter matrix \(N\) is given by

$$\begin{aligned} N=QP^{-1}, \end{aligned}$$
(9)

and the sliding surface can be designed as

$$\begin{aligned} s(t)=[-QP^{-1}\ I_m]z(t)=0. \end{aligned}$$
(10)

Proof

The proof process is similar to that of Theorem 2 in [13], we omit it here.\(\square \)

After the switching surface is designed, the next step is to design a reaching control law which will drive the state trajectory to the switching surface and maintain a sliding-mode condition in spite of the uncertainties.

As we all know, the parameter variations of the system are difficult to measure, and the exact value of the external load disturbance is also difficult to know in advance for practical applications in industry. Therefore, an adaptive sliding-mode position controller is proposed here, in which an adaptive algorithm is used to estimate the upper bound of lumped uncertainty.

System (3) can be rewritten as follows

$$\begin{aligned} D^\alpha z(t)&= (\bar{{A_0}}+{\varDelta } \bar{A})z(t)+\bar{B}(u(t)+f(T^{-1}z(t),t))\nonumber \\&= \bar{{A_0}}z(t)+\bar{B}u(t)+E(z,u), \end{aligned}$$
(11)

where \(E(z,t)={\varDelta } \bar{A}z(t)+\bar{B}f(T^{-1}z(t),t))\) is the lumped uncertainty.

Let \(\bar{N}=[-QP^{-1}\ I_m]\), from (10), it is obvious that

$$\begin{aligned} D^\alpha s(t)&= \bar{N}(\bar{{A_0}}+{\varDelta } \bar{A})z(t)\nonumber \\&+B_m(u(t)+f(T^{-1}z(t),t))\nonumber \\&= \bar{{A_0}}z(t)+B_mu(t)+\bar{E}(z,u), \end{aligned}$$
(12)

where \(\bar{E}(z,t)=\bar{N}{\varDelta } \bar{A}z(t)+B_mf(T^{-1}z(t),t))\).

Assumption 4

\(\bar{E}(z,t)\) is unknown but bounded, i.e., \(\Vert \bar{E}(z,t)\Vert <\beta \), where \(\beta \) is an unknown but bounded positive constant.

Furthermore, the following adaptive algorithm for the bound of \(\Vert \bar{E}(z,t)\Vert \) is considered as

$$\begin{aligned} D^\alpha \hat{\beta }=k\Vert s(t)\Vert , \end{aligned}$$
(13)

where \(\hat{\beta }\) is the estimated value of \(\beta \), and \(k>1\) is denoted as the adaptation gain, the adaptation speed of \(\hat{\beta }\) can be tuned by \(k\).

A sliding-mode controller with adaptive algorithm is designed as follows:

$$\begin{aligned} u(t)=-B_m^{-1}\left( \bar{N}\bar{A_0}z(t)+\rho \frac{s(t)}{\Vert s(t)\Vert ^2}+\hat{\beta }k\frac{s(t)}{\Vert s(t)\Vert }\right) .\nonumber \\ \end{aligned}$$
(14)

where \(\rho >0\).

Theorem 2

Under assumption 4 and the obtained sliding surface function (10), the trajectories of system (3) with the controller (14) and the adaptive law (13) can be driven asymptotically onto the sliding surface in limited time \(t\le \root \alpha \of {\frac{\Vert s(0)\Vert ^2{\varGamma }(\alpha +1)}{2\rho }}\).

Proof

Define the adaptation error as \(\tilde{\beta }=\hat{\beta }-\beta \). Combining (12) with (13), one has

$$\begin{aligned} \left\{ \begin{array}{lll} D^\alpha s(t)=\bar{N}(\bar{{A_0}}+{\varDelta } \bar{A})z(t)\\ \quad +B_m(u(t)+f(T^{-1}z(t),t)),\\ D^\alpha \hat{\beta }=D^\alpha \tilde{\beta }=k\Vert s(t)\Vert \end{array} \right. \end{aligned}$$
(15)

Let \(F_\beta (z,s)=(\bar{N}(\bar{{A_0}}+{\varDelta } \bar{A})z(t)+B_m(u(t)+f(T^{-1}z(t),t)),k\Vert s(t)\Vert )^T\) and \(S_\beta =(s,\tilde{\beta })^T\), then, it follows from Lemma 2 that

$$\begin{aligned} S_\beta ^T(t) D^\alpha S_\beta (t)&= S_\beta ^T(t)F_\beta (z,s)\nonumber \\&= s^T(t)\frac{\mathrm{d}^\alpha s(t)}{\mathrm{d}t^\alpha }+\tilde{\beta }(t)\frac{\mathrm{d}^\alpha \tilde{\beta }(t)}{\mathrm{d}t^\alpha }\nonumber \\&= s^T(t)\frac{\mathrm{d}^\alpha s(t)}{\mathrm{d}t^\alpha }+\tilde{\beta }(t)\frac{\mathrm{d}^\alpha \hat{\beta }(t)}{\mathrm{d}t^\alpha }\nonumber \\&= s^T(t)\big [\bar{N}\bar{{A_0}}z(t)+B_mu(t)+E(z,u)\big ]\nonumber \\&+\,(\hat{\beta }-\beta )k\Vert s(t)\Vert . \end{aligned}$$
(16)

Substituting control input (14) into (16), then

$$\begin{aligned} S_\beta ^T(t)D^\alpha S_\beta (t)&= s^T(t)\big [-\rho \frac{s(t)}{\Vert s(t)\Vert ^2}-\hat{\beta }k\frac{s(t)}{\Vert s(t)\Vert }\nonumber \\&+E(z,u)\big ]+(\hat{\beta }-\beta )k\Vert s(t)\Vert \nonumber \\&\le -\rho \frac{\Vert s(t)\Vert ^2}{\Vert s(t)\Vert ^2}+\Vert E(z,u)\Vert \Vert s(t)\Vert \nonumber \\&-\beta k\Vert s(t)\Vert \nonumber \\&= -\rho -(k\beta -\Vert E(z,u)\Vert )\Vert s(t)\Vert \nonumber \\&\le -\rho \nonumber \\&< 0. \end{aligned}$$
(17)

Hence, the convergence of \(s(t)\) and \(\tilde{\beta }\) is proven by Lemma 2. Both \(s(t)\) and \(\tilde{\beta }\) reach zero in finite time, i.e., \(s(t)\rightarrow 0\) and \(\tilde{\beta }\rightarrow 0\). In order to show that the sliding motion occurs in finite time, the reaching time can be obtained as follows.

It follows from Lemma 1 and (17) that

$$\begin{aligned} D^\alpha \Vert s(t)\Vert ^2 \le 2s^T(t)D^\alpha s(t)\le -2\rho , \end{aligned}$$
(18)

which means that there exists \(M(t)\ge 0\) such that

$$\begin{aligned} D^\alpha \Vert s(t)\Vert ^2=-2\rho -M(t). \end{aligned}$$
(19)

Taking Laplace transform on both sides of (19), one has

$$\begin{aligned} s^{\alpha }Y(s)-s^{\alpha -1}y(0)=-2\rho \frac{1}{s}-M(s), \end{aligned}$$

where

$$\begin{aligned}&y(t)=\Vert s(t)\Vert ^2, Y(s)=\int ^{+\infty }_{0}e^{-st}y(t)\mathrm{d}t,\\&M(s)=\int ^{+\infty }_{0}e^{-st}M(t)\mathrm{d}t. \end{aligned}$$

Then,

$$\begin{aligned} Y(s)=\frac{1}{s}y(0)-2\rho \frac{1}{s^{\alpha +1}}-\frac{M(s)}{s^{\alpha }}. \end{aligned}$$
(20)

Taking inverse Laplace transform on (20), it yields

$$\begin{aligned}&\!\!\!\Vert s(t)\Vert ^2=\Vert s(0)\Vert ^2-\frac{2\rho t^{\alpha }}{{\varGamma }(\alpha +1)}\\&\quad -\int ^{t}_{0}(t-\tau )^{\alpha -1}M(\tau )\mathrm{d}\tau . \end{aligned}$$

In this way, \(\Vert s(t)\Vert ^2=0\) implies that the system trajectories converge to the sliding surface \(s(t)=0\), that is

$$\begin{aligned} \Vert s(0)\Vert ^2-\frac{2\rho t^{\alpha }}{{\varGamma }(\alpha +1)}-\int ^{t}_{0}(t-\tau )^{\alpha -1}M(\tau )\mathrm{d}\tau =0.\nonumber \\ \end{aligned}$$
(21)

Since \(\int ^{t}_{0}(t-\tau )^{\alpha -1}M(\tau )\mathrm{d}\tau \ge 0\), from (21) one has

$$\begin{aligned} \Vert s(0)\Vert ^2-\frac{2\rho t^{\alpha }}{{\varGamma }(\alpha +1)}\ge 0. \end{aligned}$$

It is apparent that

$$\begin{aligned} t\le \root \alpha \of {\frac{\Vert s(0)\Vert ^2{\varGamma }(\alpha +1)}{2\rho }}. \end{aligned}$$

Therefore, the trajectories of system (3) with the control input (14) will converge to the sliding surface in the finite time \(t\le \root \alpha \of {\frac{\Vert s(0)\Vert ^2{\varGamma }(\alpha +1)}{2\rho }}\). Thus the proof is completed.\(\square \)

Remark 1

When the disturbances \(h(x(t),t)=0\), system (1) will degenerate into modes discussed in paper [8–14]. It is clear that these results are not applied for system (1).

Remark 2

Fractional-order linear time-invariant interval systems have been discussed in paper [8–14], but without considering external disturbances. Since Lyapunov stability theory for fractional-order systems has not yet been developed, to design controller for system (1) is very challenging, and there is no effective way to cope with. In this paper, control of a class of FO-LTI system with Caputo derivative and the external disturbances is first discussed. By introducing adaptive SMC method, the control problem for such systems has been successfully solved. The proposed method has the computation advantages since the conditions are represented by the LMI, which can be easily solved by using the LMI Toolbox in Matlab.

Remark 3

In recent years, there exist some results about control and synchronization of fractional-order chaotic systems via SMC [25–33], in which the traditional Lyapunov stability theory has been used to show the convergence of system trajectories to the sliding surface. Since the dynamics of the considered system and the sliding surface involve fractional-order terms, it may be not appropriate to design reaching control law based on the traditional Lyapunov stability theory.

Remark 4

Problems about sliding-mode controller design for a lot of fractional-order chaotic systems with fractional Caputo derivatives have been discussed in [25–35]. Some integral type sliding surfaces including fractional integral term \(D^{\alpha -1}x(t)\) are constructed, where \(0<\alpha <1\), \(D^{\alpha -1}x(t)=D^{-(1-\alpha )}x(t)=\frac{1}{{\varGamma }(1-\alpha )}\int _{t_0}^t(t-\tau )^{-\alpha }x(\tau )\mathrm{d}\tau \) denotes the Riemann–Liouville fractional integral of order \(1-\alpha \) of a function \(x(t)\). Then take the first-order derivative, it follows that \(\frac{\mathrm{d}(D^{\alpha -1}x(t))}{\mathrm{d}t}=\frac{\mathrm{d}}{\mathrm{d}t}\frac{1}{{\varGamma }(1-\alpha )}\int _{t_0}^t(t-\tau )^{-\alpha }x(\tau )\mathrm{d}\tau =_{\mathrm{RL}}D^{\alpha }x(t)\ne _{C}D^{\alpha }x(t)\), which implies that these obtained theoretical results are applicable only for fractional-order systems with Riemann–Liouville derivative, not for Caputo derivative. Here, sliding-mode controller for fractional-order systems with Caputo derivative has been designed, and the correct sliding surface for such system is presented.

4 Numerical example

In this section, to verify and demonstrate the effectiveness of the proposed methods, a simple numerical example is presented.

Consider the uncertain system (1) with the following parameters:

$$\begin{aligned} A&= \left[ \begin{array}{ccc} \left[ \begin{array}{cc}-6,-4\end{array} \right] &{} [-3.5,-1.5] &{} [-5,-3] \\ \left[ \begin{array}{cc}-4.5,3.5\end{array} \right]&\left[ \begin{array}{cc}1,3\end{array} \right]&\left[ \begin{array}{cc}0.5,2.5\end{array} \right] \\ \left[ \begin{array}{cc}2,4\end{array} \right]&\left[ \begin{array}{cc}-4,4\end{array} \right]&\left[ \begin{array}{cc}-6,-4\end{array} \right] \\ \end{array} \right] ,\\ B&= \left[ \begin{array}{ccc} 0&1&0 \end{array} \right] ^T, h(x(t)){=}0.2\sin x_1(t)-0.4\cos x_2(t),\\ \alpha&= 0.65. \end{aligned}$$

Based on the analysis proposed in [13], it is very easy to obtain that \( A_0=\left[ \begin{array}{ccc} -5 &{} 2.5 &{} -4 \\ -0.5 &{} 2 &{} 1.5\\ 3 &{} 0 &{} -5 \end{array} \right] .\) Then, take the transform matrix \(T=\left[ \begin{array}{ccc} 0 &{} 0 &{} 1 \\ 1 &{} 0 &{} 0\\ 0 &{} 1 &{} 0 \end{array} \right] \), and according to (3), it can be shown that

$$\begin{aligned} \bar{A}_{11}=&\left[ \begin{array}{cc} -5 &{} 3 \\ -4 &{} -5\\ \end{array} \right] , \bar{A}_{12}=\left[ \begin{array}{c} 0 \\ -2.5\\ \end{array} \right] ,\\ \bar{A}_{21}=&[1.5\ \ -0.5], \bar{A}_{22}=2, B_2=1\\ D_1=&\left[ \begin{array}{ccccccccc} 0 &{} 0 &{} 1 &{} 0 &{} 0 &{} 2 &{} 0 &{} 0 &{} 1 \\ 1 &{} 0 &{} 0 &{} 1 &{} 0 &{} 0 &{} 1 &{} 0 &{} 0 \end{array} \right] ,\\ D_2=&\left[ \begin{array}{ccccccccc} 0&2&0&0&1&0&0&1&0 \end{array} \right] ,\\ E_1=&\left[ \begin{array}{ccccccccc} 0 &{} 0 &{} 1 &{} 0 &{} 0 &{} 1 &{} 0 &{} 0 &{} 1 \\ 1 &{} 0 &{} 0 &{} 2 &{} 0 &{} 0 &{} 1 &{} 0 &{} 0 \end{array} \right] ^T,\\ E_2=&\left[ \begin{array}{ccccccccc} 0&1&0&0&1&0&0&2&0 \end{array} \right] ^T. \end{aligned}$$

It follows from Theorem 1 that LMI (8) has feasible solutions \(\varepsilon _{11}=\varepsilon _{21}=7.2320\), \(\eta _{11}=\eta _{21}=7.0402\), \(Q=[0.3376\ 2.1620]\), \(P=\left[ \begin{array}{cc} 10.5916 &{} -3.0279\\ -3.0279 &{} 4.5312 \end{array} \right] \). When \(k=2, \rho =2\), in view of (10) and (14), the sliding surface and the control law are given by

$$\begin{aligned} s(t)&= [-0.2080 \ -0.6161 \ 1]z(t),\\ u(t)&= -\left( [4.3480 \ -1.7522 \ -5.0922]z(t)\right. \\&\quad +\,\left. 2 \frac{s(t)}{\Vert s(t)\Vert ^2}+2\hat{\beta }\frac{s(t)}{\Vert s(t)\Vert }\right) \\ \end{aligned}$$

with the adaptive laws

$$\begin{aligned} D^\alpha \hat{\beta }=2\Vert s(t)\Vert , \end{aligned}$$

where \(z(t)=Tx(t)\).

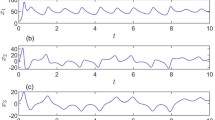
In the simulation, Adams–Bashforth–Moulton predictor–corrector algorithm [37] is used for the numerical calculation of fractional system. The simulation results are illustrated with the initial condition \((x_1(0), x_2(0), x_3(0),\hat{\beta }(0))=(0.1, -0.1, 0.2, 0.1)\). From Figs. 1 and 2, system is asymptotically stable and the sliding motion trends to the origin in finite time. Input control is shown in Fig. 3. Figure 4 shows the time responses of the updating vector parameter \(\hat{\beta }\). Obviously, the updating vector parameters approach to some bounded values. The simulation results illustrate that the proposed controller has quite a good performance and is very effective in coping with system uncertainties.

Fig. 1
figure 1

The state time response of the system in example

Full size image
Fig. 2
figure 2

The time evolution of sliding surface in example

Full size image
Fig. 3
figure 3

The time evolution of control input in example

Full size image
Fig. 4
figure 4

The time response of adaptive parameter

Full size image

5 Conclusion

This paper has proposed the method for designing sliding-mode controller for a class of fractional-order linear interval systems with the external disturbances. Sufficient conditions in terms of LMIs are presented for the existence of a linear sliding surfaces guaranteeing asymptotic stability of the reduced-order equivalent system restricted to the surface. By using stability of fractional-order nonlinear systems, a reaching motion controller is proposed to drive the state trajectory to the switching surface and maintain a sliding-mode condition in spite of the uncertainties. Sliding-mode control for fractional-order nonlinear systems with Caputo derivative will be considered in the future.